Analysis of Vibration Characteristics of Planetary Gearbox with Broken Sun Gear Based on Phenomenological Model
Abstract
:1. Introduction
2. Vibration Mechanism of Planetary Gearbox
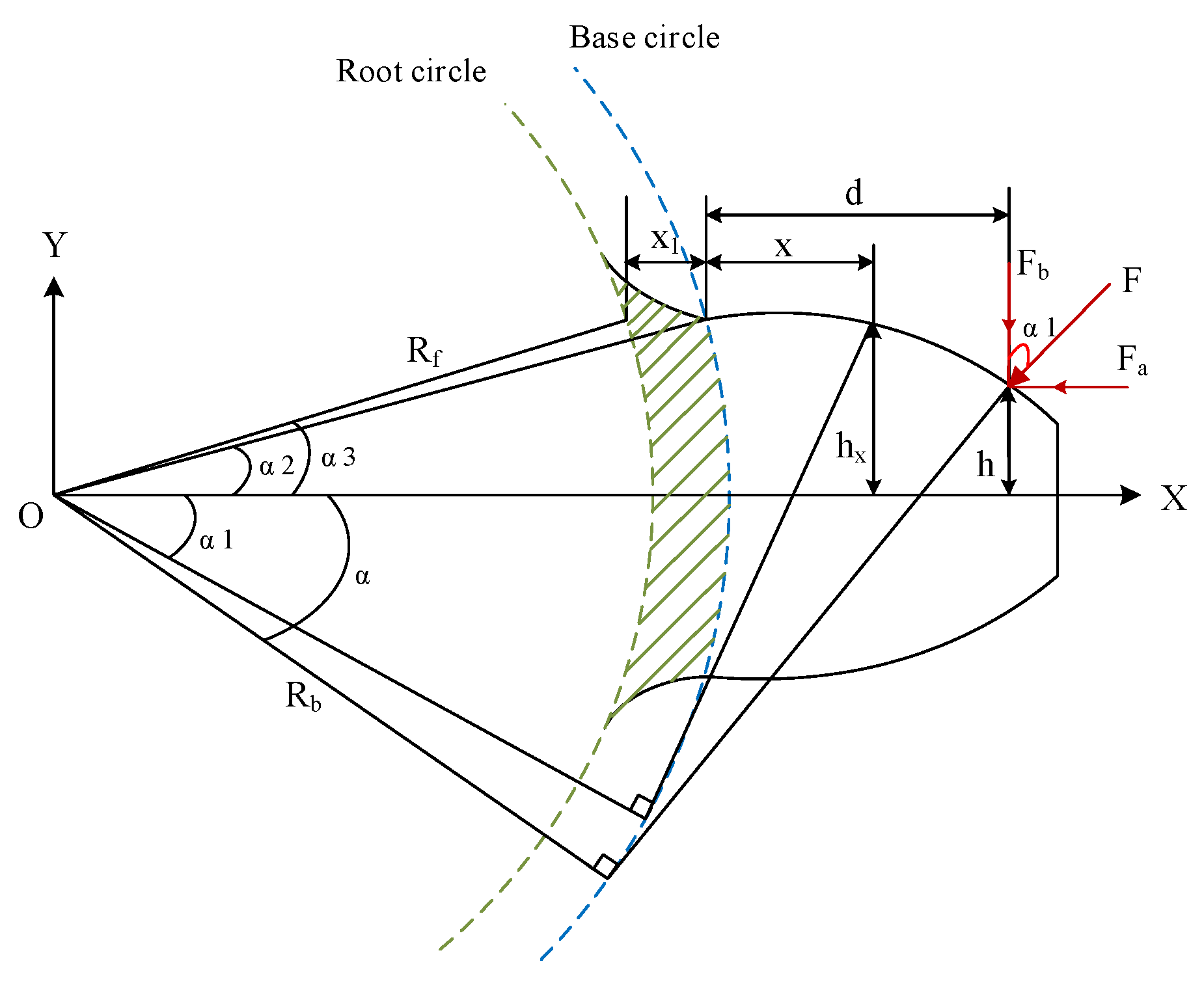
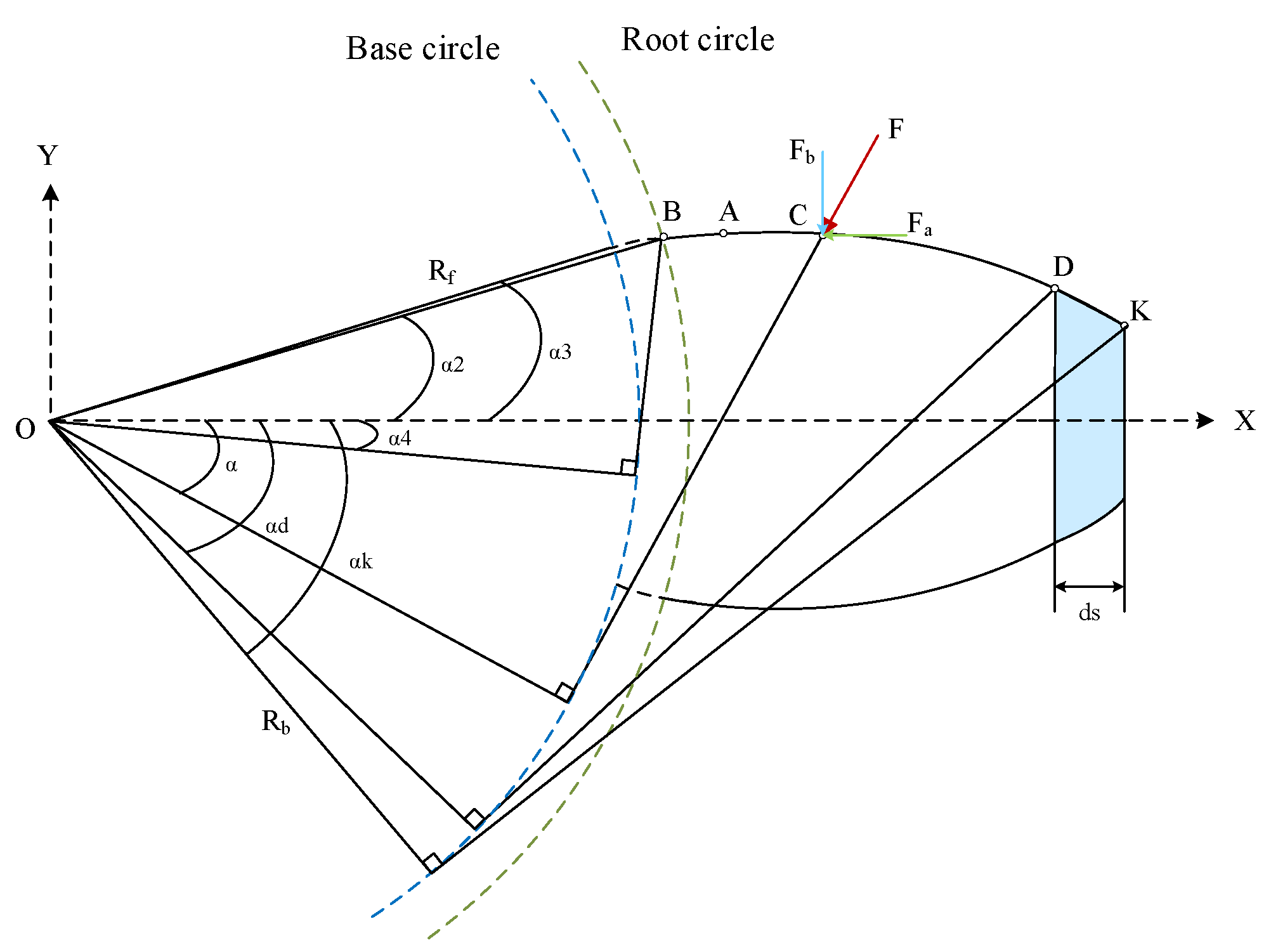
2.1. Time-Varying Meshing Stiffness
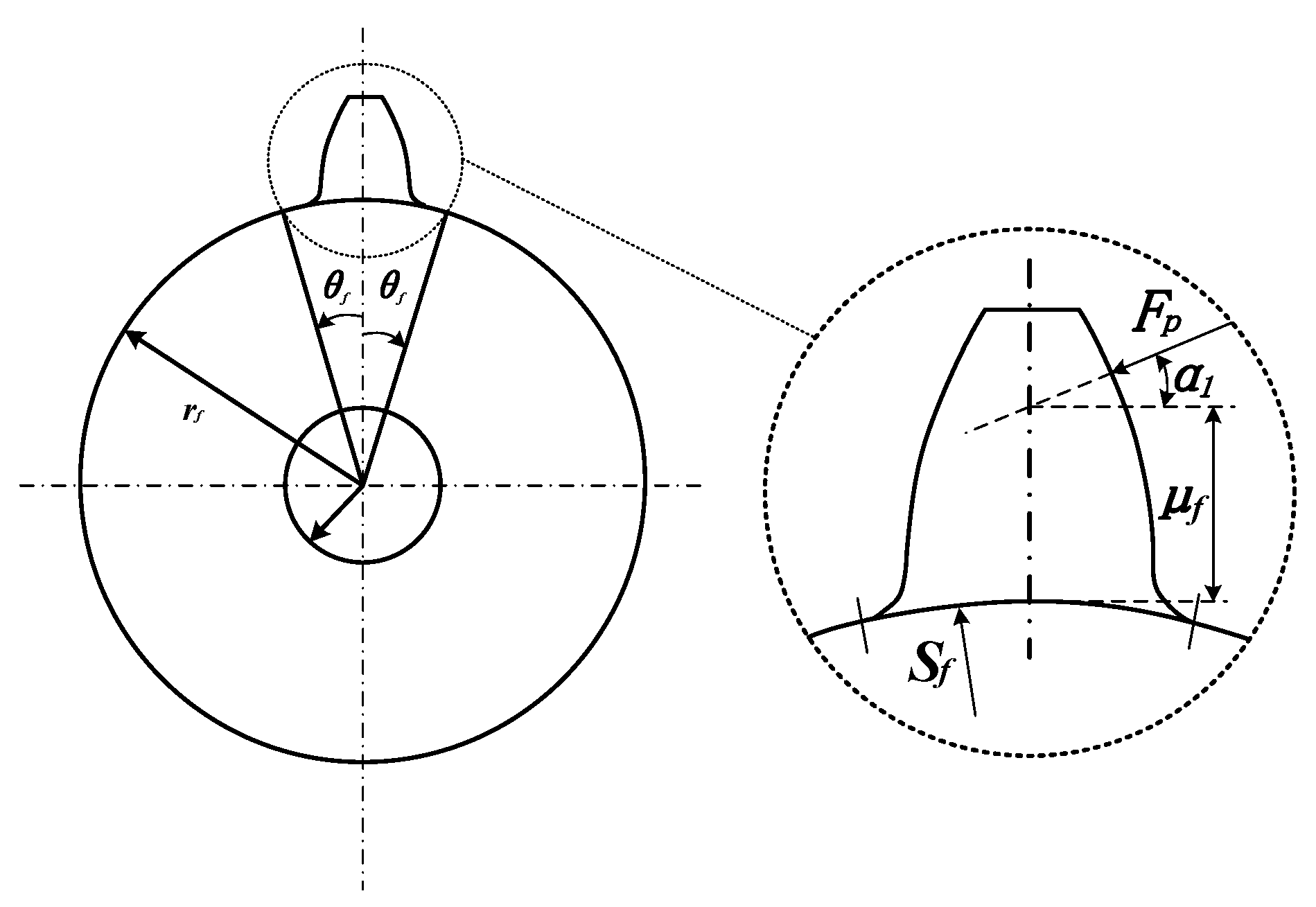
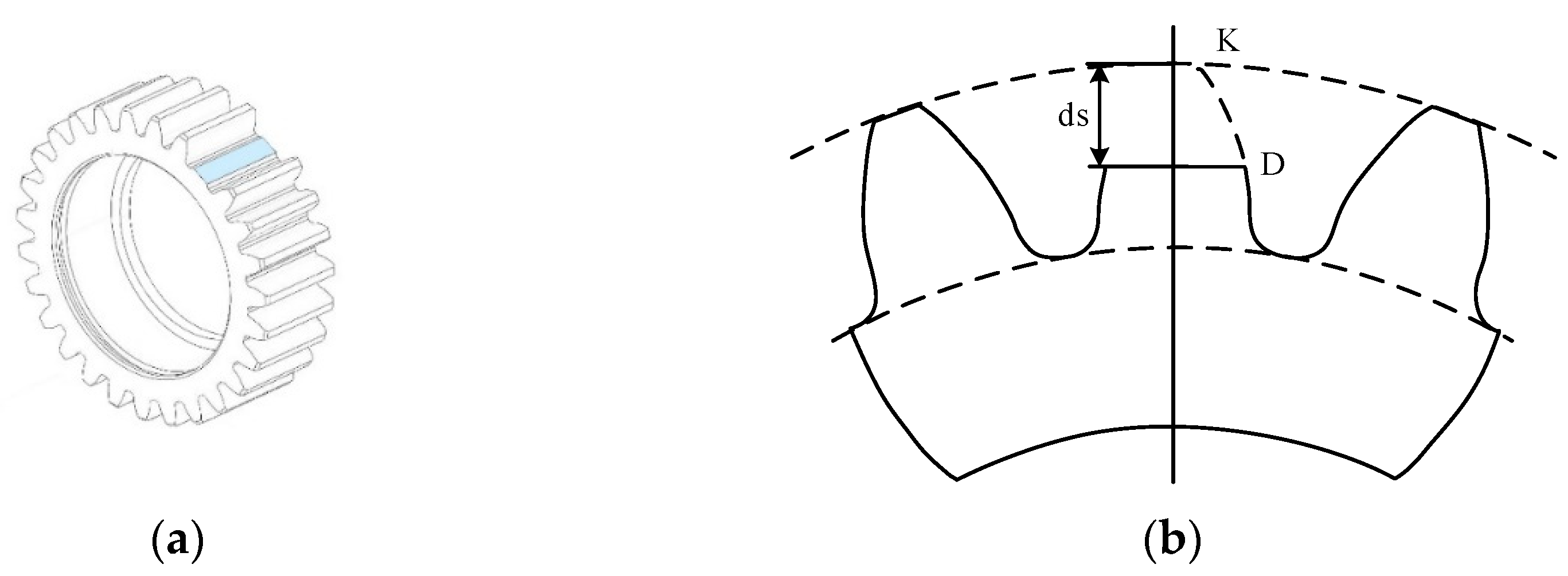
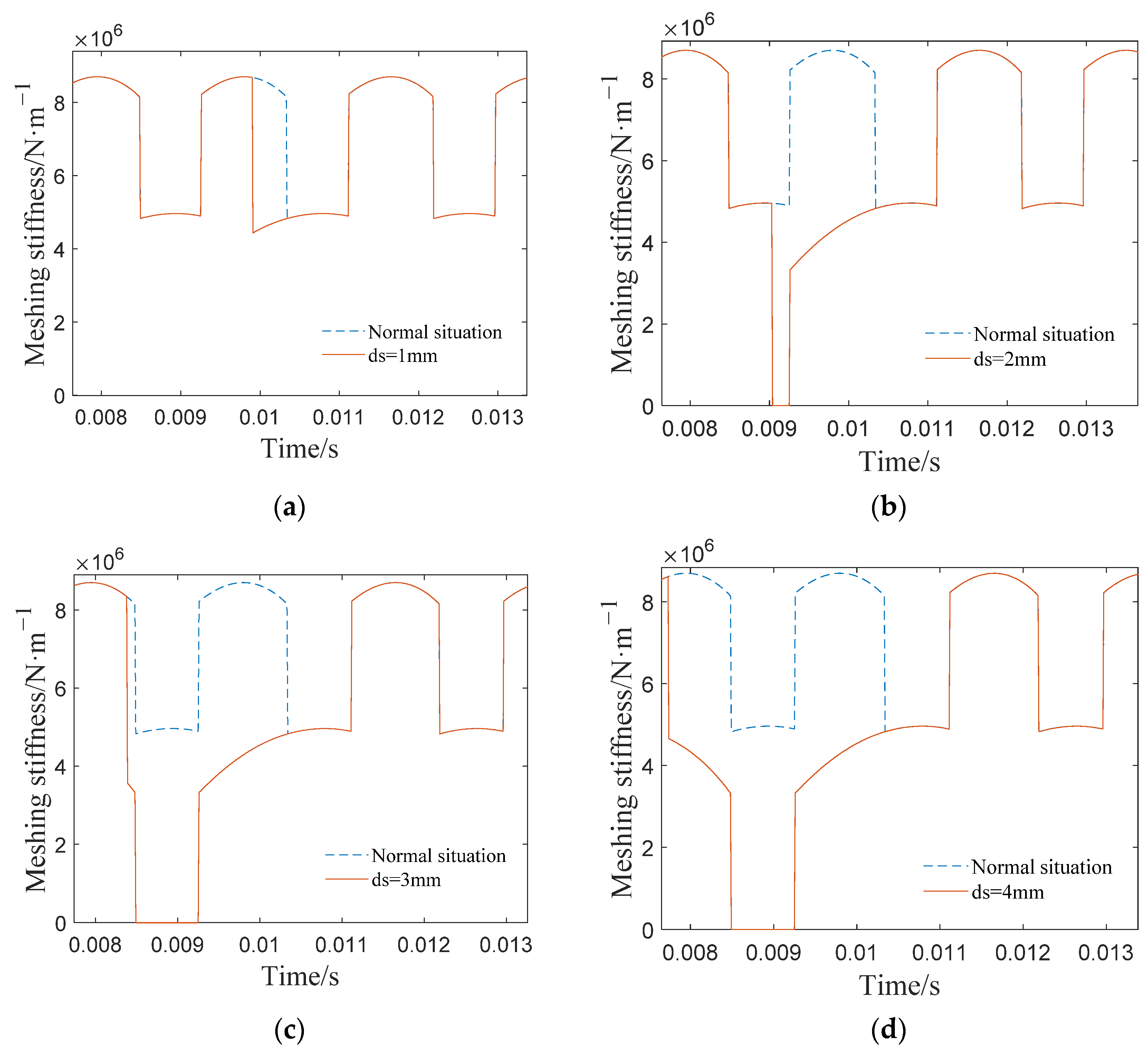
2.2. Meshing Stiffness of the Fault External Gear Pair
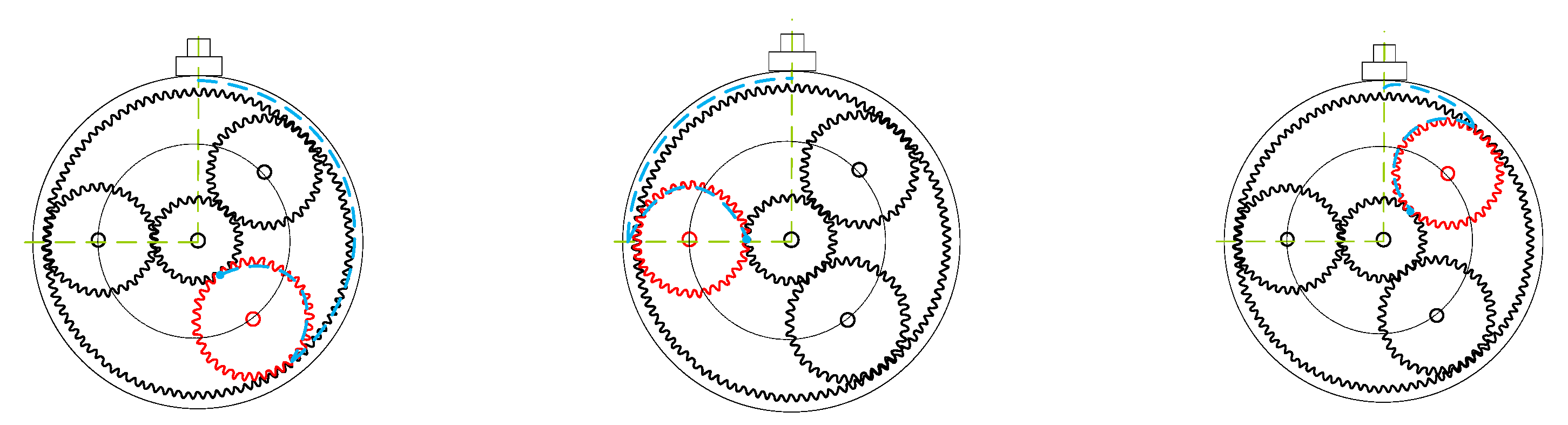
3. Phenomenological Model of Gearbox with Broken Sun Gear Fault
3.1. Phenomenological Model of Planetary Gearbox under Healthy Condition
3.2. Phenomenological Model of Planetary Gearbox under Fault Condition
4. Experiment and Analysis of Experimental Results
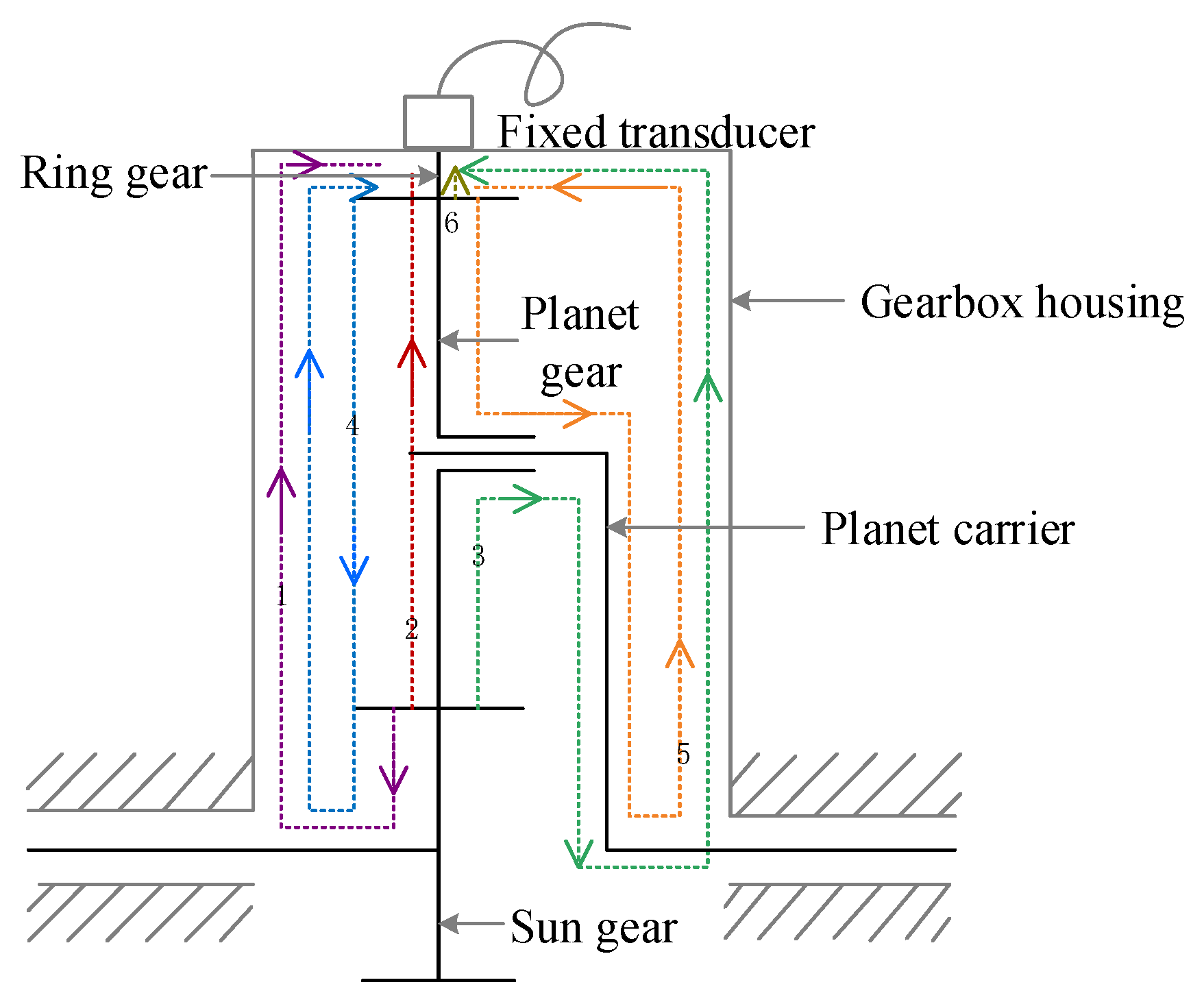
4.1. Introduction of the Test Rig
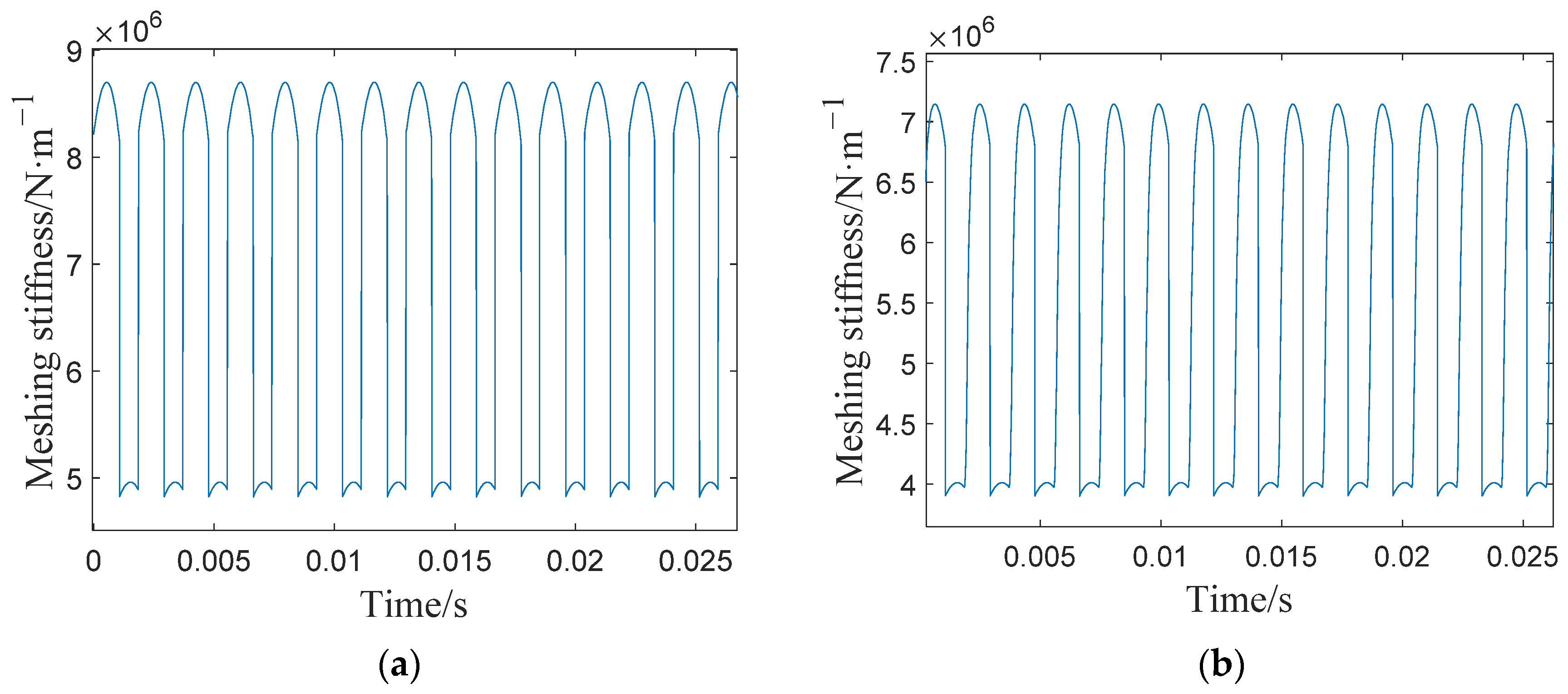
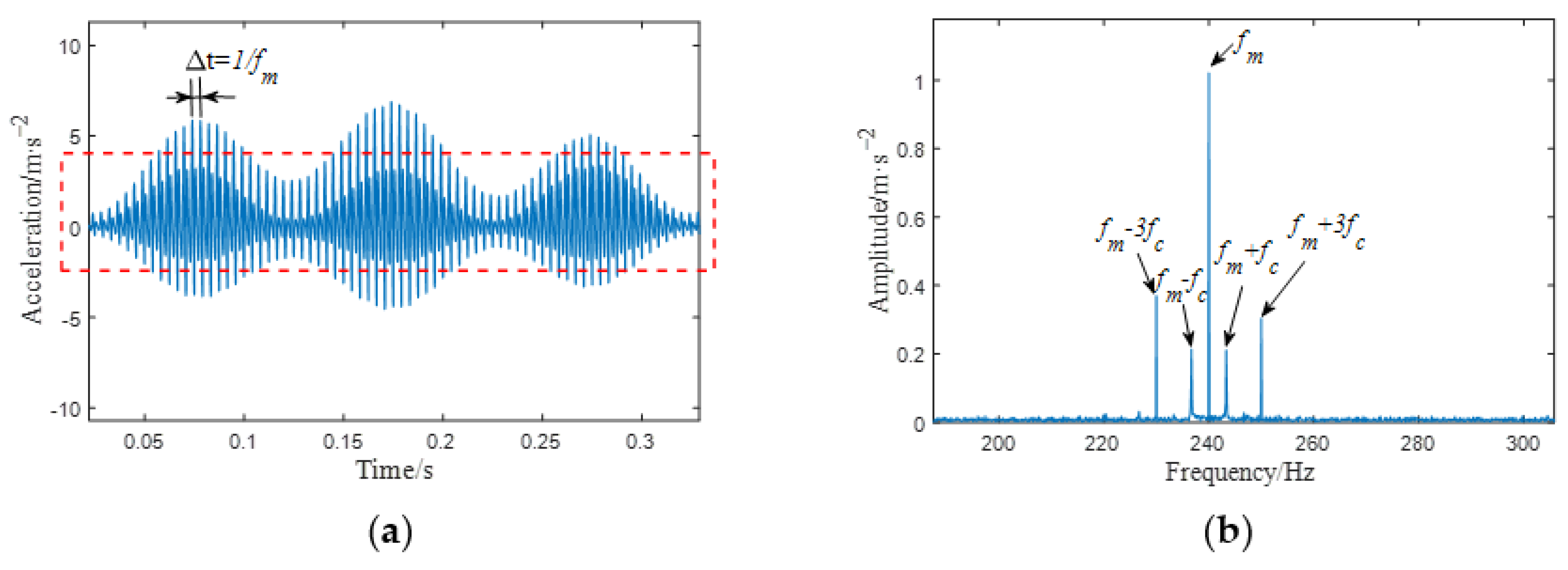
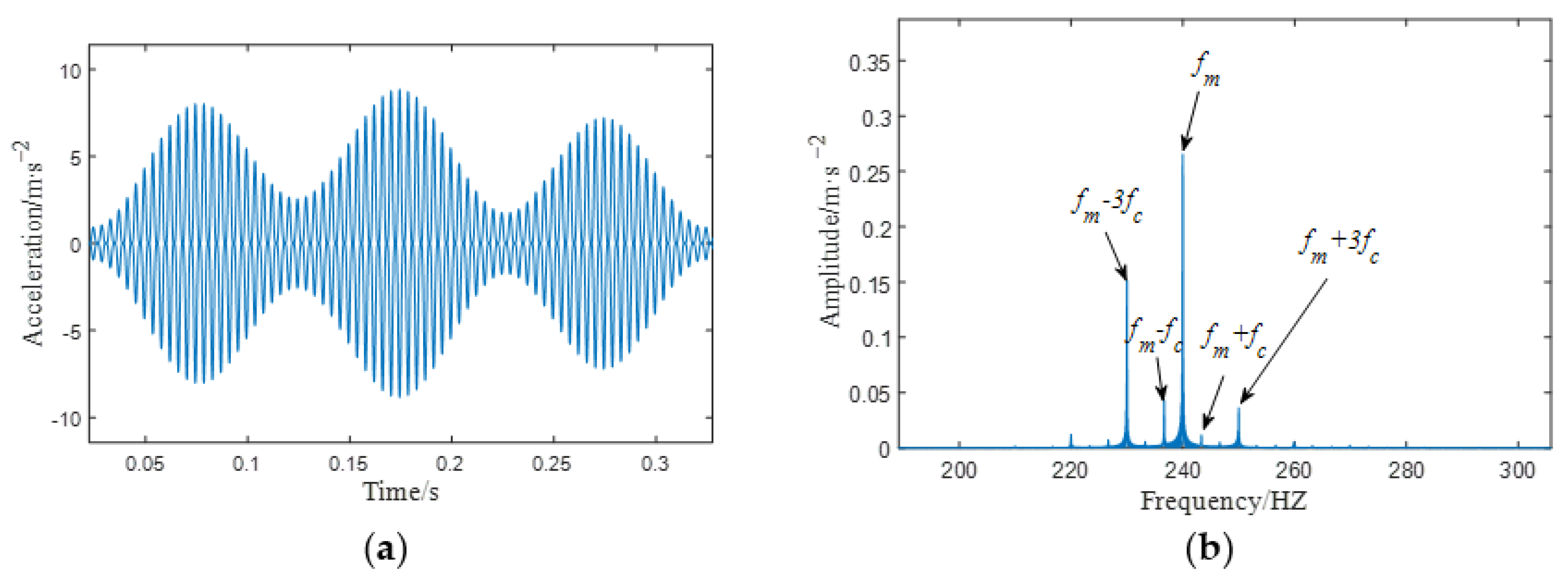
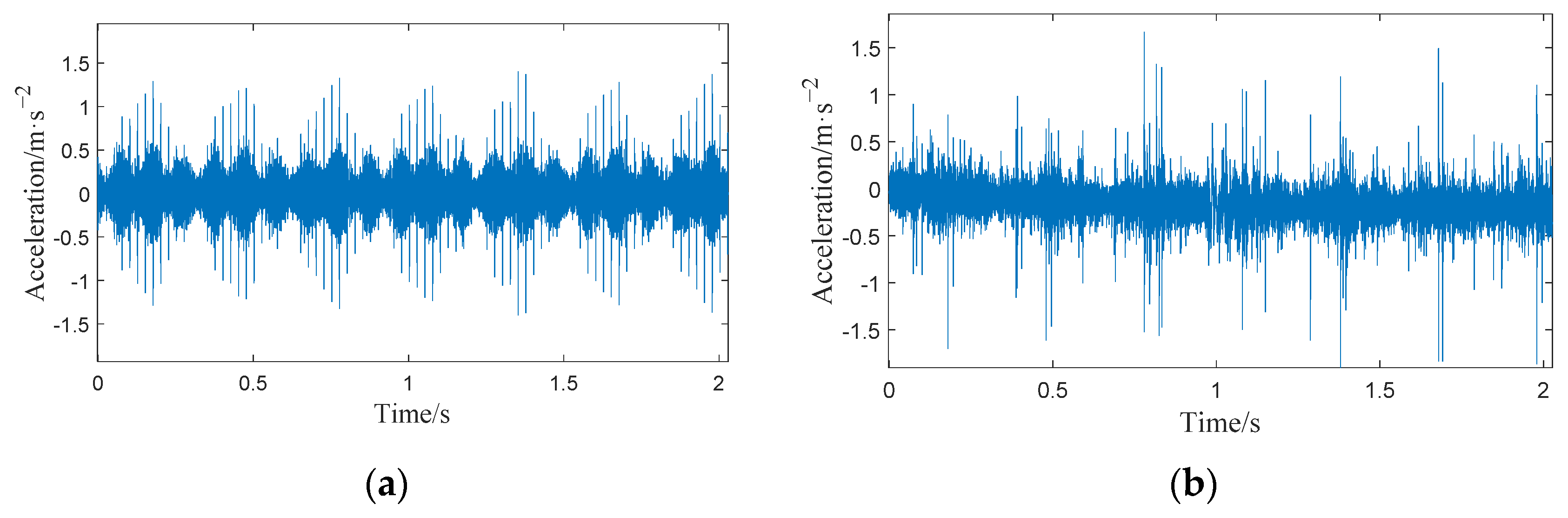
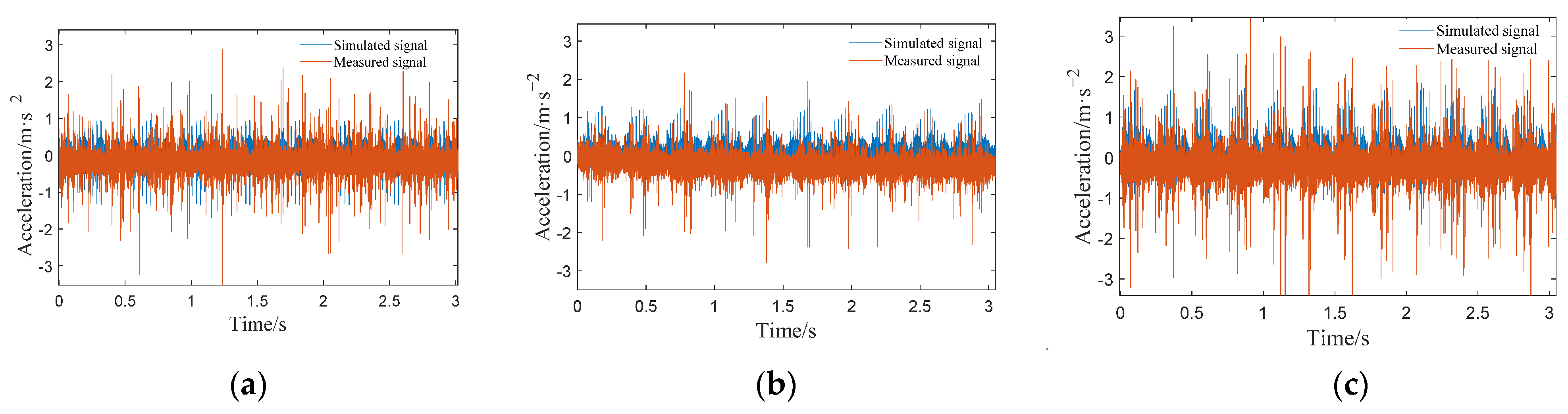
4.2. Comparison Analysis between Simulated and Measured Vibration Signals under Healthy Condition
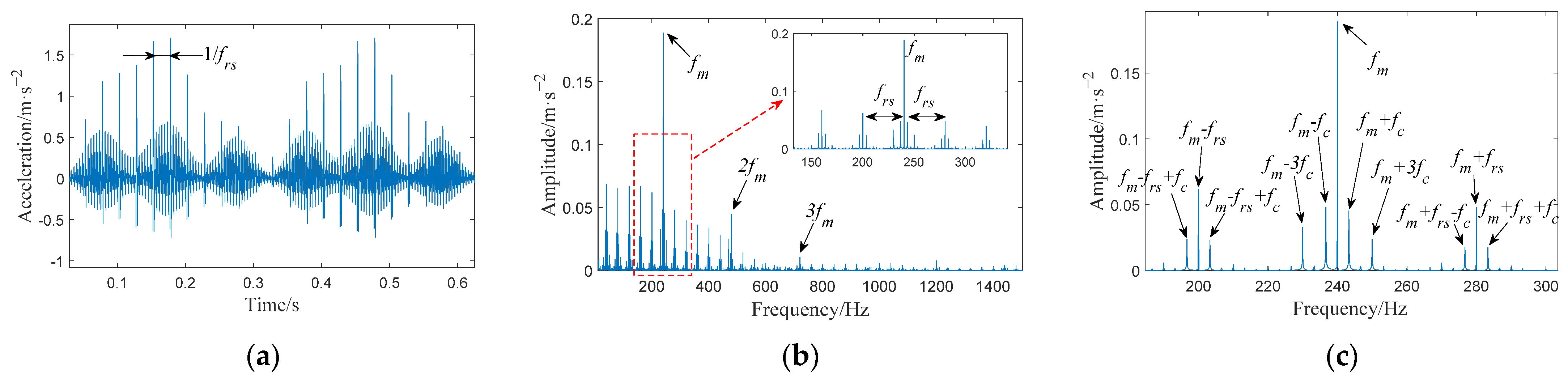
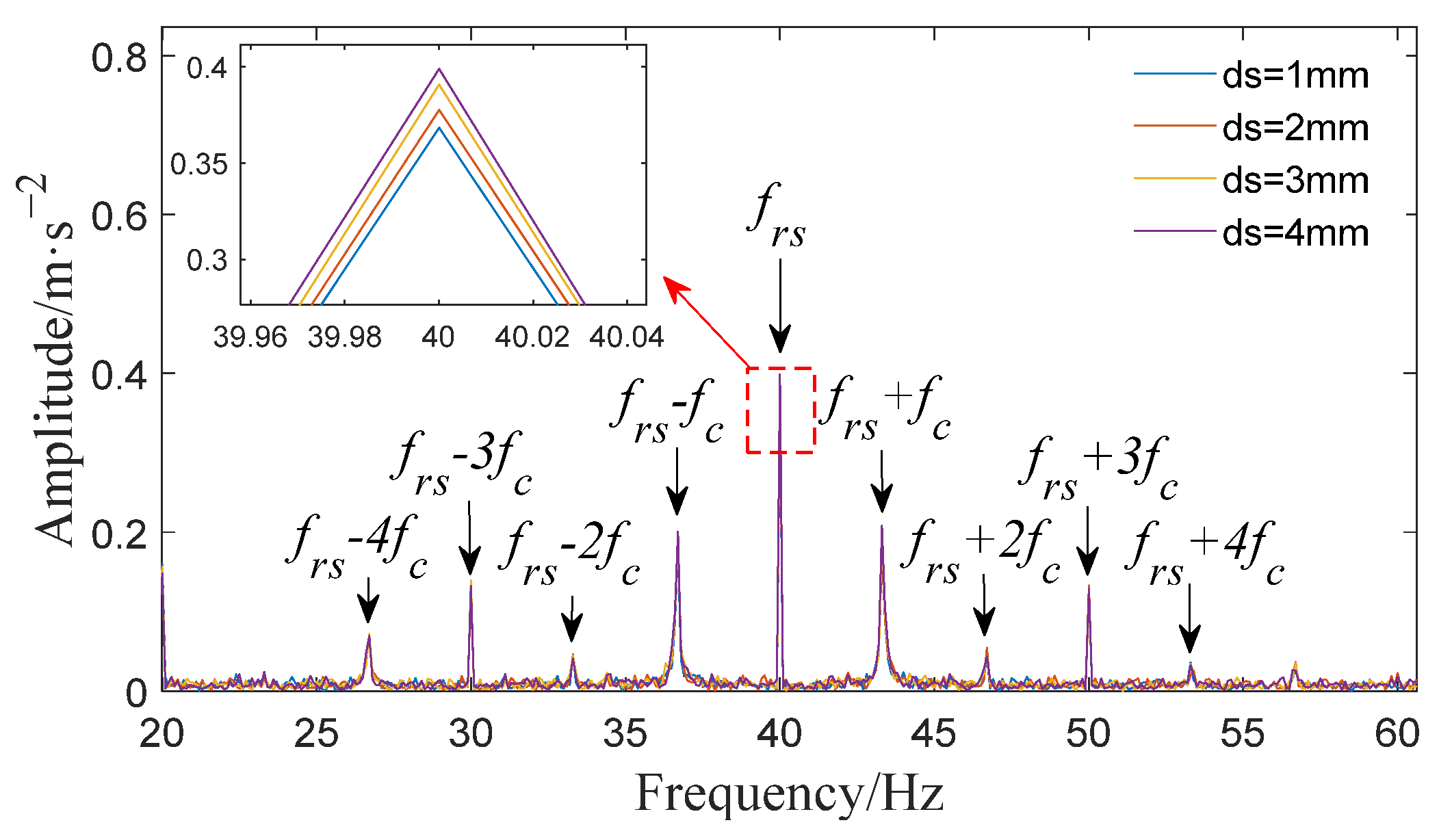
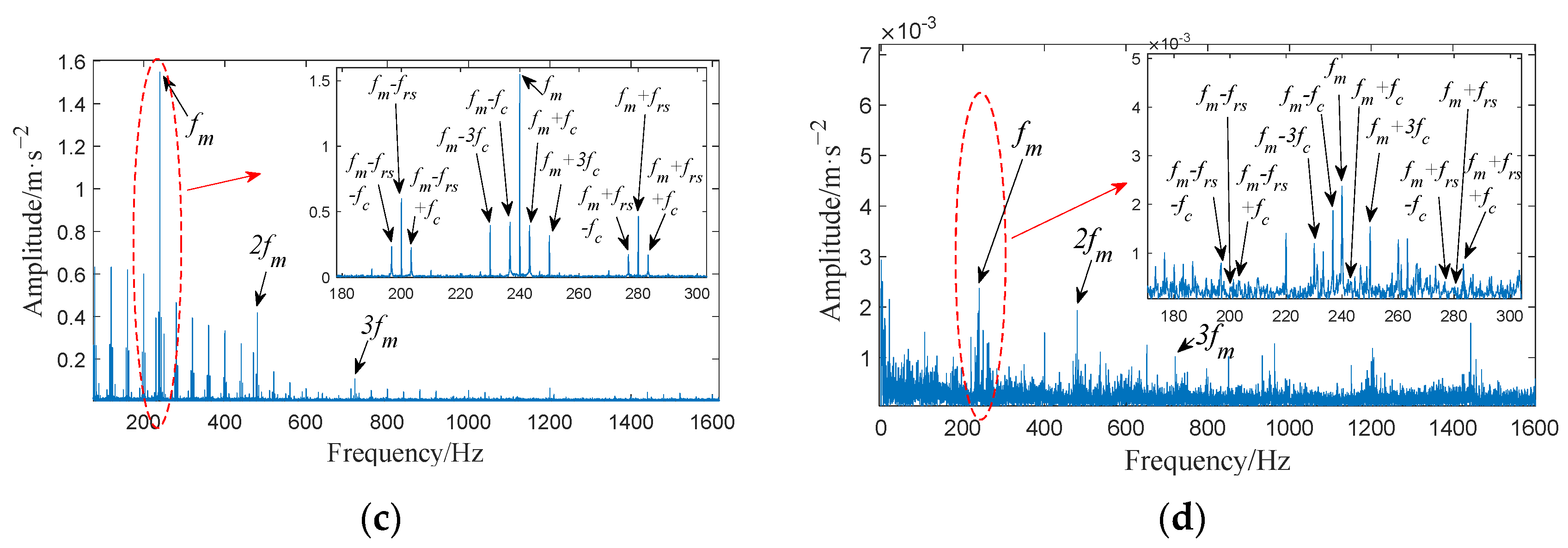
4.3. Comparison Analysis between Simulated and Measured Vibration Signals under Fault Condition
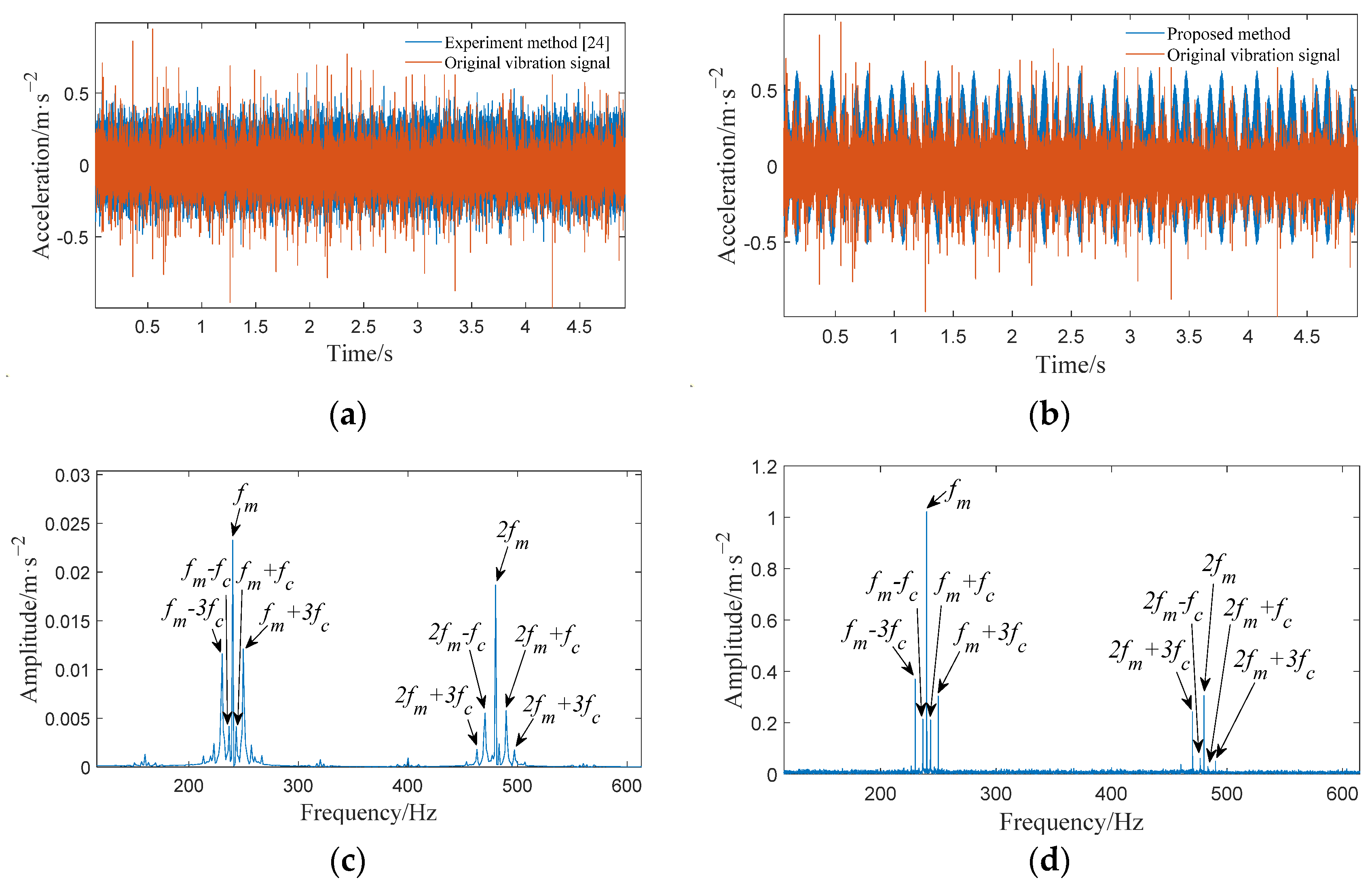
4.4. Comparative of the Model Descriptive Capability
5. Discussion and Conclusions
5.1. Discussion
5.2. Conclusions
- (1)
- When calculating the mesh stiffness via the potential energy method, the flexibility between the root circle and the base circle should be considered.
- (2)
- The movement of the falling edge with the stiffness of the faulty gear pair caused by the fault shows a tendency to advance as the fault size increases. When the fault size is large (≥1/2 of tooth height), the stiffness of the faulty gear pair may be 0, leading to the unstable state of the gear system.
- (3)
- Meshing impact is an important vibration excitation in the planetary gearbox. Compared with the traditional phenomenological model constructed by a series of cosine functions, the phenomenological model established in this paper considers the influence of the meshing impact and obtains a simulation signal that is more in line with the time–frequency domain characteristics of the actual signal.
- (4)
- Under healthy conditions, the frequency components at the meshing point of the gearbox are the meshing frequency and its frequency doubling; the amplitude shows a gradual decreasing trend; and the sidebands appear at , . Under the sun gear broken tooth fault, the same frequency component and sidebands appear at the meshing point as in the healthy case. In addition, there are also sidebands with the sun gear fault frequency as the interval near the meshing frequency under the fault condition, and a symmetrical sideband with as the interval appears on both sides of . Analyzing the vibration signal characteristics of the planetary gearbox under normal conditions and with sun gear broken tooth faults is helpful in the local fault diagnosis of the planetary gearbox.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| F | The meshing force | Poisson’s ratio | |
| Rb | Base circle radius | E | Young’s modulus |
| Rf | Root circle radius | L | Width of gear |
| ka | Axial compression stiffness | G | Shear modulus |
| kb | Bending stiffness | Ax | Cross-sectional area of the section in X direction |
| ks | Shear stiffness | Ix | Area moment of inertia |
| kh | Hertz contact stiffness | ds | Size of the broken tooth |
| kf | Matrix stiffness | Vibration generated at the meshing point between the ring and the planet i | |
| c, s, r, p | Planet carrier, sun gear, ring gear, and planet gear | Vibration generated at the meshing point between the sun and the planet i | |
| frs | Fault frequency of sun gear | Vibration amplitude of the harmonic of | |
| fc, fs, fr, fp | Rotational frequencies of the planet carrier, sun gear, ring gear, and planet gear | PG | Planetary gearbox |
| Fa | The meshing force is divided in the X-direction | LPDM | Lumped-parameter dynamic model |
| Fb | The meshing force is divided in the Y-direction |
References
- Buzzoni, M.; Elia, G.; Cocconcelli, M. A tool for validating and benchmarking signal processing techniques applied to machine diagnosis. Mech. Syst. Signal Process. 2020, 139, 106618. [Google Scholar] [CrossRef]
- Hu, Y.; Du, Q.; Xie, S. Nonlinear dynamic modeling and analysis of spur gears considering uncertain interval shaft misalignment with multiple degrees of freedom. Mech. Syst. Signal Process. 2023, 193, 110261. [Google Scholar] [CrossRef]
- Inalpolat, M.; Kahraman, A. A dynamic model to predict modulation sidebands of a planetary gear set having manufacturing errors. J. Sound Vib. 2009, 329, 371–393. [Google Scholar] [CrossRef]
- Hu, J.; Hu, N.; Yang, Y.; Zhang, L.; Shen, G. Nonlinear dynamic modeling and analysis of a helicopter planetary gear set for tooth crack diagnosis. Measurement 2022, 198, 111347. [Google Scholar] [CrossRef]
- Yang, X.; Niaki, E.; Zuo, M.; Tian, Z.; Safizadeh, M.; Qin, D. Analysis of spur gearbox dynamics considering tooth lubrication and tooth crack severity progression. Tribol. Int. 2023, 178, 108027. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, X.; Li, Y. Influence of Temperature on Friction and Wear Characteristics of Gear Investigated by Oil Particle Analysis. J. Shenyang Inst. Eng. (Nat. Sci.) 2023, 19, 87–91. [Google Scholar]
- Yue, K.; Kang, Z.; Zhang, M.; Wang, L.; Shao, Y.; Chen, Z. Study on gear meshing power loss calculation considering the coupling effect of friction and dynamic characteristics. Tribol. Int. 2023, 183, 108378. [Google Scholar] [CrossRef]
- Zhang, M.; Li, D.; Zuo, M.; Liu, J.; Xiang, H.; Song, Y.; Wang, K. An improved phenomenological model of vibrations for planetary gearboxes. J. Sound Vib. 2020, 496, 115919. [Google Scholar] [CrossRef]
- Zhou, P.; Chen, S.; He, Q.; Wang, D.; Peng, Z. Rotating machinery fault-induced vibration signal modulation effects: A review with mechanisms, extraction methods and applications for diagnosis. Mech. Syst. Signal Process. 2023, 200, 110489. [Google Scholar] [CrossRef]
- Yu, X.; Feng, Z.; Liang, M. Analytical vibration signal model and signature analysis in resonance region for planetary gearbox fault diagnosis. J. Sound Vib. 2021, 498, 115962. [Google Scholar] [CrossRef]
- Liu, Z.; Lei, Y.; Liu, H.; Yang, X.; Song, W. A phenomenological model for investigating unequal planet load sharing in epicyclic gearboxes. Mech. Syst. Signal Process. 2020, 135, 106414. [Google Scholar] [CrossRef]
- Parra, J.; Vicuña, M.C. Two methods for modeling vibrations of planetary gearboxes including faults: Comparison and validation. Mech. Syst. Signal Process. 2017, 92, 213–225. [Google Scholar] [CrossRef]
- Luo, Y.; Cui, L.; Ma, J. An Improved Phenomenological Model of the Planetary Gearbox Based on Meshing Vibration Characteristics. IEEE Access 2020, 8, 103462–103475. [Google Scholar] [CrossRef]
- Luo, Y.; Cui, L.; Zhang, J.; Ma, J. Vibration Mechanism and Improved Phenomenological Model of Planetary Gearbox with Broken Sun Gear Fault. Measurement 2021, 178, 109356. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Wang, Y.; Feng, W.; Zhang, K. A phenomenological model of vibration signals of epicyclic gearboxes under meshing impact excitations. Mech. Syst. Signal Process. 2023, 187, 109904. [Google Scholar] [CrossRef]
- Xu, L.; Ding, K.; He, G.; Li, Y.; Chen, Z. Resonance modulation vibration mechanism of equally-spaced planetary gearbox with a localized fault on sun gear. Mech. Syst. Signal Process. 2022, 166, 108450. [Google Scholar] [CrossRef]
- Nie, Y.; Li, F.; Wang, L.; Li, J.; Sun, M.; Wang, M.; Li, J. A mathematical model of vibration signal for multistage wind turbine gearboxes with transmission path effect analysis. Mech. Mach. Theory 2022, 167, 104428. [Google Scholar] [CrossRef]
- Ma, H.; Zeng, J.; Feng, R.; Pang, X.; Wen, B. An improved analytical method for mesh stiffness calculation of spur gears with tip relief. Mech. Mach. Theory 2016, 98, 64–80. [Google Scholar] [CrossRef]
- Ma, J.; Liu, T.; Zha, C.; Song, L. Simulation Research on the Time-Varying Meshing Stiffness and Vibration Response of Micro-Cracks in Gears under Variable Tooth Shape Parameters. Appl. Sci. 2019, 9, 1512. [Google Scholar] [CrossRef]
- Liang, X.; Zuo, M.; Pandey, M. Analytically evaluating the influence of crack on the mesh stiffness of a planetary gear set. Mech. Mach. Theory 2014, 76, 20–38. [Google Scholar] [CrossRef]
- Wan, Z.; Cao, H.; Zi, Y.; He, W.; He, Z. An improved time-varying mesh stiffness algorithm and dynamic modeling of gear-rotor system with tooth root crack. Eng. Fail. Anal. 2014, 42, 157–177. [Google Scholar] [CrossRef]
- Sainsot, P.; Velex, P.; Duverger, O. Contribution of Gear Body to Tooth Deflections—A New Bidimensional Analytical Formula. J. Mech. Des. 2004, 126, 748–752. [Google Scholar] [CrossRef]
- Chaari, F.; Fakhfakh, T.; Haddar, M. Analytical modelling of spur gear tooth crack and influence on gear mesh stiffness. Eur. J. Mech. A Solids 2009, 28, 461–468. [Google Scholar] [CrossRef]
- Fan, J.; Guo, Y.; Wu, X.; Lin, Y.; Chen, X. Vibration simulation and experiment of planetary gearbox with planetary gear local fault. J. Vib. Eng. 2022, 35, 1270–1277. [Google Scholar]
- Nie, Y.; Li, F.; Wang, L.; Li, J.; Wang, M.; Sun, M.; Li, G.; Li, Y. Phenomenological vibration models of planetary gearboxes for gear local fault diagnosis. Mech. Mach. Theory 2022, 170, 104698. [Google Scholar] [CrossRef]
- Lei, Y.; Liu, Z.; Lin, J.; Lu, F. Phenomenological models of vibration signals for condition monitoring and fault diagnosis of epicyclic gearboxes. J. Sound Vib. 2016, 369, 266–281. [Google Scholar] [CrossRef]
- Inalpolat, M.; Kahraman, A. A theoretical and experimental investigation of modulation sidebands of planetary gear sets. J. Sound Vib. 2009, 323, 677–696. [Google Scholar] [CrossRef]
- Lei, Y.; Tang, W.; Kong, D.; Lin, J. Vibration Signal Simulation and Fault Diagnosis of Planetary Gearboxes Based on Transmission Mechanism Analysis. J. Mech. Eng. 2014, 50, 61–68. [Google Scholar] [CrossRef]



| Ai | Bi | Ci | Di | Ei | Fi | |
|---|---|---|---|---|---|---|
| L* | −5.574 × 10−5 | −1.9986 × 10−3 | −2.3015 × 10−4 | 4.7702 × 10−3 | 0.0271 | 6.8045 |
| M* | 60.111 × 10−5 | −28.100 × 10−3 | −83.431 × 10−4 | −9.9256 × 10−3 | 0.1624 | 0.9086 |
| P* | −50.952 × 10−5 | 185.50 × 10−3 | 0.0538 × 10−4 | 53.3 × 10−3 | 0.2895 | 0.9236 |
| Q* | −6.2042 × 10−5 | 9.0889 × 10−3 | −4.0964 × 10−4 | 7.8297 × 10−3 | −0.1472 | 0.6904 |
| Item | Sun Gear | Plant Gear | Ring Gear |
|---|---|---|---|
| Tooth number | 18 | 27 | 72 |
| Module(mm) | 2 | ||
| Width of teeth (mm) | 20 | ||
| Addendum coefficient | 1 | ||
| Pressure angle (°) | 20 | ||
| Young’s modulus (Pa) | 2.06 × 107 | ||
| Poisson’s ratio | 0.3 | ||
| Item | Symbolization | Value |
|---|---|---|
| Meshing frequency | 240 Hz | |
| Rotational frequency of planet carrier | 3.34 Hz | |
| Rotational frequency of sun gear | 16.67 Hz | |
| Fault frequency of sun gear | 40 Hz |
| Theoretical Value | Simulated Value | Measured Value | |
|---|---|---|---|
| 240 Hz | 240 Hz | 239.94 Hz | 0.025% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, M.; Ma, J.; Xiong, X.; Li, R. Analysis of Vibration Characteristics of Planetary Gearbox with Broken Sun Gear Based on Phenomenological Model. Appl. Sci. 2023, 13, 9413. https://doi.org/10.3390/app13169413
Zou M, Ma J, Xiong X, Li R. Analysis of Vibration Characteristics of Planetary Gearbox with Broken Sun Gear Based on Phenomenological Model. Applied Sciences. 2023; 13(16):9413. https://doi.org/10.3390/app13169413
Chicago/Turabian StyleZou, Mengting, Jun Ma, Xin Xiong, and Rong Li. 2023. "Analysis of Vibration Characteristics of Planetary Gearbox with Broken Sun Gear Based on Phenomenological Model" Applied Sciences 13, no. 16: 9413. https://doi.org/10.3390/app13169413
APA StyleZou, M., Ma, J., Xiong, X., & Li, R. (2023). Analysis of Vibration Characteristics of Planetary Gearbox with Broken Sun Gear Based on Phenomenological Model. Applied Sciences, 13(16), 9413. https://doi.org/10.3390/app13169413






