Performance Analysis of Multiple Steel Corrugated Pipe Arch Culvert under Construction and Periodic Vehicle Load
Abstract
:1. Introduction
2. Project Background
2.1. Culvert and Foundation
2.2. Foundation Treatment
3. Finite-Element Model
3.1. Two-Dimensional Model
- (1)
- The construction of a 0.5 m gravel cushion and 1.5 m C20 stone concrete foundation was completed in one step.
- (2)
- The installation of the steel corrugated pipe and C15 fine stone concrete protective masonry around the pipe was completed in one step.
- (3)
- The gravel soil around the pipe was backfilled in one step, and then the supporting structure of the foundation pit was removed.
- (4)
- The pavement structure was constructed in one step, and a 20 kPa load was applied to the pavement to simulate the action of construction machinery.
3.2. Three-Dimensional FE Model
4. Results and Analysis
4.1. Simulation Results of Arch Culvert Construction
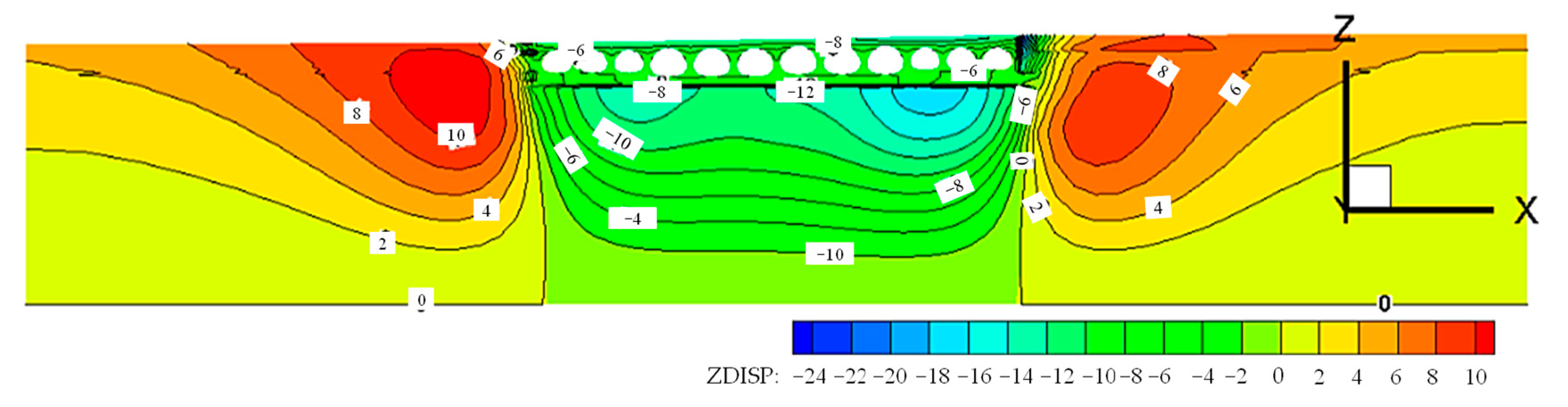
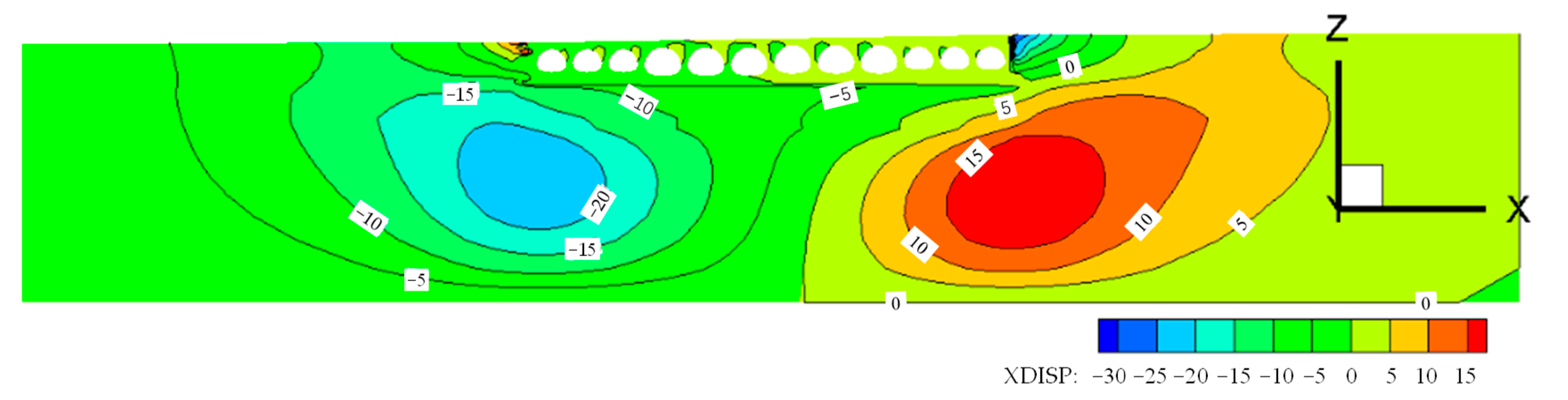
4.1.1. Displacement of Strata
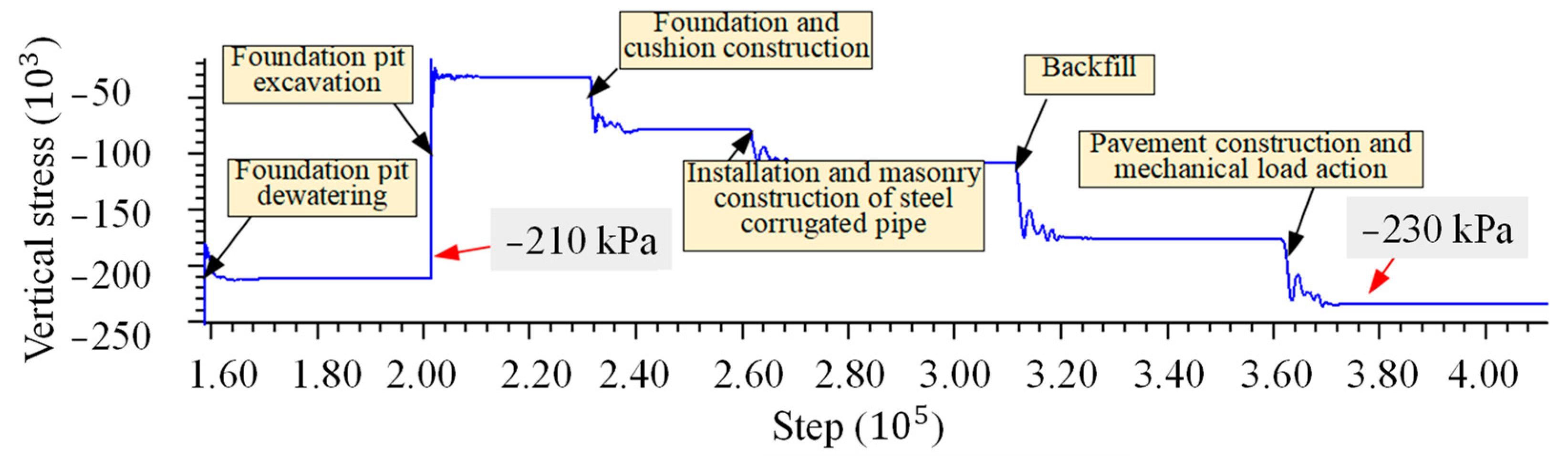
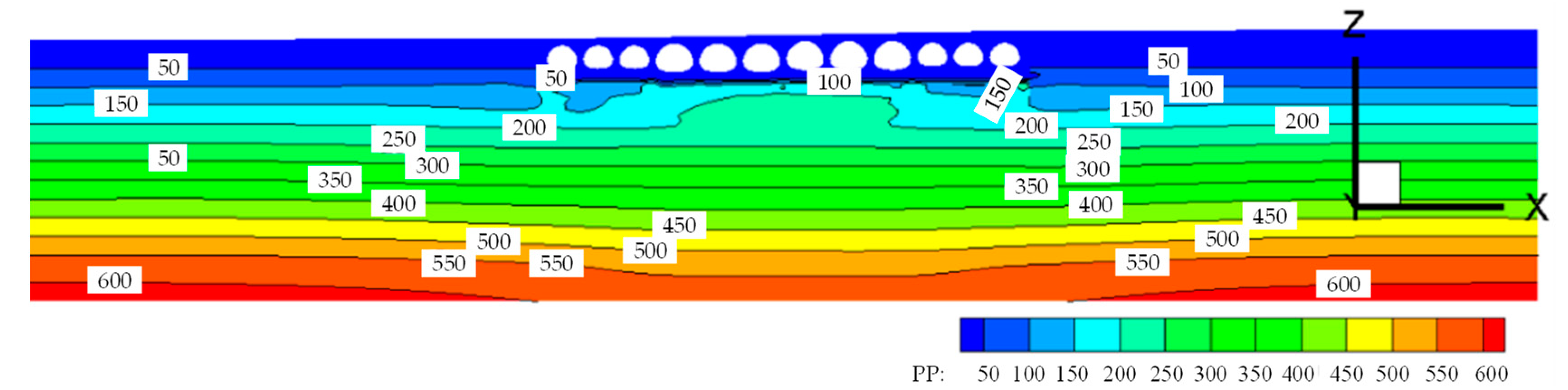
4.1.2. Soil Stress and Pore Water Pressure
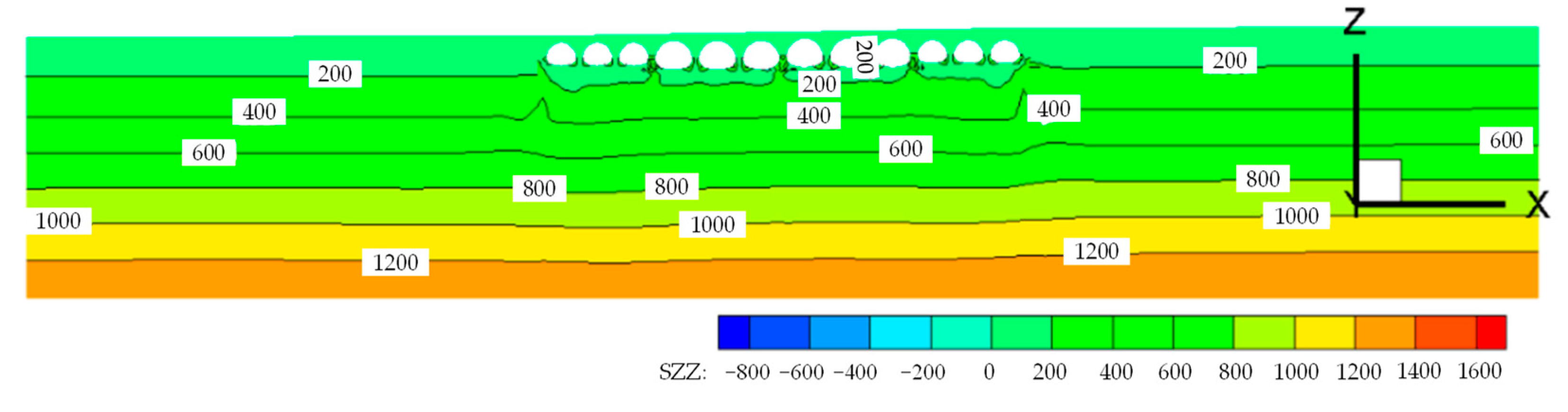
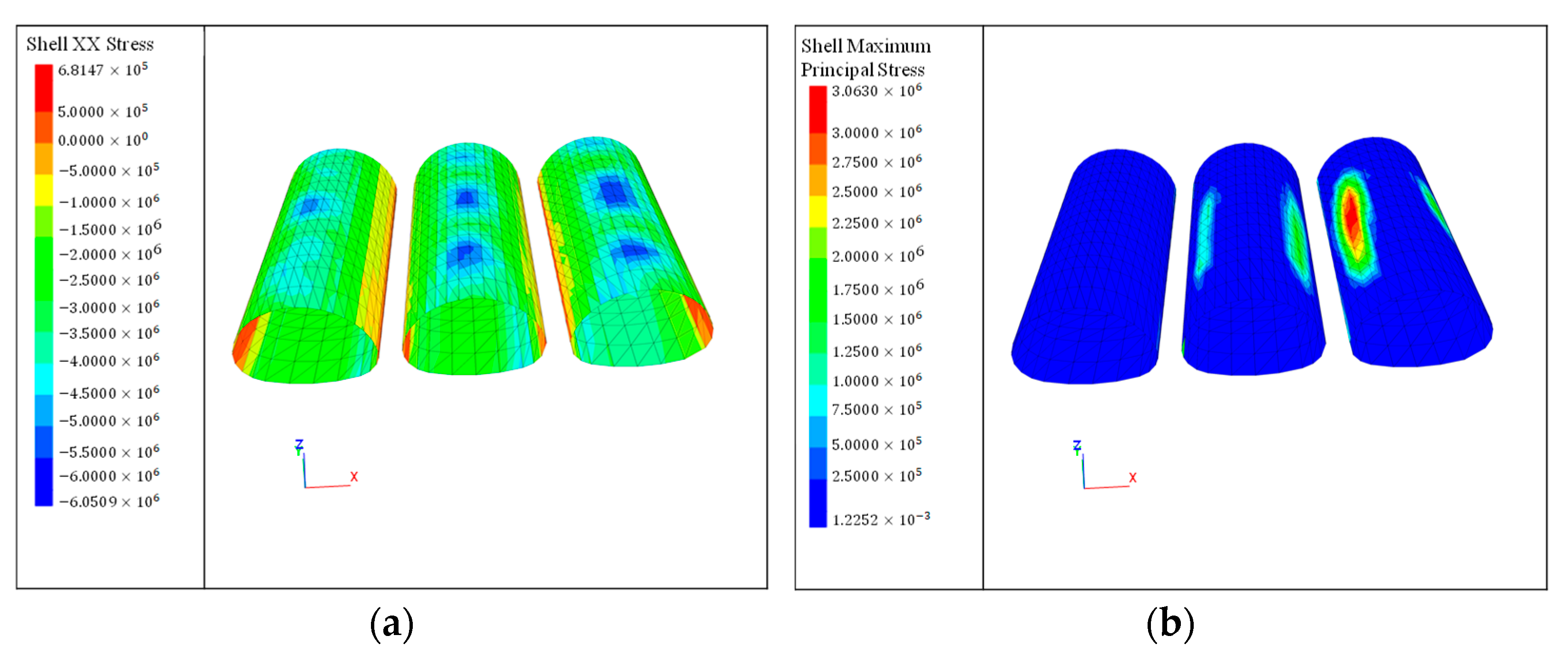
4.1.3. Structural Stress and Deformation
4.2. Simulation Results of Arch Culvert under Periodic Vehicle Load
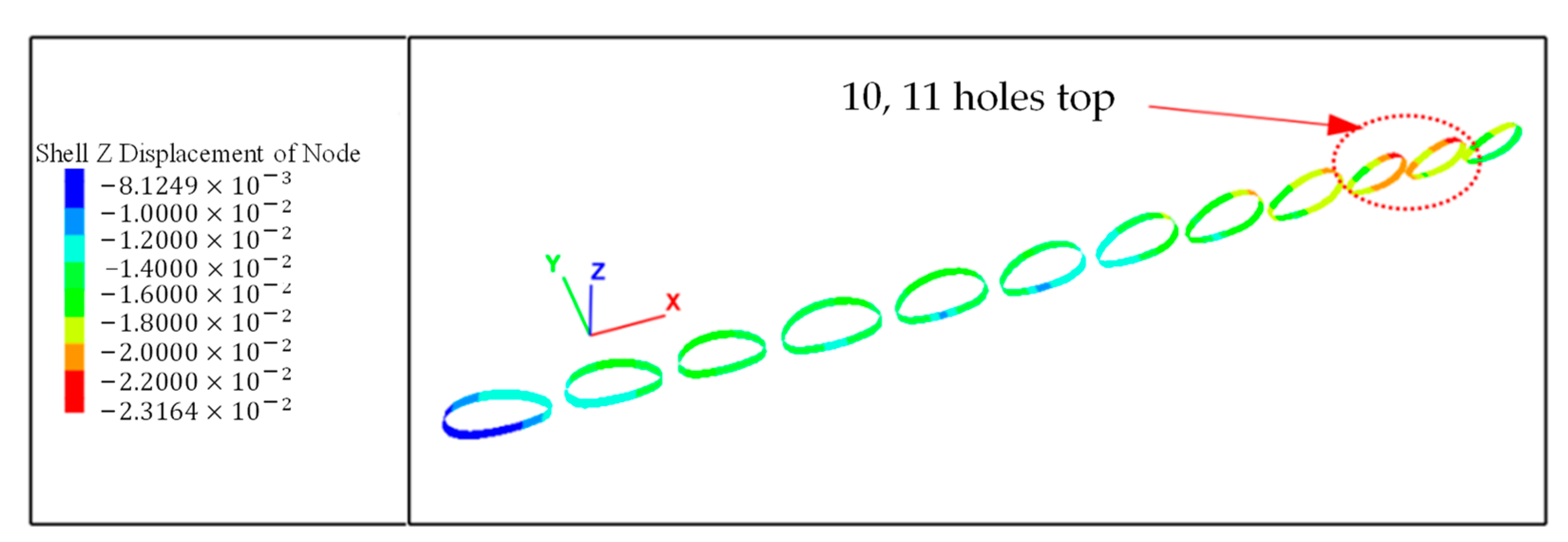
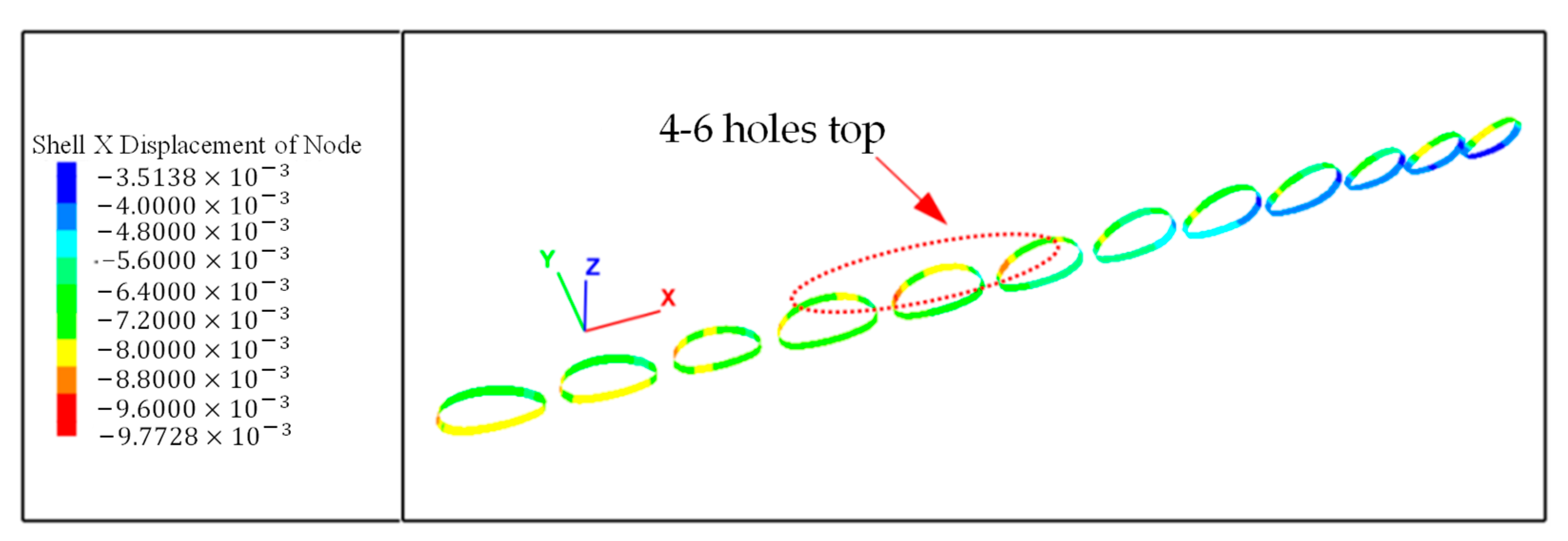
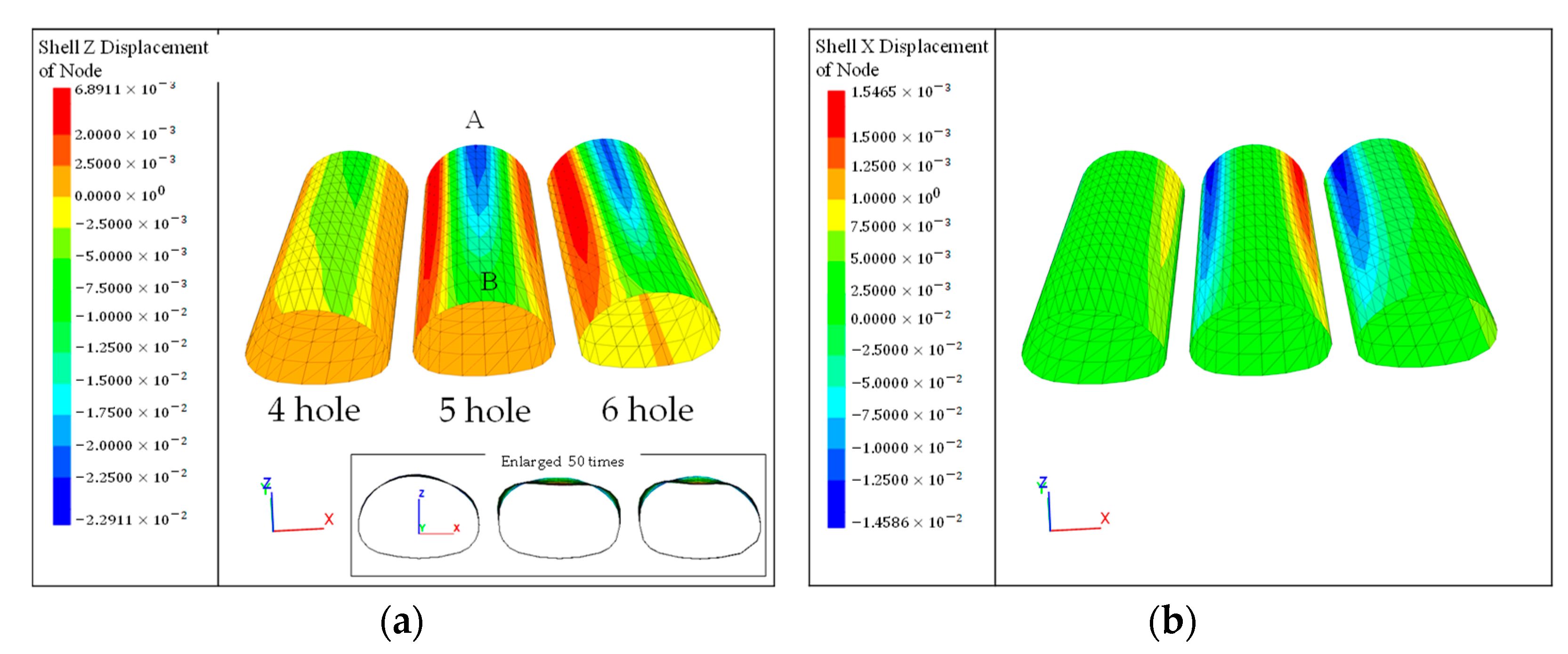
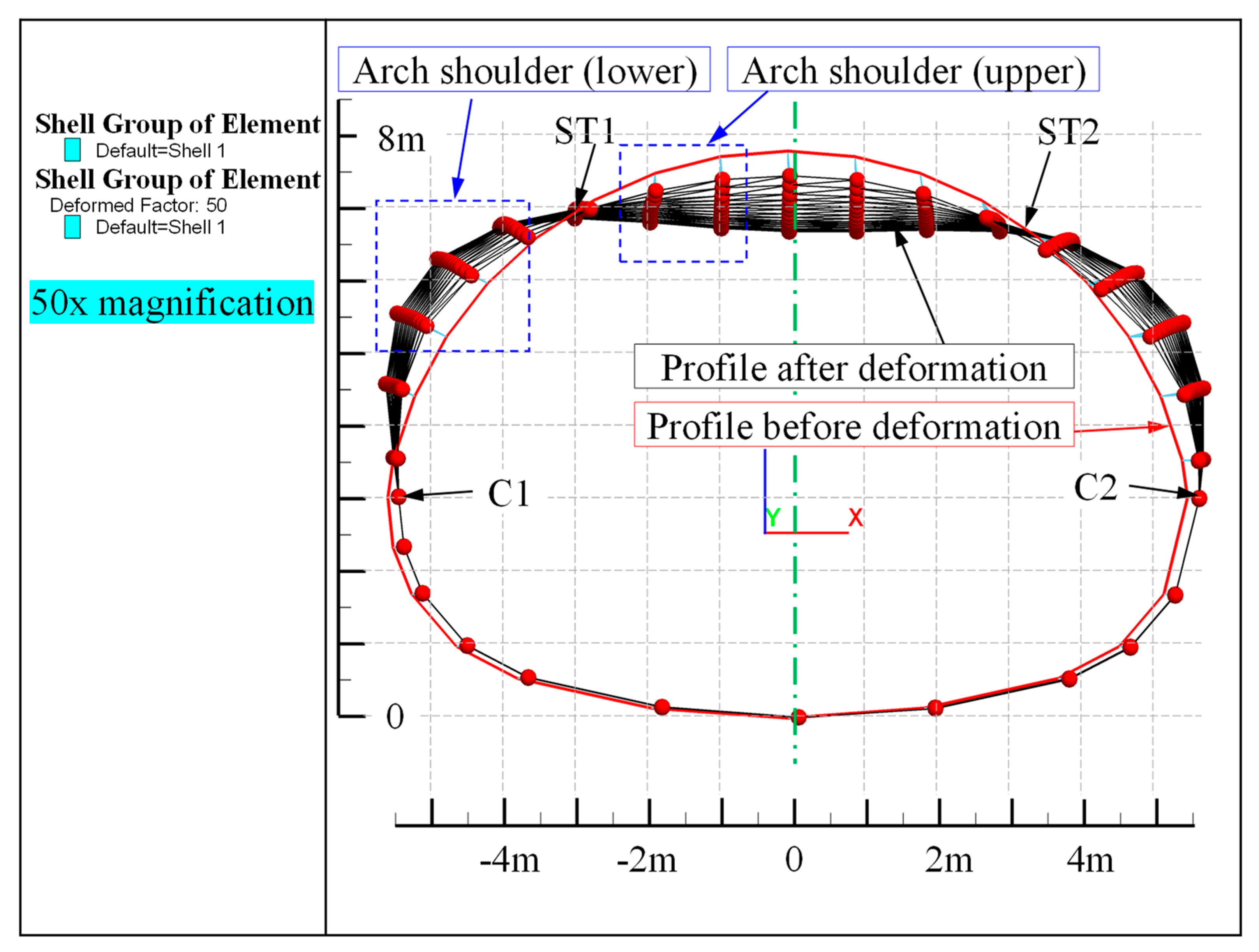
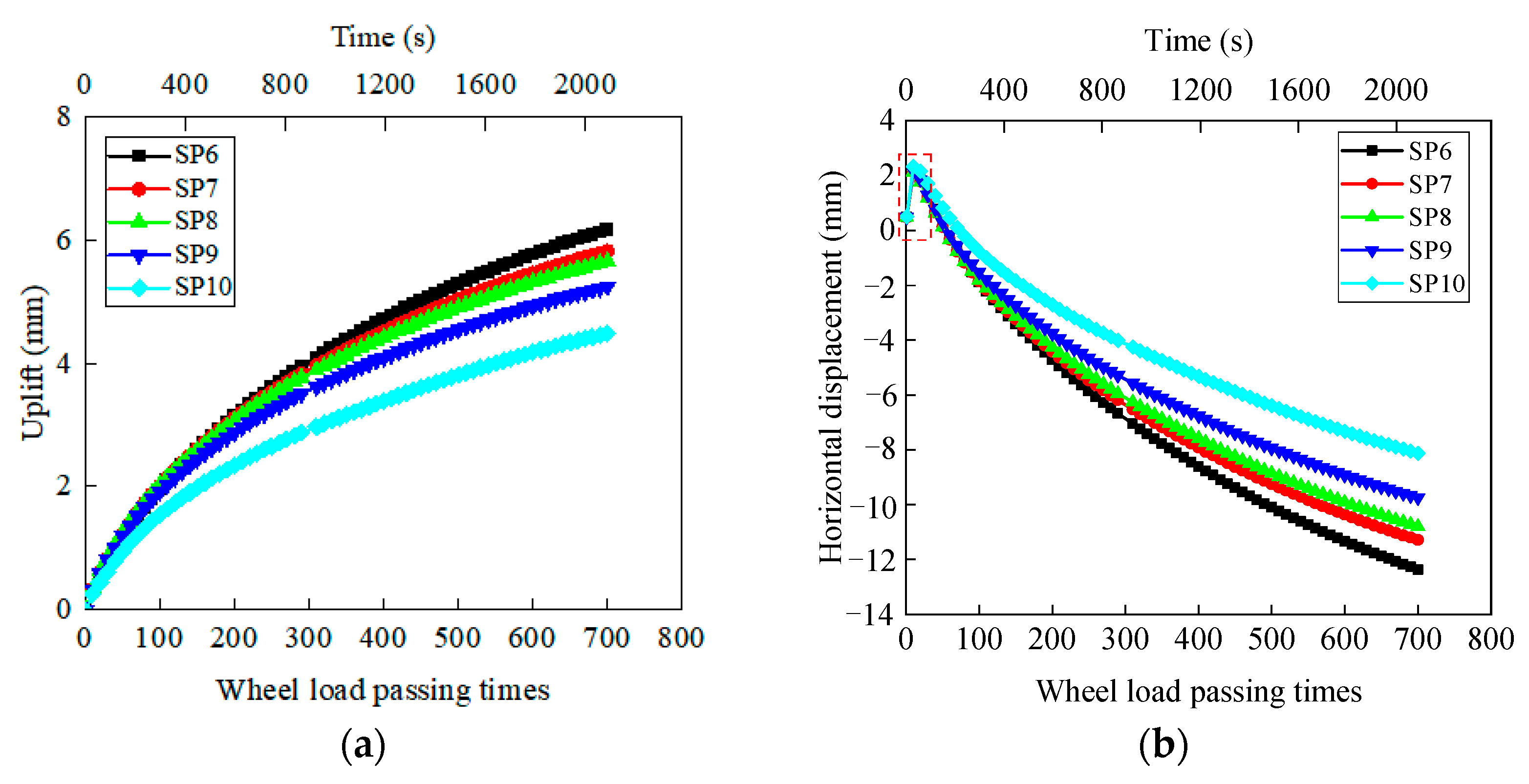
4.2.1. Deformation of Steel Corrugated Pipe
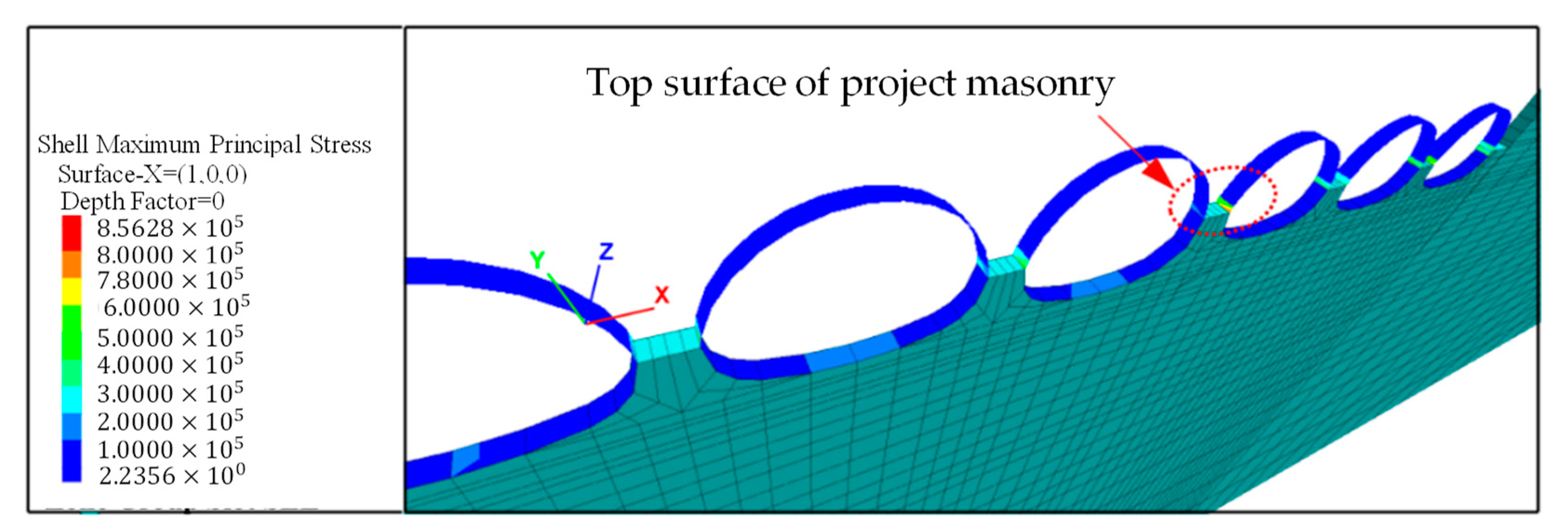
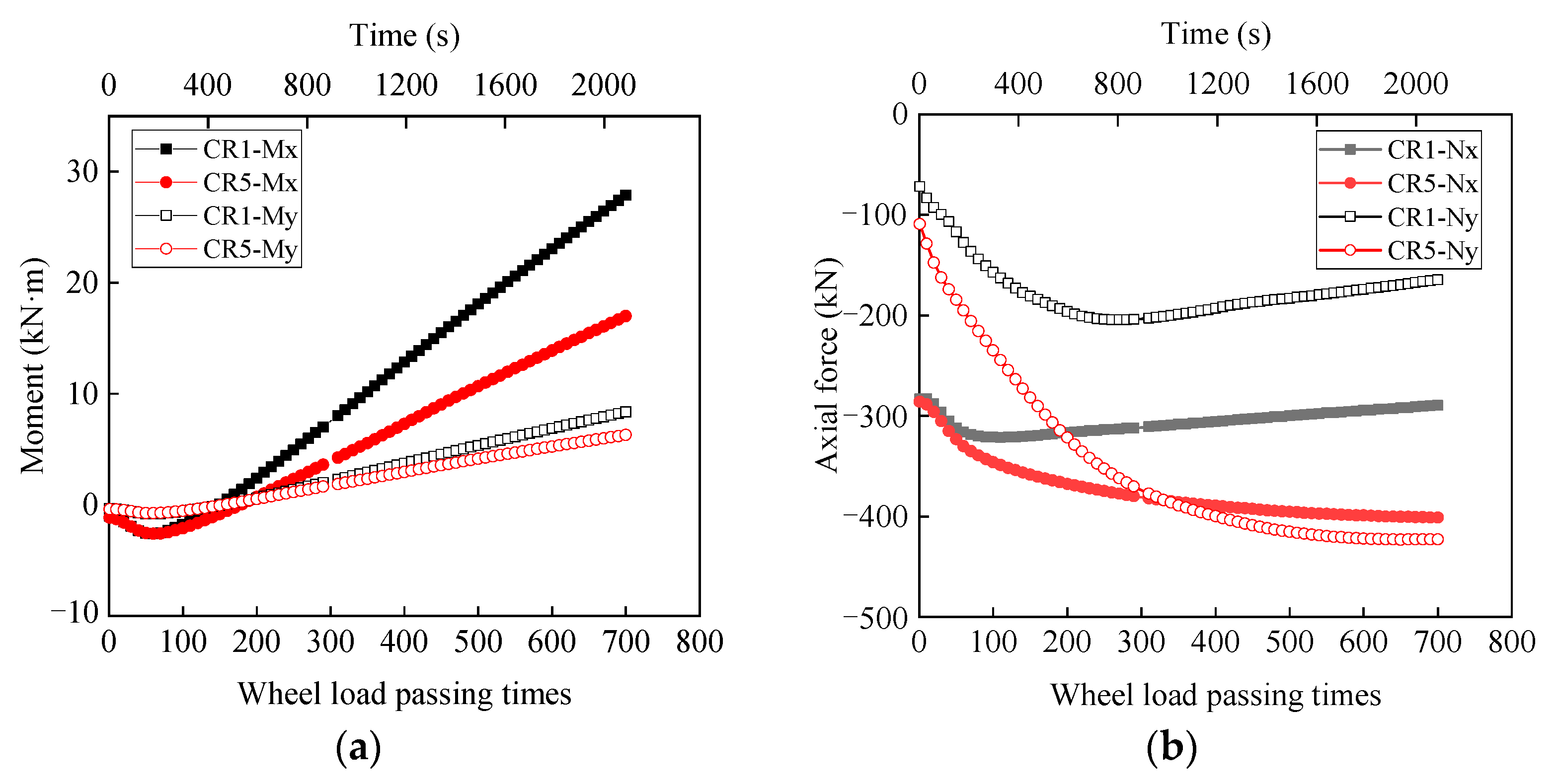
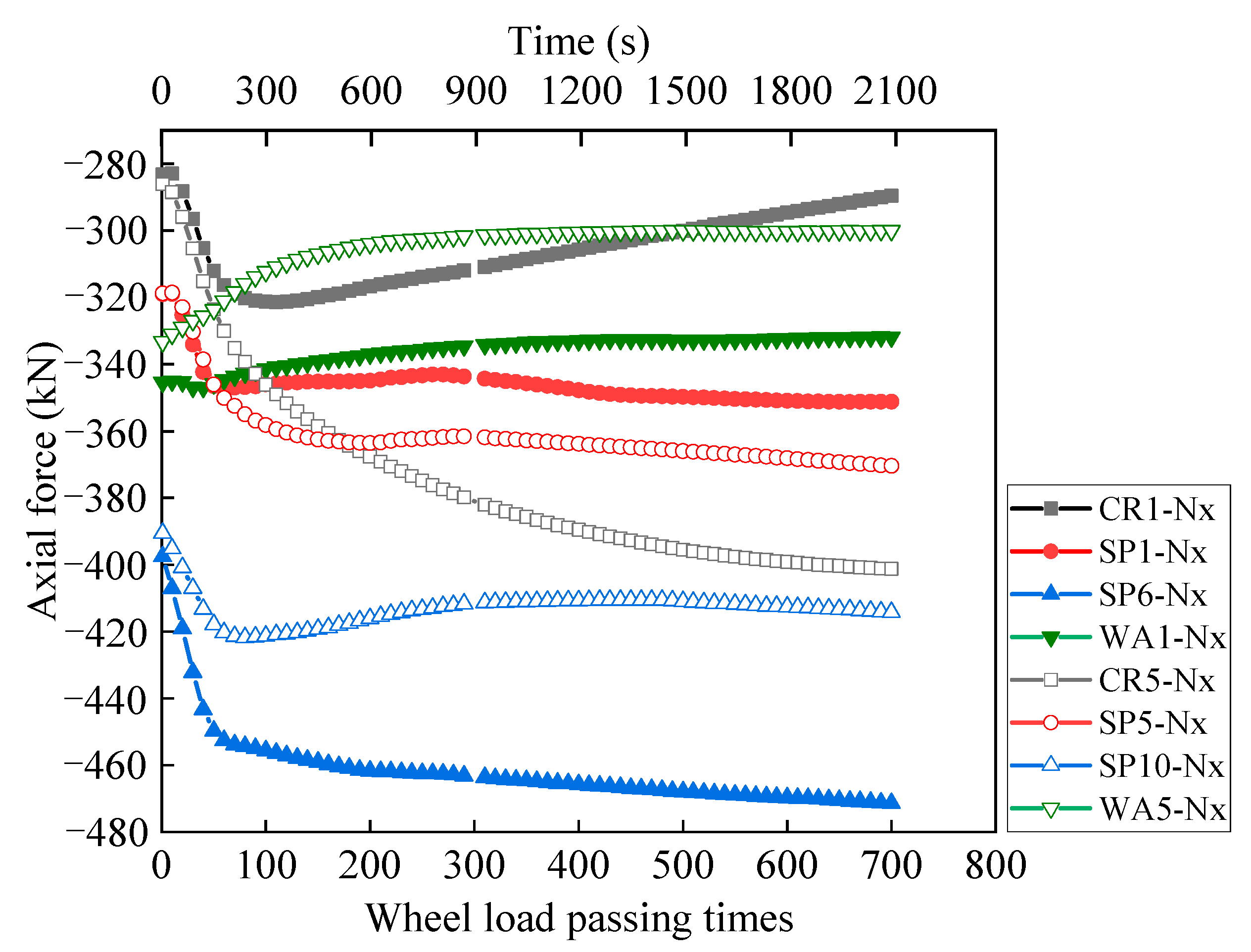
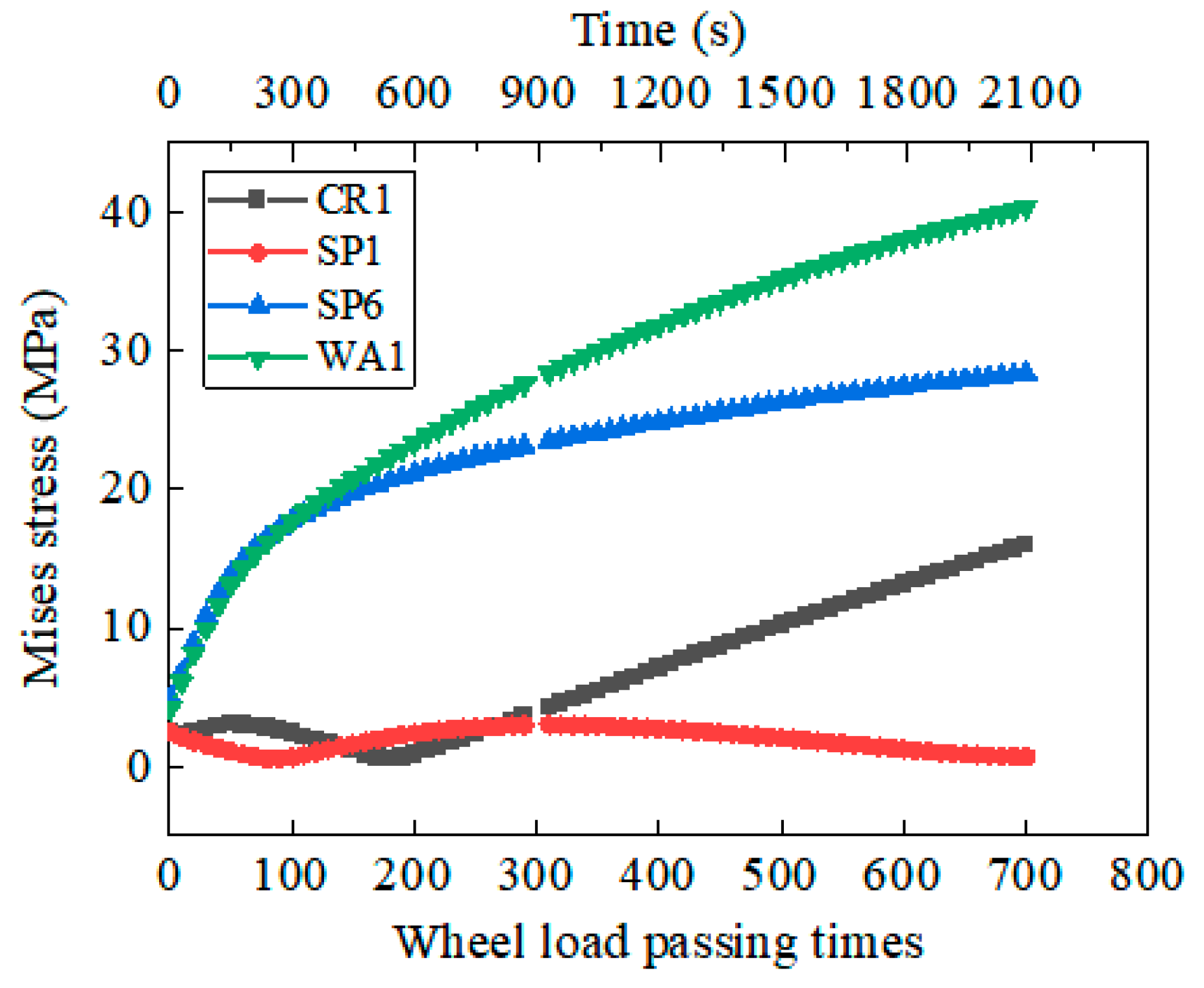
4.2.2. Internal Force of Steel Corrugated Pipe Structure
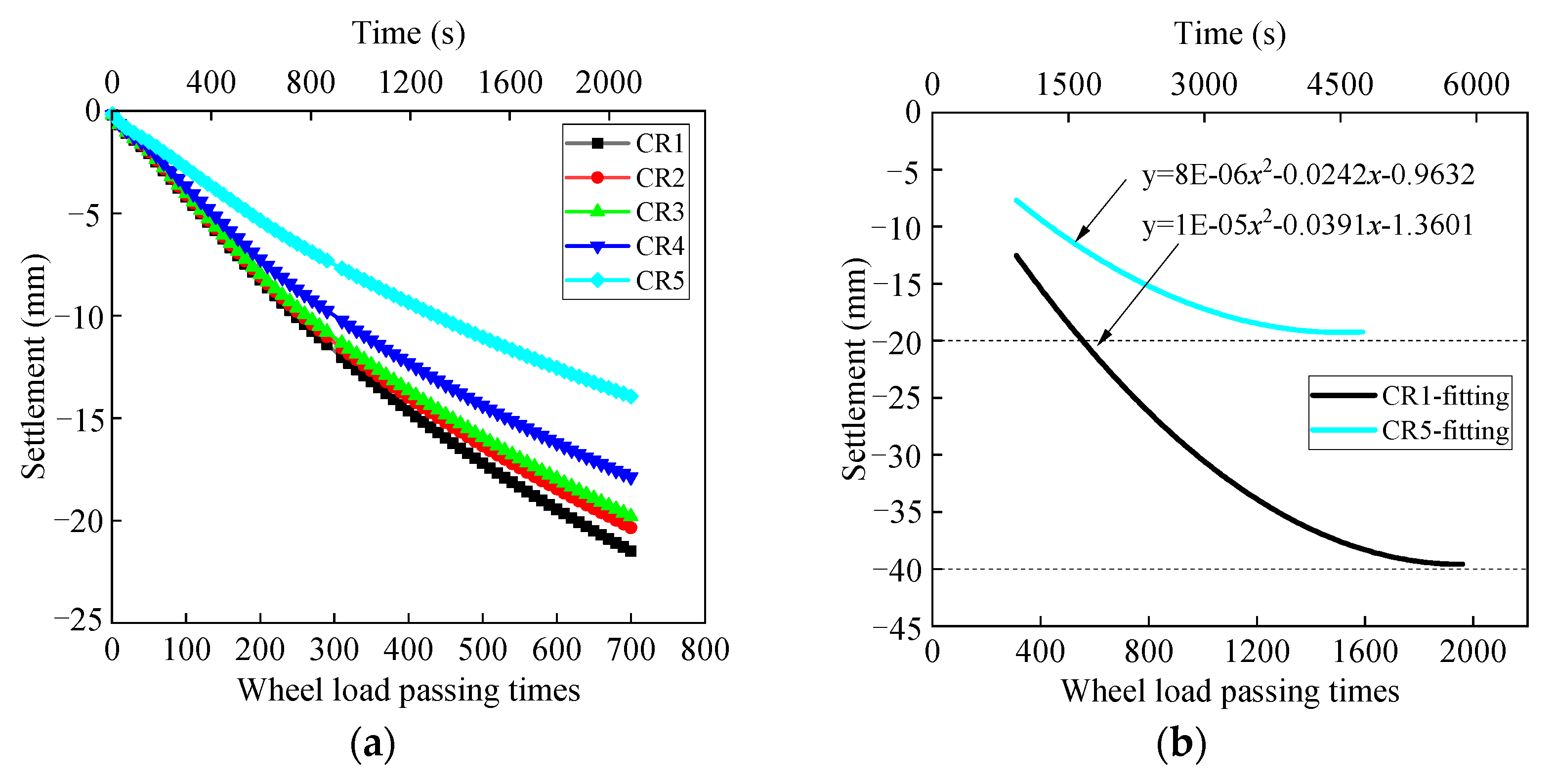
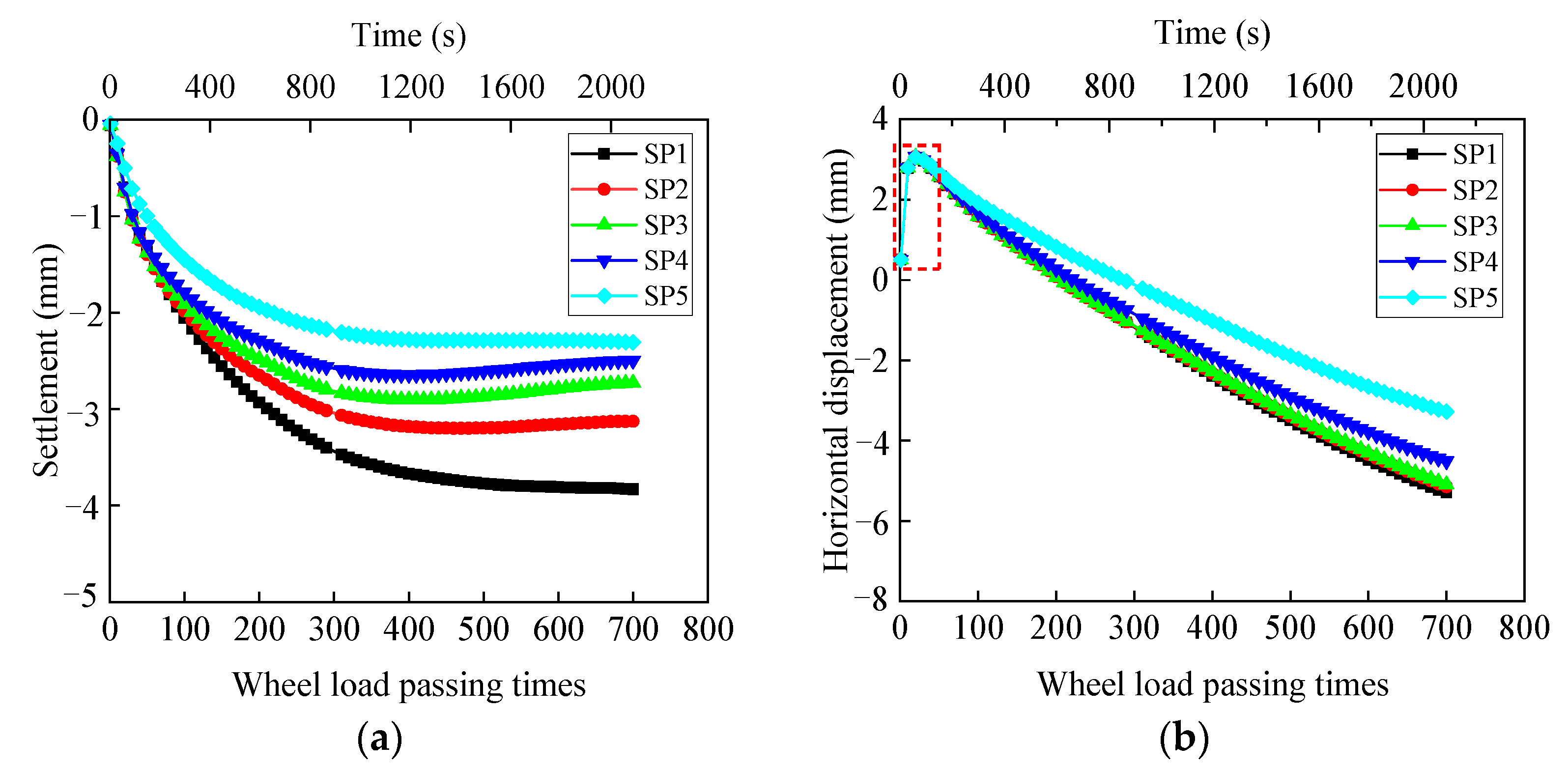
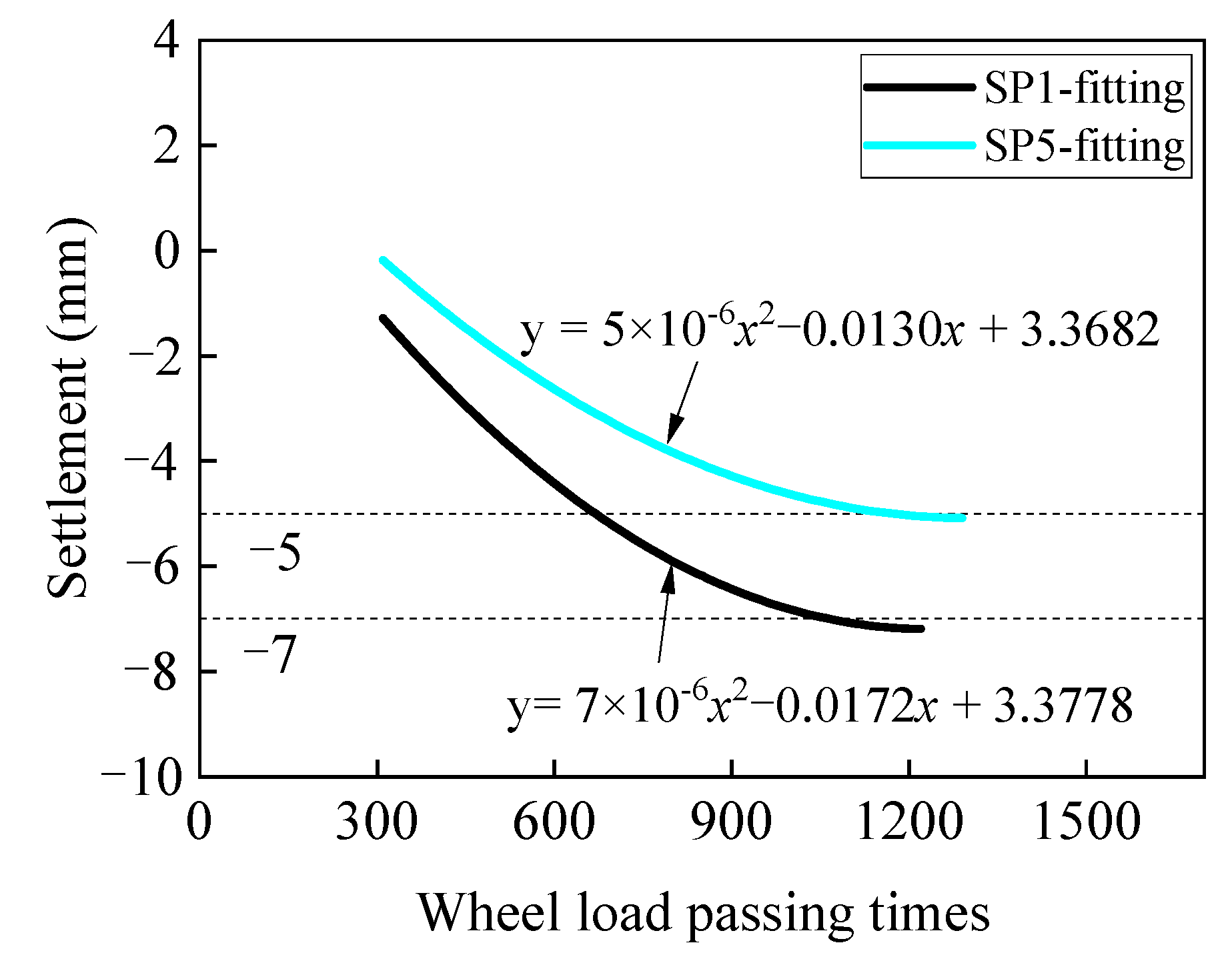
4.2.3. Settlement of Pavement of Steel Corrugated Pipe Arch Culvert
5. Conclusions
- (1)
- After construction, due to the influence of filling thickness, the settlement of the east side of the arch culvert is larger. The maximum settlement of the soil in the arch culvert area is at the junction of the two different arch culverts. The different structure sizes have caused the soil to be discontinuous and uneven in space, and the response to the load is greater. The maximum vertical deformation of the structure appears at the vault, and the arch waist is prone to stress concentration. Therefore, the vault and haunch need to be considered in the design stage.
- (2)
- The stress and deformation of the structure increase rapidly with an increase in the number of times the load passes through the steel corrugated pipe arch culverts and then stabilizes rapidly. The structure can reach the cooperative state of deformation with the soil in the initial stage of arch culvert operation. However, the subgrade soil between the arch culvert and the structure itself will produce some unrecoverable deformation or internal force accumulation.
- (3)
- After structural deformation, there is a relatively constant deformation point around the pipe. The vertical deformation of the left side of the structure at this point is opposite to that on the right side. In addition, the circumferential stress transformation point appears at the arch’s shoulder of the structure. From the vault to the arch’s waist, the circumferential stress first increases gradually and then decreases gradually towards the arch’s waist after reaching its maximum at this point.
- (4)
- Although the arch’s crown had a large vertical deformation, the von Mises stress of the arch’s waist increased rapidly and was highest. Based on the fourth strength criterion, the arch’s waist is the most dangerous for structural damage. Therefore, utmost care must be taken during the design and construction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Che, H.B.; Tong, L.Y.; Liu, S.Y.; Yang, Q. Field investigation on the mechanical performance of corrugated steel utility tunnel (CSUT). J. Constr. Steel Res. 2021, 183, 106693. [Google Scholar] [CrossRef]
- Marquez, A.; Fazzini, P.G.; Otegui, J.L. Failure analysis of flexible metal hose at compressor discharge. Eng. Fail. Anal. 2009, 16, 1912–1921. [Google Scholar] [CrossRef]
- Korusiewicz, L.; Kunecki, B. Behaviour of the steel box-type culvert during backfilling. Arch. Civ. Mech. Eng. 2011, 11, 637–650. [Google Scholar] [CrossRef]
- Bian, X.C.; Tang, X.W.; Shen, W.M.; Ling, D.S.; Chen, Y.M. An Experimental Study on a Culvert Buried in Granular Soil Subjected to Vehicle Loads. Adv. Struct. Eng. 2012, 15, 1031–1040. [Google Scholar] [CrossRef]
- Beben, D. Field Performance of Corrugated Steel Plate Road Culvert under Normal Live-Load Conditions. J. Perform. Constr. Facil. 2013, 27, 807–817. [Google Scholar] [CrossRef]
- Abuhajar, O.; Newson, T.; El, N.H. Scaled physical and numerical modelling of static soil pressures on box culverts. Can. Geotech. J. 2015, 52, 1637–1648. [Google Scholar] [CrossRef]
- Beben, D. The Role of Backfill Quality on Corrugated Steel Plate Culvert Behaviour. Balt. J. Road Bridge Eng. 2017, 12, 1–11. [Google Scholar] [CrossRef]
- Wang, T.Y.; Tan, L.X.; Xie, S.Y.; Ma, B.S. Development and applications of common utility tunnels in China. Tunn. Undergr. Space Technol. 2018, 76, 92–106. [Google Scholar] [CrossRef]
- Yue, F.; Liu, B.W.; Zhu, B. Shaking table investigations on seismic performance of prefabricated corrugated steel utility tunnels. Tunn. Undergr. Space Technol. 2020, 105, 103579. [Google Scholar] [CrossRef]
- Kells, J.A. Hydraulic performance of damaged-end corrugated steel pipe culverts. Can. J. Civ. Eng. 2008, 35, 918–924. [Google Scholar] [CrossRef]
- Katona, M.G. Improved Methods for Simulating Live Loads for Two-Dimensional Structural Analysis of Buried Culverts. Transp. Res. Rec. 2019, 2673, 449–462. [Google Scholar] [CrossRef]
- Liu, B.D.; Sun, H.B.; Xu, W.B.; Shi, Y.F.; Zhang, B.C.; Yao, M.M. Research on the Law of Stress Development Along Backfilling Process Between Crest and Valley of Buried Corrugated Steel Pipe Culverts. Int. J. Steel Struct. 2021, 21, 142–153. [Google Scholar] [CrossRef]
- Sezen, H.; Yeau, K.Y.; Fox, P.J. In-Situ load testing of corrugated steel pipe-arch culverts. J. Perform. Constr. Facil. 2008, 22, 245–252. [Google Scholar] [CrossRef]
- Tehrani, A.D.; Kouchesfehani, Z.K.; Chimauriya, H.R.; Raut, S.; Najafi, M.; Yu, X.B. Structural evaluation of invert-cut circular and arch shape corrugated steel pipes through laboratory testing. Can. J. Civ. Eng. 2021, 48, 187–201. [Google Scholar] [CrossRef]
- Yeau, K.Y.; Sezen, H.; Fox, P.J. Simulation of Behavior of In-Service Metal Culverts. J. Pipeline Syst. Eng. Pract. 2014, 5, 04013016. [Google Scholar] [CrossRef]
- Chaallal, O.; Arockiasamy, M.; Godat, A. Numerical Finite-Element Investigation of the Parameters Influencing the Behavior of Flexible Pipes for Culverts and Storm Sewers under Truck Load. J. Pipeline Syst. Eng. Pract. 2015, 6, 04014015. [Google Scholar] [CrossRef]
- Hwang, J.H.; Kikumoto, M.; Kishida, K.; Kimura, M. Dynamic stability of multi-arch culvert tunnel using 3-D FEM. Tunn. Undergr. Space Technol. 2006, 21, 384. [Google Scholar] [CrossRef]
- Sawamura, Y.; Kishida, K.; Kimura, M. Centrifuge Model Test and FEM Analysis of Dynamic Interactive Behavior between Embankments and Installed Culverts in Multiarch Culvert Embankments. Int. J. Geomech. 2015, 15, 04014050. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, B.D.; Meng, L.W. Structural behavior and soil arching state of underground corrugated steel utility tunnel. J. Constr. Steel Res. 2023, 203, 107798. [Google Scholar] [CrossRef]
- JTGB01-2014; Technical Standard of Highway Engineering. China Communications Press Co., Ltd.: Beijing, China, 2014.
- Wadi, A.; Pettersson, L.; Karoumi, R. Flexible culverts in sloping terrain: Numerical simulation of soil loading effects. Eng. Struct. 2015, 101, 111–124. [Google Scholar] [CrossRef]
- Yang, W.; Hussein, M.F.M.; Marshall, A.M. Centrifuge and numerical modelling of ground-borne vibration from an underground tunnel. Soil Dyn. Earthq. Eng. 2013, 51, 23–34. [Google Scholar] [CrossRef]
- Uddin, K.; Balasubramaniam, A.S.; Bergado, D.T. Engineering behavior of cement-treated Bangkok soft clay. Geotech. Eng. 1997, 28, 89–119. [Google Scholar]
- Lee, F.H.; Lee, Y.; Chew, S.H.; Yong, K.Y. Strength and modulus of marine clay-cement mixes. J. Geotech. Geoenviron. Eng. 2005, 131, 178–186. [Google Scholar] [CrossRef]
- Lorenzo, G.A.; Bergado, D.T. Fundamental Characteristics of Cement-Admixed Clay in Deep Mixing. J. Mater. Civ. Eng. 2006, 18, 161–174. [Google Scholar] [CrossRef]
- Ren, R.B.; Geng, L.T.; Qi, W.Y. Analysis of the Dynamic Response for Saturated Asphalt Pavement under Moving Vehicle Loads by Three-Dimensional Finite Element Method. Appl. Mech. Mater. 2011, 97, 305–310. [Google Scholar] [CrossRef]
- Kuhlmeyer, R.L.; Lysmer, J. Finite element method accuracy for wave propagation problems. ASCE Soil Mech. Found. Div. J. 1973, 99, 421–427. [Google Scholar] [CrossRef]
- Cui, X.Z. Dynamic Numerical Analysis of Antimoisture-Damage Mechanism of Permeable Pavement Base. Int. J. Geomech. 2010, 10, 230–235. [Google Scholar] [CrossRef]
- Liu, P.F.; Wang, D.W.; Otto, F.; Oeser, M. Application of semi-analytical finite element method to analyze the bearing capacity of asphalt pavements under moving loads. Front. Struct. Civ. Eng. 2018, 12, 215–221. [Google Scholar] [CrossRef]
- TB 10001-2016; Code for Design of Railway Earth Structure. China Communications Press Co., Ltd.: Beijing, China, 2016.
- Wadi, A.; Pettersson, L.; Karoumi, R. Flexible culverts in sloping terrain: Numerical simulation of avalanche load effects. Cold Reg. Sci. Technol. 2016, 124, 95–109. [Google Scholar] [CrossRef]
- DBJT45-T 014-2020; Technical Guide for Design and Construction of Highway Steel Corrugated Pipe Culverts. Guangjsih Bouxcuengh Swcigih Guauhdungh Yinsuh Dingh: Nanning, China, 2020.
- GB 50017-2017; Standard for Design of Steel Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China; China Architecture Publishing & Media Co., Ltd.: Beijing, China, 2017.
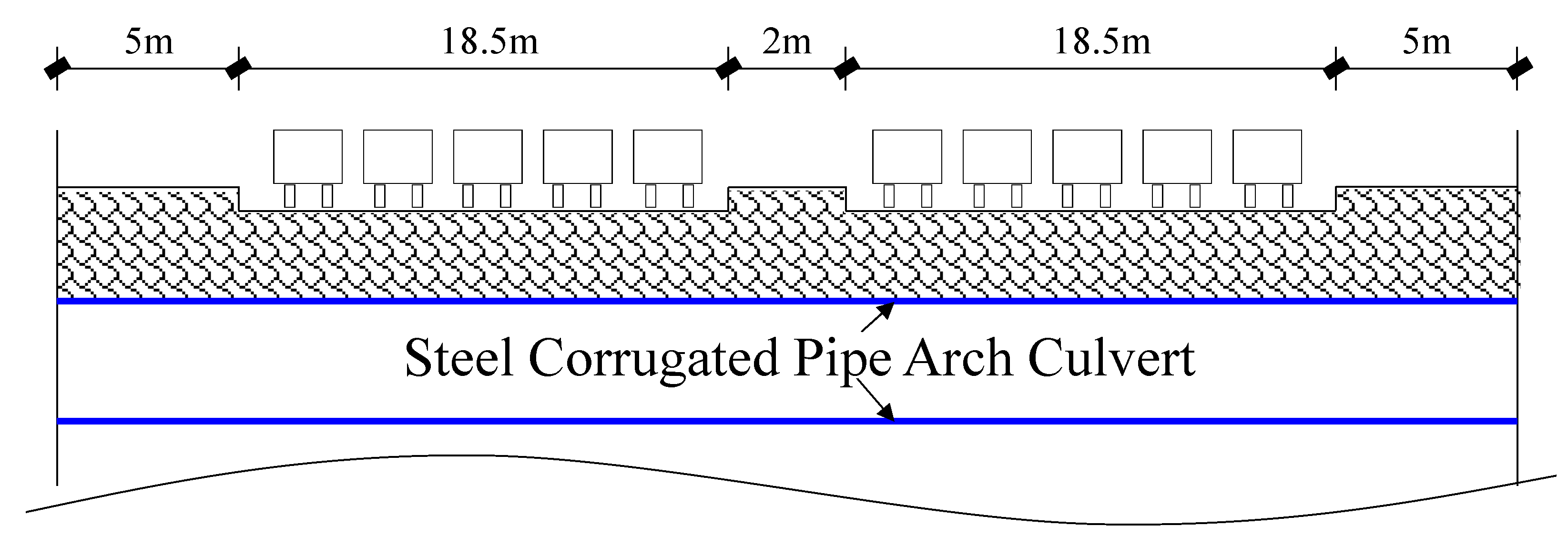
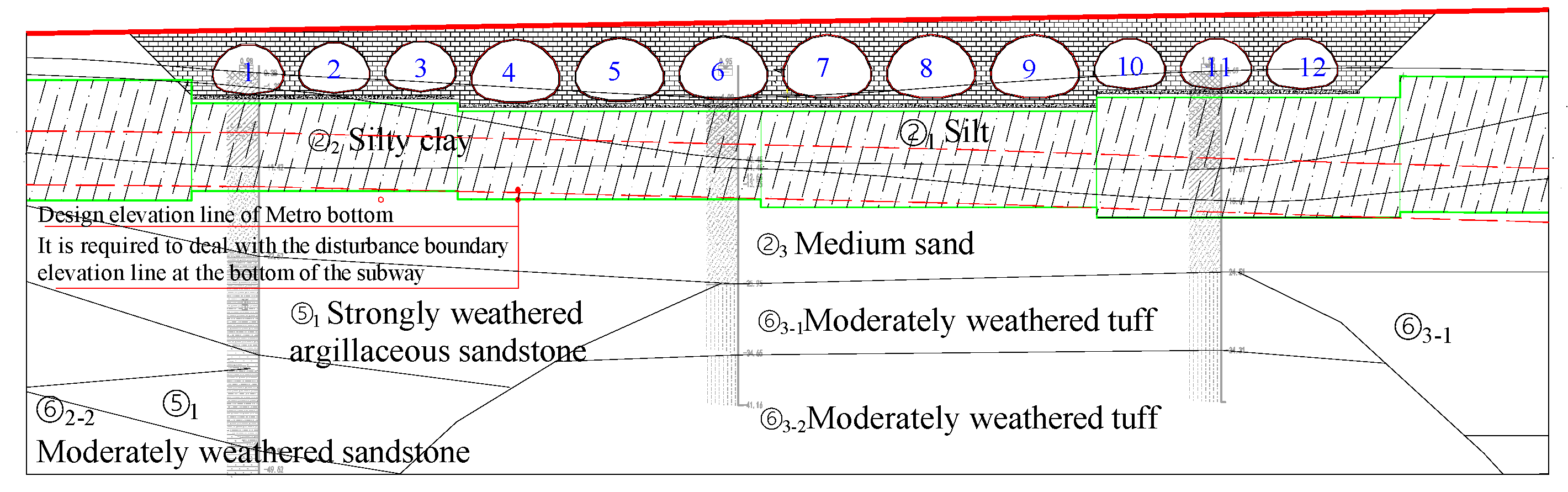
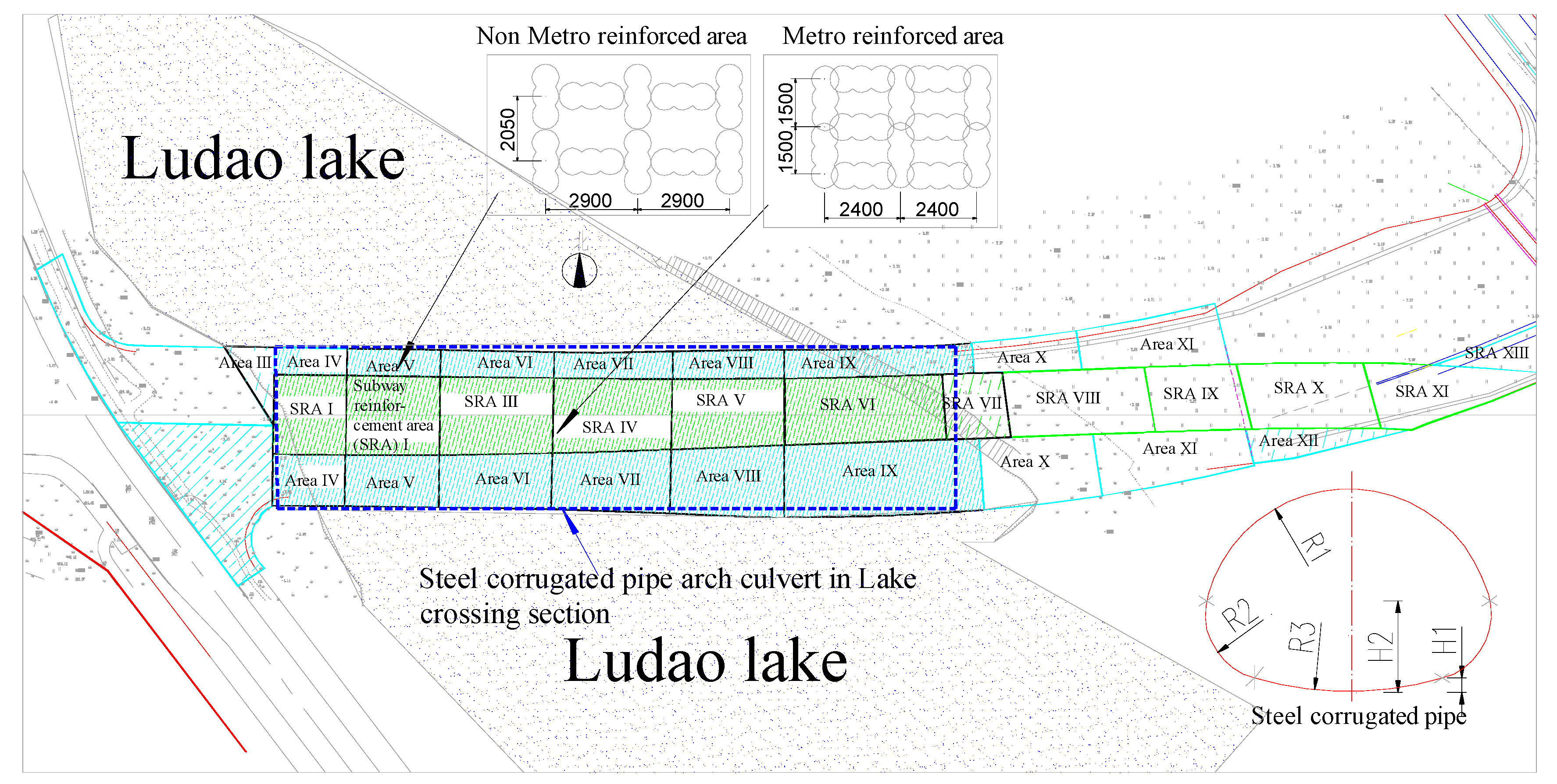

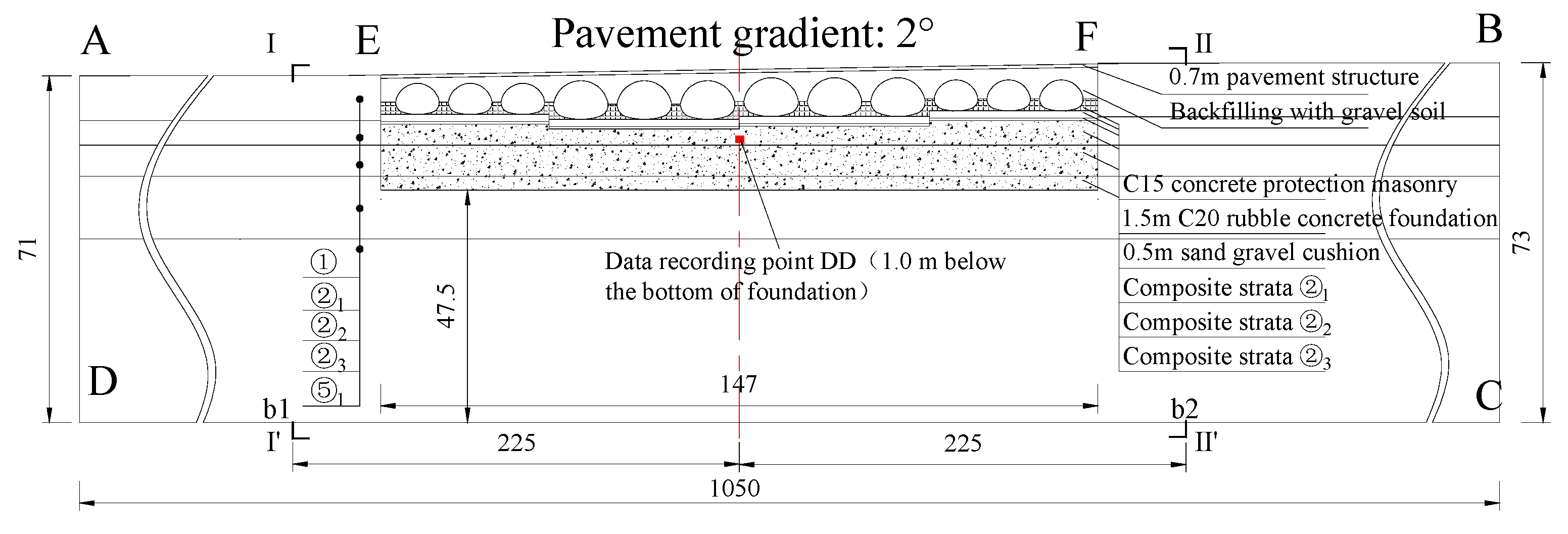


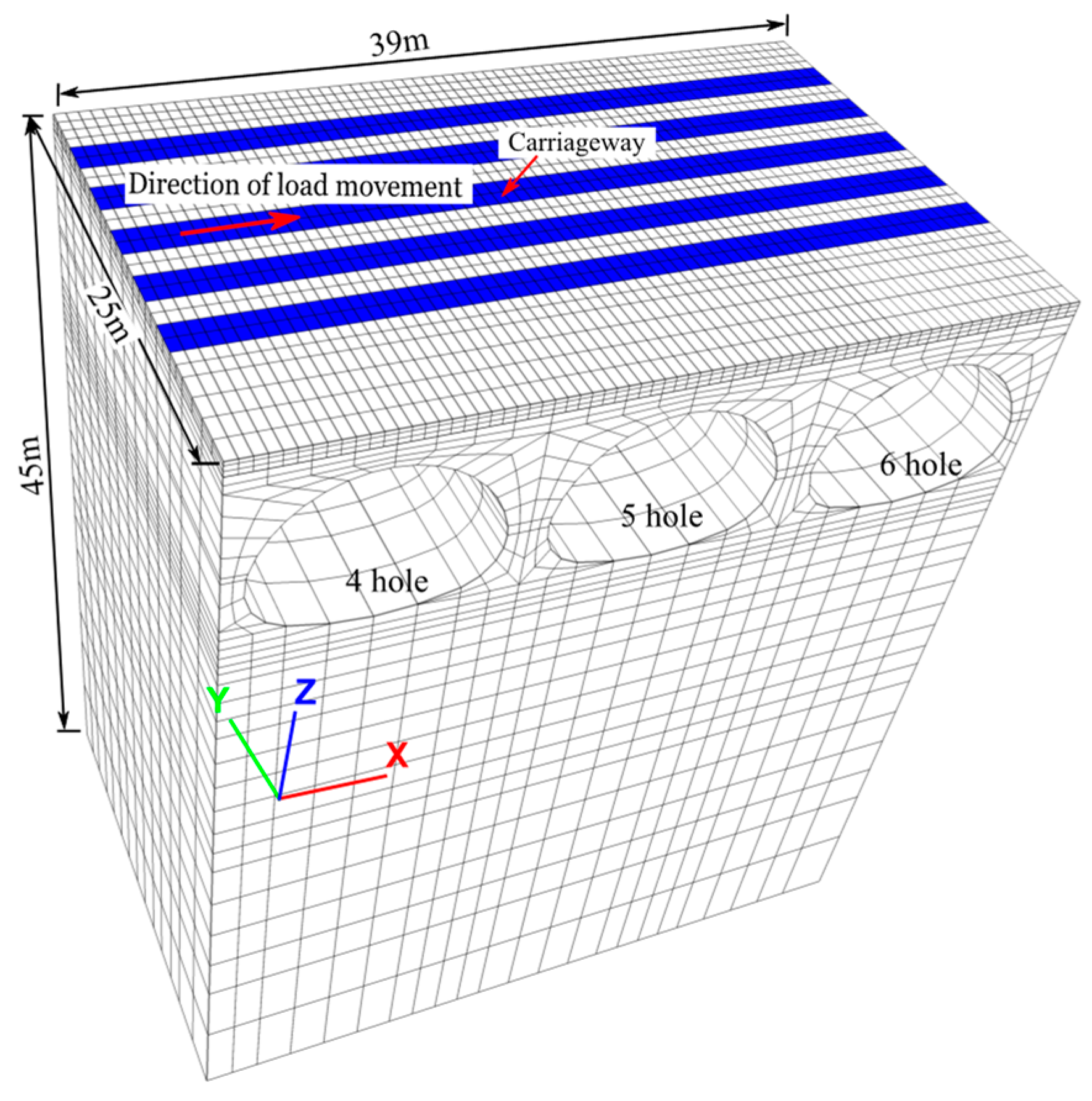
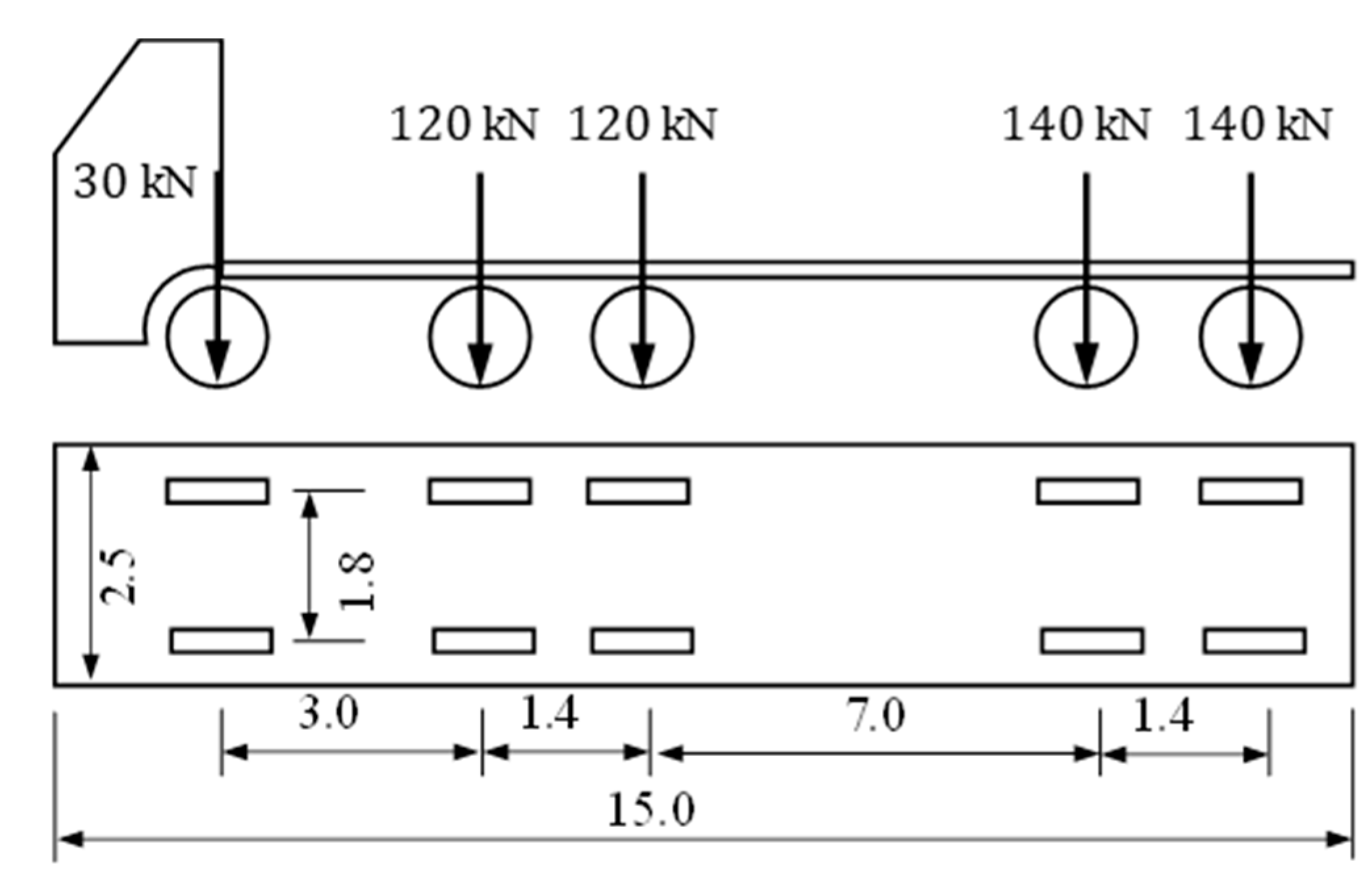
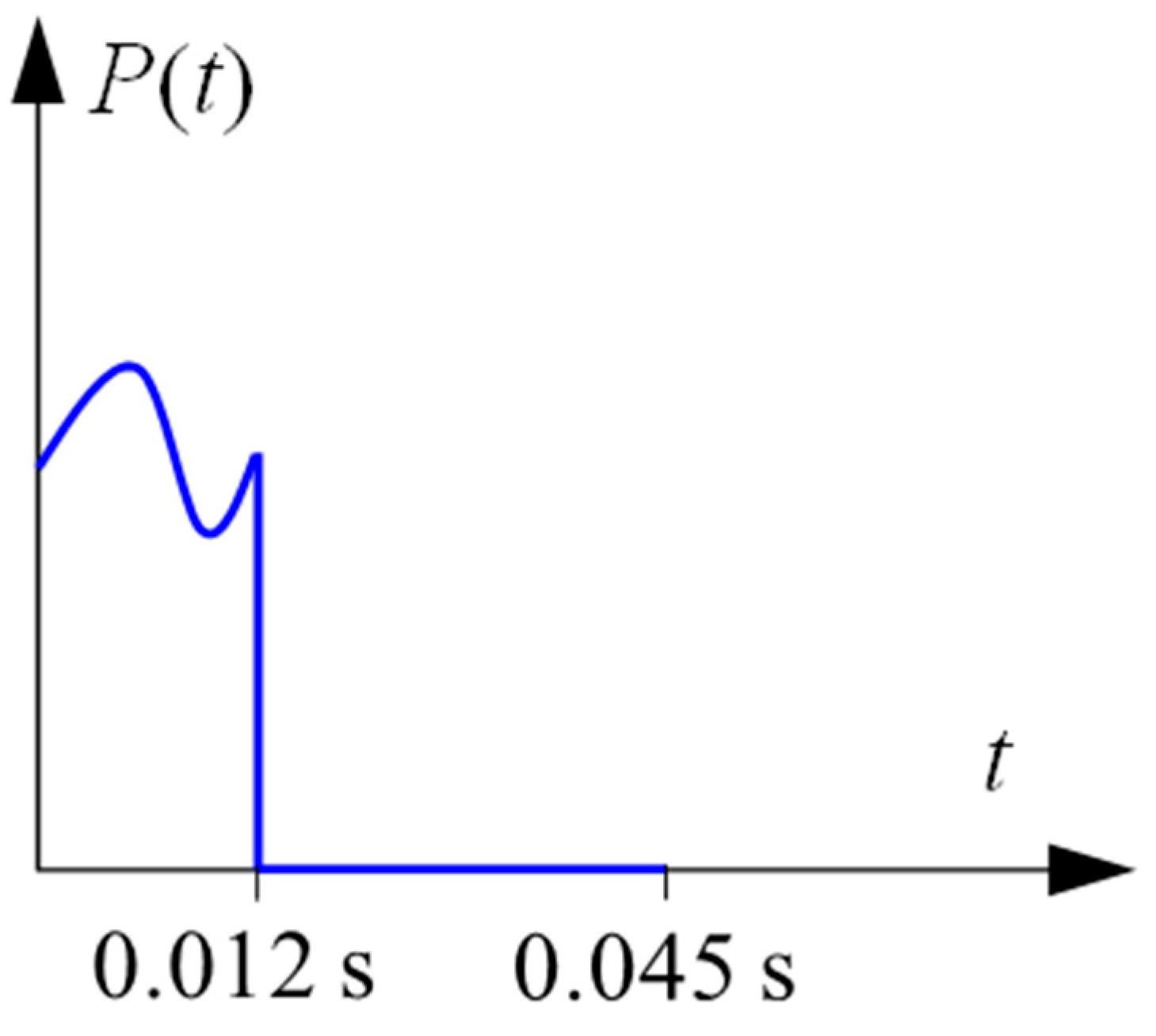
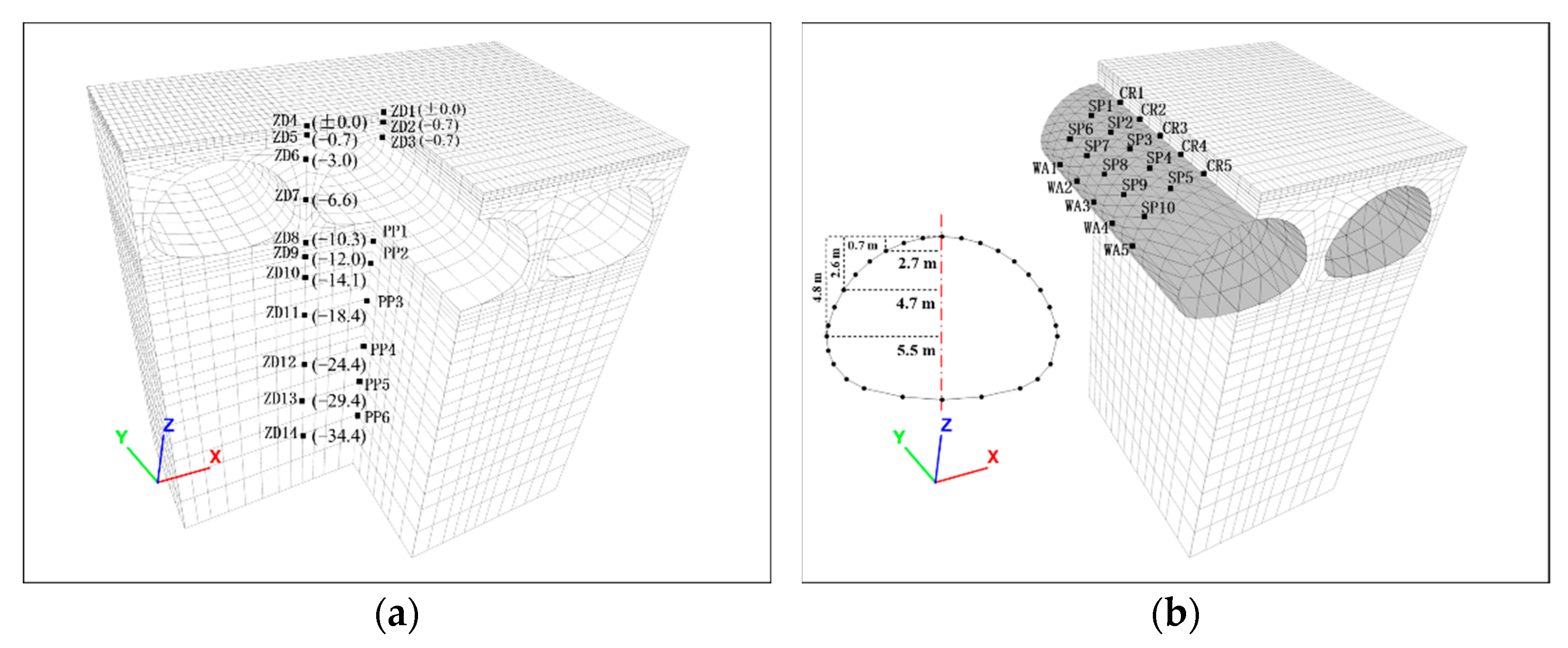

| Type | Thickness | High × Span | Steel Type | H1 | H2 | R1 | R2 | R3 |
|---|---|---|---|---|---|---|---|---|
| See Figure 3 for Parameter Meanings | ||||||||
| Other holes | 0.00775 | 6.21 × 8.7 | Q345 steel | 0.441 | 2.805 | 4.471 | 2.007 | 10.667 |
| 4–9 holes | 0.00975 | 7.77 × 11 | Q345 steel | 0.561 | 3.525 | 5.615 | 2.527 | 12.617 |
| Foundation Name (ID) | Unit Weight γ (kN/m3) | Cohesion C (kPa) | Internal Friction Angle φ (°) | Poisson Ratio v | Compression Modulus Es (MPa) | Deformation Modulus E0 (MPa) |
|---|---|---|---|---|---|---|
| Fill (①) | 18.8 | 20 | 10 | 0.4 | 3.5 | - |
| Mud (②1) | 16.5 | 6.8 | 3.4 | 0.35 | 2.4 | - |
| Silty clay (②2) | 19.7 | 24.7 | 11.2 | 0.32 | 5.7 | - |
| Medium sand (②3) | 19.2 | 0 | 30.0 | 0.25 | 15.0 | 12.0 |
| Mealy sand (②4) | 18.8 | 0 | 26.0 | 0.25 | - | 8.0 |
| Silty clay (③1) | 19.5 | 35.0 | 13.0 | 0.32 | 6.5 | 7.0 |
| Medium-coarse sand (③2) | 19.8 | 0 | 32.0 | 0.25 | - | 13.0 |
| Fully weathered shaly sand (④1) | 19.8 | 35.0 | 20.0 | 0.35 | 8.0 | 60.0 |
| Fully weathered sandstone (④2) | 20.0 | 15.0 | 35.0 | 0.35 | - | 60.0 |
| Strong weathering muddy sand (⑤1) | 21.0 | 40.0 | 25.0 | 0.28 | 12.0 | 80.0 |
| Strong weathering sand (⑤2) | 21.2 | 20.0 | 40.0 | - | - | 80.0 |
| Strong weathering tuff rock (⑤3) | 21.0 | 30.0 | 35.0 | - | - | 80.0 |
| Strata | t (m) | Es (kPa) | v | E0 (MPa) | Ei (MPa) | αi (%) | E0c (MPa) | E0m (MPa) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ar | r | Ar | r | Ar | r | ||||||
| ②1 | 5.0 | 2.4 | 0.4 | 1.1 | 490 | 72 | 59 | 353 | 287 | 338 | 275 |
| ②2 | 6.4 | 5.7 | 0.4 | 2.7 | 245 | 72 | 59 | 177 | 144 | ||
| ②3 | 2.8 | 15.0 | 0.3 | 7.0 | 945 | 72 | 59 | 682 | 556 | ||
| Strata | Dry Density ρd (g/cm3) | Cohesion C (kPa) | Internal Friction Angle φ (°) | Compression Modulus Es (MPa) | Deformation Modulus E0 (MPa) | Poisson Ratio v | Permeability Coefficient K (cm/s) | Porosity n |
|---|---|---|---|---|---|---|---|---|
| Natural strata | ||||||||
| ① | 1.60 | 20.0 | 10.0 | 3.5 | / | 0.40 | 2.0 × 10−3 | 0.33 |
| ②1 | 1.10 | 6.8 | 3.40 | 2.4 | / | 0.35 | 1.0 × 10−7 | 0.50 |
| ②2 | 1.50 | 24.7 | 11.2 | 5.7 | / | 0.32 | 6.0 × 10−5 | 0.40 |
| ②3 | 1.80 | 0.0 | 30.0 | 15.0 | 12.0 | 0.25 | 2.4 × 10−2 | 0.33 |
| ⑤1 | 1.78 | 40.0 | 25.0 | / | 80.0 | 0.28 | 1.0 × 10−3 | 0.30 |
| Composite strata | ||||||||
| ②1 | 1.28 | 209 | 20.0 | / | 287 | 0.35 | 1 × 10−7 | 0.50 |
| ②2 | 1.68 | 104 | 12.8 | / | 144 | 0.32 | 1 × 10−7 | 0.50 |
| ②3 | 1.83 | 324 | 34.0 | / | 556 | 0.25 | 1 × 10−7 | 0.50 |
| Material Type | Density ρ (g/cm3) | Cohesion C (kP) | Internal Friction Angle φ (°) | Deformation Modulus E0 (MPa) | Elastic Modulus E (GPa) | Poisson Ratio v |
|---|---|---|---|---|---|---|
| C15 concrete protects masonry | 2400 | / | / | / | 22 | 0.2 |
| C20 concrete foundation | 2400 | / | / | / | 25 | 0.2 |
| Asphalt concrete pavement | 2400 | / | / | / | 1.4 | 0.35 |
| Backfill or stratigraphic gravel soil | 1900 | 0 | 30 | 12 | 3E0 | 0.3 |
| Steel Corrugated Pipe Type | Material Density ρ (g/cm3) | Equivalent Density ρ1 (g/cm3) | Equivalent Thickness t (mm) | Elastic Modulus E (GP) | Poisson Ratio v |
|---|---|---|---|---|---|
| 4–9 holes | 7.85 | 1.411 | 70 | 206 | 0.3 |
| Other holes | 7.85 | 1.171 | 65 | 206 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, X.; Wu, X.; Shen, J.; Wu, S.; Chen, X.; Cui, H. Performance Analysis of Multiple Steel Corrugated Pipe Arch Culvert under Construction and Periodic Vehicle Load. Appl. Sci. 2023, 13, 9441. https://doi.org/10.3390/app13169441
Bao X, Wu X, Shen J, Wu S, Chen X, Cui H. Performance Analysis of Multiple Steel Corrugated Pipe Arch Culvert under Construction and Periodic Vehicle Load. Applied Sciences. 2023; 13(16):9441. https://doi.org/10.3390/app13169441
Chicago/Turabian StyleBao, Xiaohua, Xianlong Wu, Jun Shen, Shidong Wu, Xiangsheng Chen, and Hongzhi Cui. 2023. "Performance Analysis of Multiple Steel Corrugated Pipe Arch Culvert under Construction and Periodic Vehicle Load" Applied Sciences 13, no. 16: 9441. https://doi.org/10.3390/app13169441
APA StyleBao, X., Wu, X., Shen, J., Wu, S., Chen, X., & Cui, H. (2023). Performance Analysis of Multiple Steel Corrugated Pipe Arch Culvert under Construction and Periodic Vehicle Load. Applied Sciences, 13(16), 9441. https://doi.org/10.3390/app13169441







