Teleportation-Based Error Correction Protocol of Time–Frequency Qubit States

Abstract

We present a linear optical protocol for teleporting and correcting both temporal and frequency errors in two time–frequency qubit states. The first state is the frequency (or time-of-arrival) cat qubit, which is a single photon in a superposition of two frequencies (or time-of-arrival), while the second is the time–frequency Gottesman–Kitaev–Preskill (GKP) state, which is a single photon with a frequency comb structure. The proposed optical scheme could be valuable for reducing the error rate in quantum communication protocols involving one of these qubits.

1. Introduction

Quantum information harnesses the foundational principles of quantum mechanics, such as superposition and entanglement, to manipulate and transmit data in fundamentally novel ways. For instance, quantum entanglement establishes correlations between distant particles, a phenomenon exploited in quantum communication for secure key distribution and teleportation protocols. The pertinence of single photons in encoding quantum information emanates from their unique attributes, including minimal susceptibility to environmental decoherence, and the fact that single photons travel at the speed of light.

Quantum information can be encoded in various degrees of freedom of single photons, which can be described by either discrete or continuous variables (CV). Frequency (or energy) and time of arrival are natural pairs of conjugate quantum continuous variables in the single photon subspace, along with the transverse position and momentum degrees of freedom [1,2,3,4]. Discretizing the frequency or time of arrival into temporal or frequency bins, or performing the mode decomposition of the continuous variable distribution of the single photon, can be experimentally motivated due to the finite resolution of detection devices or specific requirements of a quantum protocol, such as in quantum metrology for super-resolution [5]. We should stress that in any dimensional single-photon encoding, photon losses do not correspond to a logical error. The second way of encoding information is through particle number sensitive encoding, which can be used to define physical systems with either discrete or continuous variables. In this encoding, CV corresponds to the quadratures of the electromagnetic field, i.e., the amplitude and phase of the quantum field, in a particular mode. With the particle-sensitive encoding, photon loss corresponds to a logical error. Mathematically, the quadrature of an electromagnetic field in a given mode can be treated as the continuous degree of freedom of a single photon [4], as long as an auxiliary discrete mode is occupied by only one single photon.

Error correction code for continuous variables encoding is defined by discretizing them. Three bosonic qubit codes have been studied, such as the cat code [6,7,8], Gottesman, Kitaev, and Preskill (GKP) code [9,10,11,12,13,14,15] and the binomial code [16,17]. Cat and GKP codes are candidates for achieving universal quantum computation; see [7,18,19,20]. GKP code could be employed for building quantum repeaters [21], and for sensing applications [22,23]. The mathematical analogy between time–frequency and quadrature CV allows defining time–frequency qubit states, called the time–frequency cat state [2,24] and time–frequency GKP state [1,2,25]. Both of these types of code are ways to discretize time–frequency continuous variables at the single photon level to define a qubit. CV or time–frequency CV codes possess an equivalent mathematical structure; they are common eigenvectors of non-commuting displacements operators [1] and they are thus designed to be robust against a small shift in one continuous variable (cat state) and the two canonically conjugated ones (GKP state).

In this paper, we start by reminding the reader of the mathematical structure of the time–frequency cat and GKP codes and discuss the temporal and frequency errors that they were designed to be robust against. From the standard method for quantum error correction for quadrature GKP states [26], we propose the analogous protocol to perform correcting the time–frequency GKP state. In such a quantum error correction scheme, a temporally and spectrally broadened (corresponding to errors in this encoding) time–frequency GKP state is first entangled with a less noisy ancilla GKP, and finally temporal- or frequency-resolved detection is performed on the ancilla state. The resulting time–frequency GKP state is either corrected in the time (resp. frequency) if the frequency (resp. temporal) resolved measurement has been performed. However, the creation of the frequency entanglement structure for single photon encoding is difficult to realize experimentally with the current technology, as it requires performing a frequency entanglement operation between two single photons [27]. Therefore, inspired by the teleportation-based error correction protocol for quadrature encoding [28,29], we develop a teleportation-based error correction protocol for frequency qubit states that uses only linear optical elements and allows the simultaneous correction of both time and frequency variables. In the teleportation-based error correction protocol, the noisy frequency qubit state is entangled with a less noisy frequency entangled state. One of the members of the entangled pair is combined into a balanced beam splitter with the noisy single-photon state, and then Bell measurements are performed. The error correction is performed naturally since the remaining frequency single-photon state belongs to the entangled state that was less noisy in the time and frequency domains compared to the initial state. Since the protocol requires the use of a Bell measurement, we also describe how to experimentally implement such a measurement for the two types of frequency qubits by using Mach–Zehnder interferometry. The proposed protocol is intrinsically probabilistic and consists of the teleportation of non-orthogonal states [30], instead of orthogonal ones [31,32]. The non-orthogonality of the state reduces the efficiency of the teleportation-based error correction protocol. For that reason, we mention that photon number-resolving detectors can help increase the probability of success of the protocol by reducing the number of rejected measurement events. Finally, the advantage of discretizing a grid state into a qubit state by combining the even and odd peaks, rather than considering the state as a time–frequency qudit, is convenient because it simplifies the optical implementation of grid state manipulations.

The paper is organized as follows. In Section 2, we provide a reminder of the definition of the time–frequency cat and GKP states and the reason for the experimental difficulty behind the natural error correction scheme of the time–frequency GKP states which requires frequency entanglement gates. In Section 3, we explain the optical equivalent of the polarizing beam splitter, a Mach–Zehnder interferometer, which allows separating spatially the two logical states of the time–frequency cat and GKP qubits. Such an interferometer is crucial for implementing Bell’s measurement in the time–frequency degree of freedom. In Section 4, we present a teleportation-based error correction protocol for the time–frequency GKP state, which makes use of Bell’s measurement. The protocol is intrinsically probabilistic and can be achieved with the current experimental devices. Finally, in Section 5, we summarize our results and present new perspectives.

2. Time–Frequency Qubit States

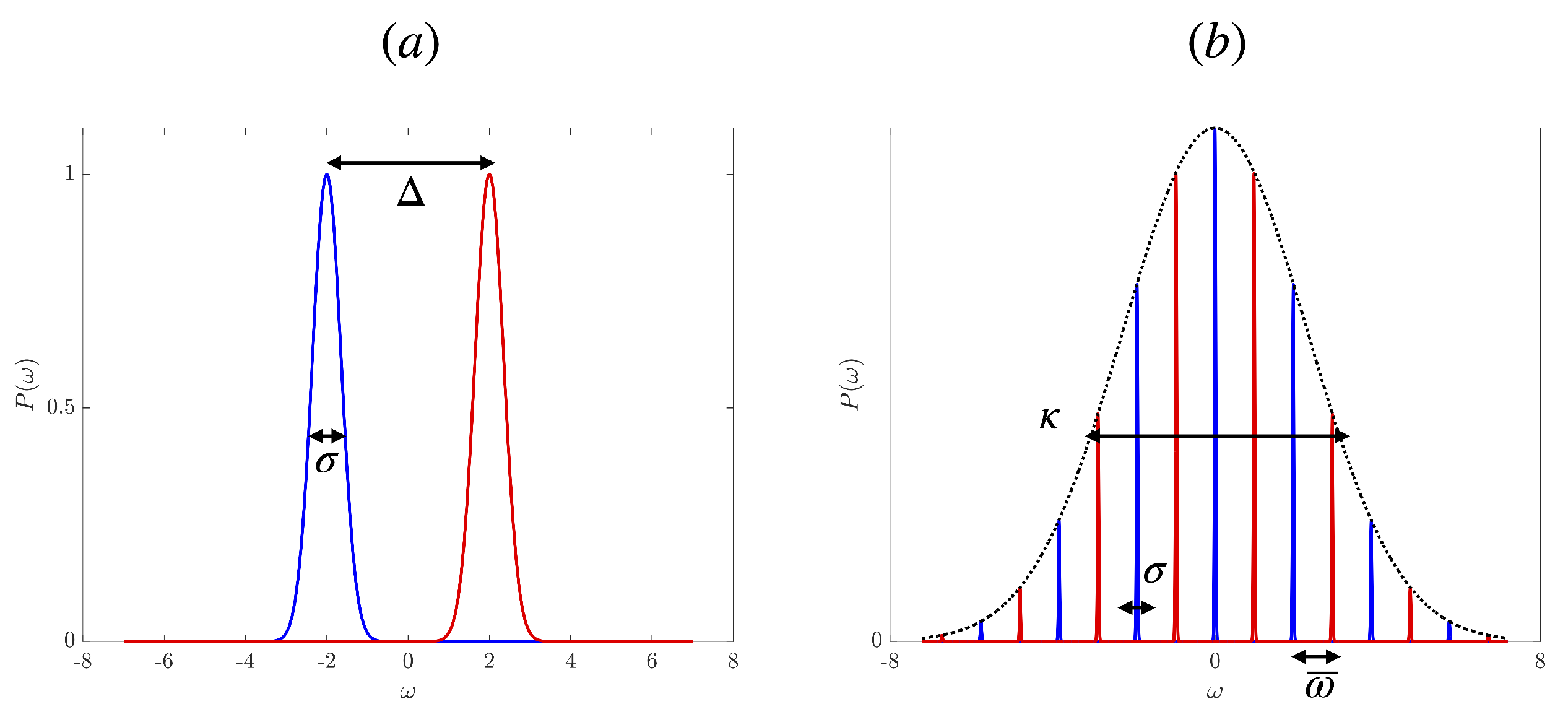
2.1. Time–Frequency Cat State

We denote $\left|\Omega \right.〉$ as the vacuum state. A single-photon state at frequency $\omega$ in the spatial port a is denoted as ${\left|\omega \right.〉}_a={\hat{a}}^{†}\left(\omega \right)\left|\Omega \right.〉$. The frequency cat state as introduced in [24] is defined as the superposition of a single photon into two different frequency Gaussian distributions (see Figure 1a):

$$\left|\psi \right.〉=N_{\alpha \beta }(\alpha {\left|{\omega }_1\right.〉}_a+\beta {\left|{\omega }_2\right.〉}_a)=N_{\alpha \beta }(\alpha {\left|0\right.〉}_a+\beta {\left|1\right.〉}_a),$$

(1)

where ${\left|{\omega }_1\right.〉}_a=\frac{1}{\sqrt{2\pi {\sigma }^2}}\mathit{\int }d\omega \exp (-{(\omega -{\omega }_1)}^2/2{\sigma }^2){\left|\omega \right.〉}_a$, $\sigma$ is the frequency width of the spectral Gaussian distribution and the normalization of the state is given by $1=N_{\alpha \beta }^2{\left(\right|\alpha |}^2+{\left|\beta \right|}^2+2\mathrm{Re}\left(\alpha {\beta }^{\ast }\right)e^{-{({\omega }_1-{\omega }_2)}^2/2{\sigma }^2})$. This is a non-orthogonal qubit state, as their overlap is ${}_a{\langle 0|1\rangle }_a=\exp (-{({\omega }_1-{\omega }_2)}^2/2{\sigma }^2)$. Experimental proposals for manipulating such a state were proposed in [33,34] with pulse shapers, and electro-optic modulators were used in the cascade. The results showed an operation fidelity close to 100%, but the successive optical elements drastically decreased the probability of single photon detection. The wave function of the time of the cat state is defined as

$$\left|{\psi }_t\right.〉=N_{\alpha \beta }(\alpha {\left|t_1\right.〉}_a+\beta {\left|t_2\right.〉}_a).$$

(2)

Note that for avoiding having a normalization constant depending on the coefficients $\alpha ,\beta$, and writing the wave function on an orthogonal basis, we can employ the Gram–Schmidt decomposition procedure. The normalized orthogonal basis $\left|a\right.〉$ and $\left|b\right.〉$ can be written as

$$\left|a\right.〉=\left|0\right.〉,\left|b\right.〉=N[\left|1\right.〉-\langle 0|1\rangle \left|0\right.〉],$$

(3)

where $N=1/\sqrt{1-r^2}$ and $r=|\langle 0|1\rangle |$. The frequency Equation (1) (or time cat state Equation (2)) can be written in the orthogonal basis as

$$\left|\psi \right.〉=(\alpha +\beta \langle 0|1\rangle )\left|a\right.〉+\frac{\beta }{N}\left|b\right.〉,$$

(4)

where we have now ${\left|(\alpha +\beta \langle 0|1\rangle )\right|}^2+{\left|\frac{\beta }{N}\right|}^2=1$.

The frequency entangled cat state, an EPR state, can be written as

$$\begin{array}{c}\hfill \left|{\varphi }^{\pm }\right.〉=N_{\mathrm{EPR}}({\left|{\omega }_1{\omega }_1\right.〉}_{ab}\pm {\left|{\omega }_2{\omega }_2\right.〉}_{ab})\end{array}$$

(5)

$$\begin{array}{c}\hfill \left|{\psi }^{\pm }\right.〉=N_{\mathrm{EPR}}({\left|{\omega }_1{\omega }_2\right.〉}_{ab}\pm {\left|{\omega }_2{\omega }_1\right.〉}_{ab})\end{array}$$

(6)

where $N_{\mathrm{EPR}}^2(2+2e^{-{({\omega }_1-{\omega }_2)}^2/2{\sigma }^2})=1$. When ${\omega }_1-{\omega }_2\gg \sigma$, we recover the normalization of an EPR state composed of orthogonal qubits $N_{\mathrm{EPR}}=1/\sqrt{2}$. The frequency cat state can be produced by an integrated optical wave guide [35] and bulk system [36]. The wave function of a temporal entangled EPR state Equation (5) has the same mathematical structure, and such a quantum state can be produced by quantum dots, for instance [37]. This type of quantum state has potential applications in quantum communications [38].

2.2. Time–Frequency GKP State

We define a frequency lattice of period $\overline{\omega }$. Centered on each of these intervals, we define the ideal time–frequency GKP state as the following frequency comb at the single photon level:

$${\left|{\overline{\mu }}_{\omega }\right.〉}_a=\sum _{n\in \mathbb{Z}}{\left|(2n+\mu )\overline{\omega }\right.〉}_a$$

(7)

where $\mu =0,1$ index the two logical states. Note that the equal weight superposition of the zero and the one logical time–frequency GKP states in the frequency domain are the zero and one in the temporal domain:

$$\begin{array}{c}\hfill {\left|{\overline{+}}_{\omega }\right.〉}_a=\frac{1}{\sqrt{2}}({\left|{\overline{0}}_{\omega }\right.〉}_a+{\left|{\overline{1}}_{\omega }\right.〉}_a)={\left|{\overline{0}}_t\right.〉}_a\end{array}$$

(8)

$$\begin{array}{c}\hfill {\left|{\overline{-}}_{\omega }\right.〉}_a=\frac{1}{\sqrt{2}}({\left|{\overline{0}}_{\omega }\right.〉}_a-{\left|{\overline{1}}_{\omega }\right.〉}_a)={\left|{\overline{1}}_t\right.〉}_a.\end{array}$$

(9)

The periodicity of the state in the temporal domain: $\overline{\omega }=2\pi /\overline{\omega }$. Such a state is not physical since the state is an infinite sum of monochromatic states and will require infinite energy to prepare it. The physical time–frequency GKP state can be built upon this ideal state by applying time and frequency noise, which are frequency- and time-displacement operations multiplied by the Gaussian distribution, which is detailed in [1]. The wave function of the two logical states can be written as follows:

$${\left|{\mu }_{\omega }\right.〉}_a=N_{\mu }\sum _{n\in \mathbb{Z}}\mathit{\int }d\omega G^{\kappa }\left(\omega \right)G^{\sigma }(\omega -(2n+\mu )\overline{\omega }){\left|\omega \right.〉}_a$$

(10)

where G are Gaussian functions representing the envelope of the comb of width $\kappa$ and the peaks of the comb of width $\sigma$. The frequency probability distribution of the grid state is represented in Figure 1. Alternatively, for large comb $\overline{\omega }/\sigma \gg 1$ [39], we can write

$${\left|{\mu }_{\omega }\right.〉}_a=N_{\mu }\sum _{n\in \mathbb{Z}}{c}_{2n+\mu }\mathit{\int }d\omega G^{\sigma }(\omega -(2n+\mu )\overline{\omega }){\left|\omega \right.〉}_a$$

(11)

with the envelope coefficients $c_n=\exp (-{(n\overline{\omega }/\kappa )}^2/2)$. $N_{\mu }$ is the normalization constant found thanks to the relation $1=|{}_a\langle {\mu }_{\omega }|{\mu }_{\omega \rangle }{}_a{|}^2=N_{\mu }^2{\sum }_{n\in \mathbb{Z}}{\left|c_{2n+\mu }\right|}^2\sqrt{\pi {\sigma }^2}$.

In general, the physical GKP state can be in a superposition of the two logical states:

$$\left|\psi \right.〉=N_{\alpha \beta }(\alpha {\left|0_{\omega }\right.〉}_a+\beta {\left|1_{\omega }\right.〉}_a),$$

(12)

where $N_{\alpha \beta }={\left(\right|\alpha |}^2+{\left|\beta \right|}^2+2\mathrm{Re}\left({\alpha }^{\ast }\beta {}_a{\langle 0_{\omega }|1_{\omega }\rangle }_a\right){\left)\right)}^{-1/2}$. The two logical states are not orthogonal when a Gaussian wave packet enters the frequency bin of its neighbor. The overlap ${}_a{\langle 0_{\omega }|1_{\omega }\rangle }_a$ is different from zero and is equal to

$${}_a{\langle 0_{\omega }|1_{\omega }\rangle }_a=e^{-{\overline{\omega }}^2/4{\sigma }^2}\frac{{\sum }_n{c}_{2n}{c}_{2n+1}^{\ast }}{(\sqrt{{\sum }_n|c_{2n}{|}^2{\sum }_n|c_{2n+1}{|}^2)}}.$$

(13)

The full state is thus described by five important parameters. The complex parameters $\alpha$ and $\beta$ where the quantum information is encoded, the frequency width $\sigma ,\kappa$, and the periodicity of the state $\overline{\omega }$. If the state is not too noisy, meaning that ${}_a{\langle 0_{\omega }|1_{\omega }\rangle }_a\sim 0$, then the normalization condition of Equation (12) is given by ${\left|\alpha \right|}^2+{\left|\beta \right|}^2=1$. Finally, in [1,4], we define the time-of-arrival and frequency operators, which do not commute and verify the Heisenberg algebra. This is mathematically equivalent to the non-commutativity of time–frequency displacement operators. This property leads to consider the temporal and frequency bandwidth as quantum noise at the single photon level.

The GKP states which are defined as the sum of squeezed states in a given mode [9,40] are designed to be robust against small shifts in position and momentum, which can be caused by a Gaussian quantum channel, but they are also robust against photon losses [40]. On the other hand, time–frequency GKP states are designed to be robust against small shifts in time and frequency. The major difference between GKP states and time–frequency GKP states is that photon losses do not result in errors for the latter. In general, temporal errors are the dominant source of errors, while frequency is considered a robust degree of freedom, as it is barely affected by linear physical processes. Additionally, GKP states can be used for fault-tolerant universal quantum computation [20]. Due to their mathematical similarity with time–frequency GKP states, it is expected that they will lead to the same mathematical result. However, the generation of non-Gaussian states using the degree of freedom of a single photon is relatively simple to implement experimentally. As a result, the experimental implementation of a time–frequency GKP state is considered straightforward. In contrast, creating entanglement gates between two single photons is a more challenging task. For particle-number sensitive encoding, non-Gaussian operations involving the quadrature degree of freedom can be difficult to implement, while two-mode Gaussian operations, such as with a beam splitter, are easier to perform.

2.3. Sources of Time–Frequency Noise

In this section, we discuss the physical processes that lead to temporal–spectral broadening or distortion. Coherent and incoherent errors will lead to either pure or mixed states, respectively.

Temporal errors for both codes arise from the temporal spreading of each wave packet composing the state due to the linear dispersion effect, described by a coherent model (see, for instance, [41] for an example in the single photon regime). After such a second-order dispersion effect, the temporal width of the Gaussian wave packet becomes $\tau ={\tau }_0\sqrt{1+{\tau }_c^4/{\tau }_0^4}$, where ${\tau }_0$ is the initial width of the pulse and ${\tau }_c=\sqrt{{\beta }_{2}L}$, L being the length of the dispersive medium and ${\beta }_2$ the dispersion coefficient. Such a dispersion process is described by a unitary operation, and it can, in principle, be undone by a reverse transformation. However, it requires knowledge of the full characterization of the propagation channel. For the time–frequency GKP state, the dispersive effect not only leads to a temporal spreading of each wave packet, but also leads to the formation of replica temporal images, called the temporal Talbot effect (see, for instance, [42]). One has to consider the specific length of the fiber or dispersive coefficient to recover the initial state, which will be also temporally broadened. Polarizing mode dispersion is one of incoherent temporal broadening [43,44,45]. Due to a coupling between the polarization and frequency degree of freedom, if the polarization is not measured, the single-photon state becomes mixed in frequency [46]. Thus, the error correction protocol that is presented in Section 2.4 becomes particularly relevant because we cannot cancel the error simply by a unitary operation.

Frequency noise that causes spectral broadening while the spectral distribution remains Gaussian is not typically dominant at the single-photon level. Spectral broadening induced by the self-phase modulation effect [47] results from the accumulated phase ${\varphi }_{NL}\left(t\right)=\frac{2\pi }{\lambda }{n}_{2}I\left(t\right)L$, where $n_2$ is the non-linear refractive index, and L is the length of the medium and depends on the intensity $I\left(t\right)$ of the field, leading to a non-Gaussian spectral distribution. At the single-photon level, this non-linear process does not occur naturally. In [1], we also argue that the frequency noise arises from frequency broadening caused by the generation of photon pairs itself, and we describe one method to correct such noise. There are numerous processes that can distort the spectral distribution of single photons, such as distortions caused by frequency shifts induced by electro-optic modulators [48,49], or the presence of a filter during single-photon heralding.

An error correction protocol is implemented to mitigate the effects of potential errors from various sources. Its objective is to restore the Gaussian distribution of each frequency peak. This is because Gaussian probability distributions are better understood for setting confidence intervals and error thresholds as discussed in [50]. Both qubits are sensitive to temporal and frequency broadening. While the time–frequency cat state is designed to be robust against errors over one variable, the time–frequency GKP state can correct errors along both orthogonal variables. It is not necessary to use the time–frequency GKP state if the main error is in the temporal domain. We now develop two error correction methods, one based on a direct frequency entanglement between the noisy state of interest and a less noisy ancilla (Section 2.4), and the other method using only linear optics and also less noisy ancilla (Section 4).

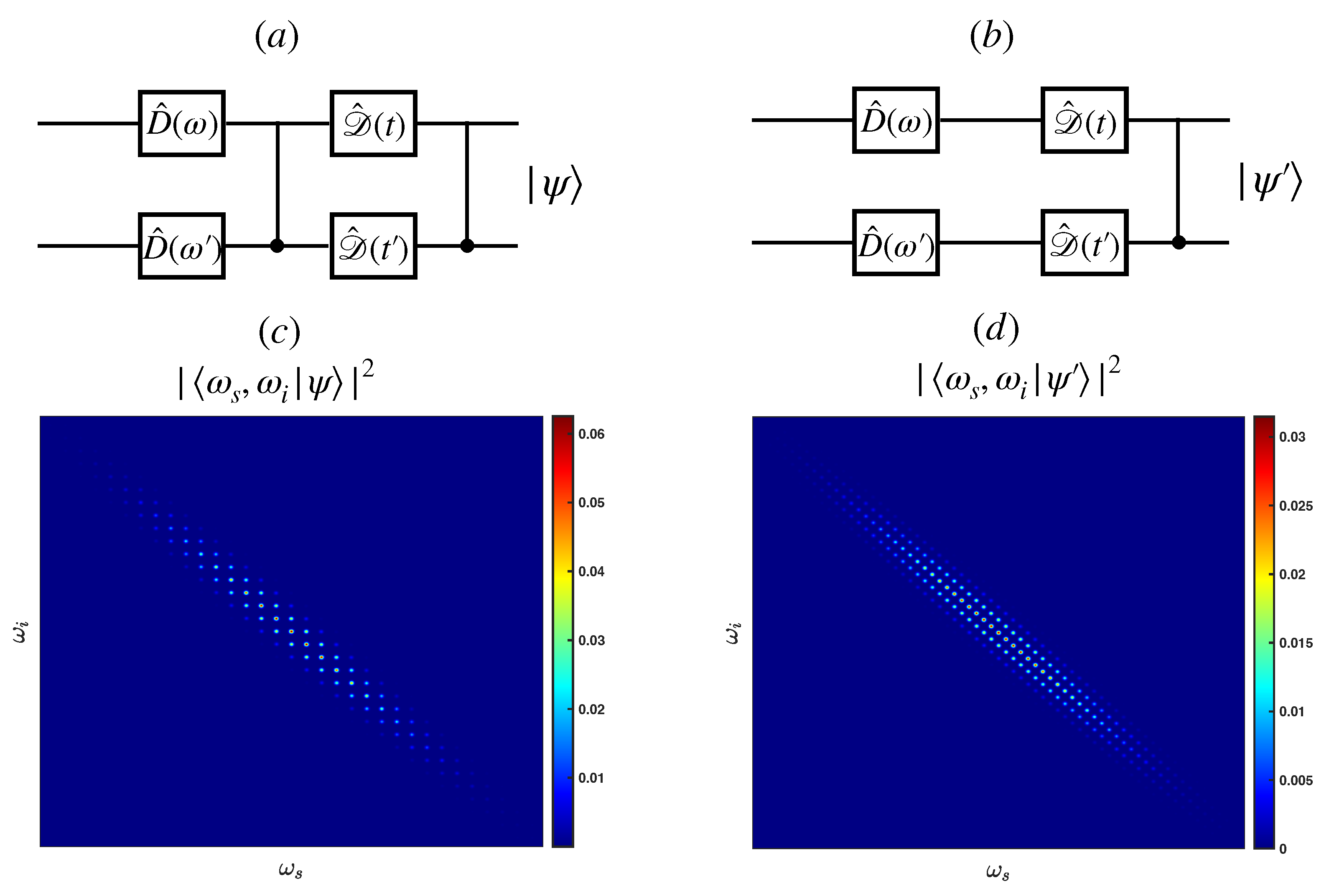
2.4. Time–Frequency Entangled GKP State and Error Correction Protocols

The error correction of continuous variables states can be performed with a Steane error correction protocol for the quadrature degree of freedom [51] and for the time–frequency one [1]. For the two encodings, the protocol consists of entangling the state of interest with one less noisy ancilla (a $\left|+\right.〉$ logical state in one variable, time or frequency) with a beam splitter (resp. with frequency beam splitter that will be explicated below), and performing one homodyne (resp. single-photon frequency measurement) detection at the spatial output of the ancilla for correcting the error along one variable. The protocol is repeated to correct errors in the orthogonally (or canonically) conjugated variable. To achieve this, one must entangle the state of interest with a less noisy state using a $\left|+\right.〉$ state in the canonically conjugated variable compared to the first step. Then, perform the entangling operation, project a measurement in the canonically conjugated variable (compared to step one), and finally conduct a conditional displacement operation. An important tool for quantifying the threshold of noise from which it is still possible to correct the GKP states, a Steane error correction protocol was used in [50]. Figures of merit for quantifying the probability of measuring the one logical state while this is zero were obtained in [26,50]. We will refer to these figures of merit when we note one logical state is noisier (or less noisy) than the other. From now on, we develop two entanglement structures of time–frequency GKP state that can be generated in the laboratory, and the method for performing the error correction in each case.

The first entanglement structure of the time–frequency GKP state that we can study is the one obtained by using a spontaneous parametric downconversion process (SPDC) from a non-linear crystal placed into an optical cavity [1,52]. The corresponding wave function can be cast as

$$\left|\psi \right.〉=\mathit{\int }\mathit{\int }d{\omega }_{s}d{\omega }_i{f}_{+}\left({\omega }_{+}\right)f_{-}\left({\omega }_{-}\right)f\left({\omega }_s\right)f\left({\omega }_i\right)\left|{\omega }_s,{\omega }_i\right.〉.$$

(14)

The functions $f_{\pm }$ model, respectively, the energy conservation and the phase matching of the SPDC process, and f models the cavity function. The joint spectrum intensity is represented in Figure 2c. Instead of the traditional view, where the wave function of two photons is written by applying a quadratic Hamiltonian on the vacuum state, it can also be expressed with a quantum circuit representation as shown in Figure 2a. This starts with two ideal separable GKP states (fictitious), which undergo initial frequency broadening, which can be interpreted as a frequency noise [1]. Then, the state is entangled through the gate performed by the non-linear crystal:

$$\hat{U}\left|{\omega }_s,{\omega }_i\right.〉=\left|\frac{{\omega }_s+{\omega }_i}{\sqrt{2}},\frac{{\omega }_s-{\omega }_i}{\sqrt{2}}\right.〉$$

(15)

that we called a frequency beam splitter by analogy with the beam splitter, which acts mathematically similarly in the quadrature position–momentum degree of freedom [4,53]. The state then undergoes a temporal broadening, which can be interpreted as a temporal noise and a final frequency beam-splitter operation is performed. The mathematical reason behind these four successive operations is that the envelope of the grid state is a function of the collective variables ${\omega }_{\pm }$, while the cavity of the local variable is ${\omega }_{s,i}$. The form of the frequency entanglement between the two single photon grid states generated by the non-linear process (see Equation (15)) allows for the reduction in the temporal broadening of one of the single photons by performing a temporally resolved measurement of the other. The form of the pure wave function after the conditioned operation is written in [1].

After correcting the single-photon state in the temporal domain, the next step is to correct the state in the frequency domain. For that, we must first entangle the single photon to correct with a less noisy ancilla single-photon state using the entanglement gate Equation (15). Since now we have two separable single-photon states, we cannot directly entangle them by using a non-linear crystal, which is inefficient. Nevertheless, such a frequency entangled gate could be implemented with a quantum emitter embedded into a wave guide, which assists in the interaction between the two single photons [27,54].

The second entanglement structure of the time–frequency GKP state that can be considered is to start with two initially separable GKP states, with one being less noisy than the other. These states are then entangled using Equation (15). The resulting wave function is

$$\left|{\psi }^{\prime }\right.〉=\mathit{\int }\mathit{\int }d{\omega }_{s}d{\omega }_i{f}_{+}\left({\omega }_{+}\right)f_{-}\left({\omega }_{-}\right)f\left({\omega }_{+}\right)f\left({\omega }_{-}\right)\left|{\omega }_s,{\omega }_i\right.〉.$$

(16)

In this new spectral function (see Figure 2d, the cavity function is now dependent on the collective variables, and thus, the periodicity of the grid state is not the same as in Equation (14). The corresponding quantum circuit representation is pictured in Figure 2b. The error correction protocol is followed by a temporally resolved measurement followed by a conditional displacement operation to correct only the temporal noise in the state of interest. A second entanglement operation is performed using a less noisy ancilla state, followed by a resolved frequency measurement followed by a conditional displacement operation to correct the frequency noise. The difference in the joint spectral amplitude of the photon pairs results— Equations (14) and (16)—in a different wave function when one of the photons undergoes a temporally resolved (and frequency) measurement and a conditional displacement operation.

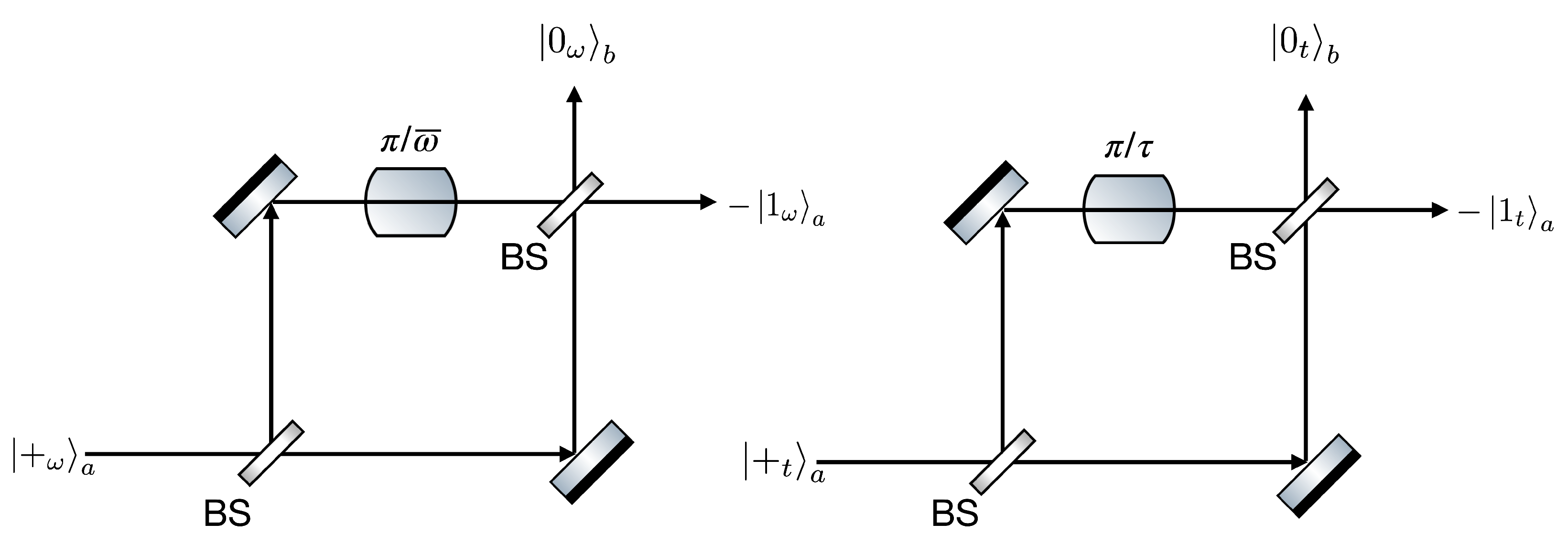
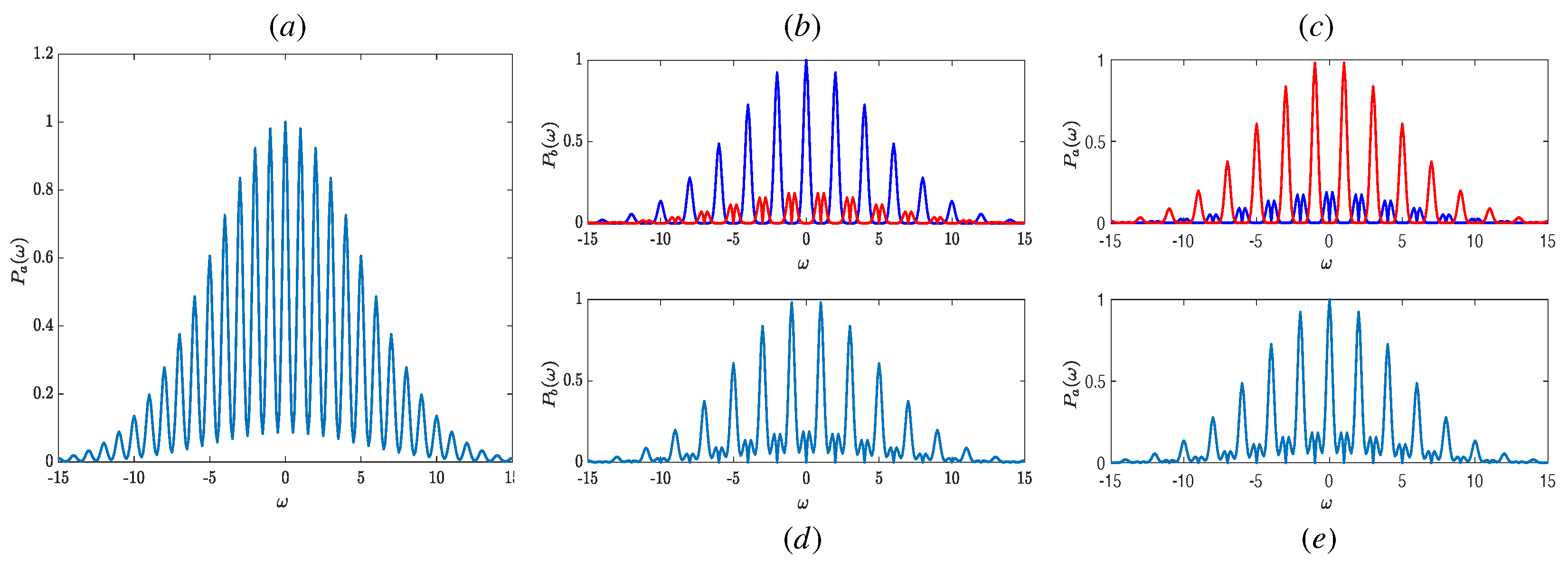
3. Spatial Separation of the Two Logical Time–Frequency Qubit States

In this section, we develop the equivalent of the polarizing beam-slitter operation for the time–frequency cat and GKP state, which is the crucial optical component for the teleportation-based error correction described in the next section. Such an optical element is called the frequency qubit beam splitter (FQBS) in what follows.

3.1. Spatial Separation of the Two Logical Time–Frequency Cat States

In this section, we explicitly show how to separate spatially the two Gaussian wave packets with linear optics, using a Mach–Zehnder interferometer. The frequency cat state as described by Equation (1) is introduced into a balanced beam splitter and the associated wave function is

$$\left|\psi \right.〉=\frac{1}{2}({\left|{\omega }_1\right.〉}_a+{\left|{\omega }_2\right.〉}_a+{\left|{\omega }_1\right.〉}_b+{\left|{\omega }_2\right.〉}_b).$$

(17)

We assume for simplicity that the two frequency states are well separated ${\omega }_1-{\omega }_2\gg \sigma$. Then, a pulse shaper is placed at the spatial port b, described by the following unitary operation:

$$\hat{U}{\left|{\omega }_1\right.〉}_b={\left|{\omega }_1\right.〉}_b,\hat{U}{\left|{\omega }_2\right.〉}_b=e^{i\varphi }{\left|{\omega }_2\right.〉}_b.$$

(18)

Such an operation can be implemented, for instance, by mapping the spectral to the spatial degree of freedom with a grating, a spatial light modulator at the focal length of two lenses, and then performing back the mapping from the spatial to the spectral degree of freedom [2,55]. We assume that the frequency peaks are spaced enough so that the pulse shaper acts on each logical state independently. The two spatial paths are then recombined into another balanced beam splitter. The output state has the final form:

$$\left|\psi \right.〉=\frac{1}{\sqrt{2}}{\left|{\omega }_1\right.〉}_a{\left|\Omega \right.〉}_b+\frac{1}{2\sqrt{2}}((1+e^{i\varphi }){\left|{\omega }_2\right.〉}_a{\left|\Omega \right.〉}_b+(1-e^{i\varphi }){\left|\Omega \right.〉}_a{\left|{\omega }_2\right.〉}_b).$$

(19)

If $\varphi =\pi$, the two logical states are spatially separated $\left|\psi \right.〉=\frac{1}{\sqrt{2}}({\left|{\omega }_1\right.〉}_a{\left|\Omega \right.〉}_b+{\left|\Omega \right.〉}_a{\left|{\omega }_2\right.〉}_b)$. This optical interferometer is the equivalent of the polarizing beam splitter that separates the vertical and horizontal polarization of optical fields into two distinct spatial paths.

3.2. Spatial Separation of the Two Logical Time–Frequency GKP States

In this part, we introduce how to separate spatially the odd and the even frequencies with a Mach–Zehnder interferometer. Such a scheme was already proposed for manipulating large quadrature position–momentum continuous variables cluster states [56], and was described in [2,25].

We start with a time–frequency GKP state with a finite envelop but with infinitely narrow frequency width $\left|+\right.〉=\frac{1}{\sqrt{2}}({\left|0\right.〉}_a+{\left|1\right.〉}_a$), and is introduced into a balanced beam splitter. The spatial output port of the beam splitter is denoted as a and b. A time-shift operation is performed in spatial port b, and then the two spatial ports are recombined into a balanced beam splitter (see Figure 3). The final wave function can be written as

$$\left|\psi \right.〉=\frac{1}{2}\sum _{n\in \mathbb{Z}}[c_n(e^{in\overline{\omega }t}-1){\left|n\overline{\omega }\right.〉}_a{\left|\Omega \right.〉}_b-(e^{in\overline{\omega }t}+1){\left|\Omega \right.〉}_a{\left|n\overline{\omega }\right.〉}_b].$$

(20)

If we set $t=\pi /\overline{\omega }$, after the second beam splitter, the wave function is (see [2])

$$\left|\psi \right.〉=\frac{1}{\sqrt{2}}(-{\left|1\right.〉}_a{\left|\Omega \right.〉}_b+{\left|\Omega \right.〉}_a{\left|0\right.〉}_b).$$

(21)

The odd and even frequency components are spatially separated, allowing for individual manipulation, such as correcting the phase accumulation of the one logical state. It is possible to achieve the same result in the temporal domain by shifting the frequency instead of the time as shown in Figure 3.

If each frequency peak is not infinitely narrow, then the output wave function after the Mach–Zehnder interferometer can be written as

$$\left|\psi \right.〉=\frac{1}{2}\sum _{n\in \mathbb{Z}}{c}_n\left[\right(\mathit{\int }d\omega (e^{i\pi \omega /\overline{\omega }}-1)G^{\sigma }(\omega -n\overline{\omega }){\left|\omega \right.〉}_a{\left|\Omega \right.〉}_b-(\mathit{\int }d\omega (e^{i\pi \omega /\overline{\omega }}+1)G^{\sigma }(\omega -n\overline{\omega }){\left|\Omega \right.〉}_a{\left|\omega \right.〉}_b.$$

(22)

The corresponding probability frequency distributions at spatial port a and b are

$$\begin{array}{c}\hfill P_a\left(\omega \right)=\frac{1}{4}{|\sum _{n\in \mathbb{Z}}{c}_n(e^{i\pi \omega /\overline{\omega }}-1)G^{\sigma }(\omega -n\overline{\omega })|}^2,\end{array}$$

(23)

$$\begin{array}{c}\hfill P_b\left(\omega \right)=\frac{1}{4}{|\sum _{n\in \mathbb{Z}}{c}_n(e^{i\pi \omega /\overline{\omega }}+1)G^{\sigma }(\omega -n\overline{\omega })|}^2.\end{array}$$

(24)

We represent in Figure 4a and Figure 5a the spectral probability density distribution of two $\left|{+}_{\omega }\right.〉$ states for $\sigma =0.1\overline{\omega }$ and $\sigma =0.2\overline{\omega }$. The output probability density distribution after the Mach–Zehnder interferometer if we start with the zero or one logical state is represented in Figure 4b,c. We observe that when $\sigma =0.1\overline{\omega }$, it is valid to consider the zero and one logical states independently since they do not interfere due to their central frequencies being too far apart to overlap. However, the spatial separation is imperfect; the one logical state does not emerge from the correct spatial port. When $\sigma =0.2\overline{\omega }$ (see Figure 5b,c), there is an interference term between the zero and one logical state because they now overlap significantly. The resulting state is outside the GKP subspace; it can be seen with the distortion because the probability at the center of the odd and even frequency bins is zero. The addition of a periodic frequency filter can enhance the projection into the GKP subspace and the choice of a frequency width would be crucial for rejecting the logical states emerging from the incorrect spatial port.

We represent in Figure 4d,e and Figure 5d,e, the output probability distribution in the spatial ports a and b when the initial state is $\left|{+}_{\omega }\right.〉$. We observe a peculiar interference effect due to the increasing of the overlap between the zero and one logical state. In practice, for instance, we have to filter out the single-photon state that enters the wrong spatial port by placing appropriate frequency filters.

In Appendix A, we also investigate the separation of the odd and even components of the comb when the two-photon state is an input of the frequency qubit beam splitter. This is relevant to the teleportation-based error correction protocol because the state to be teleported is combined with a single photon from an EPR pair during the Bell measurement. The spatial separation is, in that case, also completely effective when each Gaussian distribution approaches a Dirac distribution, and not otherwise. Explicitly, for the two-photon state, we obtain ${\left|0\tilde{1}\right.〉}_{aa}\to {\left|0_G\right.〉}_a{\left|{\tilde{1}}_G\right.〉}_{a^{\prime }}+{\left|0_E\right.〉}_{a^{\prime }}{\left|{\tilde{1}}_E\right.〉}_a$, whose corresponding expressions are given in Appendix A. The case to combine two different single-photon states also plays a role in quantum communication scenarios, where the second qubit is from an attacker who tries to collect the information about the qubit carrying the information of interest.

4. Teleportation-Based Error Correction of Time–Frequency Qubit States

In this section, we propose a protocol for correcting and teleporting frequency qubit states without relying on frequency-entangling operations. This protocol is similar to the one used for teleporting polarization qubit states as described in [57], and is inspired by the GKP analog [28,29]. Since the EPR state has a lower level of noise in both temporal and frequency variables, the protocol includes an additional component for correcting errors in the state being teleported.

The single-photon state $\left|\psi \right.〉$ to be teleported and corrected is described by the wave function $\left|\psi \right.〉=N_{\alpha \beta }(\alpha {\left|0\right.〉}_a+\beta {\left|1\right.〉}_a)$, where the two logical states are either the time–frequency cat or GKP qubits (see Equation (12)). The wave function of the entangled EPR time–frequency state in spatial ports b and c that assists with the teleportation and the correction is

$${\left|{\varphi }^{+}\right.〉}_{bc}=N_{\mathrm{EPR}}({\left|\tilde{0}\tilde{1}\right.〉}_{bc}+{\left|\tilde{1}\tilde{0}\right.〉}_{bc})$$

(25)

composed of logical states which are less noisy, indicated with the tilde notation, than the state to be teleported. Upon completion of the protocol, the single-photon state $\left|\psi \right.〉$ is localized to spatial port c, and the correction is automatically performed since the EPR state is less noisy than the state of interest.

We now write the protocol for the error correction and teleportation of the time–frequency cat state, considering that the Bell measurement perfectly separates the two logical states. This protocol allows for correcting frequency errors affecting the frequency qubit states. The protocol is shown in Figure 6, and we will now proceed to write the evolution of the wave function at each step of the protocol. The initial wave function, composed of the state to be corrected and teleported, and the EPR state, written in Bell’s basis is

$$\begin{array}{cc}\hfill \left|\psi \right.〉=& \frac{N_{\alpha \beta }{N}_{\mathrm{EPR}}}{2}(\left|{\omega }_1{\tilde{\omega }}_1\right.〉+\left|{\omega }_2{\tilde{\omega }}_2\right.〉)(\alpha {\left|\widetilde{{\omega }_1}\right.〉}_c+\beta {\left|\widetilde{{\omega }_2}\right.〉}_c)\hfill \\ \hfill & +(\left|{\omega }_1{\tilde{\omega }}_1\right.〉-\left|{\omega }_2{\tilde{\omega }}_2\right.〉)(\alpha {\left|\widetilde{{\omega }_1}\right.〉}_c-\beta {\left|\widetilde{{\omega }_2}\right.〉}_c)\hfill \\ \hfill & +(\left|{\omega }_1{\tilde{\omega }}_2\right.〉+\left|{\omega }_2{\tilde{\omega }}_1\right.〉)(\beta {\left|\widetilde{{\omega }_1}\right.〉}_c+\alpha {\left|\widetilde{{\omega }_2}\right.〉}_c)\hfill \\ \hfill & +(-\left|{\omega }_1{\tilde{\omega }}_2\right.〉+\left|{\omega }_2{\tilde{\omega }}_1\right.〉)(\beta {\left|\widetilde{{\omega }_1}\right.〉}_c-\alpha {\left|\widetilde{{\omega }_2}\right.〉}_c).\hfill \end{array}$$

(26)

The single-photon state and one member of the EPR pair are then combined into a beam splitter, followed by two parity–frequency beam splitters placed in the spatial ports $a^{\prime }$ and $b^{\prime }$. The first and second Bell states are transformed as

$$\begin{array}{cc}\hfill \frac{N_{\mathrm{EPR}}}{2}[{\left|{\omega }_1{\tilde{\omega }}_1\right.〉}_a& -{\left|{\omega }_1\right.〉}_a{\left|{\tilde{\omega }}_1\right.〉}_b+{\left|{\omega }_1\right.〉}_b{\left|{\tilde{\omega }}_1\right.〉}_a-{\left|{\omega }_1{\tilde{\omega }}_1\right.〉}_b\hfill \\ \hfill & +{\left|{\omega }_2{\tilde{\omega }}_2\right.〉}_a-{\left|{\omega }_2\right.〉}_a{\left|{\tilde{\omega }}_2\right.〉}_b+{\left|{\omega }_2\right.〉}_b{\left|{\tilde{\omega }}_2\right.〉}_a-{\left|{\omega }_2{\tilde{\omega }}_2\right.〉}_b].\hfill \end{array}$$

(27)

The presence of a single photon in each port is a consequence of the distinguishability of the photons. While if the photons are indistinguishable, only bunching events are measured, as in the case of polarization encoding for two orthogonal logical states. In order to suppress these coincidence events that lead to errors in the teleportation protocol, the use of frequency filters with the same frequency width (envelope and peak) as the EPR state is a possible solution. Explicitly, after the filtering operation, the state becomes ${\left|{\tilde{\omega }}_1{\tilde{\omega }}_1\right.〉}_a-{\left|{\omega }_1{\tilde{\omega }}_1\right.〉}_b+{\left|{\tilde{\omega }}_2{\tilde{\omega }}_2\right.〉}_a-{\left|{\omega }_2{\tilde{\omega }}_2\right.〉}_b$, which leads only to two bunching events, which are ignored when single photon detectors are used. The same analysis can be employed for the second Bell state.

For the third and fourth Bell states, they are transformed as

$$\begin{array}{cc}\hfill \frac{N_{\mathrm{EPR}}}{2}[& \pm {\left|{\omega }_1{\tilde{\omega }}_2\right.〉}_{a{a}^{\prime }}\mp {\left|{\omega }_1{\tilde{\omega }}_2\right.〉}_{a{b}^{\prime }}\pm {\left|{\omega }_1{\tilde{\omega }}_2\right.〉}_{b{a}^{\prime }}\mp {\left|{\omega }_1{\tilde{\omega }}_2\right.〉}_{b{b}^{\prime }}\hfill \\ \hfill & +{\left|{\omega }_2{\tilde{\omega }}_1\right.〉}_{a^{\prime }a}-{\left|{\omega }_2{\tilde{\omega }}_1\right.〉}_{a^{\prime }b}+{\left|{\omega }_2{\tilde{\omega }}_1\right.〉}_{b^{\prime }a}-{\left|{\omega }_2{\tilde{\omega }}_1\right.〉}_{b^{\prime }b}].\hfill \end{array}$$

(28)

The use of frequency filters is again imperative since the measurement of coincidence once filtered of $a,a^{\prime }$ (or $b,b^{\prime }$) permits to ensure that the quantum state $N_{\alpha \beta }(\beta \left|\widetilde{{\omega }_1}\right.〉+\alpha \left|\widetilde{{\omega }_2}\right.〉)$ is teleported. In the same way, the measurement of the coincidence of $a,b^{\prime }$ (or $b,a^{\prime }$) allows teleporting the state $N_{\alpha \beta }(\beta \left|\widetilde{{\omega }_1}\right.〉-\alpha \left|\widetilde{{\omega }_2}\right.〉)$. The receiver sends to spatial port c which detectors have measured coincidences, and then a product of Pauli matrix gates must be applied to recover the initial state of interest. The Pauli matrices for the time–frequency cat states are frequency and temporal shifts operations [1], which can be implemented by either an electro-optical modulator [48,49] and a delay line, respectively. The full optical scheme of the teleportation-based error correction protocol is represented in Figure 6, along with an illustration of the effect of the error correction for qubit cat states.

The corresponding probability of each event is $P=\frac{1}{8(1+e^{-{\Delta }^2/2{\sigma }^2})}$, and the overall probability success of the teleportation is

$$P=\frac{1}{2(1+e^{-{\Delta }^2/2{\sigma }^2})},$$

(29)

which is then lower than 50% since only linear optics is used [57] and because the non-orthogonality of the encoding further decreases the probability of success. Note that the use of photon number-resolving (PNR) detectors will be able to not discard the bunching events coming from the first and second Bell states. The single nanowire superconductivity detector can also differentiate two and one single photons since the amplitude of the resistance of the hotspot over time is higher for two photons. With the use of such a PNR detector, the overall probability of success of the teleportation protocol is

$$P_{\mathrm{PNR}}=\frac{3}{4(1+e^{-{\Delta }^2/2{\sigma }^2})}$$

(30)

and thus allows to increase the probability of success of the protocol despite the non-orthogonality of the state. Experimentally, the choice of the PNR detector could be the one described in [58]. Reaching a $3/4$ probability of success was also found by using a non-linear process or ancilla entangled states [59,60].

We can formulate the previous protocol for time–frequency GKP states. If we employ an EPR state which is less noisy in the temporal and frequency domain, the teleported state is corrected in both the temporal and frequency variables at once. It is in contrast with the error correction protocol based on the frequency entanglement described in Section 2.4, where we have to repeat twice the same protocol to correct both variables. In Appendix B, we tackle the case of the teleportation error correction protocol when the spatial separation of the non-orthogonal qubit state is imperfect, discussing the special case of time–frequency GKP state and Bell measurement relying on the spatial separation of the two logical states described in Section 3.2. The imperfect spatial separation affects both the efficiency and the fidelity of the teleportation protocol. The fidelity is always equal to one when the logical states are orthogonal, but this is not the case for non-orthogonal time–frequency qubit states. The use of frequency filters can eliminate detection events caused by imperfect spatial separation, but it comes at the cost of decreased brightness.

5. Conclusions

In this paper, we started to present two time–frequency qubit states, time–frequency cat and GKP states, and the errors from which they are robust against. Then, we explained two different optical scenarios that lead to different entanglement structures of time–frequency GKP states and gave different periodicities for the joint spectral intensity of the photon pair. This time–frequency GKP state entanglement structure leads naturally to a first error correction method that requires non-linear processes [1] or quantum dot embedded into a wave guide [27] to realize it. We then developed a method to perform the Bell measurement for these two time–frequency qubits using Mach–Zehnder interferometry.

Since this error correction method is not scalable and difficult to implement experimentally, we discussed the teleportation-based error correction protocol for the frequency qubit state, and developed the case of the time–frequency GKP state in the appendix. The teleportation-based error correction protocol is well suited for the single-photon encoding, as it requires only linear optics. The single-photon state carrying the quantum information of interest is first combined into a balanced beam splitter with one member of a less noisy pair, and then the Bell measurement is performed. Therefore, if the initial state is broadened in the temporal or frequency domain, because the remaining single-photon state belongs to a less noisy entangled pair, such a state is less broadened in the temporal (or frequency) domain and carries the information of interest (see Figure 6). By contrast with the polarization degree of freedom, since the frequency qubit is defined from the discretization of a continuous variable, the two logical states composing the qubit are intrinsically non-orthogonal such that this fact leads to a decrease in the overall probability of success of the teleportation protocol.

We can envision the scenario where the single-photon frequency is the carrier of the quantum information and is moving through different nodes of a quantum network, and the entangled states could be generated locally and allow healing the temporally and frequency-broadened single-photon state carrying the quantum information of interest. This teleportation-based error correction optical scheme has the same objective as a quantum relay, that is, reducing the error rate of a quantum key distribution protocol by reducing the overlap of the two logical states composing the qubit.

One perspective is to study the case where the logical qubit states are not infinitely frequency-narrowed. The Bell measurement will lead to wrong detections because the spatial separation of the two logical states into two spatial ports, realized with Mach–Zehnder interferometry, is imperfect. This can be corrected by using frequency filters but at the cost of losing single photon detection events. To tackle this issue, the use of frequency-resolved detection and the fault-tolerance threshold defined in [50] could be valuable for avoiding the use of frequency filters. We showed that our protocol can correct the errors of the qubit composed of two colors by reducing their spectral width. As a direct perspective, a single photon qubit composed of two Gaussian centered on two temporal bins (see Equation (2)) could be corrected from the temporal dispersion with the teleportation-based error correction scheme by using a less temporally broadened entangled state, thereby reducing the error rate of quantum communication protocols [61,62,63].