The Calibration Process and Setting of Image Brightness to Achieve Optimum Strain Measurement Accuracy Using Stereo-Camera Digital Image Correlation
Abstract
:1. Introduction
- the size, manufacturing accuracy, and the number of different registered positions of the calibration target used in the calibration, and
- the image brightness on the values of the average deviations obtained in strain/stress analyses on a small area of the flat specimen with a hole.
2. Experimental Analyses Performed by DIC
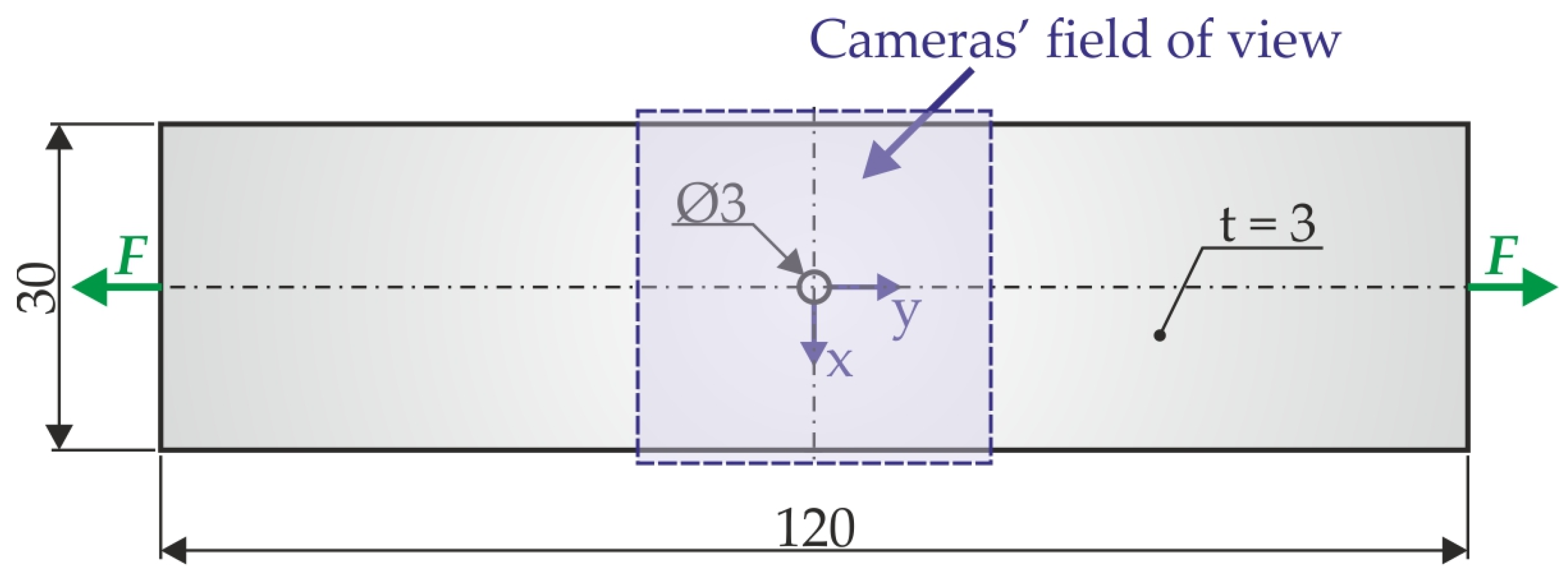
2.1. Experimental Analysis of the Influence of Calibration Parameters on the Results of Strain/Stress Analysis
2.2. Experimental Analysis of the Influence of Image Brightness on the Results of Strain/Stress Analysis
3. Results
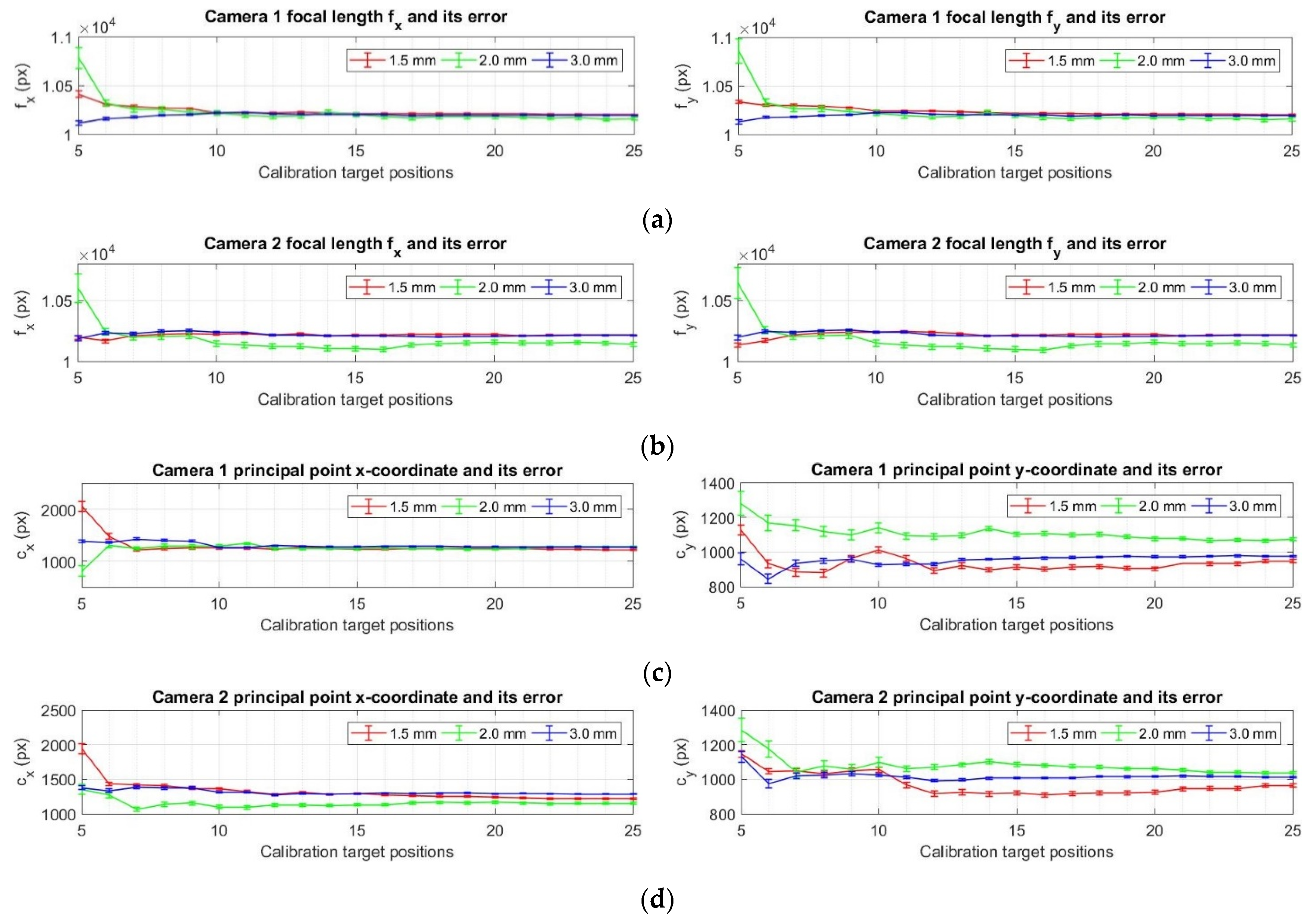
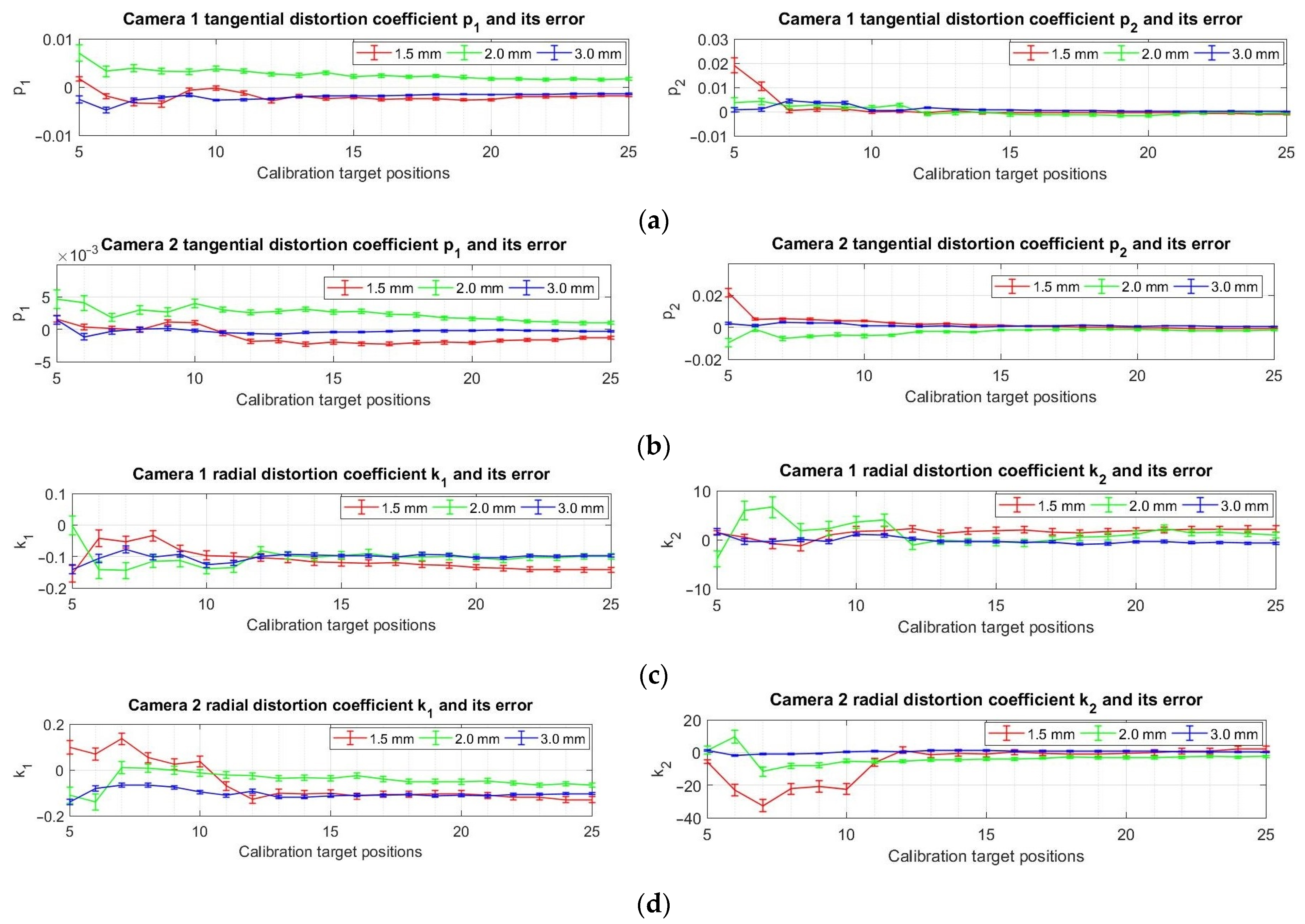
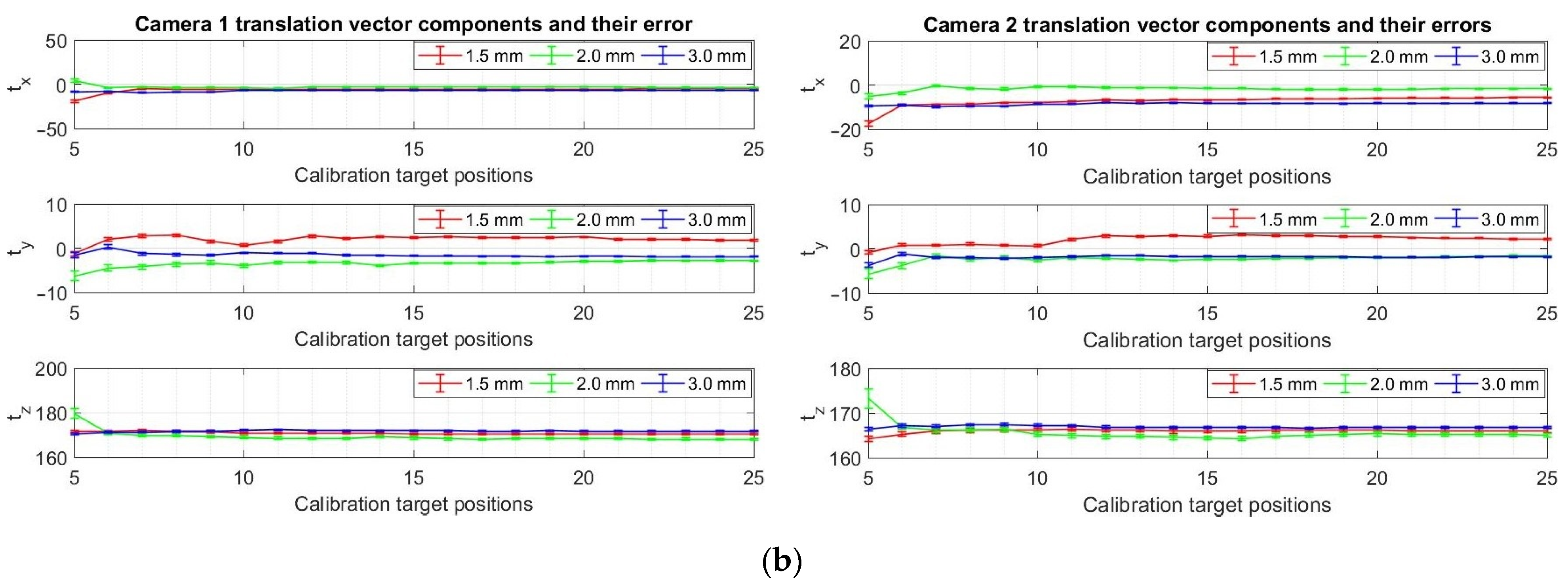
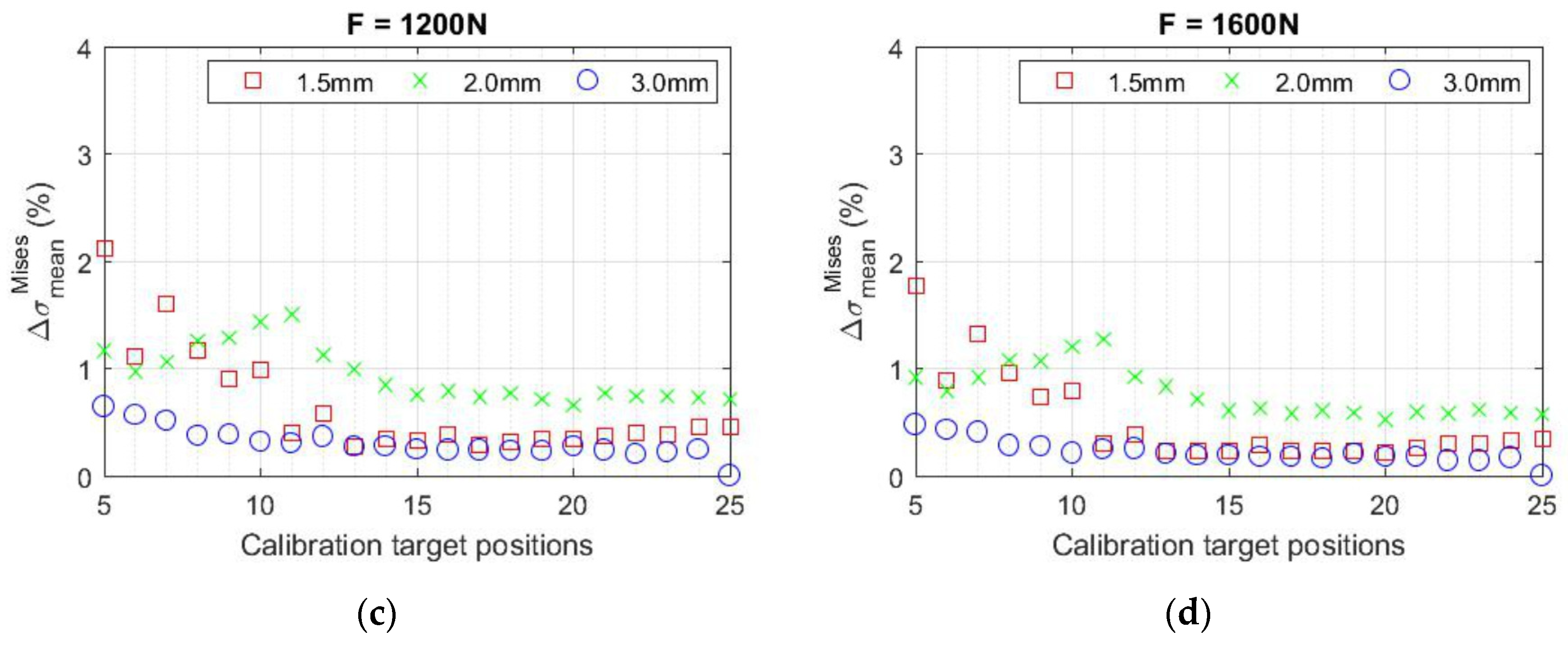
3.1. Investigation of the Influence of Calibration Parameters on the Results of Strain/Stress Analysis
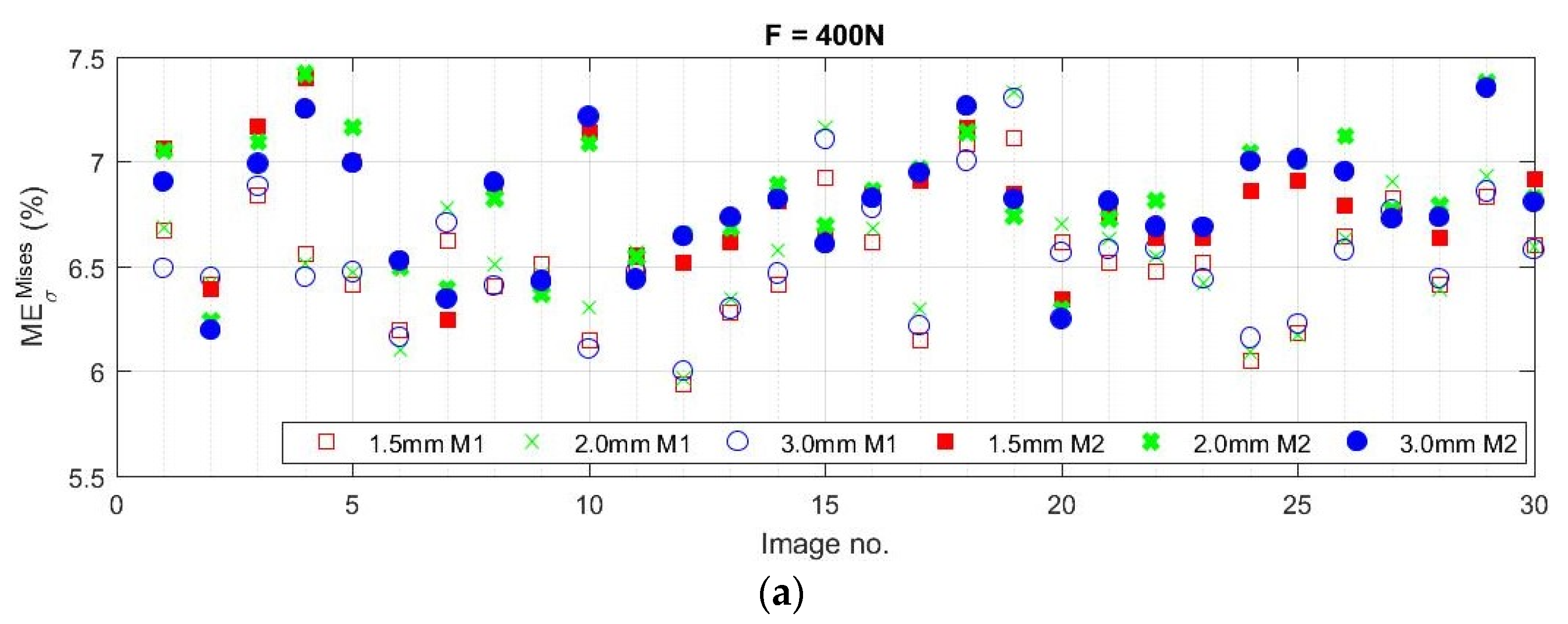
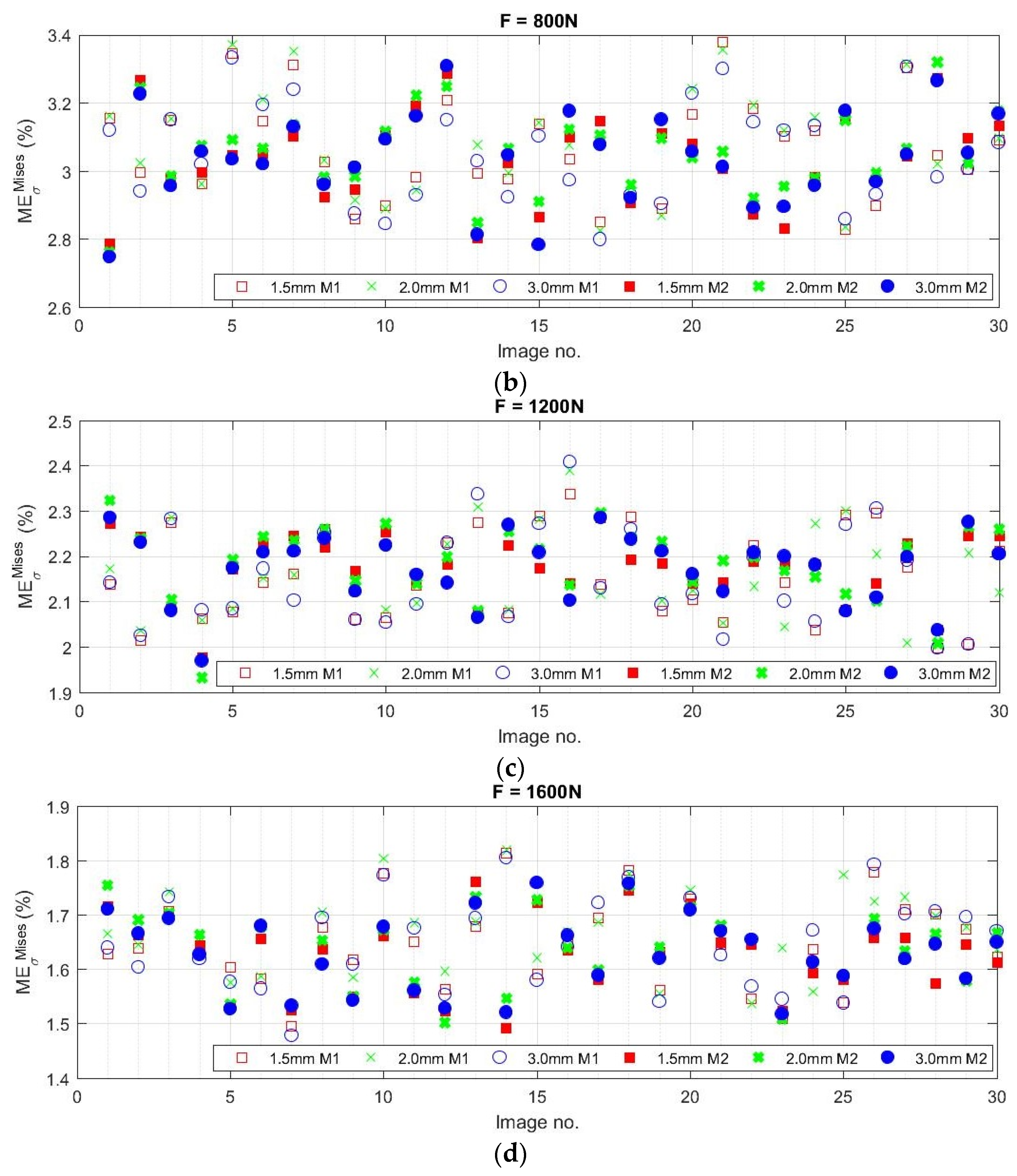
3.2. Investigation of the Influence of Image Brightness on the Results of Strain/Stress Analysis
4. Discussion
- the problem of applying a standard digital image correlation system with commercially available drilling equipment;
- the lower sensitivity of the cameras compared to specialised strain gauge rosettes.
- if possible, use calibration targets whose size corresponds approximately to the field of view of the cameras used in correlation mode;
- if the calibration target used is significantly smaller than the field of view of the cameras, there is a risk that some of the calibration parameters will not be estimated correctly if the number of registered target positions is less than 10; it is, therefore, recommended to register as many different positions of the target chosen for calibrating the cameras as possible (minimum 15);
- a target with a lower manufacturing accuracy should be used for the calibration of the cameras only in case of necessity—however—it has to be taken into account that the measurement results will be obtained with a higher measurement uncertainty than in the case of targets manufactured with a guaranteed higher manufacturing accuracy.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Lecompte, D.; Smits, A.; Bossuyt, S.; Sol, H.; Vantomme, J.; Van Hemelrijck, D.; Habraken, A.M. Quality assessment of speckle patterns for digital image correlation. Opt. Laser Eng. 2006, 44, 1132–1145. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. On errors of digital image correlation due to speckle patterns. In Proceedings of the International Conference on Experimental Mechnics 2008 and Seventh Asian Conference on Experimental Mechanics, Nanjing, China, 8–11 November 2008. [Google Scholar]
- Hua, T.; Xie, H.; Wang, S.; Hu, Z.; Chen, P.; Zhang, Q. Evaluation of the quality of a speckle pattern in the digital image correlation method by mean subset fluctuation. Opt. Laser Technol. 2011, 43, 9–13. [Google Scholar] [CrossRef]
- Haddadi, H.; Belhabib, S. Use of rigid-body motion for the investigation and estimation of the measurement errors related to digital image correlation technique. Opt. Laser Eng. 2008, 46, 185–196. [Google Scholar] [CrossRef]
- Barranger, Y.; Doumalin, P.; Dupré, J.C.; Germaneau, A. Digital Image Correlation accuracy: Influence of kind of speckle and recording setup. EPJ Web Conf. 2010, 6, 31002. [Google Scholar] [CrossRef]
- Crammond, G.; Boyd, S.W.; Dulieu-Barton, J.M. Speckle pattern quality assessment for digital image correlation. Opt. Laser Eng. 2013, 51, 1368–1378. [Google Scholar] [CrossRef]
- Kammers, A.D.; Daly, S. Small-scale patterning methods for digital image correlation under scanning electron microscopy. Meas. Sci. Technol. 2011, 22, 125501. [Google Scholar] [CrossRef]
- Cannon, A.H.; Hochhalter, J.D.; Mello, A.W.; Bomarito, G.F.; Sangid, M.D. Microstamping for improved speckle patterns to enable digital image correlation. Microsc. Microanal. 2015, 21, 451–452. [Google Scholar] [CrossRef]
- Bossuyt, S. Optimized patterns for digital image correlation. In Proceedings of the 2012 Annual Conference on Experimental and Applied Mechanics, Volume 3: Imaging Methods for Novel Materials and Challenging Applications, Costa Mesa, CA, USA, 11–14 June 2012. [Google Scholar]
- Bomarito, G.F.; Hochhalter, J.D.; Ruggles, T.J.; Cannon, A.H. Increasing accuracy and precision of digital image correlation through pattern optimization. Opt. Laser Eng. 2017, 91, 73–85. [Google Scholar] [CrossRef]
- Song, J.; Zang, J.; Liu, F.; Lu, K. Quality assessment of laser speckle patterns for digital image correlation by a Multi-Factor Fusion Index. Opt. Laser Eng. 2020, 124, 105822. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, C.; Xu, Z. High-Accuracy Three-Dimensional Deformation Measurement System Based on Fringe Projection and Speckle Correlation. Sensors 2023, 23, 680. [Google Scholar] [CrossRef]
- Souto Janeiro, A.; Fernández López, A.; Chimeno Manguan, M.; Pérez-Merino, P. Three-Dimensional Digital Image Correlation Based on Speckle Pattern Projection for Non-Invasive Vibrational Analysis. Sensors 2022, 22, 9766. [Google Scholar] [CrossRef]
- Craig, W.D.; Leeuwen, F.B.; Jarrett, S.R.; Hansen, R.S.; Berke, R.B. Using text as a native speckle pattern in digital image correlation. J. Strain Anal. Eng. Des. 2022, 57, 539–555. [Google Scholar] [CrossRef]
- Hu, X.; Xie, Z.; Liu, F. Assessment of speckle pattern quality in digital image correlation from the perspective of mean bias error. Measurement 2021, 173, 108618. [Google Scholar] [CrossRef]
- Sun, Y.; Pang, J.H. Study of optimal subset size in digital image correlation of speckle pattern images. Opt. Lasers Eng. 2007, 45, 967–974. [Google Scholar]
- Pan, B.; Xie, H.; Wang, Z.; Qian, K.; Wang, Z. Study on subset size selection in digital image correlation for speckle patterns. Opt. Express 2008, 16, 7037–7048. [Google Scholar] [CrossRef]
- Lane, C.; Burguete, R.L.; Shterenlikht, A. An objective criterion for the selection of an optimum dic pattern and subset size. In Proceedings of the XIth International Congress and Exposition on Experimental and Applied Mechanics, Orlando, FL, USA, 2–5 June 2008. [Google Scholar]
- Wang, M.; Cen, Y.; Hu, X.; Yu, X.; Xie, N.; Wu, Y.; Xu, P.; Xu, D. A weighting window applied to the digital image correlation method. Opt. Laser Technol. 2009, 41, 154–158. [Google Scholar] [CrossRef]
- Huang, J.; Pan, X.; Peng, X.; Yuan, Y.; Xiong, C.; Fang, J.; Yuan, F. Digital image correlation with self-adaptive Gaussian windows. Exp. Mech. 2013, 53, 505–512. [Google Scholar] [CrossRef]
- Li, B.J.; Wang, Q.; Duan, D.P.; Chen, J.A. Modified digital image correlation for balancing the influence of subset size choice. Opt. Eng. 2017, 56, 054104. [Google Scholar] [CrossRef]
- Wang, X.; Liu, X.; Zhu, H.; Ma, S. Spatial-temporal subset based digital image correlation considering the temporal continuity of deformation. Opt. Laser Eng. 2017, 90, 247–253. [Google Scholar] [CrossRef]
- Xing, T.; Zhu, H.; Wang, L.; Liu, G.; Ma, Q.; Wang, X.; Ma, S. High accuracy measurement of heterogeneous deformation field using spatial-temporal subset digital image correlation. Measurement 2020, 156, 107605. [Google Scholar] [CrossRef]
- Hagara, M.; Bocko, J. The aspects of stress analysis performed by digital image correlation method related with smoothing and its influence on the results. Acta Mechatron. 2018, 3, 15–21. [Google Scholar] [CrossRef]
- Peng, B.; Zhang, Q.; Zhou, W.; Hao, X.; Ding, L. Modified correlation criterion for digital image correlation considering the effect of lighting variations in deformation measurements. Opt. Eng. 2012, 51, 017004. [Google Scholar] [CrossRef]
- Pan, B.; Wu, D.; Xia, Y. An active imaging digital image correlation method for deformation measurement insensitive to ambient light. Opt. Laser Technol. 2012, 44, 204–209. [Google Scholar] [CrossRef]
- Poncelet, M.; Leclerc, H. A Digital Image Correlation algorithm with light reflection compensation. Exp. Mech. 2015, 55, 1317–1327. [Google Scholar] [CrossRef]
- Simončič, S.; Podržaj, P. An improved digital image correlation calculation in the case of substantial lighting variation. Exp. Mech. 2017, 57, 743–753. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, P.; Zhao, Y. Neighborhood binary speckle pattern for deformation measurements insensitive to local illumination variation by digital image correlation. Appl. Opt. 2017, 56, 4708–4719. [Google Scholar] [CrossRef]
- Li, B.J.; Wang, Q.B.; Duan, D.P.; Chen, J.A. Using grey intensity adjustment strategy to enhance the measurement accuracy of digital image correlation considering the effect of intensity saturation. Opt. Lasers Eng. 2018, 104, 173–180. [Google Scholar] [CrossRef]
- Hu, X.; Xie, Z.; Liu, F. Estimating gray intensities for saturated speckle to improve the measurement accuracy of digital image correlation. Opt. Laser Eng. 2021, 139, 106510. [Google Scholar] [CrossRef]
- ASTM E837-13a; Standard Test Method for Determining Residual Stresses by the Hole-Drilling Strain-Gage Method. American Society for Testing and Materials: West Conshohocken, PA, USA, 2013.
- Rendler, N.J.; Vigness, I. Hole-drilling strain-gage method of measuring residual stresses. Exp. Mech. 1966, 6, 577–586. [Google Scholar] [CrossRef]
- Schajer, G.S. Application of finite element calculations to residual stress measurements. J. Eng. Mater. Technol. 1981, 103, 157–163. [Google Scholar] [CrossRef]
- Schajer, G.S. Measurement of non-uniform residual stress using the hole-drilling method: Part II-Practical application of the integral method. J. Eng. Mater. Technol. 1988, 110, 344–349. [Google Scholar] [CrossRef]
- Schajer, G.S.; Tootonian, M. A new rosette design for more reliable hole-drilling residual stress measurements. Exp. Mech. 1997, 37, 299–306. [Google Scholar] [CrossRef]
- Schajer, G.S.; Whitehead, P.S. Hole-Drilling Method for Measuring Residual Stresses, 1st ed.; Springer Nature Switzerland AG: Cham, Switzerland, 2018; pp. 1–186. [Google Scholar]
- Viotti, M.R.; Dolinko, A.E.; Galizzi, G.E.; Kaufmann, G.H. A portable digital speckle pattern interferometry device to measure residual stresses using the hole drilling technique. Opt. Lasers Eng. 2006, 44, 1052–1066. [Google Scholar] [CrossRef]
- Brynk, T.; Romelczyk-Baishya, B. Residual stress estimation based on 3D DIC displacement filed measurement around drilled holes. Procedia Struct. Integr. 2018, 13, 1267–1272. [Google Scholar] [CrossRef]
- Pástor, M.; Hagara, M.; Virgala, I.; Kaľavský, A.; Sapietová, A.; Hagarová, L. Design of a Unique Device for Residual Stresses Quantification by the Drilling Method Combining the PhotoStress and Digital Image Correlation. Materials 2021, 14, 314. [Google Scholar] [CrossRef]
- Hagara, M.; Trebuňa, F.; Pástor, M.; Huňady, R.; Lengvarský, P. Analysis of the aspects of residual stresses quantification performed by 3D DIC combined with standardized hole-drilling method. Measurement 2019, 137, 238–256. [Google Scholar] [CrossRef]
- Hagara, M.; Pástor, M. A Complex Review of the Possibilities of Residual Stress Analysis Using Moving 2D and 3D Digital Image Correlation System. J. Mech. Eng. 2021, 71, 61–78. [Google Scholar]
- Zhang, Z. A Flexible New Technique for Camera Calibration; Microsoft Research Technical Report MSR-TR-98-71; Microsoft: Redmond, WA, USA, 1998. [Google Scholar]
- Zhang, Z. Flexible Camera Calibration by Viewing a Plane from Unknown Orientations. In Proceedings of the 7th IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999. [Google Scholar]
- Dantec Dynamics. Calibration Targets (DIC): High-Precision DIC Reference Measurement Objects; Data Sheet 0752_v3; Dantec Dynamics: Skovlunde, Denmark, 2022. [Google Scholar]
- Dantec Dynamics. Q-400 User Manual; Dantec Dynamics: Skovlunde, Denmark, 2012. [Google Scholar]
- Dantec Dynamics. Influence of Filter Parameter on Q-4xx Measurement Results; Technical Note; Dantec Dynamics: Skovlunde, Denmark, 2013. [Google Scholar]
- Hagara, M.; Pástor, M.; Delyová, I. Set-up of the Standard 2D-DIC System for Quantification of Residual Stresses. In Proceedings of the EAN 2019—57th Conference on Experimental Stress Analysis, Luhačovice, Czech Republic, 3–6 June 2019. [Google Scholar]




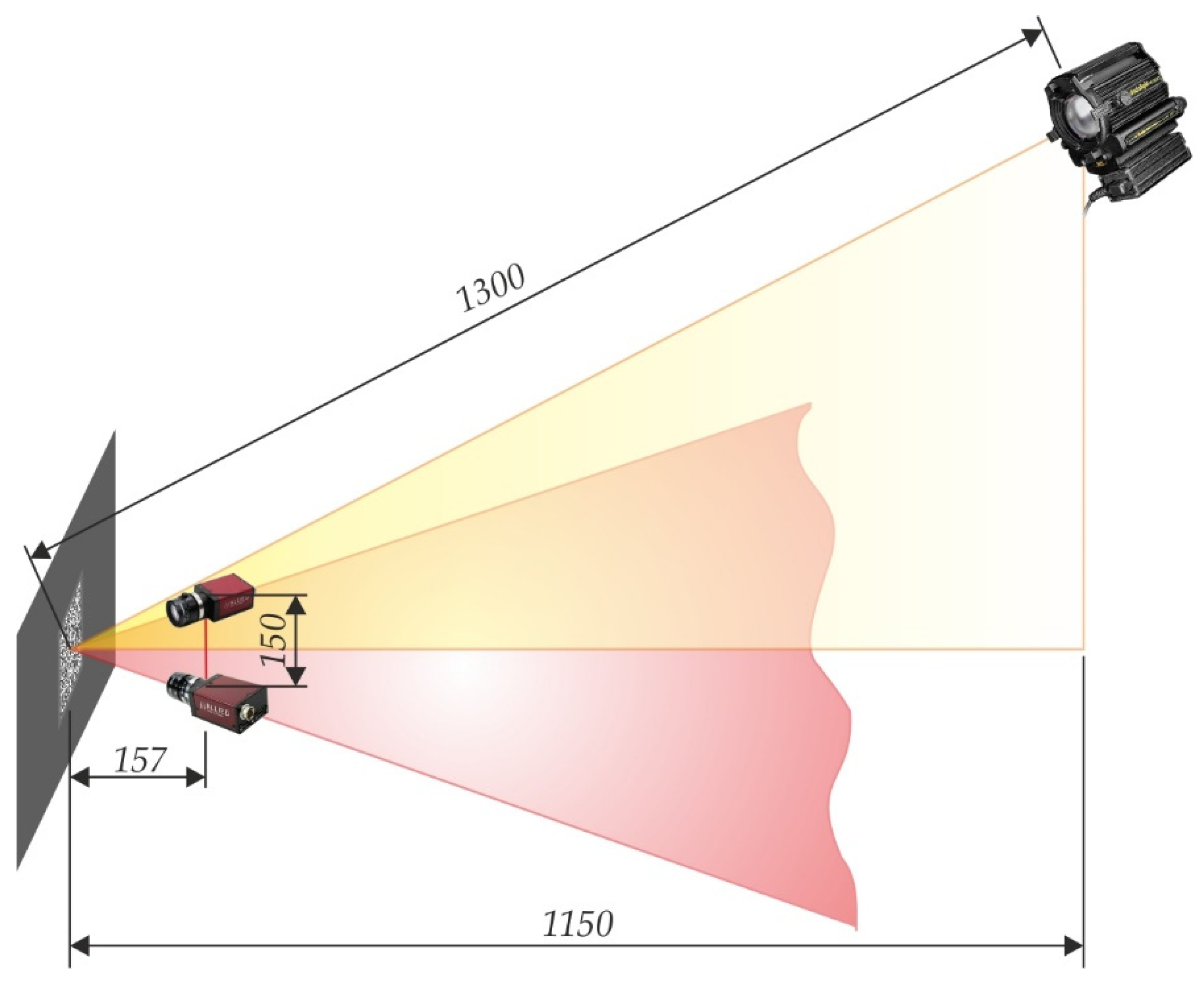
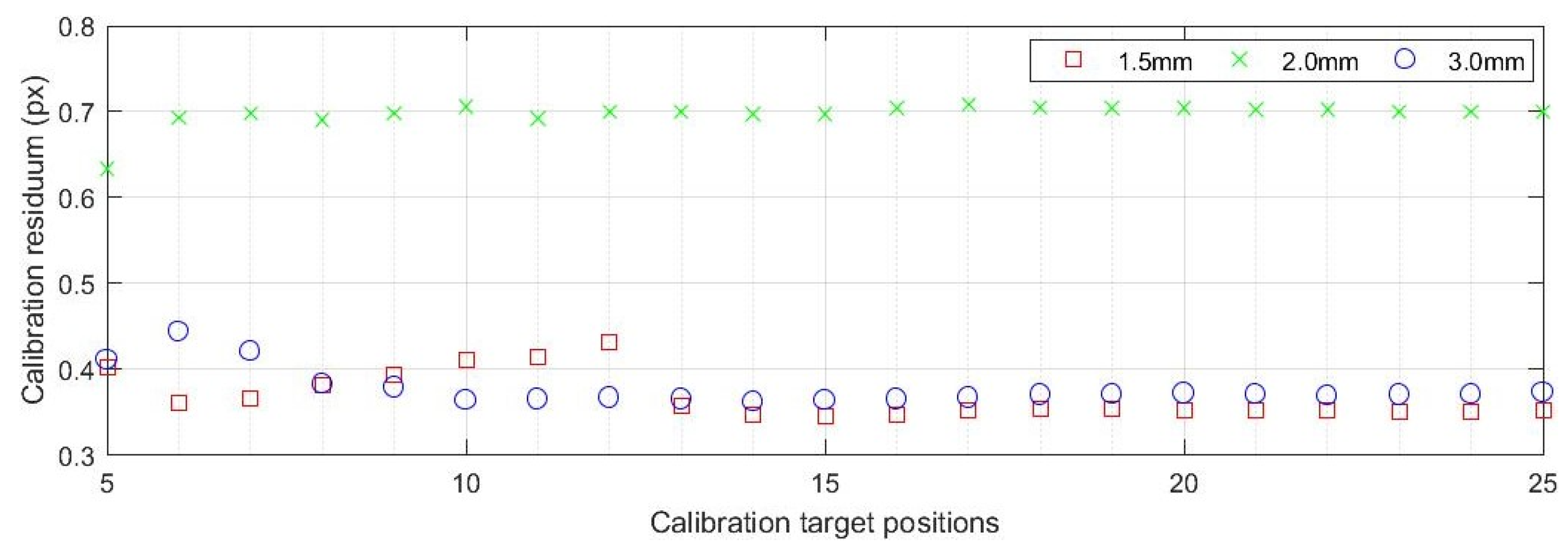


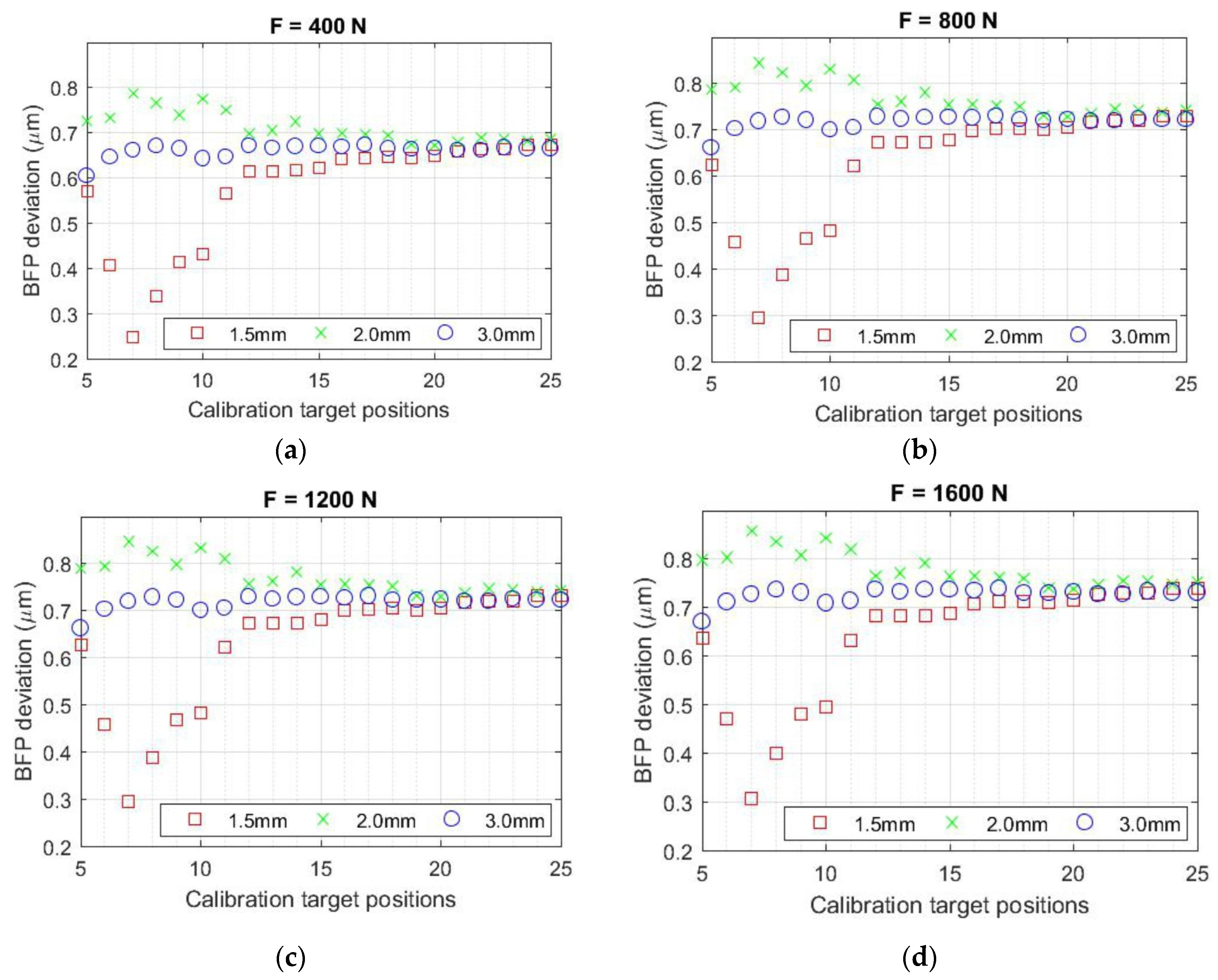
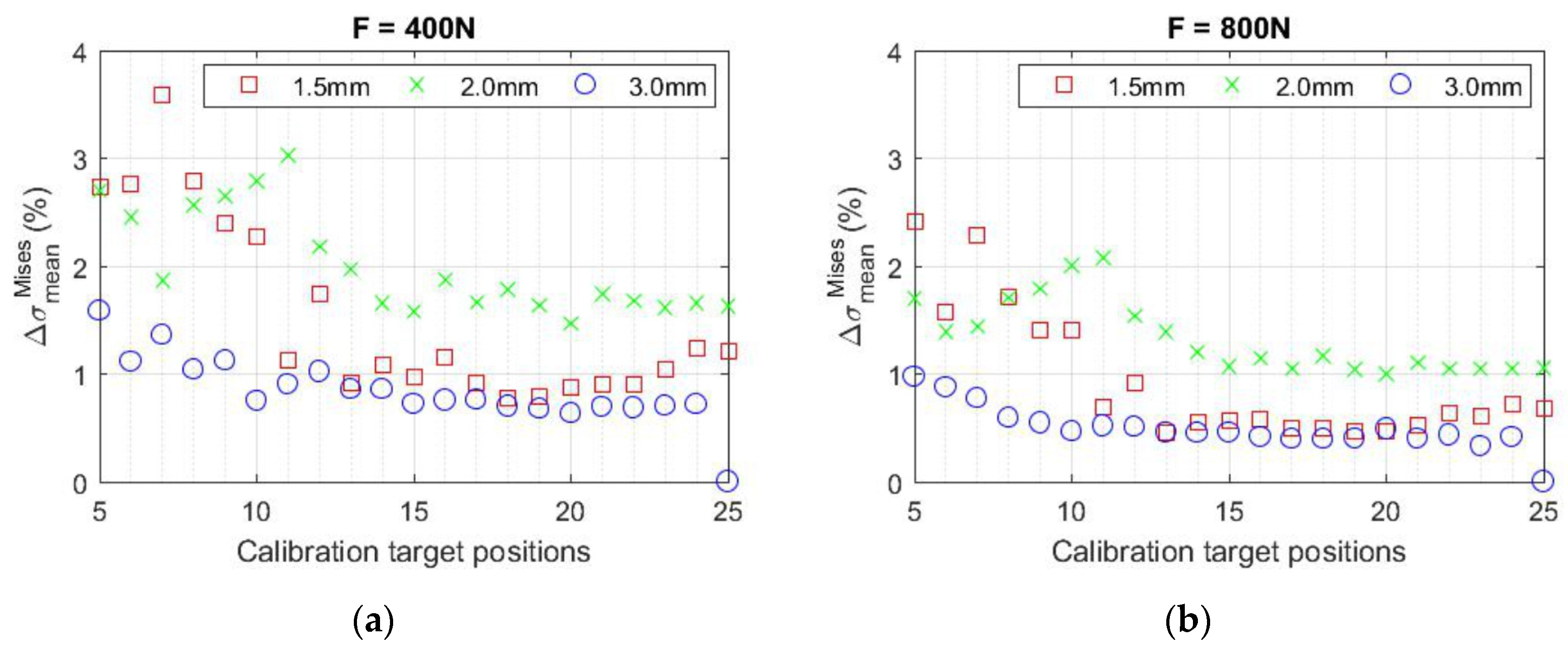

| Parameter | Value |
|---|---|
| Adjusted power of the light source | 200 W |
| Distance between the light source and the specimen | 1.3 m |
| Illumination angle of the specimen surface | 28° |
| Adjusted focus angle of the light source | 30° |
| Colour temperature of the lamp | 5600 K |
| F-number of the lenses | F/16 |
| Camera gain | 0 dB |
| Exposure Time | Exposure Time | ||
|---|---|---|---|
| Measurement 1 | 0.004 s | Measurement 7 | 0.022 s |
| Measurement 2 | 0.007 s | Measurement 8 | 0.025 s |
| Measurement 3 | 0.01 s | Measurement 9 | 0.028 s |
| Measurement 4 | 0.013 s | Measurement 10 | 0.031 s |
| Measurement 5 | 0.016 s | Measurement 11 | 0.034 s |
| Measurement 6 | 0.019 s | Measurement 12 | 0.037 s |
| F = 400 N | F = 800 N | F = 1200 N | F = 1600 N | |
|---|---|---|---|---|
| from 6.8 up to 7.5 | from 3.1 up to 3.6 | from 2.1 up to 2.6 | from 1.6 up to 1.9 |
| Tensile Force | Mean Relative Measurement Errors and Their Standard Deviations (%) | ||
|---|---|---|---|
| Calibration target 1.5 mm | Calibration target 2.0 mm | Calibration target 3.0 mm | |
| F = 400 N | 6.65 ± 0.31 | 6.70 ± 0.33 | 6.66 ± 0.32 |
| F = 800 N | 3.05 ± 0.14 | 3.07 ± 0.14 | 3.04 ± 0.14 |
| F = 1200 N | 2.17 ± 0.10 | 2.17 ± 0.09 | 2.16 ± 0.09 |
| F = 1600 N | 1.63 ± 0.08 | 1.65 ± 0.08 | 1.64 ± 0.08 |
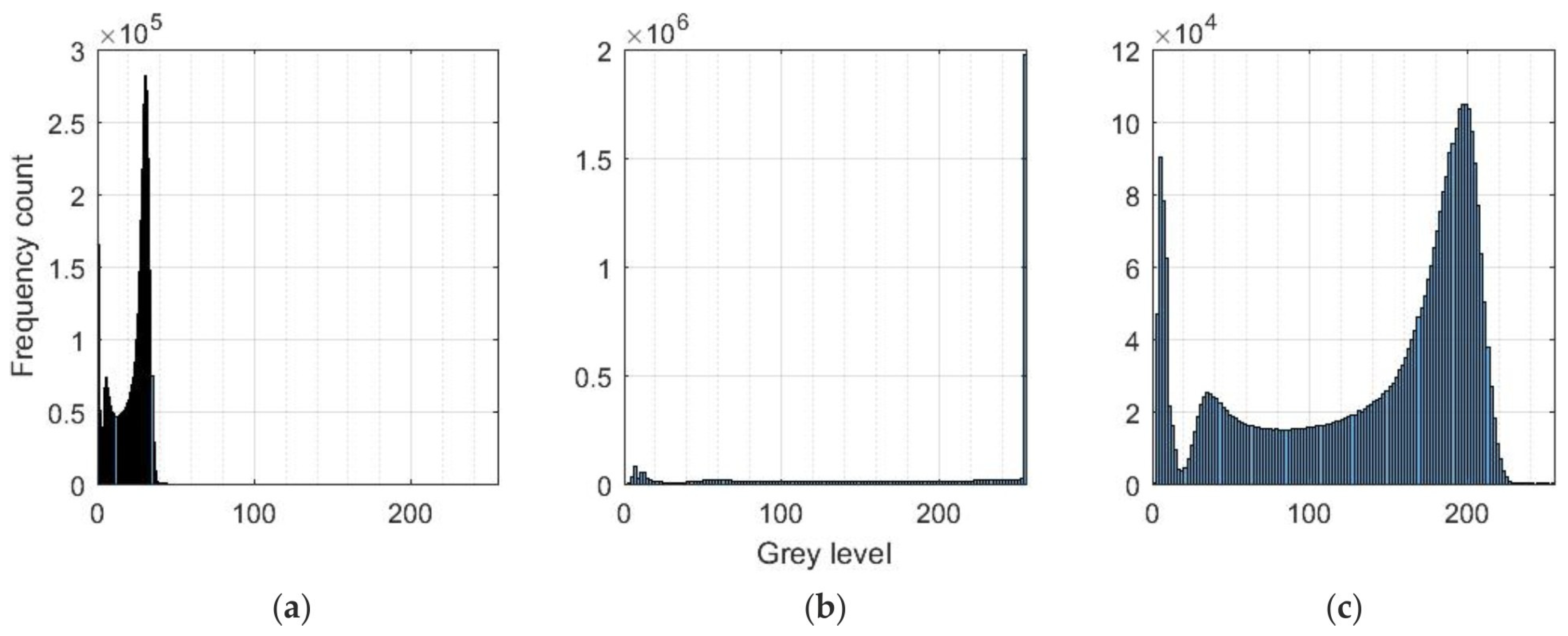
| Image Quality | MGV | Consequence |
|---|---|---|
| unsuitable too dark images | less than 22 | measurement evaluation issues |
| underexposed images | from 22 up to 55 | increase in deviation in the evaluated stresses |
| suitable image brightness | from 56 up to 171 | deviation in the evaluated stresses approximately at the measurement error level |
| overexposed images | from 172 up to 194 | increase in deviation in the evaluated stresses |
| unsuitable too bright images | more than 194 | measurement evaluation issues |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hagara, M.; Huňady, R.; Lengvarský, P.; Vocetka, M.; Palička, P. The Calibration Process and Setting of Image Brightness to Achieve Optimum Strain Measurement Accuracy Using Stereo-Camera Digital Image Correlation. Appl. Sci. 2023, 13, 9512. https://doi.org/10.3390/app13179512
Hagara M, Huňady R, Lengvarský P, Vocetka M, Palička P. The Calibration Process and Setting of Image Brightness to Achieve Optimum Strain Measurement Accuracy Using Stereo-Camera Digital Image Correlation. Applied Sciences. 2023; 13(17):9512. https://doi.org/10.3390/app13179512
Chicago/Turabian StyleHagara, Martin, Róbert Huňady, Pavol Lengvarský, Michal Vocetka, and Peter Palička. 2023. "The Calibration Process and Setting of Image Brightness to Achieve Optimum Strain Measurement Accuracy Using Stereo-Camera Digital Image Correlation" Applied Sciences 13, no. 17: 9512. https://doi.org/10.3390/app13179512
APA StyleHagara, M., Huňady, R., Lengvarský, P., Vocetka, M., & Palička, P. (2023). The Calibration Process and Setting of Image Brightness to Achieve Optimum Strain Measurement Accuracy Using Stereo-Camera Digital Image Correlation. Applied Sciences, 13(17), 9512. https://doi.org/10.3390/app13179512






