Surface Motion for P-Wave Scattering by an Arbitrary-Shaped Canyon in Saturated Half-Space
Abstract
:1. Introduction
2. Computational Model and Governing Equations
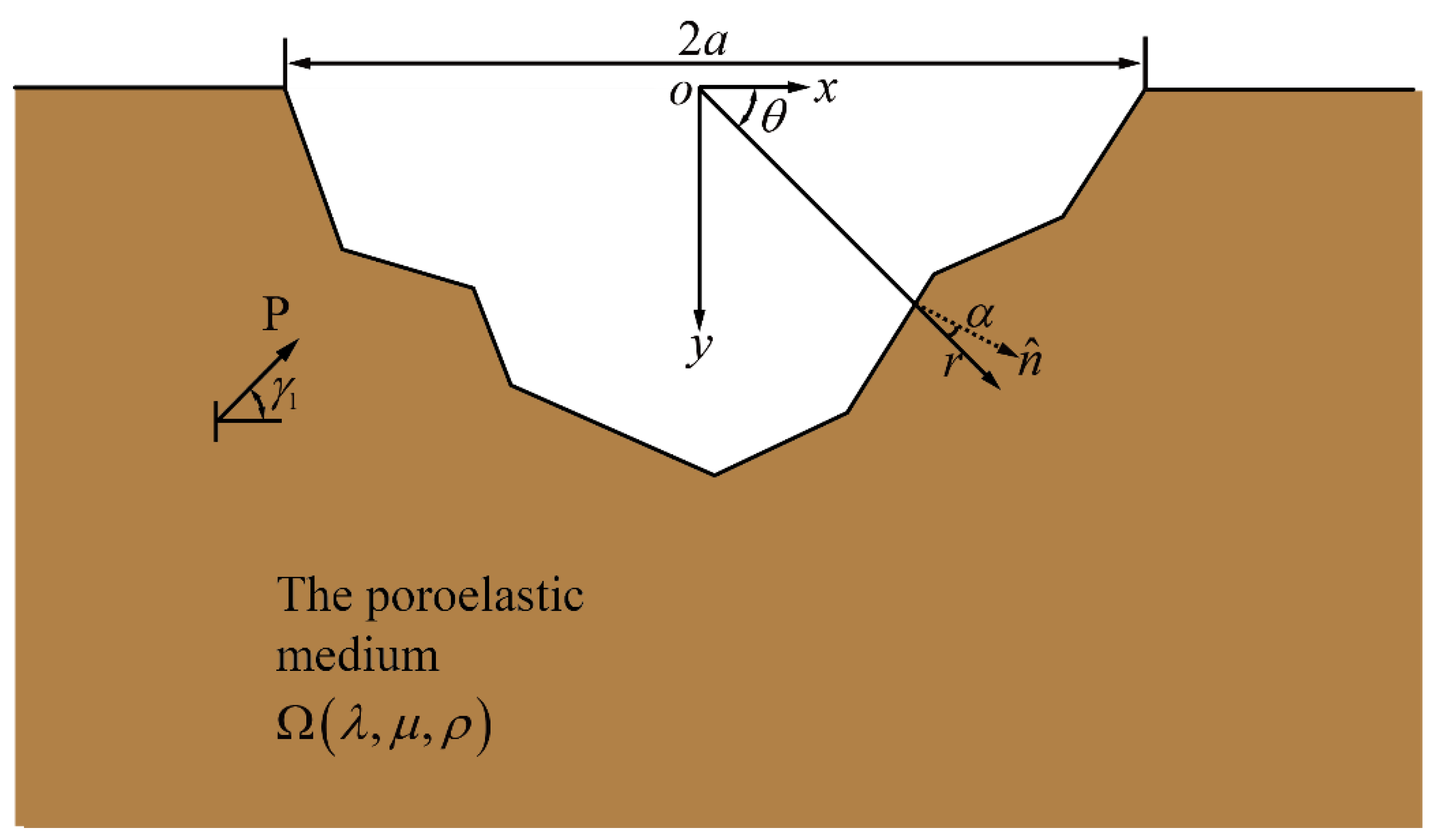
2.1. Computational Model
2.2. Biot’s Theory
3. Methodology
3.1. Boundary Conditions
3.2. Wavefield Analysis
3.2.1. Free-Field
3.2.2. Scattering Waves
3.3. Expression of Stress and Displacement
3.4. The Solution
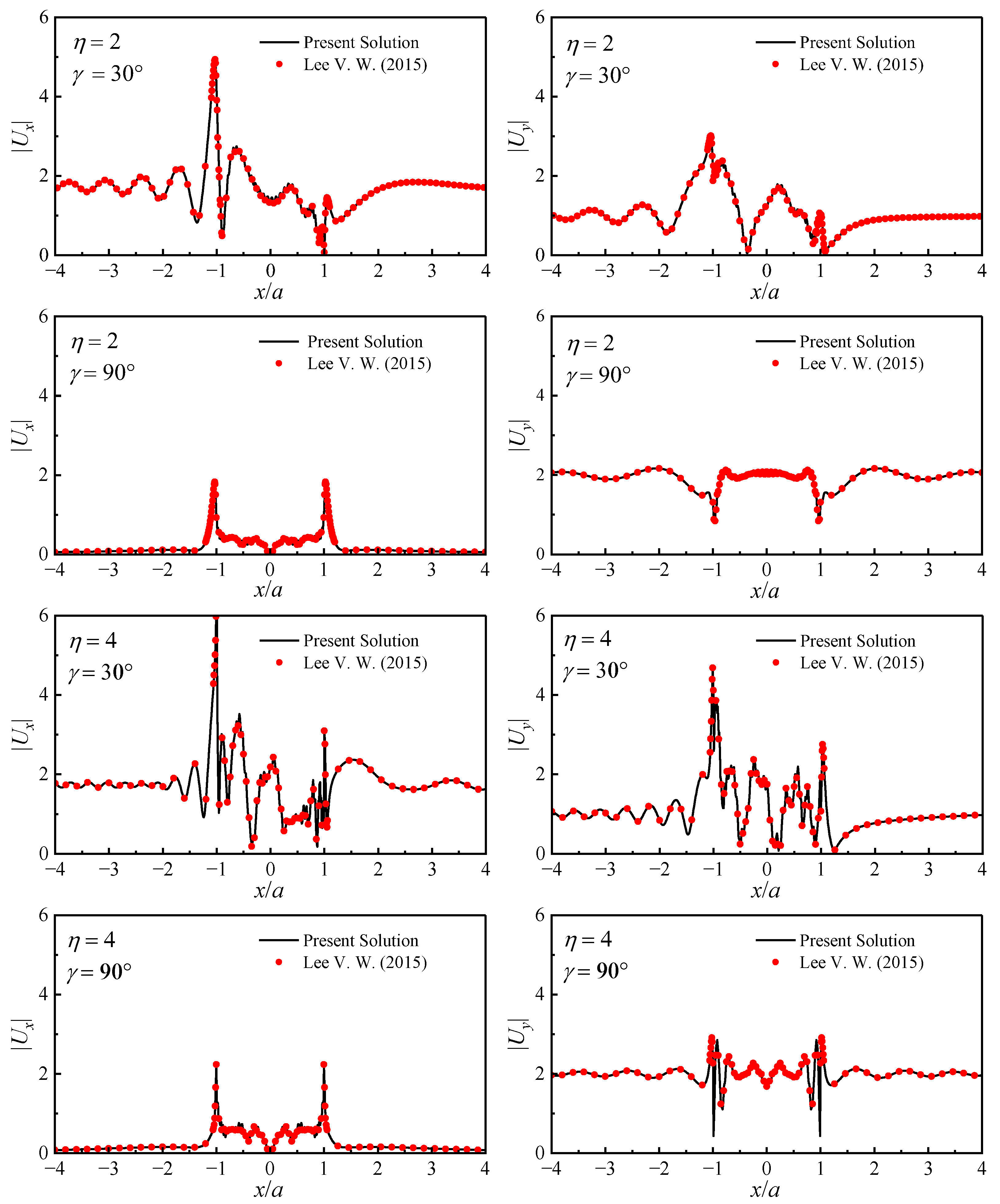
4. Verification
5. Parameter Analysis
5.1. Semicircular Canyon
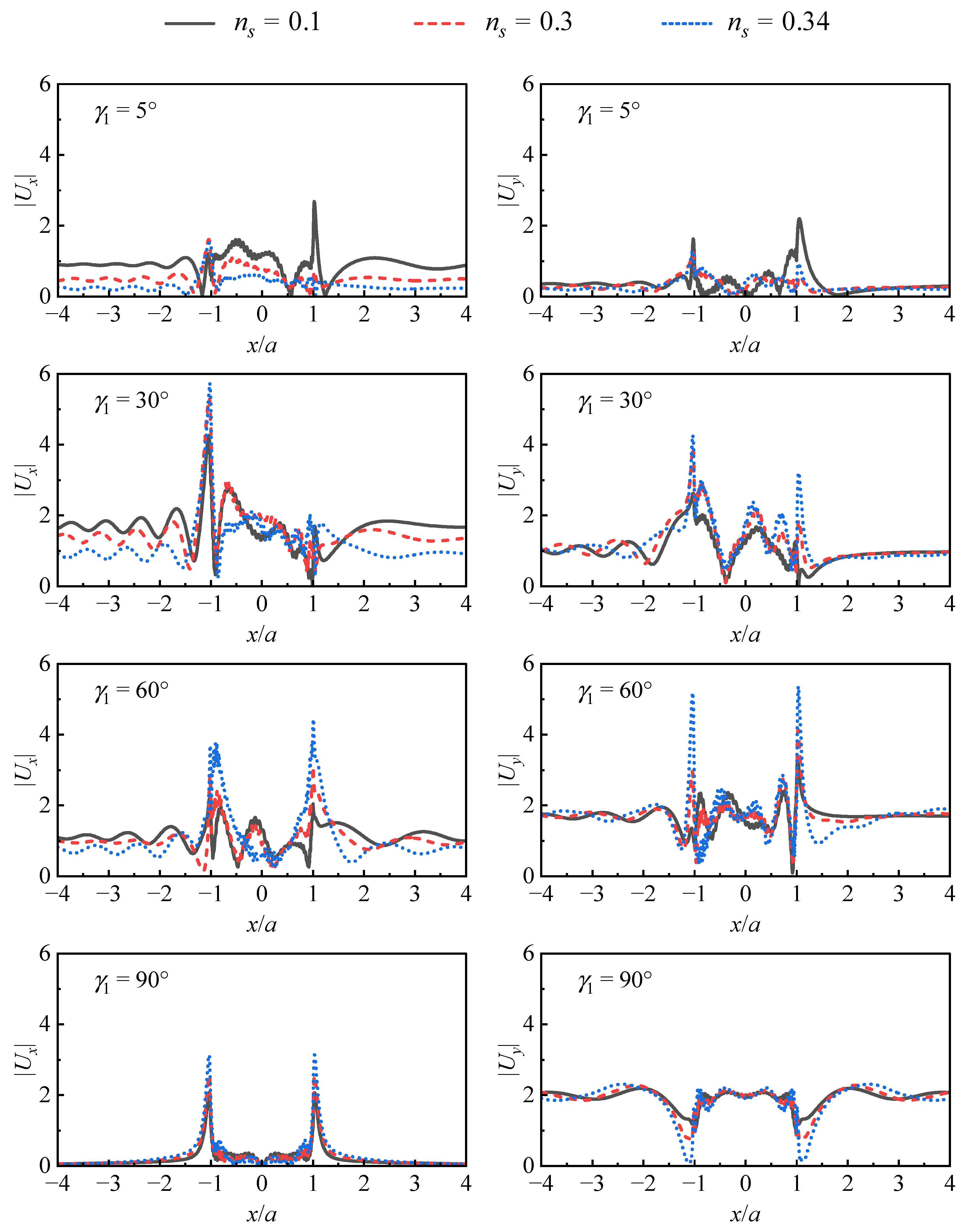
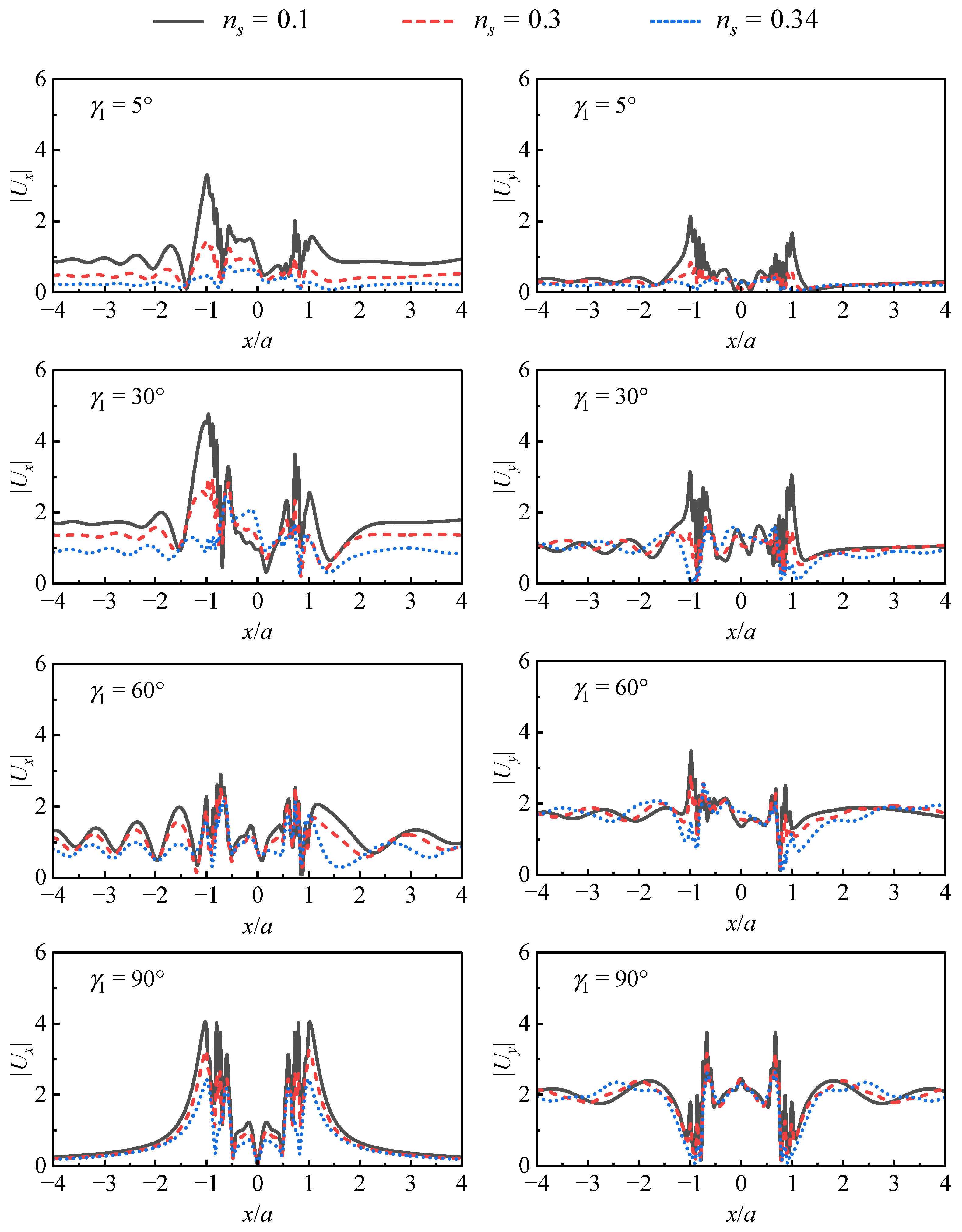
5.1.1. Medium Porosity
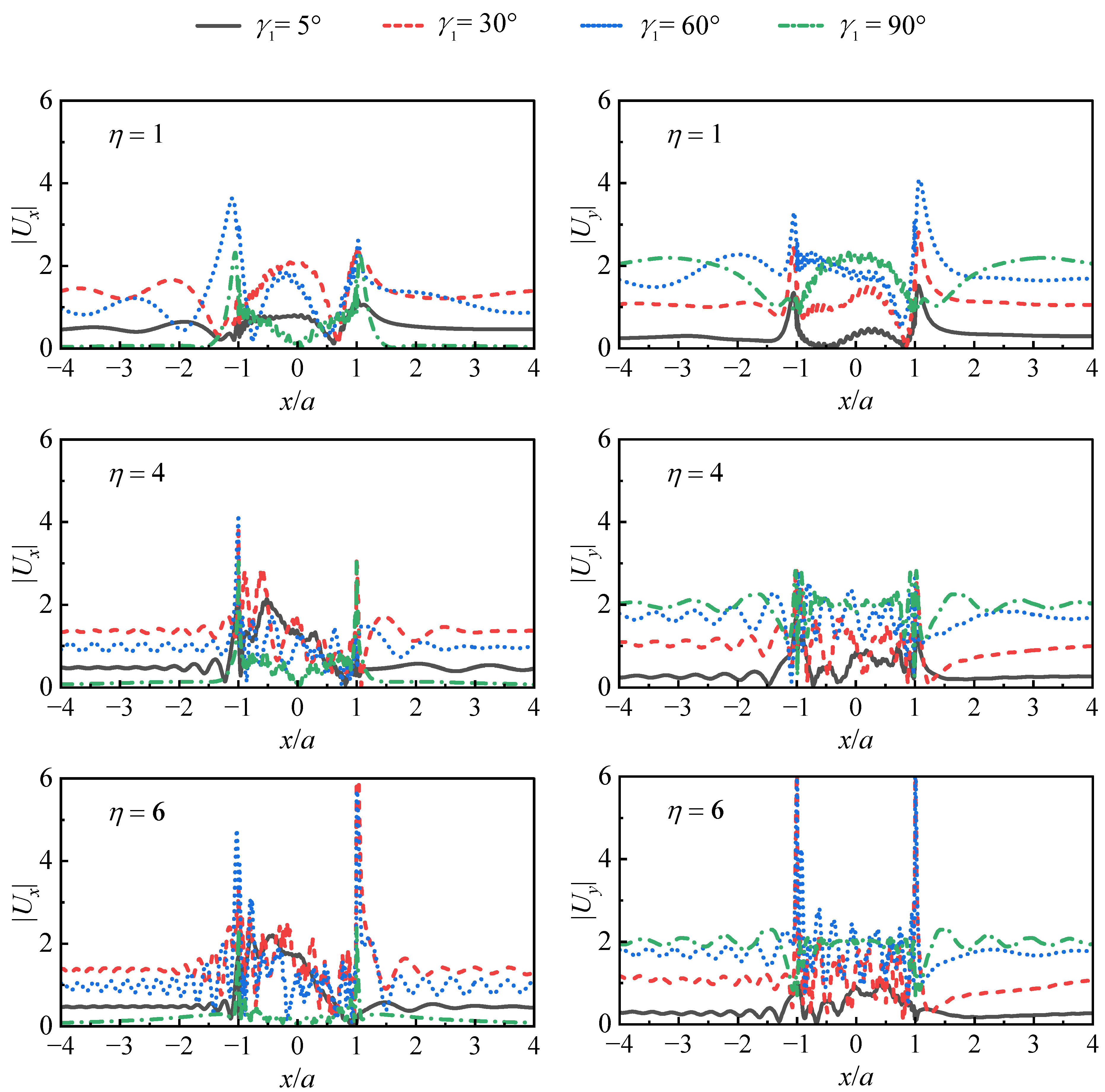
5.1.2. Incident Angle
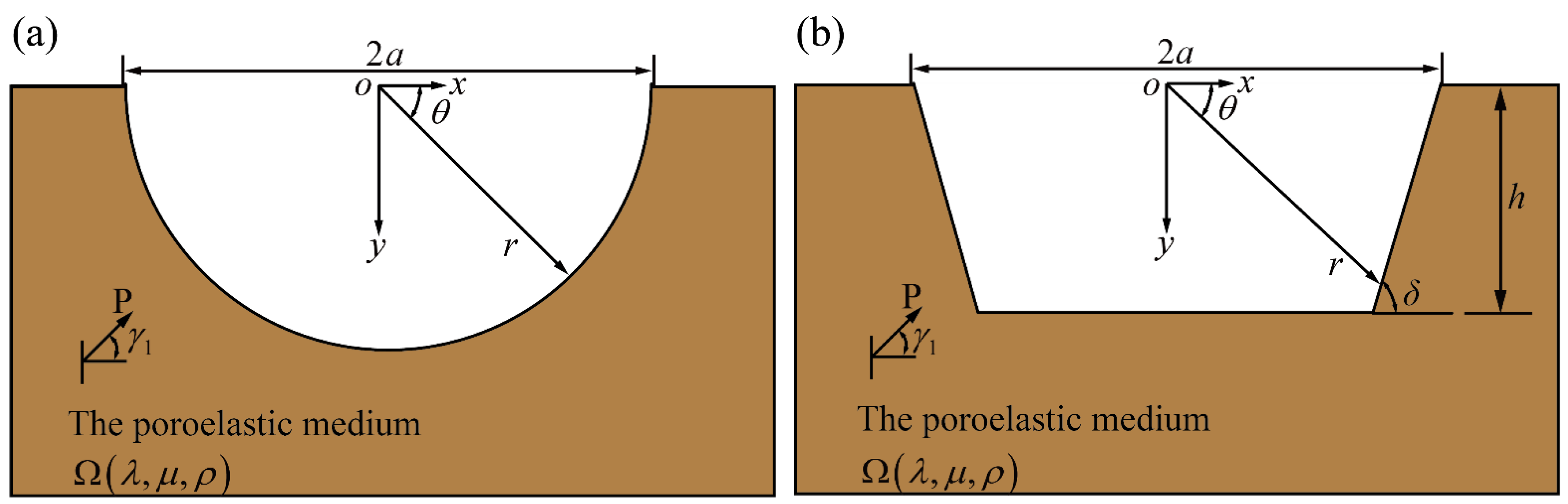
5.2. Trapezoidal Canyon
5.2.1. Medium Porosity
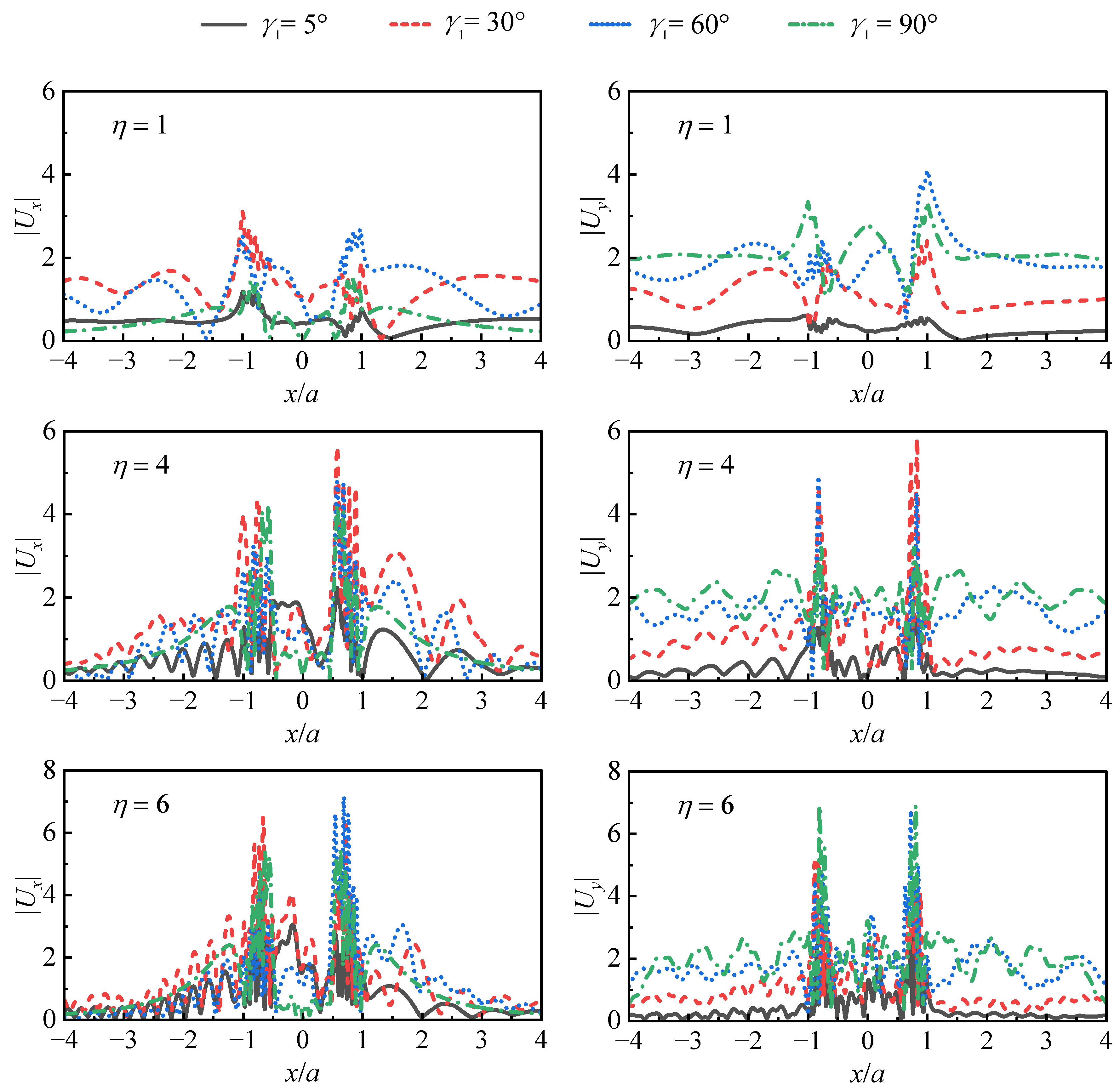
5.2.2. Incident Angle
6. Conclusions
- The incidence angle has an obvious influence on the displacement amplitude. For the solved cases, almost all of them meet the following rules: for x-component displacement, when the P-wave is oblique incident at the incidence angle γ1 = 30°, the displacement amplitude is the largest, followed by 60°, 5°, and 90°; for y-component displacement, the amplitude of displacement is the largest when the P-wave is vertically incident at the incident angle γ1 = 90°, which is 60°, 30°, and 5°, successively.
- Compared with the incidence angle, porosity has little influence on the amplitude of displacement, especially for y-component displacement. The displacement curves of the three kinds of porosity almost coincide on the front side and backside of the canyon, but there is a slight difference in the inner part of the canyon. The effect on the displacement amplitude in the horizontal direction is more significant, and the displacement amplitude is smaller and smaller as the porosity increases on the whole.
- The influence of the shape of the canyon on displacement amplitude is mainly reflected in the shielding effect on the incident wave. At the same dimensionless frequency, the ground surface displacement of the trapezoidal canyon is more oscillating than that of the semicircular canyon, indicating that the trapezoidal canyon has a more shielding effect on the incident wave.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Gao, Y.; Dai, D.; Zhang, N. Progress and prospect of topographic amplification effects of seismicwave in canyon sites. J. Disaster Prev. Mitig. Eng. 2021, 41, 734–752. [Google Scholar]
- Fu, L.; Chen, S.; Li, J.; Zhang, L.; Xie, J.; Li, X. Regional Spectral Characteristics Derived Using the Generalized Inversion Technique and Applications to Stochastic Simulation of the 2021 Mw 6.1 Yangbi Earthquake. Bull. Seismol. Soc. Am. 2023, 113, 378–400. [Google Scholar] [CrossRef]
- Trifunac, M.D. Scattering of plane SH waves by a semi-cylindrical canyon. Earthq. Eng. Struct. Dyn. 1972, 1, 267–281. [Google Scholar] [CrossRef]
- Cao, H.; Lee, V.W. Scattering and diffraction of plane P waves by circular cylindrical canyons with variable depth-to-width ratio. Eur. J. Obstet. Gynecol. Reprod. Biol. 1979, 9, 141–150. [Google Scholar] [CrossRef]
- Lee, V.W.; Cao, H. Diffraction of SV waves by circular canyons of various depths. J. Eng. Mech. 1989, 115, 2035–2056. [Google Scholar] [CrossRef]
- Gregory, R.D. An expansion theorem applicable to problems of wave propagation in an elastic half-space containing a cavity. Math. Proc. Camb. Philos. Soc. Camb. Univ. Press 1967, 63, 1341–1367. [Google Scholar] [CrossRef]
- Tsaur, D.H.; Chang, K.H. An analytical approach for the scattering of SH waves by a symmetrical V-shaped canyon: Shallow case. Geophys. J. Int. 2008, 174, 255–264. [Google Scholar] [CrossRef]
- Tsaur, D.H.; Chang, K.H.; Hsu, M.S. An analytical approach for the scattering of SH waves by a symmetrical V-shaped canyon: Deep case. Geophys. J. Int. 2010, 183, 1501–1511. [Google Scholar] [CrossRef]
- Zhang, N.; Pan, J.; Gao, Y.; Zhang, Y.; Dai, D.; Chen, X. Analytical approach to scattering of SH waves by an arbitrary number of semicircular canyons in an elastic half space. Soil Dyn. Earthq. Eng. 2021, 146, 106762. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, Y.; Gao, Y.; Pak, R.; Yan, J. Site amplification effects of a radially multi-layered semi-cylindrical canyon on seismic response of an earth and rockfill dam. Soil Dyn. Earthq. Eng. 2019, 116, 145–163. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, Y.; Gao, Y.; Pak, R.; Wu, Y.; Zhang, F. An exact solution for SH-wave scattering by a radially multilayered inhomogeneous semicylindrical canyon. Geophys. J. Int. 2019, 217, 1232–1260. [Google Scholar] [CrossRef]
- Panji, M. A half-space TD-BEM model for a seismic corrugated orthotropic stratum. Eng. Anal. Bound. Elem. 2023, 152, 655–677. [Google Scholar] [CrossRef]
- Mojtabazadeh-Hasanlouei, S.; Panji, M.; Kamalian, M. Scattering attenuation of transient SH-wave by an orthotropic gaussian-shaped sedimentary basin. Eng. Anal. Bound. Elem. 2022, 140, 186–219. [Google Scholar] [CrossRef]
- Parvanova, S.; Vasilev, G.; Dineva, P. Hybrid modelling of multi-layered geological structure under seismic excitation. J. Seismol. 2020, 24, 183–202. [Google Scholar] [CrossRef]
- Lee, V.W.; Liu, W. Two-dimensional scattering and diffraction of P- and SV-waves around a semi-circular canyon in an elastic half-space: An analytic solution via a stress-free wave function. Soil Dyn. Earthq. Eng. 2014, 63, 110–119. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Q.; Deng, P. Surface motion of a half-space with a semicylindrical canyon under P, SV, and Rayleigh waves. Bull. Seismol. Soc. Am. 2017, 107, 809–820. [Google Scholar] [CrossRef]
- Liu, D.; Gai, B.; Tao, G. Applications of the method of complex functions to dynamic stress concentrations. Wave Motion 1982, 4, 293–304. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, T.; Zhang, J. A new series solution method for two–dimensional elastic wave scattering along a canyon in half-space. Soil Dyn. Earthq. Eng. 2016, 89, 128–135. [Google Scholar] [CrossRef]
- Hans, S. Boundary Methods: An Algebraic Theory. SIAM Rev. 1986, 28, 278–279. [Google Scholar]
- Lee, V.W.; Wu, X. Application of the weighted residual method to diffraction by 2D canyons of arbitrary shape: II. Incident P, SV and Rayleigh waves. Soil Dyn. Earthq. Eng. 1994, 13, 365–375. [Google Scholar] [CrossRef]
- Lee, V.W.; Brandow, H.P. Weighted residual method for diffraction of plane P-waves in a 2D elastic half-space revisited: On an almost circular arbitrary-shaped canyon. J. Earthq. 2015, 2015, 543128. [Google Scholar] [CrossRef]
- Brandow, H.P.; Lee, V.W. Scattering and diffraction of plane P-waves in a 2D elastic half-space II: Shallow arbitrary shaped canyon. Earthq. Eng. Eng. Vib. 2017, 16, 459–485. [Google Scholar] [CrossRef]
- Brandow, H.P.; Lee, V.W. Weighted residual method for diffraction of plane P-waves in a 2D elastic half-space Ⅲ: On an almost circular arbitrary-shaped alluvial valley. Earthq. Sci. 2018, 31, 19–34. [Google Scholar] [CrossRef]
- Biot, M.A.; Willis, D.G. The elastic coefficients of the theory of consolidation. J. Appl. Mech. 1957, 24, 594–601. [Google Scholar] [CrossRef]
- Deresiewicz, H. The effect of boundaries on wave propagation in a liquid-filled porous solid. Bull. Seismol. Soc. Am. 1960, 50, 599–607. [Google Scholar] [CrossRef]
- Carcione, J.M. Wave Fields in Real Media: Wave Propagation in Anisotropic, Anelastic, Porous and Electromagnetic Media; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Li, W.; Zhao, C. Scattering of plane SV waves by cylindrical canyons in saturated porous medium. Solid Dyn. Earthq. Eng. 2005, 25, 981–995. [Google Scholar]
- Liang, J.; Ba, Z.; Lee, V.W. Diffraction of plane SV waves by a shallow circular-arc canyon in a saturated poroelastic half-space. Solid Dyn. Earthq. Eng. 2006, 26, 582–610. [Google Scholar] [CrossRef]
- Satyam, N.D.; Towhata, I. Site-Specific Ground Response Analysis and Liquefaction Assessment of Vijayawada City (India). Nat. Hazards 2016, 81, 705–724. [Google Scholar] [CrossRef]
- Zhang, G.; Yang, Y.; Song, Y.; Cao, Y. Ground motion around a semi-cylindrical canyon in saturated soil: P wave incidence. Waves Random Complex Media 2022, 1–12. [Google Scholar] [CrossRef]
- Barak, M.S.; Kumar, M.; Kumari, M.; Singh, A. Inhomogeneous wave propagation in partially saturated soils. Wave Motion 2020, 93, 102470. [Google Scholar] [CrossRef]
- Kumari, M.; Singh, A.; Barak, M.S.; Kumar, M. Horizontal and vertical motion at the surface of partially saturated soils layer sandwiched between water and elastic solid. Waves Random Complex Media 2022, 1–25. [Google Scholar] [CrossRef]
- Feng, G.; Xie, L.; Chow Su, T. SV-wave scattering by an underwater circular cylindrical canyon in a saturated poroelastic half-space. Waves Random Complex Media 2023, 1–44. [Google Scholar] [CrossRef]
- Martínez Calzada, V.; Arizpe Carreón, P.; Basaldúa Sanchez, J.; Rodríguez Castellanos, A. A Numerical Based Parametric Study on Seismic Amplifications Due to Soft Deposits on Seabed. J. Earthq. Eng. 2022, 26, 3660–3679. [Google Scholar] [CrossRef]
- Lin, C.; Lee, V.W.; Trifunac, M.D. The reflection of plane waves in a poroelastic half-space saturated with inviscid fluid. Solid Dyn. Earthq. Eng. 2005, 25, 205–223. [Google Scholar] [CrossRef]
- Liu, Q.; Yue, C.; Zhao, M. Scattering of harmonic P1 and SV waves by a shallow lined circular tunnel in a poroelastic half-plane. Solid Dyn. Earthq. Eng. 2022, 158, 107306. [Google Scholar] [CrossRef]
- Hasheminejad, S.M.; Avazmohammadi, R. Harmonic wave diffraction by two circular cavities in a poroelastic formation. Soil Dyn. Earthq. Eng. 2007, 27, 29–41. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, X.; Jin, L.; Zhou, Z. Surface Motion for P-Wave Scattering by an Arbitrary-Shaped Canyon in Saturated Half-Space. Appl. Sci. 2023, 13, 9566. https://doi.org/10.3390/app13179566
Duan X, Jin L, Zhou Z. Surface Motion for P-Wave Scattering by an Arbitrary-Shaped Canyon in Saturated Half-Space. Applied Sciences. 2023; 13(17):9566. https://doi.org/10.3390/app13179566
Chicago/Turabian StyleDuan, Xueliang, Liguo Jin, and Zhenghua Zhou. 2023. "Surface Motion for P-Wave Scattering by an Arbitrary-Shaped Canyon in Saturated Half-Space" Applied Sciences 13, no. 17: 9566. https://doi.org/10.3390/app13179566
APA StyleDuan, X., Jin, L., & Zhou, Z. (2023). Surface Motion for P-Wave Scattering by an Arbitrary-Shaped Canyon in Saturated Half-Space. Applied Sciences, 13(17), 9566. https://doi.org/10.3390/app13179566






