Runtime Construction of Large-Scale Spiking Neuronal Network Models on GPU Devices
Abstract
:1. Introduction
2. Materials and Methods
2.1. Creation of Connections Directly in GPU Memory
- One-to-one (one_to_one):with .
- All-to-all (all_to_all):with .
- Random, fixed out-degree with multapses (fixed_outdegree):where K is the out-degree, i.e., the number of output connections per source node, is a random integer between 0 and sampled from a uniform distribution, and .
- Random, fixed in-degree with multapses (fixed_indegree):where K is the in-degree, i.e., the number of input connections per target node, and .
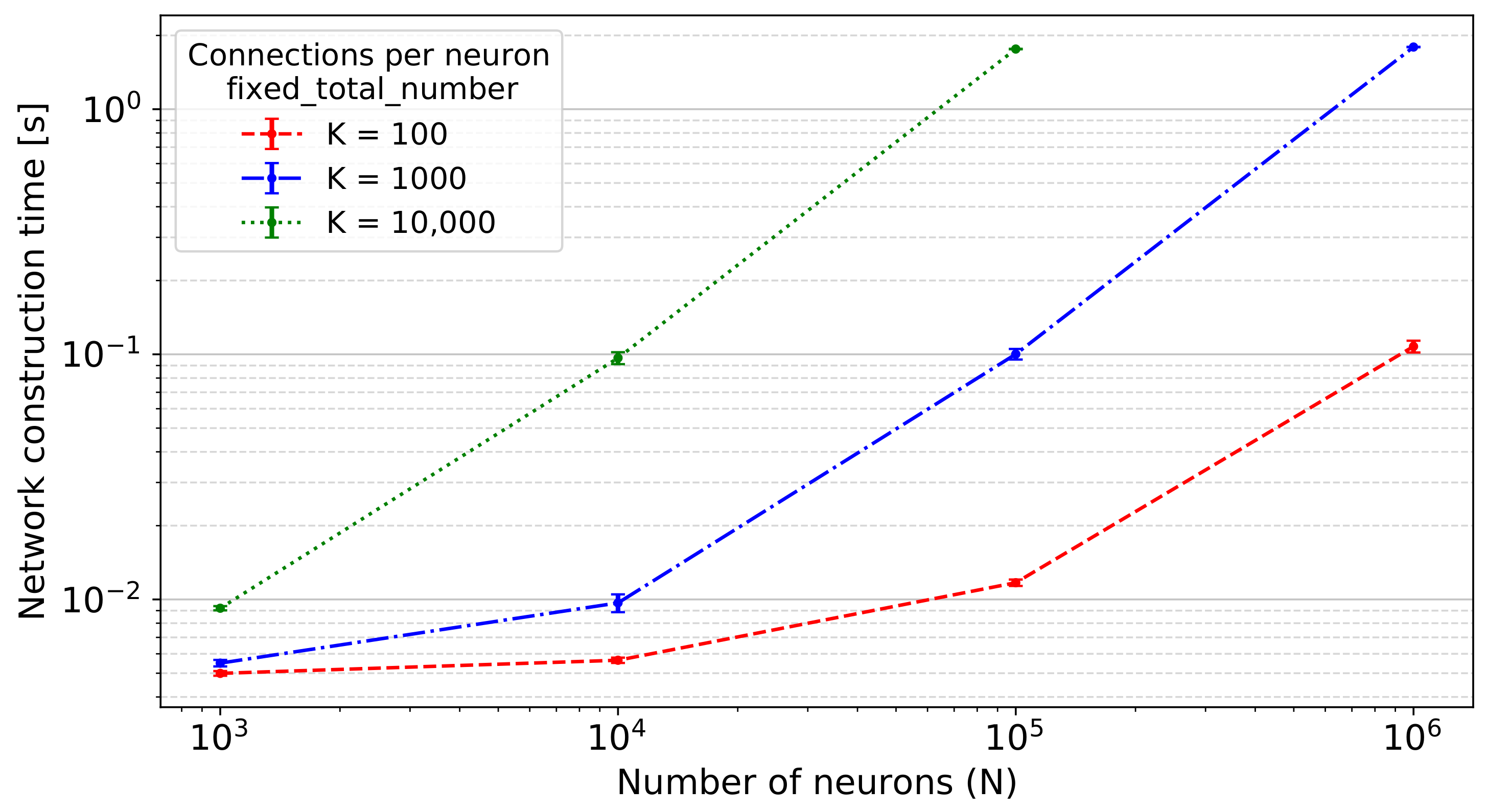
- Random, fixed total number with multapses (fixed_total_number):where pairs of sources and targets are sampled until the specified total number of connections is reached.
2.2. Data Structures Used for Connections
2.3. The Spike Buffer
2.4. Models Used for Performance Evaluation
- fixed_total_number:The total number of connections used in each connect call is set to .
- fixed_indegree:The in-degree used in each connect call is set to .
- fixed_outdegree:The out-degree used in each connect call is set to .
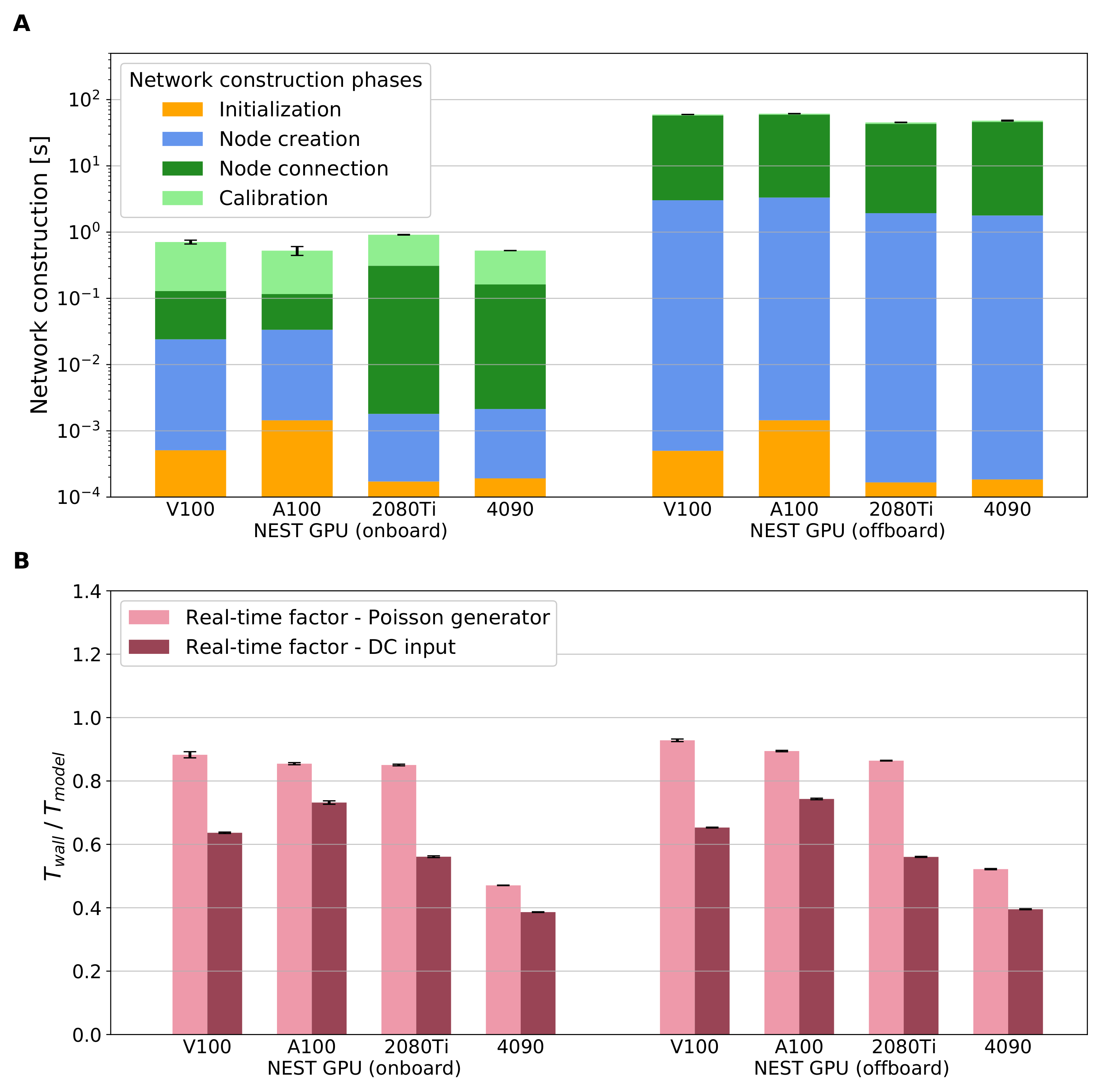
2.5. Hardware and Software of Performance Evaluation
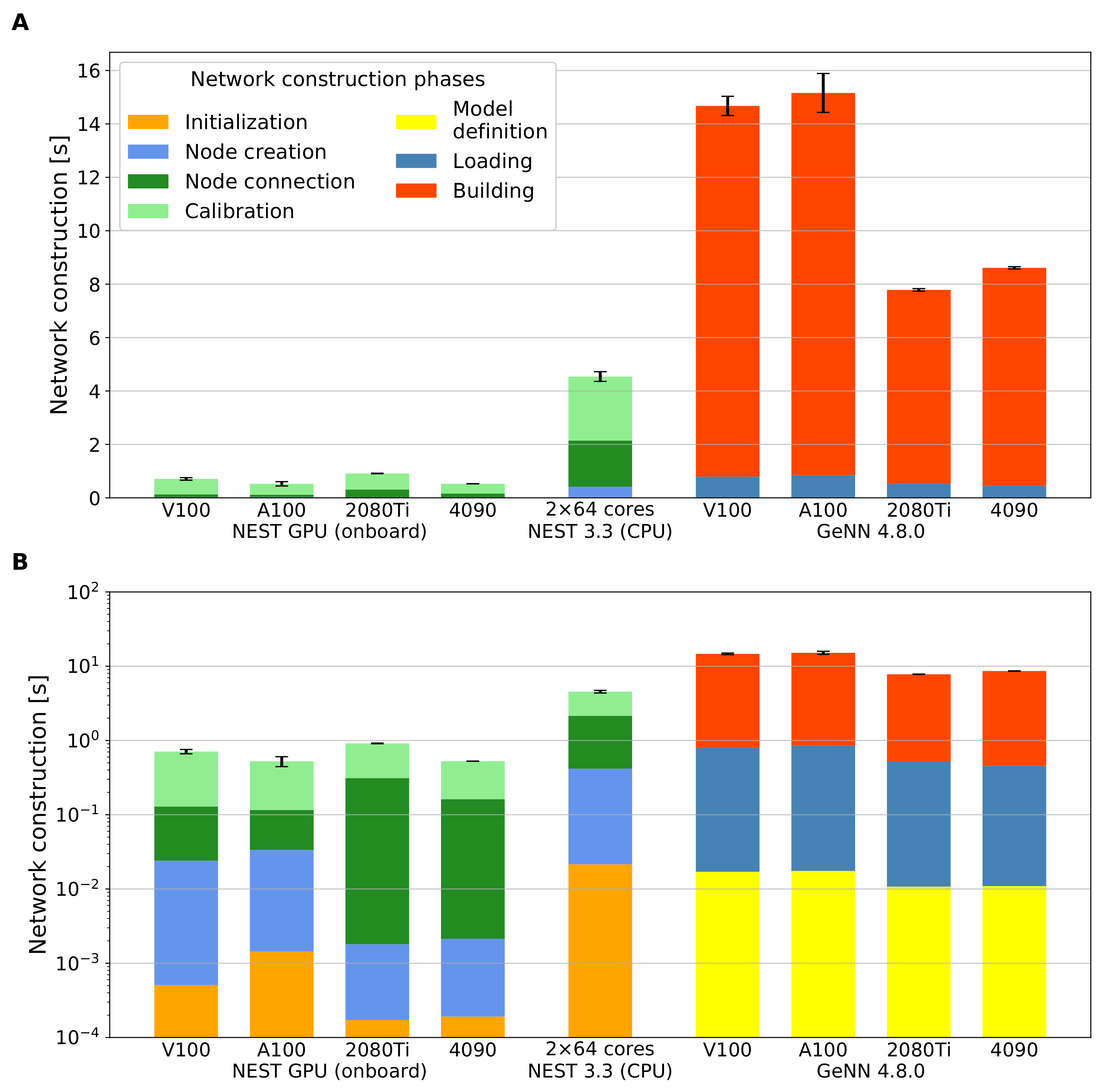
2.6. Simulation Phases
- Initialization is a setup phase in the Python script for preparing both model and simulator by importing modules, instantiating a class, or setting parameters, etc.
- import nestgpu
- Node creation instantiates all the neurons and devices of the model.
- nestgpu.Create()
- Node connection instantiates the connections among network nodes.
- nestgpu.Connect()
- Calibration is a preparation phase that orders the connections and initializes data structures for the spike buffers and the spike arrays just before the state propagation begins. In the CPU code, the pre-synaptic connection infrastructure is set up here. This stage can be triggered by simulating just one time step h.
- nestgpu.Simulate(h)
Previously, the calibration phase of NEST GPU was used to finish moving data to the GPU memory and instantiate additional data structures like the spike buffer (cf. Section 2.3). Now, as no data transfer is needed and connection sorting is carried out instead (cf. Section 2.2), the calibration phase is now conceptually closer to the operations carried out in the CPU version of NEST [37].
- Model definition defines neurons and devices and synapses of the network model.
- from pygenn import genn_model
- model = genn_model.GeNNModel()
- model.add_neuron_population()
- Building generates and compiles the simulation code.
- model.build()
- Loading allocates memory and instantiates the network on the GPU.
- model.load()
2.7. Validation of the Proposed Network Construction Method
- Time-averaged firing rate for each neuron;
- Coefficient of variation of inter-spike intervals (CV ISI);
- Pairwise Pearson correlation of the spike trains obtained from a subset of 200 neurons for each population.
3. Results
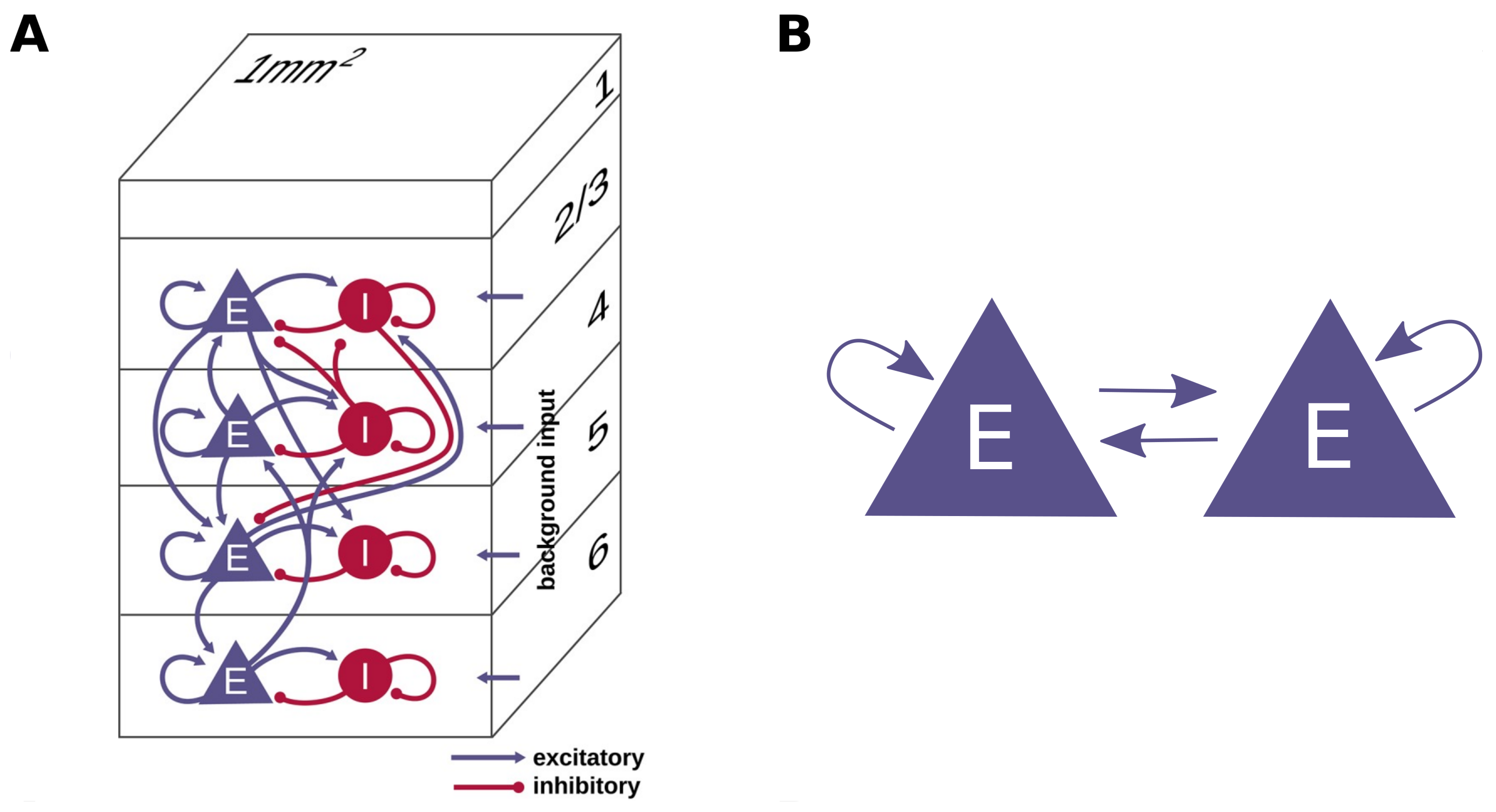
3.1. Cortical Microcircuit Model
3.2. Two-Population Network
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Block Sorting
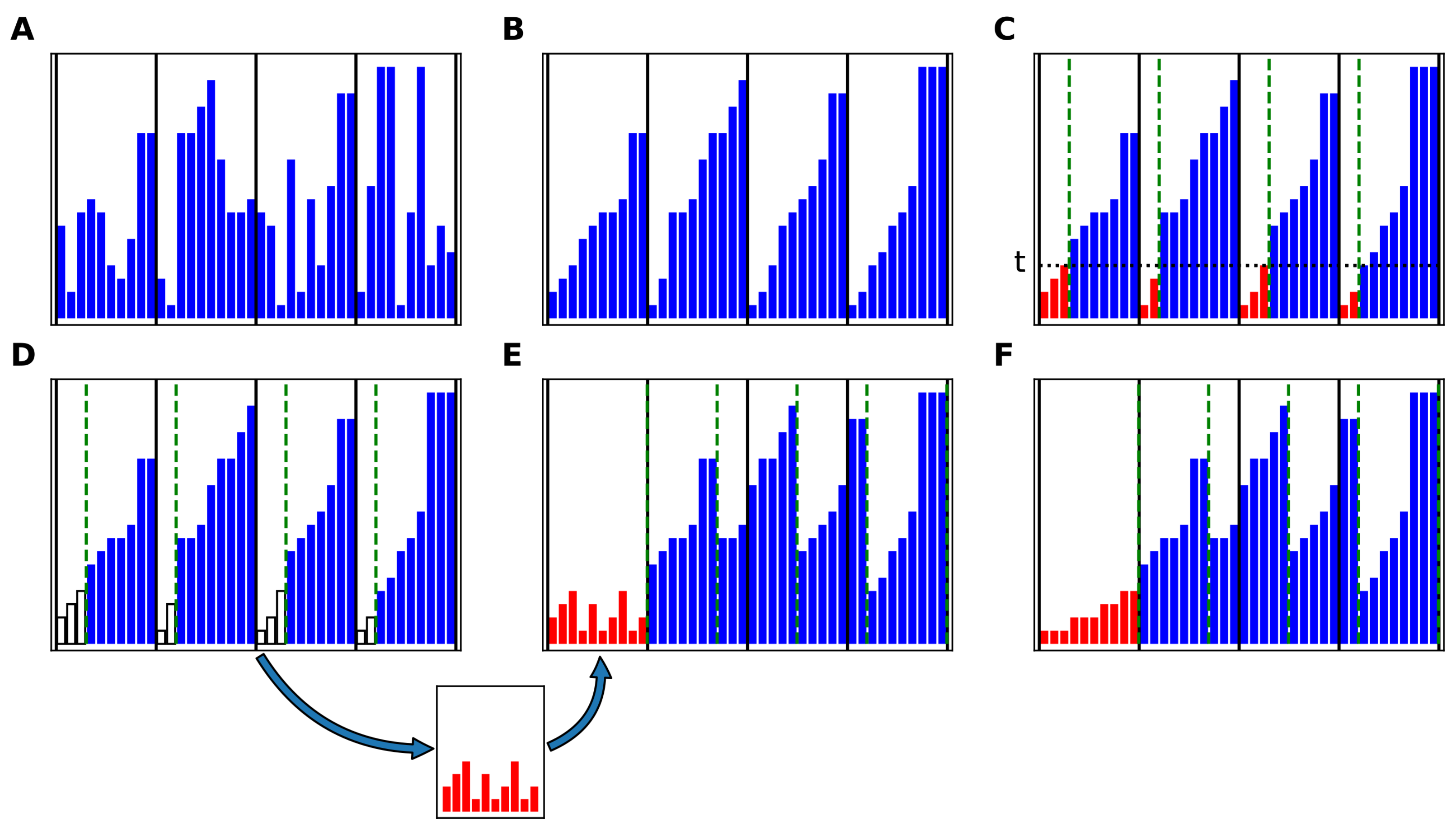
Appendix A.1. The COPASS (Constrained Partition of Sorted Subarrays) Block-Sort Algorithm
Appendix A.2. The COPASS Partition Algorithm
- Case 1In this case, . The iteration is concluded, and the partition sizes are computed using the procedure described in Appendix A.4.
- Case 2In this case, we setand continue with the next iteration. Equations (A30)–(A32) ensure that the condition of Equation (A19) is satisfied for the next iteration index .
- Case 3In this case, we setand continue with the next iteration. Equations (A33)–(35) ensure that the condition of Equation (A19) is satisfied for the next iteration index .
Appendix A.3. The COPASS Partition Last Step, Case 1
Appendix A.4. The COPASS Partition Last Step, Case 2
Appendix B. Validation Details
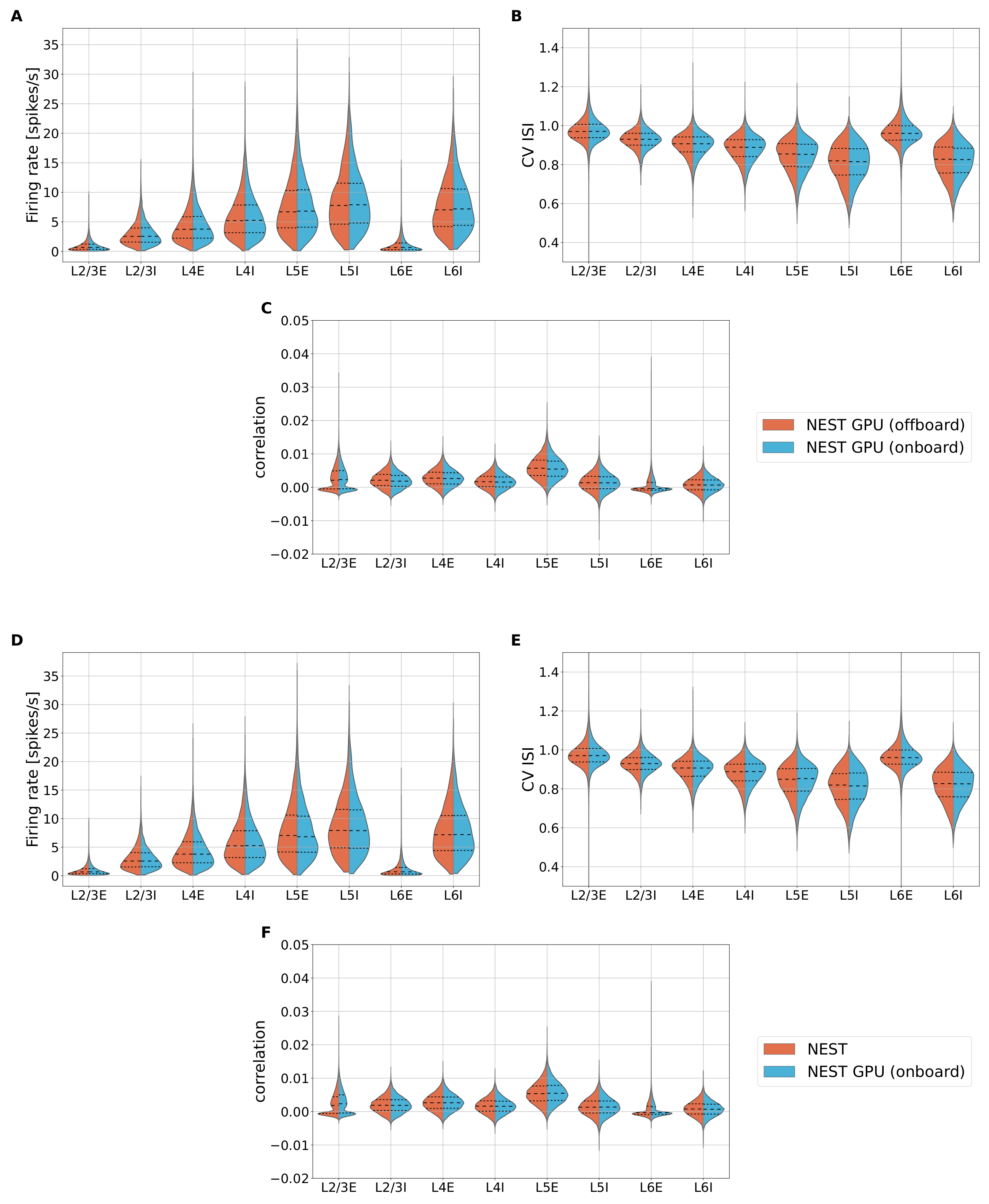

Appendix C. Additional Data for Cortical Microcircuit Simulations

Appendix D. Additional Data for the Two-Population Network Simulations

References
- Gewaltig, M.O.; Diesmann, M. NEST (NEural Simulation Tool). Scholarpedia 2007, 2, 1430. [Google Scholar] [CrossRef]
- Carnevale, N.T.; Hines, M.L. The NEURON Book; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
- Stimberg, M.; Brette, R.; Goodman, D.F. Brian 2, an intuitive and efficient neural simulator. eLife 2019, 8, e47314. [Google Scholar] [CrossRef] [PubMed]
- Bekolay, T.; Bergstra, J.; Hunsberger, E.; DeWolf, T.; Stewart, T.; Rasmussen, D.; Choo, X.; Voelker, A.; Eliasmith, C. Nengo: A Python tool for building large-scale functional brain models. Front. Neuroinform. 2014, 7, 48. [Google Scholar] [CrossRef]
- Vitay, J.; Dinkelbach, H.U.; Hamker, F.H. ANNarchy: A code generation approach to neural simulations on parallel hardware. Front. Neuroinform. 2015, 9, 19. [Google Scholar] [CrossRef]
- Yavuz, E.; Turner, J.; Nowotny, T. GeNN: A code generation framework for accelerated brain simulations. Sci. Rep. 2016, 6, 18854. [Google Scholar] [CrossRef]
- Nageswaran, J.M.; Dutt, N.; Krichmar, J.L.; Nicolau, A.; Veidenbaum, A.V. A configurable simulation environment for the efficient simulation of large-scale spiking neural networks on graphics processors. Neural Netw. 2009, 22, 791–800. [Google Scholar] [CrossRef]
- Niedermeier, L.; Chen, K.; Xing, J.; Das, A.; Kopsick, J.; Scott, E.; Sutton, N.; Weber, K.; Dutt, N.; Krichmar, J.L. CARLsim 6: An Open Source Library for Large-Scale, Biologically Detailed Spiking Neural Network Simulation. In Proceedings of the 2022 International Joint Conference on Neural Networks (IJCNN), Padua, Italy, 18–23 July 2022; pp. 1–10. [Google Scholar] [CrossRef]
- Golosio, B.; Tiddia, G.; De Luca, C.; Pastorelli, E.; Simula, F.; Paolucci, P.S. Fast Simulations of Highly-Connected Spiking Cortical Models Using GPUs. Front. Comput. Neurosci. 2021, 15, 627620. [Google Scholar] [CrossRef] [PubMed]
- Kumbhar, P.; Hines, M.; Fouriaux, J.; Ovcharenko, A.; King, J.; Delalondre, F.; Schürmann, F. CoreNEURON: An Optimized Compute Engine for the NEURON Simulator. Front. Neuroinform. 2019, 13, 63. [Google Scholar] [CrossRef]
- Golosio, B.; De Luca, C.; Pastorelli, E.; Simula, F.; Tiddia, G.; Paolucci, P.S. Toward a possible integration of NeuronGPU in NEST. In Proceedings of the NEST Conference, Aas, Norway, 29–30 June 2020; Volume 7. [Google Scholar]
- Stimberg, M.; Goodman, D.F.M.; Nowotny, T. Brian2GeNN: Accelerating spiking neural network simulations with graphics hardware. Sci. Rep. 2020, 10, 410. [Google Scholar] [CrossRef]
- Tiddia, G.; Golosio, B.; Albers, J.; Senk, J.; Simula, F.; Pronold, J.; Fanti, V.; Pastorelli, E.; Paolucci, P.S.; van Albada, S.J. Fast Simulation of a Multi-Area Spiking Network Model of Macaque Cortex on an MPI-GPU Cluster. Front. Neuroinform. 2022, 16, 883333. [Google Scholar] [CrossRef]
- Alevi, D.; Stimberg, M.; Sprekeler, H.; Obermayer, K.; Augustin, M. Brian2CUDA: Flexible and Efficient Simulation of Spiking Neural Network Models on GPUs. Front. Neuroinform. 2022, 16, 883700. [Google Scholar] [CrossRef]
- Awile, O.; Kumbhar, P.; Cornu, N.; Dura-Bernal, S.; King, J.G.; Lupton, O.; Magkanaris, I.; McDougal, R.A.; Newton, A.J.H.; Pereira, F.; et al. Modernizing the NEURON Simulator for Sustainability, Portability, and Performance. Front. Neuroinform. 2022, 16, 884046. [Google Scholar] [CrossRef] [PubMed]
- Abi Akar, N.; Cumming, B.; Karakasis, V.; Küsters, A.; Klijn, W.; Peyser, A.; Yates, S. Arbor—A Morphologically-Detailed Neural Network Simulation Library for Contemporary High-Performance Computing Architectures. In Proceedings of the 2019 27th Euromicro International Conference on Parallel, Distributed and Network-Based Processing (PDP), Pavia, Italy, 13–15 February 2019; pp. 274–282. [Google Scholar] [CrossRef]
- Knight, J.C.; Komissarov, A.; Nowotny, T. PyGeNN: A Python Library for GPU-Enhanced Neural Networks. Front. Neuroinform. 2021, 15, 659005. [Google Scholar] [CrossRef]
- Balaji, A.; Adiraju, P.; Kashyap, H.J.; Das, A.; Krichmar, J.L.; Dutt, N.D.; Catthoor, F. PyCARL: A PyNN Interface for Hardware-Software Co-Simulation of Spiking Neural Network. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–10. [Google Scholar] [CrossRef]
- Eppler, J.; Helias, M.; Muller, E.; Diesmann, M.; Gewaltig, M.O. PyNEST: A convenient interface to the NEST simulator. Front. Neuroinform. 2009, 2, 12. [Google Scholar] [CrossRef]
- Davison, A.P. PyNN: A common interface for neuronal network simulators. Front. Neuroinform. 2008, 2, 11. [Google Scholar] [CrossRef] [PubMed]
- Senk, J.; Kriener, B.; Djurfeldt, M.; Voges, N.; Jiang, H.J.; Schüttler, L.; Gramelsberger, G.; Diesmann, M.; Plesser, H.E.; van Albada, S.J. Connectivity concepts in neuronal network modeling. PLoS Comput. Biol. 2022, 18, e1010086. [Google Scholar] [CrossRef]
- Morrison, A.; Diesmann, M. Maintaining Causality in Discrete Time Neuronal Network Simulations. In Lectures in Supercomputational Neurosciences: Dynamics in Complex Brain Networks; Graben, P.b., Zhou, C., Thiel, M., Kurths, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 267–278. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; The MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Potjans, T.C.; Diesmann, M. The Cell-Type Specific Cortical Microcircuit: Relating Structure and Activity in a Full-Scale Spiking Network Model. Cereb. Cortex 2014, 24, 785–806. [Google Scholar] [CrossRef] [PubMed]
- Rotter, S.; Diesmann, M. Exact digital simulation of time-invariant linear systems with applications to neuronal modeling. Biol. Cybern. 1999, 81, 381–402. [Google Scholar] [CrossRef]
- Van Albada, S.J.; Rowley, A.G.; Senk, J.; Hopkins, M.; Schmidt, M.; Stokes, A.B.; Lester, D.R.; Diesmann, M.; Furber, S.B. Performance Comparison of the Digital Neuromorphic Hardware SpiNNaker and the Neural Network Simulation Software NEST for a Full-Scale Cortical Microcircuit Model. Front. Neurosci. 2018, 12, 291. [Google Scholar] [CrossRef]
- Dasbach, S.; Tetzlaff, T.; Diesmann, M.; Senk, J. Dynamical Characteristics of Recurrent Neuronal Networks Are Robust Against Low Synaptic Weight Resolution. Front. Neurosci. 2021, 15, 757790. [Google Scholar] [CrossRef]
- Schmidt, M.; Bakker, R.; Shen, K.; Bezgin, G.; Diesmann, M.; van Albada, S.J. A multi-scale layer-resolved spiking network model of resting-state dynamics in macaque visual cortical areas. PLoS Comput. Biol. 2018, 14, e1006359. [Google Scholar] [CrossRef] [PubMed]
- Knight, J.C.; Nowotny, T. GPUs Outperform Current HPC and Neuromorphic Solutions in Terms of Speed and Energy When Simulating a Highly-Connected Cortical Model. Front. Neurosci. 2018, 12, 941. [Google Scholar] [CrossRef]
- Rhodes, O.; Peres, L.; Rowley, A.G.D.; Gait, A.; Plana, L.A.; Brenninkmeijer, C.; Furber, S.B. Real-time cortical simulation on neuromorphic hardware. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2019, 378, 20190160. [Google Scholar] [CrossRef]
- Kurth, A.C.; Senk, J.; Terhorst, D.; Finnerty, J.; Diesmann, M. Sub-realtime simulation of a neuronal network of natural density. Neuromorphic Comput. Eng. 2022, 2, 021001. [Google Scholar] [CrossRef]
- Heittmann, A.; Psychou, G.; Trensch, G.; Cox, C.E.; Wilcke, W.W.; Diesmann, M.; Noll, T.G. Simulating the Cortical Microcircuit Significantly Faster Than Real Time on the IBM INC-3000 Neural Supercomputer. Front. Neurosci. 2022, 15, 728460. [Google Scholar] [CrossRef] [PubMed]
- Izhikevich, E. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef] [PubMed]
- Spreizer, S.; Mitchell, J.; Jordan, J.; Wybo, W.; Kurth, A.; Vennemo, S.B.; Pronold, J.; Trensch, G.; Benelhedi, M.A.; Terhorst, D.; et al. NEST 3.3. Zenodo 2022. [Google Scholar] [CrossRef]
- Vieth, B.V.S. JUSUF: Modular Tier-2 Supercomputing and Cloud Infrastructure at Jülich Supercomputing Centre. J. Large-Scale Res. Facil. JLSRF 2021, 7, A179. [Google Scholar] [CrossRef]
- Thörnig, P. JURECA: Data Centric and Booster Modules implementing the Modular Supercomputing Architecture at Jülich Supercomputing Centre. J. Large-Scale Res. Facil. JLSRF 2021, 7, A182. [Google Scholar] [CrossRef]
- Jordan, J.; Ippen, T.; Helias, M.; Kitayama, I.; Sato, M.; Igarashi, J.; Diesmann, M.; Kunkel, S. Extremely Scalable Spiking Neuronal Network Simulation Code: From Laptops to Exascale Computers. Front. Neuroinform. 2018, 12, 2. [Google Scholar] [CrossRef]
- Azizi, A. Introducing a Novel Hybrid Artificial Intelligence Algorithm to Optimize Network of Industrial Applications in Modern Manufacturing. Complexity 2017, 2017, 8728209. [Google Scholar] [CrossRef]
- Schmitt, F.J.; Rostami, V.; Nawrot, M.P. Efficient parameter calibration and real-time simulation of large-scale spiking neural networks with GeNN and NEST. Front. Neuroinform. 2023, 17, 941696. [Google Scholar] [CrossRef] [PubMed]
- Waskom, M.L. Seaborn: Statistical data visualization. J. Open Source Softw. 2021, 6, 3021. [Google Scholar] [CrossRef]
- Rosenblatt, M. Remarks on Some Nonparametric Estimates of a Density Function. Ann. Math. Stat. 1956, 27, 832–837. [Google Scholar] [CrossRef]
- Parzen, E. On Estimation of a Probability Density Function and Mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman and Hall: London, UK, 1986. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Albers, J.; Pronold, J.; Kurth, A.C.; Vennemo, S.B.; Mood, K.H.; Patronis, A.; Terhorst, D.; Jordan, J.; Kunkel, S.; Tetzlaff, T.; et al. A Modular Workflow for Performance Benchmarking of Neuronal Network Simulations. Front. Neuroinform. 2022, 16, 837549. [Google Scholar] [CrossRef]

| System | CPU | GPU |
|---|---|---|
| JUSUF cluster | 2× AMD EPYC 7742, 2× 64 cores, 2.25 GHz | NVIDIA V100 1, 1530 MHz, 16 GB HBM2e, 5120 CUDA cores |
| JURECA-DC cluster | 2× AMD EPYC 7742, 2× 64 cores, 2.25 GHz | NVIDIA A100 2, 1410 MHz, 40 GB HBM2e, 6912 CUDA cores |
| Workstation 1 | Intel Core i9-9900K, 8 cores, 3.60 GHz | NVIDIA RTX 2080 Ti 3, 1545 MHz, 11 GB GDDR6, 4352 CUDA cores |
| Workstation 2 | Intel Core i9-10940X, 14 cores, 3.30 GHz | NVIDIA RTX 4090 4, 2520 MHz, 24 GB GDDR6X, 16384 CUDA cores |
| Metrics | NEST GPU (onboard) | NEST GPU (offboard) | NEST 3.3 (CPU) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| V100 | A100 | 2080Ti | 4090 | V100 | A100 | 2080Ti | 4090 | 2 64 Cores | |
| Initialization | × 10−4 | × 10−3 | × 10−4 | × 10−4 | × 10−4 | × 10−3 | × 10−4 | × 10−4 | |
| Node creation | × 10−3 | × 10−3 | (0.018) | ||||||
| Node connection | (0.0003) | (0.009) | (0.0005) | ||||||
| Calibration | (0.001) | (0.005) | (0.0006) | (0.0004) | (0.014) | ||||
| Network construction | (0.001) | (0.0008) | |||||||
| Simulation (10 s) | (0.008) | (0.018) | |||||||
| Metrics | NEST GPU (onboard) | NEST GPU (offboard) | NEST 3.3 (CPU) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| V100 | A100 | 2080Ti | 4090 | V100 | A100 | 2080Ti | 4090 | 2 64 Cores | |
| Initialization | × 10−4 | × 10−3 | × 10−4 | × 10−4 | × 10−4 | × 10−3 | × 10−4 | × 10−4 | (0.003) |
| Node creation | × 10−3 | × 10−3 | × 10−3 | × 10−3 | (0.003) | ||||
| Node connection | (0.0004) | (0.0013) | (0.009) | (0.0005) | |||||
| Calibration | (0.0013) | (0.008) | (0.0006) | (0.0003) | (0.012) | (0.016) | (0.015) | (0.015) | (0.005) |
| Network construction | (0.0018) | (0.0005) | |||||||
| Simulation (10 s) | (0.012) | (0.016) | (0.013) | ||||||
| Metrics | GeNN | |||
|---|---|---|---|---|
| V100 | A100 | 2080Ti | 4090 | |
| Model definition | × 10−2 | × 10−2 | × 10−2 | × 10−2 |
| Building | ||||
| Loading | ||||
| Network construction (no building) | ||||
| Network construction | ||||
| Simulation (10 s) | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Golosio, B.; Villamar, J.; Tiddia, G.; Pastorelli, E.; Stapmanns, J.; Fanti, V.; Paolucci, P.S.; Morrison, A.; Senk, J. Runtime Construction of Large-Scale Spiking Neuronal Network Models on GPU Devices. Appl. Sci. 2023, 13, 9598. https://doi.org/10.3390/app13179598
Golosio B, Villamar J, Tiddia G, Pastorelli E, Stapmanns J, Fanti V, Paolucci PS, Morrison A, Senk J. Runtime Construction of Large-Scale Spiking Neuronal Network Models on GPU Devices. Applied Sciences. 2023; 13(17):9598. https://doi.org/10.3390/app13179598
Chicago/Turabian StyleGolosio, Bruno, Jose Villamar, Gianmarco Tiddia, Elena Pastorelli, Jonas Stapmanns, Viviana Fanti, Pier Stanislao Paolucci, Abigail Morrison, and Johanna Senk. 2023. "Runtime Construction of Large-Scale Spiking Neuronal Network Models on GPU Devices" Applied Sciences 13, no. 17: 9598. https://doi.org/10.3390/app13179598
APA StyleGolosio, B., Villamar, J., Tiddia, G., Pastorelli, E., Stapmanns, J., Fanti, V., Paolucci, P. S., Morrison, A., & Senk, J. (2023). Runtime Construction of Large-Scale Spiking Neuronal Network Models on GPU Devices. Applied Sciences, 13(17), 9598. https://doi.org/10.3390/app13179598






