Microseism Detection Method in Coal Mine Based on Spatiotemporal Characteristics and Support Vector Regression Algorithm
Abstract
:1. Introduction
2. Detection Method of Microseisms in Coal Mines
2.1. Extraction of Temporal and Spatial Characteristics of Coal Mine Microseisms Based on Markov Chain
2.1.1. Coal Mine Data Acquisition Based on Spatiotemporal Sliding Window
2.1.2. Continuous Attribute Discretization Processing of Coal Mine Data
- (1)
- Calculate initial state entropy ;
- (2)
- Make ’s attribute perform and ascending arrangement, and then, select two adjacent intervals from the ordered sequence to merge;
- (3)
- Calculate the entropy value after merging every two adjacent intervals one by one ; connect it with to make a difference; select the merge interval with the smallest entropy difference as the best merge interval;
- (4)
- Calculate Formula (2) to compare the size of and ; if , the merged continuous attributes will be , and repeat Steps (2) and (3); otherwise, the algorithm stops, and all discrete point sets are output. Complete the discretization of the real-time coal mine data in the spatiotemporal sliding window.
2.1.3. Extraction of Time Characteristics of Microseismic Signal of Target Node Coal Mine
2.1.4. Spatial Feature Extraction of Microseismic Signal of Target Node Coal Mine
2.2. Microseism Detection Method in Coal Mine
2.2.1. Regression Solution of Microseism Detection Signal in Coal Mine
2.2.2. Optimal Microseism Detection Results of Coal Mine
- (1)
- Sett and , the maximum particle speed , the number of particles , and the maximum iterations , and randomly select the position vector of particles and velocity vector .
- (2)
- Check whether the particles in section are in the solution space; if their current positions exceeds the range of the solution space, it will be reset to the position of the previous time .
- (3)
- From the root-mean-squared error , calculate the fitness value of the current particle and the global fitness values .
- (4)
- Find the optimal self-state variable according to the fitness value of each particle and global state variables . By comparison of ’s fitness and the objective function, if the objective function is better, update it with the current position . If the fitness value of the objective function is not only better than , but is also better than , the current position is used to update .
- (5)
- Update random particle vector at each step of the iteration process; a passively attractive individual of the particles should be randomly selected from the population .
- (6)
- Calculate the velocity vector and position vector coordinates of the particles and update all vector coordinate values of each particle.
- (7)
- Check whether the iteration termination conditions are met. If not, repeat Steps (2) to (6), and run the PSO algorithm several times until the global optimal solution is obtained. If the parameter combination of the output optimal SVR model is satisfied, the SVR with the optimal parameter combination is used to complete the precise detection of coal mine microseisms.
3. Experimental Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Lund, B.; Schmidt, P.; Shomali, Z.H.; Roth, M. The modern swedish national seismic network: Two decades of intraplate microseismic observation. Seism. Res. Lett. 2021, 92, 1747–1758. [Google Scholar] [CrossRef]
- Li, X.; Chen, S.; Wang, E.; Li, Z. Rockburst mechanism in coal rock with structural surface and the microseismic (ms) and electromagnetic radiation (emr) response. Eng. Fail. Anal. 2021, 124, 105396. [Google Scholar] [CrossRef]
- Liu, Y.; Huff, O.; Luo, B.; Jin, G.; Simmons, J. Convolutional neural network-based classification of microseismic events originating in a stimulated reservoir from distributed acoustic sensing data. Geophys. Prospect. 2022, 70, 904–920. [Google Scholar] [CrossRef]
- Liu, L.; Song, W.; Zeng, C.; Yang, X. Microseismic event detection and classification based on convolutional neural network. J. Appl. Geophys. 2021, 192, 104380. [Google Scholar] [CrossRef]
- Nguyen, H.; Bui, X.N.; Hieu, T.Q.; Long, N.Q.; Vu, N.P. Developing an advanced soft computational model for estimating blast-induced ground vibration in nui beo open-pit coal mine (vietnam) using artificial neural network. Inz. Miner. 2020, 2, 57–72. [Google Scholar] [CrossRef]
- Ozkan, H.; Temelli, R.; Gurbuz, O.; Koksal, O.K.; Ipekoren, A.K.; Canbal, F.; Karahan, B.D.; Kuran, M. Multimedia traffic classification with mixture of markov components. Ad Hoc Netw. 2021, 121, 102608. [Google Scholar] [CrossRef]
- Narwal, P.; Kumar, D.; Singh, S.N.; Tewari, P. Stochastic intrusion detection game-based arrangement using controlled markov chain for prevention of dos and ddos attacks in cloud. J. Inf. Technol. Res. 2021, 14, 45–57. [Google Scholar] [CrossRef]
- Mohamed, Z.E.; Saleh, H.H. Potential of machine learning based support vector regression for solar radiation prediction. Comput. J. 2021, 66, 399–415. [Google Scholar] [CrossRef]
- Soleimani, N.; Trinchero, R. Compressed complex-valued least squares support vector machine regression for modeling of the frequency-domain responses of electromagnetic structures. Electronics 2022, 11, 551. [Google Scholar] [CrossRef]
- Chen, C. An analysis of mandarin emotional tendency recognition based on expression spatiotemporal feature recognition. Int. J. Biom. 2021, 13, 211–228. [Google Scholar] [CrossRef]
- Li, T.; Xu, H.; Liu, Z.; Dong, Z.; Liu, Q.; Li, J.; Fan, S.; Sun, X. A spatiotemporal multi-feature extraction framework for opinion mining. Neurocomputing 2022, 490, 337–346. [Google Scholar] [CrossRef]
- Shah, Z.; Dunn, A.G. Event detection on twitter by mapping unexpected changes in streaming data into a spatiotemporal lattice. IEEE Trans. Big Data 2022, 8, 508–522. [Google Scholar] [CrossRef]
- Dai, F.; Prymak, A.; Shadrin, A.; Temlyakov, V.; Tikhonov, S. Entropy numbers and marcinkiewicz-type discretization. J. Funct. Anal. 2021, 281, 109090. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, Z. Optimal hybrid framework for carbon price forecasting using time series analysis and least squares support vector machine. J. Forecast. 2021, 41, 615–632. [Google Scholar] [CrossRef]
- Bhat, H.F.; Wani, M.A. Novel pssm-based approaches for gene identification using support vector machine. J. Inf. Technol. Res. 2021, 14, 152–173. [Google Scholar] [CrossRef]
- Wen, L.; Li, Y.; Zhang, H.; Liu, Y.; Zhou, H. Predicting the crest settlement of concrete face rockfill dams by combining threshold regression and support vector machine. Int. J. Geomech. 2022, 22, 04022074. [Google Scholar] [CrossRef]
- Bingul, Z.; Karahan, O. Real-time trajectory tracking control of stewart platform using fractional order fuzzy pid controller optimized by particle swarm algorithm. Ind. Robot. 2022, 49, 708–725. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, C. Surface Quality and Parameter Optimization of AeroMet100 Ultra High Strength Steel Milling. Weapon Mater. Sci. Eng. 2020, 43, 5–10. [Google Scholar]
- Li, Z.; Feng, Y.; Lin, Z.; Xu, H. Optimization of SVM model for facial color recognition based on improved PSO algorithm. Comput. Simul. 2022, 39, 241–247. [Google Scholar]


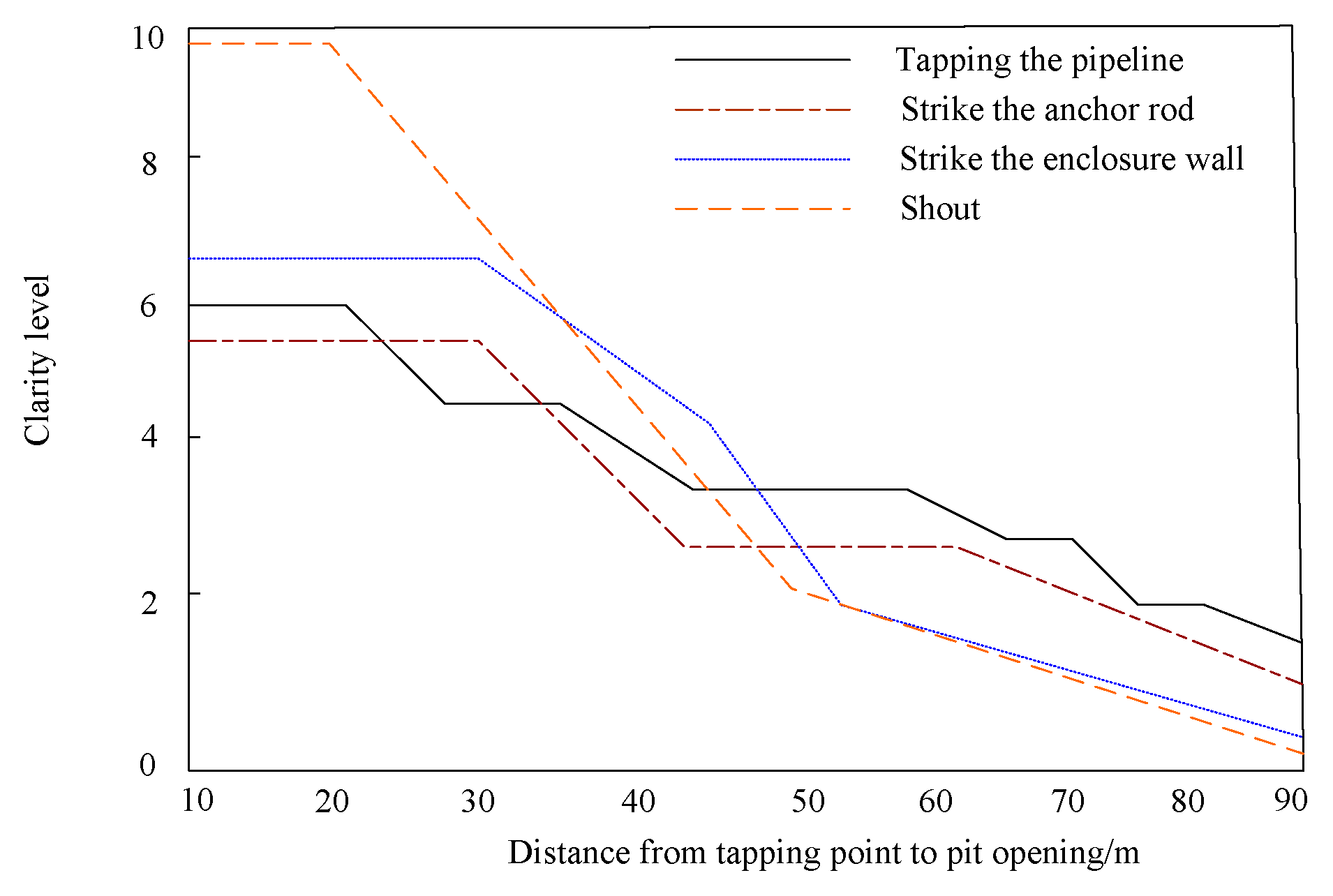

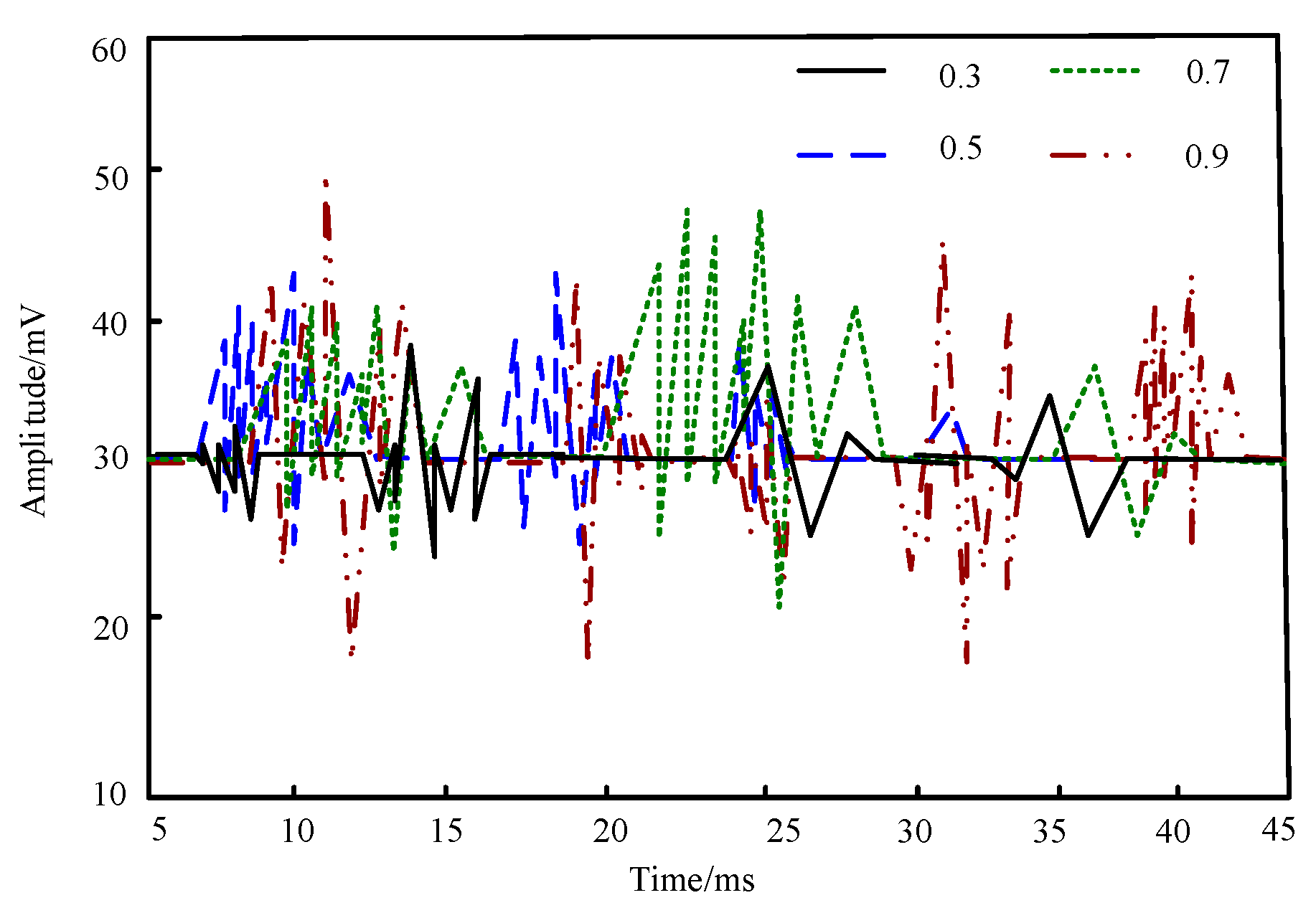

| Serial Number | Date Time | The Original System of the Group Detects Microseismic Energy (J) | The Method Used in This Article to Detect Microseismic Energy (J) | Actual Energy (J) | Notes |
|---|---|---|---|---|---|
| 1 | 2023.1.8T1:30:15 | 2.20 × 102 | 2.32 × 102 | 2.35 × 101 | Coal mine microseismic impact event |
| 2 | 2023.1.8T1:31:16 | 3.82 × 103 | 3.98 × 104 | 4.00 × 103 | |
| 3 | 2023.1.8T1:32:35 | 2.53 × 102 | 2.64 × 101 | 2.67 × 102 | |
| 4 | 2023.1.8T1:33:26 | 4.56 × 105 | 7.34 × 104 | 7.37 × 105 | |
| 5 | 2023.1.8T1:34:54 | 6.46 × 106 | 5.23 × 101 | 5.46 × 103 | |
| 6 | 2023.1.8T1:35:12 | 4.23 × 103 | 4.45 × 103 | 4.47 × 106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Mu, C.; Sun, H. Microseism Detection Method in Coal Mine Based on Spatiotemporal Characteristics and Support Vector Regression Algorithm. Appl. Sci. 2023, 13, 9917. https://doi.org/10.3390/app13179917
Gao H, Mu C, Sun H. Microseism Detection Method in Coal Mine Based on Spatiotemporal Characteristics and Support Vector Regression Algorithm. Applied Sciences. 2023; 13(17):9917. https://doi.org/10.3390/app13179917
Chicago/Turabian StyleGao, Hong, Chaomin Mu, and Hui Sun. 2023. "Microseism Detection Method in Coal Mine Based on Spatiotemporal Characteristics and Support Vector Regression Algorithm" Applied Sciences 13, no. 17: 9917. https://doi.org/10.3390/app13179917




