Closed-Form Analytical Solutions for the Deflection of Elastic Beams in a Peridynamic Framework

Abstract

Peridynamics is a continuum theory that operates with non-local deformation measures as well as long-range internal force/moment interactions. The resulting equations are of the integral type, in contrast to the classical theory, which deals with differential equations. The aim of this paper is to analyze peridynamic governing equations for elastic beams. To this end, the strain energy density is formulated as a function of the non-local curvature. By applying the Lagrange principle, the peridynamic equations of motion are derived. Examples of non-local boundary conditions, including simple support, clamped edge, roller clamped edge, and free edge, are presented by introducing the interaction domain. Novel closed-form analytical solutions to integral equations are presented for beams with various boundary conditions, including clamped—simply supported, clamped–clamped, simply supported–roller-clamped, and clamped–roller-clamped beams. Furthermore, different types of loadings, including uniformly distributed load, concentrated force, and concentrated moment, are considered. The results are validated by comparing the derived solutions against solutions to the classical Bernoulli–Euler beam theory. A very good agreement between the non-local and the classical theories is observed for the case of the small horizon sizes, which shows the capability of the derived equations of motion and proposed boundary conditions.

1. Introduction

In recent years, non-local theories of solid mechanics have become of increasing interest, due to many applications such as analysis of micro- and nanometer-scale components, laminates with thin layers, composite materials with extreme differences in properties of constituents, among others.

One way to develop a non-local theory is to extend the classical continuum mechanics (CCM) by introducing higher-order strain gradients as arguments of the strain energy density [1]. By applying a variational principle, the governing equations of motion and boundary conditions can be derived. For linear-elastic material behavior, and in the case of statics, a strain gradient theory of the nth order provides a 2nth-order system of linear partial differential equations, e.g., [2]. In addition, higher-order stress tensors are introduced, and many boundary conditions are required to pose the boundary-value problem. Strain gradient theories were recently applied to the analysis of micro- and nanometer structures in, e.g., [3,4] (see also the works cited therein).

Alternatively, non-local continuum theories can be formulated within the peridynamics (PD) framework [5,6]. Here, the balance equations for long-range internal forces are introduced. The deformation gradient, higher strain gradients, or gradients of internal state variables are not required. Peridynamic theories for three-dimensional solids are discussed in [5].

Thin-walled structural components can be modeled by using classical three-dimensional continuum mechanics or alternatively by applying classical theories of beams, plates, and shells, as discussed in many textbooks, e.g., [7]. Within the framework of peridynamics, a three-dimensional theory can be used in the analysis of thin-walled structures, e.g., [8]. However, a very high computational effort is required for the numerical solution, as the thickness direction must be discretized by many node layers to to provide satisfactory accuracy. Furthermore, for components with a very low thickness-to-span-length ratio, for example, soft polymeric layers in laminated glass [9], the PD horizon size may be comparable to or even larger than the layer thickness. This would lead to non-physical long-range force interactions between the layers in a laminate. Therefore, robust peridynamic theories for beams, plates, and shells are required to analyze slender components.

Similarly to classical theories, PD theories for thin-walled structures can be derived from balance laws for a deformable line in the case of a beam, a deformable plane for a plate, and a deformable surface for a shell. These types of theories can be referred to as direct theories by analogy to the classical continuum mechanics. A direct PD beam theory proposed in [10] assumes the strain energy density to be a function of a non-local curvature. Discretized PD equations of motion with respect to the displacements of a straight beam are derived in [11]. For initially curved beams, PD equations of motion are presented in [12]. Discretized forms of PD equations of motion for plates and shells are derived in [13] based on the Lagrange variational principle. Peridynamic theories for membranes and fibers are presented in [14]. A direct PD shell theory in terms of displacements and linearized rotations is proposed in [15]. In [16], a non-linear direct PD plate theory is developed. Points of the plate midplane are assumed to have the rigid body-type degrees of freedom: displacements and finite rotations. Long-range force and moment interactions between the points of a plate are introduced. Governing balance laws are formulated directly for the plate.

Alternatively, applying the through-the-thickness approximations for the kinematic variables, a three-dimensional PD theory can be reduced to one- or two-dimensional cases. In [17], a PD plate theory is developed from the three-dimensional bond-based PD theory by applying asymptotic analysis. A peridynamic beam theory proposed in [18] is derived from three-dimensional PD equations and cross-section approximations for the deformation vector.

The governing peridynamic equations of motion are of integro-differential type, unlike CCM and strain gradient theories, where partial differential equations are introduced. To solve PD equations numerically, various approaches such as the mesh-free method [19] and discontinuous finite element formulation [20] have been proposed. Various numerical solutions are presented to demonstrate the ability of PD to represent complex phenomena such as crack initiation [8], delamination [21], and propagation of cracks [22,23].

However, only several closed-form analytical solutions to PD integral equations are derived. Examples include solutions for straight axially loaded rods [24,25,26]. For initially straight beams with specific boundary constraints, series solutions to PD equations are presented in [27]. Series solutions for rectangular plates under special boundary conditions are given in [28]. General solutions to peristatics and peridynamics for three-dimensional media are presented in [29,30].

Analytical solutions explicitly illustrate the effect of non-locality on the deformation state. In particular, the PD horizon size enters the results for the beam deformations and can be varied to analyze the convergence to the classical solution. This gives an advantage over numerical methods, where the horizon size is related to the size of the spatial discretization and can be only varied in a small range. Furthermore, different types of constraints can be introduced and analyzed, as they affect the final results, by applying the analytical solutions. Furthermore, closed-form analytical solutions are useful as reference solutions in order to validate the numerical methods developed to solve PD equations, such as the mesh-free method, and to analyze the convergence of numerical results.

The aim of this study is to derive a family of novel closed-form analytical solutions to both peristatic and peridynamic equations of shear-rigid beams. In addition to results presented in [27] for simply supported cantilever beams, various boundary conditions, including clamped–simply supported, clamped–clamped, simply supported–roller-clamped, and clamped–roller-clamped beams, will be considered. Furthermore, novel closed-form solutions for different types of loadings, including uniformly distributed load, concentrated force, and concentrated moment, will be introduced. The results will be validated by comparing the derived solutions against available solutions to the classical Bernoulli–Euler beam theory (CBT).

2. Peridynamic Beam Theory

2.1. Classical Equations and Assumptions

Let x be the coordinate for a point of the centerline of the initially straight beam, and z is the transverse coordinate of cross-section points with the origin at the centroid of the cross-section. The corresponding Cartesian base vectors will be specified by ${\mathbf{e}}_x$ and ${\mathbf{e}}_z$, respectively. In what follows, let us analyze the plane-bending of the beam. In this case, the deformed centerline belongs to the $x-z$ plane. In the case of small cross-sectional rotations, the displacement vector $\mathfrak{u}$ can be represented as follows:

$$\mathfrak{u}(x,z)=w\left(x\right){\mathbf{e}}_z+\theta \left(x\right)z{\mathbf{e}}_x,$$

(1)

where w is the deflection and $\theta$ is the small angle of cross-sectional rotation.

Assuming small strains, the linear strain tensor $\mathit{\epsilon }$ is related to the displacement field according to the following equation:

$$\mathit{\epsilon }=\frac{1}{2}\left(\mathbf{\nabla }\mathfrak{u}+{(\mathbf{\nabla }\mathfrak{u})}^{\mathrm{T}}\right),\mathbf{\nabla }(\dots )={\mathbf{e}}_x\frac{\partial (\dots )}{\partial x}+{\mathbf{e}}_z\frac{\partial (\dots )}{\partial z}.$$

(2)

With Equation (1) inserted into Equation (2), the strain tensor is computed as follows:

$$\mathbf{\epsilon }=\epsilon {\mathbf{e}}_x\otimes {\mathbf{e}}_x+\frac{1}{2}\gamma ({\mathbf{e}}_x\otimes {\mathbf{e}}_z+{\mathbf{e}}_z\otimes {\mathbf{e}}_x),$$

(3)

with the following expressions for normal strain $\epsilon$ and the transverse shear strain $\gamma$:

$$\epsilon =z\frac{\mathrm{d}\theta }{\mathrm{d}x},\gamma =\theta +\frac{\mathrm{d}w}{\mathrm{d}x}.$$

(4)

For the shear rigid beams, $\gamma =0$ is assumed, resulting in

$$\theta =-\frac{\mathrm{d}w}{\mathrm{d}x},\epsilon =-z\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{x}^2}.$$

(5)

For the linear-elastic material behavior, the strain energy per unit length is defined as follows:

$$\mathcal{U}=\frac{1}{2}\underset{A}{\int }E{\epsilon }^2\mathrm{d}A,$$

(6)

where E is the Young’s modulus, and A is the cross-sectional area. With Equation (5), the strain energy density (6) takes the following form:

$$\mathcal{U}=\frac{EI}{2}{\kappa }^2,\kappa =-\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{x}^2}$$

(7)

where I is the second area moment of the beam cross-section.

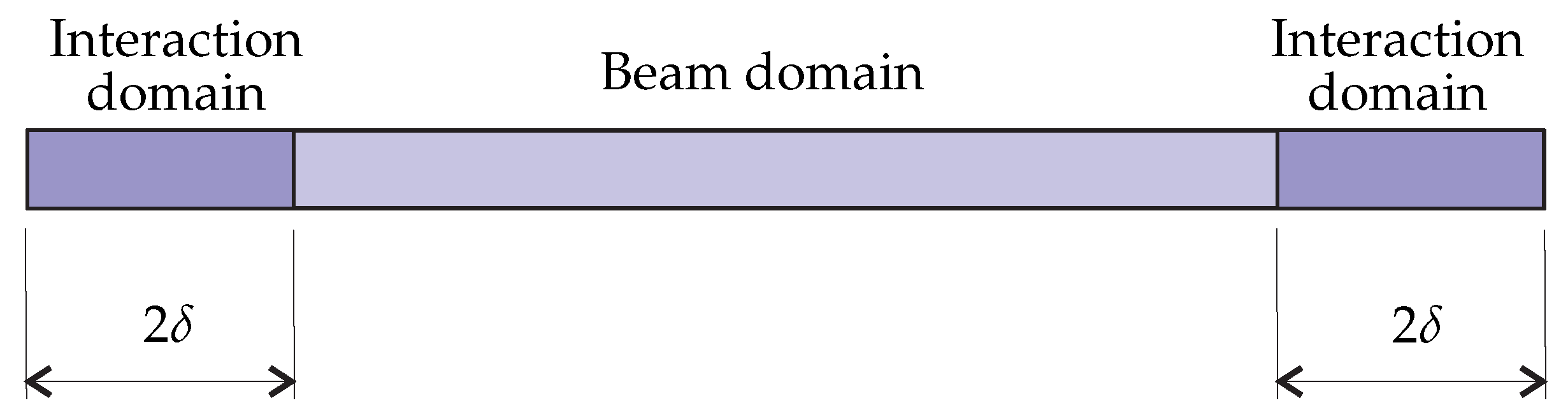
2.2. Peridynamic Equations of Motion

Unlike the CCM and the classical beam theory (CBT), where strains are defined in terms of derivatives with respect to the coordinates, non-local deformation measures are introduced in the PD framework. The PD deformations can be introduced as work conjugates to the bond force and moment densities considering the energy balance equation, e.g., [5,16]. Assuming the linear-elastic material behavior, a class of PD theories for beams and plates can be derived with the correspondence of the strain energy density from the CCM as a function of the PD deformation measures [27,28].

Let $\Gamma$ be the collection of points of the beam centerline. Introduce the PD horizon as an open ball centered at point x with the PD horizon size $\delta$ defined as $\forall x\in \Gamma$, i.e.,

$$H_x:=\left\{x^{\prime }\in \Gamma :\left|x^{\prime }-x\right|<\delta \right\}.$$

(8)

In PD, the strain energy density of any arbitrary material point x depends upon both the displacement of itself and the displacement fields within its horizon $H_x$, i.e.,

$$\overline{U}\left(x\right)=\overline{U}\left(w\left(H_x\right)\right).$$

(9)

To formulate the PD strain energy density, consider the following non-local curvature:

$$\overline{\kappa }\left(x\right)=-\frac{1}{\delta }\underset{x-\delta }{\overset{x+\delta }{\int }}\frac{w\left(x^{\prime }\right)-w\left(x\right)}{{(x^{\prime }-x)}^2}\mathrm{d}{x}^{\prime }.$$

(10)

For smooth deflection function $w\left(x\right)$, it can be shown that $\overline{\kappa }\left(x\right)$ approaches the local curvature (7) ${}_2$ as $\delta \to 0$. With Equations (7) ${}_1$ and (10), the PD bending strain energy density is formulated as follows:

$$\overline{U}\left(x\right)=\frac{1}{2}\frac{EI}{{\delta }^2}{\left[\underset{x-\delta }{\overset{x+\delta }{\int }}\frac{w\left(x^{\prime }\right)-w\left(x\right)}{{(x^{\prime }-x)}^2}\mathrm{d}{x}^{\prime }\right]}^2.$$

(11)

For elastic beams, the PD equation of motion can be derived using Lagrange’s equation,

$$\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial \mathcal{L}}{\partial \dot{w}}-\frac{\partial \mathcal{L}}{\partial w}=0,$$

(12)

where $\mathcal{L}=\mathcal{T}-\overline{\mathcal{U}}+\mathcal{W}$ is the Lagrangian. The kinetic energy $\mathcal{T}$ is computed as follows:

$$\mathcal{T}=\frac{1}{2}\underset{0}{\overset{L}{\int }}\rho A{\dot{w}}^2\mathrm{d}x$$

(13)

in which $\rho$ is the density and L is the length of the beam. The strain energy of the beam $\overline{\mathcal{U}}$ and the work of external forces $\mathcal{W}$ are

$$\overline{\mathcal{U}}=\underset{0}{\overset{L}{\int }}\overline{U}\left(x\right)\mathrm{d}x,\mathcal{W}=\underset{0}{\overset{L}{\int }}p\left(x\right)w\left(x\right)\mathrm{d}x,$$

(14)

where $p\left(x\right)$ is the distributed lateral load.

With Equations (11)–(14), the following equation of motion is derived:

$$\rho A\ddot{w}\left(x\right)=\frac{EI}{{\delta }^2}\underset{x-\delta }{\overset{x+\delta }{\int }}\frac{1}{{\left(x^{\prime }-x\right)}^2}\left[\underset{x-\delta }{\overset{x+\delta }{\int }}\frac{w\left(\zeta \right)-w\left(x\right)}{{\left(\zeta -x\right)}^2}\mathrm{d}\zeta -\underset{x^{\prime }-\delta }{\overset{x^{\prime }+\delta }{\int }}\frac{w\left(\zeta \right)-w\left(x^{\prime }\right)}{{\left(\zeta -x^{\prime }\right)}^2}\mathrm{d}\zeta \right]\mathrm{d}{x}^{\prime }+p\left(x\right).$$

(15)

By changing the integration variables, Equation (15) can be put in the following form:

$$\rho A\ddot{w}\left(x\right)=\frac{EI}{{\delta }^2}\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{w\left(x+\eta \right)-w\left(x\right)}{{\eta }^2}\mathrm{d}\eta -\underset{-\delta }{\overset{\delta }{\int }}\frac{w\left(x+\xi +\eta \right)-w\left(x+\xi \right)}{{\eta }^2}\mathrm{d}\eta \right]\mathrm{d}\xi +p\left(x\right).$$

(16)

For the static case, the PD governing equation for the Bernoulli–Euler beam (16) can be expressed as follows:

$$\frac{EI}{{\delta }^2}\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{w\left(x+\eta \right)-w\left(x\right)}{{\eta }^2}\mathrm{d}\eta -\underset{-\delta }{\overset{\delta }{\int }}\frac{w\left(x+\xi +\eta \right)-w\left(x+\xi \right)}{{\eta }^2}\mathrm{d}\eta \right]\mathrm{d}\xi =-p\left(x\right).$$

(17)

2.3. Peridynamic Boundary Conditions

The governing equation, Equation (16), is valid only if the material points are completely embedded in its PD influence domain. For material points adjacent to the boundary, it is necessary to introduce a fictitious interaction material region. For the introduced beam theory, the width of the fictitious region is double the PD horizon size, $2\delta$, as shown in Figure 1.

2.3.1. Simple Support

Suppose the beam is subjected to the simply supported boundary condition on the left. In this case, the deflection and curvature must vanish, i.e.,

$$\left\{\begin{array}{c}{\displaystyle w\left(0\right)=0,}\hfill \\ {\displaystyle {\left.\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{x}^2}\right|}_{x=0}=0.}\hfill \end{array}\right.$$

(18)

Applying the central difference for Equation (18) ${}_2$ yields

$${\left.\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{x}^2}\right|}_{x=0}\approx \frac{w\left(-\Delta x\right)-2w\left(0\right)+w\left(\Delta x\right)}{\Delta x^2}=0.$$

(19)

Replacing $\Delta x$ with $\xi$ and associating it with Equation (18) ${}_1$ gives the PD simply supported condition as

$$w\left(-\xi \right)=-w\left(\xi \right),\mathrm{for}0\le \xi \le 2\delta .$$

(20)

It indicates that the simply supported end enforces in the fictitious region an anti-symmetric relation with respect to the real material domain, as shown in Figure 2.

2.3.2. Roller Clamped Edge

In the case of a roller-clamped edge, Figure 3, a rotational rigidity is required such that

$${\left.\frac{\mathrm{d}w}{\mathrm{d}x}\right|}_{x=0}=0.$$

(21)

With the central difference, the PD boundary condition for the roller-clamped boundary condition takes the form

$${\left.\frac{\mathrm{d}w}{\mathrm{d}x}\right|}_{x=0}\approx \frac{w\left(\xi \right)-w\left(-\xi \right)}{2\xi }=0\Rightarrow w\left(-\xi \right)=w\left(\xi \right).$$

(22)

One can observe that roller-clamped boundary condition in PD enforces a mirror relation between the fictitious region and the real region.

3. Analytical Solutions to Peristatic Problems

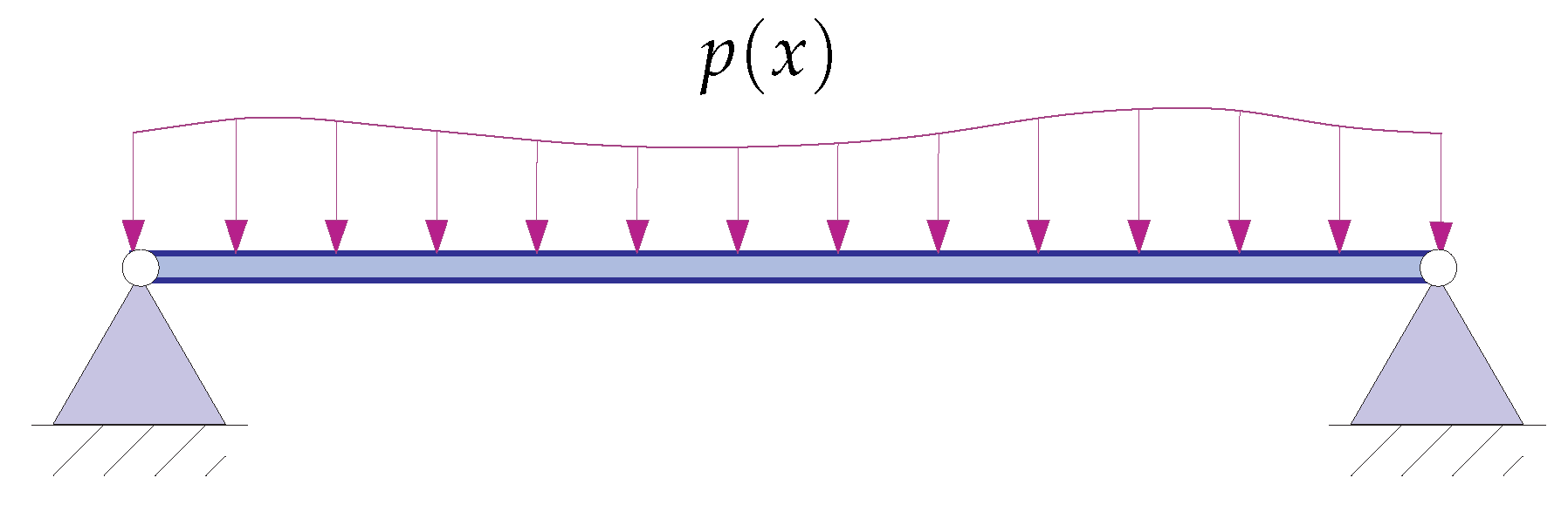
3.1. Simply Supported Beam

Consider a simply supported beam subjected to a transverse load $p\left(x\right)$, as shown in Figure 4. In this case, the PD boundary conditions can be given as follows:

$$w\left(-\xi \right)=-w\left(\xi \right),w\left(L+\xi \right)=-w\left(L-\xi \right),\left(0<\xi \le 2\delta \right).$$

(23)

With the BCs (23), the deflection field can be extended periodically with the period of $2L$, as shown in Figure 5.

Therefore, the deflection function can be expanded by applying the following Fourier series:

$$w\left(x\right)=\sum _{n=1}^{\infty }{b}_{n}sin\frac{n\pi x}{L}.$$

(24)

Substituting Equation (24) into (17) provides, after some simplifications,

$$\frac{EI}{{\delta }^2}\sum _{n=1}^{\infty }{b}_{n}sin\frac{n\pi x}{L}{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-cos\frac{n\pi \xi }{L}\right)\mathrm{d}\xi ,\right]}^2=p\left(x\right)$$

(25)

where the unknown coefficients can be determined by invoking the orthogonality of trigonometric functions:

$$b_n=\frac{2{\delta }^2}{LEI}\underset{0}{\overset{L}{\int }}p\left(x\right)sin\frac{n\pi x}{L}dx{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-cos\frac{n\pi \xi }{L}\right)\mathrm{d}\xi \right]}^{-2}.$$

(26)

Plugging Equation (26) back into (24) gives the following explicit PD solution for the simply supported beam:

$$w\left(x\right)=\frac{2{\delta }^2}{LEI}\sum _{n=1}^{\infty }\underset{0}{\overset{L}{\int }}p\left(x\right)sin\frac{n\pi x}{L}\mathrm{d}x{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-cos\frac{n\pi \xi }{L}\right)\mathrm{d}\xi \right]}^{-2}sin\frac{n\pi x}{L}.$$

(27)

3.2. Clamped–Simply Supported Beam

For the clamped–simply supported beam, Figure 6a shows the solution that can be applied. The rotational constraint of the clamped end can be released by introducing the moment $M_0$, as shown in Figure 6b. By applying Castigliano’s theorem, moment $M_0$ can be computed as follows:

$$M_0=-\frac{1}{L}\underset{0}{\overset{L}{\int }}\left[\underset{0}{\overset{x}{\int }}\left(x-a\right)p\left(a\right)da\right]\mathrm{d}x-\frac{3}{2L^2}\underset{0}{\overset{L}{\int }}\left[\underset{0}{\overset{x}{\int }}\left(x-a\right)p\left(L-x\right)da\right]x\mathrm{d}x+\frac{L}{2}\underset{0}{\overset{L}{\int }}p\left(x\right)\mathrm{d}x$$

(28)

In the case of the shear rigid beam, the bending moment can be transformed into body force associated with a derivative of the Dirac delta. Indeed, a moment can be replaced with the force couple, as shown in Figure 7.

For such a case, the external load term can be formulated as follows:

$$\begin{array}{ccc}\hfill p\left(x\right)& =& {\displaystyle \underset{\Delta x\to 0}{lim}F\left[\delta \left(x-\left(x_0-\frac{\Delta x}{2}\right)\right)-\delta \left(x-\left(x_0+\frac{\Delta x}{2}\right)\right)\right]}\hfill \\ \hfill & =& {\displaystyle \underset{\Delta x\to 0}{lim}}M\frac{{\displaystyle \left[\delta \left(x-x_0+\frac{\Delta x}{2}\right)-\delta \left(x-x_0-\frac{\Delta x}{2}\right)\right]}}{{\displaystyle \Delta x}}\hfill \\ \hfill {\displaystyle }& =& M{\delta }^{\prime }\left(x-x_0\right).\hfill \end{array}$$

(29)

With Equations (27)–(29), the solution to the clamped–simply supported beam can be formulated as follows:

$$\begin{array}{c}{\displaystyle w\left(x\right)=\frac{2{\delta }^2}{LEI}\sum _{n=1}^{\infty }\underset{0}{\overset{L}{\int }}\left[p\left(x\right)+M_0{\delta }^{\prime }\left(x-0\right)\right]\sin \frac{n\pi x}{L}\mathrm{d}x{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{n\pi \xi }{L}\right)\mathrm{d}\xi \right]}^{-2}\sin \frac{n\pi x}{L}}\hfill \\ {\displaystyle =\frac{2{\delta }^2}{LEI}\sum _{n=1}^{\infty }\left[\underset{0}{\overset{L}{\int }}p\left(x\right)\sin \frac{n\pi x}{L}\mathrm{d}x+\underset{0}{\overset{L}{\int }}{M}_0{\delta }^{\prime }\left(x-0\right)\sin \frac{n\pi x}{L}\mathrm{d}x\right]{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{n\pi \xi }{L}\right)\mathrm{d}\xi \right]}^{-2}\sin \frac{n\pi x}{L}}\hfill \\ {\displaystyle =\frac{2{\delta }^2}{LEI}\sum _{n=1}^{\infty }\left\{\underset{0}{\overset{L}{\int }}p\left(x\right)\sin \frac{n\pi x}{L}\mathrm{d}x+M_0\left[{\left.\delta \left(x-0\right)\sin \frac{n\pi x}{L}\mathrm{d}x\right|}_0^L-\underset{0}{\overset{L}{\int }}\frac{n\pi }{L}\delta \left(x-0\right)\cos \frac{n\pi x}{L}dx\right]\right\}}\hfill \\ {\displaystyle \times {\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{n\pi \xi }{L}\right)\mathrm{d}\xi \right]}^{-2}\sin \frac{n\pi x}{L}}\hfill \\ {\displaystyle =\frac{2{\delta }^2}{LEI}\sum _{n=1}^{\infty }\left[\underset{0}{\overset{L}{\int }}p\left(x\right)\sin \frac{n\pi x}{L}dx-M_0\frac{n\pi }{L}\right]{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{n\pi \xi }{L}\right)\mathrm{d}\xi \right]}^{-2}\sin \frac{n\pi x}{L}.}\hfill \end{array}$$

(30)

3.3. Clamped–Clamped Beam

The clamped–clamped beam, Figure 8a, can be considered as a simply supported beam subjected to bending moments $M_0$ and $M_L$ at the boundaries, as shown in Figure 8b, if the two rotational constrains are released. By applying Castigliano’s theorem, we obtain

$$\begin{array}{c}{\displaystyle M_0=\frac{6}{L^2}\underset{0}{\overset{L}{\int }}\left[{\int }_0^{x}p\left(a\right)\left(x-a\right)\mathrm{d}a\right]x\mathrm{d}x-\frac{4}{L}\underset{0}{\overset{L}{\int }}\left[\underset{0}{\overset{x}{\int }}p\left(a\right)\left(x-a\right)\mathrm{d}a\right]\mathrm{d}x}\hfill \\ {\displaystyle M_L=-\underset{0}{\overset{L}{\int }}p\left(x\right)\left(L-x\right)\mathrm{d}x+\frac{6}{L^2}\underset{0}{\overset{L}{\int }}\left[\underset{0}{\overset{x}{\int }}p\left(a\right)\left(x-a\right)da\right]x\mathrm{d}x-\frac{2}{L}\underset{0}{\overset{L}{\int }}\left[\underset{0}{\overset{x}{\int }}p\left(a\right)\left(x-a\right)\mathrm{d}a\right]\mathrm{d}x.}\hfill \end{array}$$

(31)

With the PD solution for simply supported beam (27) and (31), the PD solution for the clamped–clamped beam can be cast as

$$\begin{array}{c}{\displaystyle w\left(x\right)=\frac{2{\delta }^2}{LEI}\sum _{n=1}^{\infty }\underset{0}{\overset{L}{\int }}\left[p\left(x\right)+M_0{\delta }^{\prime }\left(x-0\right)+M_L{\delta }^{\prime }\left(x-L\right)\right]\sin \frac{n\pi x}{L}\mathrm{d}x\times }\hfill \\ {\displaystyle \times {\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{n\pi \xi }{L}\right)\mathrm{d}\xi \right]}^{-2}\sin \frac{n\pi x}{L}}\hfill \\ {\displaystyle =\frac{2{\delta }^2}{LEI}\sum _{n=1}^{\infty }\left[\underset{0}{\overset{L}{\int }}p\left(x\right)\sin \frac{n\pi x}{L}\mathrm{d}x+\underset{0}{\overset{L}{\int }}{M}_0{\delta }^{\prime }\left(x-0\right)\sin \frac{n\pi x}{L}\mathrm{d}x+\underset{0}{\overset{L}{\int }}{M}_L{\delta }^{\prime }\left(x-L\right)\sin \frac{n\pi x}{L}\mathrm{d}x\right]}\hfill \\ {\displaystyle \times {\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{n\pi \xi }{L}\right)\mathrm{d}\xi \right]}^{-2}\sin \frac{n\pi x}{L}}\hfill \\ {\displaystyle =\frac{2{\delta }^2}{LEI}\sum _{n=1}^{\infty }\left\{\underset{0}{\overset{L}{\int }}p\left(x\right)\sin \frac{n\pi x}{L}\mathrm{d}x+M_0\left[-\underset{0}{\overset{L}{\int }}\frac{n\pi }{L}\delta \left(x-0\right)\cos \frac{n\pi x}{L}dx\right]\right.}\hfill \\ {\displaystyle \left.{\displaystyle +M_L\left[-\underset{0}{\overset{L}{\int }}\frac{n\pi }{L}\delta \left(x-L\right)\cos \frac{n\pi x}{L}\mathrm{d}x\right]}\right\}{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{n\pi \xi }{L}\right)\mathrm{d}\xi \right]}^{-2}\sin \frac{n\pi x}{L}}\hfill \\ {\displaystyle =\frac{2{\delta }^2}{LEI}\sum _{n=1}^{\infty }\left\{\underset{0}{\overset{L}{\int }}p\left(x\right)\sin \frac{n\pi x}{L}\mathrm{d}x-\frac{n\pi }{L}\left[M_0+M_L{\left(-1\right)}^n\right]\right\}{\left[{\int }_{-\delta }^{\delta }\frac{1}{{\xi }^2}\left(1-\cos \frac{n\pi \xi }{L}\right)\mathrm{d}\xi \right]}^{-2}\sin \frac{n\pi x}{L}.}\hfill \end{array}$$

(32)

3.4. Simply Supported–Roller-Clamped Beam

A simply supported–roller-supported beam subjected to transverse loading $p\left(x\right)$ is illustrated in Figure 9. The PD boundary conditions in this case admit an anti-symmetric and symmetric relation between the fictitious and real domains

$$w(-\xi )=-w\left(\xi \right),w(L-\xi )=w(L+\xi ).$$

(33)

Based on relation (33), the displacement field can be extended over the entire real line such that it has a periodicity of $4L$ and is anti-symmetric about the origin and symmetric about $x=L$, as illustrated in Figure 10.

Therefore, the displacement can be expanded using the Fourier series as follows:

$$\begin{array}{ccc}\left\{\begin{array}{c}w\left(-x\right)=-w\left(x\right)\hfill \\ w\left(L-x\right)=w\left(L+x\right)\hfill \end{array}\right.& \Rightarrow & {\displaystyle w\left(x\right)=\sum _{n=1}^{\infty }{b}_{n}sin\frac{\left(2n-1\right)\pi x}{2L}}.\end{array}$$

(34)

Following the similar approach given in Section 3.1, the PD solution to the simply supported–roller-supported beam can be expressed explicitly as follows:

$$w\left(x\right)=\frac{2{\delta }^2}{LEI}\sum _{n=1}^{\infty }\underset{0}{\overset{L}{\int }}p\left(x\right)sin\frac{\left(2n-1\right)\pi x}{2L}\mathrm{d}x{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-cos\frac{\left(2n-1\right)\pi \xi }{2L}\right)\mathrm{d}\xi \right]}^{-2}sin\frac{\left(2n-1\right)\pi x}{2L}.$$

(35)

3.5. Clamped–Roller-Clamped Beam

Figure 11a illustrates a clamped–roller-clamped beam. To derive the analytical solution, the rotational constraint in the left clamped edge is removed, and the moment $M_0$ is introduced, as shown in Figure 11b. By applying Castigliano’s theorem, we obtain

$$M_0=-\frac{1}{L}\underset{0}{\overset{L}{\int }}\left[\underset{0}{\overset{x}{\int }}p\left(a\right)\left(x-a\right)da\right]\mathrm{d}x+\frac{L}{2}\underset{0}{\overset{L}{\int }}p\left(x\right)dx.$$

(36)

Again, the boundary moment $M_0$ can be absorbed as a part of the body force, and hence, based on the solution form of simply supported–roller-clamped beam, the solution for the clamped–roller-clamped beam can be given as

$$\begin{array}{c}{\displaystyle w\left(x\right)=\frac{2{\delta }^2}{LEI}\sum _{n=1}^{\infty }\left[\underset{0}{\overset{L}{\int }}p\left(x\right)sin\frac{\left(2n-1\right)\pi x}{2L}dx-M_0\frac{\left(2n-1\right)\pi }{2L}\right]}\hfill \\ {\displaystyle \times {\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-cos\frac{\left(2n-1\right)\pi \xi }{2L}\right)\mathrm{d}\xi \right]}^{-2}sin\frac{\left(2n-1\right)\pi x}{2L}.}\hfill \end{array}$$

(37)

3.6. Cantilever Beam

Consider a cantilever beam subjected to the transverse load $p\left(x\right)$. The solution can be identically decomposed using the following steps (see Figure 12).

• Place a fictitious simple support at the free end.
• Transit the origin to be level with the free end and then subtract the corresponding rigid body motion.
• Release the vertical displacement constraint and replace it with the corresponding shear force Q.

The shear force Q must balance with the resultant of the external loading such that

$$Q=-\underset{0}{\overset{L}{\int }}p\left(x\right)dx.$$

(38)

By modifying the PD solution for the simply supported–roller-clamped beam (35) with consideration of shear force Q at the left end, the explicit PD solution for the cantilever beam can be given as follows:

$$\begin{array}{c}{\displaystyle w\left(x\right)=\frac{2{\delta }^2}{LEI}\sum _{n=1}^{\infty }\frac{{\displaystyle \underset{0}{\overset{L}{\int }}p\left(x\right)\cos \frac{\left(2n-1\right)\pi x}{2L}\mathrm{d}x+Q}}{{\displaystyle {\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{\left(2n-1\right)\pi \xi }{2L}\right)\mathrm{d}\xi \right]}^2}}\left[\cos \frac{\left(2n-1\right)\pi x}{2L}-1\right]}\hfill \\ {\displaystyle =\frac{2{\delta }^2}{LEI}\sum _{n=1}^{\infty }\frac{{\displaystyle \underset{0}{\overset{L}{\int }}p\left(x\right)\left(\cos \frac{\left(2n-1\right)\pi x}{2L}-1\right)\mathrm{d}x}}{{\displaystyle {\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{\left(2n-1\right)\pi \xi }{2L}\right)\mathrm{d}\xi \right]}^2}}\left[\cos \frac{\left(2n-1\right)\pi x}{2L}-1\right].}\hfill \end{array}$$

(39)

4. Analytical Solutions to Peridynamic Problems

Let us recall the PD equation of motion (16):

$$\rho A\ddot{w}\left(x\right)=\frac{EI}{{\delta }^2}\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{w\left(x+\zeta \right)-w\left(x\right)}{{\zeta }^2}\mathrm{d}\zeta -\underset{-\delta }{\overset{\delta }{\int }}\frac{w\left(x+\xi +\eta \right)-w\left(x+\xi \right)}{{\eta }^2}\mathrm{d}\eta \right]\mathrm{d}\xi +p\left(x\right).$$

(40)

To formulate the analytical solutions to Equation (40), we apply the Laplace transform as follows:

$$\begin{array}{c}\rho A\left[s^{2}W\left(x,s\right)-s{w}_0\left(x\right)-v_0\left(x\right)\right]\hfill \\ {\displaystyle =c\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left[\begin{array}{c}{\displaystyle \underset{-\delta }{\overset{\delta }{\int }}\frac{W\left(x+\zeta ,s\right)-W\left(x,s\right)}{{\zeta }^2}d\zeta }\hfill \\ {\displaystyle -\underset{-\delta }{\overset{\delta }{\int }}\frac{W\left(x+\xi +\eta ,s\right)-W\left(x+\xi ,s\right)}{{\eta }^2}d\eta .}\hfill \end{array}\right]d\xi +P\left(x,s\right),}\hfill \end{array}$$

(41)

where

$$W\left(x,s\right)=L\left[w\left(x,t\right)\right],P\left(x,s\right)=L\left[p\left(x,t\right)\right],w_0\left(x\right)=w\left(x,0\right),v_0\left(x\right)=\dot{w}\left(x,0\right).$$

(42)

Consider a simply supported beam subjected to some arbitrary dynamic load. By analogy to Section 2.3.1, we can assume that the solution to Equation (41) has the following form:

$$W\left(x,s\right)=\sum _{n=1}^{\infty }{B}_n\left(s\right)\sin \frac{n\pi x}{L}.$$

(43)

After plugging Equation (43) into Equation (41), we obtain

$$\sum _{n=1}^{\infty }{B}_n\left(s\right)\left\{c{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{n\pi \xi }{L}\right)d\xi \right]}^2+\rho A{s}^2\right\}\sin \frac{n\pi x}{L}=P\left(x,s\right)+s\rho A{w}_0\left(x\right)+\rho A{v}_0\left(x\right).$$

(44)

According to orthogonality, we obtain

$$\begin{array}{c}{\displaystyle B_n\left(s\right)=\frac{2}{L}\frac{\underset{0}{\overset{L}{\int }}\left[P\left(x,s\right)+s\rho A{w}_0\left(x\right)+\rho A{v}_0\left(x\right)\right]\sin \frac{n\pi x}{L}dx}{\rho A{s}^2+c{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{n\pi \xi }{L}\right)d\xi \right]}^2}}\hfill \\ {\displaystyle =\frac{2}{L}\frac{\frac{1}{\rho A}\underset{0}{\overset{L}{\int }}P\left(x,s\right)\sin \frac{n\pi x}{L}dx+s{\widehat{w}}_n+{\widehat{v}}_n}{\left(s-i{\omega }_n\right)\left(s+i{\omega }_n\right)},}\hfill \end{array}$$

(45)

where

$$\begin{array}{c}{\displaystyle {\widehat{w}}_n=\underset{0}{\overset{L}{\int }}{w}_0\left(x\right)\sin \frac{n\pi x}{L}dx,{\widehat{v}}_n=\underset{0}{\overset{L}{\int }}{v}_0\left(x\right)\sin \frac{n\pi x}{L}dx,}\hfill \\ {\displaystyle {\omega }_n=\sqrt{\frac{c}{\rho A}}\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{n\pi \xi }{L}\right)d\xi .}\hfill \end{array}$$

(46)

Applying partial fractions to Equation (45) it follows that

$$B_n\left(s\right)=\frac{2}{L}\left[\frac{1}{\rho A}\frac{\underset{0}{\overset{L}{\int }}P\left(x,s\right)\sin \frac{n\pi x}{L}dx}{\left(s-i{\omega }_n\right)\left(s+i{\omega }_n\right)}+\frac{i{\omega }_n{\widehat{w}}_n+{\widehat{v}}_n}{2i{\omega }_n}\frac{1}{s-i{\omega }_n}+\frac{i{\omega }_n{\widehat{w}}_n-{\widehat{v}}_n}{2i{\omega }_n}\frac{1}{s+i{\omega }_n}\right].$$

(47)

After performing the inverse Laplace transform on (47), we obtain

$$\begin{array}{c}{\displaystyle b_n\left(t\right)=\frac{2}{L}\left\{\frac{1}{\rho A}\frac{1}{2i{\omega }_n}\underset{0}{\overset{t}{\int }}\left(e^{i{\omega }_{n}u}-e^{-i{\omega }_{n}u}\right)\left[\underset{0}{\overset{L}{\int }}b\left(x,t-u\right)\sin \widehat{n}xdx\right]du\right.}\hfill \\ {\displaystyle +\left.\frac{i{\omega }_n{\widehat{w}}_n+{\widehat{v}}_n}{2i{\omega }_n}{e}^{i{\omega }_{n}t}+\frac{i{\omega }_n{\widehat{w}}_n-{\widehat{v}}_n}{2i{\omega }_n}{e}^{-i{\omega }_{n}t}\right\}}\hfill \\ {\displaystyle =\frac{2}{L}\left\{{\widehat{w}}_n\cos {\omega }_{n}t+\frac{{\widehat{v}}_n}{{\omega }_n}\sin {\omega }_{n}t+\frac{1}{\rho A}\frac{1}{{\omega }_n}{\int }_0^t\sin {\omega }_{n}u\left[\underset{0}{\overset{L}{\int }}p\left(x,t-u\right)\sin \frac{n\pi x}{L}dx\right]du\right\}.}\hfill \end{array}$$

(48)

In this case, the solution is

$$w\left(x,t\right)=L^{-1}\left[W\left(x,s\right)\right]=\sum _{n=1}^{\infty }{b}_n\left(t\right)\sin \frac{n\pi x}{L}.$$

(49)

Coupling (48) with (49) yields the complete solution for a simply supported beam as follows:

$$\begin{array}{c}{\displaystyle w\left(x,t\right)=\frac{2}{L}\sum _{n=1}^{\infty }\left\{{\widehat{w}}_n\cos {\omega }_{n}t+\frac{{\widehat{v}}_n}{{\omega }_n}\sin {\omega }_{n}t\right.}\hfill \\ {\displaystyle \left.+\frac{1}{\rho A}\frac{1}{{\omega }_n}\underset{0}{\overset{t}{\int }}\sin {\omega }_{n}u\left[\underset{0}{\overset{L}{\int }}p\left(x,t-u\right)\sin \frac{n\pi x}{L}dx\right]du\right\}\sin \frac{n\pi x}{L}}\hfill \end{array}$$

(50)

where

$$\begin{array}{c}{\displaystyle {\widehat{w}}_n=\underset{0}{\overset{L}{\int }}{w}_0\left(x\right)\sin \frac{n\pi x}{L}dx,{\widehat{v}}_n=\underset{0}{\overset{L}{\int }}{v}_o\left(x\right)\sin \frac{n\pi x}{L}dx,}\hfill \\ {\displaystyle {\omega }_n=\sqrt{\frac{c}{\rho A}}\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{n\pi \xi }{L}\right)d\xi .}\hfill \end{array}$$

(51)

Regarding the dynamic response of the clamped–simply supported and clamped–clamped case, we will have to add moments on the boundaries accordingly and absorb them into the body force as follows:

$$\overline{p}\left(x,t\right)=M_0\left(t\right){\delta }^{\prime }\left(x\right)+M_L\left(t\right)\delta \left(x-L\right)+p\left(x,t\right).$$

(52)

Here, $M_0\left(t\right)$ and $M_L\left(t\right)$ must balance the net effect of external loading and inertial force, and it can be computed using Castigliano’s theorem. Regarding simply supported–roller-clamped case and its ramifications, we can replace the term $\frac{n\pi }{L}$ by $\frac{\left(2n-1\right)\pi }{2L}$ and follow a similar procedure.

5. Examples

5.1. Peristatic Solutions

The derived closed-form solutions can be applied to a large class of beam problems for various boundary conditions and loading cases, including distributed and concentrated loads. Below, we present plots of derived solutions for the deflection function for several examples. In addition, well-known analytical solutions to the classical beam theory will be plotted in order to demonstrate the validation of both the PD beam theory and the derived results.

Consider a beam with a rectangular cross-section with high $h=0.01$ m and width $b=0.01$ m. The length of the beam is assumed to be $L=1$ m, and Young’s modulus of the beam material is $E=200$ GPa. conditions. The PD horizon size is chosen as $\delta =0.001$ m. Figure 13 illustrates the plots of closed-form series solutions developed in this study. Different cases of loadings, including concentrated moment applied at different points of the beam, uniformly distributed load over the beam length, concentrated force at different points of the beam, and the load distributed over a part of the beam are considered. Furthermore, different examples of boundary conditions, including simply supported–simply supported, clamped–simply supported, clamped–clamped, simply supported–roller-clamped, clamped–roller-clamped, and clamped–free, are analyzed. For comparison, solutions according to the classical beam theory for the same loadings and boundary conditions are presented. A very good agreement between the results for the selected value of the horizon size can be observed.

Let us note that the horizon size is an important parameter in PD, providing a length-scale influence and the non-locality of the system. If the horizon size tends to zero, the PD solution converges to that of the classical beam theory in the case of elastic material behavior. The horizon size enters the derived analytical solutions in the explicit form. Plots of deflection vs. horizon size for a simply supported beam are presented in [27].

Let us summarize the closed-form analytical solutions for the six cases presented in Figure 13 as follows:

• Simply supported–simply supported

  $$w\left(x\right)=\frac{2}{cL}\sum _{n=1}^{\infty }\frac{-\frac{n\pi }{L}M\cos \left(\frac{n\pi }{2}\right)}{{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{n\pi \xi }{L}\right)d\xi \right]}^2}\sin \frac{n\pi x}{L}$$

  based on PD and

  $$w\left(x\right)=-\frac{M}{24LEI}\left\{\left[-3L^3+12L^{2}x-12L{x}^2\right]H\left(2x-L\right)-L^{2}x+4x^3\right\}$$

  based on CBT.
• Clamped–simply supported

  $$w\left(x\right)=-\frac{2}{cL}\sum _{n=1}^{\infty }\frac{\underset{0}{\overset{L}{\int }}p\sin \frac{n\pi x}{L}dx-\frac{n\pi }{L}\frac{p}{8}{L}^2}{{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{n\pi \xi }{L}\right)d\xi \right]}^2}\sin \frac{n\pi x}{L}$$

  based on PD and

  $$w\left(x\right)=-\frac{p{x}^2}{48EI}\left(3L^2-5Lx+2x^2\right)$$

  based on CBT.
• Clamped–clamped

  $$w\left(x\right)=-\frac{2p}{cL}\sum _{n=1}^{\infty }\frac{\sin \frac{n\pi a}{L}-\frac{4}{27}n\pi +n\pi {\left(-1\right)}^n\frac{2}{27}}{{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{n\pi \xi }{L}\right)d\xi \right]}^2}\sin \frac{n\pi x}{L}$$

  based on PD and

  $$w\left(x\right)=\frac{F}{162EI}\left[4x^2\left(3L-5x\right)-{\left(L-3x\right)}^{3}H\left(3x-L\right)\right]$$

  based on CBT.
• Simply supported–roller-clamped

  $$w\left(x\right)=-\frac{2p}{cL}\sum _{n=1}^{\infty }\frac{\underset{\frac{L}{4}}{\overset{\frac{3L}{4}}{\int }}\sin \frac{\left(2n-1\right)\pi x}{2L}d\xi }{{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{\left(2n-1\right)\pi \xi }{2L}\right)d\xi \right]}^2}\sin \frac{\left(2n-1\right)\pi x}{2L}$$

  based on PD and

  $$w\left(x\right)=-\frac{p}{6144EI}\left\{\begin{array}{c}\left[L^4-16L^{3}x+96L^2{x}^2-256L{x}^3+256x^4\right]H\left(L-4x\right)\hfill \\ +\left[-81L^4+432L^{3}x-864L^2{x}^2-256x^4+768L{x}^3\right]H\left(3L-4x\right)\hfill \\ -L^3\left(L-16x\right)+27L^3\left(3L-16x\right)+768L^2{x}^2\hfill \end{array}\right\}$$

  based on CBT.
• Clamped–roller-clamped

  $$w\left(x\right)=-\frac{2p}{cL}\sum _{n=1}^{\infty }\frac{\sin \frac{\left(2n-1\right)\pi }{4}-\frac{3}{16}\left(2n-1\right)\pi }{{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{\left(2n-1\right)\pi \xi }{2L}\right)d\xi \right]}^2}\sin \frac{\left(2n-1\right)\pi x}{2L}$$

  based on PD and

  $$w\left(x\right)=\frac{F}{48EI}\left[x^2\left(9L-8x\right)-{\left(L-2x\right)}^{3}H\left(2x-L\right)\right]$$

  based on CBT
• Cantilever beam

  $$w\left(x\right)=-\frac{2}{cL}\sum _{n=1}^{\infty }\frac{M\frac{\left(2n-1\right)\pi }{2L}{\left(-1\right)}^{n+1}}{{\left[\underset{-\delta }{\overset{\delta }{\int }}\frac{1}{{\xi }^2}\left(1-\cos \frac{\left(2n-1\right)\pi \xi }{2L}\right)d\xi \right]}^2}\left[1-\cos \frac{\left(2n-1\right)\pi x}{2L}\right]$$

  based on PD and

  $$w\left(x\right)=-\frac{M}{2EI}{x}^2$$

  based on CBT

5.2. Peridynamic Solutions

Consider the simply supported beam subjected to a harmonic load, as shown in Figure 14.

Let us set L = 2 m, A = 0.01 × 0.01 m${}^2$, $E=200\times {10}^9$ Pa, $\rho$ = 7850 kg/m${}^3$, $\delta$ = 0.01 m. The initial conditions are assumed as follows: $u\left(x,0\right)=0.01x\left(x-L\right)$ and $\dot{u}\left(x,0\right)=\sin \frac{\pi x}{L}$. The harmonic concentrated load is

$$p\left(x,t\right)=50sin\left(\frac{{\omega }_1}{3}t\right)\delta \left(x-\frac{L}{2}\right),$$

where $\delta$ is the Dirac delta function. Figure 15 illustrates the transverse displacement vs. time plots for two different points along the beam axis.

We observe that for the considered value of the PD horizon, the results according to the PD beam theory and the classical beam theory almost coincide. As the next example, consider a mass drop on the midpoint of a simply supported beam; see Figure 16.

As in the previous example, we set L = 2 m, A = 0.01 × 0.01 m${}^2$, $E=200\times {10}^9$ Pa, $\rho$ = 7850 kg/m${}^3$, and $\delta$ = 0.01 m. The balance of momentum for the mass yields

$$-mv\left(t_{1^{+}}\right)-mv\left(t_{1^{-}}\right)=-m\left[v\left(t_{1^{+}}\right)+v\left(t_{1^{-}}\right)\right]=-m\overline{v},\overline{v}=-\left[v\left(t_{1^{+}}\right)+v\left(t_{1^{-}}\right)\right].$$

Specifying the concentrated force acting on the beam by F and considering the interaction over $\Delta t$, we obtain

$$m\overline{v}\left\{H\left(t-t_1\right)-H\left[t-\left(t_1+\Delta t\right)\right]\right\}=F\Delta t,$$

where H is the Heaviside function. Consequently, the force is obtained as follows

$$F=m\overline{v}\frac{H\left(t-t_1\right)-H\left[t-\left(t_1+\Delta t\right)\right]}{\Delta t}$$

or

$$F\left(t\right)=m\overline{v}\delta \left(t-t_1\right)$$

as $\Delta t\to 0$. The initial conditions are $u\left(x,0\right)=0.01x\left(x-L\right)$ and $\dot{u}\left(x,0\right)=\sin \frac{\pi x}{L}$ The load is assumed as follows:

$$p\left(x,t\right)=F\left(t\right)\delta \left(x-\frac{L}{2}\right),F\left(t\right)=10\delta \left(t-0.5\right).$$

Plots of the transverse displacement vs. time for two different points along the beam axis are shown in Figure 17.

Again, the results according to the PD beam theory and the classical beam theory agree if the horizon size is considered small.

6. Conclusions

In this paper, straight elastic beams are analyzed within the framework of peridynamics. Closed-form analytical solutions to both peristatic and peridynamic equations are presented for various examples with different types of loadings and boundary conditions. In addition to the cases analyzed in the literature, novel solutions for the clamped edge, roller-clamped edge, free edge, concentrated force, and concentrated moment are presented. The validation of PD formulations and solutions is accomplished by comparing the deflections against the corresponding results according to the Bernoulli–Euler beam theory. A very good agreement between the non-local and the classical theories is observed for the case of the small horizon sizes, which shows the capability of the derived PD equations and proposed boundary conditions.

The derived closed-form solutions include the horizon size in the explicit form such that the non-locality of the PD theory can be analyzed in a natural way. Furthermore, the results are useful to validate the numerical methods and numerical codes developed to solve PD equations.

It is worth noting that, unlike the classical beam theory, many different types of constraints can be applied within the peridynamic framework. Indeed, the deflection function can be specified over the interaction domain in many different ways, in addition to the cases discussed in this paper. Future studies should be related to aalyzing different types of PD constraints as they influence the deformed shape of the beam and deriving the corresponding analytical solutions.