Dynamic Modeling of Motorized Spindle System with Unbalanced Mass and Spindle Inclination
Abstract
1. Introduction
2. Dynamic Modeling
2.1. Dynamic Modeling of Motorized Spindle without Fault
2.2. Dynamic Modeling of Motorized Spindle with Unbalanced Mass Fault
2.3. Dynamic Modeling of Motorized Spindle with Spindle Inclination Fault
3. Results and Discussion
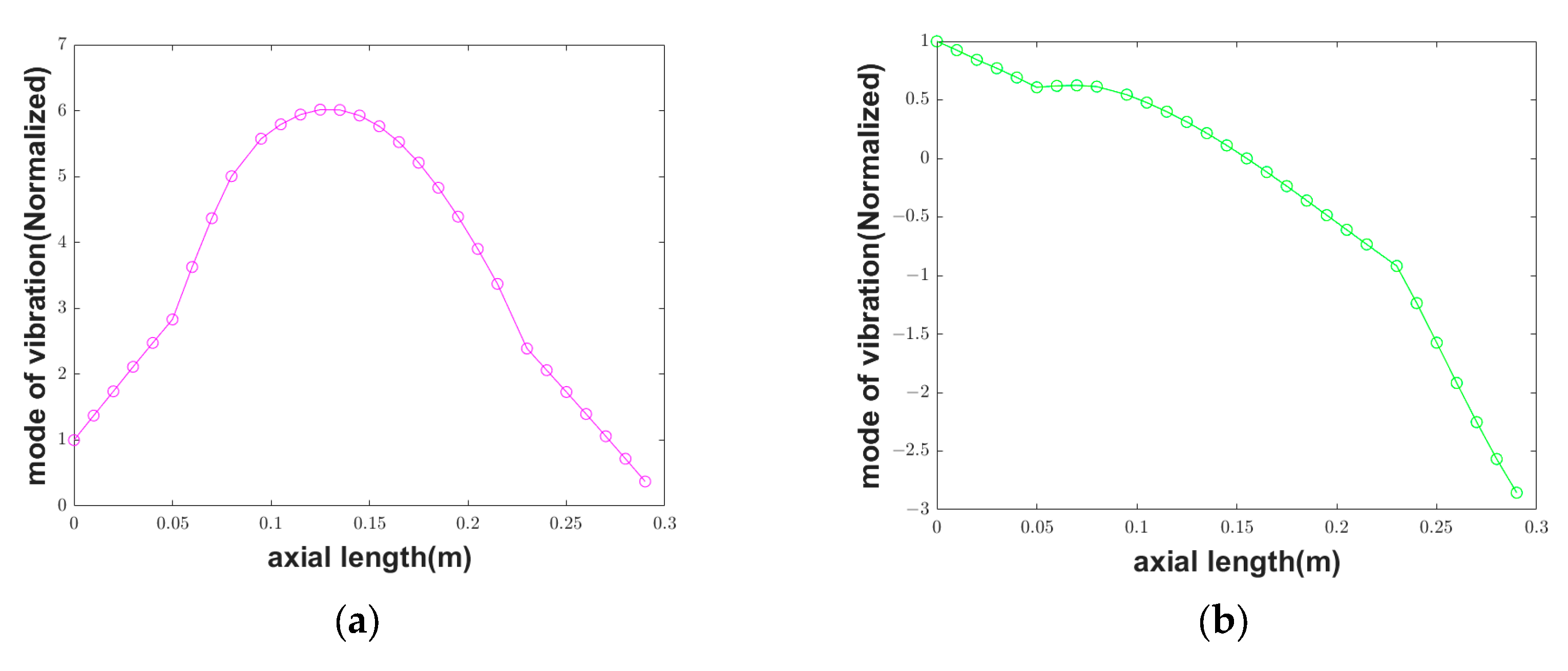
3.1. Dynamic Characteristics of Motorized Spindle without Fault
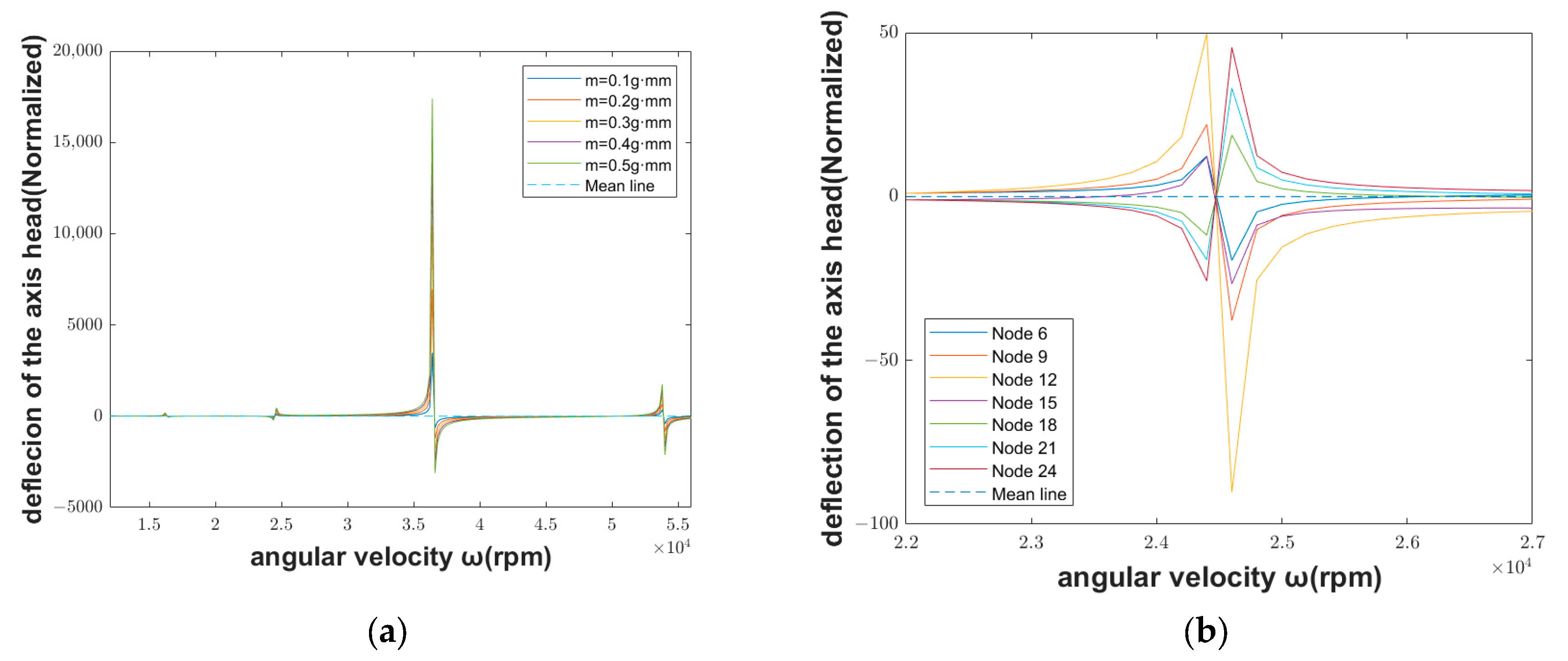
3.2. Dynamic Characteristics of Motorized Spindle with Unbalanced Mass Fault
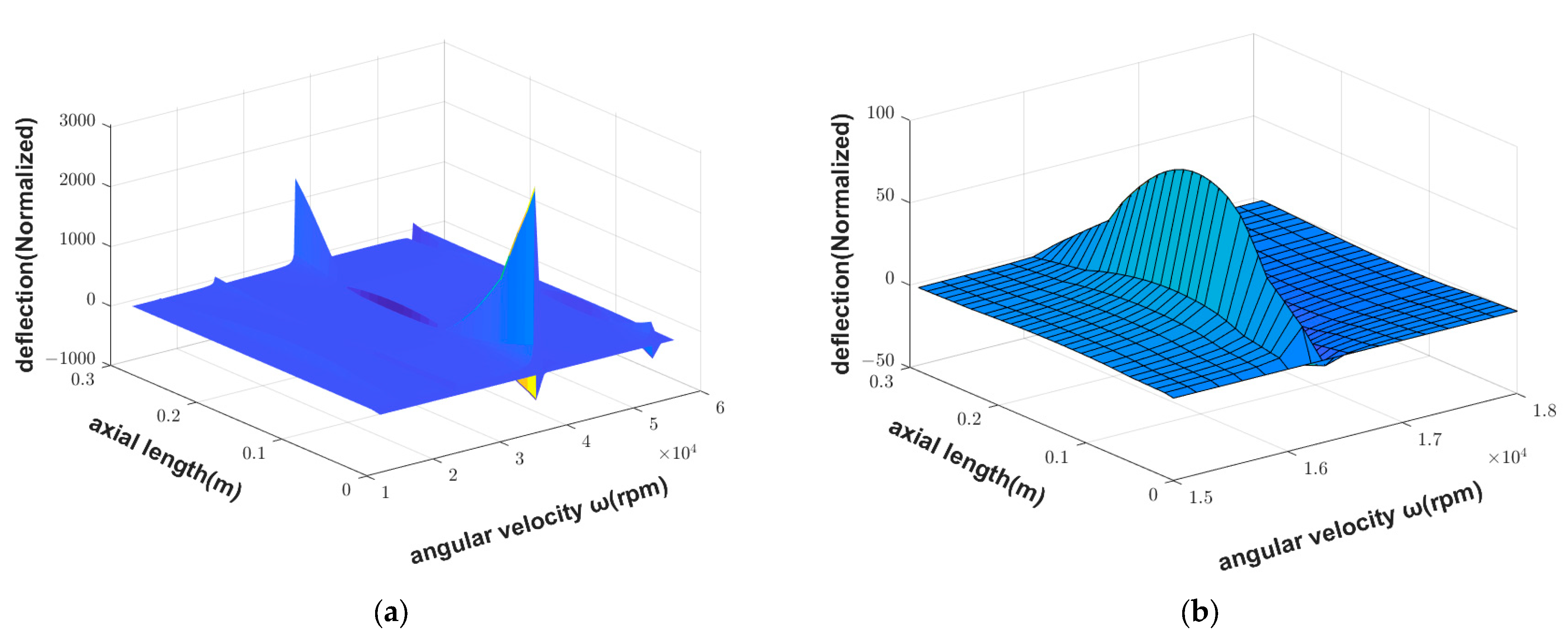
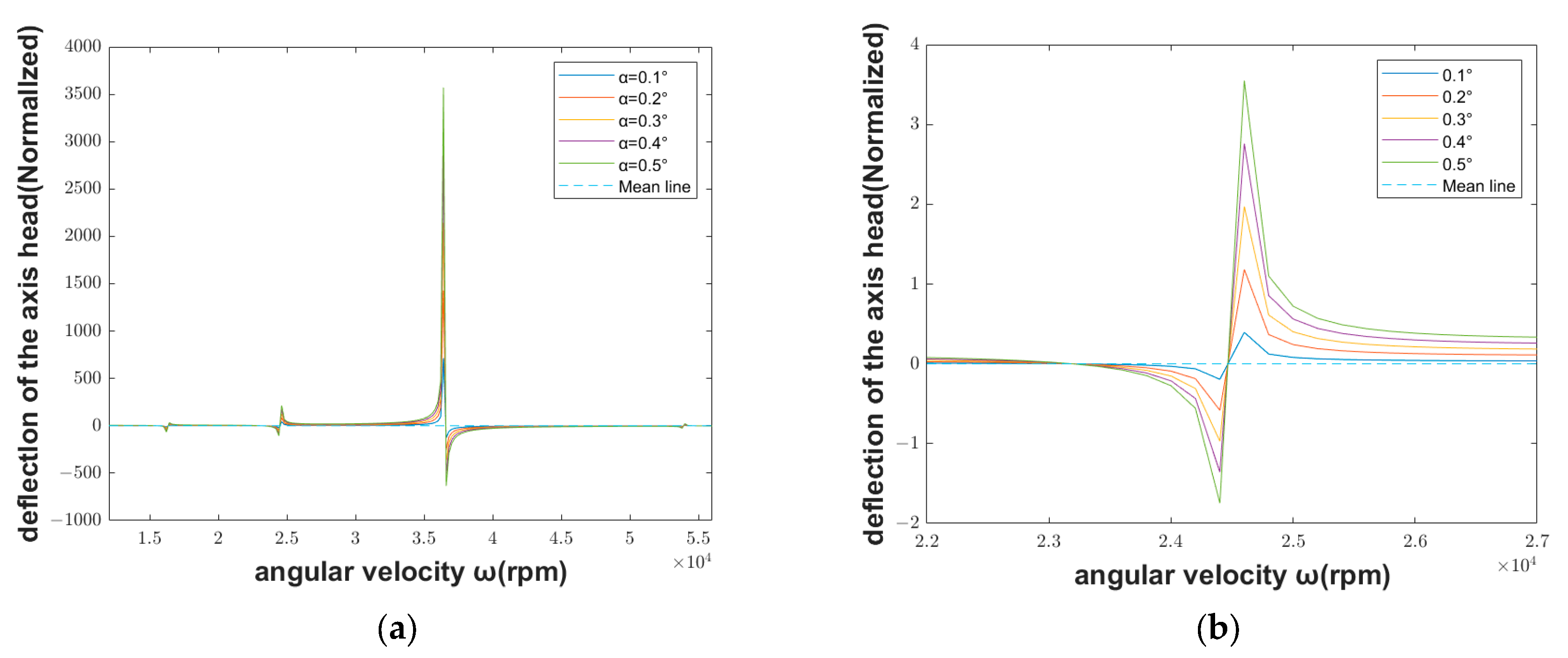
3.3. Dynamic Characteristics of Motorized Spindle with Spindle Inclination Fault
4. Conclusions
- (1)
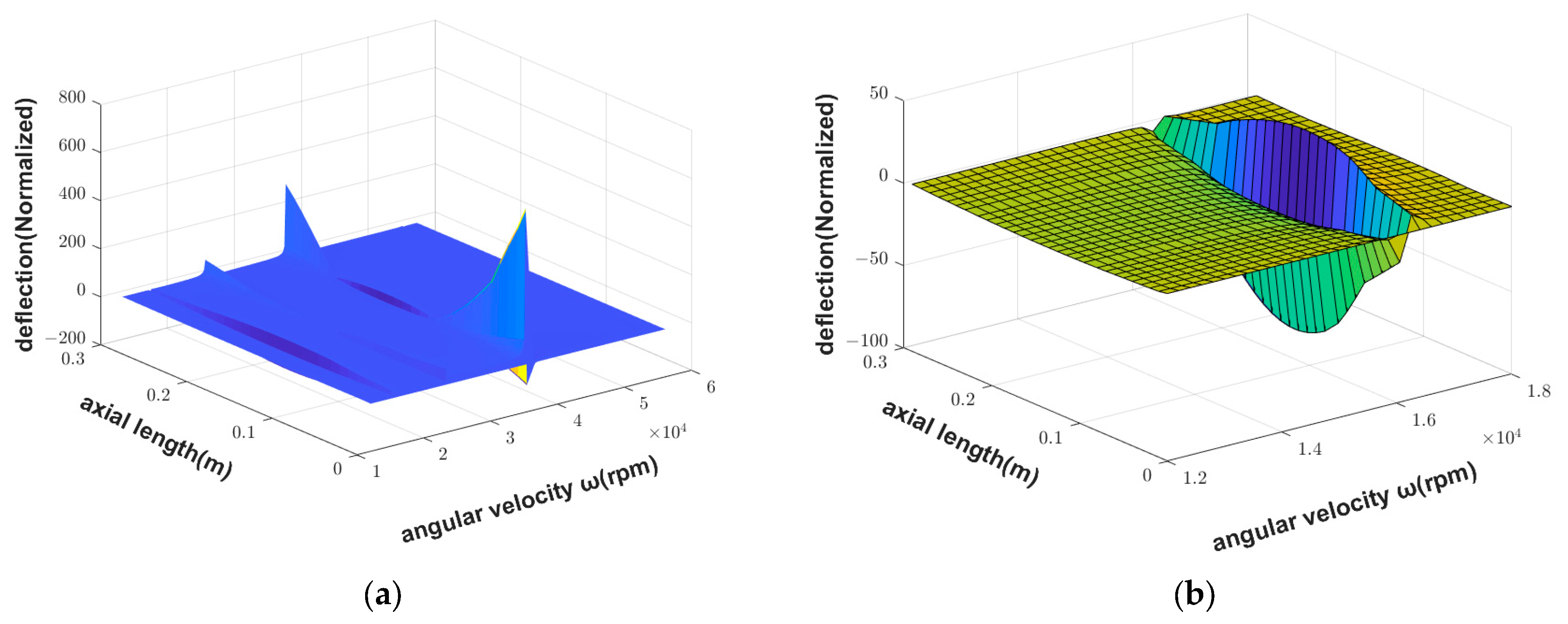
- If the unbalanced mass fault occurs, when the spindle speed is close to the first-order or second-order critical speed, the deflection at the initial end of the spindle is small; when the spindle speed is close to the fourth-order critical speed, the deflection is large. The opposite is true when the spindle inclination fault occurs. It can be seen that the motorized spindle is more sensitive at high rotating speeds when the unbalanced mass fault occurs, and it is more sensitive at low rotating speed when the spindle inclination fault occurs.
- (2)
- CNC machine tools are vibration systems with high stiffness, and the support system is flexible or nearly flexible. The rotor may exhibit rigid behavior, manifested as a smaller rotor vibration and larger bearing seat vibration. So, regardless of whether the spindle has an unbalanced mass fault or spindle inclination fault, when the spindle speed reaches the third-order critical speed, the deflection at the initial end of the spindle is the largest.
- (3)
- When the spindle speed approaches the first-order critical speed, an unbalanced mass fault will make the middle part of the spindle bend upward, while the spindle inclination fault will make the middle part of the spindle bend downward.
- (4)
- When the unbalanced mass fault occurs, the deflection will be increased first, then suddenly decrease until the direction change, and the deflection will continue to increase along this direction. When the spindle inclination fault occurs, the deflection will be increased first in the opposite direction, then gradually decreases after reaching the maximum value, and then gradually continues to increase along the original direction when it returns to the original direction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lin, C.-W.; Lin, Y.-K.; Chu, C.-H. Dynamic models and design of spindle-bearing systems of machine tools: A review. Int. J. Precis. Eng. Manuf. 2013, 14, 513–521. [Google Scholar] [CrossRef]
- Gu, D.; Wei, Y.; Xiong, B.; Liu, S.; Zhao, D.; Wang, B. Three degrees of freedom chatter stability prediction in the milling process. J. Mech. Sci. Technol. 2020, 34, 3489–3496. [Google Scholar] [CrossRef]
- Xiong, B.; Wei, Y.; Gu, D.; Zhao, D.; Wang, B.; Liu, S. Chatter stability analysis of variable speed milling with helix angled cutters. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2021, 235, 850–861. [Google Scholar] [CrossRef]
- Appana, D.K.; Prosvirin, A.; Kim, J.-M. Reliable fault diagnosis of bearings with varying rotational speeds using envelope spectrum and convolution neural networks. Soft Comput. 2018, 22, 6719–6729. [Google Scholar] [CrossRef]
- Tra, V.; Kim, J.; Kim, J.-M. Fault Diagnosis of Bearings with Variable Rotational Speeds Using Convolutional Neural Networks. In Advances in Computer Communication and Computational Sciences; Springer: Singapore, 2019; pp. 71–81. [Google Scholar]
- Feng, H.; Jiang, S. Dynamics of a motorized spindle supported on water-lubricated bearings. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 459–472. [Google Scholar] [CrossRef]
- Ma, J.; Wu, L.; Zhu, Z.Q. Effect of magnet thickness on electromagnetic performance of high speed permanent magnet machines. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–7. [Google Scholar]
- Wang, B.; Wei, Y.; Liu, S.; Gu, D.; Zhao, D. Intelligent chatter detection for CNC machine based on RFE multi-feature selection strategy. Meas. Sci. Technol. 2021, 32, 095904. [Google Scholar] [CrossRef]
- Shan, W.; Chen, X.; He, Y.; Zhou, J. A novel experimental research on vibration characteristics of the running high-speed motorized spindles. J. Mech. Sci. Technol. 2013, 27, 2245–2252. [Google Scholar] [CrossRef]
- Fan, K.; Xiao, J.; Wang, R.; Gao, R. Thermoelectric-based cooling system for high-speed motorized spindle I: Design and control mechanism. Int. J. Adv. Manuf. Technol. 2022, 121, 3787–3800. [Google Scholar] [CrossRef]
- Wang, N.; Jiang, D. Vibration response characteristics of a dual-rotor with unbalance-misalignment coupling faults: Theoretical analysis and experimental study. Mech. Mach. Theory 2018, 125, 207–219. [Google Scholar] [CrossRef]
- Xu, X.; Han, Q.; Chu, F. Nonlinear vibration of a generator rotor with unbalanced magnetic pull considering both dynamic and static eccentricities. Arch. Appl. Mech. 2016, 86, 1521–1536. [Google Scholar] [CrossRef]
- Liu, H.; Wu, Y.; Wang, X.; Yan, P.; Zhang, X. Nonlinear normal modes and primary resonance for permanent magnet synchronous motors with a nonlinear restoring force and an unbalanced magnetic pull. Nonlinear Dyn. 2019, 97, 1197–1213. [Google Scholar] [CrossRef]
- Werner, U. Influence of electromagnetic field damping on forced vibrations of induction rotors caused by dynamic rotor eccentricity. ZAMM—J. Appl. Math. Mech./Z. Für Angew. Math. Und Mech. 2017, 97, 38–59. [Google Scholar] [CrossRef]
- Zuo, S.; Li, D.; Mao, Y.; Deng, W. Longitudinal vibration analysis and suppression of electric wheel system driven by in-wheel motor considering unbalanced magnetic pull. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 2729–2745. [Google Scholar] [CrossRef]
- Xiang, C.; Liu, F.; Liu, H.; Han, L.; Zhang, X. Nonlinear dynamic behaviors of permanent magnet synchronous motors in electric vehicles caused by unbalanced magnetic pull. J. Sound Vib. 2016, 371, 277–294. [Google Scholar] [CrossRef]
- Kumar, G.; Kalita, K. Vibration control using BCW induction motor. Procedia Eng. 2016, 144, 94–101. [Google Scholar] [CrossRef][Green Version]
- Bossmanns, B.; Tu, J.F. A power flow model for high speed motorized spindles—Heat generation characterization. J. Manuf. Sci. Eng. 2000, 123, 494–505. [Google Scholar] [CrossRef]
- Li, H.; Shin, Y.C. Integrated dynamic thermo-mechanical modeling of high speed spindles, Part 1: Model development. J. Manuf. Sci. Eng. 2004, 126, 148–158. [Google Scholar] [CrossRef]
- Li, H.; Shin, Y.C. Integrated dynamic thermo-mechanical modeling of high speed spindles, Part 2: Solution procedure and validations. J. Manuf. Sci. Eng. 2004, 126, 159–168. [Google Scholar] [CrossRef]
- Xul, J.; Zheng, X.; Zhang, J.; Liu, X. Vibration characteristics of unbalance response for motorized spindle system. Procedia Eng. 2017, 174, 331–340. [Google Scholar] [CrossRef]
- Liu, J.; Lai, T.; Chen, X. Dynamics analysis of unbalanced motorized spindles supported on ball bearings. Shock Vib. 2016, 2016, 2787524. [Google Scholar] [CrossRef]
- Su, X.; Lu, H.; Zhang, X.; Fan, W.; Zhang, Y. Analysis of dynamic characteristic for misalignment-spline gear shaft based on whole transfer matrix method. J. Vibroeng. 2018, 20, 1392–1408. [Google Scholar] [CrossRef]
- Huang, S.; Chi, X.; Xu, Y.; Sun, Y. Dynamic characteristics of coupling shaft system in tufting machine based on the Riccati whole transfer matrix method. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 356–371. [Google Scholar] [CrossRef]
- Jiang, S.; Zheng, S. A modeling approach for analysis and improvement of spindle-drawbar-bearing assembly dynamics. Int. J. Mach. Tools Manuf. 2010, 50, 131–142. [Google Scholar] [CrossRef]
- Zhong, Y.; He, Y.; Wang, Z.; Li, F. Rotor Dynamics; Tsinghua University Press: Beijing, China, 1987. [Google Scholar]
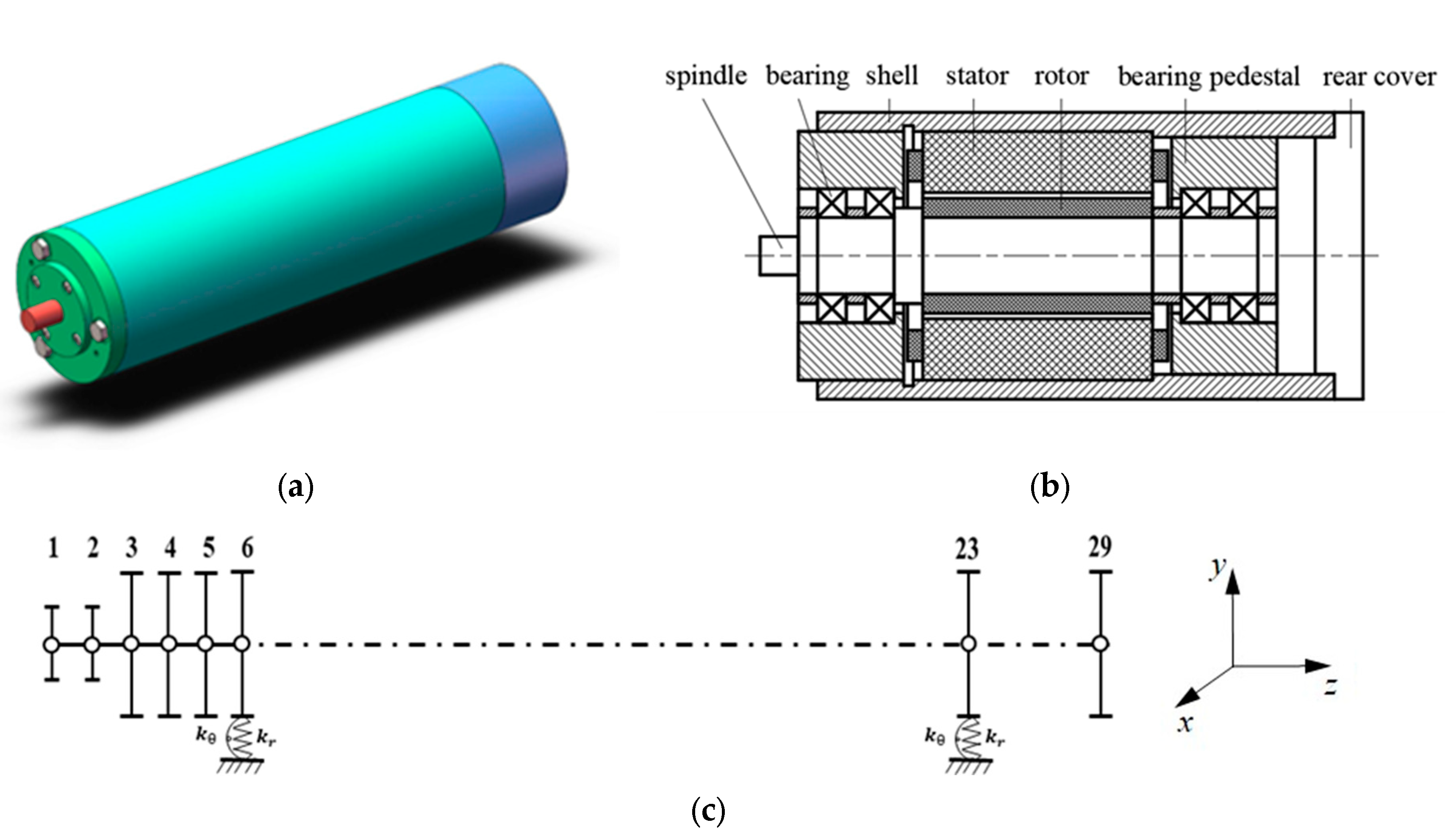





| Parameter | Value |
|---|---|
| Spindle length/mm | 290 |
| Mass/kg | 9.87 |
| Current/A | 10 |
| Inner diameter of motor rotor/mm | 42 |
| Outer diameter of rotating spindle/mm | 40 |
| Outer diameter of motor rotor/mm | 100 |
| Type of bearing | 71,908 CE/HCP4A |
| Maximum speed/rpm | 58,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, D.; Xie, Y.; Liu, S.; Wei, Y.; Shen, J. Dynamic Modeling of Motorized Spindle System with Unbalanced Mass and Spindle Inclination. Appl. Sci. 2023, 13, 10053. https://doi.org/10.3390/app131810053
Gu D, Xie Y, Liu S, Wei Y, Shen J. Dynamic Modeling of Motorized Spindle System with Unbalanced Mass and Spindle Inclination. Applied Sciences. 2023; 13(18):10053. https://doi.org/10.3390/app131810053
Chicago/Turabian StyleGu, Dan, Yufeng Xie, Shulin Liu, Yuan Wei, and Jiayi Shen. 2023. "Dynamic Modeling of Motorized Spindle System with Unbalanced Mass and Spindle Inclination" Applied Sciences 13, no. 18: 10053. https://doi.org/10.3390/app131810053
APA StyleGu, D., Xie, Y., Liu, S., Wei, Y., & Shen, J. (2023). Dynamic Modeling of Motorized Spindle System with Unbalanced Mass and Spindle Inclination. Applied Sciences, 13(18), 10053. https://doi.org/10.3390/app131810053









