Spatial Overlay Analysis of Geochemical Singularity Index α-Value of Porphyry Cu Deposit in Gangdese Metallogenic Belt, Tibet, Western China
Abstract
:1. Introduction
2. Geological Setting and Geochemical Data
2.1. Regional Geological Background
2.2. Geochemical Data
3. Methods
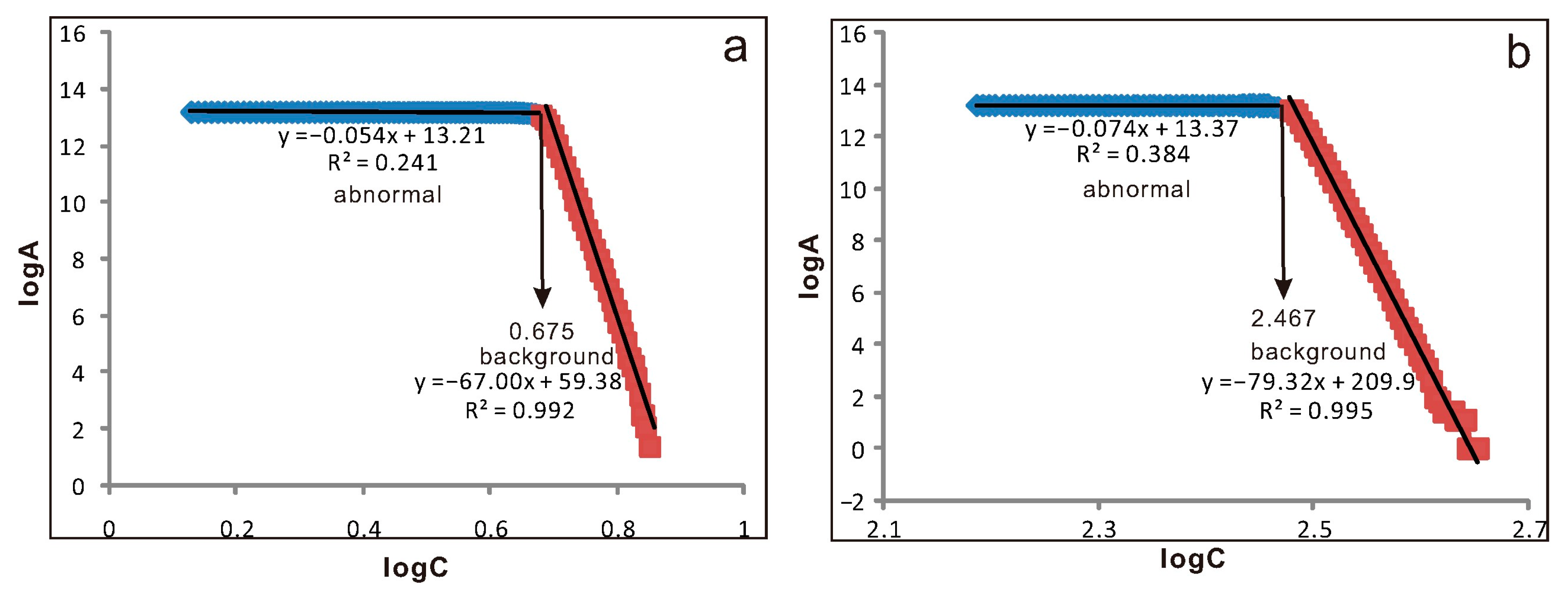
3.1. Multifractal Inverse Distance Weighted (MIDW)
3.2. Local Singularity Spatial Overlay Analysis (α-Value)
3.3. Concentration–Area Model (C–A)
4. Results and Discussion
4.1. The Question of ilr-RPCA-Back clr
4.2. Selection of Element Association Associated with Porphyry Copper Mineralization
4.3. Spatial Overlay Analysis of Geochemical Singularity Index α-Value of Porphyry Copper Deposit
5. Conclusions
- The ilr-RPCA-back CLR model has two issues. (1) The change in element position severely affects the relationship between geochemical elements. (2) The score and load transformation to clr space disrupts the corresponding relationship between the elements. Therefore, it is important to carefully consider the use of this model for the identification of geochemical element combinations.
- The proposed method of singular value overlay analysis has clear advantages in identifying porphyry copper deposits. However, it is difficult to distinguish skarn-type copper related to porphyry from porphyry molybdenum. Additionally, the distinction between porphyry skarn-type copper deposits and porphyry gold deposits is not well defined. Nevertheless, this method can reduce the anomaly grade.
- This paper investigates the geochemical laws, geochemical markers, and geochemical models based on geological foundations. It provides objective geological connotations for the identification and evaluation of anomalies using geochemical data. By overcoming the limitations of traditional technical methods and single element analysis, which are influenced by elemental chemical properties, redox environment, weathering erosion, and other factors, these methods offer significant advantages in anomaly screening. They greatly reduce multiple solutions and subjectivity, highlighting the prospecting value of anomalous regularity.
Author Contributions
Funding
Conflicts of Interest
References
- Rui, Z.; Huang, C.; Qi, G.; Xu, J.; Zhang, H. Porphyry Copper (Molybdenum) Deposits of China; Geological Phblishing House: Bejing, China, 1984; Volume 350. [Google Scholar]
- Wang, Z.T.; Qin, K.Z.; Zhang, S.L. Geology and Exploration of Large Copper Deposits [Z]; Metallurgical Industry Press: Beijing, China, 1994. [Google Scholar]
- Qin, K.Z.; Sun, S.; Li, J.L.; Fang, T.H.; Wang, S.L.; Liu, W. Paleozoic epithermal Au and porphyry Cu deposits in North Xinjiang, China: Epochs, features, tectonic linkage and exploration significance. Resour. Geol. 2002, 52, 291–300. [Google Scholar] [CrossRef]
- Cooke, D.R. Giant Porphyry Deposits: Characteristics, Distribution, and Tectonic Controls. Econ. Geol. 2005, 100, 801–818. [Google Scholar] [CrossRef]
- Zheng, Y.Y.; Xue, Y.X.; Cheng, L.J.; Fan, Z.H.; Gao, S.B. Finding, Characteristics and Significances of Qulong Superlarge Porphyry Copper (Molybdenum) Deposit. Earth Sci. J. China Univ. Geosci. 2004, 29, 103–108. (In Chinese) [Google Scholar]
- Cheng, Q.M. Singularity Modeling of Geo-Anomalies and Recognition of Anomalies Caused by Buried Sources. Earth Sci.-J. Univ. Geosci. 2011, 36, 307–316. (In Chinese) [Google Scholar]
- Xie, Y.S. The Study of the Complexity of Tectonic\Fluid\Mineralization System and its Dynamic Mechanism: A Case Study of Shuikoushan Pb\Zn\Au Polymetallic ore Field in Hunan Province, China; Guangzhou Institute of Geochemistry Chinese Academy of Science: Guangzhou, China, 2004. [Google Scholar]
- Filzmoser, P.; Hron, K.; Reimann, C.; Garrett, R. Robust factor analysis for compositional data. Comput. Geosci. 2009, 35, 1854–1861. [Google Scholar] [CrossRef]
- Grunsky, E.C.; Mueller, U.A.; Corrigan, D. A study of the lake sediment geochemistry of the Melville Peninsula using multivariate methods: Applications for predictive geological mapping. J. Geochem. Explor. 2014, 141, 15–41. [Google Scholar] [CrossRef]
- Sadeghi, M.; Billay, A.; Carranza, E. Analysis and mapping of soil geochemical anomalies: Implications for bedrock mapping and gold exploration in Giyani area, South Africa. J. Geochem. Explor. 2015, 154, 180–193. [Google Scholar] [CrossRef]
- Wang, H.C.; Zuo, R.G. A comparative study of trend surface analysis and spectrum–area multifractal model to identify geochemical anomalies. J. Geochem. Explor. 2015, 155, 84–90. [Google Scholar] [CrossRef]
- Zuo, R.G.; Wang, J. Fractal/multifractal modeling of geochemical data: A review. J. Geochem. Explor. 2016, 164, 33–41. [Google Scholar] [CrossRef]
- Chen, X.; Xu, R.K.; Zheng, Y.Y.; Jiang, X.J.; Du, W.Y. Identifying potential Au-Pb-Ag mineralization in SE Shuangkoushan, North Qaidam, Western China: Combined log-ratio approach and singularity mapping. J. Geochem. Explor. 2018, 189, 109–121. [Google Scholar] [CrossRef]
- Wang, H. The Effects of Compositional Data Closure Problem on Geochemical Data Analysis. Master’s Thesis, China University of Geosciences, Wuhan, China, 2013; pp. 1–46. (In Chinese). [Google Scholar]
- Jiang, X.J.; Chen, X.; Zheng, Y.Y.; Gao, S.B.; Ouyang, S.; Zhang, Y.C.; Zheng, L.; Huang, J. The recognition and extraction of Au, Cu geochemical composite anomalies: A case study of the east of Laji Mountains. Geophys. Geochem. Explor. 2017, 41, 459–467. (In Chinese) [Google Scholar]
- Cheng, Q.M. Mapping singularities with stream sediment geochemical data for prediction of undiscovered mineral deposits in Gejiu, Yunnan Province, China-ScienceDirect. Ore Geol. Rev. 2007, 32, 314–324. [Google Scholar] [CrossRef]
- Bai, J.; Porwal, A.; Hart, C.; Ford, A.; Yu, L. Mapping geochemical singularity using multifractal analysis: Application to anomaly definition on stream sediments data from Funin Sheet, Yunnan, China. J. Geochem. Explor. 2010, 104, 1–11. [Google Scholar] [CrossRef]
- Sun, X.; Gong, Q.J.; Wang, Q.F.; Yang, L.Q.; Wang, C.M.; Wang, Z.L. Application of local singularity model to delineate geochemical anomalies in Xiong’ershan gold and molybdenum ore district, Western Henan province, China. J. Geochem. Explor. 2010, 107, 21–29. [Google Scholar] [CrossRef]
- Agterberg, F.P. Multifractals and geostatistics. J. Geochem. Explor. 2012, 122, 113–122. [Google Scholar] [CrossRef]
- Cheng, Q.M. Singularity theory and methods for mapping geochemical anomalies caused by buried sources and for predicting undiscovered mineral deposits in covered areas. J. Geochem. Explor. 2012, 122, 55–70. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, Q.M.; Xia, Q.L.; Wang, X.Q. Geochemical Evaluation of Exploration Prospect in the Xiongxcun Copper-Gold District and Peripheral Areas, Xietongmen County, Tibet. J. Geochem. Explor. 2013, 134, 61–72. [Google Scholar] [CrossRef]
- Zuo, R.G.; Wang, J.; Chen, G.X.; Yang, M.G. Identification of weak anomalies: A multifractal perspective. J. Geochem. Explor. 2015, 148, 12–24. [Google Scholar] [CrossRef]
- Zuo, R.G.; Carranza, E.J.M.; Wang, J. Spatial analysis and visualization of exploration geochemical data. Earth-Sci. Rev. 2016, 158, 9–18. [Google Scholar] [CrossRef]
- Gao, S.B. Copper-Iron Polymetal Metallogenesis and Exploration Direction in the Western of Gangdese Metallogenic Belt, Tibet. China Univ. Geosci. 2015, 212, 1–21. (In Chinese) [Google Scholar]
- Pan, G.T.; Mo, X.X.; Hou, Z.Q.; Zhu, D.C.; Wang, L.Q.; Li, G.M.; Zhao, Z.D.; Geng, Q.R.; Liao, Z.L. Spatial-temporal framework of the Gangdese Orogenic Belt and its evolution. Acta Petrol. Sin. 2006, 22, 521–533. (In Chinese) [Google Scholar]
- Kaiser, H.F. The varimax criterion for analytic rotation in factor analysis. Educ. Psychol. Meas. 1958, 23, 187–200. [Google Scholar] [CrossRef]
- Zuo, R.G. Decomposing of mixed pattern of arsenic using fractal model in Gangdese belt, Tibet, China. Appl. Geochem. 2011, 26, S271–S273. [Google Scholar] [CrossRef]
- Wang, X.; Xie, X.; Zhang, B.; Hou, Q. Geochemical probe into China’s continental crust. Acta Geosci. Sinica. 2011, 32, 65–83. [Google Scholar]
- Cheng, Q.M. Multifractal and geostatistic methods forcharacterizing local structure and singularityproperties of exploration geochemical anomalies. Earth Sci. (J. China Univ. Geosci.) 2001, 26, 161–166. (In Chinese) [Google Scholar]
- Cheng, Q.M. Spatial and scaling modelling for geochemical anomaly separation. J. Geochem. Explor. 1999, 65, 175–194. [Google Scholar] [CrossRef]
- Zuo, R.G. Identifying geochemical anomalies associated with Cu and Pb-Zn skarn mineralization using principal component analysis and spectrum-area fractal modeling in the Gangdese Belt, Tibet (China). J. Geochem. Explor. 2011, 111, 13–22. [Google Scholar] [CrossRef]
- Zuo, R.G.; Xia, Q.L.; Wang, H.C. Compositional data analysis in the study of integrated geochemical anomalies associated with mineralization. Appl. Geochem. 2013, 28, 202–211. [Google Scholar] [CrossRef]
- Cheng, Q.M.; Agterberg, F.P.; Ballantyne, S.B. The Separation of Geochemical Anomalies from Background by Fractal Methods. J. Geochem. Explor. 1994, 51, 109–130. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Geochemical Anomaly and Mineral Prospectivity Mapping in GIS; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Gao, Y.; Zhang, Z.J.; Xiong, Y.H.; Zuo, R.G. Mapping mineral prospectivity for Cu polymetallic mineralization in southwest Fujian Province, China. Ore Geol. Rev. 2016, 75, 16–28. [Google Scholar] [CrossRef]
- Lang, X.H.; Tang, J.X.; Li, Z.J.; Dong, S.Y.; Ding, F.; Wang, Z.Z.; Zhang, L.; Huang, Y. Geochemical evaluation of exploration prospect in the Xiongcun copper-gold district and peripheral areas, Xietongmen County, Tibet. Geol. Explor. 2012, 48, 12–23. [Google Scholar]
- Sun, X.; Zheng, Y.Y.; Li, M.; Ouyang, H.T.; Liu, Q.Q.; Jing, X.K.; Sun, G.P.; Song, Q.J. Genesis of Luobuzhen Pb–Zn veins: Implications for porphyry Cu systems and exploration targeting at Luobuzhen-Dongshibu in western Gangdese belt, southern Tibet. Ore Geol. Rev. 2017, 82, 252–267. [Google Scholar] [CrossRef]
- Yang, S.P.; Zhang, H.; Liu, Y.H.; Kong, M.; Liu, H.Z.; Dong, G.F.; Luo, Y.P. Geochemical Evaluation of Potential Ore in the Qulong Copper Deposit and Its Peripheral Region in Tibet. Acta Geol. Sin. 2006, 10, 1558–1565. [Google Scholar]
- Zheng, W.B. The Study on Metallogenic Model and Prospecting Pattern for Jiama Polymetallic Copper Deposit, Tibet; Chengdu University of Technology: Chengdu, China, 2012; Volume 229. (In Chinese) [Google Scholar]
- She, H.Q.; Li, G.M.; Dong, Y.J.; Pan, G.; Li, J.; Zhang, D.; Feng, C. Regional metallogenic prognosis and mineral reserves estimation for porphyry copper deposits in Gangdese polymetallic ore belt, Tibet. Miner. Depos. 2009, 28, 803–814. [Google Scholar]
- Zuo, R.G. Synthetic information prediction of porphyry copper in Tibet. Cent. South Univ. Technol. 2007, 38, 368–373. [Google Scholar]
- Li, G.M.; She, H.Q.; Zhang, L.; Liu, B.; Dong, Y.J. Based on mineral resource assessment system (MRAS) for the metallogenic prognosis in Gangdese metallogenic belt, Tibet. Geol. Explor. 2009, 45, 645–652. [Google Scholar]
- Sun, X.; Zheng, Y.Y.; Wang, C.M.; Zhao, Z.Y.; Geng, X.B. Identifying geochemical anomalies associated with Sb–Au–Pb–Zn–Ag mineralization in North Himalaya, southern Tibet. Ore Geol. Rev. 2016, 73, 1–12. [Google Scholar] [CrossRef]





| No. | Elements | Detection Limit | No. | Elements | Detection Limit | No. | Elements | Detection Limit |
|---|---|---|---|---|---|---|---|---|
| 1 | Ag | 0.02 | 14 | La | 30 | 27 | U | 0.5 |
| 2 | As | 1 | 15 | Li | 5 | 28 | V | 20 |
| 3 | Au | 0.0003 | 16 | Mn | 30 | 29 | W | 0.5 |
| 4 | B | 5 | 17 | Mo | 0.4 | 30 | Y | 5 |
| 5 | Ba | 50 | 18 | Nb | 5 | 31 | Zn | 10 |
| 6 | Be | 0.5 | 19 | Ni | 2 | 32 | Zr | 10 |
| 7 | Bi | 0.1 | 20 | P | 100 | 33 | SiO2 | 0.10% |
| 8 | Cd | 0.05 | 21 | Pb | 2 | 34 | Al2O3 | 0.10% |
| 9 | Co | 1 | 22 | Sb | 0.1 | 35 | TFe2O3 | 0.05% |
| 10 | Cr | 15 | 23 | Sn | 1 | 36 | MgO | 0.05% |
| 11 | Cu | 1 | 24 | Sr | 5 | 37 | CaO | 0.05% |
| 12 | F | 100 | 25 | Th | 4 | 38 | Na2O | 0.05% |
| 13 | Hg | 0.0005 | 26 | Ti | 100 | 39 | K2O | 0.05% |
| Sequence 1 (Figure 3a) | Sequence 2 (Figure 3b) | Sequence 3 (Figure 3c) | Sequence 4 (Figure 3d) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Elements | PC1 | PC2 | Elements | PC1 | PC2 | Elements | PC1 | PC2 | Elements | PC1 | PC2 |
| Bi | 0.17 | 0.86 | W | −0.08 | 0.42 | W | 0.29 | 0.24 | W | 0.26 | −0.31 |
| W | −0.33 | 0.04 | Ag | −0.57 | −0.36 | Au | −0.44 | −0.38 | Bi | −0.47 | −0.66 |
| Au | 0.29 | −0.42 | Bi | 0.30 | 0.58 | Cu | −0.69 | 0.20 | Mo | 0.34 | 0.07 |
| Cu | 0.68 | −0.19 | Au | 0.22 | −0.49 | Mo | 0.29 | −0.20 | Cu | −0.52 | 0.30 |
| Ag | −0.38 | −0.21 | Cu | 0.58 | −0.30 | Ag | 0.34 | −0.52 | Au | −0.16 | 0.61 |
| Mo | −0.42 | −0.08 | Mo | −0.44 | 0.14 | Bi | 0.21 | 0.67 | Ag | 0.55 | −0.01 |
| Cumulative Proportion | 0.34 | 0.58 | Cumulative Proportion | 0.32 | 0.61 | Cumulative Proportion | 0.37 | 0.63 | Cumulative Proportion | 0.31 | 0.58 |
| Deposits and Metallogenic Belts | Geochemical Anomaly Element Combination | Sampling Mode | References |
|---|---|---|---|
| Xiong Cun | Cu, Au, Mo | regional geochemical anomalies | [35] |
| Xiong Cun | Cu, Au, Ag, Pb, Zn | soil anomaly | [36] |
| Ji Ru | Cu, Mo, W, Bi | regional geochemical anomalies | [35] |
| Zhu Nuo | Au, Cu, Mo, W | regional geochemical anomalies | [35] |
| Zhu Nuo | Cu, Mo, W, Au, Pb, Zn, Ag | stream sediment | [37] |
| Chong Jiang | Cu, Mo, Au, Ag, Pb, Zn, Hg, Sb | stream sediment | [37] |
| Chong Jiang | Cu, Mo, W, Bi, Pb, Ag | regional geochemical anomalies | [37] |
| Qu Long | Cu, Mo, W, Bi, Pb, Ag | stream sediment | [38] |
| Qu Long | Cu, Mo, W, Bi, Sn | regional geochemical anomalies | [5] |
| Jia Ma | Cu, Bi, Au, Ag, Pb, Zn | stream sediment | [39] |
| Jia Ma | Cu, Mo, Au, Ag, Bi, Sn | soil geochemistry | [39] |
| Gangdese polymetallic metallogenic belt | Cu, Mo, W, Au, Ag, Bi | geochemical anomaly | [40] |
| Gangdese polymetallic metallogenic belt | Cu-Mo, Au-Ag, Cu-Mo-Au, Cu-Au-Ag | combination geochemical anomaly | [40] |
| Gangdese porphyry copper deposit | Cu, Mo, Pb, Zn, Ag | [41] | |
| Gangdese copper polymetallic metallogenic belt | Cu, Au, Ag, W, Mo, Bi | geochemical anomaly | [42] |
| Gangdese copper polymetallic metallogenic belt | Cu-Mo, Cu, Cu-Mo-Au, Cu-Au | geochemical anomaly | [42] |
| statistical results | Cu(21), Mo(16), Au(14), Ag(12), W(8), Bi(8), Pb(7), Zn(5), Hg(1), Sb(1), Sn(1) | final choice | Cu(21), Mo(16), Au(14), Ag(12), W(8), Bi(8) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, S.; Jiang, X.; Gao, S. Spatial Overlay Analysis of Geochemical Singularity Index α-Value of Porphyry Cu Deposit in Gangdese Metallogenic Belt, Tibet, Western China. Appl. Sci. 2023, 13, 10123. https://doi.org/10.3390/app131810123
Zheng S, Jiang X, Gao S. Spatial Overlay Analysis of Geochemical Singularity Index α-Value of Porphyry Cu Deposit in Gangdese Metallogenic Belt, Tibet, Western China. Applied Sciences. 2023; 13(18):10123. https://doi.org/10.3390/app131810123
Chicago/Turabian StyleZheng, Shunli, Xiaojia Jiang, and Shunbao Gao. 2023. "Spatial Overlay Analysis of Geochemical Singularity Index α-Value of Porphyry Cu Deposit in Gangdese Metallogenic Belt, Tibet, Western China" Applied Sciences 13, no. 18: 10123. https://doi.org/10.3390/app131810123
APA StyleZheng, S., Jiang, X., & Gao, S. (2023). Spatial Overlay Analysis of Geochemical Singularity Index α-Value of Porphyry Cu Deposit in Gangdese Metallogenic Belt, Tibet, Western China. Applied Sciences, 13(18), 10123. https://doi.org/10.3390/app131810123





