Featured Application
The algorithm can be applied to unmanned storage and automatic driving.
Abstract
Aimed at the problems of low search efficiency of the A* algorithm in global path planning, not considering the size of AGV and too many turns, and the DWA algorithm easily falling into local optimization, an AGV path planning algorithm based on improved A* and DWA fusion is proposed. To begin, the obstacle rate coefficient is added to the A* algorithm’s evaluation function to build an adaptive cost function; the search efficiency and path safety are increased by improving the search mode; by extracting key nodes, a global path containing only the starting point, key nodes, and endpoints is obtained. The DWA algorithm’s evaluation function is then optimized and the starting azimuth is optimized based on information from the first key node. The experimental results show that in a static environment, compared with the traditional A* algorithm and the improved A* algorithm, the path length is reduced by 1.3% and 5.6%, respectively, and the turning times are reduced by 62.5% and 70%, respectively; compared with the improved ant colony algorithm in the literature, the turning angle is reduced by 29%. In the dynamic environment, the running time of this fusion algorithm is reduced by 12.6% compared with the other hybrid algorithms.
1. Introduction
With the continuous development and progress in science and technology, the increasing number of private cars makes traffic network congestion a topic of both theoretical interest and practical importance [1]. The Automated Guided Vehicle (AGV), serving as the primary tool for intelligent material transportation, has gained widespread utilization in modern production systems. The incorporation of AGVs offers several advantages, including enhanced productivity, reduced labor costs, improved energy utilization, and heightened safety [2]. Path planning stands as a pivotal aspect of AGVs, with key metrics for assessing path quality encompassing path length, smoothness, and safety.
Currently, numerous AGV path-planning algorithms cater to diverse environments. Common static global path planning algorithms encompass the A* algorithm [3,4], Dijkstra’s algorithm [5,6], ant colony algorithm [7,8], genetic algorithm [9], and particle swarm optimization algorithm [10,11]. Meanwhile, local path planning algorithms comprise the dynamic window approach (DWA) [12,13], the artificial potential field method [14,15], and the time elastic band (TEB) algorithm [16]. Among the global path planning algorithms, the A* algorithm stands out as the most prominent and widely employed. However, several issues arise in the paths generated by the A* algorithm, including an excess of redundant nodes, unnecessary turning points, simplification leading to a point without considering AGV size, and an inability to navigate temporary obstacles. Concerning local path planning algorithms, the DWA algorithm exhibits commendable local obstacle avoidance capabilities, yet it is prone to becoming trapped in local optima.
To solve the above problems, an improved A* algorithm for 8-neighborhood node search, which effectively improved work efficiency and security, was put forward [17]. An improved A* algorithm combined with the hop search algorithm, which reduced the amount of calculation, was proposed [18]. A time factor, which effectively reduced the number of turns, was introduced [19], and an improved A* algorithm for optimal path planning of robot energy consumption that takes the energy consumption value as the traffic cost between nodes was also put forward, thus obtaining an optimal path of global energy consumption [20]. By introducing the neighborhood matrix, an effect comparable to obstacle expansion is achieved during mapping, consequently enhancing path safety. Moreover, the heuristic function received an upgrade through the amalgamation of angle and distance information, effectively enhancing calculation efficiency [21]. A novel DWA algorithm was introduced to detect dense objects, allowing AGVs to adeptly navigate around congested regions [22]. An adaptive version of the DWA algorithm aimed at ensuring path safety and smoothness was also proposed [23]. To further enhance control efficacy beyond conventional methods, two fresh evaluation functions were incorporated [24]. An improved DWA approach that takes into account the spatial relationship between the mobile robot’s size and obstacles was put forth, thus contributing to better path planning [25]. However, it is worth noting that this version is susceptible to local optimization.
However, the above-mentioned improved A* algorithm only considers the globally static path and cannot realize real-time dynamic obstacle avoidance. The improved DWA algorithm can realize real-time dynamic obstacle avoidance but it cannot achieve the globally optimal path; both cannot be satisfied at the same time. Therefore, an improved fast and smooth A* algorithm designed by dynamically changing the search step length and adding a path deviation component to the evaluation function of the DWA algorithm is proposed [26]. By converting a three-dimensional city map into a two-dimensional plane map, the Floyd algorithm is used to smooth the global path so that the calculation speed is improved. The fusion algorithm not only guarantees a smoother and shorter global optimal path but also effectively avoids dynamic obstacles [27]. An improved A* algorithm combined with the dynamic window method, which reduces the number of inflection points by selecting key points, was proposed [28]. An improved A* algorithm that takes the travel time of the mobile robot as the cost and can adjust the weight of the heuristic function according to obstacle information is proposed, effectively reducing the number of turns and the turning angle during path planning [29]. An improved real-time path planning algorithm combining the A* algorithm and the dynamic window method is proposed. The search point selection strategy and the evaluation function are optimized to improve the search efficiency of the A* algorithm [30]. In the evaluation function of the traditional A* algorithm, the obstacle information in the environment and the cost information from the parent node to the target point are added to improve the efficiency of path search, optimizing the node expansion direction and effectively improving the smoothness of the path [31]. A topology map with larger granularity is built on the traditional grid map and the paths planned by the topology layer are then optimized on the grid map to remove redundant nodes and improve the smoothness of the paths [32]. By smoothing the global planning path, the stability of a USV heading in the navigation is Improved, and by adding the key points of the global path, a guide path is formed to unify the terminal heading range [33]. The extraction of key turning points combined with the Dynamic Window Approach significantly enhances the smoothness of the path [34]. An enhanced approach, which combines the A* and DWA algorithms, is introduced. This approach establishes a connection between the target point and the current point while omitting the consideration of the three rearward search directions. This reduction effectively reduces the computational load during the search process [35].
To address the aforementioned challenges comprehensively, this study presents a novel fusion algorithm that combines the enhanced A* algorithm and the DWA algorithm. This innovative approach focuses on optimizing various aspects of the A* algorithm, including the evaluation function, search methodology, key node extraction, and integration of the DWA algorithm. The experimental outcomes substantiate the effectiveness of this approach. The path planning method introduced in this study empowers AGVs with real-time obstacle avoidance capabilities while simultaneously ensuring the maintenance of a globally optimal path. The results underscore the potential of the fusion algorithm to overcome the limitations of individual algorithms and deliver a more robust and efficient path-planning solution for AGVs.
The main contributions of this study are summarized as follows:
- The path planning algorithm proposed in this study, which combines improved A* and DWA, can be widely applied across various domains, including automated unmanned warehouses, logistics and warehouse management, healthcare and medical facilities, ports and logistics centers, the hospitality and service industries, as well as autonomous driving. This algorithm has the potential to actively drive the rapid development of industrial automation.
- By incorporating an obstacle weight coefficient into the estimated cost component of the evaluation function, the algorithm adapts to changes in the number of obstacles in the environment, thereby enhancing search efficiency. Selecting different search approaches based on the obstacle positions ensures both path safety and improved search speed. The extraction of key nodes results in a final global static path that is both secure and optimal.
- Adjusting the orientation angle based on information from the first key node optimizes the path length while incorporating local target points effectively mitigates the issue of the DWA algorithm falling into local optima. In conclusion, the path planning algorithm, which integrates improved A* and DWA techniques, ensures the safe and efficient arrival of the AGV at its destination.
2. Traditional A* Algorithm with Improvements
2.1. Establishment of Environmental Modeling
In AGV path planning, several common map methods are employed, including the grid method, visibility method, and topological graph method. Among these, the grid method stands out for its ability to simplify the environment and its ease of implementation. Consequently, it has garnered significant attention from researchers in the realm of mobile robot path planning. To tackle the intricate path-planning challenges posed by AGVs in complex environments, this study adopts the grid method to model the AGV’s operational surroundings. Within this framework, the grid map is structured with distinctive representations: Black grids signify static obstacles and areas where AGVs cannot navigate; white grids denote the drivable regions accessible to AGVs. The raster maps showcasing these grid representations are depicted in Figure 1.
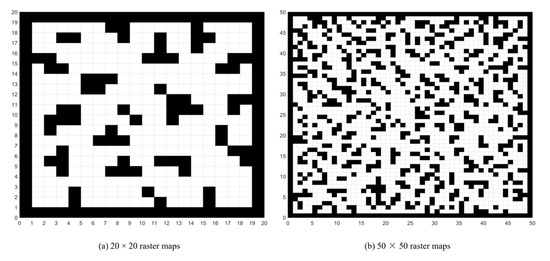
Figure 1.
Raster maps.
2.2. Traditional A* Algorithm
The fundamental concept of the A* algorithm revolves around devising a path of minimal cost from the initial point to the destination point on the map. This cost is encapsulated within a cost function , which is mathematically represented by Equation (1).
In the above formula, represents the current position node, represents the actual cost from the starting point to the current point, and represents the estimated cost from the current point to the target point.
In Equation , if is much greater than and is about equal to , then the A* algorithm is similar to Dijkstra algorithm, which will lead to an increase in node traversal and a decrease in search efficiency. If is far less than and is about equal to , the A* algorithm is similar to the best priority search algorithm, although as the speed of path planning becomes faster, it is easy to fall into the local optimal result. Therefore, the quality of the A* algorithm is determined by the heuristic function . Usually, there are three methods for estimating the heuristic function : Manhattan distance, Chebyshev distance, and Euclidean distance.
Let the coordinates of the current node be and the coordinates of the target point be . Euclidean distance heuristic function is expressed as Equation (2).
The shortcomings of the traditional A* algorithm are as follows:
- (1)
- When the difference between the estimated generation value of the heuristic function and the actual value is large, the search space becomes larger.
- (2)
- The size of AGV is not considered but is simplified to a point, which may lead to the collision of AGV with obstacles.
- (3)
- There are too many inflection points in the path, which increases the difficulty of AGV operation.
2.3. Improved A* Algorithm
2.3.1. Optimization of the Evaluation Function
To address the challenge of expanding the search space due to substantial discrepancies between the estimated cost from the heuristic function and the true value, an obstacle weight coefficient is incorporated into the estimated cost within the cost function . The exact expression of this coefficient is outlined in Equation (3).
Here, represents the total count of grids within the rectangular region bounded by the starting node and the target point while denotes the quantity of obstacle grids within the rectangular area delimited by the current node and the target point.
The provided formula illustrates that the weight coefficient applied to the estimated cost diminishes progressively as the AGV moves from the starting point toward its target. This coefficient’s value is contingent upon the count of obstacles encountered. When the obstacle count is high, the path tends to become convoluted, leading to an elevation in the weight coefficient. Consequently, the estimated cost aligns more closely with the actual value. Conversely, with a lower obstacle count, the path tends to be smoother, resulting in a reduction in the weight coefficient. This adjustment facilitates the estimated cost’s proximity to the real value in such scenarios.
2.3.2. Optimization of the Evaluation Function
Traditional search methods encompass both four-direction and eight-direction searches for node expansion. The four-direction search offers the benefit of collision-free path planning but at the cost of lower search efficiency and a surplus of turns. Conversely, the eight-direction search boasts higher search efficiency, albeit at the expense of introducing tangential points along the planned path due to obstacles. In this study, a hybrid approach is devised, combining the aforementioned search techniques. The selection of the appropriate search method is determined flexibly based on the relationship between the current node and obstacles. This approach not only enhances search efficiency but also ensures obstacle-free path planning by dynamically adapting the search method. This adaptive strategy contributes to an optimized balance between search efficiency and collision avoidance in the planned path.
In Figure 2, the middle of the nine squares is the parent node and the gray grid is the obstacle. When the distance between the parent node and the center of the obstacle is equal to 1 grid, as shown in Figure 2a, a four-direction search method is adopted to expand the node, as shown in Figure 2c. When the distance between the parent node and the center of the obstacle is greater than 1 grid, as shown in Figure 2b, the node is expanded by searching in eight directions, as shown in Figure 2d.
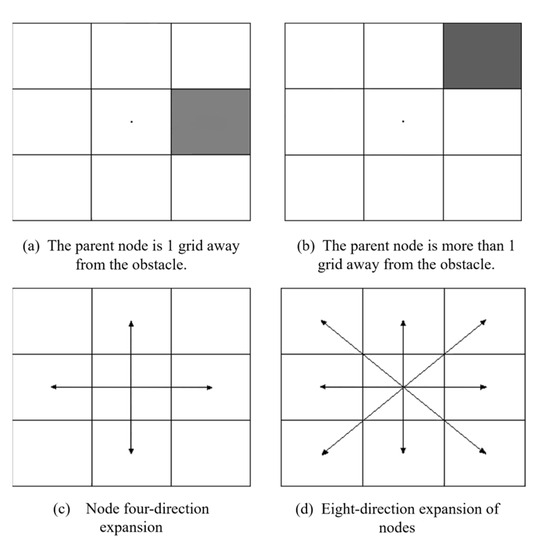
Figure 2.
Obstacle location and search method.
2.3.3. Optimization of Key Points Extraction
Upon refining the conventional A* algorithm’s single search mode in accordance with Section 2.3.2, the resulting path is visually depicted as the solid black line in Figure 3. As observed in this illustration, the planned path exhibits redundant collinear nodes and turning points. Following such a path would subject the AGV to excessive turning maneuvers, thereby increasing the vehicle’s operational load and consequently diminishing overall efficiency. Therefore, to solve this problem, this study optimizes the planned path, selects and retains the necessary key nodes, and deletes unnecessary nodes. The specific methods are as follows.
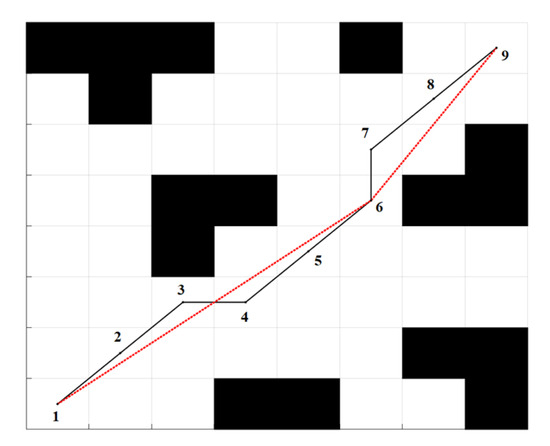
Figure 3.
Key point extraction.
First, all nodes are put into the set ; the starting point is denoted by and the target point is denoted by . Then, starting from P1, the included angle between vectors to and vectors to are solved. If the included angle is equal to zero, it means that the two vectors are collinear and is a redundant node that needs to be deleted. If the included angle is not equal to zero, it means that the two vectors are not collinear. At this point, is connected to and then the positional relationship between the line and the nearest obstacle is judged. If the distance from the center of the obstacle to the line segment is greater than the preset safe distance, it means that node is a redundant turning point and can be deleted; otherwise, it cannot be deleted. After deleting redundant nodes, the nodes in the set are updated. When key nodes that cannot be deleted are encountered, they are used as a new optimization starting point until the target point is connected. The black line represents the path searched by the traditional A* algorithm. Finally, by eliminating redundant points and retaining key points, a static global path that contains only the starting node, key points, and target points is optimized, as shown by the red dotted line in Figure 3.
3. DWA Algorithm and Improvements
The basic idea of the DWA algorithm is to sample multiple groups of velocity combinations in a simulation period from the allowable linear velocity and angular velocity based on the environmental information, kinematics model and kinematics performance of the robot, and simulation of the motion trajectory. Then, the optimal speed combination is selected as the speed in the current movement cycle through the evaluation function, and the above steps are cycled to the endpoint.
3.1. AGV Motion Model
When simulating the moving trajectory of AGV, the kinematics model is established using a four-wheel omnidirectional AGV, as shown in Figure 4.
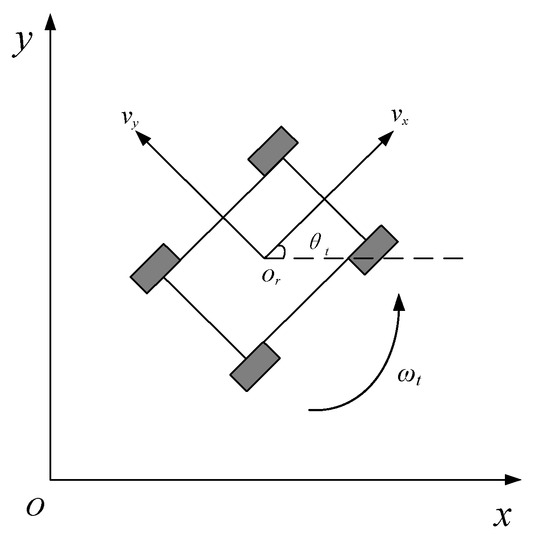
Figure 4.
AGV motion model.
As shown in Figure 5, are the horizontal and vertical velocities of AGV, is the angular velocity of AGV rotating around , and is the heading angle of AGV. Within the sampling period , the displacement can be approximated as a linear motion and its kinematics model can be expressed using Equation (4).
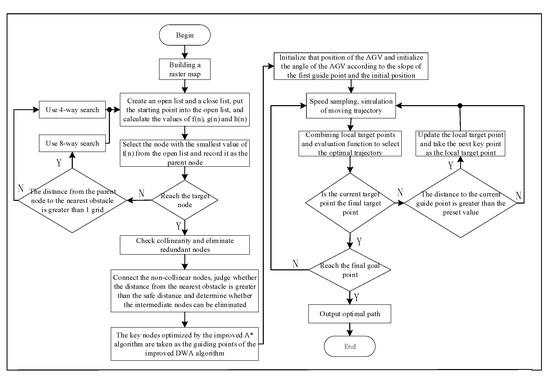
Figure 5.
Fusion algorithm flowchart.
In the above formula, represents the current moment, represents the next moment, represents the abscissa of the current moment, represents the abscissa of the next moment, represents the ordinate of the current moment, represents the ordinate of the next moment, represents the included angle between the moving direction of AGV and the -axis at the current moment, represents the included angle between the moving direction of AGV and the -axis at the next moment, and represents the angular velocity at the current moment.
3.2. Speed Sampling
In the process of running the AGV, to make the obtained speed group approach the optimal value as much as possible, it is necessary to sample multiple groups of data for simulation. However, due to some performance and the environment of AGV itself, the sampling range is limited.
- (1)
- The speed constraint of the AGV is expressed as in Equation (5).
In the above formula, and refer to the minimum and maximum linear velocities, respectively; and represent the minimum and maximum angular velocities, respectively.
- (2)
- In the predicted time range, the speed set under the constraint of acceleration and deceleration of the motor is expressed as in Equation (6).
In the above formula, and denote the linear velocity and the angular velocity at the current moment, respectively; and represent the minimum and maximum decelerations, respectively; and indicate the minimum and maximum accelerations, respectively.
- (3)
- When the AGV encounters a moving obstacle, it is necessary to ensure a safe distance between the AGV and the obstacle so that the speed of the AGV is reduced to zero before hitting the obstacle and its speed constraint is expressed as in Equation (7).
In the above formula, represents the shortest distance from the end of the simulated trajectory to the obstacle.
The final speed of the DWA is the intersection of these three constraints; the speed is expressed as in Equation (8).
3.3. Optimization of the Evaluation Function
A series of trajectories are simulated by employing a motion model and sampling approach. Subsequently, the optimal trajectory is identified among these simulations to serve as the operational path for the AGV. This selection process is facilitated by the utilization of an evaluation function. In the context of the traditional dynamic window approach (DWA) algorithm, the evaluation function is mathematically represented by Equation (9).
In the above formula, is the azimuth deviation between the end of the simulated trajectory and the target point; is the evaluation function of the predicted velocity; is the normalized parameter of the three sub-functions; is the weight coefficient, and .
The DWA algorithm’s vulnerability to local optima, especially when confronted with concave obstacles, stems from its reliance on a single target point. To mitigate this limitation, the improved A* algorithm’s key nodes are leveraged as local target points within the DWA algorithm. This enhancement aims to provide a more comprehensive navigation strategy. The resulting optimized evaluation function is mathematically depicted by Equation (10).
In the above formula, is the azimuth deviation between the endpoint of the simulated trajectory and the local target point.
4. Fusion Algorithms
While the enhanced A* algorithm excels at devising optimal paths that encompass only the starting point, ending point, and key nodes, its limitations become evident when it comes to circumventing temporary static obstacles and dynamic obstacles during AGV operation. On the other hand, the DWA algorithm demonstrates commendable proficiency in local obstacle avoidance. However, its single-target point nature renders it prone to getting ensnared in local optimal paths. The synergy between these two algorithms capitalizes on their strengths to address these shortcomings. By integrating the improved A* algorithm’s path planning capabilities with the local obstacle avoidance prowess of the DWA algorithm, an effective solution can be achieved that navigates both static and dynamic obstacles, all the while steering clear of local optima. This amalgamation contributes to a more robust and adaptable path-planning approach for AGVs. Therefore, this study combines the improved A* and DWA algorithms. The flow chart of the fusion algorithm is shown in Figure 5.
In the flowchart, an obstacle weight coefficient is first added to the evaluation function of the traditional A* algorithm. The search approach is adaptively selected based on the positions of obstacles. Next, an optimization process is applied to extract key points and remove redundant turning points. Finally, an improved A* algorithm is used to plan a global static path that includes only the starting point, key points, and destination point. Moving forward, each key waypoint assumes the role of a localized target point within the DWA algorithm. Furthermore, the initial azimuth of the AGV is meticulously adjusted, leveraging insights drawn from the first key node. The DWA algorithm undertakes speed sampling and trajectory simulation for the AGV. Through this process, a spectrum of potential motion trajectories is examined. Subsequently, an optimal set of speeds is meticulously selected through an optimized evaluation function. The AGV’s operation is then expertly regulated at this selected speed. Ultimately, the improved A* algorithm and DWA algorithm synergize to empower the AGV. This amalgamation not only enables the AGV to progress along the globally optimal path but also equips it to adeptly navigate around newly introduced static and dynamic obstacles in real-time. The culmination of these efforts ensures the AGV’s seamless and successful arrival at the designated target point.
5. Simulation Analysis
The experimental platform used to verify the feasibility of the improved algorithm in this study is MATLAB 2019b, MathWorks, Laurel, MD, USA. In the raster maps of the simulation experiment, the white grid is a passable area, the black grid represents obstacles, the blue hollow triangle represents the starting point, and the blue circle represents the final target point. The weight coefficients of the DWA algorithm evaluation function are . The motion parameters of the AGV are shown in Table 1.

Table 1.
AGV motion parameters.
5.1. Simulation Results and Analysis of Improved A* Algorithm
To validate the viability of the enhanced A* algorithm, the subsequent experiment employs a 20 × 20 raster map for simulation purposes. The outcomes of this experiment are visually depicted in Figure 6 while the accompanying numerical data are presented in Table 2. Furthermore, to bolster the credibility of the improved A* algorithm, additional experiments are conducted within randomly generated 50 × 50 raster maps. The results of these experiments are illustrated in Figure 7, while the corresponding quantitative findings are tabulated in Table 3. In Figure 6 and Figure 7, the blue triangle represents the starting point, the blue circle represents the endpoint, and the red solid line represents the planned path. (a) represents the traditional A* algorithm, (b) represents the improved A* algorithm from reference [21], (c) represents the improved ant colony algorithm from reference [8], (d) represents the improved A* algorithm in this study.

Figure 6.
20 × 20 raster maps to compare experimental results.

Table 2.
Performance indicators of 20 × 20 raster maps.

Figure 7.
50 × 50 raster maps to compare experimental results.

Table 3.
Performance indicators of 50 × 50 raster maps.
In the above experiments, the results from Figure 6a show that the path planned by the traditional A* algorithm not only disregards the vehicle’s size but also involves a higher number of turns. From the results in Figure 6b, it can be observed that the improved A* algorithm takes into account the vehicle’s size but the path still has too many turns, resulting in non-smoothness. On the other hand, as indicated by the results in Figure 6c, the improved ant colony algorithm plans a very smooth path but does not consider the vehicle’s size. However, from Figure 6d, it can be seen that in this study, the modified A* algorithm takes both the vehicle’s size and the issue of path smoothness into consideration. According to the data in Table 3, in the 20 × 20 raster maps, compared with the traditional A* algorithm, the improved A* algorithm reduces the path by 1.3%, the turning times by 62.5%, and the total turning angle by 77.8%; compared with the improved A* algorithm in the literature [21], the path is reduced by 5.6%, the turning times are reduced by 70%, and the total turning angle is reduced by 82.3%; compared with the improved ant colony algorithm in the literature [8], the path is reduced by 0.2% and the total turning angle is reduced by 29.0%. From the results in Figure 7 and Table 3, in the 50 × 50 raster maps, the improved A* algorithm in this study is better than the traditional A*, study [8], and study [21] in terms of path length, turning times, and total turning angle.
In comparison to both the traditional A* algorithm and the enhanced ant colony algorithm discussed in [8], the improved A* algorithm introduced in this study encompasses a comprehensive consideration of obstacle distances, thereby ensuring path safety is a paramount priority. Moreover, juxtaposed against the enhanced A* algorithm featured in [21], the current implementation not only reduces the number of turns but also achieves a smoother path, resulting in heightened operational efficiency for the AGV. These distinctions underscore the unique advantages and advancements in the proposed improved A* algorithm, positioning it as a compelling solution that amalgamates safety, path optimization, and operational effectiveness for AGV navigation.
5.2. Simulation Results and Analysis of Fusion Algorithm
AGV path planning, which combines the improved A* algorithm and the DWA algorithm, first plans an optimal static global path using the improved A* algorithm, then takes key nodes as local target points in the DWA algorithm and uses the DWA algorithm to avoid obstacles in real-time, and finally reaches the target point.
5.2.1. The Necessity of Algorithm Fusion
Although the DWA algorithm has good real-time obstacle avoidance performance, it easily falls into local optimum and fails at path planning when facing concave obstacles, as shown in Figure 8a. This is prevented after merging the improved A* algorithm, as shown in Figure 8b.
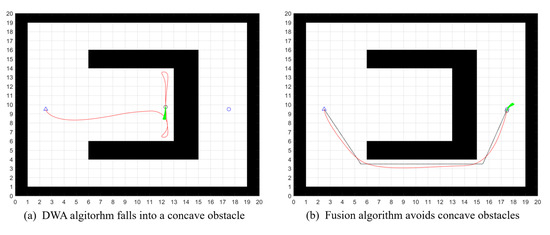
Figure 8.
Simulation results for concave obstacles.
As shown in Figure 8, the blue triangle represents the starting point, the blue circle represents the destination point, the red solid line represents the actual travel path, and the green arrowhead represents the current travel direction.
As shown in Figure 8a, using the DWA algorithm alone prevents the AGV from being driven out of concave obstacles and makes it fall into local optimization, failing to reach the target point; On the contrary, in Figure 8b, the improved A* algorithm in the hybrid algorithm provides key nodes for the DWA algorithm as local target points so that the AGV can avoid concave obstacles and reach the target point smoothly.
5.2.2. Simulation under Temporary Static Obstacle Environments
To test the ability of the hybrid algorithm in this study to deal with emergencies, the following experiments were carried out: the experiment uses 20 × 20 raster maps and adds 0, 1, 2, and 3 static obstacles on the global static path planned by the improved A* algorithm. The experimental results are shown in Figure 9. In Figure 9, the red solid line is the actual running track for the AGV, the black dotted line is the global path planned by the improved A* algorithm, "*" indicates the key nodes, and the gray square is the temporary static obstacle added.

Figure 9.
Fusion algorithm path planning in a temporary static obstacle environment.
As shown in Figure 9, the blue triangle represents the starting point, the blue circle represents the destination point, the red solid line represents the actual travel path, the black dashed line represents the global path, and the asterisk represents local target points. In the absence of temporary static obstacles, the AGV travels along the global static path under the guidance of key nodes through the fusion algorithm and successfully reaches the target point. In the case of temporary static obstacles, the AGV travels along the global static path under the guidance of key nodes through a fusion algorithm. When encountering temporary static obstacles, the improved A* algorithm provides key nodes as local target points for the DWA algorithm, completes obstacle avoidance using the DWA algorithm, and finally reaches the target point smoothly. Therefore, the fusion algorithm not only ensures that the path is globally optimal but also realizes obstacle avoidance efficiently and safely, enabling the AGV to reach the target point smoothly.
5.2.3. Simulation under Dynamic and Temporary Static Obstacle Environments
To further verify the reliability of the hybrid algorithm in this study, the following experiment adds temporary static obstacles and dynamic obstacles to the 20 × 20 raster maps and makes a simulation comparison experiment with the hybrid algorithm [34]. The experimental results are shown in Figure 10 and Figure 11, and the performance pairs are shown in Table 4.

Figure 10.
Comparison of the path planning of fusion algorithms in dynamic and temporary static obstacle environments.
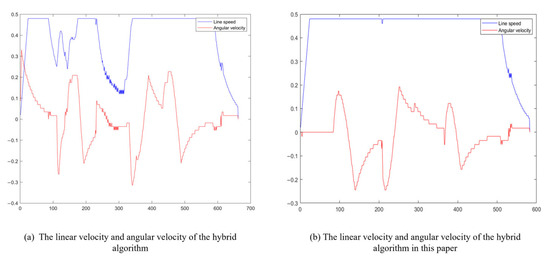
Figure 11.
Comparison of linear velocity and angular velocity of fusion algorithm in dynamic and temporary static obstacle environments.

Table 4.
Mixed experiment performance indicators.
As shown in Figure 10, the depicted elements are as follows: the blue triangle represents the starting point, the blue circle represents the destination point, the red solid line represents the actual travel path, the black dashed line represents the global path, the asterisk represents local target points, the blue solid line represents the trajectory of the moving obstacle, the black solid triangle signifies the starting point of the moving obstacle, the black five-pointed star symbolizes the endpoint of the moving obstacle, the gray square denotes the added temporary static obstacle, and the asterisk represents local target points. Figure 10a,c are the results from Ref. [34], while (b) and (d) are the results from this study. Based on the findings from Figure 10a,b, it is evident that both the hybrid algorithm mentioned in the literature and the hybrid algorithm introduced in this study can effectively detect dynamic obstacles, making adjustments to their motion directions and paths as needed. However, this study stands out due to the incorporation of an enhanced A* algorithm that takes into consideration the vehicle’s dimensions, resulting in smoother planned paths. This, in turn, offers improved local target points for subsequent AGV local path planning. Furthermore, adaptive adjustments and optimizations have been implemented for the initial orientation angle of the AGV, leading to even smoother paths. Examining Figure 10c, it is apparent that the literature’s approach neglects the AGV’s dimensions, leading to a collision between the planned path and an introduced static obstacle. Conversely, the path devised in this study adeptly circumvents obstacles, ensuring a safe and obstacle-free passage to the target point.
Figure 11a is the results from reference [34], while (b) is the results from this study. Further insights from Figure 11 reveal that, in comparison to the literature, linear velocity demonstrates greater stability and angular velocity exhibits reduced fluctuation. Additionally, Table 4 showcases a notable 12.6% reduction in running time for the hybrid algorithm implemented in this study. In summation, the AGV path planning algorithm, which leverages the enhanced A* and DWA fusion as proposed in this study, not only enhances safety but also ensures stability. These advancements collectively make it a safer, more stable, and operationally efficient solution for AGV navigation.
6. Conclusions
To address the limitations inherent in traditional A* algorithms, such as excessive turning points, suboptimal path smoothness, inability to circumvent temporary static and dynamic obstacles, and the DWA algorithm’s vulnerability to concave obstacles and local optimization, this study introduces an innovative AGV path planning algorithm rooted in the fusion of enhanced A* and DWA methodologies. The experimental findings underscore the efficacy of this approach. In static environments, the improved A* algorithm in this study consistently enhances path planning outcomes to varying degrees compared to alternative algorithms. In dynamic scenarios, the global path established by the enhanced A* algorithm serves as a foundation, designating key nodes as local targets for the refined DWA algorithm. This pivotal enhancement mitigates the DWA algorithm’s inclination towards local optima, enabling effective avoidance of temporary static and dynamic obstacles. As a result, the AGV adeptly and safely navigates the dynamic environment, ultimately achieving the target point with efficiency and precision. The amalgamation of improved A* and DWA techniques thus presents a robust and versatile solution that overcomes the shortcomings of individual algorithms, optimizing AGV path planning for both static and dynamic scenarios.
As path planning of mobile robots becomes more and more complex, more requirements will need to be improved. Therefore, further research is needed for large-scale complex environments.
Author Contributions
T.G. and Y.S. conceived and designed the research; T.G., Y.L. and L.L. carried out the experiment; T.G. and J.L. wrote the manuscript. All the authors discussed the data and revised the paper. All authors have read and agreed to the published version of the manuscript.
Funding
Supported by the Key Research and Development Project of Sichuan Transfer Payment (21ZYZFZDYF0021).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Scellato, S.; Fortuna, L.; Frasca, M.; Gómez-Gardeñes, J.; Latora, V. Traffic optimization in transport networks based on local routing. Eur. Phys. J. B 2010, 73, 303–308. [Google Scholar] [CrossRef]
- Song, X.; Gao, H.; Ding, T.; Gu, Y.; Liu, J.; Tian, K. A Review of the Motion Planning and Control Methods for Automated Vehicles. Sensors 2023, 23, 6140. [Google Scholar] [CrossRef]
- Wang, H.; Hao, C.; Zhang, P.; Yin, P.; Zhang, Y. Path Planning of Mobile Robots Based on A* Algorithm and Artificial Potential Field Algorithm. China Mech. Eng. 2019, 30, 2489–2496. [Google Scholar]
- Duan, H.; Wu, Y.; Liu, J. Path planning of reconfigurable robot based on improved A* algorithm. Electron. Meas. Technol. 2023, 46, 44–50. [Google Scholar]
- Guo, Q.; Zhang, Z.; Xu, Y. Path-Planning of Automated Guided Vehicle Based on Improved Dijkstra Algorithm. In Proceedings of the 2017 Chinese Control and Decision Conference, Chongqing, China, 28–30 May 2017. [Google Scholar]
- Gbadamosi, O.A.; Aremu, D.R. Design of a Modified Dijkstra’s Algorithm for finding alternate routes for shortest-path problems with huge costs. In Proceedings of the 2020 International Conference in Mathematics, Computer Engineering and Computer Science (ICMCECS), Lagos, Nigeria, 18–21 March 2020. [Google Scholar]
- Xiao, J.; Yu, X.; Zhou, G.; Sun, K.; Zhou, Z. An improved ant colony algorithm for indoor AGV path planning. Chin. J. Sci. Instrum. 2022, 43, 277–285. [Google Scholar]
- Jiang, M.; Wang, F.; Ge, Y.; Sun, L. Research on path planning of mobile robot based on improved ant colony algorithm. Chin. J. Sci. Instrum. 2019, 40, 113–121. [Google Scholar]
- Wu, X.; Bai, J.; Hao, F.; Cheng, G.; Tang, Y.; Li, X. Field Complete Coverage Path Planning Based on Improved Genetic Algorithm for Transplanting Robot. Machines 2023, 11, 659. [Google Scholar] [CrossRef]
- Zheng, L.; Yu, W.; Li, G.; Qin, G.; Luo, Y. Particle Swarm Algorithm Path-Planning Method for Mobile Robots Based on Artificial Potential Fields. Sensors 2023, 23, 6082. [Google Scholar] [CrossRef] [PubMed]
- Jia, H.; Wei, Z.; He, X.; Zhang, L.; He, J.; Mu, Z. Path Planning Based on Improved Particle Swarm Optimization Algorithm. Trans. Chin. Soc. Agric. Mach. 2018, 49, 371–377. [Google Scholar]
- Lu, C.; Liang, S.; Jiang, C.; Dai, Y. Reinforcement based mobile robot path planning with improved dynamic window approach in unknown environment. Auton. Robot. 2020, 45, 51–76. [Google Scholar]
- Zhang, Y.; Song, J.; Zhang, Q. Local Path Planning of Outdoor Cleaning Robot Based on an Improved DWA. Robot 2020, 42, 617–625. [Google Scholar]
- Hu, Z.; Xu, B. Dynamic Path Planning Based on the Integration of A* Algorithm and Artificial Potential Field Method. Modul. Mach. Tool Autom. Manuf. Tech. 2023, 46–49+56. [Google Scholar] [CrossRef]
- Wang, B.; Wu, H.; Niu, X. Robot Path Planning Based on Improved Potential Field Method. Comput. Sci. 2022, 49, 196–203. [Google Scholar]
- Wen, Y.; Huang, J.; Jiang, T.; Su, X. Safe and smooth improved time elastic band trajectory planning algorithm. Control Decis. 2022, 37, 2008–2016. [Google Scholar]
- Jiang, Y.; Zhang, Y. Improved path planning of A* algorithm of domain node search strategy 8. J. Electron. Meas. Instrum. 2022, 36, 234–241. [Google Scholar]
- Zhao, X.; Wang, Z.; Huang, C.; Zhao, Y. Mobile Robot Path Planning Based on an Improved A*Algorithm. Robot 2018, 40, 903–910. [Google Scholar]
- Zhang, X.; Zou, Y. Collision-free path planning for automated guided vehicles based on improved A* algorithm. Syst. Eng.-Theory Pract. 2021, 41, 240–246. [Google Scholar]
- Zhang, H.; Zhang, Y.; Liang, R.; Yang, T. Energy efficient path planning method for robots based on improved A* algorithm. Syst. Eng. Electron. 2023, 45, 513–520. [Google Scholar]
- Chen, R.; Wen, C.; Peng, L.; You, C. Application of improved A* algorithm in indoor path planning for mobile robot. J. Comput. Appl. 2019, 39, 1006–1011. [Google Scholar]
- Mai, X.; Li, D.; Ouyang, J.; Luo, Y. An improved dynamic window approach for local trajectory planning in the environment with dense objects. J. Phys. Conf. Ser. 2021, 1884, 360–369. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, Y.; Li, X.; Li, L. Self-adaptive dynamic window approach in dense obstacles. Control. Decis. 2019, 34, 927–936. [Google Scholar]
- Chang, L.; Shan, L.; Dai, Y.; Qi, Z. Multi-robot formation control in unknown environment based on improved DWA. Control. Decis. 2022, 37, 2524–2534. [Google Scholar]
- Li, X.; Liu, F.; Liu, J.; Liu, J.; Liang, S. Obstacle avoidance for mobile robot based on improved dynamic window approach. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 666–676. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, X. Path Planning Algorithm Based on Improved A* and DWA for Unmanned Surface Vehicle. Chin. J. Sens. Actuators 2021, 34, 249–254. [Google Scholar]
- Li, X.; Fang, J. Research on UAV path planning by A* algorithm and DWA method in the urban environment. Unmanned Syst. Technol. 2023, 6, 61–70. [Google Scholar]
- Lao, C.; Li, P.; Feng, Y. Path Planning of Greenhouse robot Based on Fusion of Improved A* Algorithm and Dynamic Window Approach. Trans. Chin. Soc. Agric. Mach. 2021, 52, 14–22. [Google Scholar]
- Zhao, J.; Zhao, T.; Feng, Y.; Cao, Z.; Zhong, Y. Research on robot path planning based on improved A* algorithm and DWA. Exp. Technol. Manag. 2023, 40, 87–92. [Google Scholar]
- Chi, X.; Li, H.; Fei, J. Research on robot random obstacle avoidance method based on fusion of improved A*algorithm and dynamic window method. Chin. J. Sci. Instrum. 2021, 42, 132–140. [Google Scholar]
- Zhang, Z.; Zhang, H.; Deng, Y. Real Time Path Planning of Robot by Combing Improved A∗ Algorithm and Dynamic Window Approach. Radio Eng. 2022, 52, 1984–1993. [Google Scholar]
- Zou, W.; Han, B.; Li, P.; Tian, J. Path planning based on the integration of improved A* algorithm and optimized dynamic window approach. In Computer Integrated Manufacturing Systems; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1995; pp. 1–18. [Google Scholar]
- Wei, G.; Zhang, J. Research on Unmanned Surface Vessel Aggregation Formation Based on Improved A* and Dynamic Window Approach Fusion Algorithm. Appl. Sci. 2023, 13, 8625. [Google Scholar] [CrossRef]
- Chen, J.; Xu, L.; Chen, J.; Liu, Q. Path planning based on improved A* and dynamic window approach for mobile robot. Comput. Integr. Manuf. Syst. 2022, 28, 1650–1658. [Google Scholar]
- Wu, M.; Gao, J.; Li, L.; Wang, Y. Control optimisation of automated guided vehicles in container terminal based on Petri network and dynamic path planning. Comput. Electr. Eng. 2022, 104, 108471. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).