Research and Simulation of Kinematics and Dynamics of Tracked Support Equipment Based on Multi-Body Dynamics
Abstract
:1. Introduction
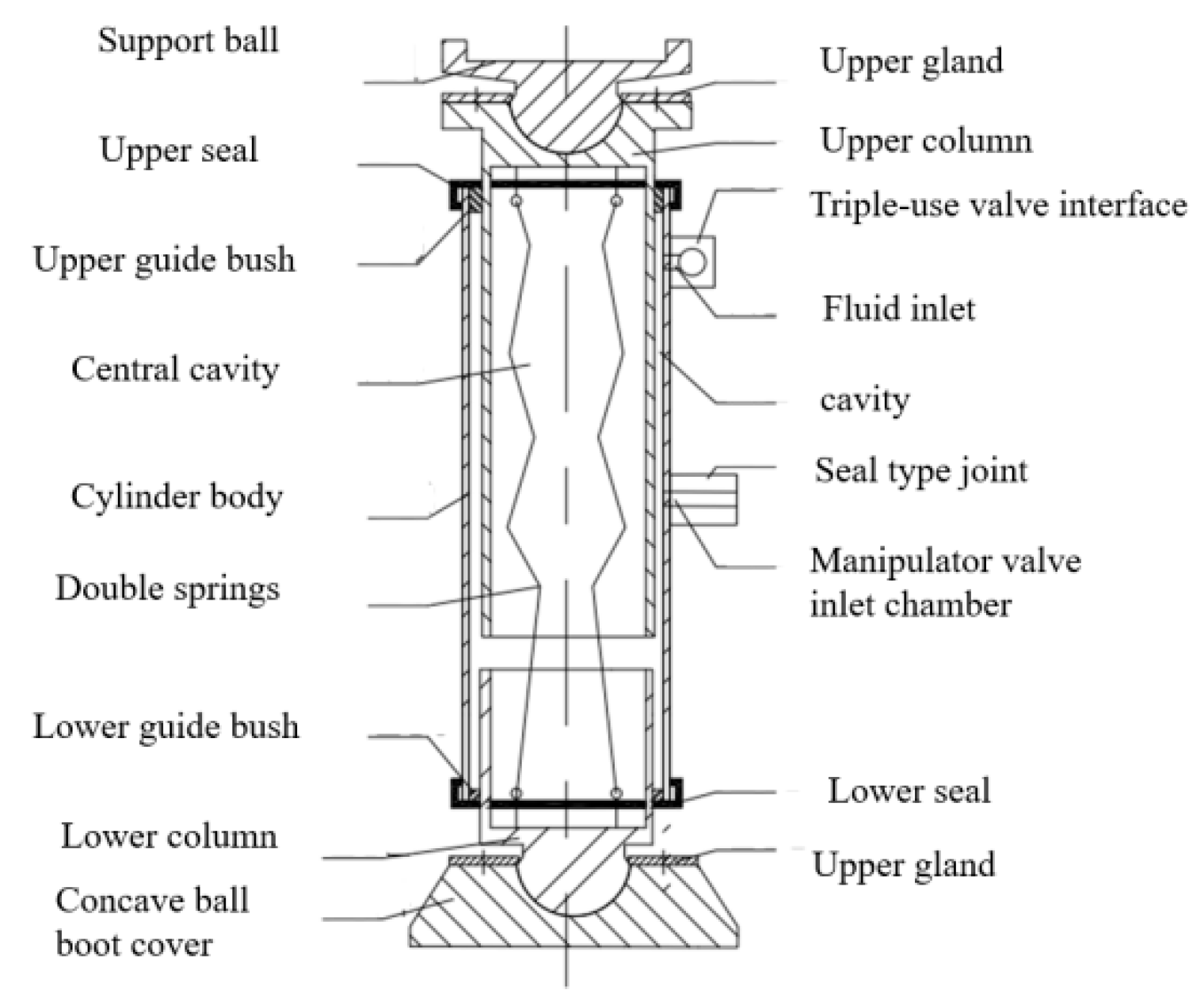
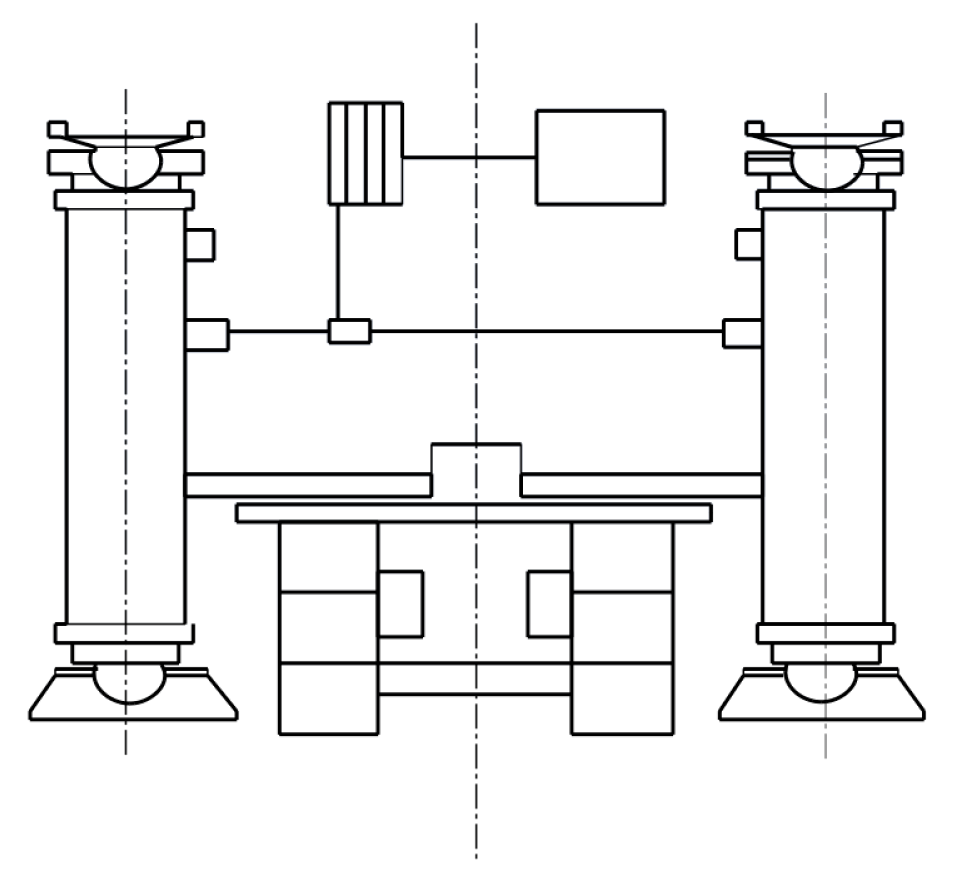
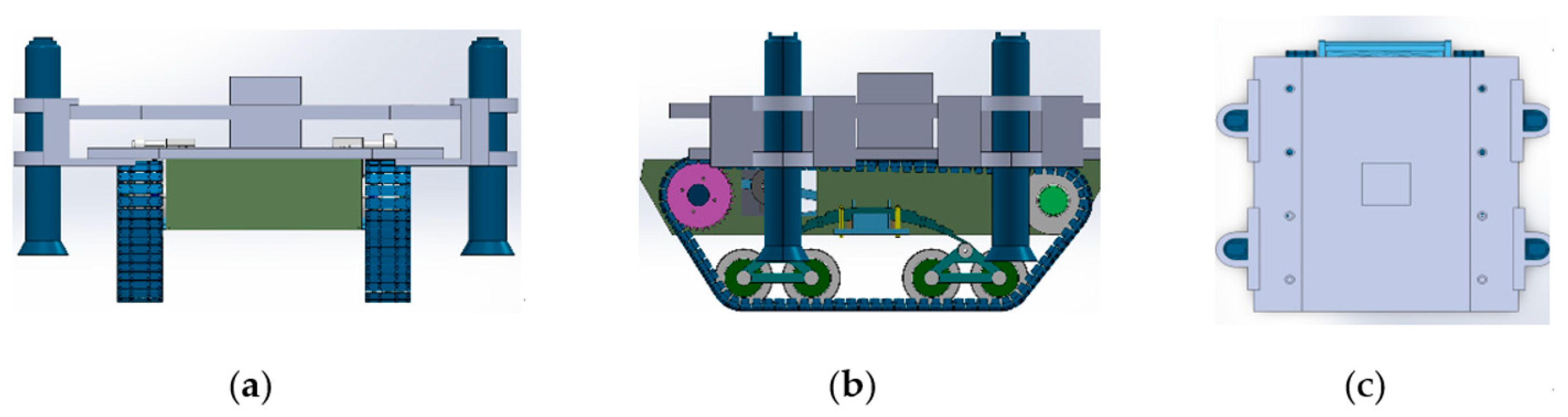
- A double live column design is adopted, and the structure realizes bidirectional live column extension together with the self-transferring traveling mechanism, which improves the supporting efficiency;
- The upper and lower double live columns are designed with a ball-type slewing structure to adapt to the changes in the angle of the bottom plate and top plate of the coal mine underground and ensure the stability of the force of the hydraulic pillar in the support process;
- The cylinder body is welded with self-sealing connecting hose fittings to prevent the air from entering the working chamber of the hydraulic pillar, preventing cavitation and rusting of the system components, thus reducing the maintenance cost and improving the working life of the components, which is in line with the concept of green mine;
- The use of coal mine three-use valves and controllers to realize dual operation and dual control mode improves operation flexibility and efficiency and ensures the safety and reliability of roof support.
2. Driving Theory Analysis
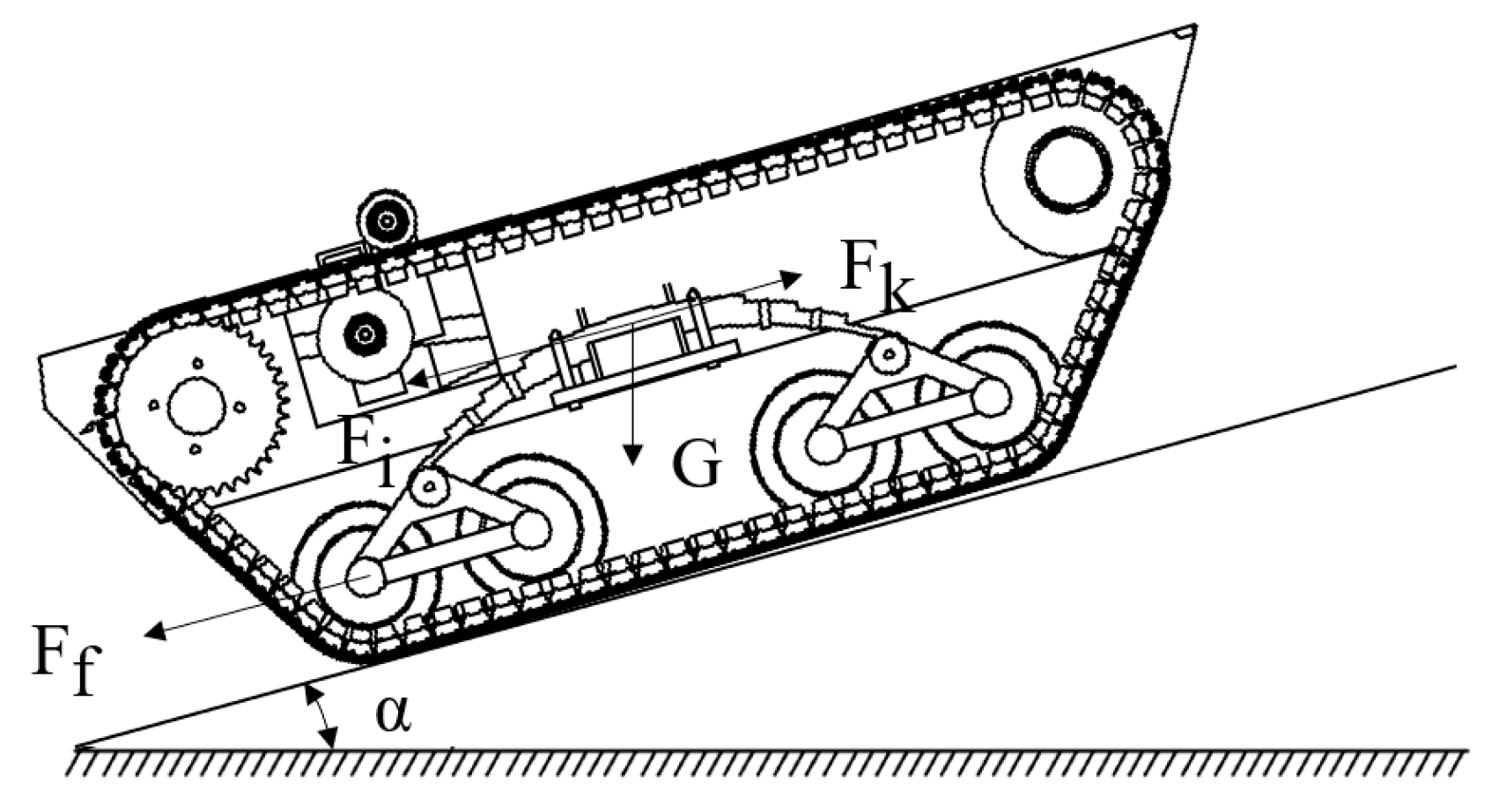
2.1. Driving Resistance Analysis
2.2. Traction and Adhesion
2.3. Stability Analysis
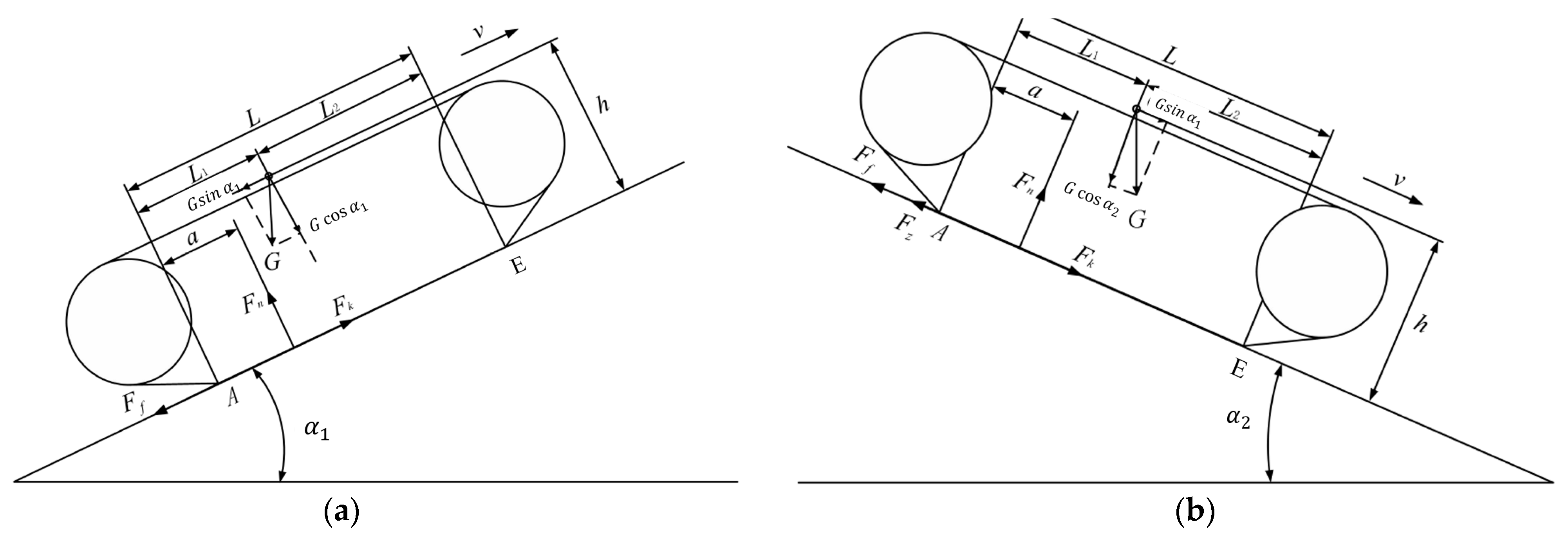
2.3.1. Uphill Rearward Tilt Limit Angle Analysis
2.3.2. Downhill Forward Tilt Limit Angle Analysis
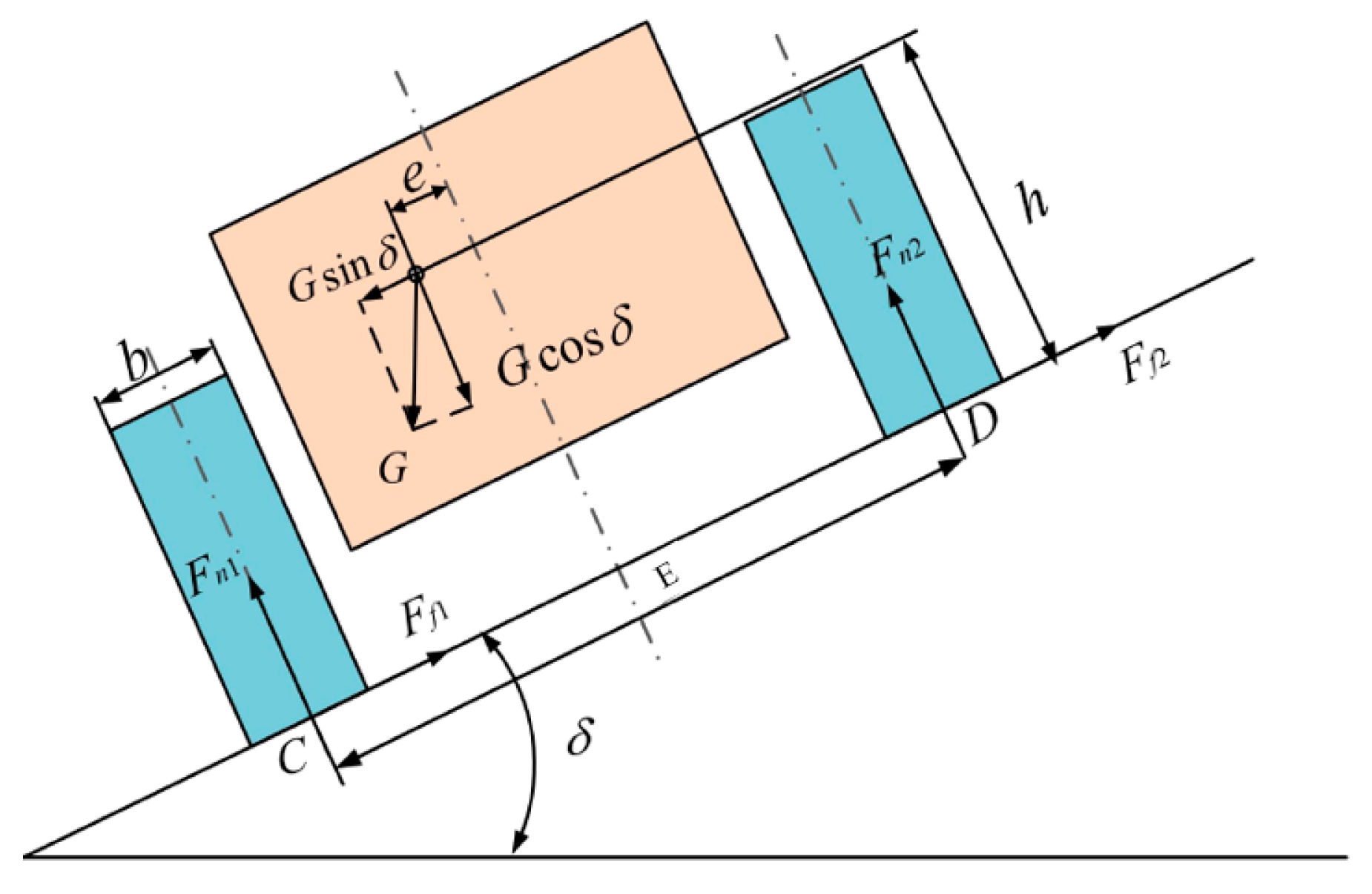
2.3.3. Cross-Slope Tilt Limit Angle Analysis
2.3.4. Slip Stability Angle Analysis
2.4. Through Performance Analysis
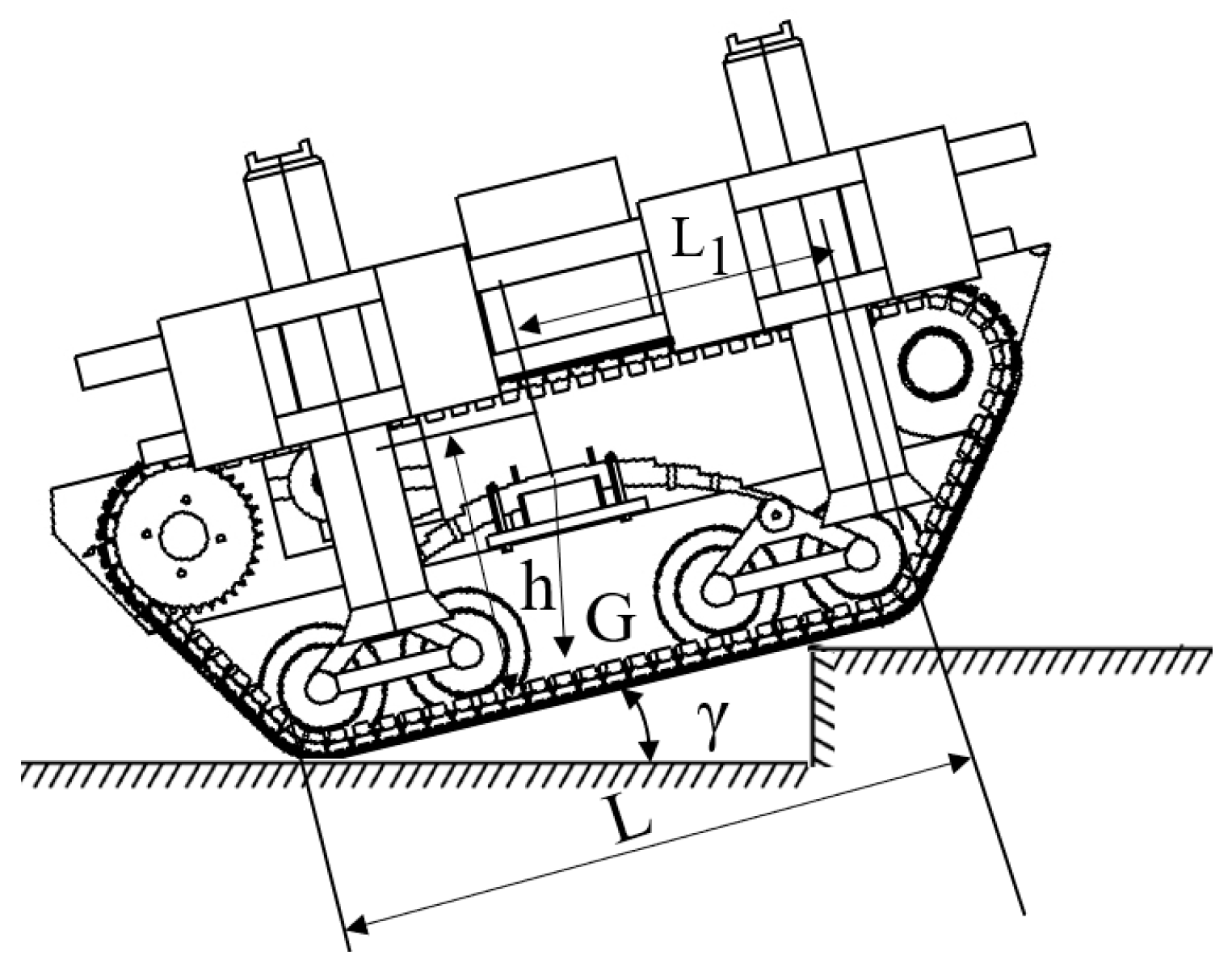
2.4.1. Obstacle Crossing Analysis
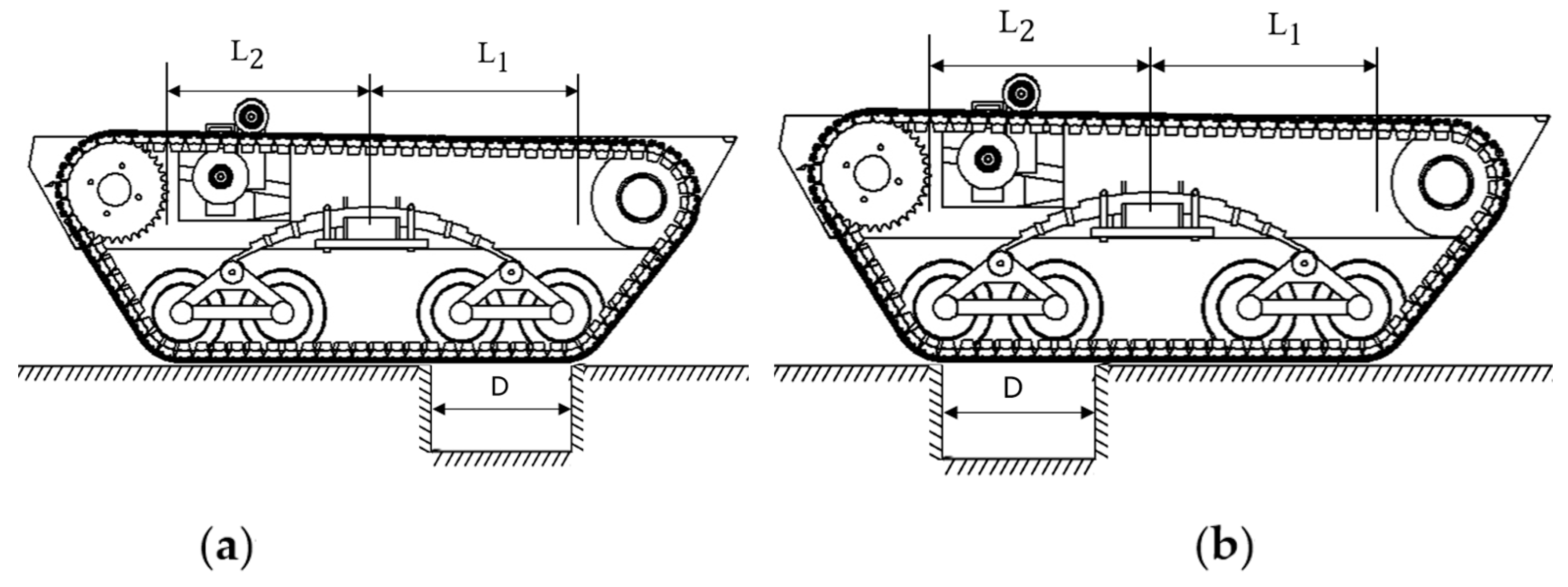
2.4.2. Over-Groove Analysis
3. Kinematic Analysis
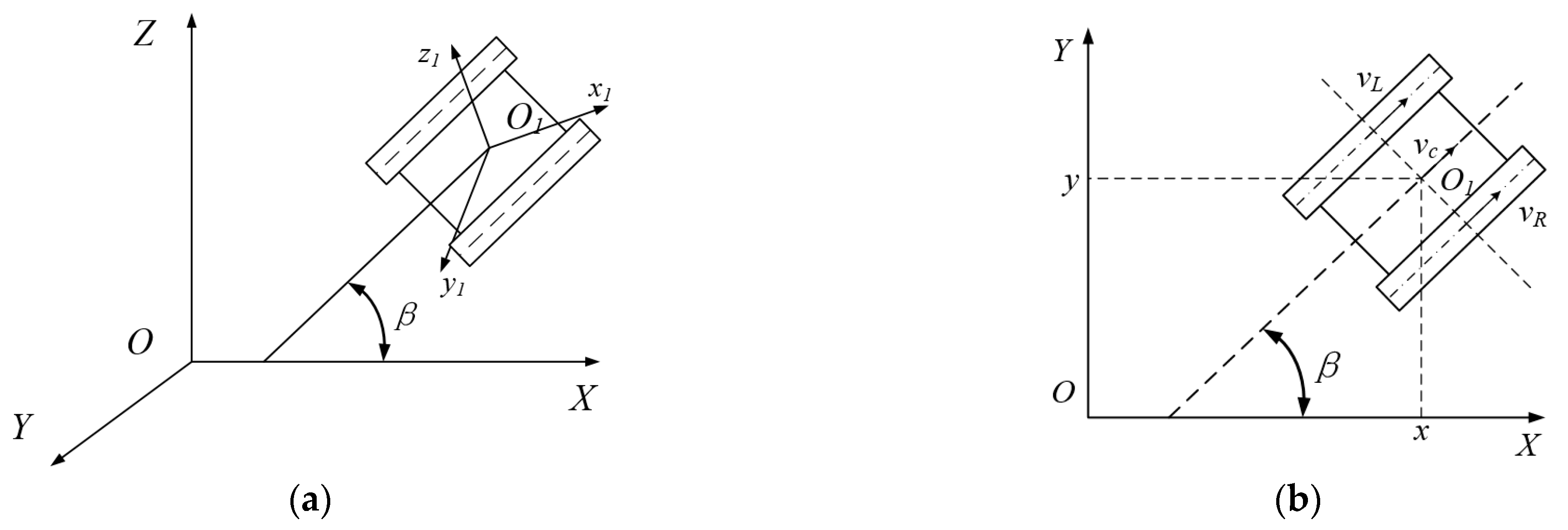
3.1. Establishment of Coordinate System
3.2. Kinematic Model of Prototype
- (1)
- The center of mass of the MSES virtual prototype is located at the center point of the vehicle, the driving surface is a hard surface, , and the shear force between the track and the ground is related to the shear displacement;
- (2)
- There is no relative sliding of the tracks against the drive wheels and no deformation of the tracks;
- (3)
- There is no lateral sliding of the prototype during steering;
- (4)
- When the prototype is steered, the coefficient of steering resistance is the same as the coefficient of resistance for straight-line driving;
- (5)
- The ground pressure of the prototype to the ground is linearly distributed.
4. Dynamics Analysis
4.1. Introduction to the Lagrange Equations
4.2. Dynamics Modeling
- (1)
- The MSES virtual prototype driving system passes through the same ground conditions on both sides of the tracks;
- (2)
- There is longitudinal symmetry of the prototype driving system, body, etc., to the center of mass;
- (3)
- The parts of the driving system of the prototype ignore their elastic variations, and the mass of each part is concentrated at the center of each part;
- (4)
- The driving system dynamics is described by a rigid system with spring stiffness and damping stiffness at the joints of the parts;
- (5)
- The track plates are of the same specification, with the same elastic properties, linear properties, stiffness coefficients and damping coefficients, and the ground attachment coefficient and sliding friction coefficient to the tracks are unchanged.
4.3. Dynamics Modeling
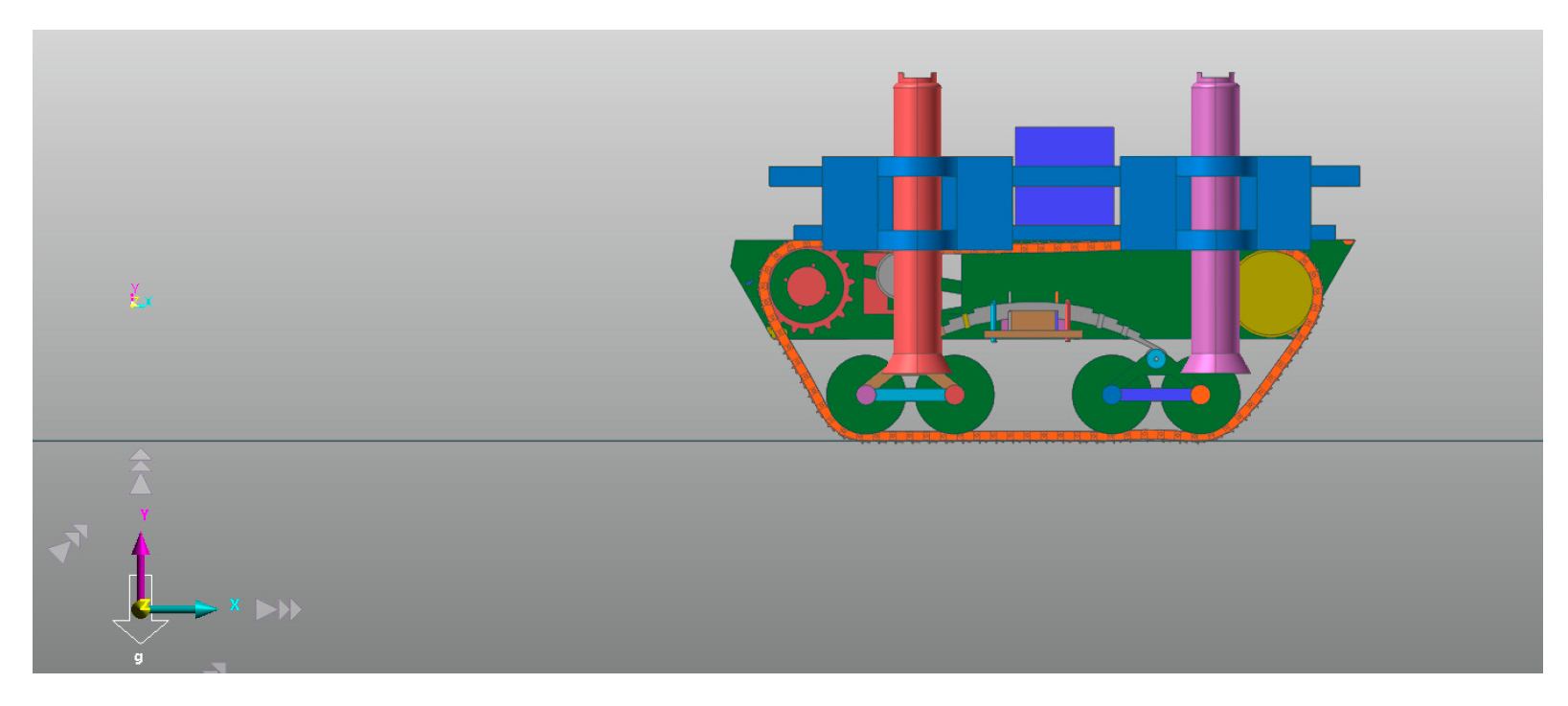
5. Multi-Body Dynamics Simulation
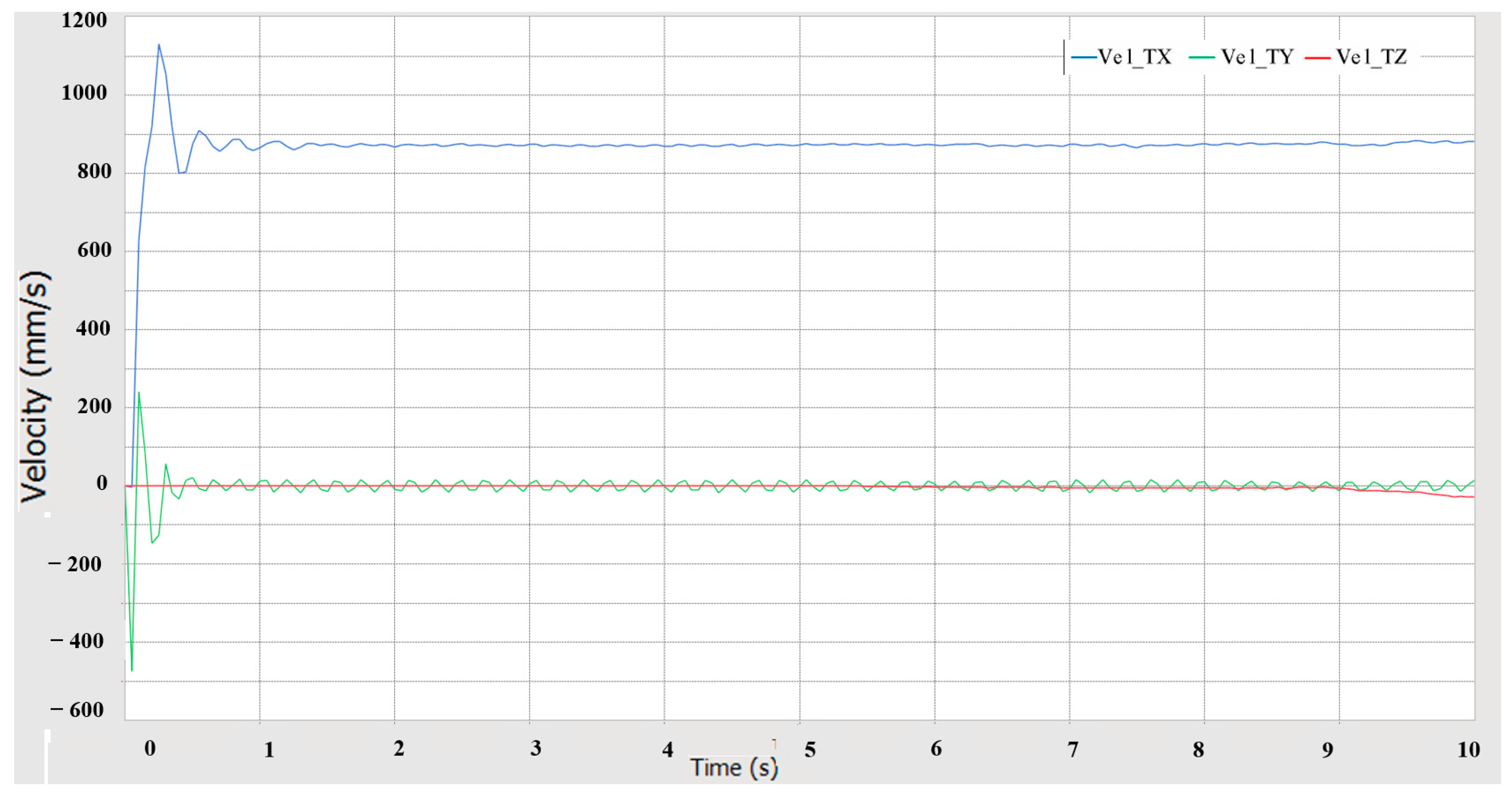
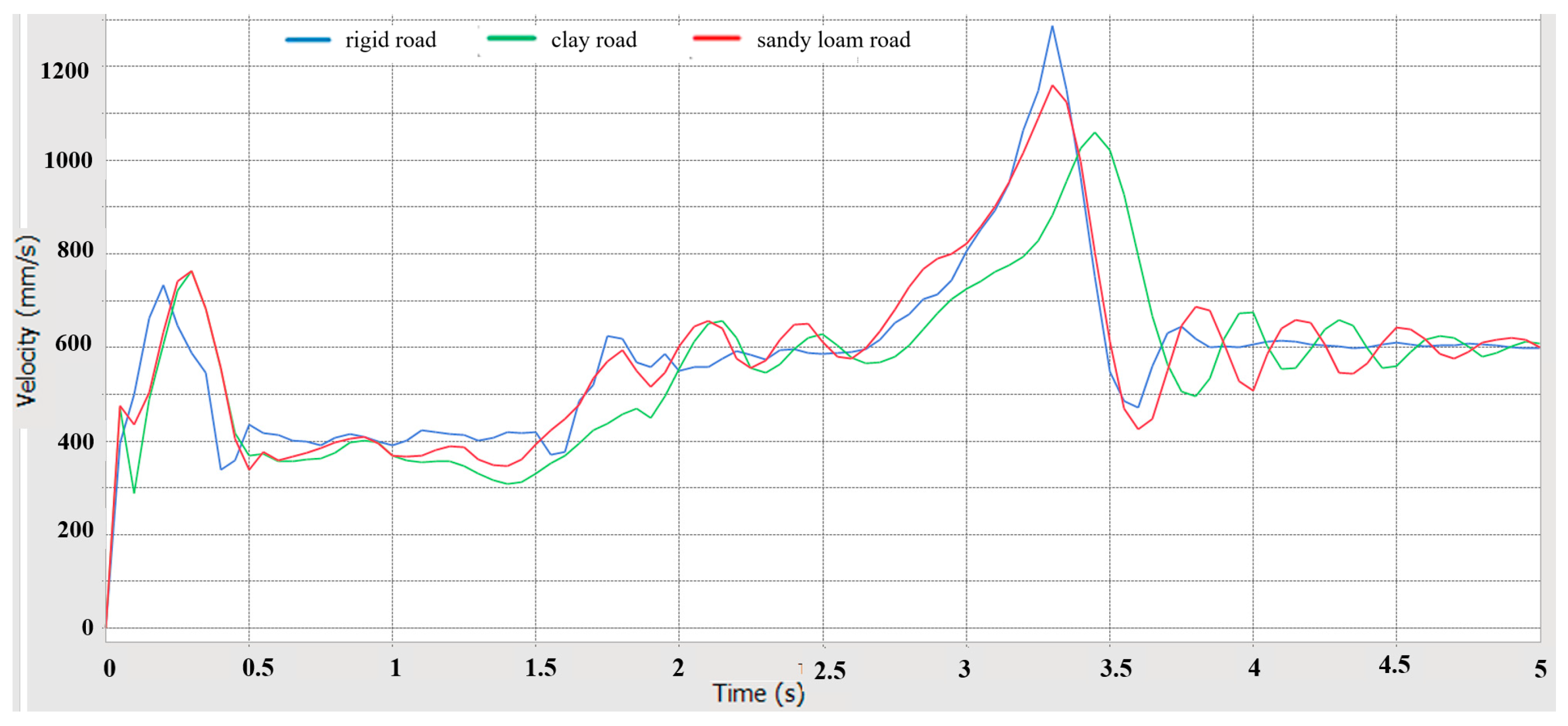
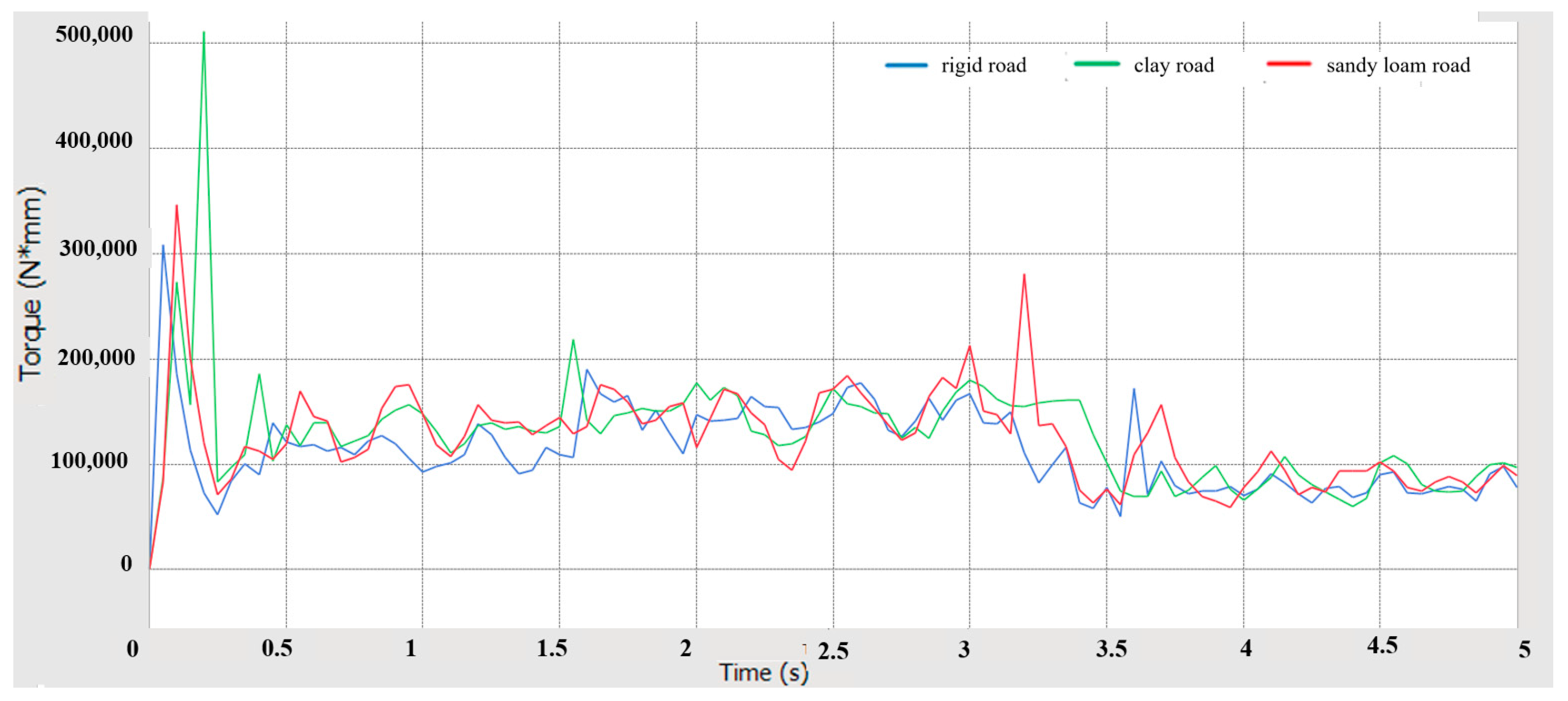
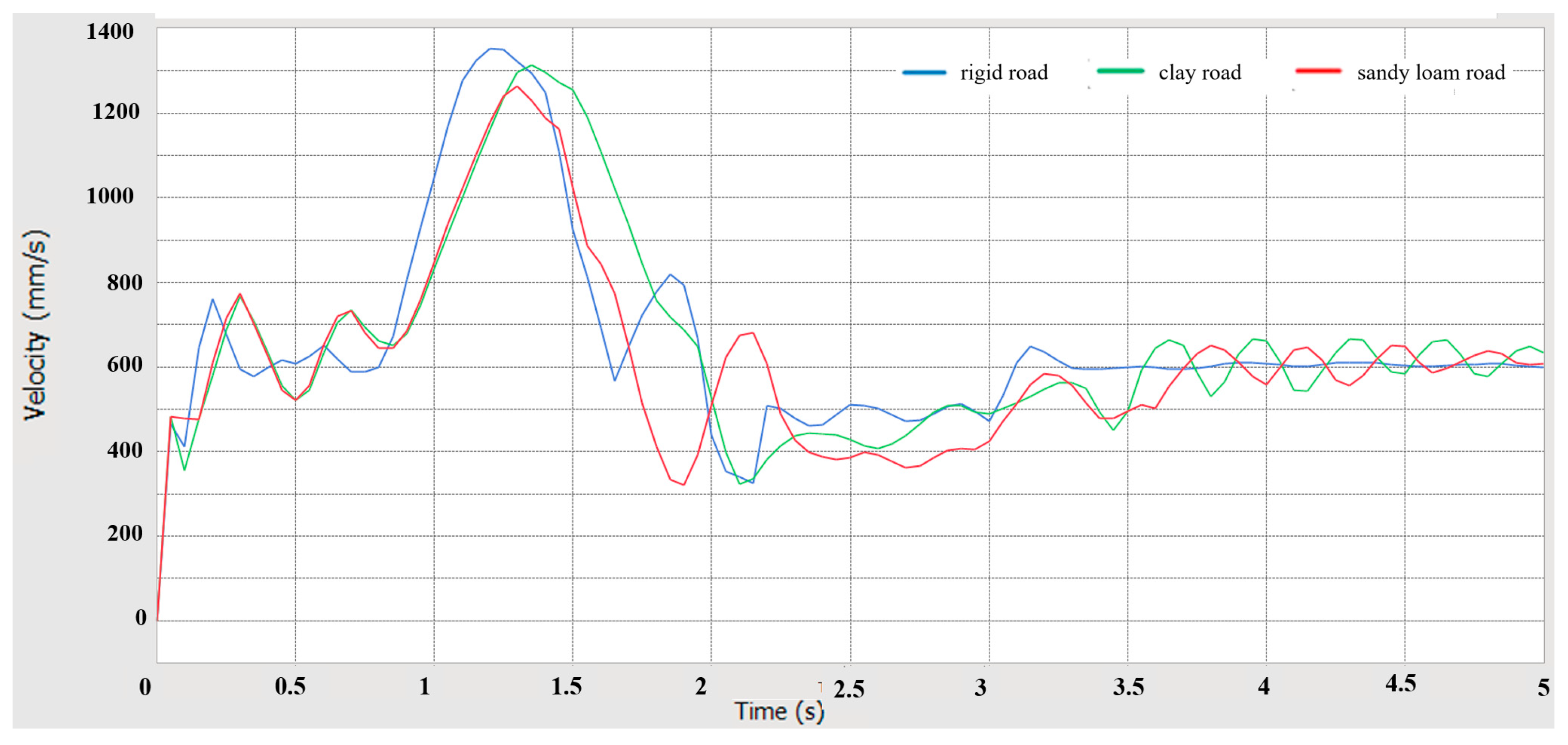
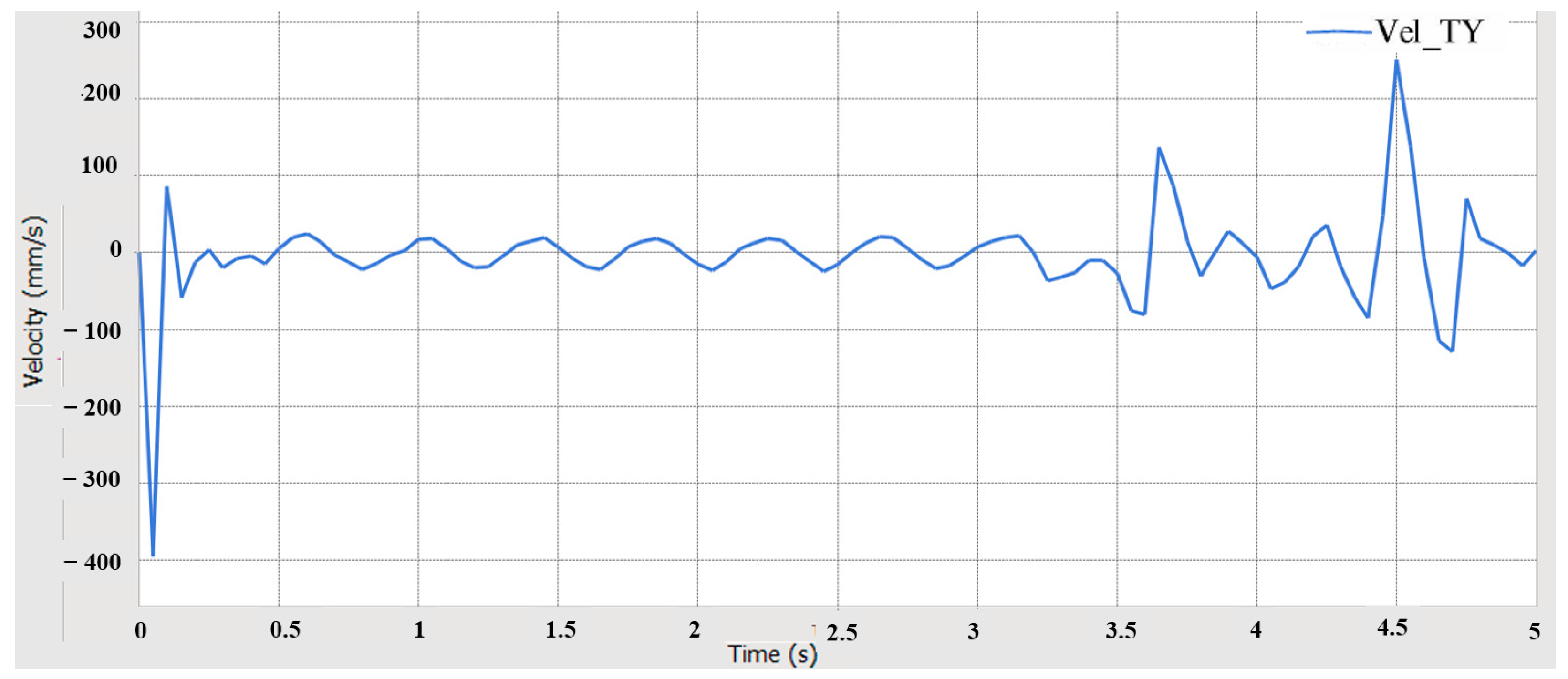
5.1. Driving Performance Simulation Analysis
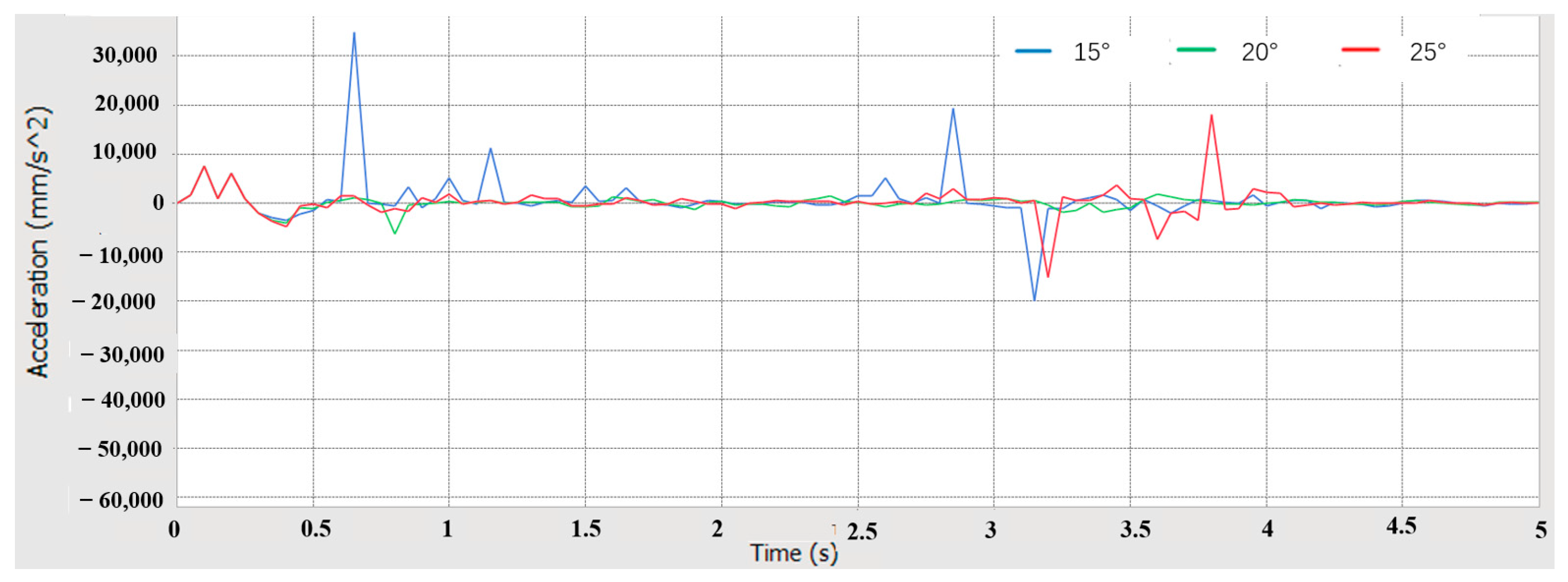
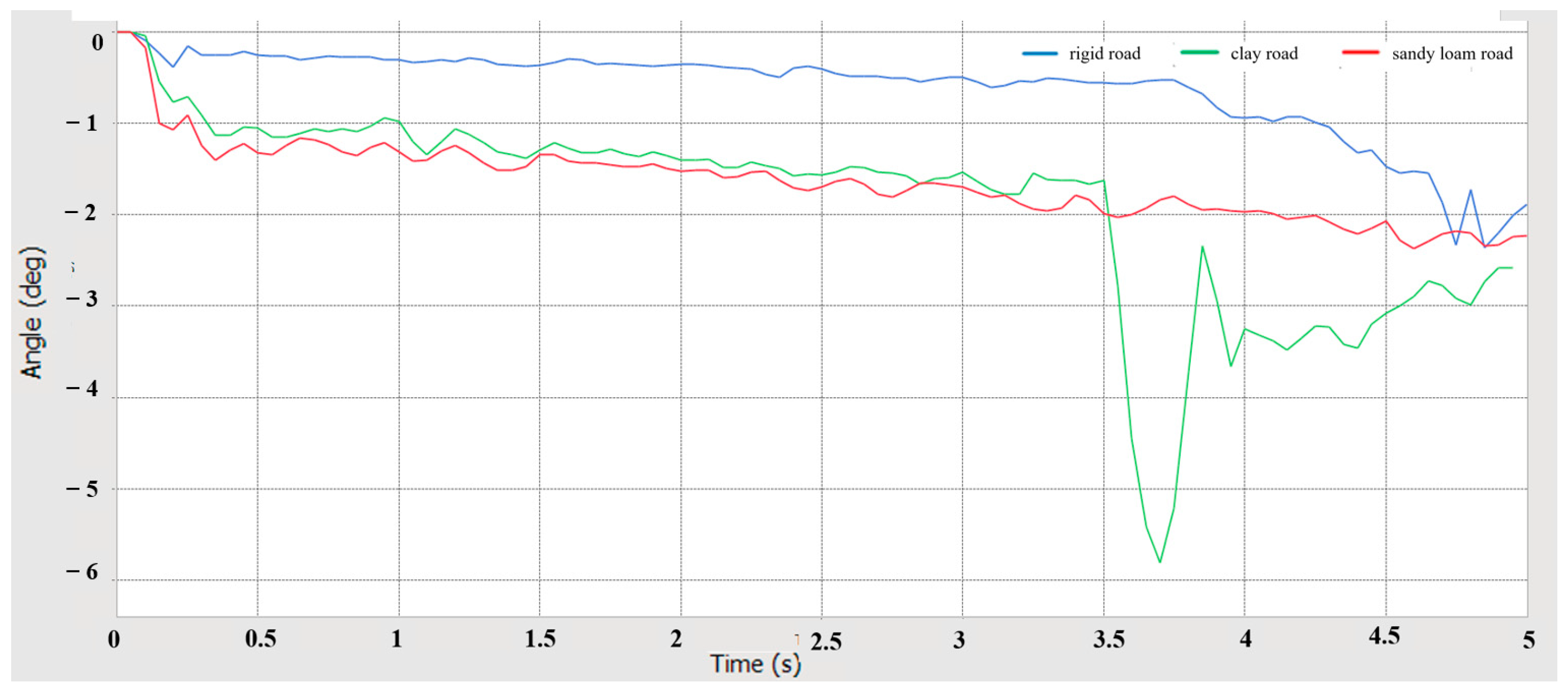
5.2. Anti-Rollover Performance Simulation Analysis
5.2.1. Uphill Driving Simulation Analysis
5.2.2. Downhill Driving Simulation Analysis
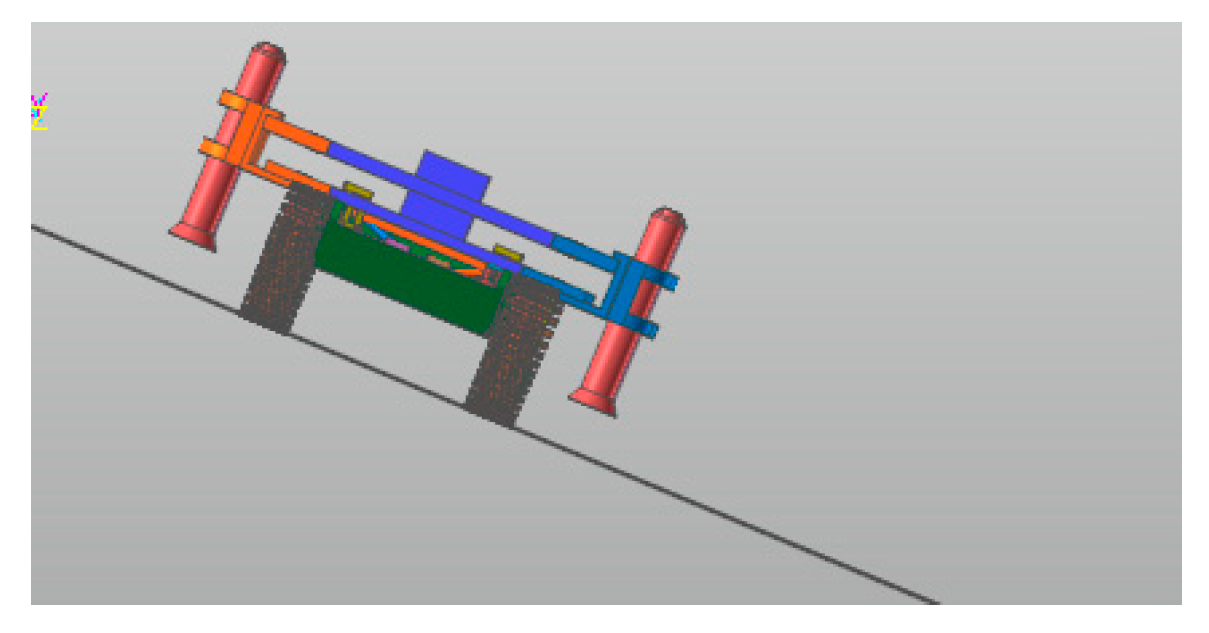
5.2.3. Cross-Slope Driving Simulation Analysis
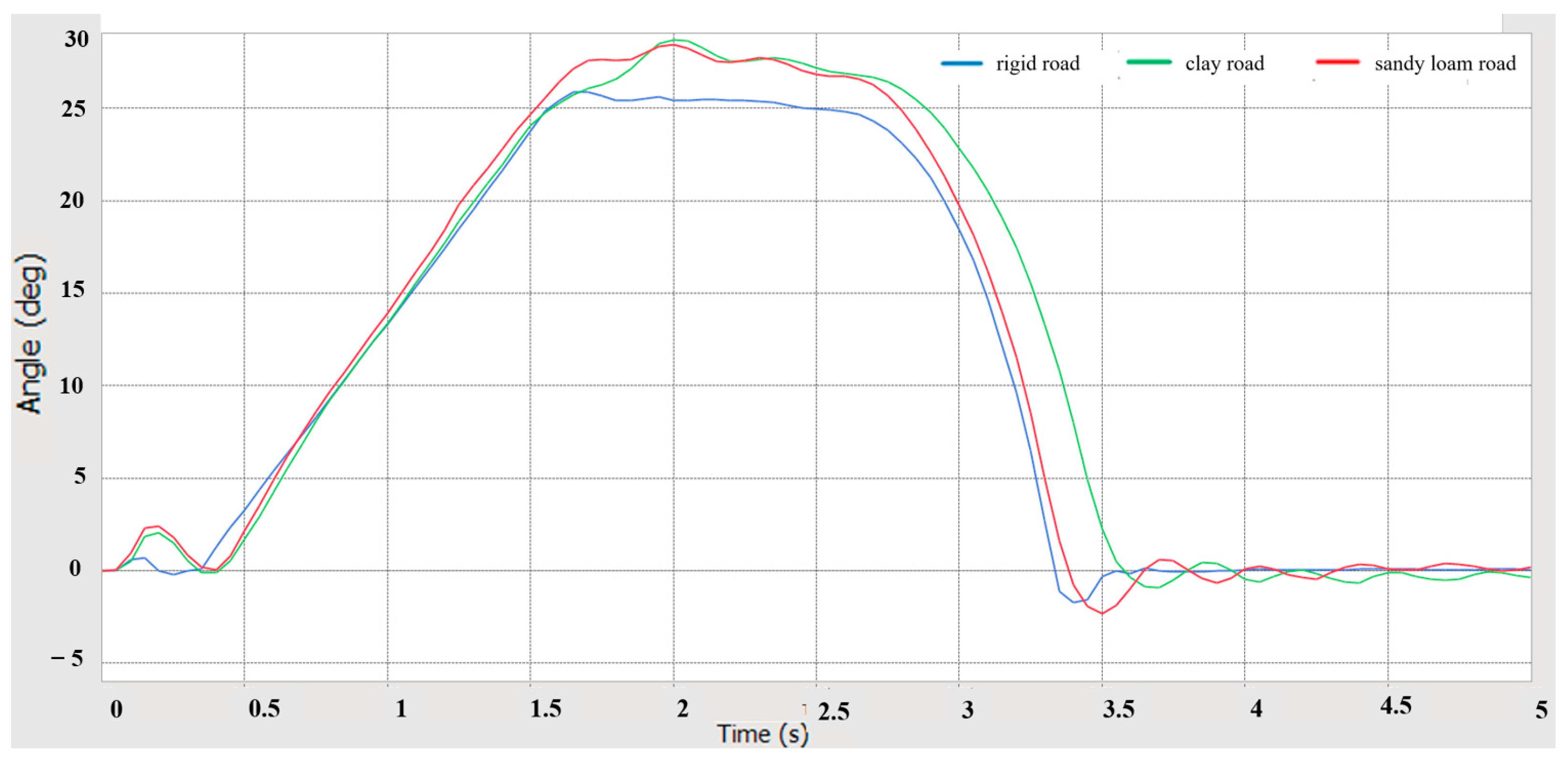
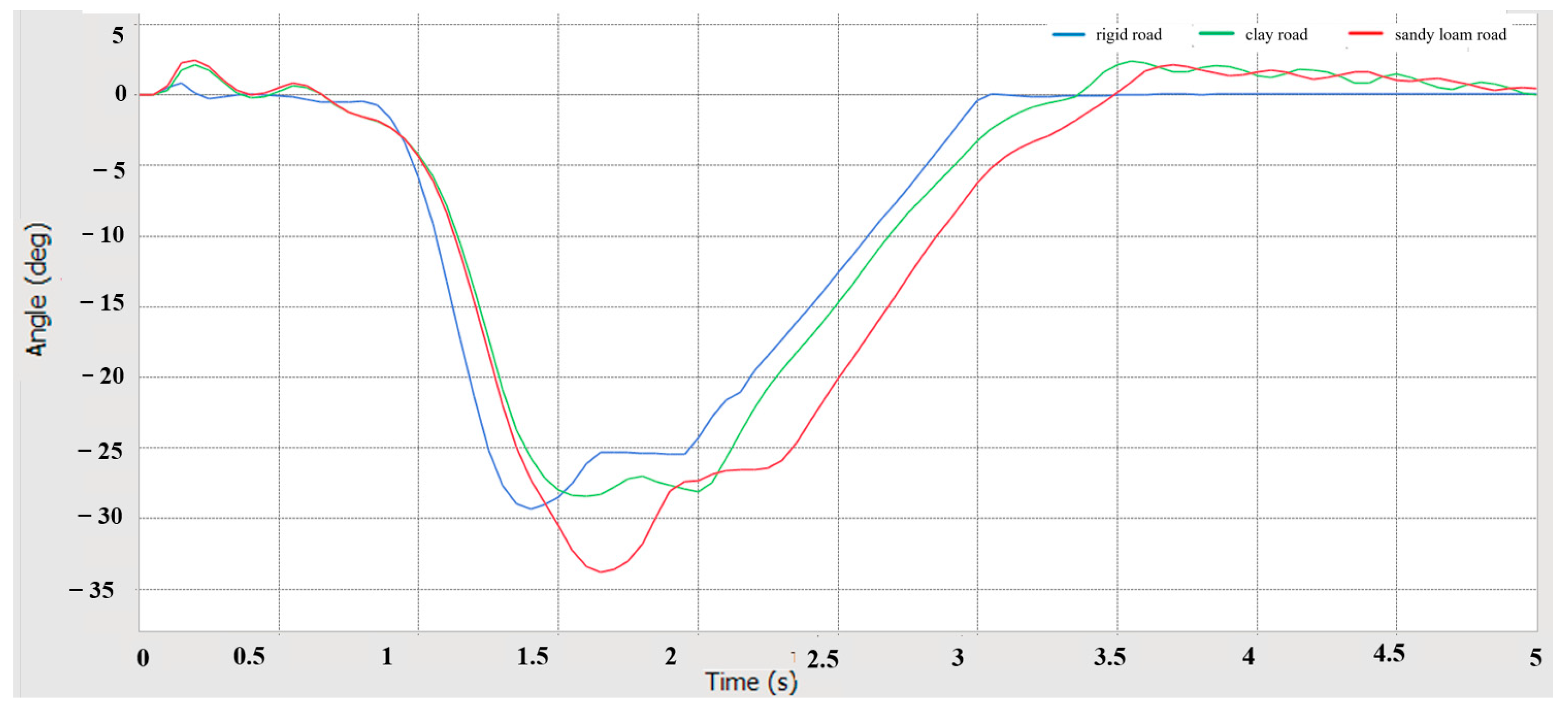
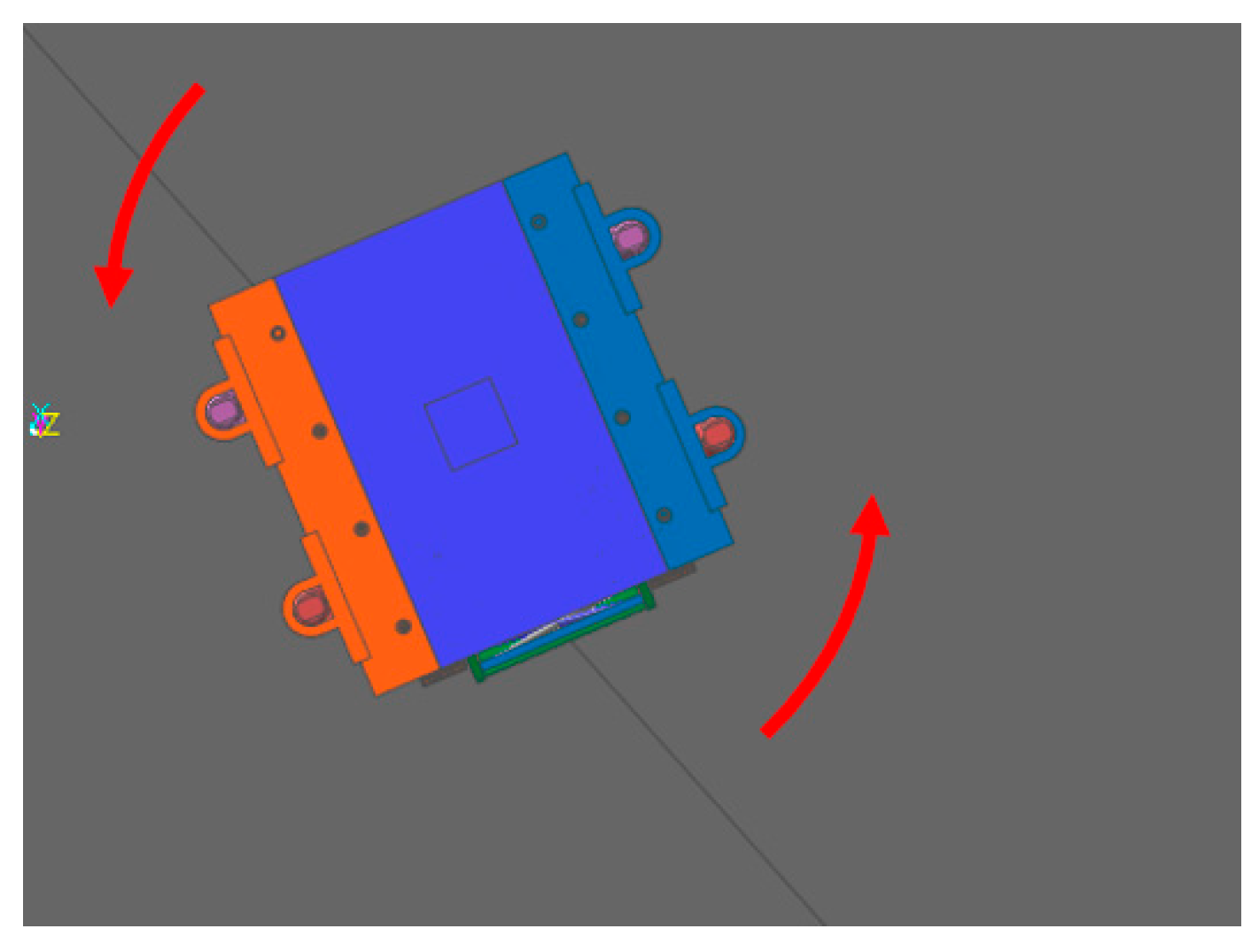
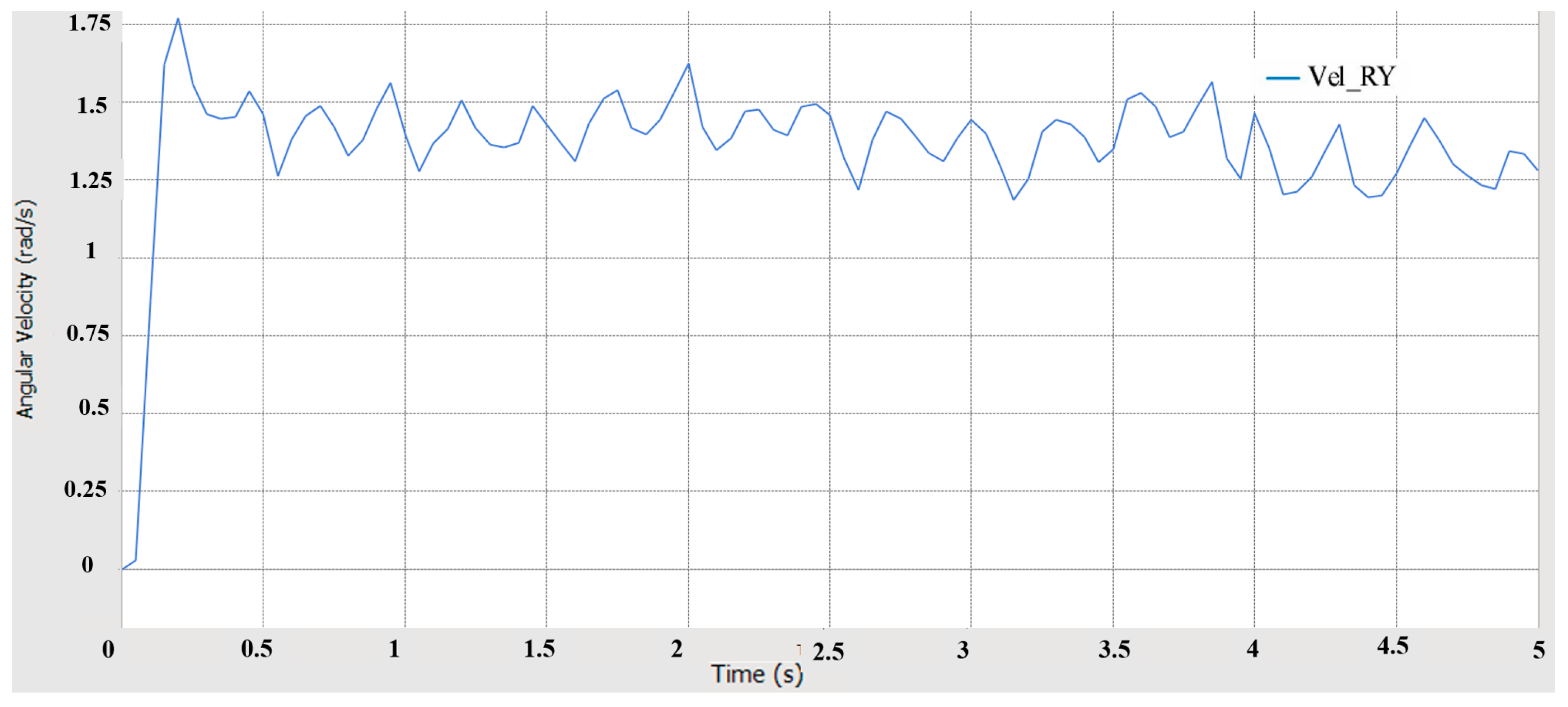
5.3. Steering Performance Simulation Analysis
5.4. Anti-Rollover Performance Simulation Analysis
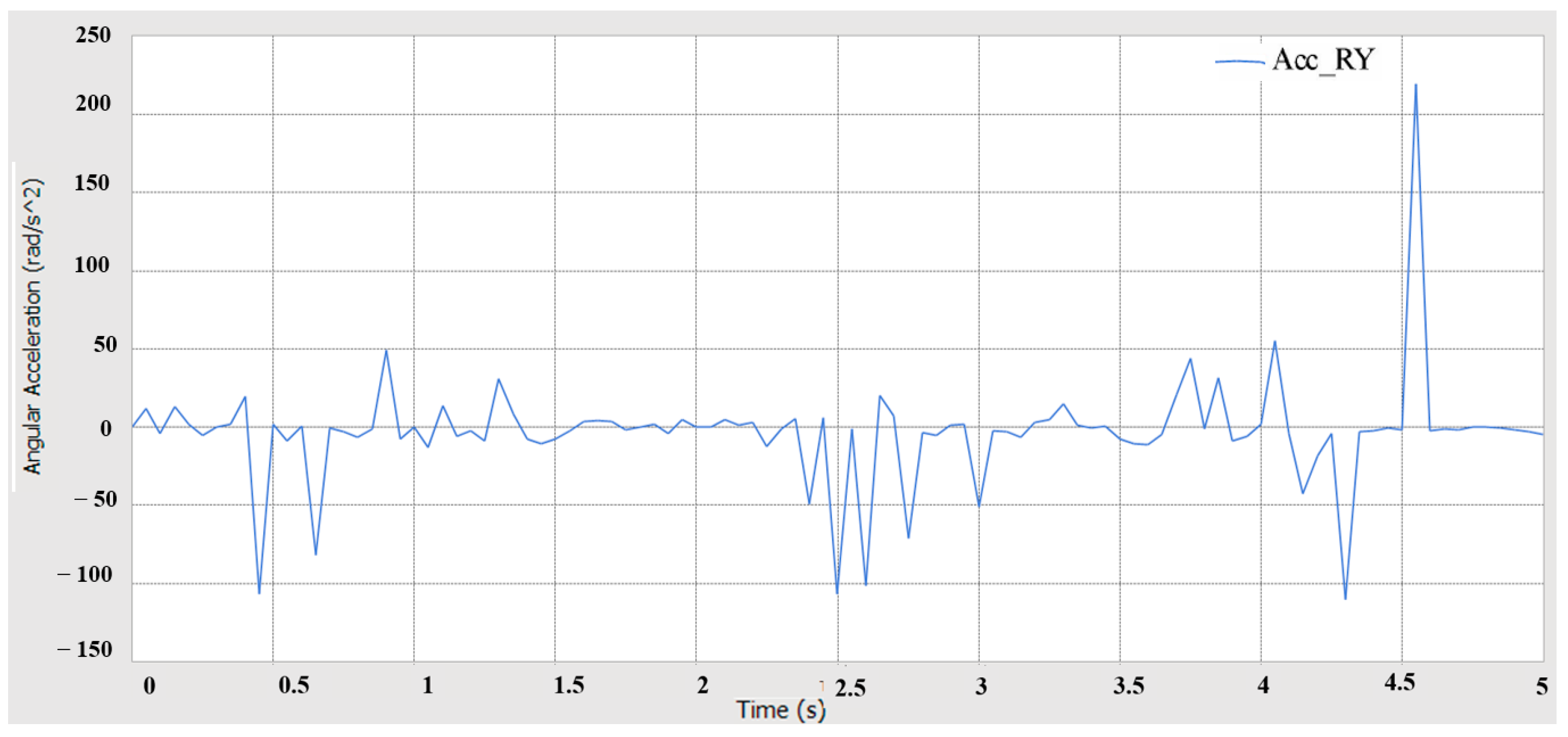
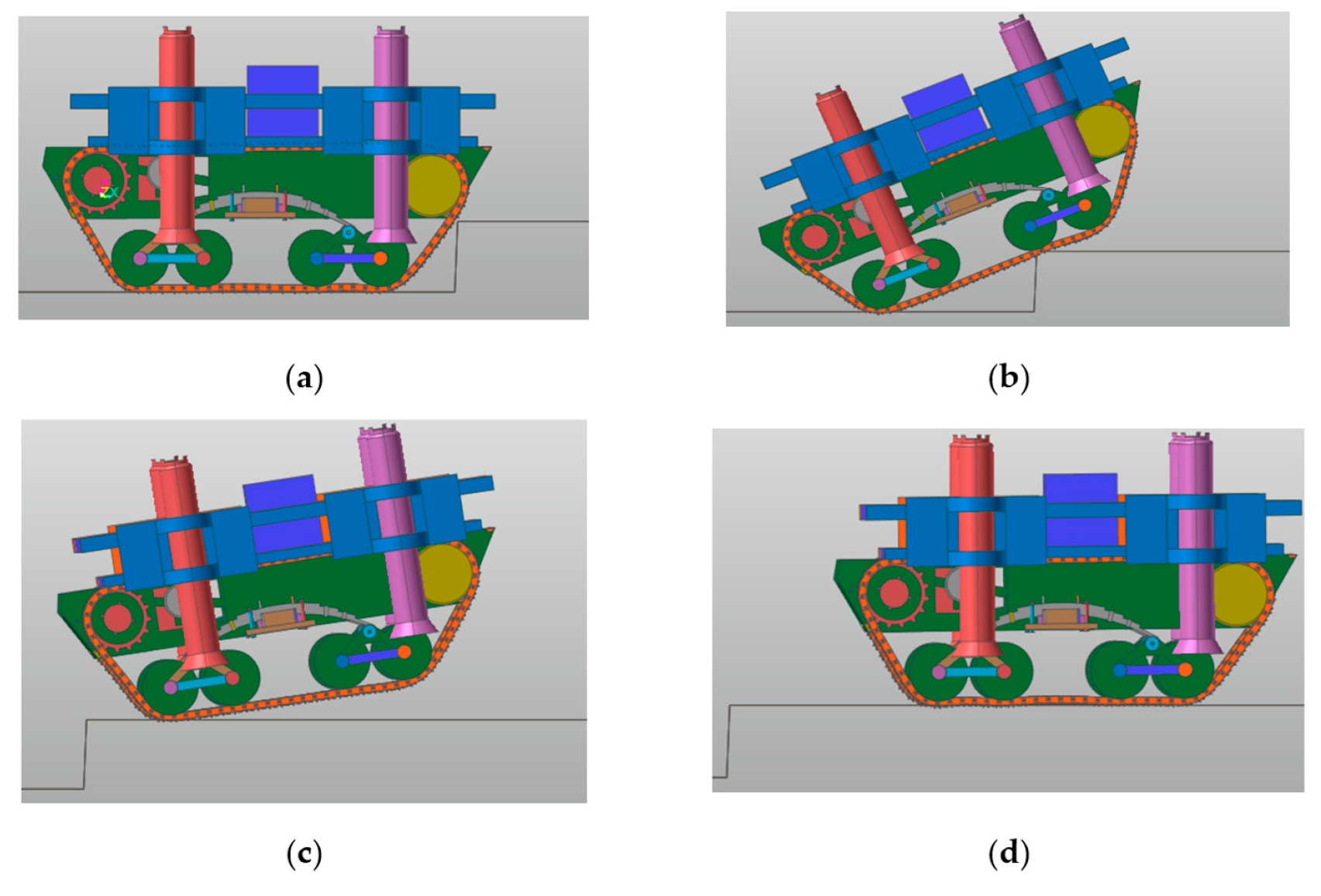
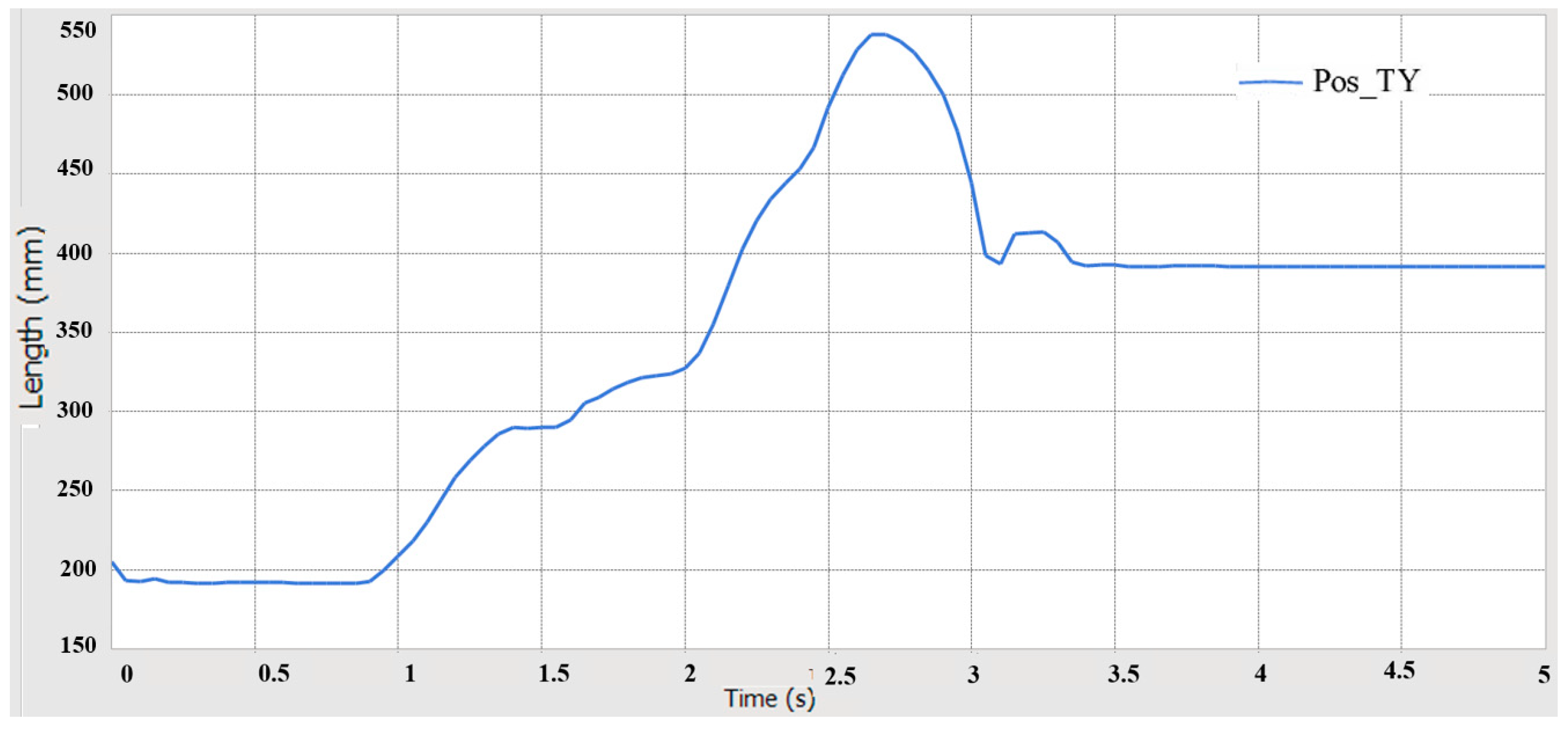
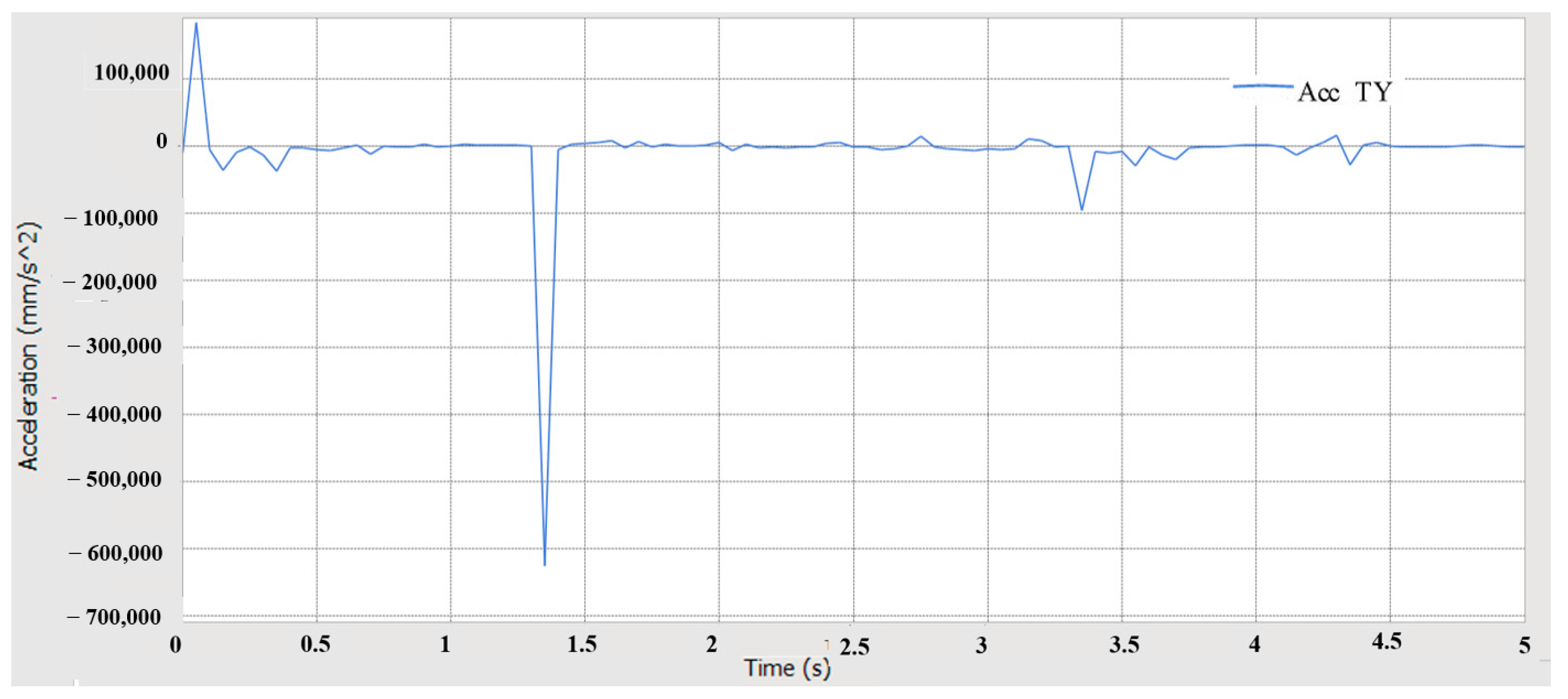
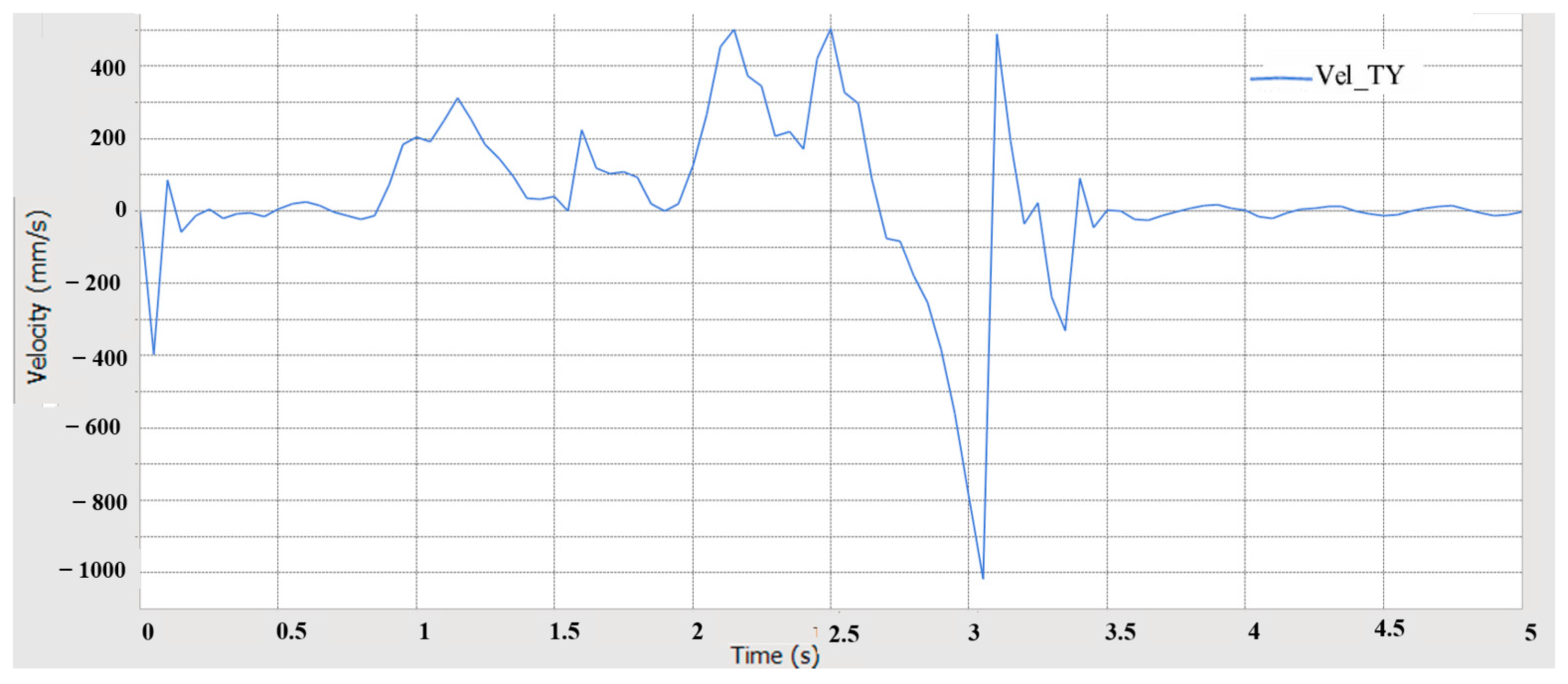
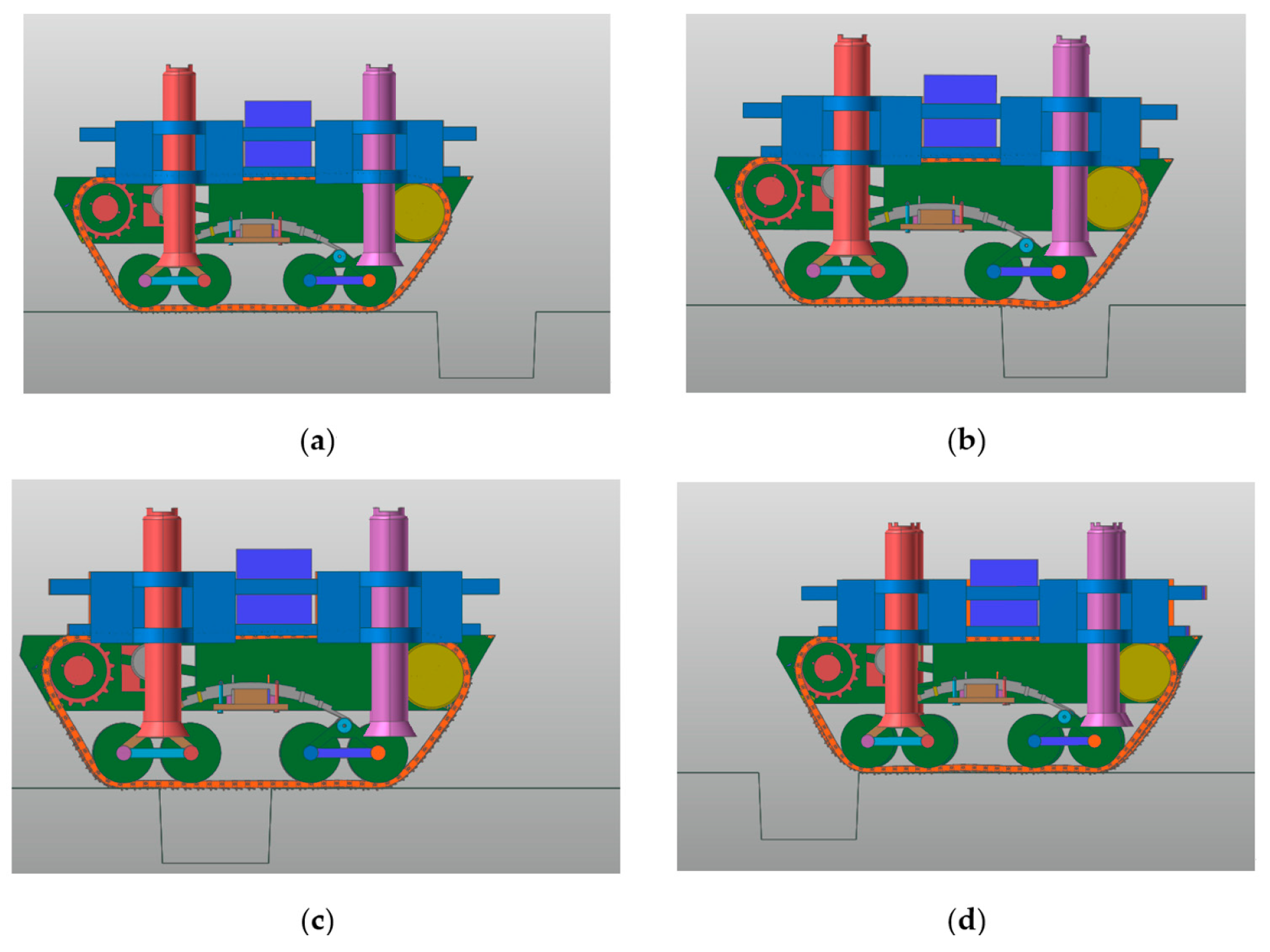
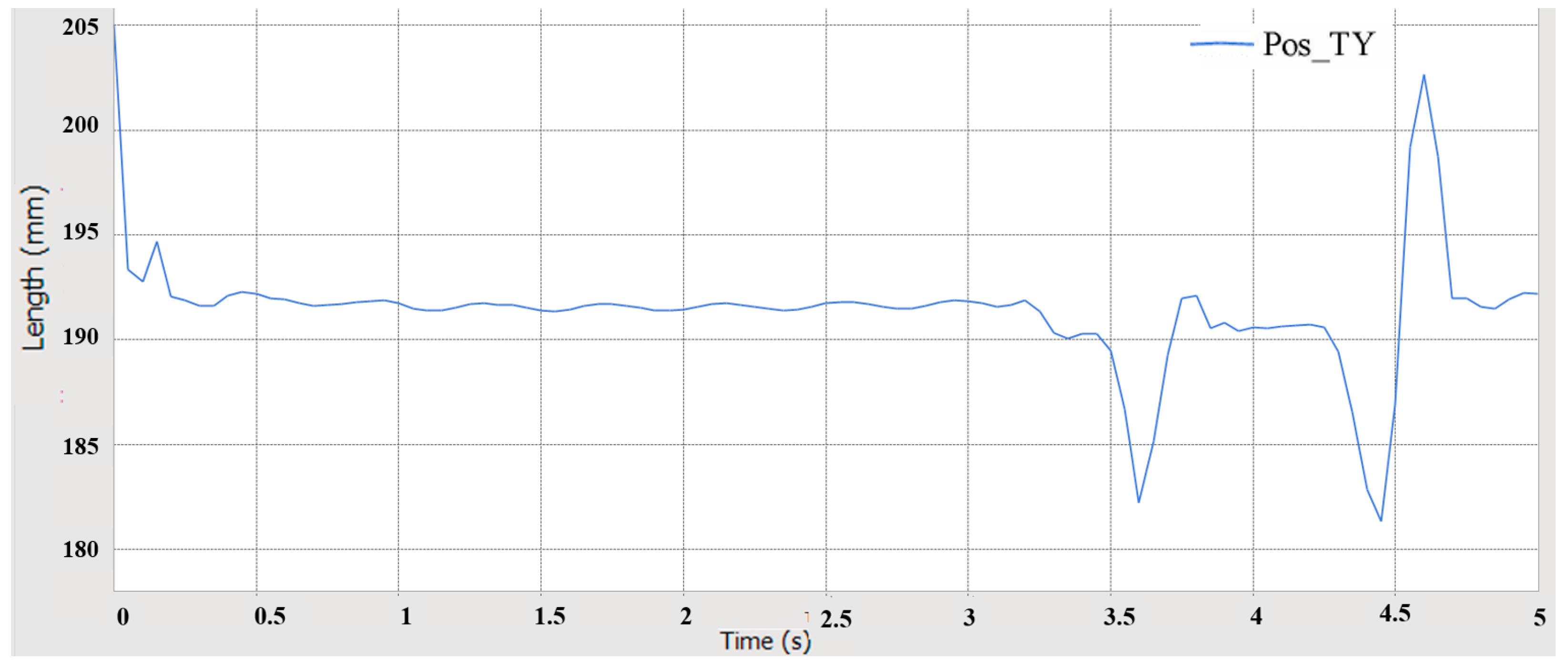
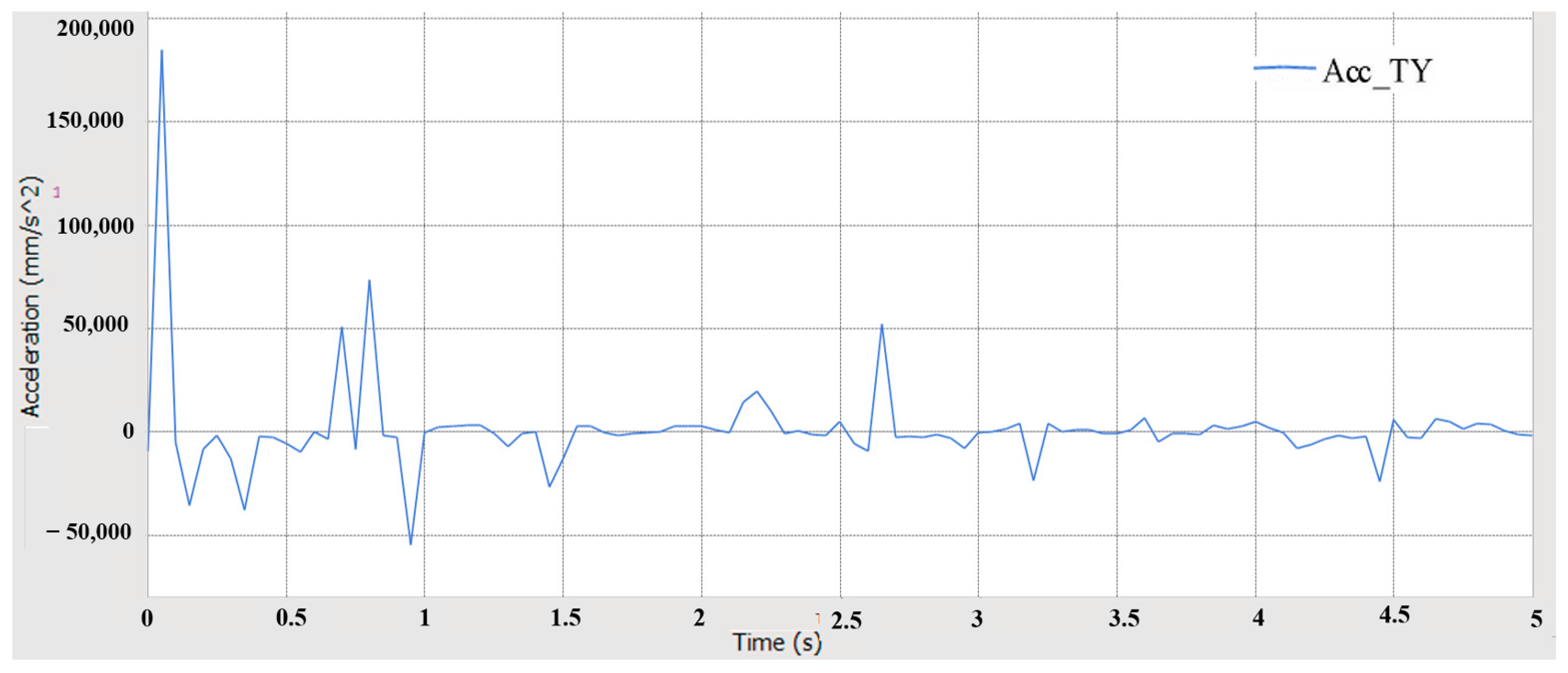
5.4.1. Crossing Obstacles Simulation Analysis
5.4.2. Over-Groove Simulation Analysis
6. Conclusions
- (1)
- The theoretical feasibility foundation of the prototype was laid through the driving theory analysis of the prototype. In the design, the height of the prototype center of mass should be reduced as far as possible to ensure that .
- (2)
- The kinematics analysis of the prototype was carried out, and the position coordinates at different times were analyzed using the RPY angles. The space coordinate system of the prototype was established, and the position coordinates of the prototype at different times were solved by establishing the plane kinematics equation.
- (3)
- By using the discrete body dynamic model method, the track was concentrated as the mass block, a 14-degree-of-freedom dynamic system model was established which can reflect the longitudinal dynamic characteristics of the driving system of the prototype, and the differential equation of motion was established by using the Lagrange dynamic equation method, which provides a theoretical basis for the dynamic simulation.
- (4)
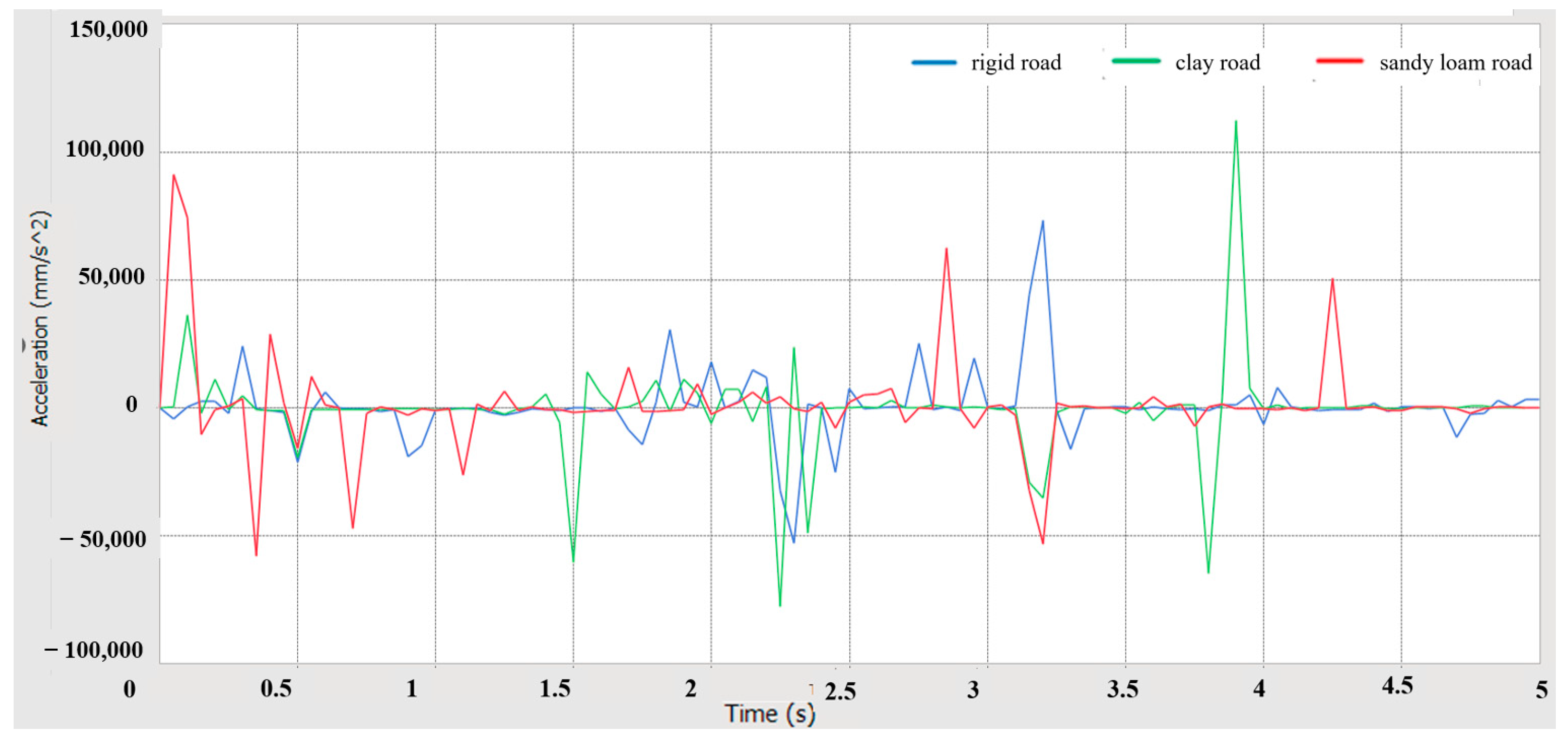
- Using RecurDyn multi-body dynamics simulation, the results verify that the prototype has good driving performance, conforms to the anti-roll design, has good steering performance, has good passing performance, and has good ride comfort and dynamic stability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Du, Y.P. Quantitative Analysis of Economic and Safety Benefits of Coal Mining Mechanization in China’s Coal Industry. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2022. [Google Scholar]
- Zhang, L.X.; Wang, Y.M.; Yang, W.J. Design and research on mechanical arm of automatic handling equipment for hydraulic pillars. J. Coal Technol. 2022, 41, 224–227. [Google Scholar]
- Zhou, K.; Wang, Q.; Tang, J.N. Tripartite Evolutionary Game and Simulation Analysis of Coal Mining Safe Production Supervision under the Chinese Central Government’s Reward and Punishment Mechanism. Math. Probl. Eng. 2021, 2021, 5298890. [Google Scholar] [CrossRef]
- Hou, L.Q. Problems and countermeasures in coal mine tunneling support. J. Energy Energy Conserv. 2023, 212, 202–204. [Google Scholar]
- Ivan, S.; Svitlana, S.; Alla, S. Field investigations of deformations in soft surrounding rocks of rocks of roadway with roof-bolting Supports by auger mining of thin coal seams. Rud.-Geol.-Naft. Zb. 2022, 37, 23–38. [Google Scholar]
- Shahzad, M.; Majeed, Y.; Emad, M.Z.; Arshad, M.; Goraya, R.; Akram, M. Assessing mechanical characteristics of typical support system being used in thin seam coal mining of Pakistan. Int. J. Min. Miner. Eng. 2022, 13, 333–351. [Google Scholar] [CrossRef]
- Xue, T.L.; Zhang, X.H.; Du, D.T. Developing History and Trend of Mine Support Equipment in China. Appl. Mech. Mater. 2010, 42, 42. [Google Scholar] [CrossRef]
- Li, J. Program design and performance study of self-moving support equipment. Electron. Technol. Softw. Eng. 2023, 246, 108–111. [Google Scholar]
- Bruzzone, L.; Nodehi, S.E.; Fanghella, P. Tracked Locomotion Systems for Ground Mobile Robots: A Review. Machines 2022, 10, 648. [Google Scholar] [CrossRef]
- Purdy, D.J.; Simner, D. A brief investigation into the effect on suspension motions of high unsprung mass. J. Battlef. Technol. 2004, 7, 15–20. [Google Scholar]
- Hetherington, J.G. Scale—Model testing of soil—Vehicle systems. J. Battlef. Technol. 2004, 7, 7–10. [Google Scholar]
- Purdy, D.J.; Kumar, R.J. Mathematical model ling of a hydro-gas suspension unit for tracked military vehicles. J. Battlef. Technol. 2005, 8, 7–14. [Google Scholar]
- Song, F.H.; Yan, C.C.; Sun, J.B. Analysis of the key points of top plate management in high-grade general mining working face. Inn. Mong. Coal Econ. 2016, 217, 51–78. [Google Scholar]
- Kleppner, D.; Kolenkow, R. An Introduction to Mechanics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Uicker, J.J.; Pennock, G.R.; Shigley, J.E. Theory of Machines and Mechanisms, 5th ed.; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Wei, D. Design of Electric Control System of Fully Hydraulic Driven Crawler Tractor; Northwest A&F University: Xianyang, China, 2013. [Google Scholar]
- Solidworks.com. Available online: https://www.solidworks.com/zh-hans (accessed on 20 September 2023).
- Ji, G.X. Design and Motion Performance Analysis of Tracked Manned Lunar Rover Mobile System; Harbin Institute of Technology: Harbin, China, 2013. [Google Scholar]
- Ou, Y. Design and Analysis of Mechanical System of Special Ground Mobile Robot; Nanjing University of Science and Technology: Nanjing, China, 2013. [Google Scholar]
- Yao, J.Q. Study on the Dynamics of Crawler System of Longitudinal Tunnel Header; Liaoning Technical University: Fuxin, China, 2012. [Google Scholar]
- Recurdyn.cn. Available online: https://www.recurdyn.cn/ (accessed on 20 September 2023).

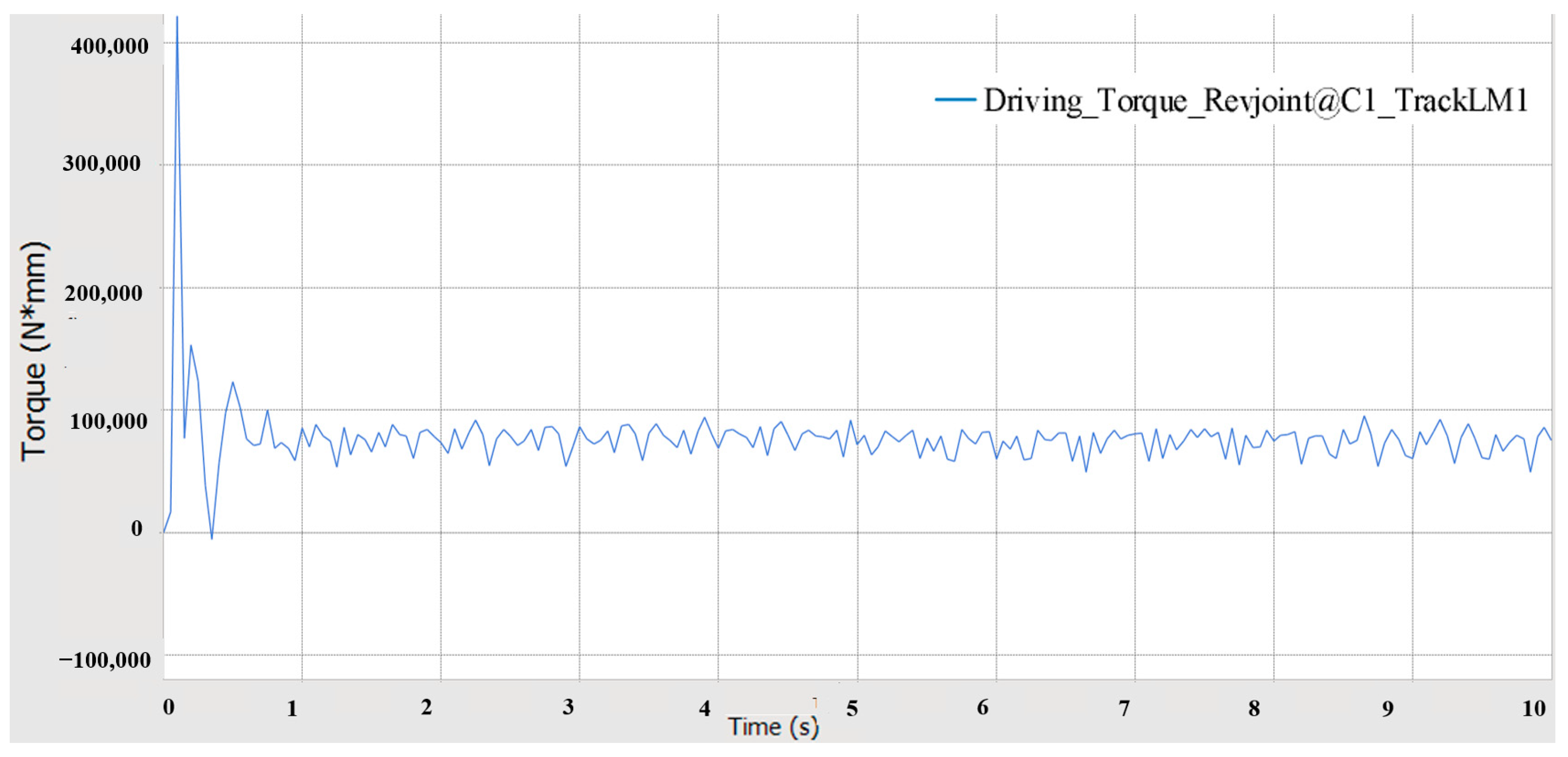




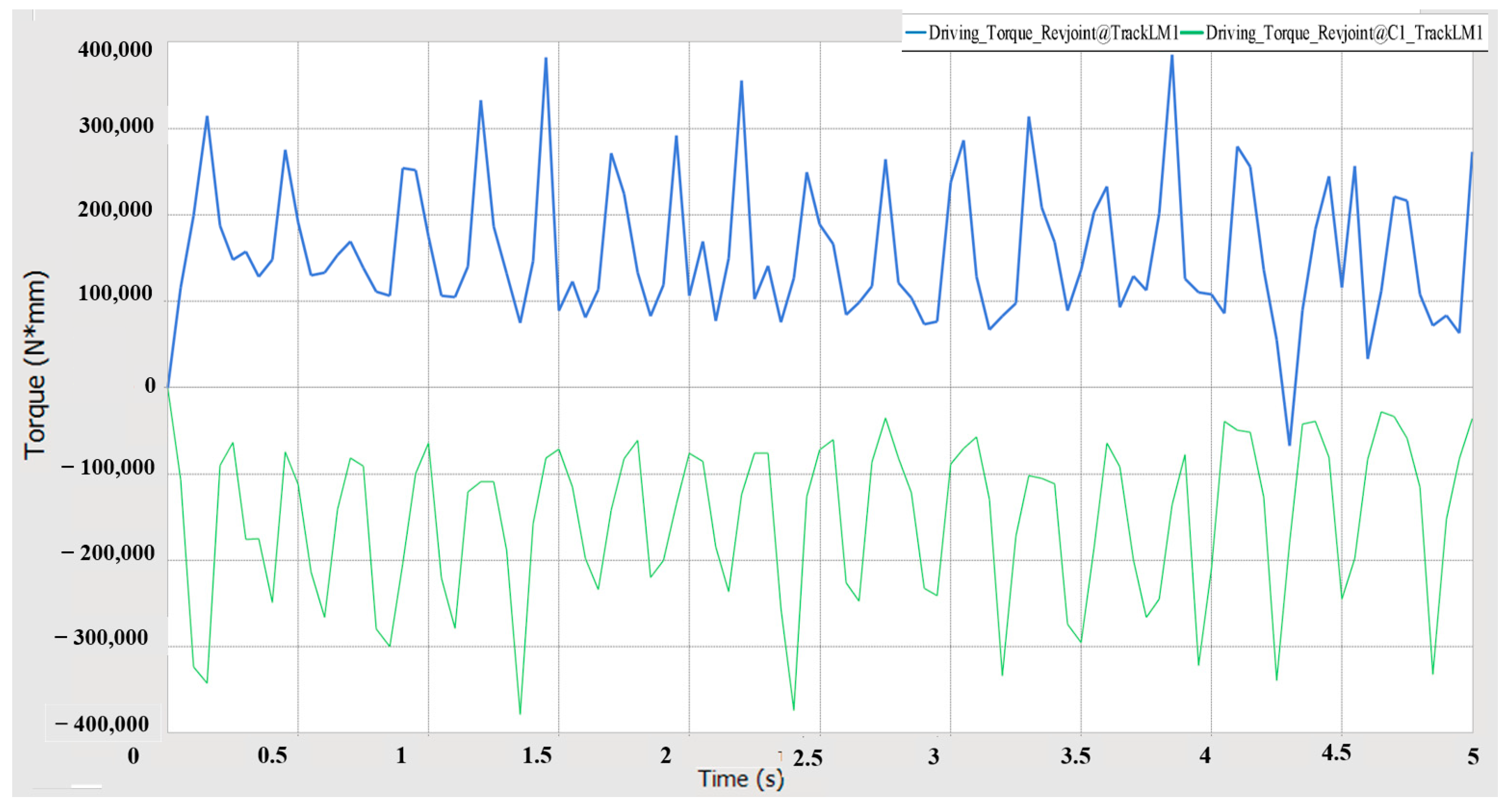
| Simulation Value | Theoretical Value | Inaccuracy | |
|---|---|---|---|
| Driving torque | 122.85 | 126.13 | 2.6% |
| Driving power | 1.24 | 1.27 | 2.6% |
| Simulation Value | Theoretical Value | Inaccuracy | |
|---|---|---|---|
| Driving torque | 287.69 | 298.05 | 3.5% |
| Driving power | 2.01 | 2.09 | 3.5% |
| Simulation Value | Theoretical Value | Inaccuracy | ||
|---|---|---|---|---|
| Driving torque | Left track | 159.64 | 165.54 | 3.6% |
| Right track | 220.72 | 228.60 | 3.4% | |
| Driving power | Left track | 1.16 | 1.2 | 3.6% |
| Right track | 1.55 | 1.6 | 3.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, C.; Shi, Y.; Hao, J.; Nie, J.; Liu, Q. Research and Simulation of Kinematics and Dynamics of Tracked Support Equipment Based on Multi-Body Dynamics. Appl. Sci. 2023, 13, 10613. https://doi.org/10.3390/app131910613
Xin C, Shi Y, Hao J, Nie J, Liu Q. Research and Simulation of Kinematics and Dynamics of Tracked Support Equipment Based on Multi-Body Dynamics. Applied Sciences. 2023; 13(19):10613. https://doi.org/10.3390/app131910613
Chicago/Turabian StyleXin, Changqing, Yongkui Shi, Jian Hao, Junlong Nie, and Qiuyue Liu. 2023. "Research and Simulation of Kinematics and Dynamics of Tracked Support Equipment Based on Multi-Body Dynamics" Applied Sciences 13, no. 19: 10613. https://doi.org/10.3390/app131910613
APA StyleXin, C., Shi, Y., Hao, J., Nie, J., & Liu, Q. (2023). Research and Simulation of Kinematics and Dynamics of Tracked Support Equipment Based on Multi-Body Dynamics. Applied Sciences, 13(19), 10613. https://doi.org/10.3390/app131910613




