Modelling the Interaction of Illuminations with a Sensor Matrix Used in Vision Systems
Abstract
:1. Introduction
2. Materials and Methods
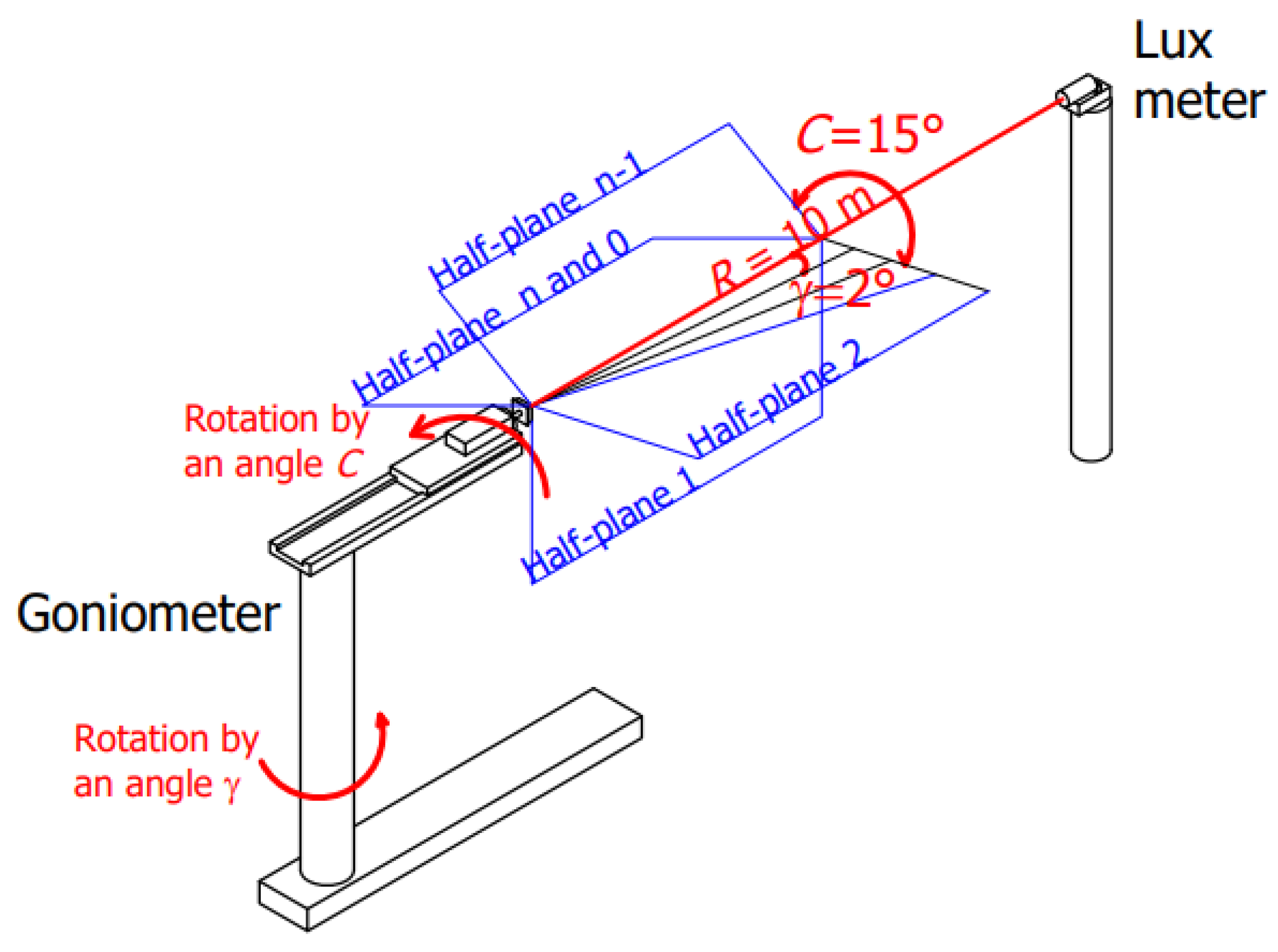
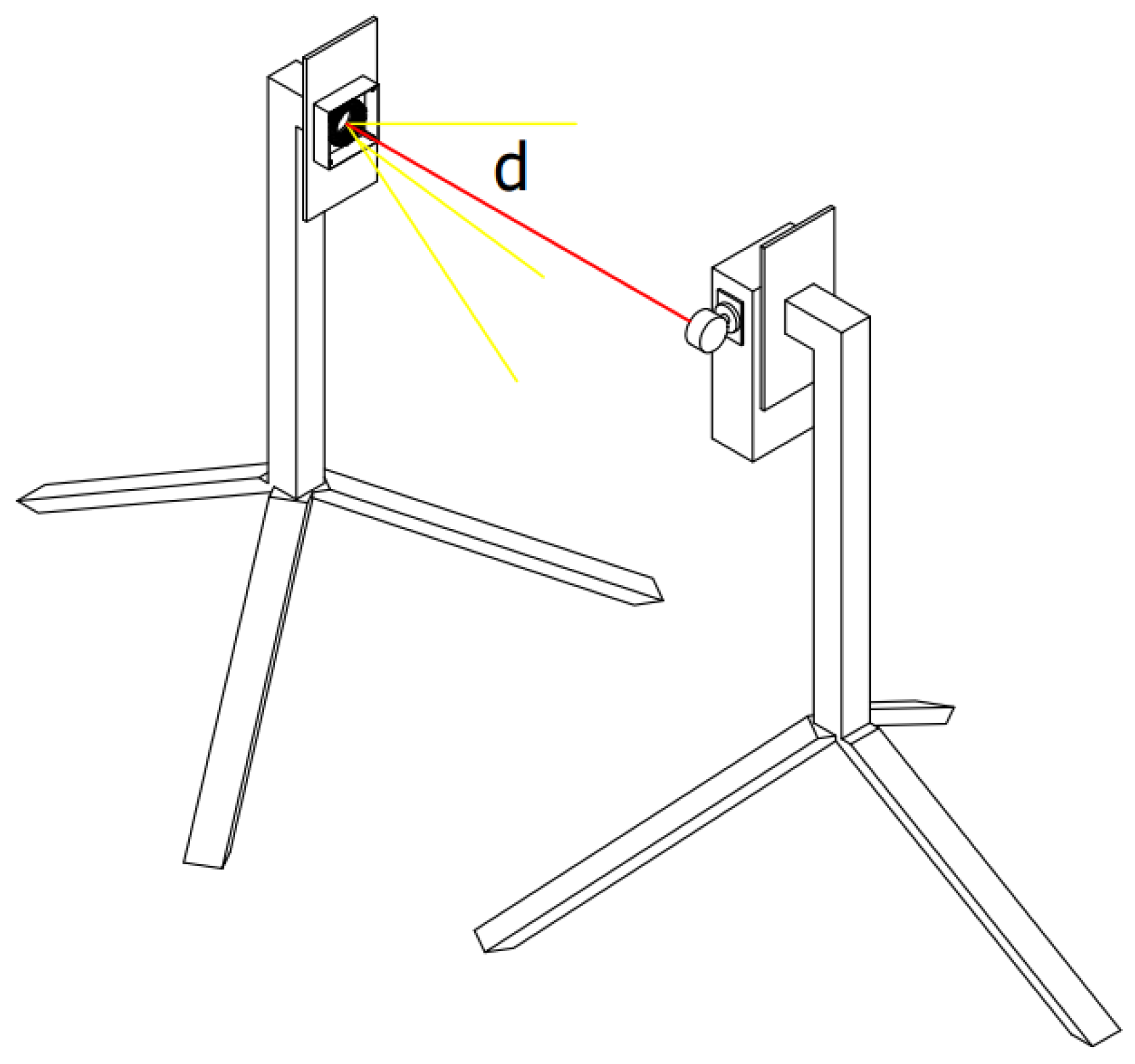
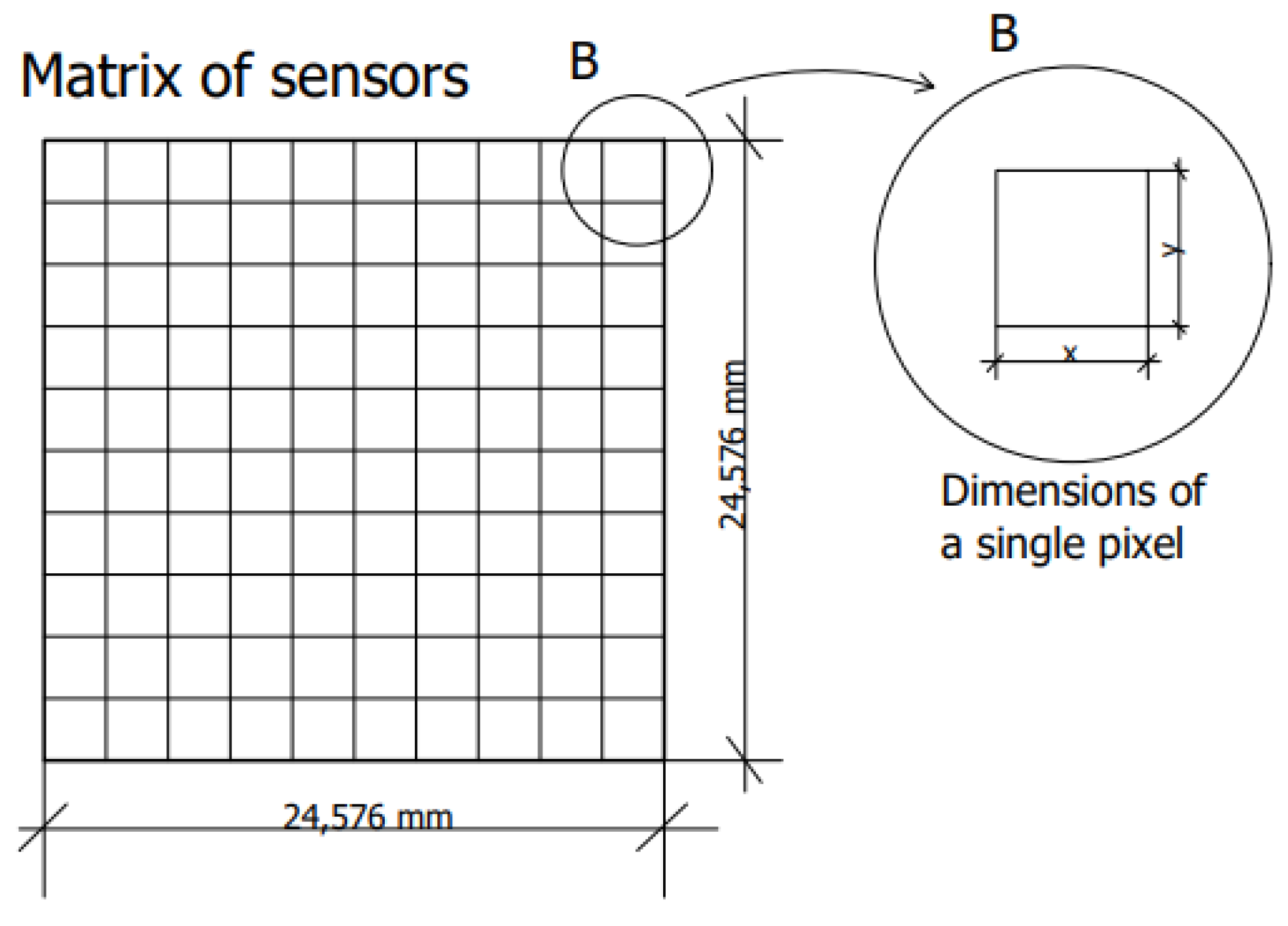
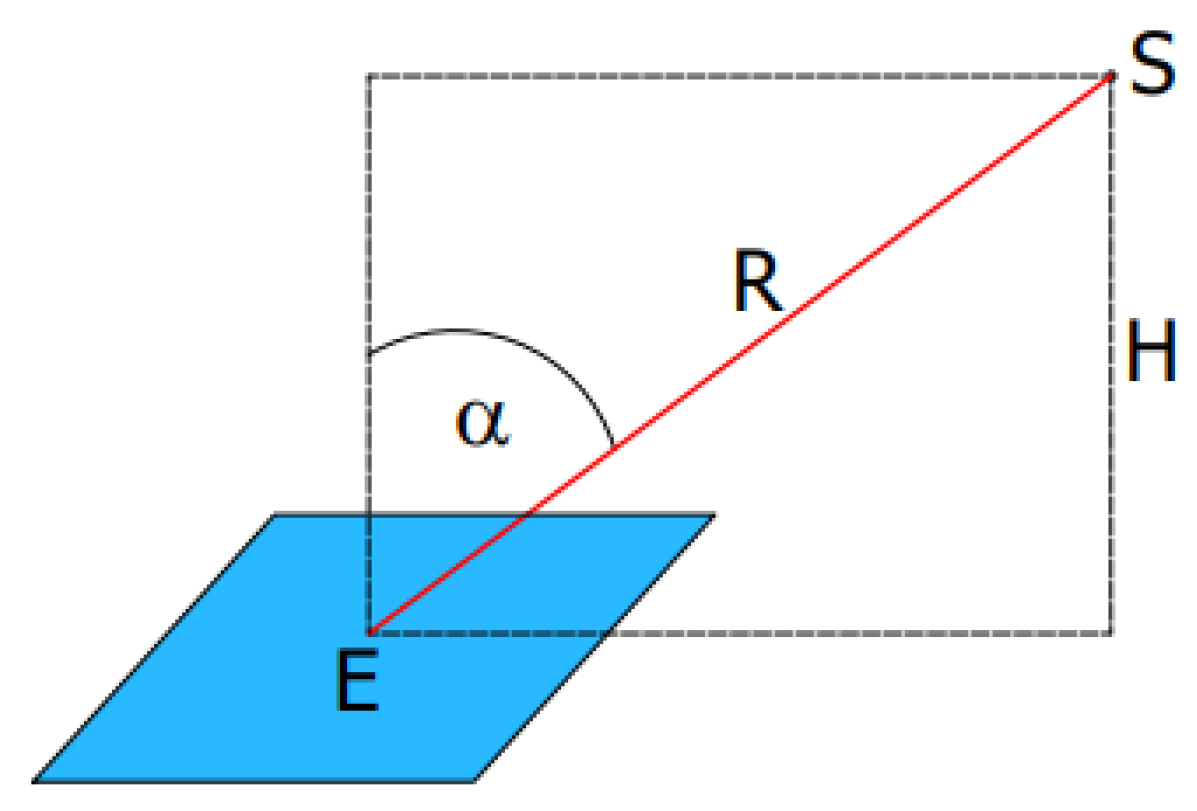
2.1. Description of the Measuring Station
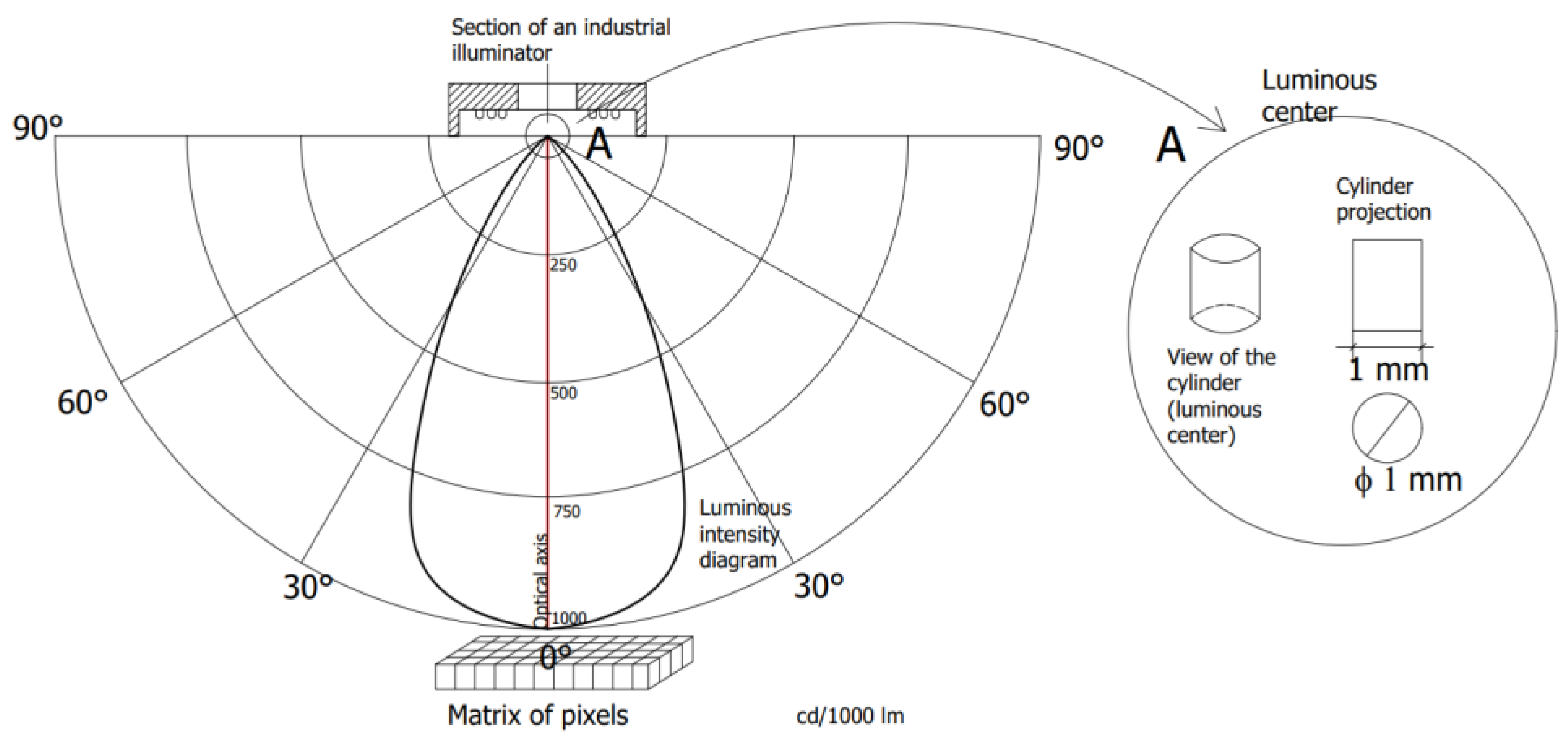
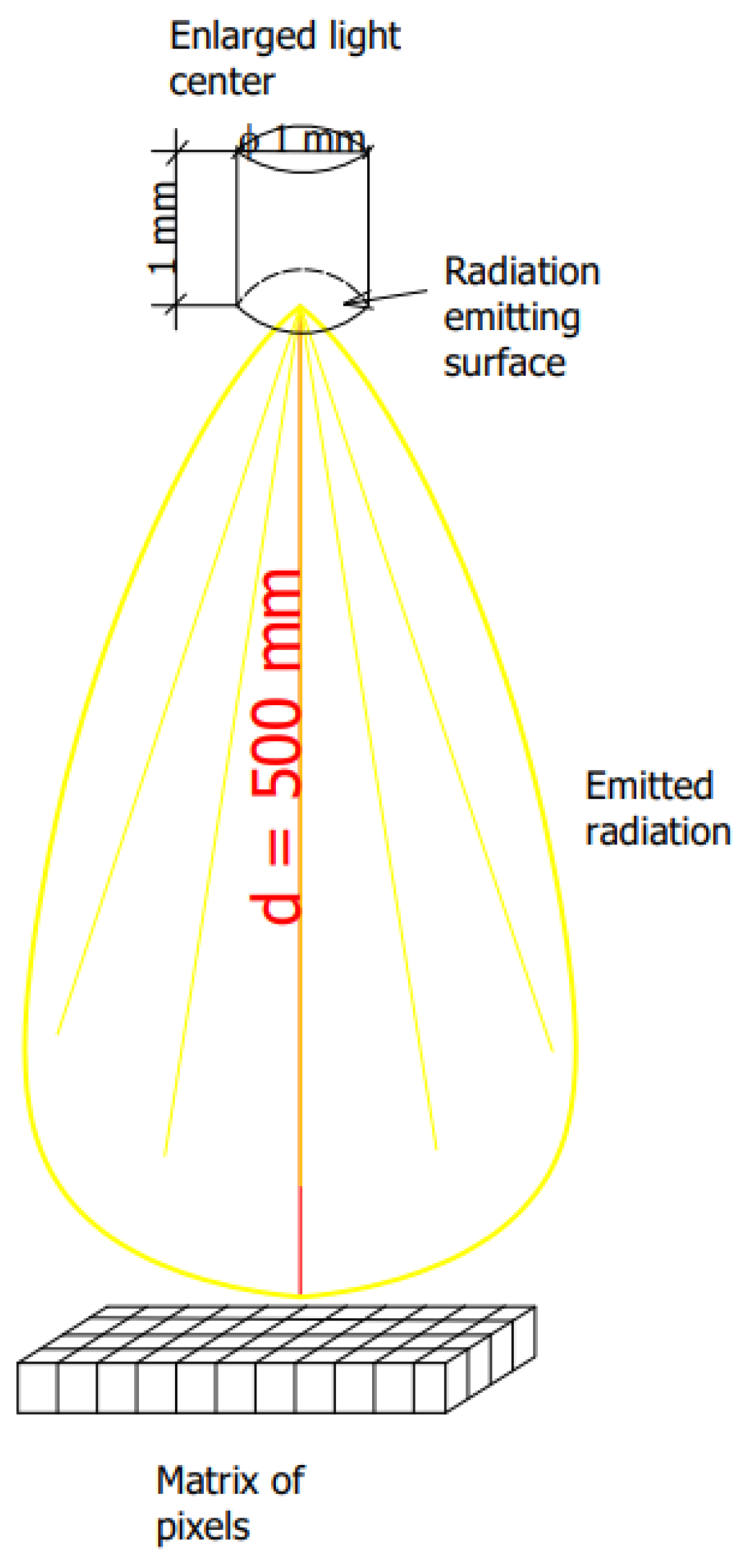
2.2. Simulation Test Method
3. Results
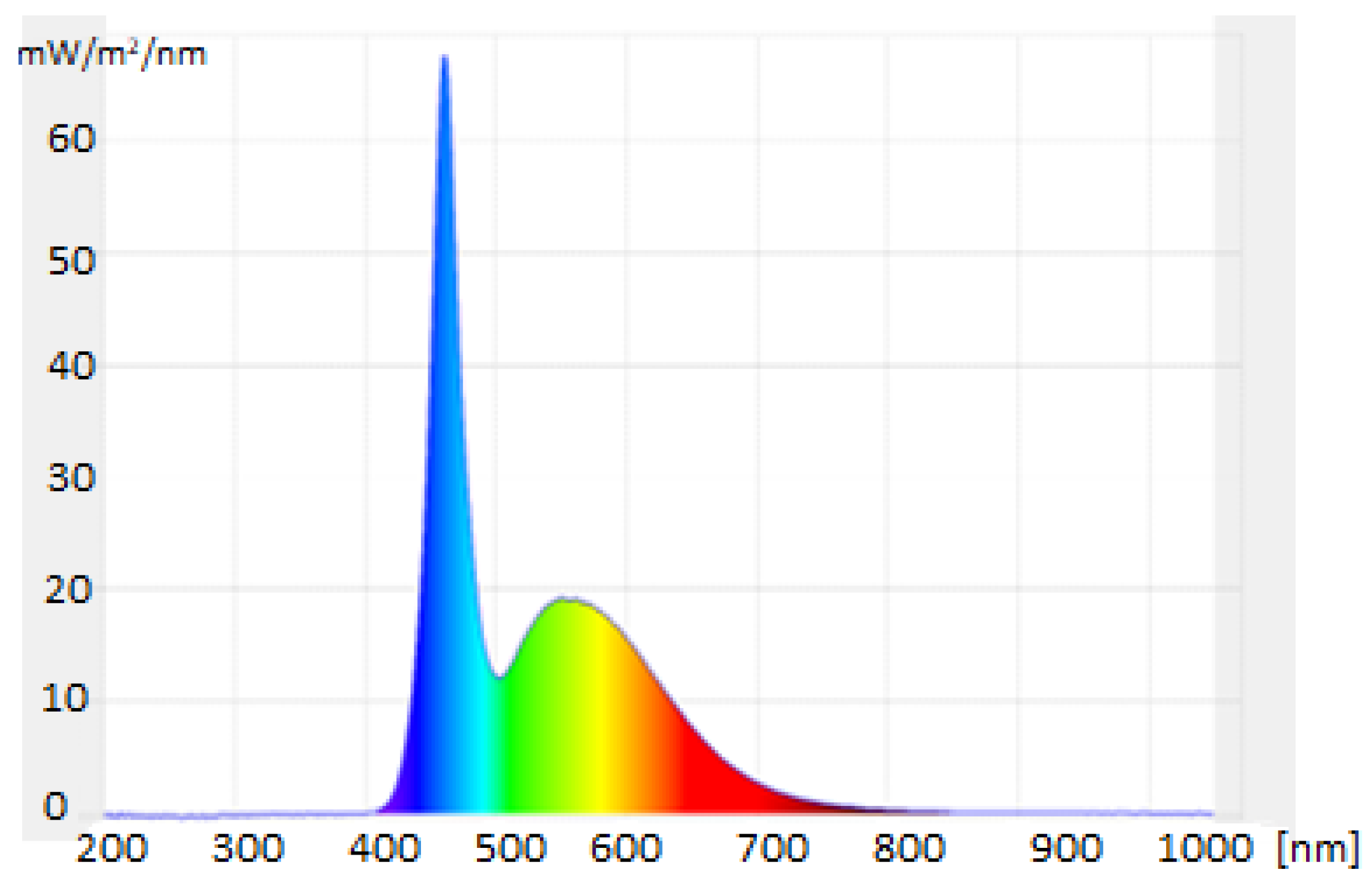
3.1. Experimental Results
3.2. Simulation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Duarte, B.; Feijão, E.; Goessling, J.W.; Caçador, I.; Matos, A.R. Pigment and Fatty Acid Production under Different Light Qualities in the Diatom Phaeodactylum Tricornutum. Appl. Sci. 2021, 11, 2550. [Google Scholar] [CrossRef]
- Song, P.; Wang, T.; Jiang, S.; Guo, C.; Wang, R.; Yang, L.; Zhou, Y.; Zheng, G. Freeform Illuminator for Computational Microscopy. Intell. Comput. 2023, 2, 0015. [Google Scholar] [CrossRef]
- Raggiunto, S.; Belli, A.; Lorenzo, P.; Piergiovanni, C.; Gattari, M.; Pierleoni, P. An Efficient Method for LED Light Sources Characterization. Electronics 2019, 8, 1089. [Google Scholar] [CrossRef]
- Zhao, F.; Van Derlofske, J.F. Side-Emitting Illuminators Using LED Sources. In Proceedings of the Design of Efficient Illumination Systems, San Diego, CA, USA, 10 November 2003; SPIE: New York, NY, USA, 2003; Volume 5186, p. 33. [Google Scholar]
- Grzybek, D.; Sioma, A. Creep Phenomenon in a Multiple-Input Single-Output Control System of a Piezoelectric Bimorph Actuator. Energies 2022, 15, 8267. [Google Scholar] [CrossRef]
- Sioma, A. 3D Imaging Methods in Quality Inspection Systems. In Proceedings of the Photonics Applications in Astronomy, Communications, Industry, and High-Energy Physics Experiments 2019, Wilga, Poland, 6 November 2019; SPIE: New York, NY, USA, 2019; p. 91. [Google Scholar]
- Struzikiewicz, G.; Sioma, A. Surface Topographic Features after Milling of Additively Manufactured AlSi10Mg Aluminum Alloy. Materials 2022, 15, 3604. [Google Scholar] [CrossRef] [PubMed]
- Dong, L.L.; Liu, P.; Lou, Q.; Xu, W.H. Study on the Influence of LED Spectrum on the Visual and Nonvisual Effects in the Interior Zone of Tunnels. J. Adv. Transp. 2021, 2021, 5339959. [Google Scholar] [CrossRef]
- Rammeloo, C.; Baumgartner, A. Spectroradiometer Calibration for Radiance Transfer Measurements. Sensors 2023, 23, 2339. [Google Scholar] [CrossRef] [PubMed]
- Sukhavasi, S.B.; Sukhavasi, S.B.; Elleithy, K.; Abuzneid, S.; Elleithy, A. Cmos Image Sensors in Surveillance System Applications. Sensors 2021, 21, 488. [Google Scholar] [CrossRef]
- Polatoğlu, A.; Özkesen, İ.C. Working Principles of CCD and CMOS Sensors and Their Place in Astronomy. Atatürk Univ. J. Anatol. Phys. Astron. 2022, 2, 51–59. [Google Scholar]
- Welden, R.; Jablonski, M.; Wege, C.; Keusgen, M.; Wagner, P.H.; Wagner, T.; Schöning, M.J. Light-Addressable Actuator-Sensor Platform for Monitoring and Manipulation of Ph Gradients in Microfluidics: A Case Study with the Enzyme Penicillinase. Biosensors 2021, 11, 171. [Google Scholar] [CrossRef]
- Legierski, M.; Michałek, P. Concept and Implementation of H-V Goniophotometer for Fast Measurement of Luminous Intensity Distribution in C-γ System. Prz. Elektrotechniczny 2020, 96, 75–78. [Google Scholar] [CrossRef]
- Voudoukis, N.; Oikonomidis, S. Inverse Square Law for Light and Radiation: A Unifying Educational Approach. Eur. J. Eng. Res. Sci. 2017, 2, 23. [Google Scholar] [CrossRef]
- ANSYS HELP. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v221/en/Optis_UG_ASP/Optis/UG_ASP/planar_illuminance_180509.html (accessed on 4 February 2023).
- ANSYS HELP. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v221/en/Optis_UG_ASP/Optis/UG_ASP/creating_an_irradiance_sensor_180507.html%23id_180507 (accessed on 4 February 2023).
- Pawlak, A.; Zaremba, K. A Monte-Carlo Simulation of an Indirect Lighting Installation Using Light Emitting Diodes (LEDs). Przegląd Elektrotechniczny 2013, 89, 215–217. [Google Scholar]
- Peterson, G.L. Stray Light Calculation Methods with Optical Ray Trace Software. In Proceedings of the Optical Design and Analysis Software, Denver, CO, USA, 27 September 1999; SPIE: New York, NY, USA, 1999; Volume 3780, pp. 132–137. [Google Scholar]
- Frasch, H.-J.J.; Steinmetz, G. Monte Carlo Methods in Ray-Tracing Software. In Proceedings of the Optical Design and Analysis Software II, Seattle, WA, USA, 5 September 2002; SPIE: New York, NY, USA, 2002; Volume 4769, p. 55. [Google Scholar]
- Freniere, E.R.; Gregory, G.G.; Hassler, R.A. Edge Diffraction in Monte Carlo Ray Tracing. In Proceedings of the Optical Design and Analysis Software, Denver, CO, USA, 27 September 1999; SPIE: New York, NY, USA, 1999; Volume 3780, pp. 151–157. [Google Scholar]


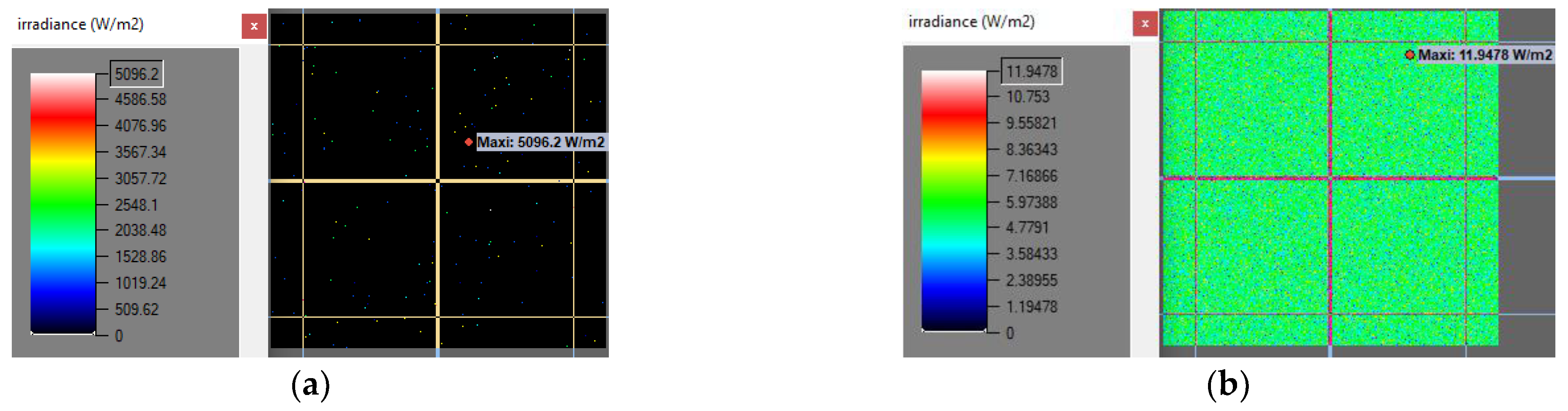
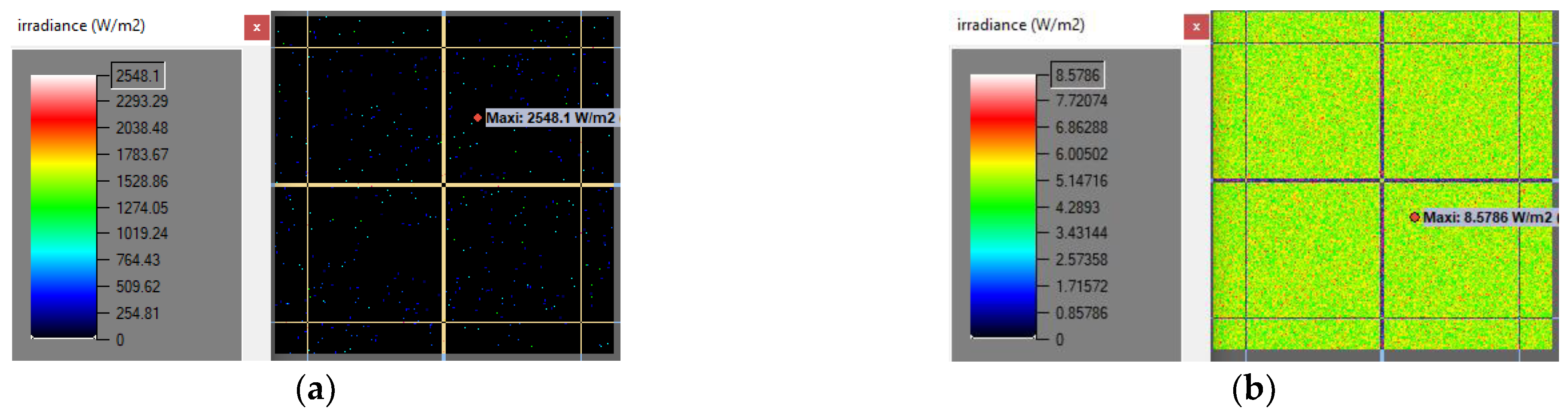
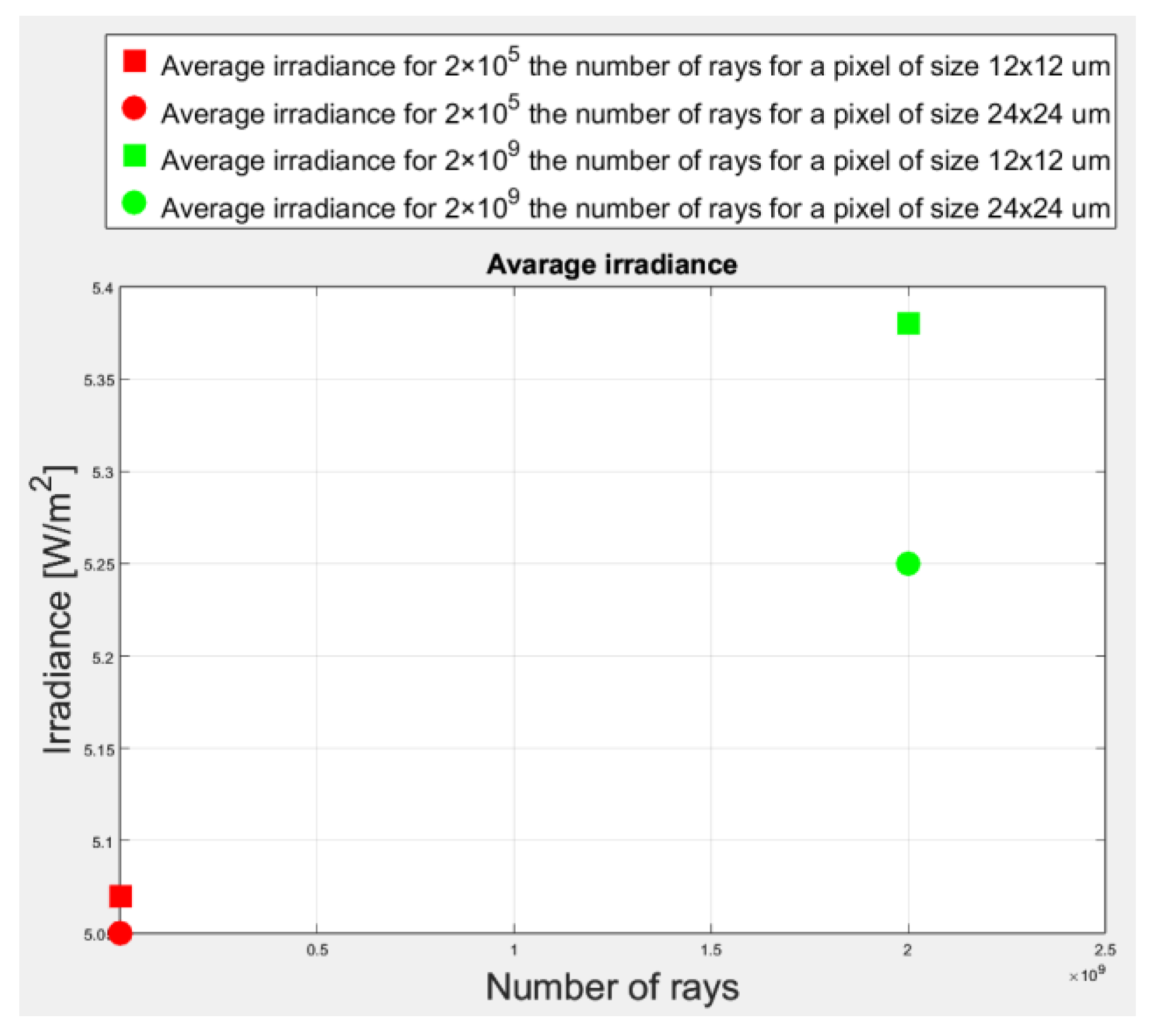
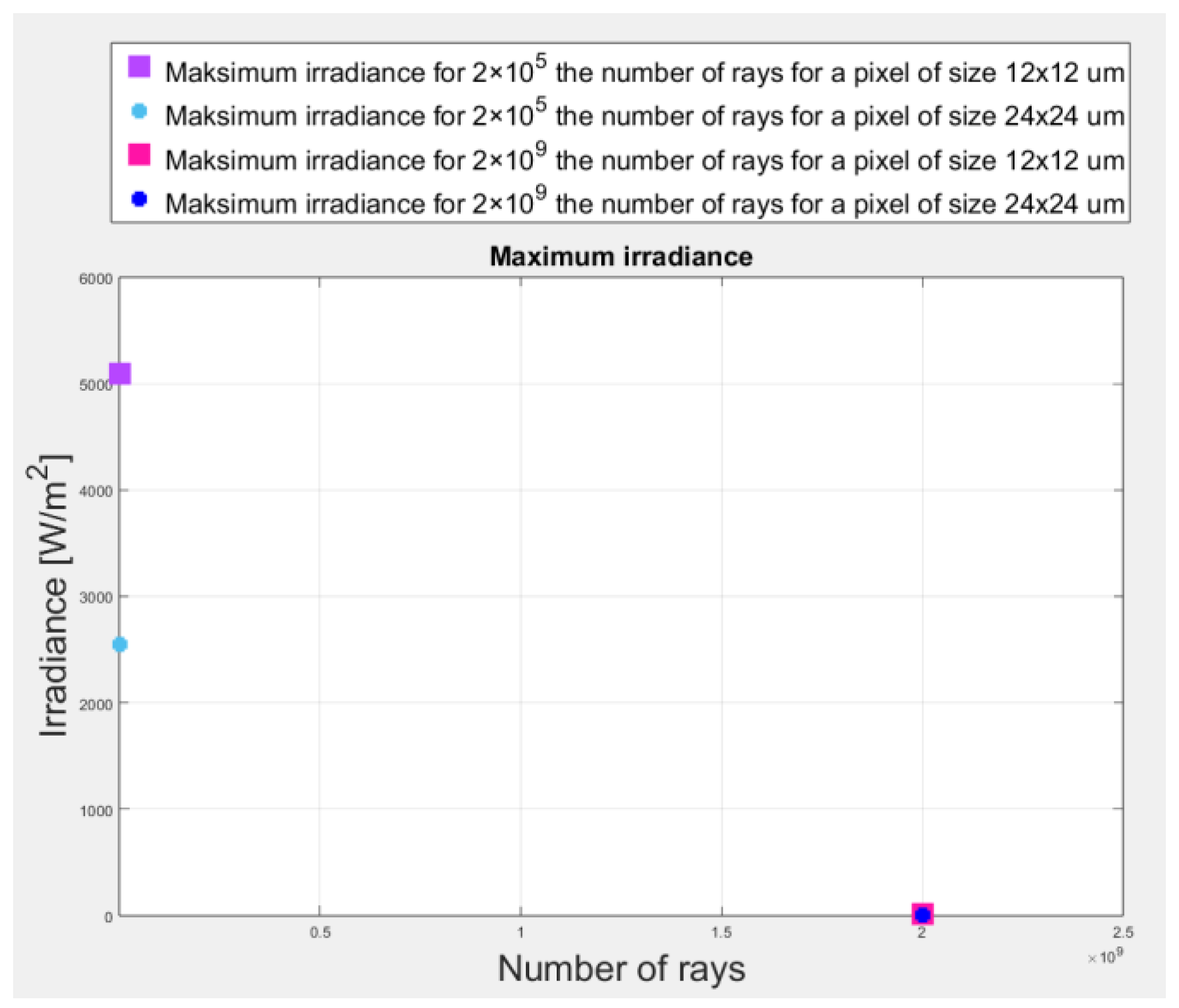
| Number of Rays | Value of Average Irradiance Recorded on the Sensor Matrix [W/m2] | The Value of the Maximum Irradiance Recorded on the Sensor Matrix [W/m2] |
|---|---|---|
| 5.07 | 5096.2 | |
| 5.38 | 11.95 |
| Number of Rays | Value of Average Irradiance Recorded on the Sensor Matrix [W/m2] | The Value of the Maximum Irradiance Recorded on the Sensor Matrix [W/m2] |
|---|---|---|
| 5.05 | 2548.1 | |
| 5.25 | 8.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waśniowska, J.; Sioma, A. Modelling the Interaction of Illuminations with a Sensor Matrix Used in Vision Systems. Appl. Sci. 2023, 13, 10641. https://doi.org/10.3390/app131910641
Waśniowska J, Sioma A. Modelling the Interaction of Illuminations with a Sensor Matrix Used in Vision Systems. Applied Sciences. 2023; 13(19):10641. https://doi.org/10.3390/app131910641
Chicago/Turabian StyleWaśniowska, Justyna, and Andrzej Sioma. 2023. "Modelling the Interaction of Illuminations with a Sensor Matrix Used in Vision Systems" Applied Sciences 13, no. 19: 10641. https://doi.org/10.3390/app131910641
APA StyleWaśniowska, J., & Sioma, A. (2023). Modelling the Interaction of Illuminations with a Sensor Matrix Used in Vision Systems. Applied Sciences, 13(19), 10641. https://doi.org/10.3390/app131910641






