Countermovement Rebound Jump: A Comparison of Joint Work and Joint Contribution to the Countermovement and Drop Jump Tests
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
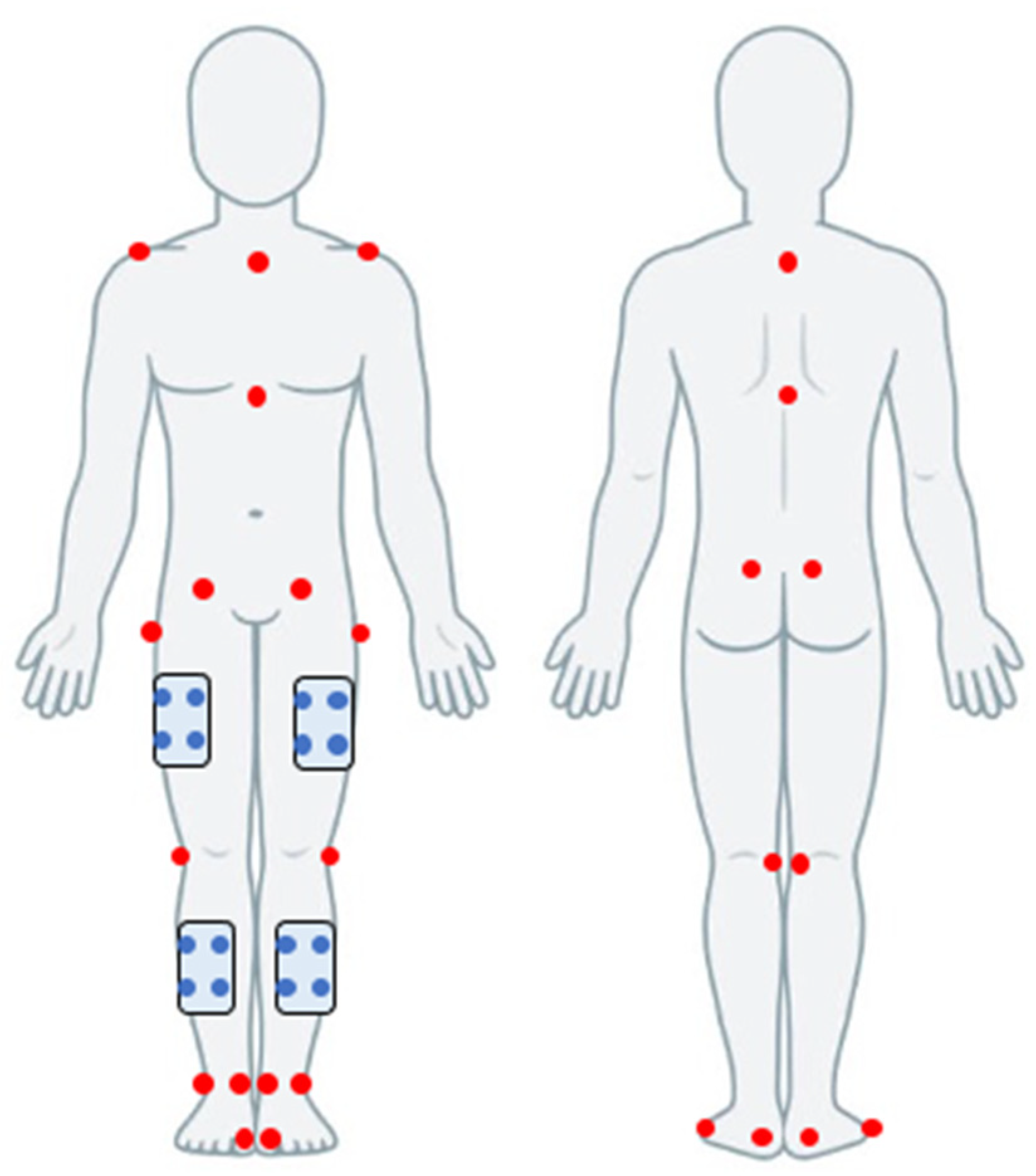
2.2. Procedures
2.3. Data Processing
2.4. Statistical Analysis
3. Results
3.1. Reliability
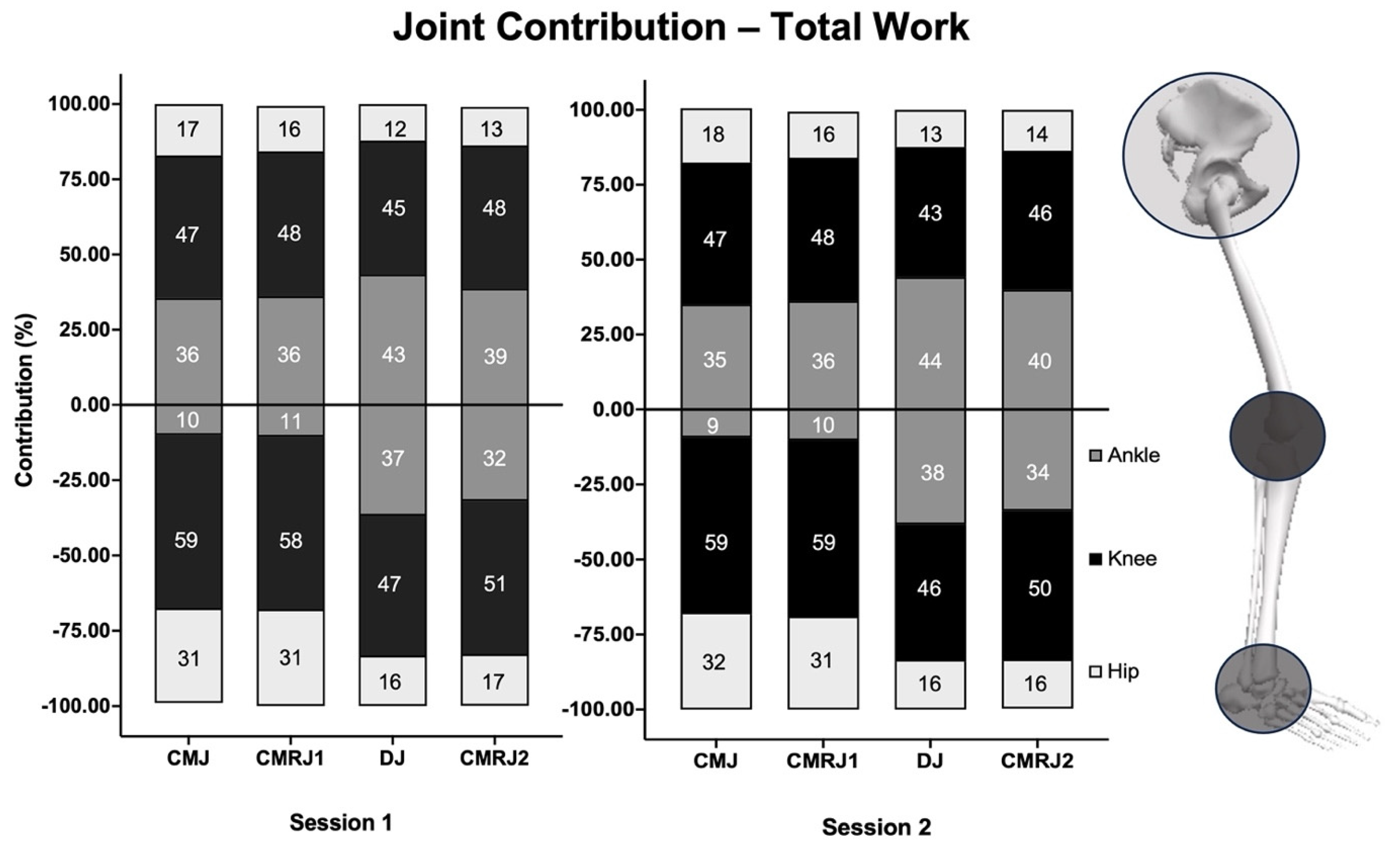
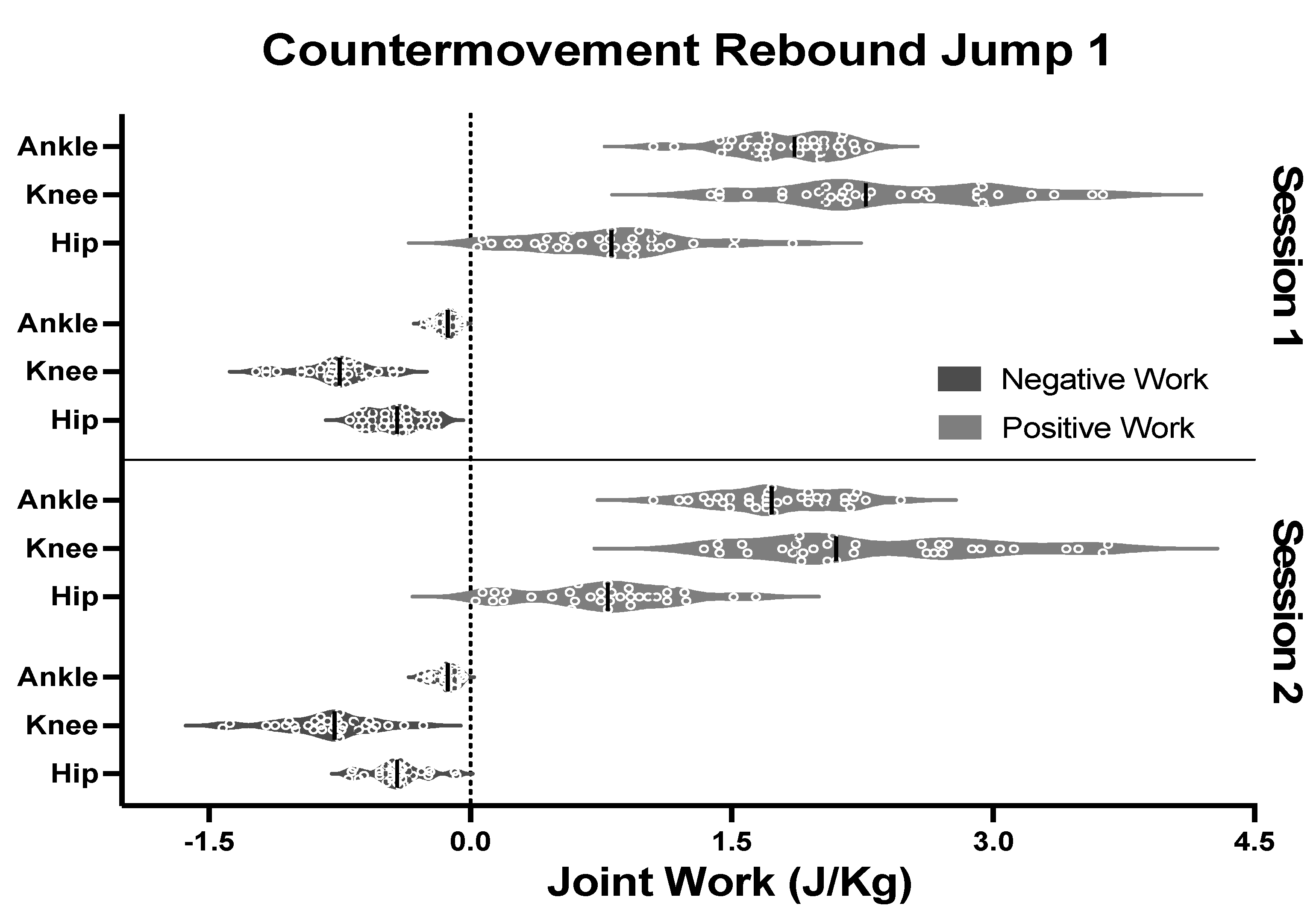
3.2. Comparison between Jump Tests
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bishop, C.; Turner, A.; Jordan, M.; Harry, J.; Loturco, I.; Lake, J.; Comfort, P. A Framework to Guide Practitioners for Selecting Metrics during the Countermovement and Drop Jump Tests. Strength Cond. J. 2021, 44, 95–103. [Google Scholar] [CrossRef]
- Chiu, L.Z.; Dæhlin, T.E. Comparing numerical methods to estimate vertical jump height using a force platform. Meas. Phys. Educ. Exerc. Sci. 2020, 24, 25–32. [Google Scholar] [CrossRef]
- Wade, L.; Lichtwark, G.A.; Farris, D.J. Comparisons of laboratory-based methods to calculate jump height and improvements to the field-based flight-time method. Scand. J. Med. Sci. Sports 2020, 30, 31–37. [Google Scholar] [CrossRef] [PubMed]
- Kipp, K.; Kiely, M.T.; Geiser, C.F. Reactive strength index modified is a valid measure of explosiveness in collegiate female volleyball players. J. Strength Cond. Res. 2016, 30, 1341–1347. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Turner, A.; Comfort, P.; Harry, J.R.; McMahon, J.J.; Chavda, S.; Bishop, C. A systematic review of the different calculation methods for measuring jump height during the countermovement and drop jump tests. Sports Med. 2023, 53, 1055–1072. [Google Scholar] [CrossRef]
- Tauchi, K.; Endo, T.; Ogata, M.; Matsuo, A.; Iso, S. The characteristics of jump ability in elite adolescent athletes and healthy males: The development of countermovement and rebound jump ability. Int. J. Sport Health Sci. 2008, 6, 78–84. [Google Scholar] [CrossRef]
- Bronze, S.H.; McMahon, J.J. Test-retest reliability of reactive strength index variants obtained from the countermovement-rebound jump. In Proceedings of the UK Strength and Conditioning Association (UKSCA) Annual Conference, 3 September 2020; Available online: https://www.uksca.org.uk/uksca-iq/article/weekly-theme-poster-week/2035/test-retest-reliability-of-reactive-strength-index-variants-obtained-from-the-countermovement-rebound-jump (accessed on 2 September 2023).
- Moir, G.L.; Garcia, A.; Dwyer, G.B. Intersession reliability of kinematic and kinetic variables during vertical jumps in men and women. Int. J. Sports Physiol. Perform. 2009, 4, 317–330. [Google Scholar] [CrossRef]
- Goldmann, J.; Braunstein, B.; Heinrich, K.; Sanno, M.; Stäudle, B.; Ritzdorf, W.; Brüggemann, G.; Albracht, K. Joint work of the take-off leg during elite high jump. In Proceedings of the 33 International Conference of Biomechanics in Sports, Poitiers, France, 29 June–3 July 2015. [Google Scholar]
- Harry, J.R.; Barker, L.A.; Paquette, M.R. Sex and acute weighted vest differences in force production and joint work during countermovement vertical jumping. J. Sports Sci. 2019, 37, 1318–1326. [Google Scholar] [CrossRef]
- Hubley, C.L.; Wells, R.P. A work-energy approach to determine individual joint contributions to vertical jump performance. Eur. J. Appl. Physiol. Occup. Physiol. 1983, 50, 247–254. [Google Scholar] [CrossRef]
- Lees, A.; Vanrenterghem, J.; De Clercq, D. The maximal and submaximal vertical jump: Implications for strength and conditioning. J. Strength Cond. Res. 2004, 18, 787–791. [Google Scholar] [CrossRef]
- Bobbert, M.F.; Huijing, P.A.; van Ingen Schenau, G.J. Drop jumping. I. The influence of jumping technique on the biomechanics of jumping. Med. Sci. Sports Exerc. 1987, 19, 332–338. [Google Scholar] [CrossRef]
- Bobbert, M.F.; Mackay, M.; Schinkelshoek, D.; Huijing, P.A.; van Ingen Schenau, G.J. Biomechanical analysis of drop and countermovement jumps. Eur. J. Appl. Physiol. Occup. Physiol. 1986, 54, 566–573. [Google Scholar] [CrossRef]
- Holcomb, W.R.; Lander, J.E.; Rutland, R.M.; Wilson, G.D. A biomechanical analysis of the vertical jump and three modified plyometric depth jumps. J. Strength Cond. Res. 1996, 10, 83–88. [Google Scholar]
- Decker, A.J.; McCaw, S.T. Target heights alter the energetics of drop jumps when drop height is held constant. J. Strength Cond. Res. 2012, 26, 3237–3242. [Google Scholar] [CrossRef]
- Yoshida, T.; Kariyama, Y.; Hayashi, R.; Takahashi, K.; Zushi, A.; Zushi, K. Development of multistep drop jump test by using different drop heights. In Proceedings of the 33 International Conference of Biomechanics in Sports, Poitiers, France, 29 June–3 July 2015. [Google Scholar]
- Kariyama, Y.; Fujii, H.; Mori, K.; Zushi, K. The comparison to the characteristics of three-dimensional joint kinetics between single leg and double leg rebound jump. In Proceedings of the 30 International Conference on Biomechanics in Sports, Melbourne, Australia, 2–6 July 2012. [Google Scholar]
- International Committee of Medical Journal Editors. Uniform requirements for manuscripts submitted to biomedical journals. Pathology 1997, 29, 441–447. [Google Scholar]
- Bishop, C.; Jarvis, P.; Turner, A.; Balsalobre-Fernandez, C. Validity and Reliability of Strategy Metrics to Assess Countermovement Jump Performance using the Newly Developed My Jump Lab Smartphone Application. J. Hum. Kinet. 2022, 83, 185–195. [Google Scholar] [CrossRef]
- Barker, L.A.; Harry, J.R.; Mercer, J.A. Relationships between countermovement jump ground reaction forces and jump height, reactive strength index, and jump time. J. Strength Cond. Res. 2018, 32, 248–254. [Google Scholar] [CrossRef]
- Comyns, T.M.; Brady, C.J.; Molloy, J. Effect of attentional focus strategies on the biomechanical performance of the drop jump. J. Strength Cond. Res. 2019, 33, 626–632. [Google Scholar] [CrossRef]
- McBride, J.M.; Nimphius, S. Biological system energy algorithm reflected in sub-system joint work distribution movement strategies: Influence of strength and eccentric loading. Sci. Rep. 2020, 10, 12052. [Google Scholar] [CrossRef]
- McMahon, J.J.; Lake, J.P.; Stratford, C.; Comfort, P. A proposed method for evaluating drop jump performance with one force platform. Biomechanics 2021, 1, 178–189. [Google Scholar] [CrossRef]
- Baca, A. A comparison of methods for analyzing drop jump performance. Med. Sci. Sports Exerc. 1999, 31, 437–442. [Google Scholar] [CrossRef]
- McMahon, J.J.; Suchomel, T.J.; Lake, J.P.; Comfort, P. Understanding the key phases of the countermovement jump force-time curve. Strength Cond. J. 2018, 40, 96–106. [Google Scholar] [CrossRef]
- Chavda, S.; Bromley, T.; Jarvis, P.; Williams, S.; Bishop, C.; Turner, A.N.; Lake, J.P.; Mundy, P.D. Force-time characteristics of the countermovement jump: Analyzing the curve in Excel. Strength Cond. J. 2018, 40, 67–77. [Google Scholar] [CrossRef]
- Vanezis, A.; Lees, A. A biomechanical analysis of good and poor performers of the vertical jump. Ergonomics 2005, 48, 1594–1603. [Google Scholar] [CrossRef]
- Weir, J.P. Quantifying test-retest reliability using the intraclass correlation coefficient and the SEM. J. Strength Cond. Res. 2005, 19, 231–240. [Google Scholar]
- Koo, T.K.; Li, M.Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef]
- Duthie, G.; Pyne, D.; Hooper, S. The reliability of video based time motion analysis. J. Hum. Mov. Stud. 2003, 44, 259–272. [Google Scholar]
- Thomas, C.; Dos’ Santos, T.; Comfort, P.; Jones, P.A. Between-Session Reliability of Common Strength-and Power-Related Measures in Adolescent Athletes. Sports 2017, 5, 15. [Google Scholar] [CrossRef]
- Rhea, M.R. Determining the magnitude of treatment effects in strength training research through the use of the effect size. J. Strength Cond. Res. 2004, 18, 918–920. [Google Scholar]
- Dufek, J.S.; Bates, B.T. Biomechanical factors associated with injury during landing in jump sports. Sports Med. 1991, 12, 326–337. [Google Scholar] [CrossRef]
- Rauch, J.; Leidersdorf, E.; Reeves, T.; Borkan, L.; Elliott, M.; Ugrinowitsch, C. Different movement strategies in the countermovement jump amongst a large cohort of NBA players. Int. J. Environ. Res. Public Health 2020, 17, 6394. [Google Scholar] [CrossRef]
- Raffalt, P.C.; Alkjær, T.; Simonsen, E.B. Joint dynamics and intra-subject variability during countermovement jumps in children and adults. J. Biomech. 2016, 49, 2968–2974. [Google Scholar] [CrossRef] [PubMed]
- Lees, A.; Vanrenterghem, J.; Clercq, D.D. Understanding how an arm swing enhances performance in the vertical jump. J. Biomech. 2004, 37, 1929–1940. [Google Scholar] [CrossRef] [PubMed]
- Moran, K.A.; Wallace, E.S. Eccentric loading and range of knee joint motion effects on performance enhancement in vertical jumping. Hum. Mov. Sci. 2007, 26, 824–840. [Google Scholar] [CrossRef] [PubMed]
- Zushi, A.; Yoshida, T.; Zushi, K.; Kariyama, Y.; Ogata, M. Characteristics of three lower limb joint kinetics affecting rebound jump performance. PLoS ONE 2022, 17, e0268339. [Google Scholar] [CrossRef] [PubMed]



| Test | Joint | Variables | Test Session 1 | Test Session 2 | Between-Session | |||
|---|---|---|---|---|---|---|---|---|
| Mean ± SD | Mean ± SD | Hedges’ g (95% CI) | Descriptor | ICC (95% CI) | CV (95% CI) | |||
| CMJ | CM Depth | 0.29 ± 0.05 | 0.29 ± 0.06 | −0.06 (−0.28, 0.16) | Trivial | 0.89 (0.78, 0.95) | 7.20 (5.38, 9.02) | |
| TTTO | 0.74 ± 0.10 * | 0.74 ± 0.13 * | 0.00 (−0.27, 0.27) | Trivial | 0.82 (0.64, 0.91) | 6.34 (4.74, 7.95) | ||
| Jump Height | 0.31 ± 0.08 | 0.32 ± 0.08 | −0.05 (−0.16, 0.06) | Trivial | 0.98 (0.95, 0.99) | 4.19 (3.13, 5.24) | ||
| Hip | Negative Work | −0.51 ± 0.21 a | −0.52 ± 0.17 a | 0.06 (−0.43, 0.55) | Trivial | 0.78 (0.55, 0.89) | 15.35 (11.64, 19.05) | |
| Positive Work | 0.93 ± 0.47 b | 0.99 ± 0.43 b | −0.14 (−0.63, 0.36) | Trivial | 0.81 (0.61, 0.91) | 20.95 (15.90, 26.00) | ||
| Knee | Negative Work | −0.91 ± 0.27 c | −0.99 ± 0.32 c | 0.25 (−0.25, 0.74) | Small | 0.89 (0.76, 0.95) | 8.83 (6.70, 10.96) | |
| Positive Work | 2.51 ± 0.62 | 2.57 ± 0.72 | −0.09 (−0.58, 0.40) | Trivial | 0.88 (0.76, 0.94) | 8.50 (6.45, 10.55) | ||
| Ankle | Negative Work | −0.16 ± 0.06 | −0.15 ± 0.07 | −0.08 (−0.57, 0.42) | Trivial | 0.89 (0.78, 0.95) | 15.35 (11.64, 19.05) | |
| Positive Work | 1.86 ± 0.29 | 1.85 ± 0.35 | 0.04 (−0.46, 0.53) | Trivial | 0.86 (0.71, 0.93) | 5.84 (4.43, 7.25) | ||
| Hip | Negative Contribution | 30.87 ± 10.75 | 31.76 ± 10.25 | −0.08 (−0.58, 0.41) | Trivial | 0.87 (0.74, 0.94) | 13.03 (9.89, 16.17) | |
| Positive Contribution | 17.04 ± 7.45 | 18.12 ± 7.15 | −0.15 (−0.64, 0.35) | Trivial | 0.76 (0.52, 0.88) | 19.29 (14.64, 23.94) | ||
| Knee | Negative Contribution | 58.02 ± 10.25 | 58.87 ± 9.98 | −0.08 (−0.58, 0.41) | Trivial | 0.85 (0.70, 0.93) | 6.74 (5.11, 8.36) | |
| Positive Contribution | 47.41 ± 7.21 | 47.29 ± 8.04 | 0.02 (−0.48, 0.51) | Trivial | 0.75 (0.50, 0.88) | 5.59 (4.24, 6.93) | ||
| Ankle | Negative Contribution | 10.08 ± 3.91 | 9.36 ± 3.87 | 0.18 (−0.31, 0.68) | Trivial | 0.87 (0.73, 0.93) | 15.57 (11.81, 19.33) | |
| Positive Contribution | 35.54 ± 4.18 | 35.12 ± 4.59 | −0.15 (−0.64, 0.35) | Trivial | 0.73 (0.44, 0.86) | 3.89 (2.95, 4.82) | ||
| CMRJ1 | CM Depth | 0.27 ± 0.05 | 0.27 ± 0.06 | 0.05 (−0.15, 0.26) | Trivial | 0.91 (0.81, 0.95) | 7.01 (5.24, 8.78) | |
| TTTO | 0.67 ± 0.11 * | 0.68 ± 0.13 * | −0.02 (−0.31, 0.27) | Trivial | 0.80 (0.59, 0.90) | 8.64 (6.45, 10.83) | ||
| Jump Height | 0.30 ± 0.07 | 0.29 ± 0.07 | 0.07 (−0.05, 0.20) | Trivial | 0.97 (0.93, 0.98) | 4.86 (3.63, 6.09) | ||
| Hip | Negative Work | −0.43 ± 0.15 a | −0.42 ± 0.15 a | −0.05 (−0.54, 0.44) | Trivial | 0.74 (0.46, 0.87) | 17.63 (13.38, 21.88) | |
| Positive Work | 0.78 ± 0.42 b | 0.76 ± 0.41 b | 0.06 (−0.44, 0.55) | Trivial | 0.90 (0.79, 0.95) | 16.69 (12.59, 20.59) | ||
| Knee | Negative Work | −0.77 ± 0.20 c | −0.81 ± 0.25 c | 0.17 (−0.32, 0.66) | trivial | 0.91 (0.82, 0.96) | 8.65 (6.56, 10.73) | |
| Positive Work | 2.41 ± 0.61 | 2.33 ± 0.68 | 0.12 (−0.37, 0.62) | Trivial | 0.90 (0.79, 0.95) | 7.92 (6.01, 9.59) | ||
| Ankle | Negative Work | −0.14 ± 0.06 | −0.14 ± 0.07 | 0.00 (−0.49, 0.49) | Trivial | 0.87 (0.73, 0.93) | 15.58 (11.82, 19.34) | |
| Positive Work | 1.81 ± 0.30 | 1.77 ± 0.34 | 0.13 (−0.37, 0.62) | Trivial | 0.93 (0.85, 0.96) | 5.26 (3.99, 6.53) | ||
| Hip | Negative Contribution | 31.52 ± 9.21 | 30.42 ± 9.96 | 0.11 (−0.38, 0.60) | Trivial | 0.86 (0.71, 0.93) | 11.64 (8.83, 15.45) | |
| Positive Contribution | 15.15 ± 7.48 | 15.35 ± 7.86 | −0.03 (−0.52, 0.47) | Trivial | 0.87 (0.73, 0.93) | 13.29 (10.08, 16.49) | ||
| Knee | Negative Contribution | 57.85 ± 9.41 | 59.23 ± 9.76 | −0.14 (−0.63, 0.35) | Trivial | 0.87 (0.74, 0.94) | 5.00 (3.80, 6.21) | |
| Positive Contribution | 48.14 ± 7.44 | 47.84 ± 8.03 | 0.04 (−0.45, 0.53) | Trivial | 0.85 (0.70, 0.93) | 3.86 (2.93, 4.79) | ||
| Ankle | Negative Contribution | 10.63 ± 3.68 | 10.35 ± 3.85 | 0.07 (−0.42, 0.57) | Trivial | 0.87 (0.73, 0.93) | 14.43 (10.95, 17.91) | |
| Positive Contribution | 36.13 ± 5.04 | 36.24 ± 5.07 | −0.02 (−0.51, 0.47) | Trivial | 0.88 (0.75, 0.94) | 3.75 (2.84, 4.65) | ||
| DJ | GCT | 0.32 ± 0.11 | 0.32 ± 0.11 | 0.05 (−0.07, 0.17) | Trivial | 0.97 (0.94, 0.99) | 5.91 (4.42, 7.41) | |
| Jump Height | 0.28 ± 0.07 | 0.27 ± 0.07 | 0.03 (−0.13, 0.19) | Trivial | 0.95 (0.89, 0.97) | 5.97 (4.46, 7.47) | ||
| Hip | Negative Work | −0.67 ± 0.28 | −0.66 ± 0.32 | −0.05 (−0.54, 0.44) | Trivial | 0.73 (0.44, 0.87) | 20.01 (15.18, 24.83) | |
| Positive Work | 0.61 ± 0.50 | 0.60 ± 0.42 | 0.03 (−0.46, 0.52) | Trivial | 0.88 (0.76, 0.94) | 25.04 (19.00, 31.09) | ||
| Knee | Negative Work | −1.97 ± 0.64 d | −1.87 ± 0.74 d | −0.14 (−0.63, 0.35) | Trivial | 0.95 (0.89, 0.97) | 9.35 (7.86, 11.85) | |
| Positive Work | 2.06 ± 0.60 e | 2.02 ± 0.72 e | 0.06 (−0.43, 0.55) | Trivial | 0.91 (0.82, 0.96) | 9.91 (7.52, 12.30) | ||
| Ankle | Negative Work | −1.47 ± 0.41 | −1.50 ± 0.52 | 0.06 (−0.43, 0.55) | Trivial | 0.93 (0.85, 0.96) | 8.46 (6.42, 10.50) | |
| Positive Work | 1.93 ± 0.29 | 1.92 ± 0.33 | 0.02 (−0.47, 0.51) | Trivial | 0.88 (0.75, 0.94) | 5.81 (4.41, 7.21) | ||
| Hip | Negative Contribution | 16.17 ± 5.57 | 16.01 ± 6.27 | 0.03 (−0.47, 0.52) | Trivial | 0.75 (0.49, 0.88) | 17.80 (13.50, 22.09) | |
| Positive Contribution | 12.14 ± 8.00 | 12.43 ± 7.77 | −0.04 (−0.53, 0.46) | Trivial | 0.88 (0.75, 0.94) | 21.99 (16.69, 27.30) | ||
| Knee | Negative Contribution | 47.01 ± 10.92 | 45.66 ± 13.38 | 0.11 (−0.38, 0.60) | Trivial | 0.93 (0.85, 0.96) | 8.64 (6.55, 10.72) | |
| Positive Contribution | 44.46 ± 7.22 | 43.34 ± 8.74 | 0.14 (−0.35, 0.63) | Trivial | 0.85 (0.70, 0.93) | 6.76 (5.13, 8.39) | ||
| Ankle | Negative Contribution | 36.82 ± 12.50 | 38.33 ± 15.07 | −0.11 (−0.60, 0.38) | Trivial | 0.93 (0.86, 0.97) | 8.96 (6.80, 11.12) | |
| Positive Contribution | 43.40 ± 8.70 f | 44.24 ± 10.42 f | −0.09 (−0.58, 0.41) | Trivial | 0.82 (0.63, 0.91) | 5.56 (4.22, 6.95) | ||
| CMRJ2 | GCT | 0.35 ± 0.12 | 0.34 ± 0.11 | 0.04 (−0.12, 0.20) | Trivial | 0.94 (0.89, 0.97) | 8.13 (6.07, 10.19) | |
| Jump Height | 0.28 ± 0.07 | 0.28 ± 0.07 | −0.02 (−0.20, 0.16) | Trivial | 0.93 (0.87, 0.97) | 6.08 (4.54, 7.62) | ||
| Hip | Negative Work | −0.82 ± 0.33 | −0.76 ± 0.44 | −0.14 (−0.64, 0.35) | Trivial | 0.64 (0.28, 0.82) | 18.94 (14.37, 23.51) | |
| Positive Work | 0.70 ± 0.52 | 0.71 ± 0.46 | −0.01 (−0.50, 0.49) | Trivial | 0.89 (0.77, 0.94) | 21.49 (16.31, 26.68) | ||
| Knee | Negative Work | −2.51 ± 0.84 d | −2.41 ± 0.84 d | −0.12 (−0.61, 0.38) | Trivial | 0.90 (0.86, 0.94) | 9.74 (7.91, 11.58) | |
| Positive Work | 2.41 ± 0.67 e | 2.30 ± 0.68 e | 0.16 (−0.33, 0.65) | Trivial | 0.91 (0.87, 0.97) | 9.22 (7.03, 11.50) | ||
| Ankle | Negative Work | −1.47 ± 0.46 | −1.54 ± 0.52 | 0.15 (−0.35, 0.64) | Trivial | 0.82 (0.63, 0.91) | 9.03 (6.85, 11.21) | |
| Positive Work | 1.90 ± 0.31 | 1.90 ± 0.34 | 0.00 (−0.49, 0.49) | Trivial | 0.90 (0.88, 0.96) | 6.18 (4.69, 7.67) | ||
| Hip | Negative Contribution | 16.54 ± 5.72 | 15.81 ± 7.27 | 0.11 (−0.38, 0.60) | Trivial | 0.85 (0.72, 0.94) | 17.24 (13.08, 21.40) | |
| Positive Contribution | 12.77 ± 8.13 | 13.65 ± 8.45 | −0.11 (−0.60, 0.39) | Trivial | 0.89 (0.77, 0.94) | 24.11 (18.30, 29.93) | ||
| Knee | Negative Contribution | 51.49 ± 11.70 | 50.07 ± 11.81 | 0.12 (−0.37, 0.61) | Trivial | 0.82 (0.63, 0.91) | 6.35 (4.82, 7.89) | |
| Positive Contribution | 47.58 ± 7.96 | 46.33 ± 7.58 | 0.16 (−0.33, 0.65) | Trivial | 0.86 (0.72, 0.93) | 5.51 (4.18, 6.84) | ||
| Ankle | Negative Contribution | 31.91 ± 12.15 | 33.82 ± 13.44 | −0.15 (−0.64, 0.35) | Trivial | 0.85 (0.69, 0.92) | 7.23 (5.49, 8.97) | |
| Positive Contribution | 38.70 ± 8.92 f | 40.02 ± 9.01 f | −0.15 (−0.64, 0.35) | Trivial | 0.83 (0.66, 0.92) | 8.82 (6.69, 10.95) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Turner, A.; Comyns, T.M.; Harry, J.R.; Chavda, S.; Bishop, C. Countermovement Rebound Jump: A Comparison of Joint Work and Joint Contribution to the Countermovement and Drop Jump Tests. Appl. Sci. 2023, 13, 10680. https://doi.org/10.3390/app131910680
Xu J, Turner A, Comyns TM, Harry JR, Chavda S, Bishop C. Countermovement Rebound Jump: A Comparison of Joint Work and Joint Contribution to the Countermovement and Drop Jump Tests. Applied Sciences. 2023; 13(19):10680. https://doi.org/10.3390/app131910680
Chicago/Turabian StyleXu, Jiaqing, Anthony Turner, Thomas M. Comyns, John R. Harry, Shyam Chavda, and Chris Bishop. 2023. "Countermovement Rebound Jump: A Comparison of Joint Work and Joint Contribution to the Countermovement and Drop Jump Tests" Applied Sciences 13, no. 19: 10680. https://doi.org/10.3390/app131910680
APA StyleXu, J., Turner, A., Comyns, T. M., Harry, J. R., Chavda, S., & Bishop, C. (2023). Countermovement Rebound Jump: A Comparison of Joint Work and Joint Contribution to the Countermovement and Drop Jump Tests. Applied Sciences, 13(19), 10680. https://doi.org/10.3390/app131910680










