A Spatial Registration Method for Multi-UAVs Based on a Cooperative Platform in a Geodesic Coordinate Information-Free Environment
Abstract
:1. Introduction
2. Problem Description
3. Target Tracking Method
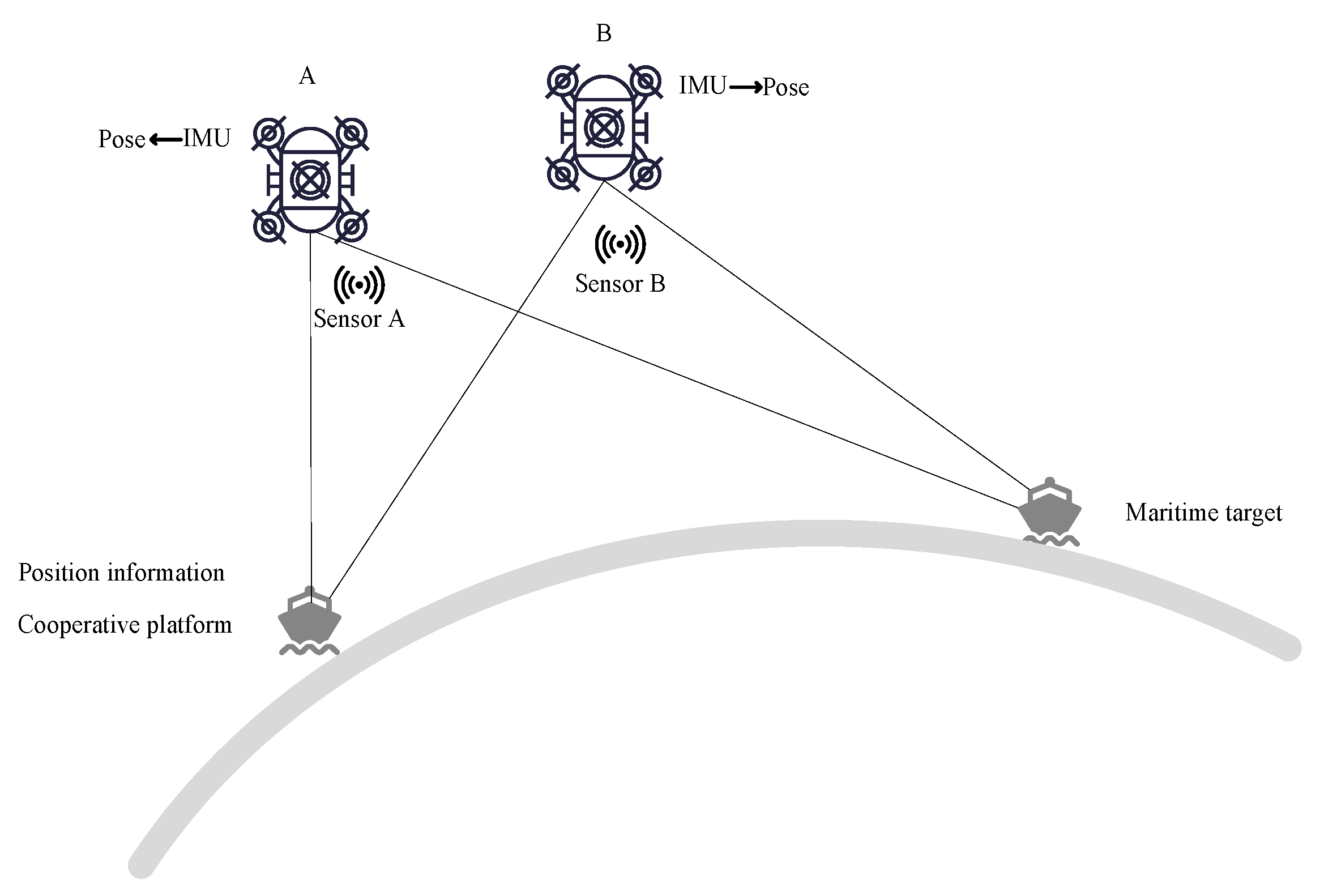
3.1. Mutual Observation Information Based on a Cooperative Platform
3.1.1. Mutual Observation Information
3.1.2. Error Analysis
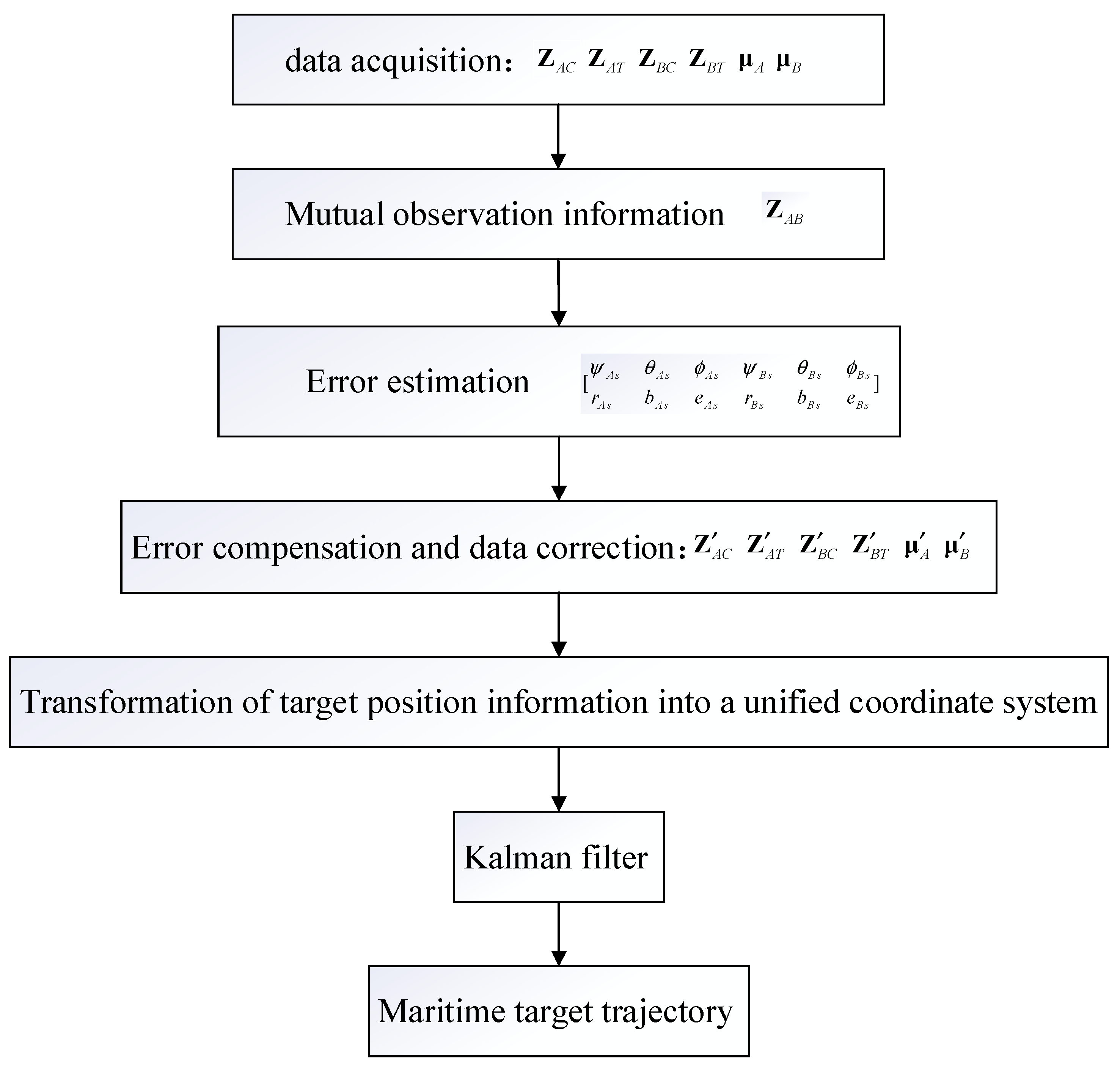
3.2. The Spatial Registration Method
3.2.1. Indirect Observation Information of the Target Based on Mutual Observation
3.2.2. Spatial Registration Based on the Right-Angle Translation Method
3.3. Maritime Target Tracking Method
4. Experimental Verification
4.1. Simulation Experiment
4.1.1. Experimental Parameter Setting
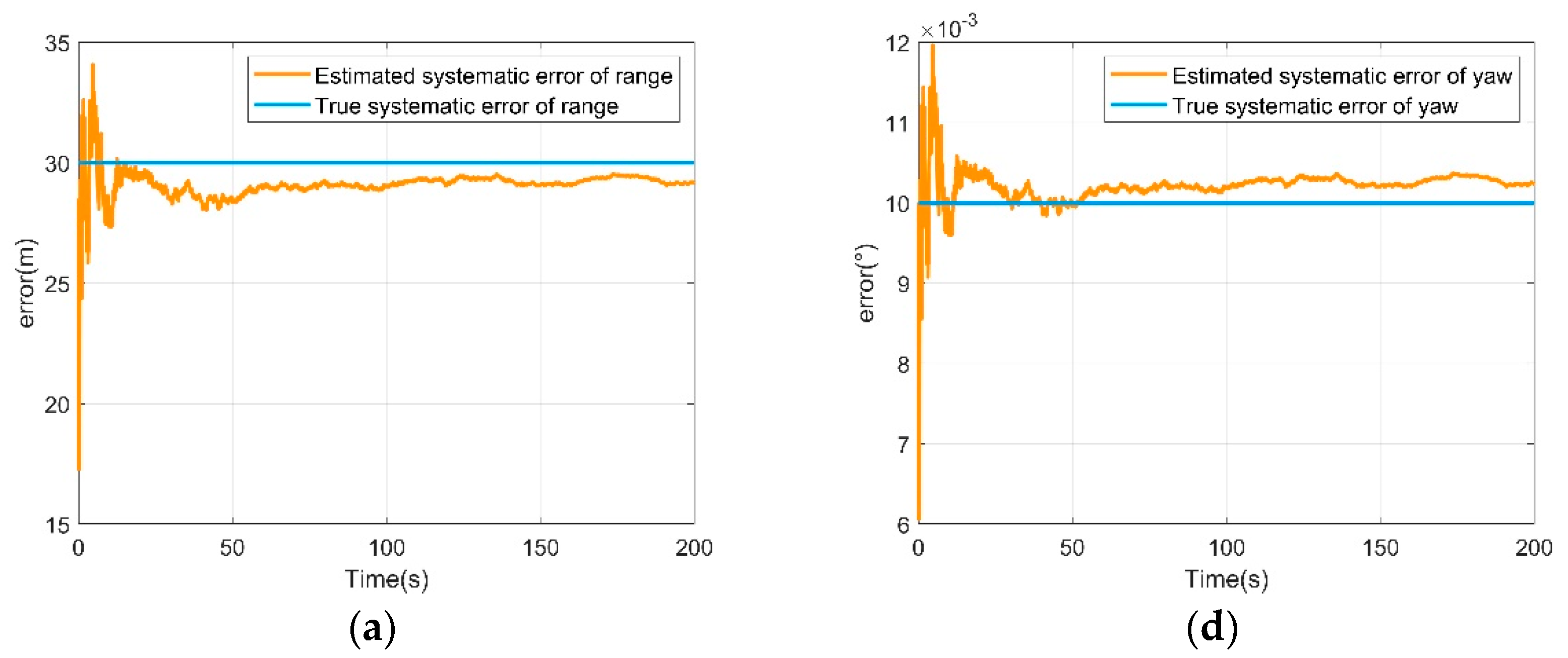
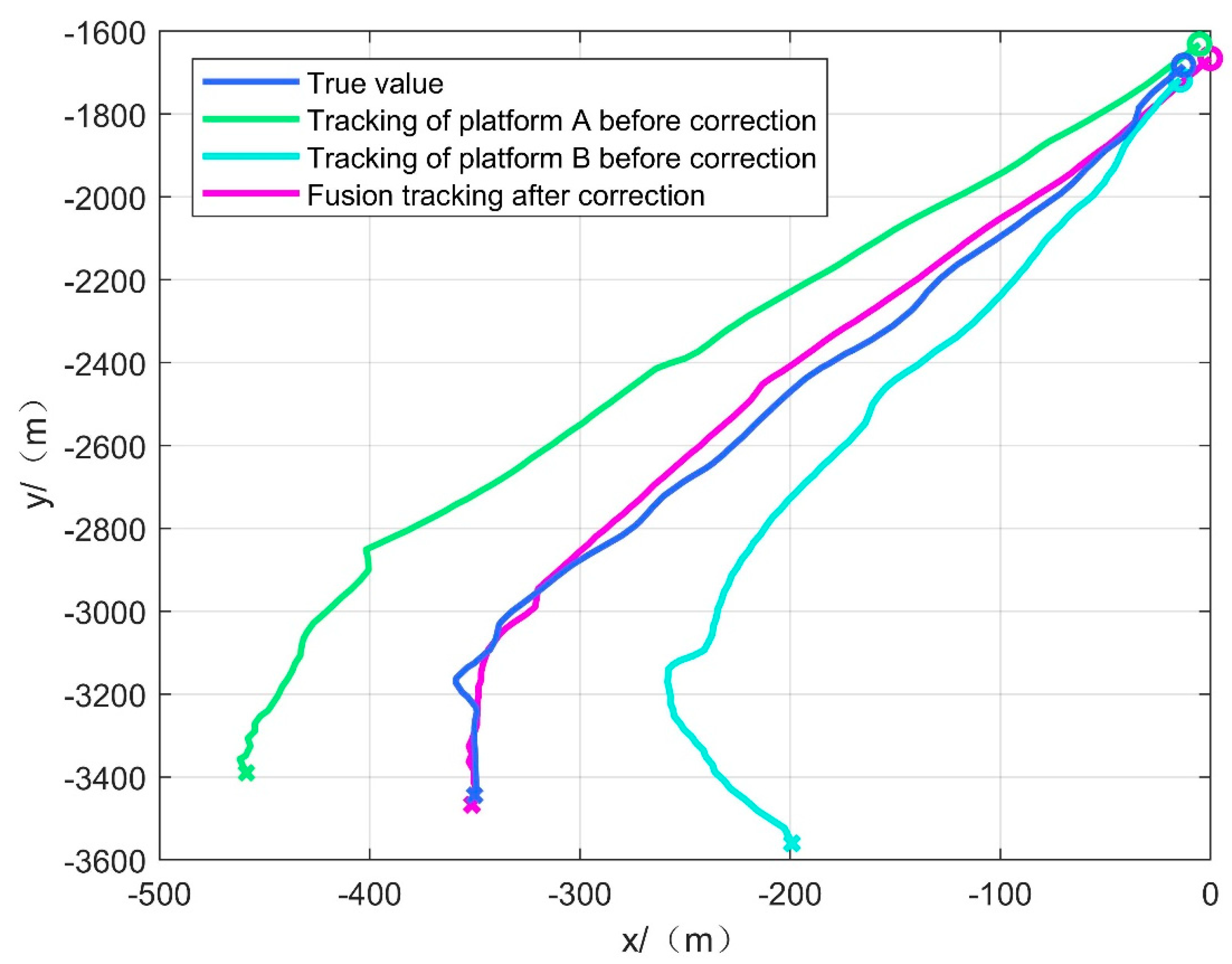
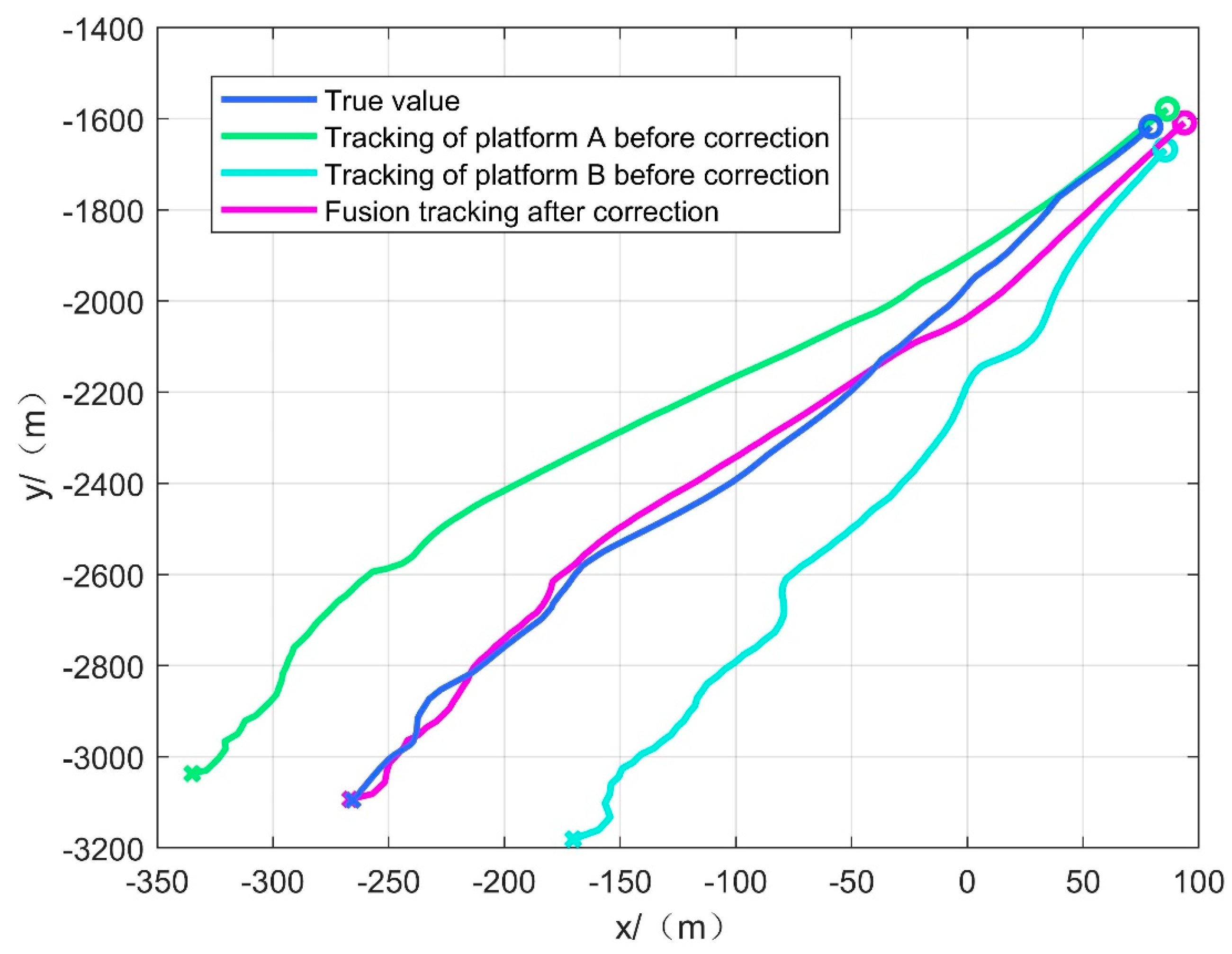
4.1.2. Simulation Experimental Result
4.2. Practical Experiment
4.2.1. Introduction to the Practical Experiment
4.2.2. Practical Experiment Result
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Leung, H.; Blanchette, M.; Gault, K. Comparison of registration error correction techniques for air surveillance radar network. Proc. SPIE—Int. Soc. Opt. Eng. 1995, 2, 211–214. [Google Scholar]
- Cai, J.; Huang, P.; Zhang, B.; Wang, D. A TSR Visual Servoing System Based on a Novel Dynamic Template Matching Method. Sensors 2015, 15, 32152–32167. [Google Scholar] [CrossRef]
- Pfeifer, T.; Lange, S.; Protzel, P. Advancing Mixture Models for Least Squares Optimization. IEEE Robot. Autom. Lett. 2021, 6, 3941–3948. [Google Scholar] [CrossRef]
- Wei, Z.; Wei, S.; Luo, F.; Yang, S.; Wang, J. A Maximum Likelihood Registration Algorithm for Moving Dissimilar Sensors. In Proceedings of the IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 24–26 May 2019. [Google Scholar]
- Zhao, S.; Yi, M.; Liu, Z. Cooperative Anti-Deception Jamming in a Distributed Multiple-Radar System under Registration Errors. Sensors 2022, 22, 7216. [Google Scholar] [CrossRef]
- Da, K.; Li, T.; Zhu, Y.; Fu, Q. A Computationally Efficient Approach for Distributed Sensor Localization and Multitarget Tracking. IEEE Commun. Lett. 2020, 24, 335–338. [Google Scholar] [CrossRef]
- Belfadel, D.; Bar-Shalom, Y.; Willett, P. Single Space Based Sensor Bias Estimation Using a Single Target of Opportunity. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1676–1684. [Google Scholar] [CrossRef]
- Lu, Z.-H.; Zhu, M.-Y.; Ye, Q.-W.; Zhou, Y. Performance analysis of two EM-based measurement bias estimation processes for tracking systems. Front. Inf. Technol. Electron. Eng. 2018, 19, 1151–1165. [Google Scholar] [CrossRef]
- Li, D.; Wu, D.; Lou, P. Exact Least Square Registration Algorithm for Multiple Dissimilar Sensors. In Proceedings of the 10th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 9–10 December 2017; pp. 338–341. [Google Scholar]
- Pu, W.; Liu, Y.; Yan, J.; Zhou, S.; Liu, H. A two-stage optimization approach to the asynchronous multi-sensor registration problem. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017. [Google Scholar]
- Shang, J.; Yao, Y. Approach of system error registration for two-station coast radars for sea surface monitoring. J. Eng. 2019, 2019, 7721–7725. [Google Scholar] [CrossRef]
- Lu, X.; Xie, Y.; Zhou, J. Improved Spatial Registration and Target Tracking Method for Sensors on Multiple Missiles. Sensors 2018, 18, 1723. [Google Scholar] [CrossRef] [PubMed]
- Drummond, O.E.; Belfadel, D.; Osborne, R.W.; Bar-Shalom, Y.; Teichgraeber, R.D. A minimalist approach to bias estimation for passive sensor measurements with targets of opportunity. In Proceedings of the Signal and Data Processing of Small Targets 2013, San Diego, CA, USA, 25–29 August 2013. [Google Scholar]
- Zhu, H.-M.; Jia, Z.-R.; Wang, H.-Y.; Sui, S.-Y. UAV target localization method for different field-of-view auxiliary beacons. J. Natl. Univ. Def. Technol. 2019, 41, 12. [Google Scholar]
- Zhao, Y.-H.; Yuan, F.; Ding, Z.-L.; Li, J. Monte Carlo estimation of cooperative target-based attitude measurement system modeling and accuracy. J. Sci. Instrum. 2010, 8, 1873–1877. [Google Scholar]
- Nguyen, V.H.; Pyun, J.Y. Location detection and tracking of moving targets by a 2D IR-UWB radar system. Sensors 2015, 15, 6740–6762. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K.; Durrant-Whyte, H.F. A new approach for filtering nonlinear systems. In Proceedings of the 1995 American Control Conference-ACC′95, Seattle, WA, USA, 21–23 June 1995. [Google Scholar]
- Huang, Y.; Zhang, Y.; Xu, B.; Wu, Z.; Chambers, J.A. A New Adaptive Extended Kalman Filter for Cooperative Localization. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 353–368. [Google Scholar] [CrossRef]
- Deng, Z.; Yin, L.; Huo, B.; Xia, Y. Adaptive Robust Unscented Kalman Filter via Fading Factor and Maximum Correntropy Criterion. Sensors 2018, 18, 2406. [Google Scholar] [CrossRef] [PubMed]
- György, K.; Kelemen, A.; Dávid, L. Unscented Kalman Filters and Particle Filter Methods for Nonlinear State Estimation. Procedia Technol. 2014, 12, 65–74. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman Filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, W.; Yuan, G. An Improved Interacting Multiple Model Filtering Algorithm Based on the Cubature Kalman Filter for Maneuvering Target Tracking. Sensors 2016, 16, 805. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.B.; Robert Jeremiah, R.J.; Su, T.L.; Bai, Y.T.; Kong, J.L. The New Trend of State Estimation: From Model-Driven to Hybrid-Driven Methods. Sensors 2021, 21, 2085. [Google Scholar] [CrossRef]
- Li, W.; Jia, Y.; Du, J.; Yu, F. Gaussian mixture PHD filter for multi-sensor multi-target tracking with registration errors. Signal Process. 2013, 93, 86–99. [Google Scholar] [CrossRef]
- Wu, W.; Jiang, J.; Liu, W.; Feng, X.; Gao, L.; Qin, X. Augmented state GM-PHD filter with registration errors for multi-target tracking by Doppler radars. Signal Process. 2016, 120, 117–128. [Google Scholar] [CrossRef]
- He, X.; Liu, G. Augmented state PHD filter for extended target tracking with bias compensation. Optik 2018, 160, 203–213. [Google Scholar] [CrossRef]
- Jain, R.; Dhingra, S.; Joshi, K.; Rana, A.K.; Goyal, N. Enhance traffic flow prediction with Real-Time Vehicle Data Integration. J. Auton. Intell. 2023, 6. [Google Scholar] [CrossRef]
- Verma, V.; Gupta, D.; Gupta, S.; Uppal, M.; Anand, D.; Ortega-Mansilla, A.; Alharithi, F.S.; Almotiri, J.; Goyal, N. A Deep Learning-Based Intelligent Garbage Detection System Using an Unmanned Aerial Vehicle. Symmetry 2022, 14, 960. [Google Scholar] [CrossRef]
- Xiong, H.; Mai, Z.; Tang, J.; He, F. Robust GPS/INS/DVL Navigation and Positioning Method Using Adaptive Federated Strong Tracking Filter Based on Weighted Least Square Principle. IEEE Access 2019, 7, 26168–26178. [Google Scholar] [CrossRef]
- Patoliya, J.; Mewada, H.; Hassaballah, M.; Khan, M.A.; Kadry, S. A robust autonomous navigation and mapping system based on GPS and LiDAR data for unconstraint environment. Earth Sci. Inform. 2022, 15, 2703–2715. [Google Scholar] [CrossRef]
- Li, F.; Chang, L. MEKF with Navigation Frame Attitude Error Parameterization for INS/GPS. IEEE Sens. J. 2019, 20, 1536–1549. [Google Scholar] [CrossRef]
- Shen, H.; Zong, Q.; Lu, H.; Zhang, X.; Tian, B.; He, L. A distributed approach for lidar-based relative state estimation of multi-UAV in GPS-denied environments. Chin. J. Aeronaut. 2022, 35, 59–69. [Google Scholar] [CrossRef]
- Sarras, I.; Marzat, J.; Bertrand, S.; Piet-Lahanier, H. Collaborative multiple micro air vehicles’ localization and target tracking in GPS-denied environment from range–velocity measurements. Int. J. Micro Air Veh. 2018, 10, 225–239. [Google Scholar] [CrossRef]
- Kim, Y.; Jung, W.; Bang, H. Visual Target Tracking and Relative Navigation for Unmanned Aerial Vehicles in a GPS-Denied Environment. Int. J. Aeronaut. Space Sci. 2014, 15, 258–266. [Google Scholar] [CrossRef]
- Tang, C.; Wang, Y.; Zhang, L.; Zhang, Y.; Song, H. Multisource Fusion UAV Cluster Cooperative Positioning Using Information Geometry. Remote Sens. 2022, 14, 5491. [Google Scholar] [CrossRef]
- Dai, Q.; Lu, F. A New Spatial Registration Algorithm of Aerial Moving Platform to Sea Target Tracking. Sensors 2023, 23, 6112. [Google Scholar] [CrossRef] [PubMed]






| Standard Deviation of Systematic Error | Standard Deviation of Random Error | |
|---|---|---|
| Sensor error | ||
| Attitude error |
| Standard Deviation of Systematic Error | Standard Deviation of Random Error | |
|---|---|---|
| Sensor error | ||
| Attitude error |
| Distance | Azimuth | Elevation | Pitch | Yaw | Roll | |
|---|---|---|---|---|---|---|
| UAV A | 1.0323 m | 0.0081° | 0.0054° | 0.0002° | 0.0002° | 0.0002° |
| UAV B | 0.9570 m | 0.0088° | 0.0054° | 0.0002° | 0.0002° | 0.0002° |
| X (m) | Y (m) | R (m) | |
|---|---|---|---|
| Uncorrected Platform A | 475.6877 | 26.5548 | 476.4284 |
| Uncorrected Platform B | 508.7279 | 39.6952 | 510.2742 |
| Uncorrected Fusion | 492.2078 | 33.1250 | 493.3212 |
| Modified Platform A | 55.4091 | 0.8984 | 55.4164 |
| Corrected Platform B | 35.6165 | 0.9326 | 35.6287 |
| Corrected Fusion | 10.7591 | 0.0235 | 10.7974 |
| X (m) | Y (m) | R (m) | |
|---|---|---|---|
| Uncorrected UAV A | 58.5292 | 58.8293 | 82.9853 |
| Uncorrected UAV B | 49.6542 | 54.4131 | 73.6636 |
| Corrected Fusion | 7.4061 | 10.3079 | 12.6927 |
| X (m) | Y (m) | R (m) | |
|---|---|---|---|
| Uncorrected UAV A | 47.8373 | 41.0663 | 63.0464 |
| Uncorrected UAV B | 61.2838 | 45.1243 | 76.1045 |
| Corrected Fusion | 8.6567 | 8.6009 | 12.2030 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, Q.; Lu, F.; Xu, J. A Spatial Registration Method for Multi-UAVs Based on a Cooperative Platform in a Geodesic Coordinate Information-Free Environment. Appl. Sci. 2023, 13, 10705. https://doi.org/10.3390/app131910705
Dai Q, Lu F, Xu J. A Spatial Registration Method for Multi-UAVs Based on a Cooperative Platform in a Geodesic Coordinate Information-Free Environment. Applied Sciences. 2023; 13(19):10705. https://doi.org/10.3390/app131910705
Chicago/Turabian StyleDai, Qiuyang, Faxing Lu, and Junfei Xu. 2023. "A Spatial Registration Method for Multi-UAVs Based on a Cooperative Platform in a Geodesic Coordinate Information-Free Environment" Applied Sciences 13, no. 19: 10705. https://doi.org/10.3390/app131910705
APA StyleDai, Q., Lu, F., & Xu, J. (2023). A Spatial Registration Method for Multi-UAVs Based on a Cooperative Platform in a Geodesic Coordinate Information-Free Environment. Applied Sciences, 13(19), 10705. https://doi.org/10.3390/app131910705








