Emphasizing the Creep Damage Constitutive Model of Hydro-Mechanical Properties of Rocks: A Case Study of Granite Gneiss
Abstract
:1. Introduction
2. Characterization of Damage Model and Hydro-Mechanical Properties Model
2.1. Damage Model in Rock Creep Process
2.2. Hydro-Mechanical Properties Model
3. Establishment of Hydro-Mechanical Properties Creep Damage Constitutive Model
3.1. Plastic Yield Surface Equation
3.2. Plastic Potential Energy Equation and Flow Law
3.3. Model Establishment
3.3.1. Instantaneous Loading Stage
3.3.2. Creep Stage
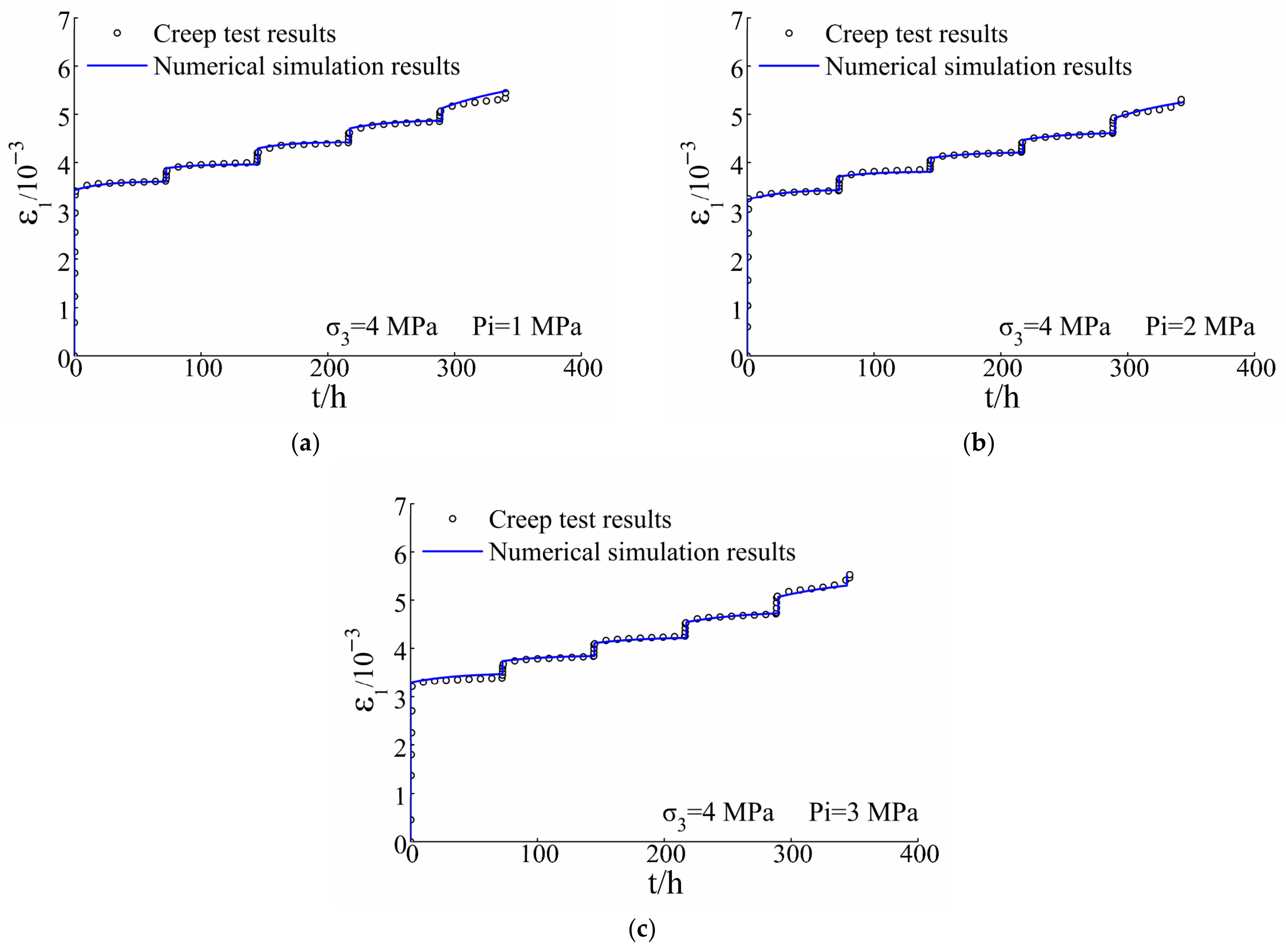
3.4. Model Validation
4. Conclusions
- (1)
- In accordance with studying the variation characteristics of porosity in rocks under the coupling effect of hydro-mechanical properties, as well as the relationship between permeability and volumetric strain, this paper proposes the concept of hydro-mechanical properties variable.
- (2)
- Through introducing the instantaneous damage variable d as the internal variable parameter of the thermodynamic state equation, the internal variable ζ is introduced in order to describe the time-dependent damage of rocks.
- (3)
- With introducing the coupling variable, instantaneous damage variable, time-dependent damage variable into the yield surface equation, plastic potential energy equation and stiffness matrix of the elastoplastic creep constitutive model, a hydro-mechanical properties creep damage coupling constitutive model is established, which can describe the creep deformation characteristics of rocks under the coupling effect of hydro-mechanical properties damage, and is consistent with the creep deformation characteristics of rocks under the coupling effect of hydro-mechanical properties.
- (4)
- Based on the triaxial creep test results of granite gneiss, the model parameters are determined. By comparing the constitutive simulation results with the experimental results, the numerical simulation results are in good agreement with the corresponding experimental results, which can better interpret the creep behavior of granite gneiss under the coupling effect of hydro-mechanical properties.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, R.; Wu, F.; Chen, J.; Zhu, C.; Ji, C. Study on creep characteristics and constitutive model of typical argillaceous salt rock in energy storage caverns in China. J. Energy Storage 2022, 50, 104248. [Google Scholar] [CrossRef]
- Shao, J.F.; Chau, K.T.; Feng, X.T. Modeling of anisotropic damage and creep deformation in brittle rocks. Int. J. Rock Mech. Min. Sci. 2006, 43, 582–592. [Google Scholar] [CrossRef]
- Lin, L.; Weiya, X. Experimental Researches on Long-Term Strength of Granite Gneiss. Adv. Mater. Sci. Eng. 2015, 2015, 187616. [Google Scholar]
- Tsai, L.S.; Hsieh, Y.M.; Weng, M.C.; Huang, T.H.; Jeng, F.S. Time-dependent deformation behaviors of weak sand-stones. Int. J. Rock. Mech. Min. Sci. 2008, 45, 144–154. [Google Scholar] [CrossRef]
- Wang, X.; Xia, C.; Zhu, Z.; Xie, W.; Song, L.; Han, G. Long-term creep law and constitutive model of extremely soft coal rock subjected to single-stage load. Rock Soil Mech. 2021, 42, 2078–2088. [Google Scholar]
- Zhao, J.; Feng, X.T.; Yang, C.; Zhou, Y.; Zhang, Y. Study on time-dependent fracturing behaviour for three different hard rock under high true triaxial stress. Rock Mech. Rock Eng. 2021, 54, 1239–1255. [Google Scholar] [CrossRef]
- Yang, S.Q.; Jing, H.W.; Cheng, L. Influences of pore pressure on short-term and creep mechanical behavior of red sandstone. Eng. Geol. 2014, 179, 10–23. [Google Scholar] [CrossRef]
- Wang, X.; Song, L.; Xia, C.; Han, G.; Zhu, Z. Nonlinear elasto-visco-plastic creep behavior and new creep damage model of dolomitic limestone subjected to cyclic incremental loading and unloading. Sustainability 2023, 13, 12376. [Google Scholar] [CrossRef]
- Yang, S.Q.; Jiang, Y.Z. Triaxial mechanical creep behavior of sandstone. Min. Sci. Technol. 2010, 20, 339–349. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Wang, W.; Wan, W.; Tang, J. Modeling of non-linear rheological behavior of hard rock using triaxial rheological experiment. Int. J. Rock Mech. Min. 2017, 93, 66–75. [Google Scholar] [CrossRef]
- Hu, B.; Yang, S.; Xu, P. A nonlinear rheological damage model of hard rock. J. Cent. South Univ. 2018, 25, 1665–1677. [Google Scholar] [CrossRef]
- Chen, H.Z.; Shao, Z.S.; Jin, D.D.; Zhang, Z.; Zhou, D.B. A numerical investigation into the effect of homogeneity on the time-dependent behavior of brittle rock. Materials 2021, 14, 6818. [Google Scholar] [CrossRef]
- Chen, L.; Wang, C.P.; Liu, J.F.; Liu, J.; Wang, J.; Jia, Y.; Shao, J.F. Damage and plastic deformation modeling of beishan granite under compressive stress conditions. Rock Mech. Rock Eng. 2015, 48, 1623–1633. [Google Scholar] [CrossRef]
- Zhou, H.W.; Wang, C.P.; Han, B.B.; Duan, Z.Q. A creep constitutive model for salt rock based on fractional derivatives. Int. J. Rock Mech. Min. Sci. 2011, 48, 116–121. [Google Scholar] [CrossRef]
- Xie, S.Y.; Shao, J.F. An experimental study and constitutive modeling of saturated porous rocks. Rock Mech. Rock Eng. 2015, 48, 223–234. [Google Scholar] [CrossRef]
- Liu, L.; Xu, W.Y.; Zhao, L.Y.; Zhu, Q.Z.; Wang, R.B. An experimental and numerical investigation of the mechanical behavior of granite gneiss under compression. Rock Mech. Rock Eng. 2017, 50, 499–506. [Google Scholar] [CrossRef]
- Lyu, C.; Liu, J.; Zhao, C.X.; Ren, Y.; Liang, C. Creep-damage constitutive model based on fractional derivatives and its application in salt cavern gas storage. J. Energy Storage 2021, 44, 103403. [Google Scholar] [CrossRef]
- Zhao, J.J.; Shen, W.Q.; Shao, J.F.; Liu, Z.B.; Vu, M.N. A constitutive model for anisotropic clay-rich rocks considering micro-structural composition. Int. J. Rock Mech. Min. Sci. 2022, 151, 105029. [Google Scholar] [CrossRef]
- Zhang, Y.; Shao, J.F.; Xu, W.Y.; Zhao, H.B.; Wang, W. Experimental and numerical investigations on strength and de-formation behavior of cataclastic sandstone. Rock Mech. Rock Eng. 2015, 48, 1083–1096. [Google Scholar] [CrossRef]
- Yin, Q.; Wu, J.Y.; Jiang, Z.; Zhu, C.; Su, H.; Jing, H.; Gu, X. Investigating the effect of water quenching cycles on me-chanical behaviors for granites after conventional triaxial compression. Geomech. Geophys. Geo-Energy Geo Resour. 2022, 8, 77. [Google Scholar] [CrossRef]
- Yang, S.Q.; Huang, Y.H.; Jiao, Y.Y.; Zeng, W.; Yu, Q.L. An experimental study on seepage behavior of sandstone material with different gas pressures. Acta Mech. Sin. 2015, 31, 837–844. [Google Scholar] [CrossRef]
- Figueiredo, B.; Tsang, C.F.; Rutqvist, J.; Niemi, A. A study of changes in deep fractured rock permeability due to coupled hydro-mechanical effects. Int. J. Rock Mech. Min. 2015, 79, 70–85. [Google Scholar] [CrossRef]
- Hideaki, Y.; Naoki, K.; Sho, O.; Dae-Sung, C.; Kiyoshi, K. Coupled thermo-hydro-mechanical-chemical modeling by incorporating pressure solution for estimating the evolution of rock permeability. Int. J. Rock Mech. Min. 2016, 86, 104–114. [Google Scholar]
- Mazars, J. A description of micro-and macroscale damage of concrete structures. Eng. Fract. Mech. 1986, 25, 729–737. [Google Scholar] [CrossRef]
- Morris, J.P.; Lomov, I.N.; Glenn, L.A. A constitutive model for stress-induced permeability and porosity evolution of Berea sandstone. J. Geophys. Res. Solid Earth 2003, 108, 237. [Google Scholar] [CrossRef]
- Rubin, M.B.; Vorobiev, O.Y.; Glenn, L.A. Mechanical and numerical modeling of a porous elastic–viscoplastic material with tensile failure. Int. J. Solids Struct. 2000, 37, 1841–1871. [Google Scholar] [CrossRef]
- Liu, L.; Xu, W.Y.; Wang, H.L.; Wang, W.; Wang, R.B. Permeability evolution of granite gneiss during triaxial creep tests. Rock Mech. Rock Eng. 2016, 49, 3455–3462. [Google Scholar] [CrossRef]
- Shao, J.F.; Zhu, Q.Z.; Su, K. Modeling of creep in rock materials in terms of material degradation. Comput. Geotech. 2003, 30, 549–555. [Google Scholar] [CrossRef]
- Pietruszczak, S.; Jiang, J.; Mirza, F.A. An elastoplastic constitutive model for concrete. Int. J. Solids Struct. 1988, 24, 705–722. [Google Scholar] [CrossRef]
- Mansouri, H.; Ajalloeian, R. Mechanical behavior of salt rock under uniaxial compression and creep tests. Int. J. Rock Mech. Min. Sci. 2018, 110, 19–27. [Google Scholar] [CrossRef]
- Firme, P.A.L.P.; Roehl, D.; Romanel, C. An assessment of the creep behaviour of Brazilian salt rocks using the multi-mechanism deformation model. Acta Geotech. 2016, 11, 1445–1463. [Google Scholar] [CrossRef]
| Pore Pressure | Parameters of the Test Data | ||||||
|---|---|---|---|---|---|---|---|
| a1 | b1 | c1 | L | a2 | b2 | c2 | |
| 1 MPa | 3.471 | 1.011 | 0.301 | 0.894 | 0.144 | 0.557 | 1.145 |
| 2 MPa | 7.213 | 1.164 | −0.062 | 1.771 | 0.857 | 0.383 | 1.075 |
| 3 MPa | 7.020 | 2.005 | 2.543 | 3.403 | 0.231 | 0.661 | 3.422 |
| Parameters | Values | Definition |
|---|---|---|
| A0 | 950 | They are obtained by obtaining the trajectories of the peak strength of each rock sample in the plane of average stress p and deviator stress q from triaxial tests under different confining pressure conditions. |
| C0 | 18 MPa | |
| 0.021 | It describes the initial yield surface position of rocks. | |
| B | 0.0005 | It is a parameter characterizing the plastic hardening rate of rock. |
| η | −0.0025 | It represents the slope of the boundary line between the compression and expansion regions of the rock sample. |
| dc | 0.9 | It represents the maximum critical value of the damage variable. |
| Bd | 125 | It can be determined by the relationship between the damage driving force and the damage variable. |
| γ | 5.0 × 10−7/s | It is determined by the creep rate. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Wen, B. Emphasizing the Creep Damage Constitutive Model of Hydro-Mechanical Properties of Rocks: A Case Study of Granite Gneiss. Appl. Sci. 2023, 13, 10967. https://doi.org/10.3390/app131910967
Liu L, Wen B. Emphasizing the Creep Damage Constitutive Model of Hydro-Mechanical Properties of Rocks: A Case Study of Granite Gneiss. Applied Sciences. 2023; 13(19):10967. https://doi.org/10.3390/app131910967
Chicago/Turabian StyleLiu, Lin, and Bo Wen. 2023. "Emphasizing the Creep Damage Constitutive Model of Hydro-Mechanical Properties of Rocks: A Case Study of Granite Gneiss" Applied Sciences 13, no. 19: 10967. https://doi.org/10.3390/app131910967
APA StyleLiu, L., & Wen, B. (2023). Emphasizing the Creep Damage Constitutive Model of Hydro-Mechanical Properties of Rocks: A Case Study of Granite Gneiss. Applied Sciences, 13(19), 10967. https://doi.org/10.3390/app131910967








