Vertically and Horizontally Reinforced End-Bearing Stone Column: An Experimental and Numerical Investigation
Abstract
:1. Introduction
2. Materials Employed
2.1. Soft Clay and Stone Aggregates
2.2. Geotextile as an Encasement Material
3. Experimental Description
3.1. Tank Size and Scale Effect
3.2. Clay Bed Preparation
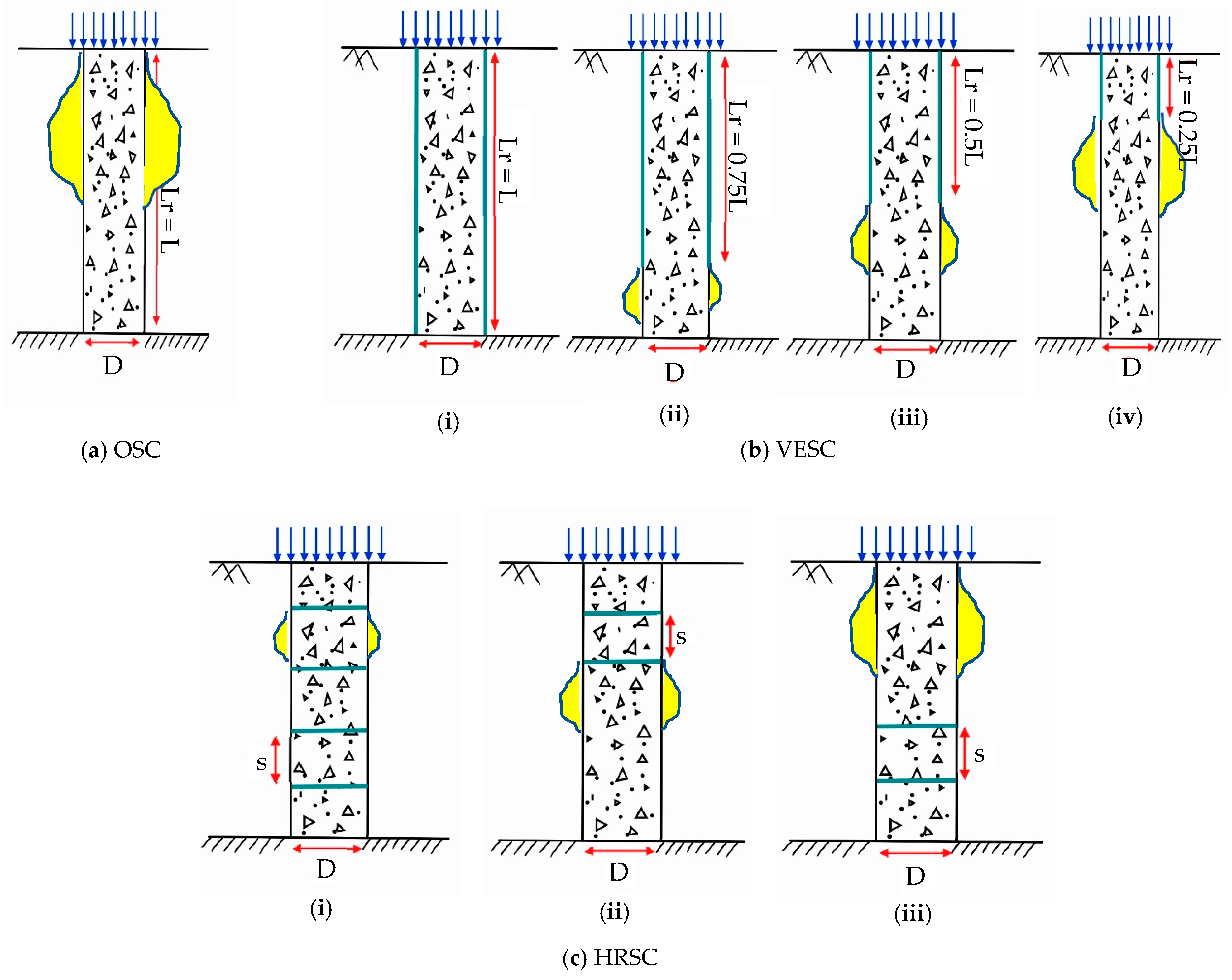
3.3. Installation and Construction Method of Stone Columns
3.4. Test Procedure
4. Numerical Analysis Using Plaxis 3D
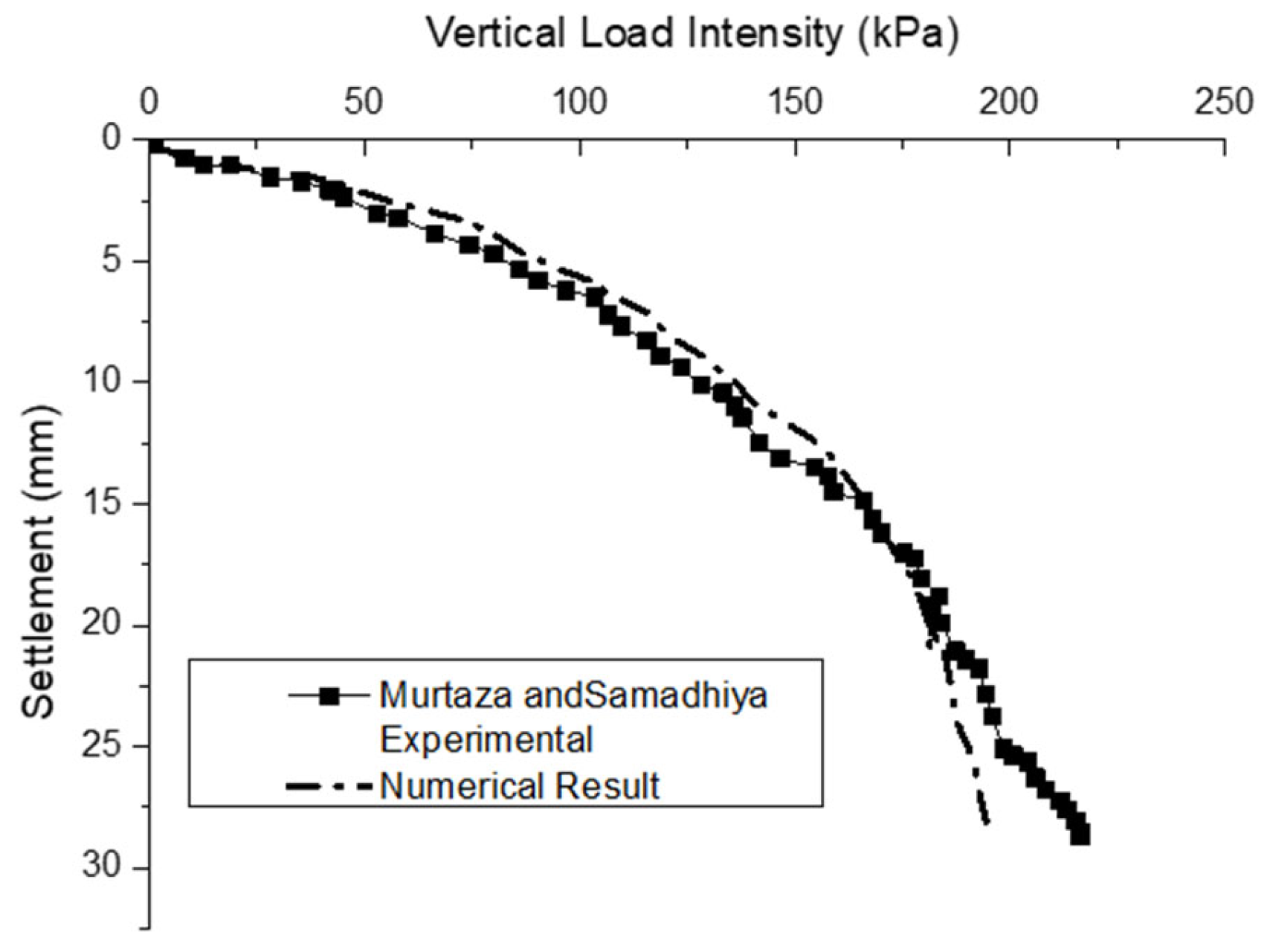
Validation
5. Results and Discussion
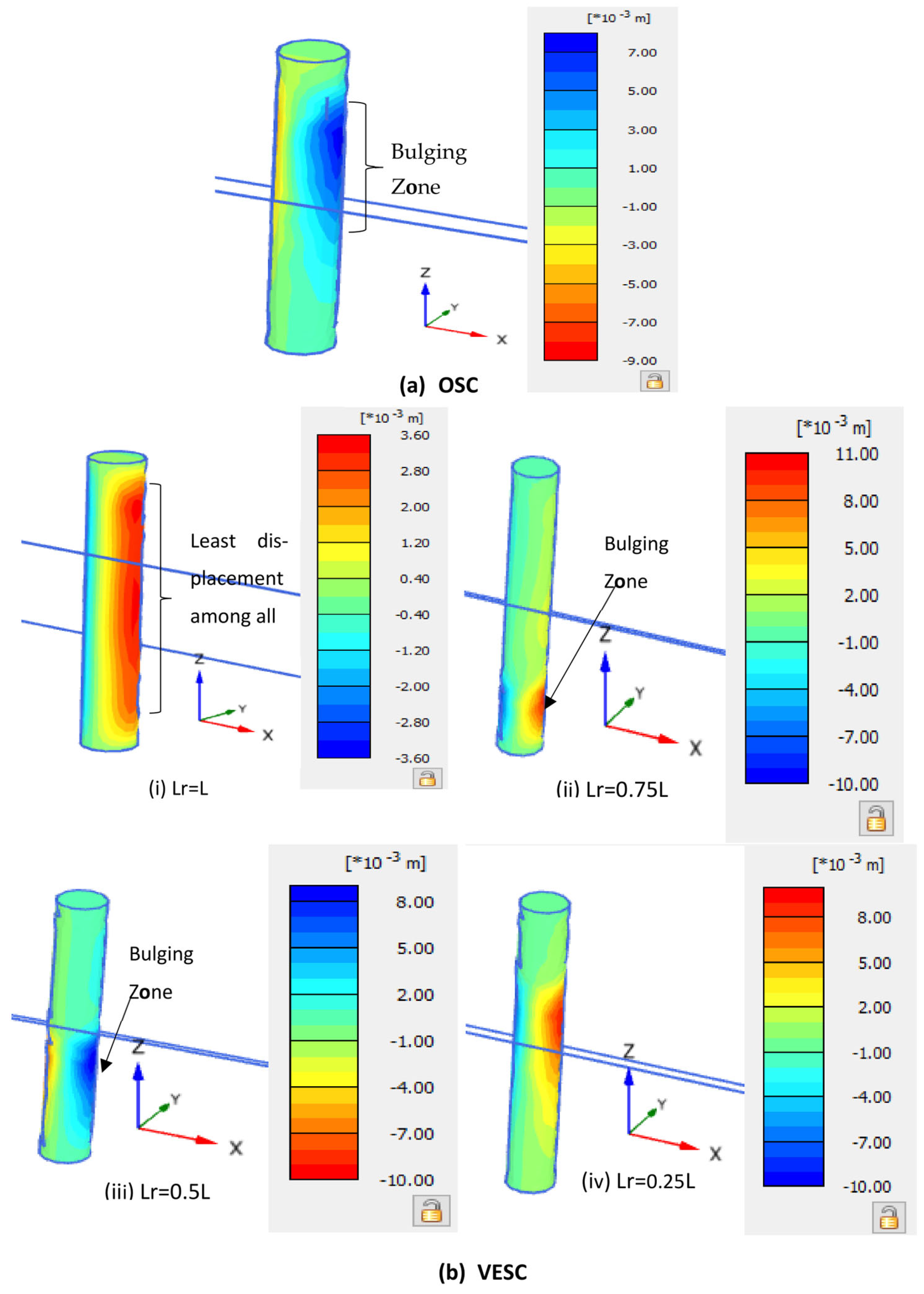
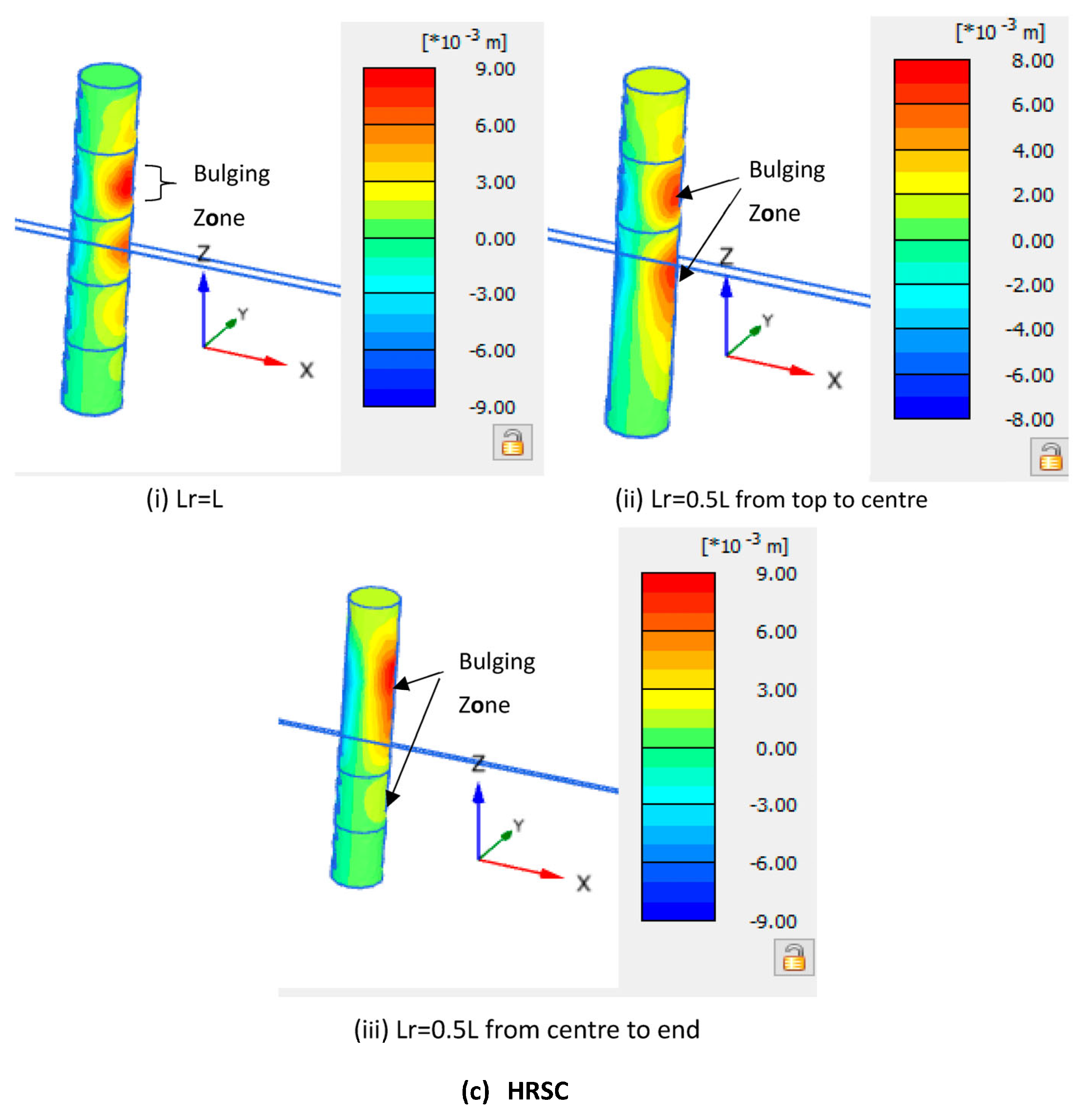
5.1. Failure Mechanism—Experimental Result
5.2. Failure Mechanism—Numerical Result
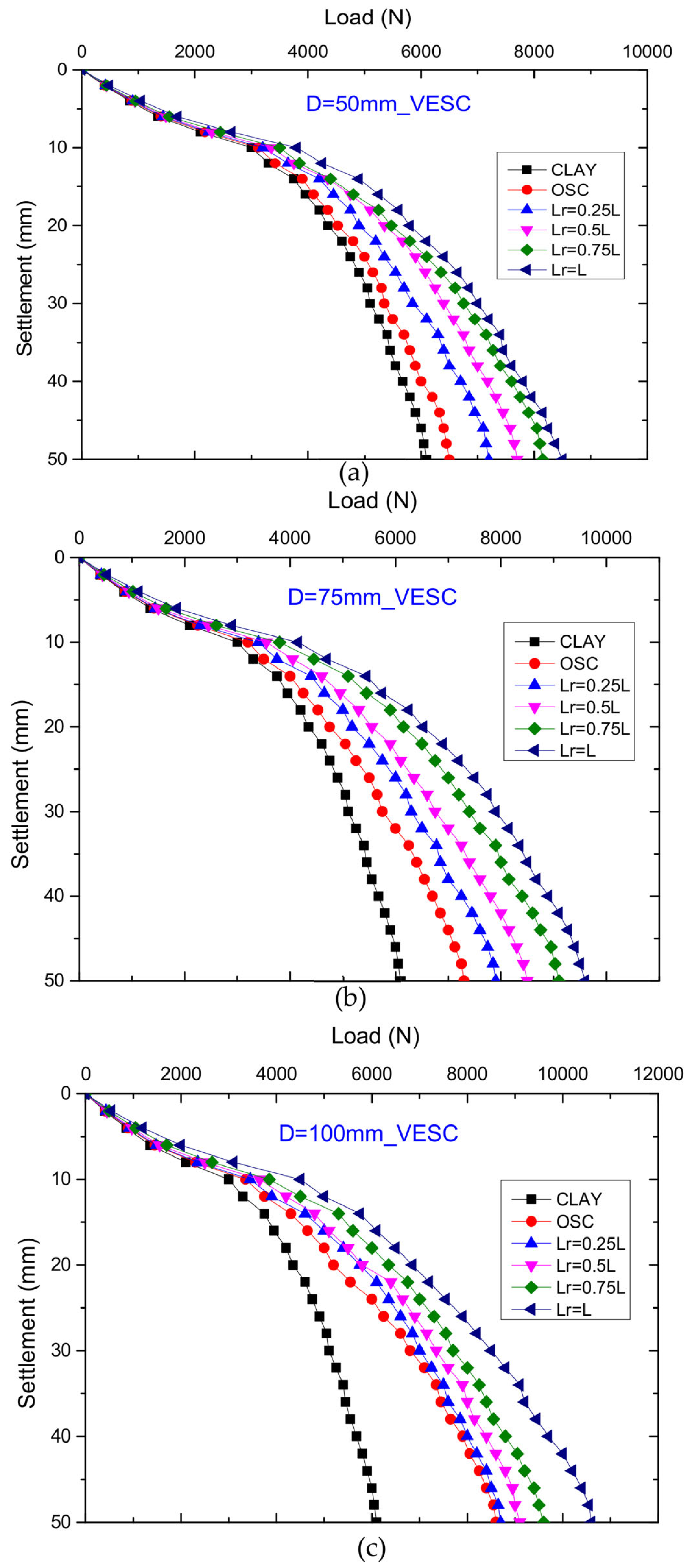
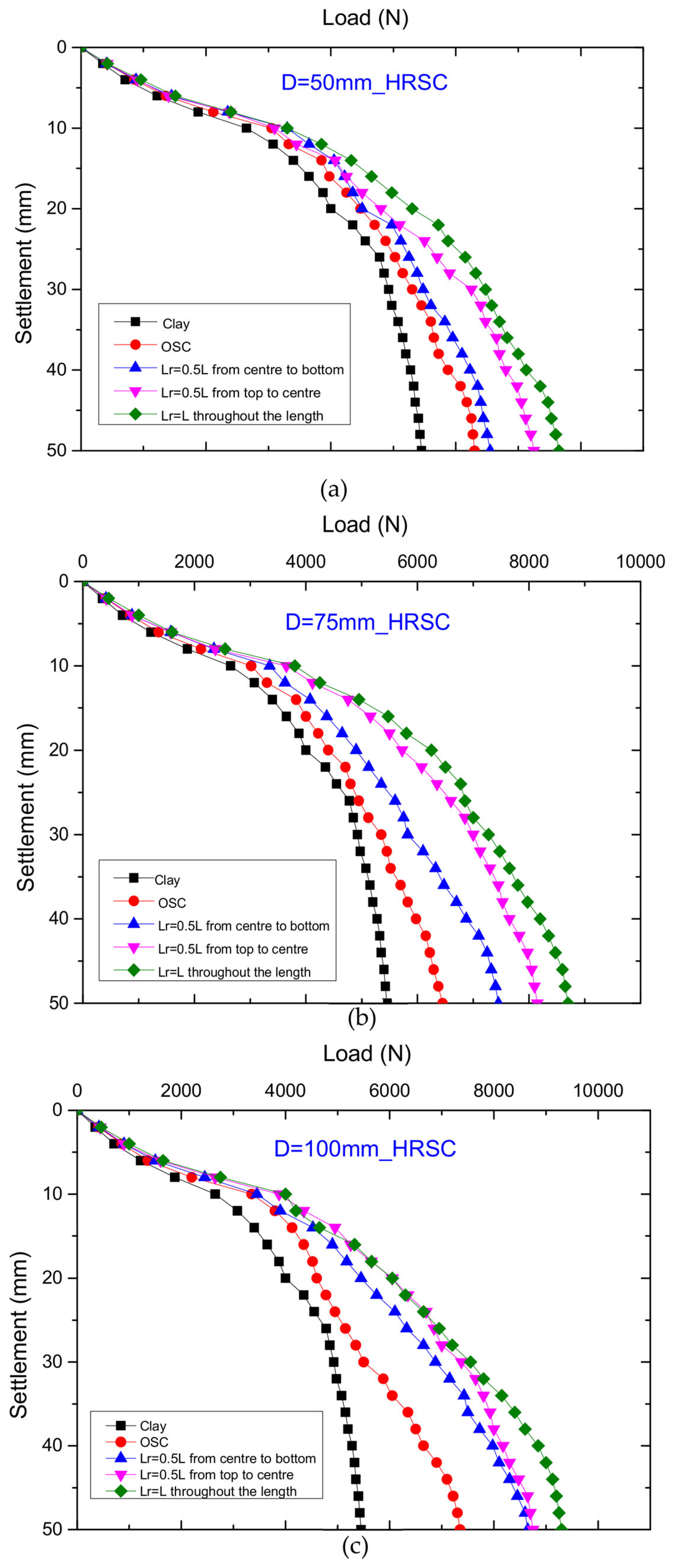
5.3. Load–Settlement Analysis—Experimental Result
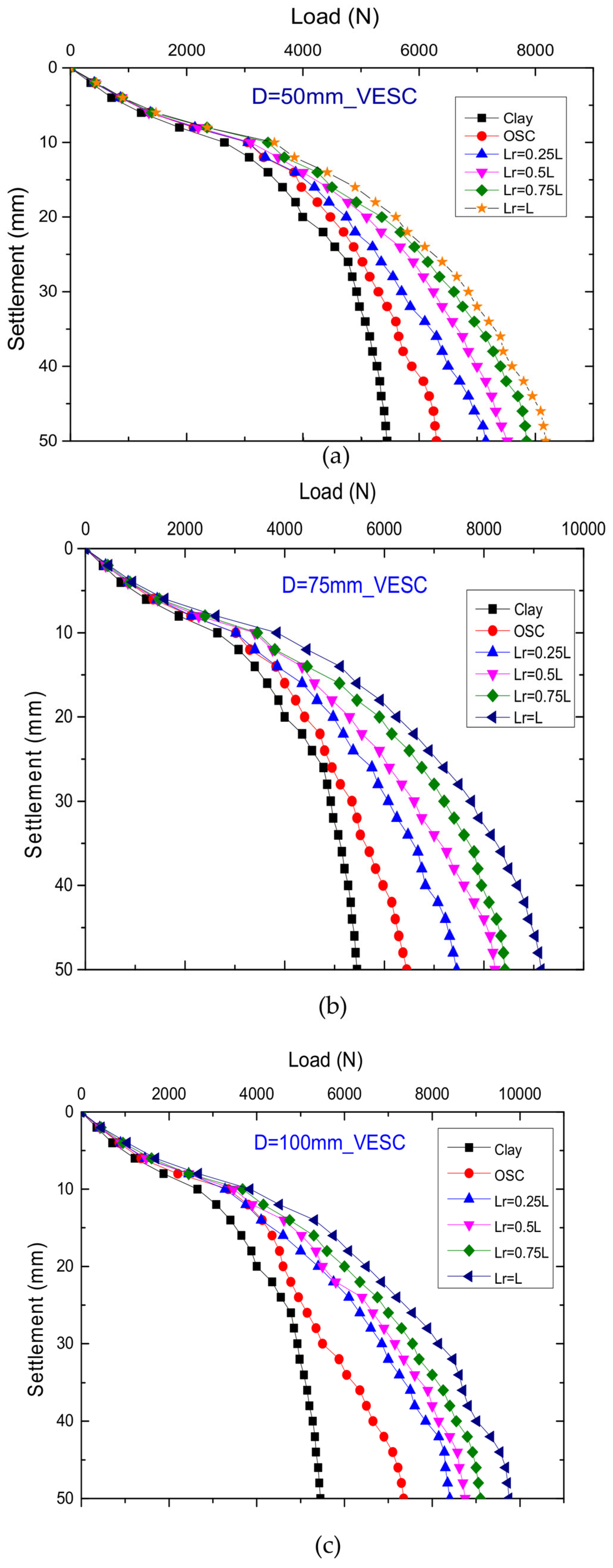
5.4. Load–Settlement Analysis—Numerical Result
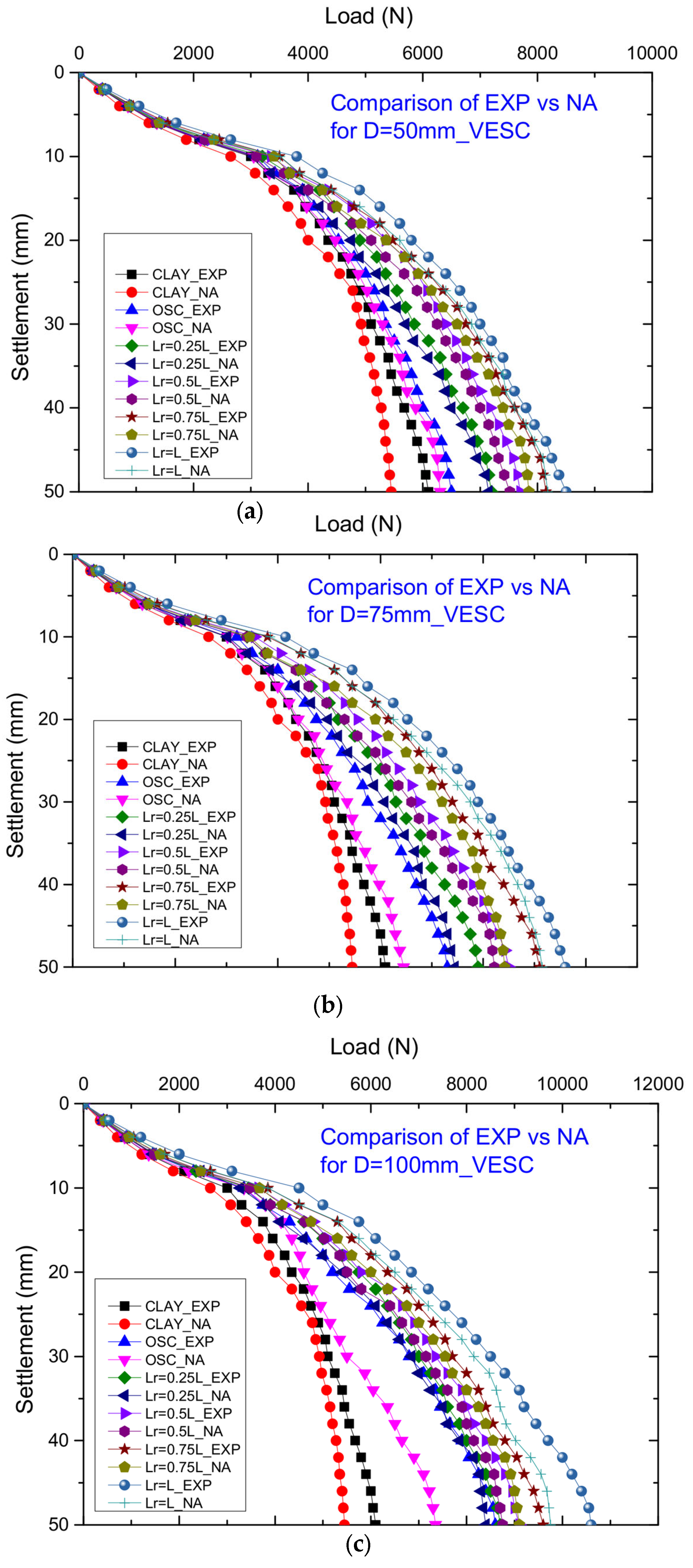
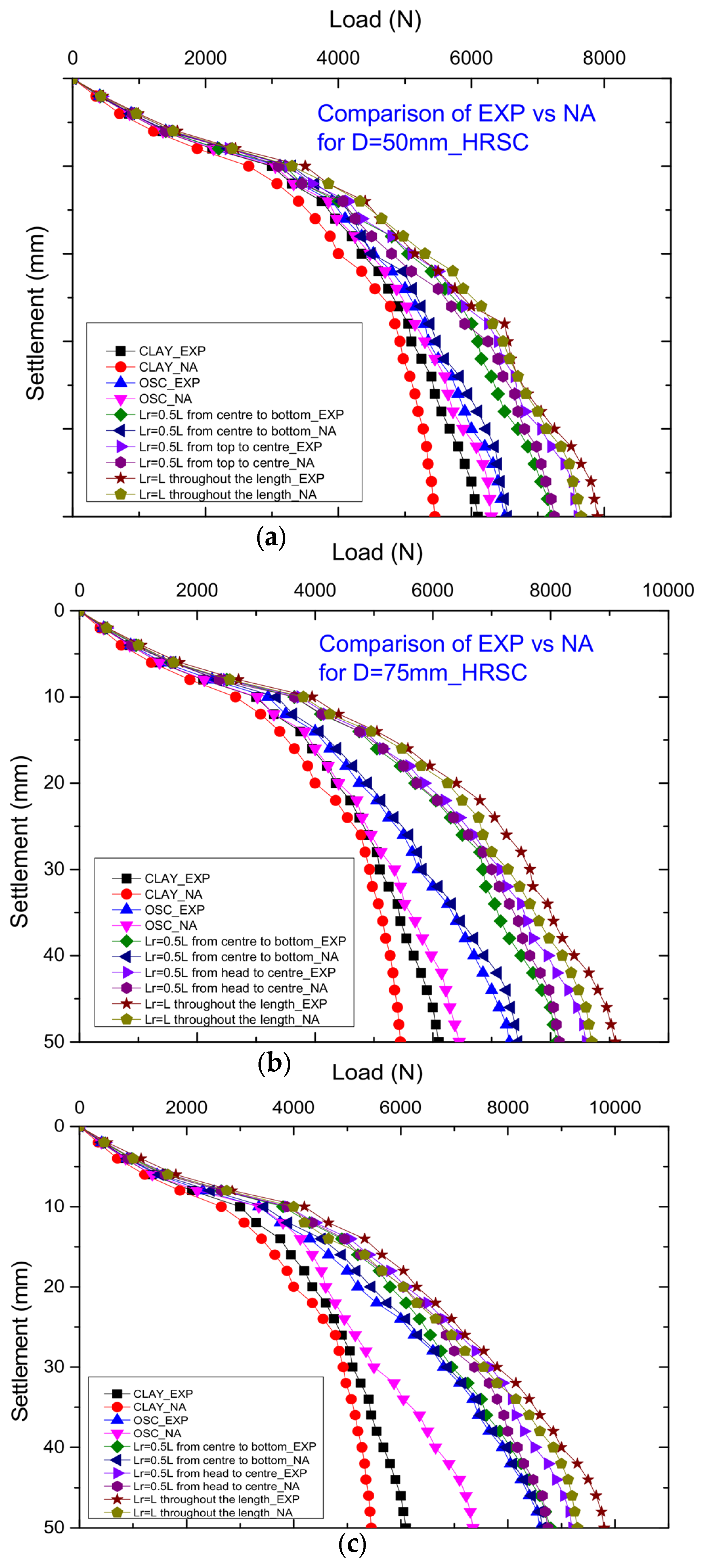
6. Comparative Analysis of Experimental and Numerical Outcomes
7. Conclusions
- The predominant failure mechanism observed in all experiments was ballooning. The occurrence of bulging failure was seen at a depth ranging from D to 2D below the head of the stone column. The occurrence of bulging in the column materials among the reinforcing sections in single HRSCs is limited.
- Increasing the area replacement ratio for an ultimate settlement of 50 mm increased the load-carrying capability in both the experimental and numerical analysis.
- For VESCs, the full-length encasement resulted in a higher load capacity of 23.52, 23.95, and 18.86% for D = 50, 75, and 100 mm, respectively, in the experimental results as compared to their OSC results. A similar trend was observed in the numerical results.
- In HRSCs, when reinforcement was provided for the full length of the column at equal intervals, the load capacity increased by 17.72, 19.78, and 12.24% for D = 50, 75, and 100 mm, respectively, when compared to their OSC values. Similar results were observed for the numerical analysis.
- Compared to the experimental results, the numerical results showed a slightly lower value for the load-carrying capability at 50 mm settlement, but the values obtained were in good agreement, with a maximum COV value of 11.08%.
- Compared to partial reinforcements, the most effective HRSCs were seen to have reinforcement sheets provided at equally spaced intervals over their entire length. In the context of VESCs, it was determined that complete encasement (Lr = L) was more effective than partial reinforcement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| OSC | Ordinary stone column |
| VESC | Vertically encased stone column |
| HRSC | Horizontally reinforced stone column |
| L | Length of the column |
| D | Diameter of the stone column |
| Lr | Length of the reinforcement |
| S | Spacing between horizontal layers of geotextile |
| E | Elastic modulus of soil |
| γbulk | Bulk unit weight of soil |
| γsat | Saturated unit weight of soil |
| c | Soil cohesion |
| φ | Friction angle of soil |
| υ | Poisson’s ratio |
| EA | Axial stiffness of geotextile |
References
- Choobbasti, A.J.; Zahmatkesh, A.; Noorzad, R. Performance of Stone Columns in Soft Clay: Numerical Evaluation. Geotech. Geol. Eng. 2011, 29, 675–684. [Google Scholar] [CrossRef]
- Srijan; Gupta, A.K. A Review article on Construction, Parametric Study and Settlement Behavior of Stone Column. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; p. 796. [Google Scholar] [CrossRef]
- Thankur, A.; Rawat, S.; Gupta, A.K. Experimental and Numerical Investigation of Load Carrying Capacity of Vertically and Horizontally Reinforced Floating Stone Column Group. Geotech. Geol. Eng. 2021, 39, 3003–3018. [Google Scholar] [CrossRef]
- Munfakh, G.A.; Sarkar, S.K.; Castelli, R.P. Performance of a test embankment founded on stone columns. In Proceedings of the International Conference on Advances in Piling and Ground Treatment for Foundations, London, UK, 2–4 March 1983; pp. 259–265. [Google Scholar]
- Yan, J.; Ye, S.L. Simplified method for consolidation rate of stone column reinforced foundations. J. Geotech. Geoenviron. Eng. (ASCE) 2001, 127, 597–603. [Google Scholar]
- Elshazly, H.A.; Hafez, D.A.; Mossaad, M.E. Reliability of conventional settlement evaluation for circular foundations on stone columns. Geotech. Geol. Eng. 2008, 26, 323–334. [Google Scholar] [CrossRef]
- Guetif, Z.; Bouassida, M.; Debats, J.M. Improved clay characteristics due to stone column installation. Comput. Geotech. 2007, 34, 104–111. [Google Scholar] [CrossRef]
- Castro, J.; Sagaseta, C. Deformation and consolidation around encased stone columns. Geotext. Geomembr. 2011, 29, 268–276. [Google Scholar] [CrossRef]
- Murugesan, S.; Rajagopal, K. Studies on the Behavior of Single and Group of Geosynthetic Encased Stone Columns. J. Geotech. Geoenviron. Eng. 2010, 136, 129–139. [Google Scholar] [CrossRef]
- Fattah, M.Y.; Zabar, B.S.; Hassan, H.A. Experimental Analysis of Embankment on Ordinary and Encased Stone Columns. Int. J. Geomech. 2016, 16, 04015102. [Google Scholar] [CrossRef]
- Srijan; Gupta, A.K. Effectiveness of triangular and square pattern of stone column with varying s/d ratio on consolidation be-haviour of soil. In Proceedings of the ASCE India Conference on Challenges of Resilient and Sustainable Infrastructure Development in Emerging Economies, Kolkata, India, 2–4 March 2020; Volume 1, pp. 1648–1654. [Google Scholar]
- Murugesan, S.; Rajagopal, K. Geosynthetic-encased stone columns: Numerical evaluation. Geotext. Geomembr. 2006, 24, 349–358. [Google Scholar] [CrossRef]
- Srijan; Gupta, A.K. The effect of using a sand column on the expansive soil’s swelling characteristics. J. Curr. Res. Eng. Sci. 2022, 5, 1–6. [Google Scholar]
- Mohanty, P.; Samanta, M. Experimental and Numerical Studies on Response of the Stone Column in Layered Soil. Int. J. Geosynth. Ground Eng. 2015, 1, 27. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, D.; Song, T.; Zhang, G.; Fan, L. A Method of Settlement Calculation of Ground Improved by Floating Deep Mixed Columns Based on Laboratory Model Tests and Finite Element Analysis. Int. J. Civ. Eng. 2022, 20, 207–222. [Google Scholar] [CrossRef]
- Shahu, J.T.; Kumar, S.; Bhowmik, R. Ground Improvement for Transportation Infrastructure: Experimental Investigations on Cyclic Behavior of a Group of Granular Columns. Int. J. Geomech. 2023, 23, 04022309. [Google Scholar] [CrossRef]
- Barksdale, R.D.; Bachus, R.C. Design and Construction of Stone Column; Report No. FHWA/R 83/026; National Technical Information Service: Springfield, VA, USA, 1983.
- Ali, M. Behavior of Ordinary and Encased Stone Columns End-Bearing and Floating in Soft Clay (Numerical Model). In Proceedings of the International Congress and Exhibition “Sustainable Civil Infrastructures: Innovative Infrastructure Geotechnology”, Cairo, Egypt, 24–28 November 2018. [Google Scholar]
- Thakur, A.; Rawat, S.; Gupta, A.K. Experimental study of ground improvement by using encased stone columns. Innov. Infrastruct. Solut. 2021, 6, 1. [Google Scholar] [CrossRef]
- Hasan, M.; Samadhiya, N.K. Performance of geosynthetic-reinforced granular piles in soft clays: Model tests and numerical analysis. Comput. Geotech. 2017, 87, 178–187. [Google Scholar] [CrossRef]
- Ali, K.; Shahu, J.T.; Sharma, K.G. Model tests on single and groups of stone columns with different geosynthetic reinforcement arrangement. Geosynth. Int. 2014, 21, 103–118. [Google Scholar] [CrossRef]
- Hosseinpour, I.; Riccio, M.; Almeida, M.S.S. Numerical evaluation of a granular column reinforced by geosynthetics using en-casement and laminated disks. Geotext. Geomembr. 2014, 42, 363–373. [Google Scholar] [CrossRef]
- Greenwood, D.A. Mechanical improvement of soils below ground surfaces. In Proceedings of the Ground Engineering Conference, Institution of Civil Engineers, London, UK, 13 September 1970; pp. 11–22. [Google Scholar]
- Priebe, H.J. The design of vibro replacement. Ground Eng. 1995, 28, 31–37. [Google Scholar]
- Baumann, V.; Bauer, G.E.A. The performance of foundations on various soils stabilized by the vibro-compaction method. Can. Geotech. J. 1974, 11, 509–530. [Google Scholar] [CrossRef]
- Ambily, A.P.; Gandhi, S.R. Behavior of stone columns based on experimental and FEM analysis. J. Geotech. Geoenviron. Eng. (ASCE) 2007, 133, 405–441. [Google Scholar] [CrossRef]
- McCabe, B.A.; Nimmons, G.J.; Egan, D. A review of field performance of stone columns in soft soils. Proc. Inst. Civ. Eng. Geotech. Eng. 2009, 162, 323–334. [Google Scholar] [CrossRef]
- Shahu, J.T.; Reddy, Y.R. Clayey soil reinforced with stone column group: Model tests and analyses. J. Geotech. Geoenviron. Eng. (ASCE) 2011, 137, 1265–1274. [Google Scholar] [CrossRef]
- Liu, K.; Qiu, R.; Yan, T.; Wu, B.; Fan, J.; Yue, F.; Mei, G. Model test of clogging effects on composite foundation of geosynthetic-encased steel slag column. Geotext. Geomembr. 2022, 50, 858–867. [Google Scholar] [CrossRef]
- Fan, J.; Rowe, R.K. Effect of subgrade on tensile strains in a geomembrane for tailings storage applications. Can. Geotech. J. 2022, 60, 18–30. [Google Scholar] [CrossRef]
- Fan, J.; Rowe, R.K. Effect of subgrade on leakage through a defective geomembrane seam below saturated tailing. Geotext. Geomembr. 2023, 51, 360–369. [Google Scholar] [CrossRef]
- Lo, S.R.; Zhang, R.; Mak, J. Geosynthetic-encased stone columns in soft clay: A numerical study. Geotext. Geomembr. 2010, 28, 292–302. [Google Scholar] [CrossRef]
- Wood, D.M.; Hu, W.; Nash, D.F.T. Group effects in stone column foundations: Model tests. Geotechnique 2000, 50, 689–698. [Google Scholar] [CrossRef]
- Hughes, J.M.O.; Withers, N.J.; Greenwood, D.A. A field trial of the reinforcing effect of a stone column in soil. Geotechnique 1975, 5, 31–44. [Google Scholar] [CrossRef]
- Murtaza, H.; Samadhiya, N.K. Experimental and numerical analysis of geosynthetic-reinforced floating granular pies in soft clays. Int. J. Geosynth. Ground Eng. 2016, 2, 22. [Google Scholar]




| Characteristics | Value |
|---|---|
| Specific gravity (SG) | 2.56 |
| Plastic limit (PL) | 27% |
| Liquid limit (LL) | 50% |
| Plasticity limit | 23% |
| Shrinkage limit (SL) | 10% |
| Maximum dry unit weight | 17.16 kN/m3 |
| Optimum moisture content | 19.23% |
| Bulk unit weight at 26.13% water content | 18 kN/m3 |
| Unified classification system | CL |
| Undrained shear strength | 20 kPa |
| Characteristics | Value |
|---|---|
| Specific gravity | 2.5 |
| Maximum dry unit weight | 16.4 kN/m3 |
| Bulk unit weight for the test at 68% relative density | 15.8 kN/m3 |
| Minimum dry unit weight | 14.4 kN/m3 |
| Internal friction angle (φ) at 68% relative density | 42° |
| Curvature coefficient (Cc) | 1.10 |
| Uniformity coefficient (Cu) | 2.14 |
| Unified classification system | GP |
| Tensile modulus from seam tests (kN/m) | 14.8 |
| Ultimate tensile strength (kN/m) | 8 |
| Tensile modulus (kN/m) | 14 |
| Strain at ultimate strength (%) | 52 |
| Strain at ultimate strength (%) from tests with seam | 46.5 |
| Ultimate tensile strength from tests with seam (kN/m) | 7 |
| Type of Column | Test Description | Length of Reinforcement | Column Diameter | Total Number of Tests Performed | ||
|---|---|---|---|---|---|---|
| 50 mm | 75 mm | 100 mm | ||||
| Solitary Stone Column | Clay | ✓ | ✓ | ✓ | 3 | |
| Ordinary Stone Column (OSC) | ✓ | ✓ | ✓ | 3 | ||
| Vertically Encased Stone Column (VESC) | Lr = L | ✓ | ✓ | ✓ | 3 | |
| Lr = 0.75 L | ✓ | ✓ | ✓ | 3 | ||
| Lr = 0.5 L | ✓ | ✓ | ✓ | 3 | ||
| Lr = 0.25 L | ✓ | ✓ | ✓ | 3 | ||
| Horizontally Reinforced Stone Column(HRSC) | Equal interval throughout the depth | ✓ | ✓ | ✓ | 3 | |
| Top half (0.5 L from column head) | ✓ | ✓ | ✓ | 3 | ||
| Bottom half (0.5 L from centre to the foot) | ✓ | ✓ | ✓ | 3 | ||
| Diameter of Stone Column | Reinforcement Type | Reinforcement Length | Experimental Result (kN) | Numerical Result (kN) | Coefficient of Variation (%) |
|---|---|---|---|---|---|
| D = 50 mm | OSC | 6.50 | 6.30 | 2.21 | |
| VESC | Lr = 0.25 L | 7.20 | 7.15 | 0.49 | |
| Lr = 0.5 L | 7.70 | 7.52 | 1.67 | ||
| Lr = 0.75 L | 8.15 | 7.85 | 2.65 | ||
| Lr = L | 8.50 | 8.18 | 2.71 | ||
| HRSC | Lr = 0.5 L from centre to bottom | 7.20 | 6.55 | 6.69 | |
| Lr = 0.5 L from head to centre | 7.60 | 7.25 | 3.33 | ||
| Lr = L throughout the length of column | 7.90 | 7.65 | 2.27 | ||
| D = 75 mm | OSC | 7.30 | 6.45 | 8.74 | |
| VESC | Lr = 0.25 L | 7.90 | 7.45 | 4.15 | |
| Lr = 0.5 L | 8.50 | 8.22 | 2.37 | ||
| Lr = 0.75 L | 9.10 | 8.42 | 5.49 | ||
| Lr = L | 9.60 | 9.15 | 3.39 | ||
| HRSC | Lr = 0.5 L from centre to bottom | 8.10 | 7.45 | 5.91 | |
| Lr = 0.5 L from head to centre | 8.60 | 8.15 | 3.80 | ||
| Lr = L throughout the length of column | 9.10 | 8.70 | 3.18 | ||
| D = 100 mm | OSC | 8.60 | 7.35 | 11.08 | |
| VESC | Lr = 0.25 L | 8.70 | 8.40 | 2.48 | |
| Lr = 0.5 L | 9.10 | 8.75 | 2.77 | ||
| Lr = 0.75 L | 9.60 | 9.10 | 3.78 | ||
| Lr = L | 10.60 | 9.75 | 5.91 | ||
| HRSC | Lr = 0.5 L from centre to bottom | 8.80 | 8.65 | 1.22 | |
| Lr = 0.5 L from head to centre | 9.20 | 8.75 | 3.55 | ||
| Lr = L throughout the length of column | 9.80 | 9.30 | 3.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srijan, S.; Gupta, A.K. Vertically and Horizontally Reinforced End-Bearing Stone Column: An Experimental and Numerical Investigation. Appl. Sci. 2023, 13, 11016. https://doi.org/10.3390/app131911016
Srijan S, Gupta AK. Vertically and Horizontally Reinforced End-Bearing Stone Column: An Experimental and Numerical Investigation. Applied Sciences. 2023; 13(19):11016. https://doi.org/10.3390/app131911016
Chicago/Turabian StyleSrijan, Srijan, and Ashok Kumar Gupta. 2023. "Vertically and Horizontally Reinforced End-Bearing Stone Column: An Experimental and Numerical Investigation" Applied Sciences 13, no. 19: 11016. https://doi.org/10.3390/app131911016
APA StyleSrijan, S., & Gupta, A. K. (2023). Vertically and Horizontally Reinforced End-Bearing Stone Column: An Experimental and Numerical Investigation. Applied Sciences, 13(19), 11016. https://doi.org/10.3390/app131911016





