The Structural Design and Optimization of Top-Stiffened Double-Layer Steel Truss Bridges Based on the Response Surface Method and Particle Swarm Optimization
Abstract
:1. Introduction
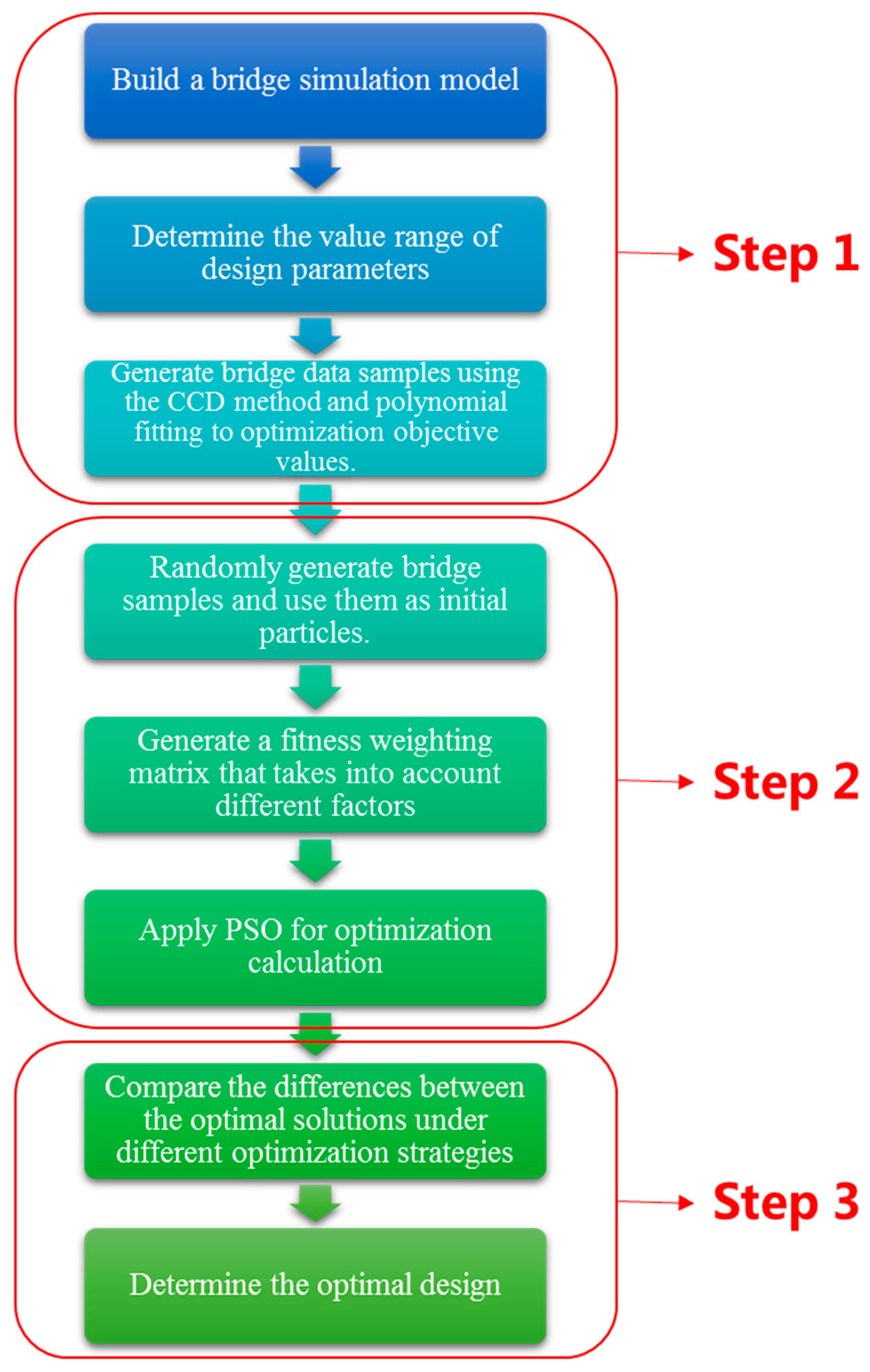
2. Capacity Optimal Design Method
2.1. Response Surface Method
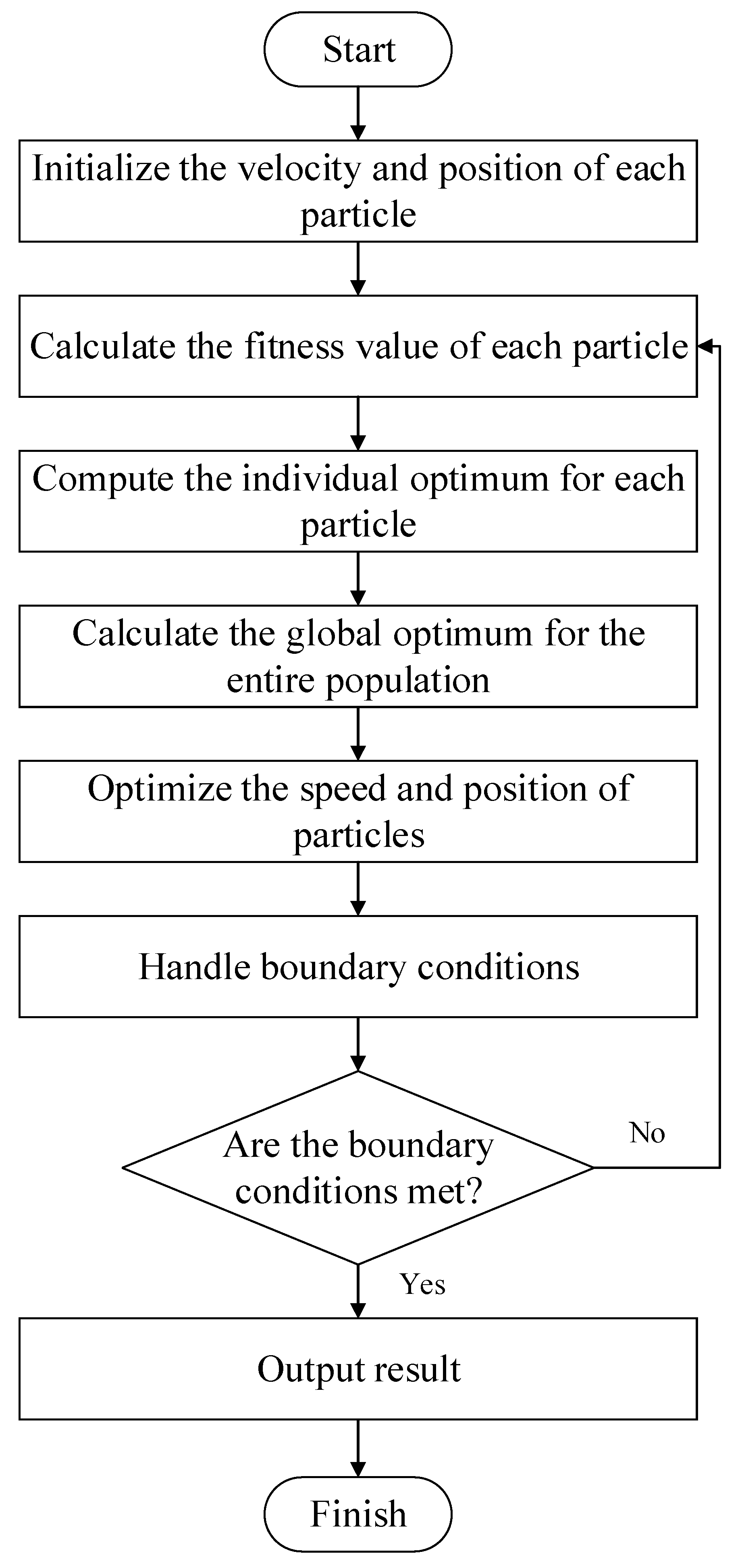
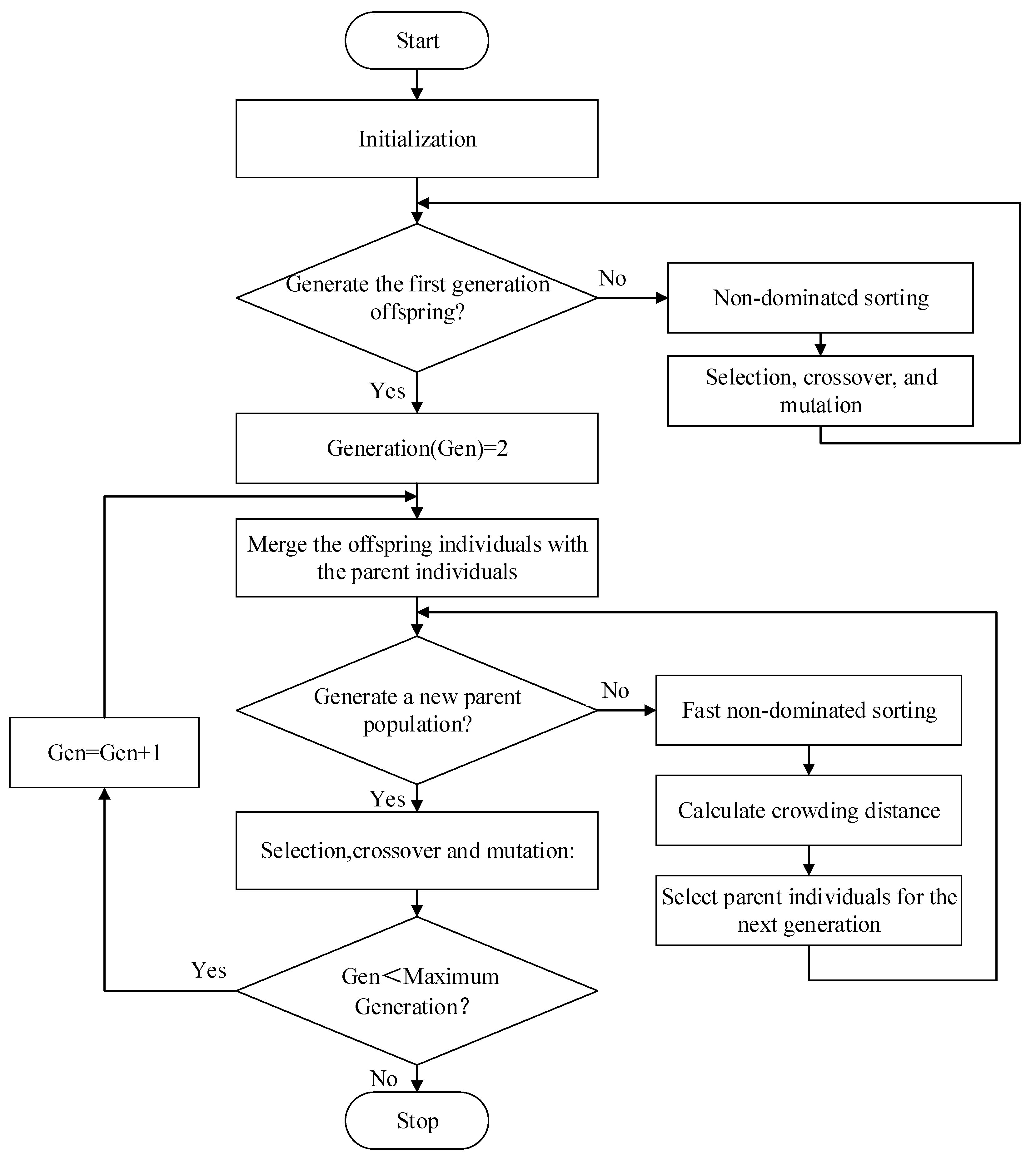
2.2. WPSO
2.3. Decision-Making
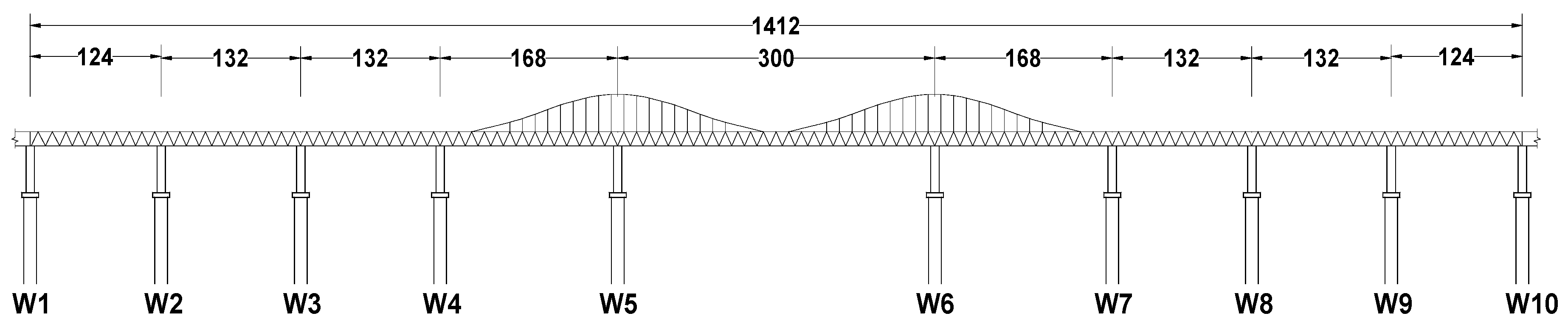
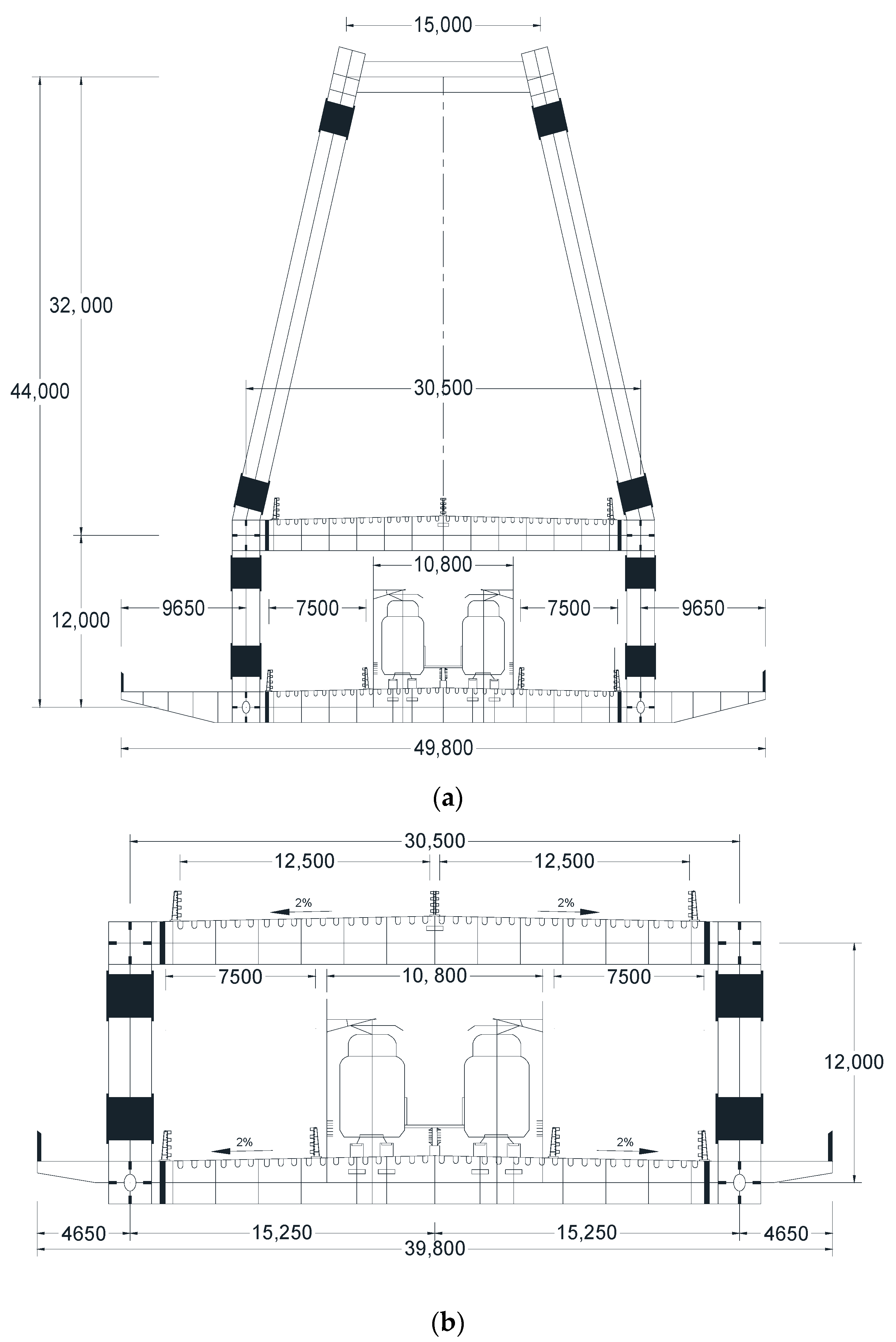
3. Bridge Case Study
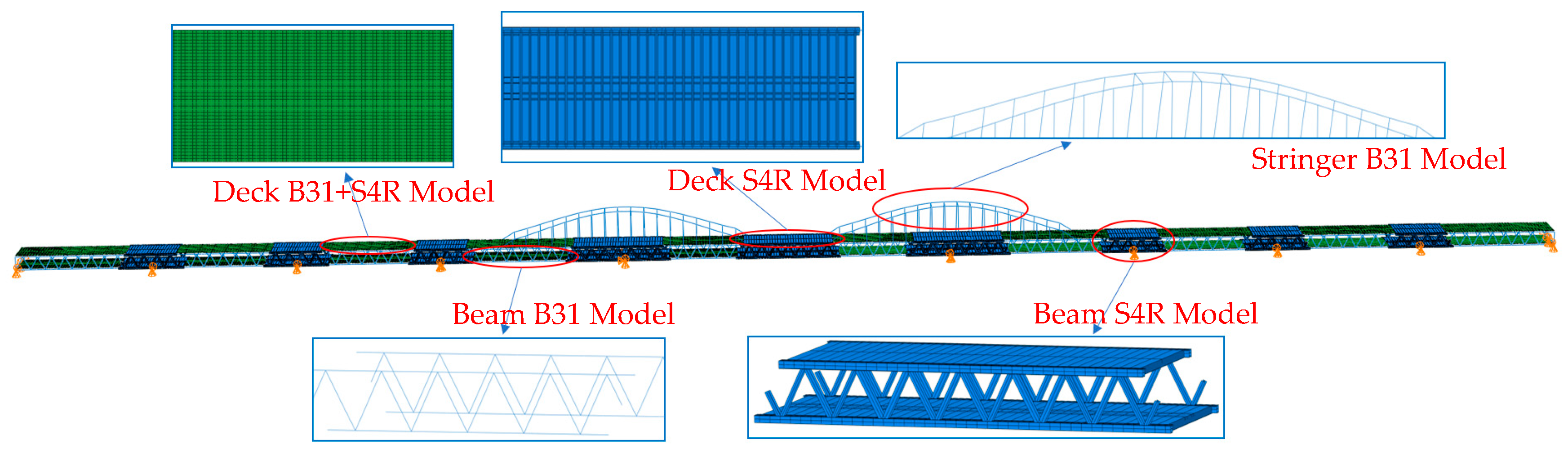
3.1. FE Modeling
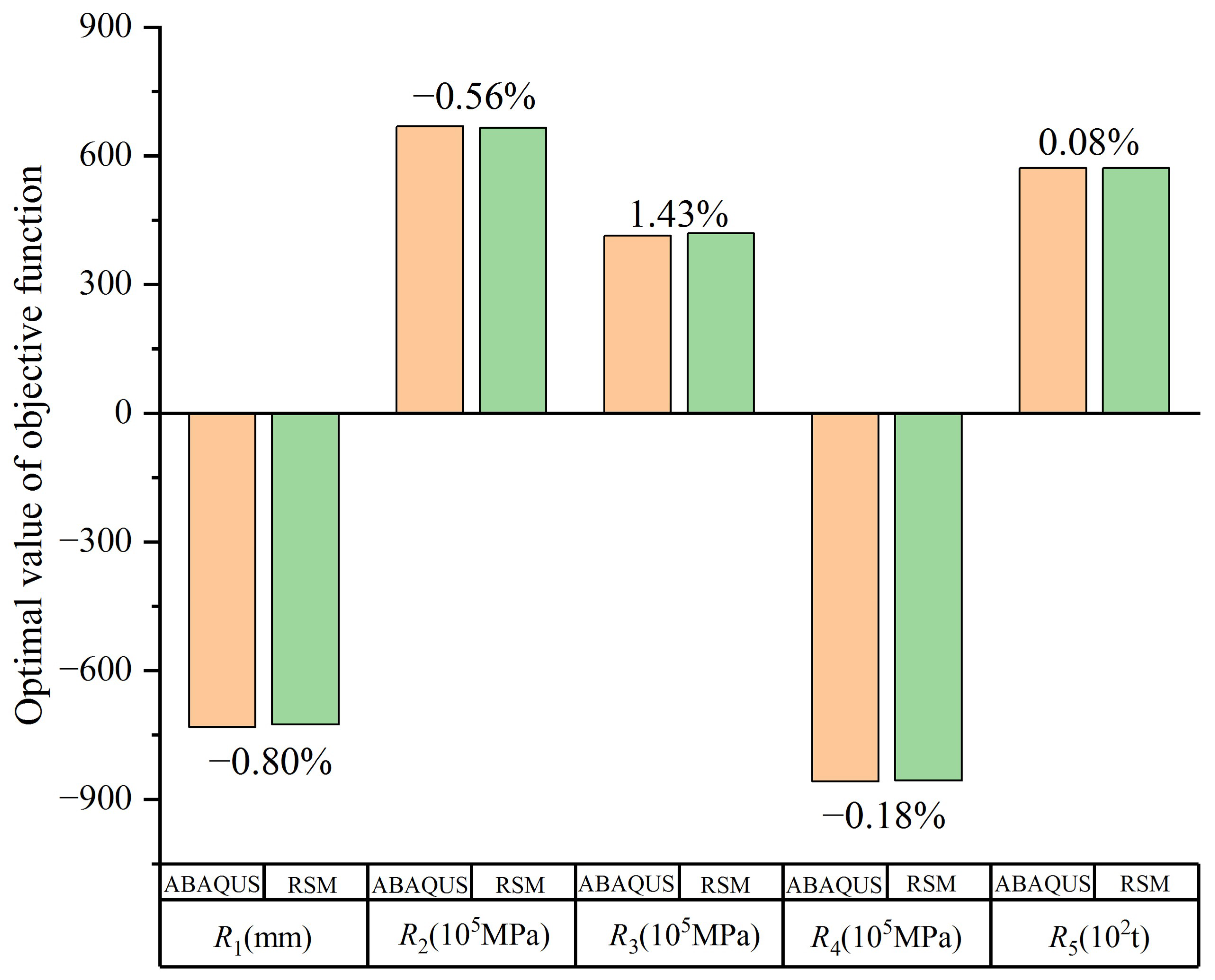
3.2. Verification of FE Modeling
4. Model Lightweight Algorithm
4.1. Choice of Optimization Parameters and Objective Function
4.2. Response Surface Analysis Fitting and Precision Testing
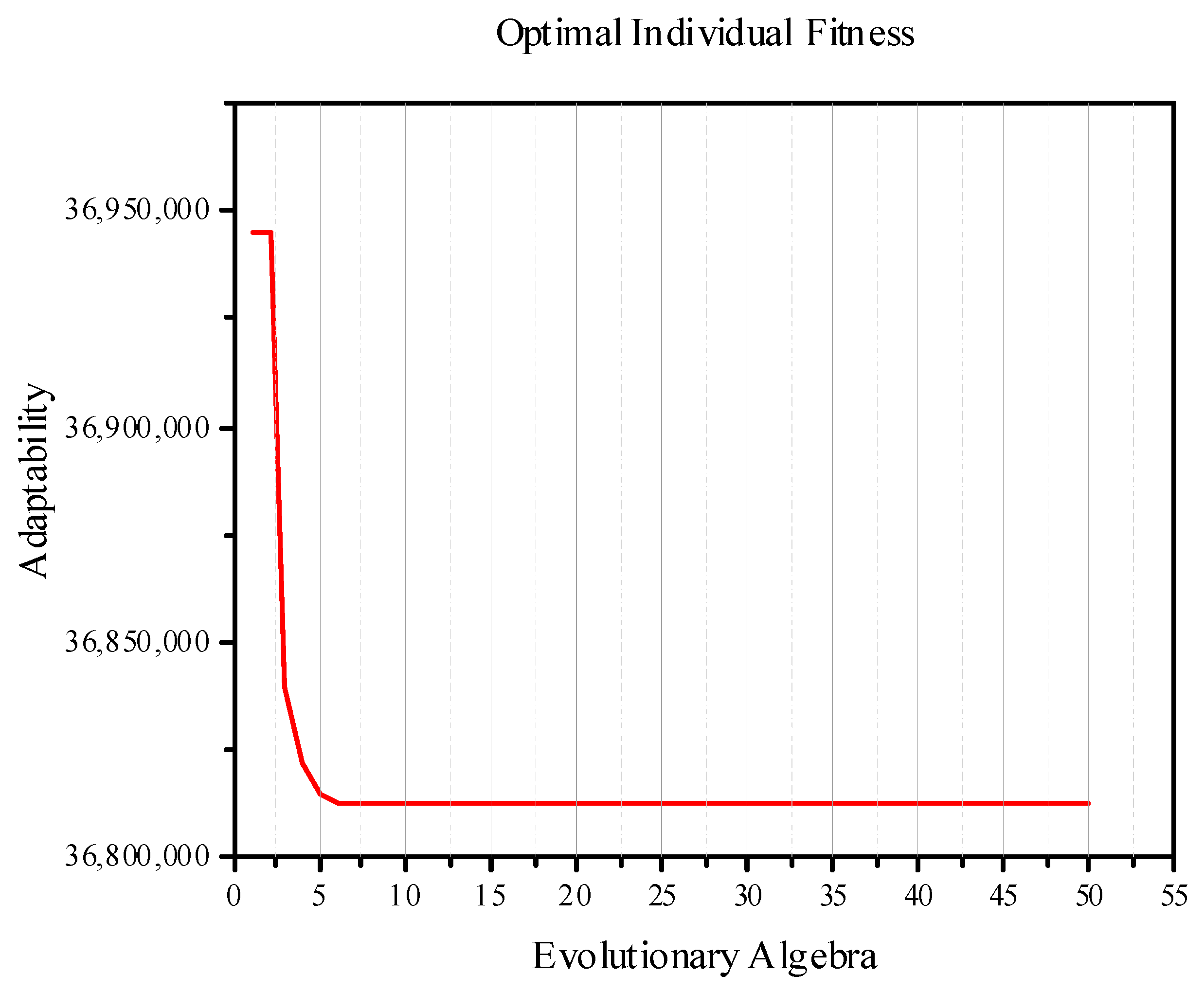
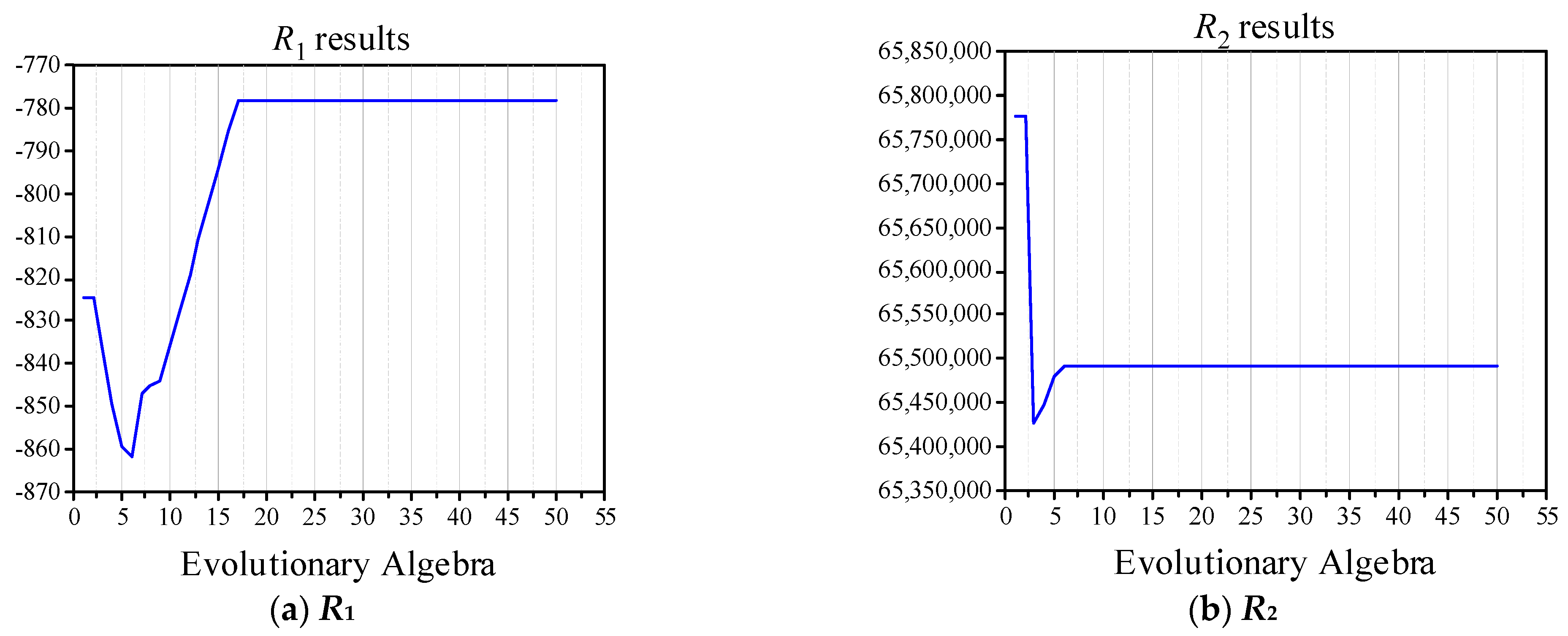
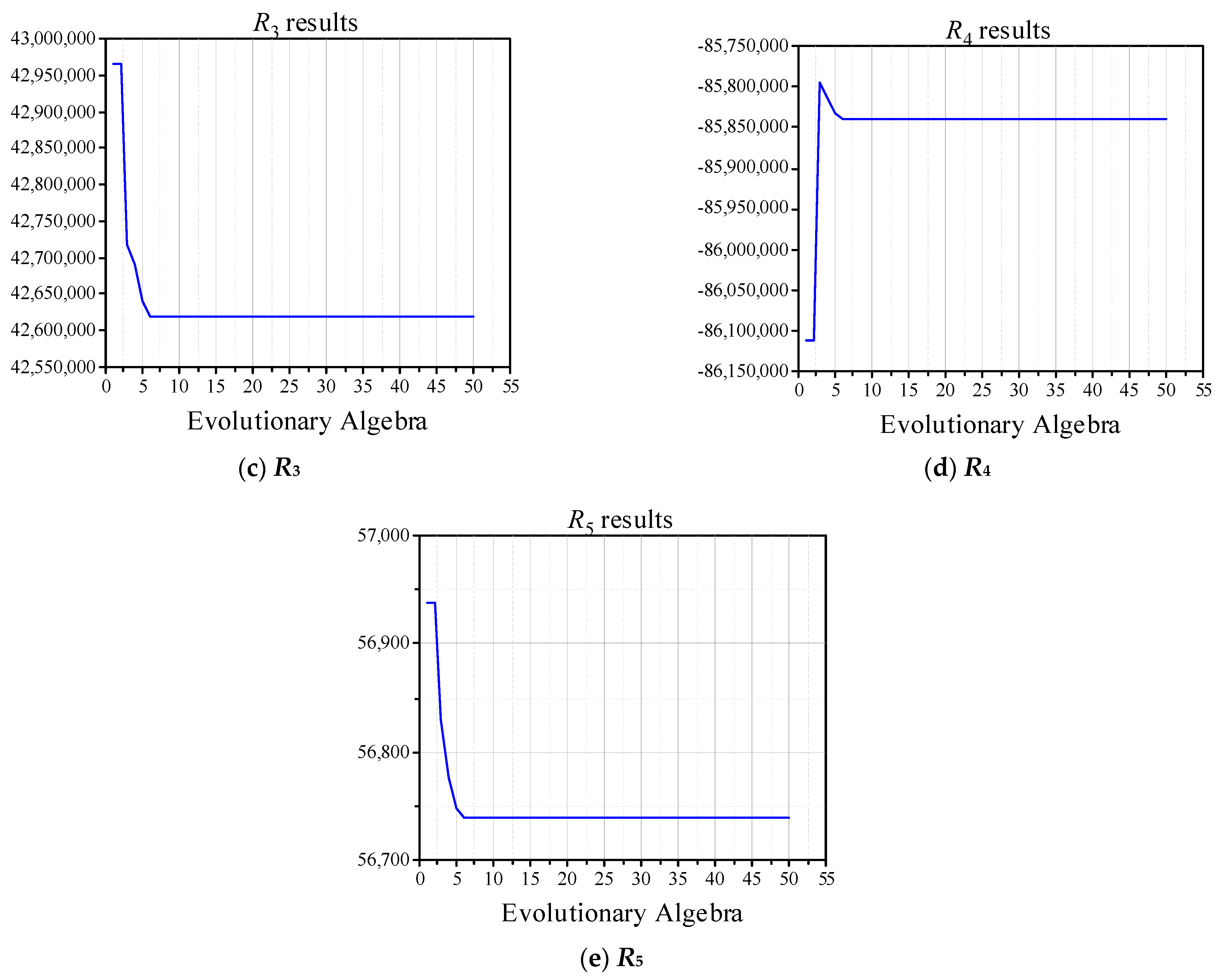
4.3. Pareto Solutions
- (1)
- Initialize the particle population size as N = 500, the particle dimension as D = 4, the maximum number of iterations as T = 50, and the learning factors as c1 = c2 = 1.49445. Determine the particle position range by Table 1; the maximum particle velocity is vmax = 1 and the minimum particle velocity is vmin = −1.
- (2)
- Initialize the population with random particle positions x and velocities v within the specified range, the individual best position p and the best value pbest for each particle, and the global best position g and best value gbest for the entire swarm.
- (3)
- Calculate the fitness function based on the response surface equation system and supplement the fitness weighting matrix to regulate the importance ranking of multi-objective parameter optimization.
- (4)
- Calculate the individual best value for each particle to screen out the global best value for the entire swarm.
- (5)
- Update all particle positions x and velocity values v, handle the boundary conditions, and update the individual best position p and best value pbest, as well as the global best position g and best value gbest for the entire swarm.
- (6)
- Check if the termination condition is met (i.e., reaching the maximum number of iterations); if so, terminate the search process and output the global optimization value; otherwise, continue with iteration optimization.
4.4. Optimization Result Certification
5. Conclusions
- (1)
- A lightweight calculation equation based on the FE model of the engineering structure supported by the RSM was established. Via significance analysis, it was found that the use of a simplified incomplete quadratic polynomial as the response surface equation can accurately fit the numerical relationships between the optimized parameters and the target response function to be corrected. The fitting accuracy was found to be high, which greatly reduces the workload of structural modeling in the optimization design and ensures the accuracy and reliability of the optimization.
- (2)
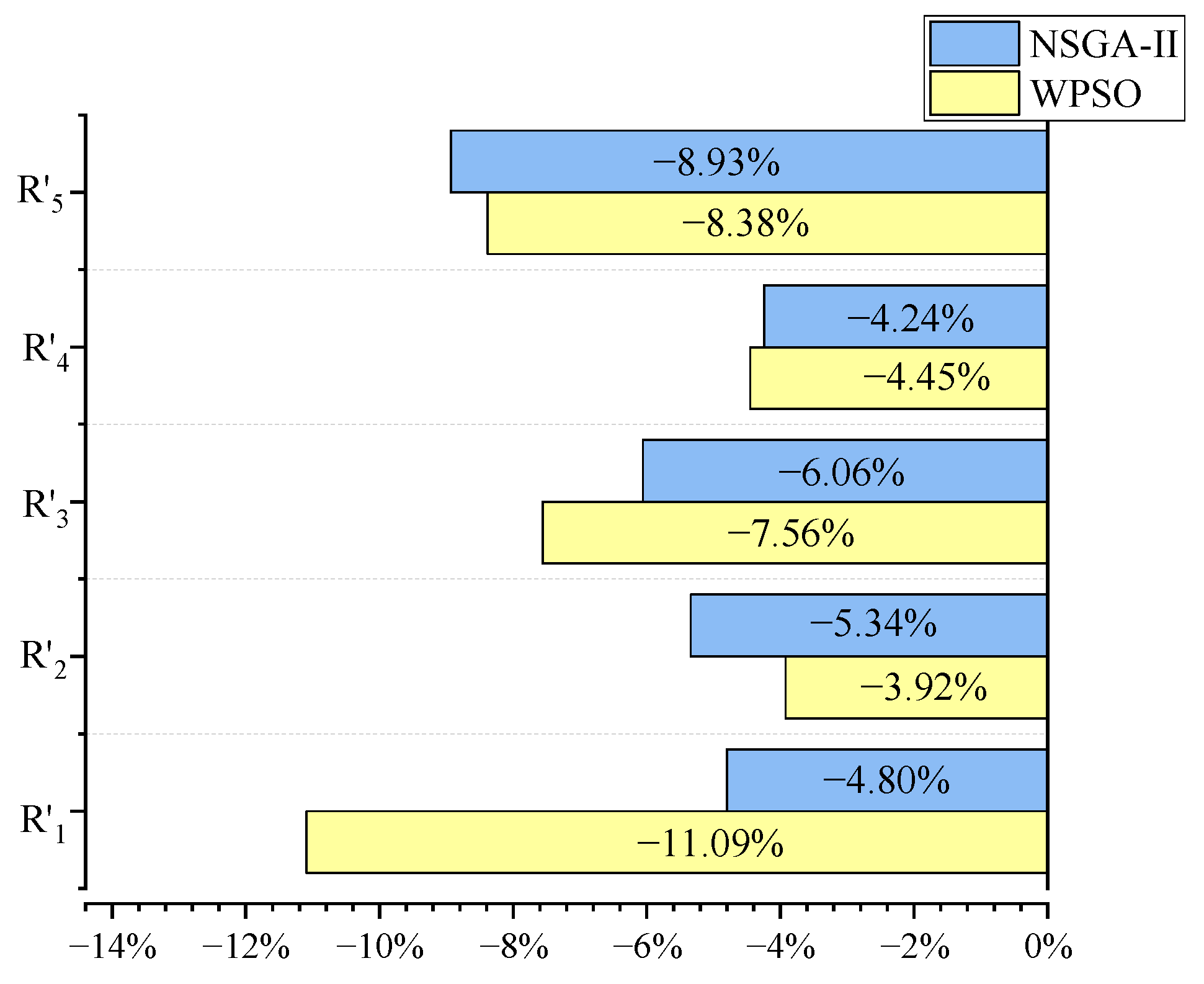
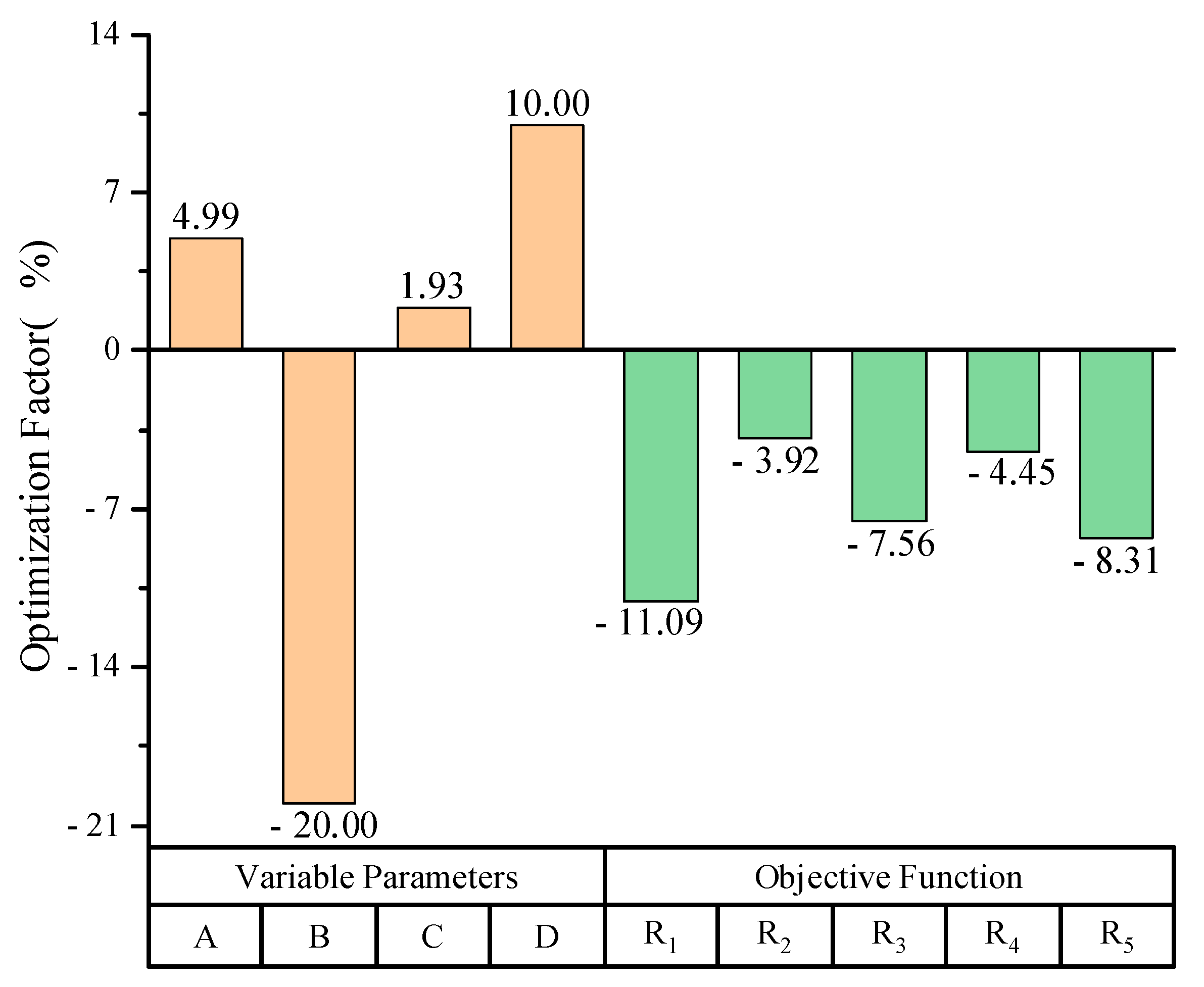
- Based on the lightweight equation established using the RSM, two optimization methods, namely, WPSO and NSGA-II, were used to minimize the quantity of upper structure engineering as the primary control objective and to minimize the mid-span vertical deflection and the axial compression force in the hollow pier top tie rod as the secondary control objectives. After comparing the optimization results, WPSO was chosen as the final optimization scheme. After optimizing the design parameters, the mid-span vertical deflection under constant load, the axial internal force of the stiffening chord, the longitudinal internal force of the bottom plate of the bridge deck panel, and the axial internal force of the compressed chord of the pier top truss were reduced by 3% to 11% as compared with the original design. Furthermore, the quantity of upper structure engineering was reduced by 8.38%, which improved the structural performance while reducing the engineering cost.
- (3)
- In the design stage, bridge structures usually require the manual adjustment of a large number of design parameters to achieve the control of the structural performance, material usage, and engineering cost. The process of establishing complex FE models and adjusting parameter combinations is time-consuming and difficult to control and involves many iterations. This article proposed a method that can achieve the accurate optimization reasoning of certain control indicators of bridge structures via mathematical optimization using lightweight response surface equations. Moreover, when bridge structures enter the service period, this method can still be used to simulate the actual parameters of the bridge structure under current conditions by using health monitoring data. Thus, the precise simulation of the entire life cycle of the bridge structure can be achieved. Therefore, this method is suitable not only for the optimization of structural parameters in the bridge design stage but also for the simulation of the structural health status of bridge structures in the operation stage.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| RSM | Response surface method |
| WPSO | Weighted particle swarm optimization |
| FE | Finite element |
| PSO | Particle swarm optimization |
| CCD | Central composite design |
| MPC | Multipoint constraint |
| C.V. | Coefficient of variation |
| NSGA-II | Non-dominated sorting genetic algorithm II |
References
- Zheng, K.; Feng, X.; Heng, J.; Zhang, Y.; Zhu, J.; Lei, M.; Wang, Y.; Hu, B.; Xiong, Z.; Tang, J.; et al. State-of-the-art review of steel bridges in 2020. J. Civ. Environ. Eng. 2021, 43, 53–69. [Google Scholar]
- Dai, J.; Qin, F.; Di, J.; Chen, Y. Review on Cable Force Optimization Method for Cable-stayed Bridge in Completed Bridge State. China J. Highw. Transp. 2019, 32, 17–37. [Google Scholar]
- Ye, D.; Xu, Z.; Liu, Y.Q. Solution to the problem of bridge structure damage identification by a response surface method and an imperialist competitive algorithm. Sci. Rep. 2022, 12, 13. [Google Scholar] [CrossRef]
- Fang, S.J. Damage detection of long-span bridge structures based on response surface model. Therm. Sci. 2020, 24, 1497–1504. [Google Scholar] [CrossRef]
- Li, F.; Liu, Y.K.; Yang, J. Durability assessment method of hollow thin-walled bridge piers under rockfall impact based on damage response surface. Sustainability 2022, 19, 12196. [Google Scholar] [CrossRef]
- Miao, C.Q.; Zhuang, M.L.; Dong, B. Stress corrosion of bridge cable wire by the response surface method. Strength Mater. 2019, 51, 646–652. [Google Scholar] [CrossRef]
- Hu, S.; Chen, B.; Song, G.; Wang, L. Resilience-based seismic design optimization of highway RC bridges by response surface method and improved non-dominated sorting genetic algorithm. Bull. Earthq. Eng. 2022, 20, 449–476. [Google Scholar] [CrossRef]
- Li, H.; Li, L.; Wu, W.; Xu, L. Seismic fragility assessment framework for highway bridges based on an improved uniform design-response surface model methodology. Bull. Earthq. Eng. 2020, 18, 2329–2353. [Google Scholar] [CrossRef]
- Chen, L.; Huang, C.; Gu, Y. Seismic vulnerability analysis of simply supported highway bridges based on an improved response surface method. Eng. Mech. 2018, 35, 208–218. [Google Scholar]
- Ma, Y.; Liu, Y.; Liu, J. multi-scale finite element model updating of CFST composite truss bridge based on response surface method. China J. Highw. Transp. 2019, 32, 51–61. [Google Scholar]
- Ji, W.; Shao, T.Y. Finite element model updating for improved box girder bridges with corrugated steel webs using the response surface method and fmincon algorithm. Ksce J. Civ. Eng. 2021, 25, 586–602. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, B.; Wang, B.; Chen, K.; Lü, J. A method for modifying dynamic model of cable-stayed bridge based on response surface method. J. Highw. Transp. Res. Dev. 2022, 39, 46–52, 61. [Google Scholar]
- Li, Y.; Liu, X.; Chen, Z.; Zhang, H. Updating of cable-stayed bridge model based on cable force response surface method. J. China Railw. Soc. 2021, 43, 168–174. [Google Scholar]
- Sun, Y. Research on Computational Model Modification of Steel-Concrete Composite Beam Self-Anchored Suspension Bridge Based on Response Surface Method. Master’s Thesis, Central South University, Changsha, China, 2020. [Google Scholar]
- Zhang, Q. Study on preparation and mechanical properties of green bridge concrete building materials: Based on response surface method. Fresenius Environ. Bull. 2021, 30, 5816–5825. [Google Scholar]
- Lehky, D.; Somodikova, M.; Lipowczan, M.; Novak, D. Inverse response surface method for prestressed concrete bridge design. In Proceedings of the 10th International Conference on Bridge Maintenance, Safety and Management (IABMAS), Electr Network, Sapporo, Japan, 11–18 April 2021; CRC Press-Balkema: Boca Raton, FL, USA, 2021. APR 11-18. [Google Scholar]
- Zhan, Y.; Hou, Z.; Shao, J.; Zhang, Y.; Sun, Y. Cable force optimization of irregular cable-stayed bridge based on response surface method and particle swarm optimization algorithm. Bridge Constr. 2022, 52, 16–23. [Google Scholar]
- Wang, D.; Zhou, W.; Li, M. Research on weight asymmetry alignment correction of main girder of long-span concrete cable-stayed bridge based on response surface method. Highw. Automot. Appl. 2022, 2, 94–96. [Google Scholar]
- Bruno, D.; Lonetti, P.; Pascuzzo, A. An optimization model for the design of network arch bridges. Comput. Struct. 2016, 170, 13–25. [Google Scholar] [CrossRef]
- Lonetti, P.; Pascuzzo, A. Design analysis of the optimum configuration of self-anchored cable-stayed suspension bridges. Struct. Eng. Mech. 2014, 51, 847–866. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, J.; Zou, D.; Wang, X.; Shi, J. Status quo and development trend of light-weight, high-strength, and durable structural materials applied in marine bridge engineering. Strateg. Study CAE 2019, 21, 31–40. [Google Scholar] [CrossRef]
- Peng, Z. Research on the Strengthening and Toughening Mechanisms of Ti Microalloyed Hot-Rolled High-Strength Steel Plates. Master’s Thesis, South China University of Technology, Guangzhou, China, 2016. [Google Scholar]
- Liu, Y. Research on the Influence of Size Parameter and Section Form on the Stress of Orthotropic Steel Deck Slab. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2018. [Google Scholar]
- Su, J.; Wang, F. Brief introduction to design of Zengjiayan Jialing river bridge of Chongqing. Technol. Highw. Transp. 2016, 32, 38–42. [Google Scholar]
- Mei, X.; Xu, W.; Duan, X.; Chen, X. Overall design of Pingtan strait combined bridges. Railw. Stand. Des. 2020, 64, 18–23. [Google Scholar]
- Yang, Z.; Wang, L.; Wang, J.; Sun, X.; Liang, L. Structural design of main bridge of Niutianyang bridge. Bridge Constr. 2021, 51, 1–8. [Google Scholar]
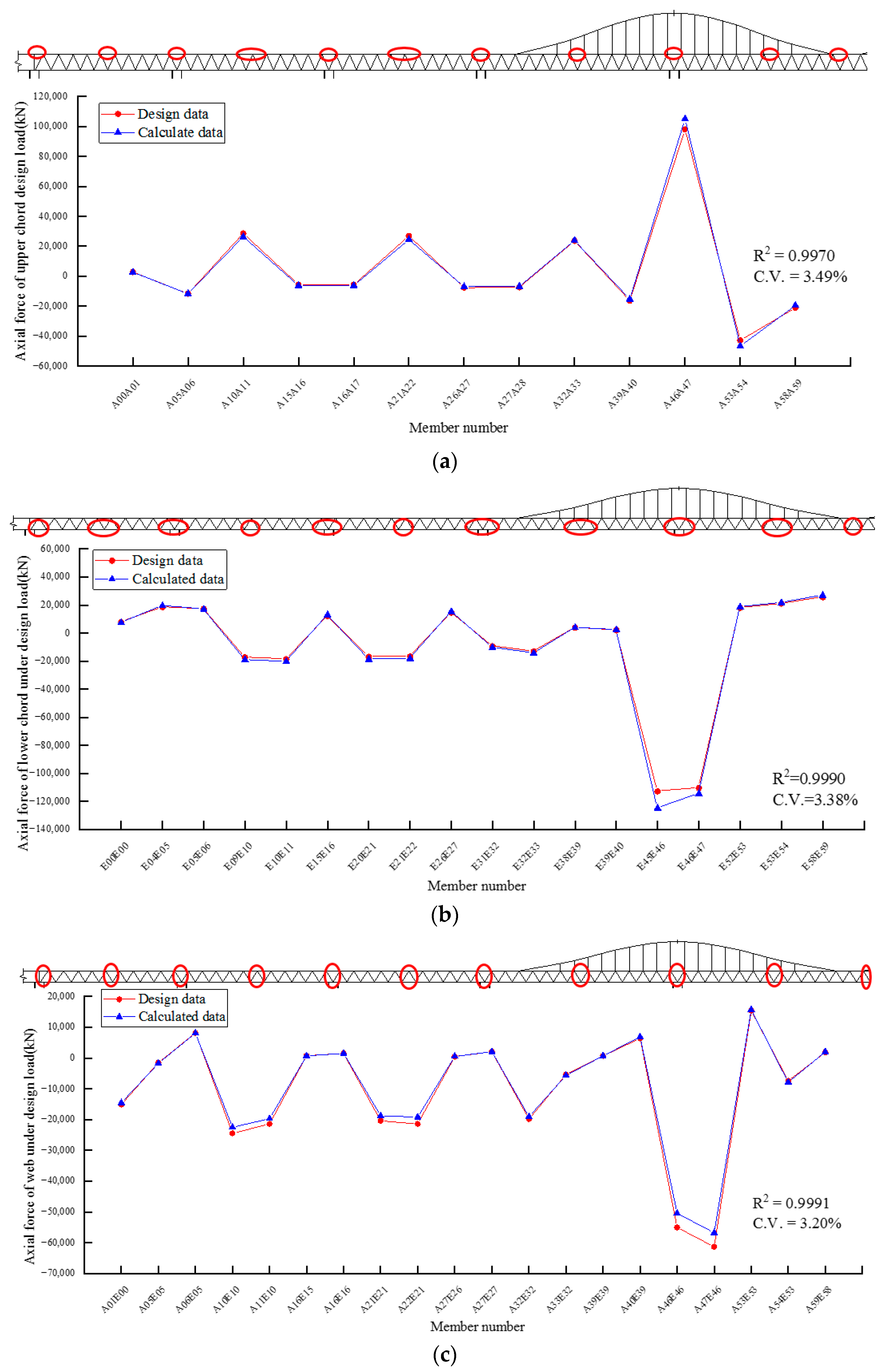
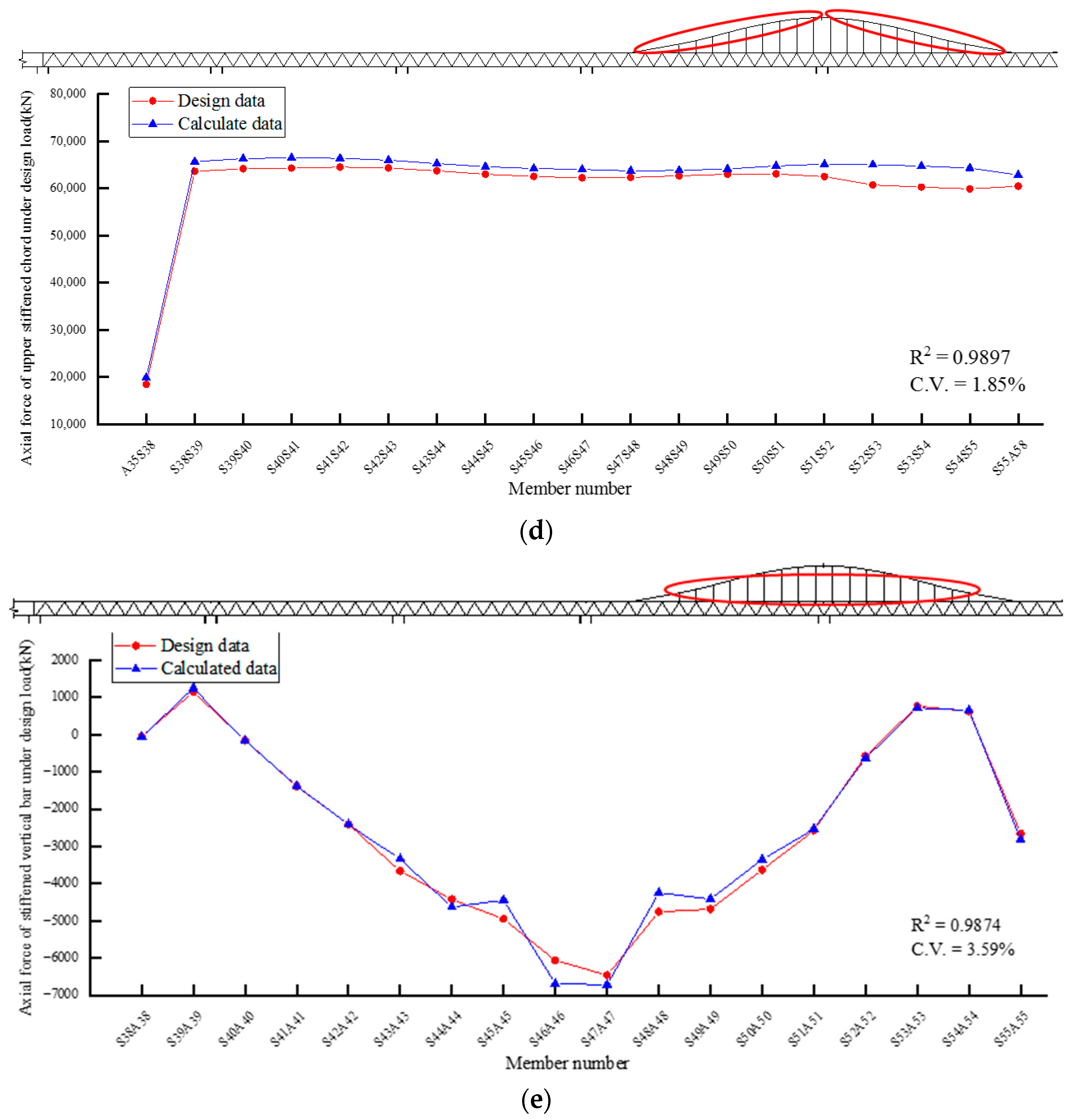
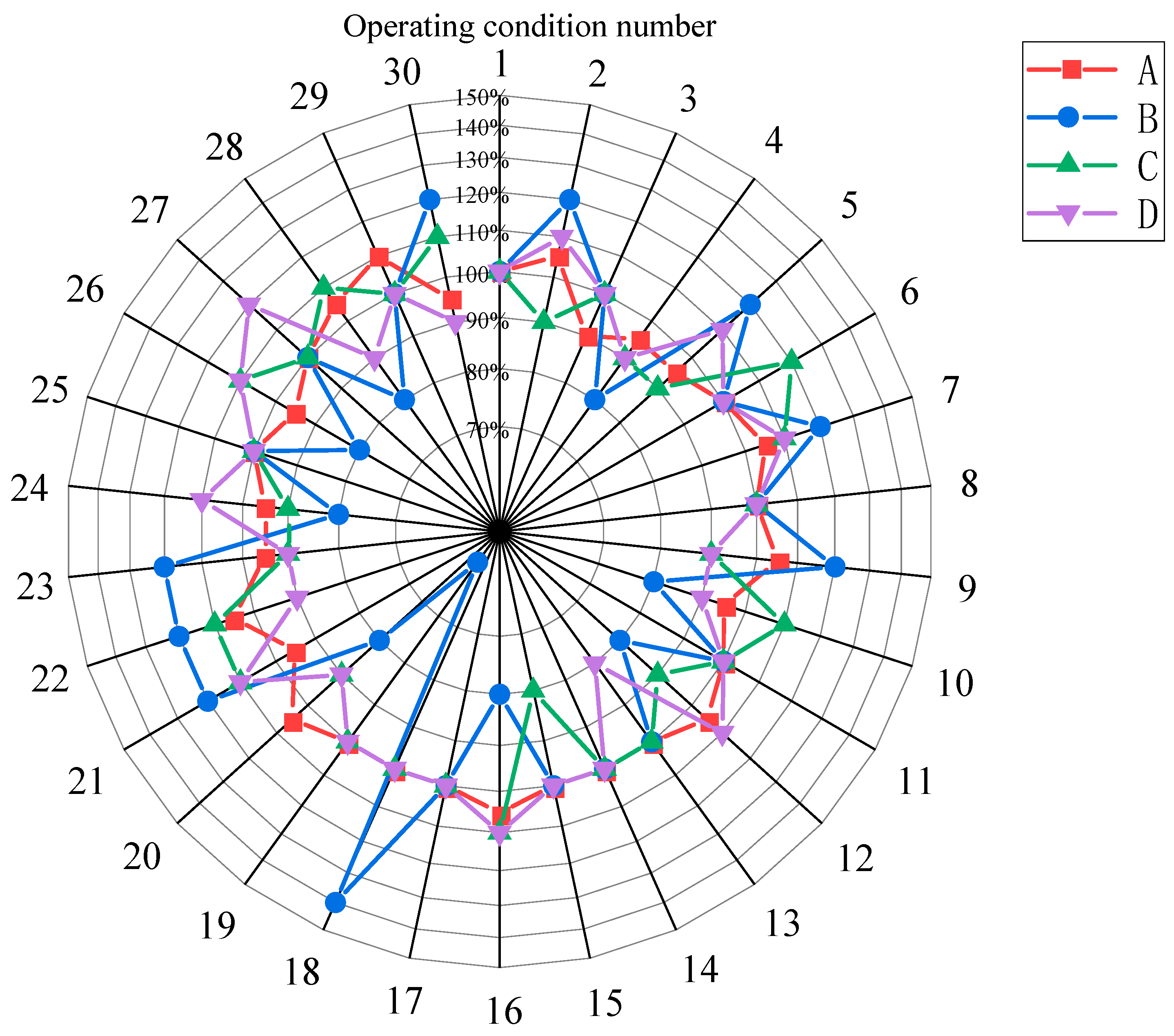
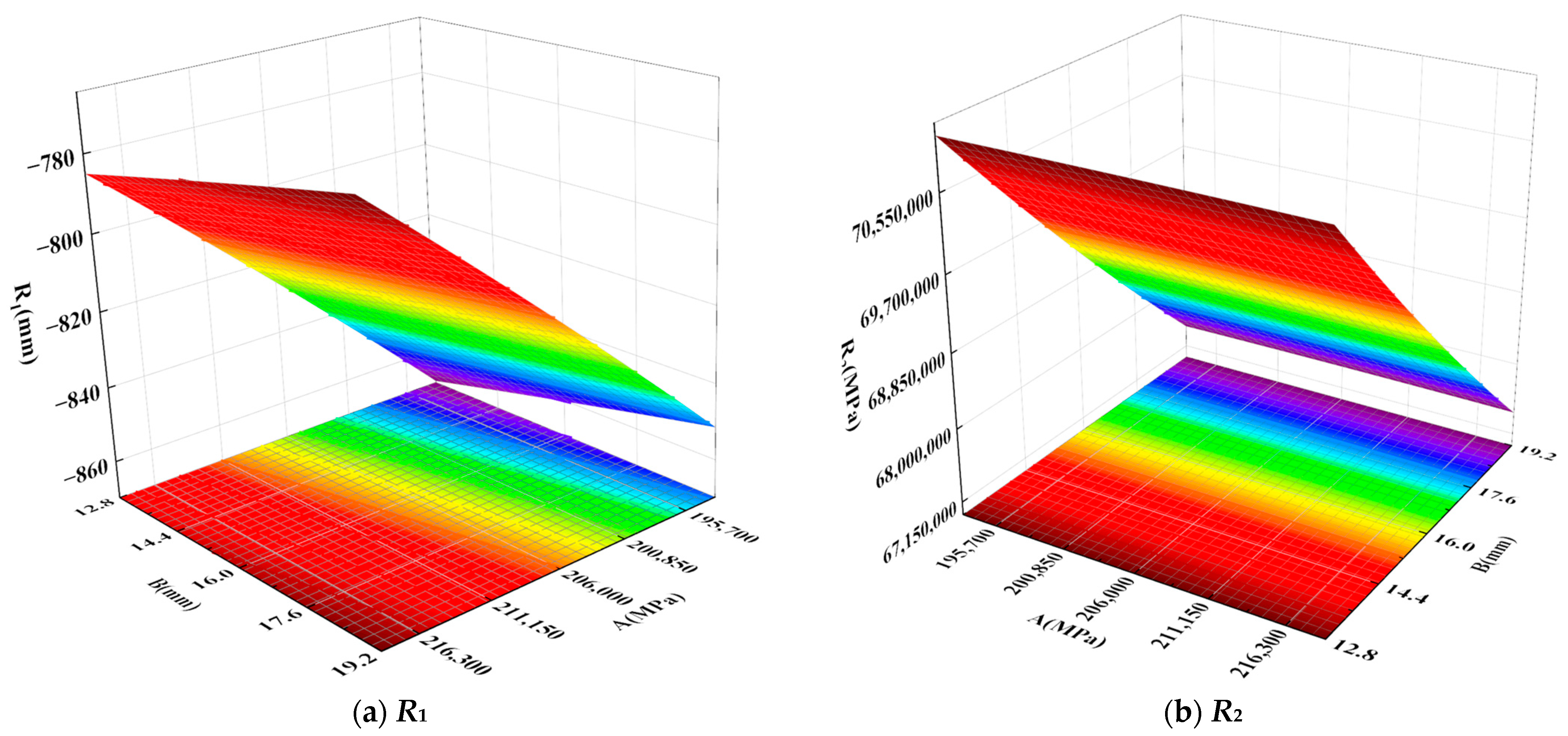
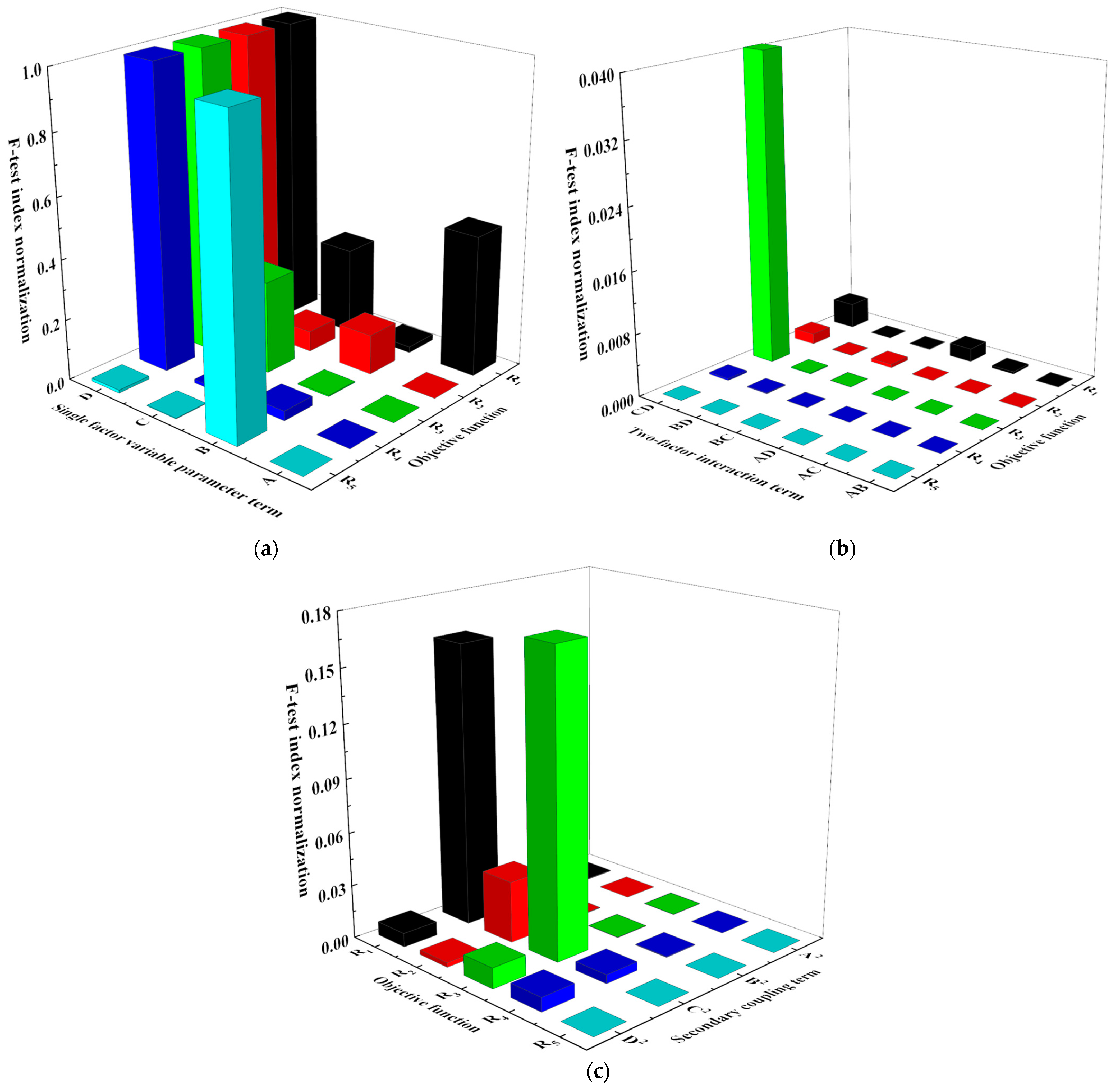
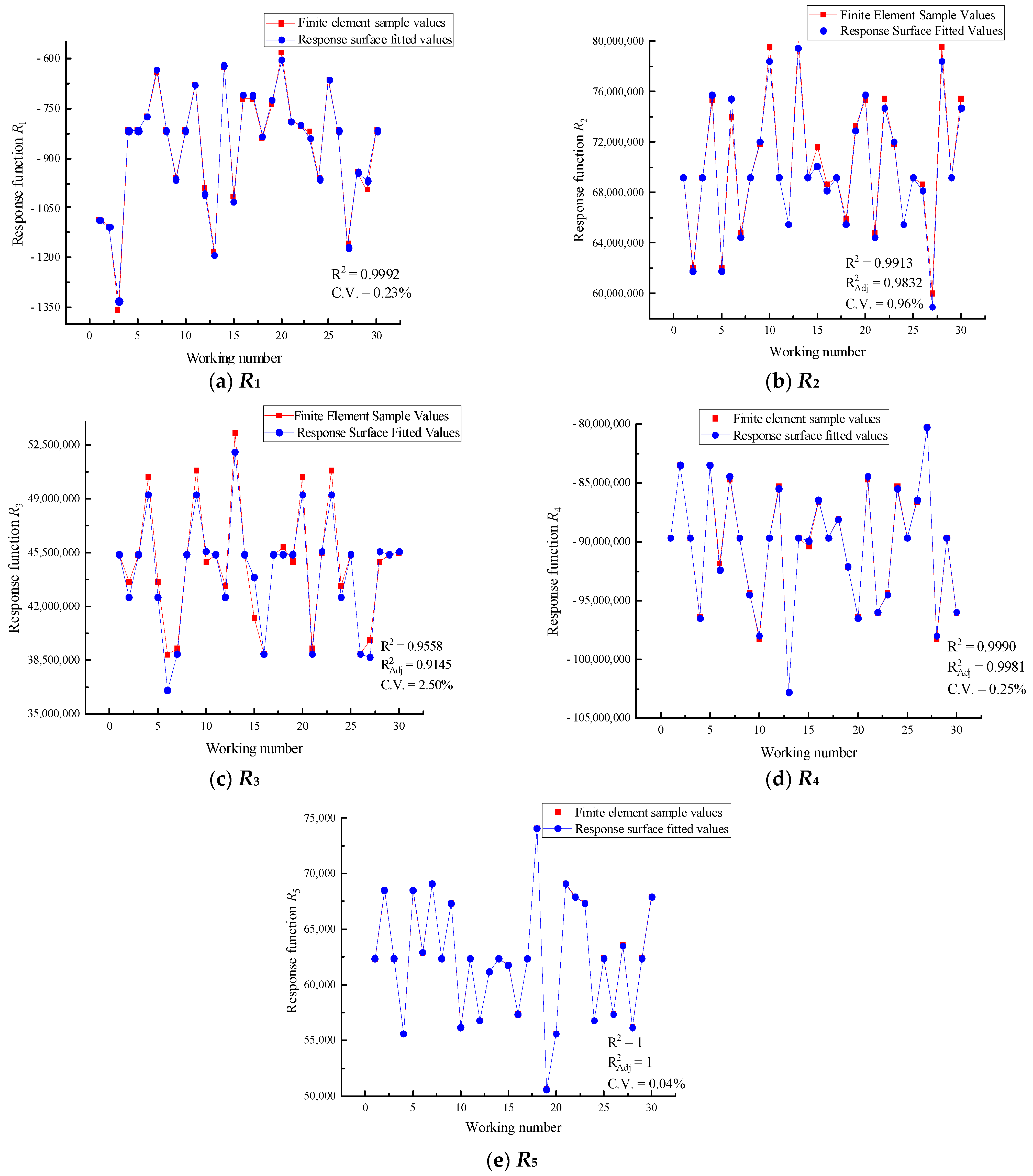
| Label | Parameter | Range of Correction (%) | Level | ||
|---|---|---|---|---|---|
| Low | Initial | High | |||
| A | Steel elastic modulus (MPa) | ±5 | 195,700 | 206,000 | 216,300 |
| B | Bridge deck thickness (mm) | ±20 | 12.8 | 16 | 19.2 |
| C | Maximum length of vertical stiffening rods (mm) | ±10 | 28,800 | 32,000 | 35,200 |
| D | Relative distance between double-layer main beams (mm) | ±10 | 10,800 | 12,000 | 13,200 |
| Label | Objective Function |
|---|---|
| Mid-span vertical deflection | |
| Axial internal force of the stiffened string | |
| Longitudinal internal force of the bridge deck bottom plate | |
| Axial internal force of the empty tube of the web bar under compression at the pier top | |
| Superstructure works |
| Experimental Design Elements | Standard Deviation | Variance Inflation Factor | Design Assessment Probability Calculation | ||
|---|---|---|---|---|---|
| 0.5 Standard Deviation | 1.0 Standard Deviation | 2.0 Standard Deviation | |||
| A | 0.20 | 1.00 | 20.9% | 63.0% | 99.5% |
| B | 0.20 | 1.00 | 20.9% | 63.0% | 99.5% |
| C | 0.20 | 1.00 | 20.9% | 63.0% | 99.5% |
| D | 0.20 | 1.00 | 20.9% | 63.0% | 99.5% |
| AB | 0.25 | 1.00 | 15.5% | 46.5% | 96.2% |
| AC | 0.25 | 1.00 | 15.5% | 46.5% | 96.2% |
| AD | 0.25 | 1.00 | 15.5% | 46.5% | 96.2% |
| BC | 0.25 | 1.00 | 15.5% | 46.5% | 96.2% |
| BD | 0.25 | 1.00 | 15.5% | 46.5% | 96.2% |
| CD | 0.25 | 1.00 | 15.5% | 46.5% | 96.2% |
| A2 | 0.19 | 1.05 | 68.7% | 99.8% | 99.9% |
| B2 | 0.19 | 1.05 | 68.7% | 99.8% | 99.9% |
| C2 | 0.19 | 1.05 | 68.7% | 99.8% | 99.9% |
| D2 | 0.19 | 1.05 | 68.7% | 99.8% | 99.9% |
| Optimization Group | Optimization Objective | Optimization Coefficient (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| A (MPa) | B (mm) | C (mm) | D (mm) | R1′ | R2′ | R3′ | R4′ | R5′ | |
| 1 | 216,237 | 12.94 | 34,599 | 13,185 | −12.97% | −2.32% | −12.36% | −3.38% | −7.67% |
| 2 | 216,237 | 12.95 | 34,599 | 12,047 | −5.80% | 4.70% | −5.38% | 2.17% | −8.57% |
| 3 | 216,237 | 12.96 | 34,999 | 13,185 | −12.87% | −1.82% | −13.48% | −3.23% | −7.57% |
| 4 | 216,279 | 13.00 | 32,618 | 13,200 | −4.80% | −5.34% | −6.06% | −4.24% | −8.93% |
| 5 | 216,236 | 12.96 | 35,135 | 13,185 | −12.81% | −1.63% | −13.88% | −3.17% | −7.55% |
| Optimization Group | Optimization Objective | Optimization Coefficient (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| A (MPa) | B (mm) | C (mm) | D (mm) | R1′ | R2′ | R3′ | R4′ | R5′ | |
| 1 | 216,300 | 12.80 | 32,838 | 13,200 | −11.25% | −3.76% | −7.90% | −4.40% | −8.35% |
| 2 | 216,300 | 12.80 | 32,723 | 13,200 | −11.18% | −3.85% | −7.72% | −4.43% | −8.35% |
| 3 | 216,279 | 12.80 | 32,618 | 13,200 | −11.09% | −3.92% | −7.56% | −4.45% | −8.38% |
| 4 | 216,300 | 12.80 | 33,088 | 13,200 | −11.38% | −3.55% | −8.30% | −4.33% | −8.31% |
| 5 | 216,300 | 12.82 | 32,816 | 13,200 | −11.24% | −3.79% | −7.86% | −4.41% | −8.29% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Xi, R.; Guo, X.; Ma, Y. The Structural Design and Optimization of Top-Stiffened Double-Layer Steel Truss Bridges Based on the Response Surface Method and Particle Swarm Optimization. Appl. Sci. 2023, 13, 11033. https://doi.org/10.3390/app131911033
Wang L, Xi R, Guo X, Ma Y. The Structural Design and Optimization of Top-Stiffened Double-Layer Steel Truss Bridges Based on the Response Surface Method and Particle Swarm Optimization. Applied Sciences. 2023; 13(19):11033. https://doi.org/10.3390/app131911033
Chicago/Turabian StyleWang, Lingbo, Rongjie Xi, Xinjun Guo, and Yinping Ma. 2023. "The Structural Design and Optimization of Top-Stiffened Double-Layer Steel Truss Bridges Based on the Response Surface Method and Particle Swarm Optimization" Applied Sciences 13, no. 19: 11033. https://doi.org/10.3390/app131911033
APA StyleWang, L., Xi, R., Guo, X., & Ma, Y. (2023). The Structural Design and Optimization of Top-Stiffened Double-Layer Steel Truss Bridges Based on the Response Surface Method and Particle Swarm Optimization. Applied Sciences, 13(19), 11033. https://doi.org/10.3390/app131911033






