Conditions for and Characteristics of the Dispersion of Gel Fuel Droplets during Ignition
Abstract
:1. Introduction
2. Materials and Methods
2.1. Component Compositions of Liquid Mixtures
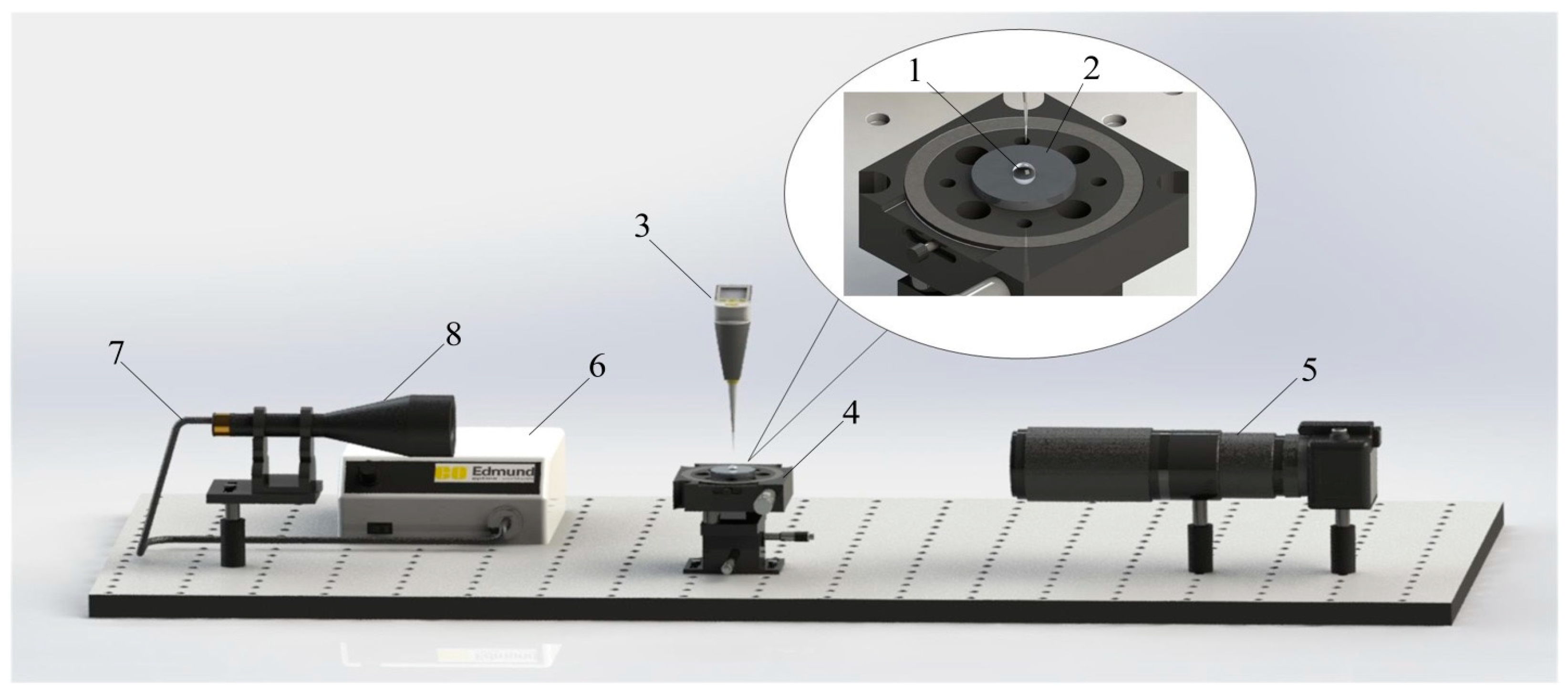
2.2. Analytical Studies
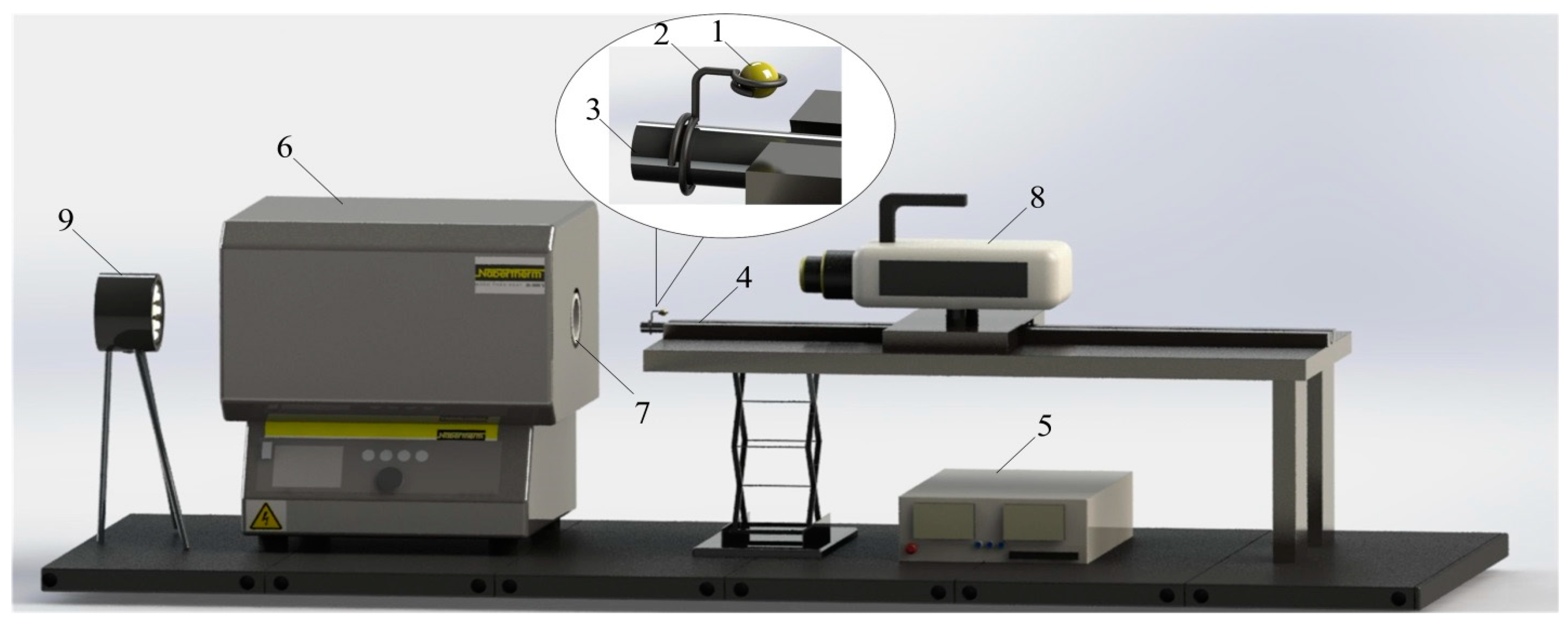
2.3. Experimental Setup for Creating the Conditions for High-Temperature Heating of Liquid Mixtures
- (1)
- The heat supply mechanism was mixed (conductive, convective, and radiation);
- (2)
- The temperature of the heating medium was 900 °C;
- (3)
- The number of components in the composition of the droplet and their concentration were two components with a concentration of 50% × 50% (vol.);
- (4)
- The droplet formation conditions were intensive mixing of the components at a temperature corresponding to laboratory conditions (from 20 to 24 °C) for at least 20 min with a magnetic armature rotation speed of at least 1200 rpm;
- (5)
- The droplet location was on a holder.
3. Results and Discussion
- Monotonic evaporation occurs if none of the components that make up the binary liquid reach the boiling point.
- The boiling of binary liquids occurs if only the low-boiling component that is part of the component composition of the mixture reaches the boiling point during heating. This is realized by mixing liquid components within one group with the mutual solubility of the components: polar; dispersive with a high value of the polar part; dispersive with a low value of the polar part; dispersive. This also occurs by mixing liquid components with partial solubility within the different groups identified above—first group + second group; first group + third group; second group + third group; second group + fourth group; third group + fourth group—when isothermal conditions are not reached at the liquid–liquid interface.
- Puffing occurs by mixing insoluble (or poorly soluble) liquid components that are characterized by a significant difference between the polar and dispersive parts of surface tension and with the obligatory achievement of isothermal conditions at the liquid–liquid interface. Puffing can occur by mixing components in the following combinations of groups: first group + fourth group; first group + second group; second group + fourth group.
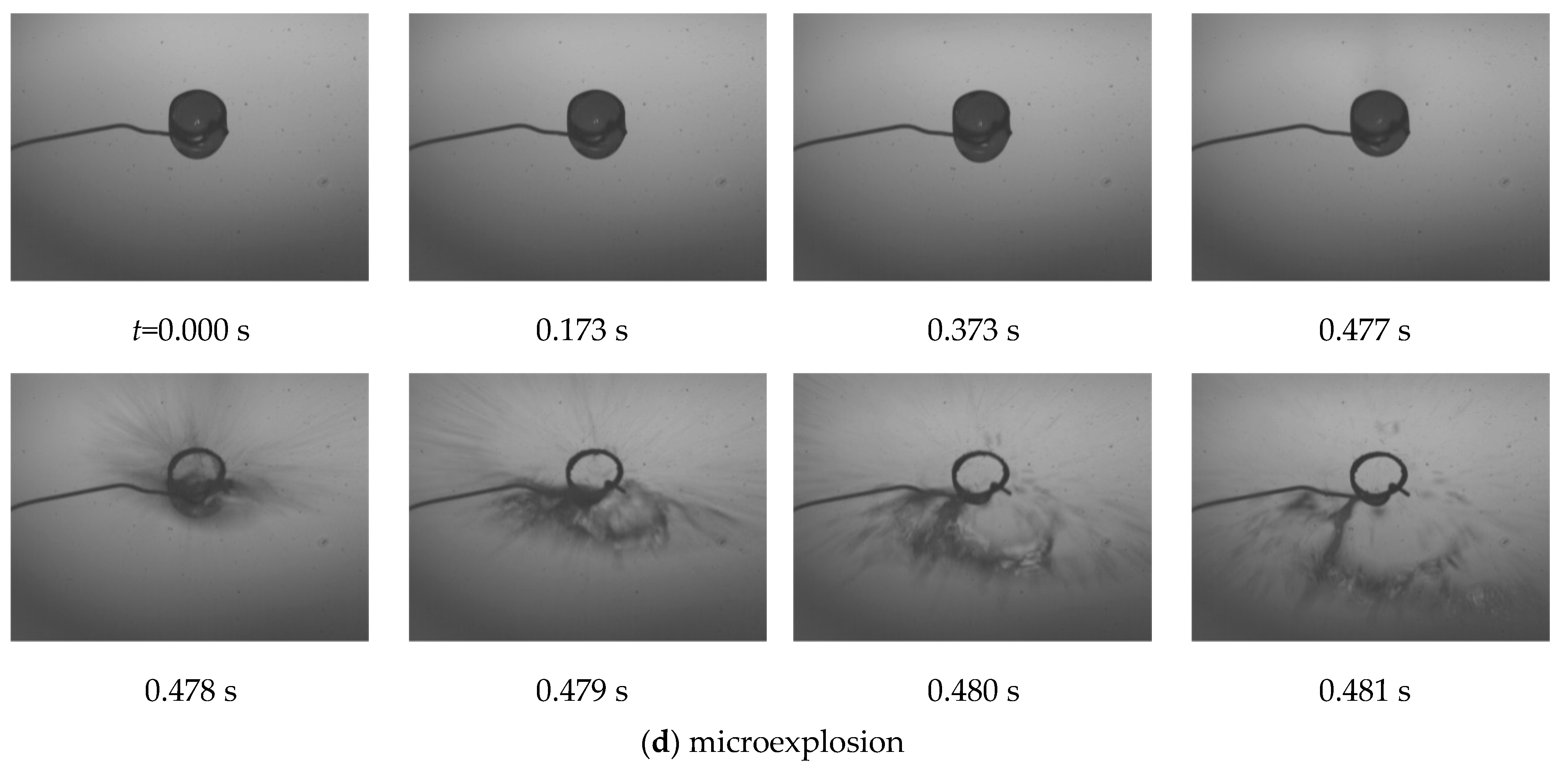
- Microexplosions occur only when isothermal conditions are necessarily reached at the liquid–liquid interface when mutually insoluble components are mixed, and one component must be characterized by the ratio of / > 1 (must be polar), and the second by the ratio of / ≤ 0.1 (must be dispersive). In addition, it is necessary to provide external heating conditions under which the value of the SFE of the liquid–liquid interface formation tends to zero.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SFE | surface free energy |
| Greek symbols | |
| surface tension for liquid, surface free energy for solid, mN/m | |
| static contact angle, ⁰ | |
| tb | boiling temperature, °C |
| Subscripts | |
| L | liquid |
| S | solid (surface) |
| P | polar part |
| D | dispersive part |
| 1,2 | serial number of the test liquid/surface |
References
- Feoktistov, D.V.; Glushkov, D.O.; Kuznetsov, G.V.; Orlova, E.G. Gel Fuels Based on Oil-Filled Cryogels: Corrosion of Tank Material and Spontaneous Ignition. Chem. Eng. J. 2020, 421, 127765. [Google Scholar] [CrossRef]
- Kadota, T.; Yamasaki, H. Recent Advances in the Combustion of Water Fuel Emulsion. Prog. Energy Combust. Sci. 2002, 28, 385–404. [Google Scholar] [CrossRef]
- Khanpit, V.; Tajane, S.P.; Mandavgane, S.A. Experimental Studies on Coal-Water Slurry Fuel Prepared from Pretreated Low-Grade Coal. Int. J. Coal Prep. Util. 2022, 42, 831–845. [Google Scholar] [CrossRef]
- Glushkov, D.O.; Nyashina, G.S.; Anand, R.; Strizhak, P.A. Composition of Gas Produced from the Direct Combustion and Pyrolysis of Biomass. Process Saf. Environ. Prot. 2021, 156, 43–56. [Google Scholar] [CrossRef]
- Nyashina, G.S.; Vershinina, K.Y.; Shlegel, N.E.; Strizhak, P.A. Effective Incineration of Fuel-Waste Slurries from Several Related Industries. Environ. Res. 2019, 176, 108559. [Google Scholar] [CrossRef] [PubMed]
- Tsue, M.; Segawa, D.; Kadota, T.; Yamasaki, H. Observation of Sooting Behavior in an Emulsion Droplet Flame by Planar Laser Light Scattering in Microgravity. Symp. Combust. 1996, 26, 1251–1258. [Google Scholar] [CrossRef]
- Watanabe, H.; Harada, T.; Matsushita, Y.; Aoki, H.; Miura, T. The Characteristics of Puffing of the Carbonated Emulsified Fuel. Int. J. Heat Mass Transf. 2009, 52, 3676–3684. [Google Scholar] [CrossRef]
- Antonov, D.V.; Kuznetsov, G.V.; Strizhak, P.A. Differences of Two-Component Droplets Breakup at the High Temperatures. J. Energy Inst. 2020, 93, 351–366. [Google Scholar] [CrossRef]
- Pilch, M.; Erdman, C.A. Use of Breakup Time Data and Velocity History Data to Predict the Maximum Size of Stable Fragments for Acceleration-Induced Breakup of a Liquid Drop. Int. J. Multiph. Flow 1987, 13, 741–757. [Google Scholar] [CrossRef]
- Mura, E.; Massoli, P.; Josset, C.; Loubar, K.; Bellettre, J. Study of the Micro-Explosion Temperature of Water in Oil Emulsion Droplets during the Leidenfrost Effect. Exp. Therm. Fluid Sci. 2012, 43, 63–70. [Google Scholar] [CrossRef]
- Strizhak, P.A.; Piskunov, M.V.; Volkov, R.S.; Legros, J.C. Evaporation, Boiling and Explosive Breakup of Oil–Water Emulsion Drops under Intense Radiant Heating. Chem. Eng. Res. Des. 2017, 127, 72–80. [Google Scholar] [CrossRef]
- Volkov, R.S.; Strizhak, P.A. Using Planar Laser Induced Fluorescence to Explore the Mechanism of the Explosive Disintegration of Water Emulsion Droplets Exposed to Intense Heating. Int. J. Therm. Sci. 2018, 127, 126–141. [Google Scholar] [CrossRef]
- Moussa, O.; Tarlet, D.; Massoli, P.; Bellettre, J. Parametric Study of the Micro-Explosion Occurrence of W/O Emulsions. Int. J. Therm. Sci. 2018, 133, 90–97. [Google Scholar] [CrossRef]
- Shinjo, J.; Xia, J.; Ganippa, L.C.; Megaritis, A. Physics of Puffing and Microexplosion of Emulsion Fuel Droplets. Phys. Fluids 2014, 26, 103302. [Google Scholar] [CrossRef]
- Califano, V.; Calabria, R.; Massoli, P. Experimental Evaluation of the Effect of Emulsion Stability on Micro-Explosion Phenomena for Water-in-Oil Emulsions. Fuel 2014, 117, 87–94. [Google Scholar] [CrossRef]
- Suzuki, Y.; Harada, T.; Watanabe, H.; Shoji, M.; Matsushita, Y.; Aoki, H.; Miura, T. Visualization of Aggregation Process of Dispersed Water Droplets and the Effect of Aggregation on Secondary Atomization of Emulsified Fuel Droplets. Proc. Combust. Inst. 2011, 33, 2063–2070. [Google Scholar] [CrossRef]
- Yahaya Khan, M.; Abdul Karim, Z.A.; Aziz, A.R.A.; Heikal, M.R.; Crua, C. Puffing and Microexplosion Behavior of Water in Pure Diesel Emulsion Droplets During Leidenfrost Effect. Combust. Sci. Technol. 2017, 189, 1186–1197. [Google Scholar] [CrossRef]
- Jarvis, T.J.; Donohue, M.D.; Katz, J.L. Bubble Nucleation Mechanisms of Liquid Droplets Superheated in Other Liquids. J. Colloid Interface Sci. 1975, 50, 359–368. [Google Scholar] [CrossRef]
- Yahaya Khan, M.; Abdul Karim, Z.A.; Aziz, A.R.A.; Tan, I.M. Experimental Study on Influence of Surfactant Dosage on Micro Explosion Occurrence in Water in Diesel Emulsion. Appl. Mech. Mater. 2016, 819, 287–291. [Google Scholar] [CrossRef]
- Antonov, D.V.; Piskunov, M.V.; Strizhak, P.A. Breakup and Explosion of Droplets of Two Immiscible Fluids and Emulsions. Int. J. Therm. Sci. 2019, 142, 30–41. [Google Scholar] [CrossRef]
- Antonov, D.V.; Volkov, R.S.; Strizhak, P.A. An Explosive Disintegration of Heated Fuel Droplets with Adding Water. Chem. Eng. Res. Des. 2018, 140, 292–307. [Google Scholar] [CrossRef]
- Cao, Q.; Liao, W.; Wu, W.T.; Feng, F. Combustion Characteristics of Inorganic Kerosene Gel Droplet with Fumed Silica as Gellant. Exp. Therm. Fluid Sci. 2019, 103, 377–384. [Google Scholar] [CrossRef]
- Feng, S.; He, B.; He, H.; Su, L.; Hou, Z.; Nie, W.; Guo, X. Experimental Studies the Burning Process of Gelled Unsymmetrical Dimethylhydrazine Droplets under Oxidant Convective Conditions. Fuel 2013, 111, 367–373. [Google Scholar] [CrossRef]
- Zhuang, B.; Ramanauskaite, G.; Koa, Z.Y.; Wang, Z.G. Like Dissolves like: A First-Principles Theory for Predicting Liquid Miscibility and Mixture Dielectric Constant. Sci. Adv. 2021, 7, 7275–7287. [Google Scholar] [CrossRef] [PubMed]
- Glushkov, D.O.; Feoktistov, D.V.; Kuznetsov, G.V.; Batishcheva, K.A.; Kudelova, T.; Paushkina, K.K. Conditions and Characteristics of Droplets Breakup for Industrial Waste-Derived Fuel Suspensions Ignited in High-Temperature Air. Fuel 2020, 265, 116915. [Google Scholar] [CrossRef]
- Vargaftik, N.B. Handbook of Thermophysical Properties of Gases and Liquids; Alekseev, V.A., Ed.; Nauka: Moscow, Russia, 1972. [Google Scholar]
- Volkov, A.I.; Zharsky, I.M. Big Chemical Reference Book; Modern School: Minsk, Belarus, 2005; ISBN 985-6751-04-7. [Google Scholar]
- Ström, G.; Fredriksson, M.; Stenius, P. Contact Angles, Work of Adhesion, and Interfacial Tensions at a Dissolving Hydrocarbon Surface. J. Colloid Interface Sci. 1987, 119, 352–361. [Google Scholar] [CrossRef]
- Panzer, J. Components of Solid Surface Free Energy from Wetting Measurements. J. Colloid Interface Sci. 1973, 44, 142–161. [Google Scholar] [CrossRef]
- Nahum, T.; Dodiuk, H.; Kenig, S.; Panwar, A.; Barry, C.; Mead, J. The Effect of Composition and Thermodynamics on the Surface Morphology of Durable Superhydrophobic Polymer Coatings. Nanotechnol. Sci. Appl. 2017, 10, 53. [Google Scholar] [CrossRef] [Green Version]
- Koerner, G.; Rossmy, G.; Sanger, G. Oberflächen und Grenzflächen. Ein Versuch, diephysikalisch-chemischen Grundgrößen darzustellen und sie mit Aspekten der Anwendungstechnik zu verbinden. In Goldschmidt Informiert Essen No. 29; Goldschmidt AG: Essen, Germany, 1974. [Google Scholar]
- Jie-Rong, C.; Wakida, T. Studies on the Surface Free Energy and Surface Structure of PTFE Film Treated with Low Temperature Plasma. J. Appl. Polym. Sci. 1997, 63, 1733–1739. [Google Scholar] [CrossRef]
- Boinovich, L.B.; Emelyanenko, A.M. Experimental Determination of the Surface Energy of Polycrystalline Ice. Dokl. Phys. Chem. 2014, 459, 198–202. [Google Scholar] [CrossRef]
- Owens, D.K.; Wendt, R.C. Estimation of the Surface Free Energy of Polymers. J. Appl. Polym. Sci. 1969, 13, 1741–1747. [Google Scholar] [CrossRef]
- Kuznetsov, G.V.; Islamova, A.G.; Orlova, E.G.; Ivashutenko, A.S.; Shanenkov, I.I.; Zykov, I.Y.; Feoktistov, D.V. Influence of Roughness on Polar and Dispersed Components of Surface Free Energy and Wettability Properties of Copper and Steel Surfaces. Surf. Coat. Technol. 2021, 422, 127518. [Google Scholar] [CrossRef]
- Hoorfar, M.; Neumann, A.W. Recent Progress in Axisymmetric Drop Shape Analysis (ADSA). Adv. Colloid Interface Sci. 2006, 121, 25–49. [Google Scholar] [CrossRef] [PubMed]
- Bateni, A.; Susnar, S.S.; Amirfazli, A.; Neumann, A.W. A High-Accuracy Polynomial Fitting Approach to Determine Contact Angles. Colloids Surf. A Physicochem. Eng. Asp. 2003, 219, 215–231. [Google Scholar] [CrossRef]
- Feoktistov, D.V.; Glushkov, D.O.; Kuznetsov, G.V.; Nikitin, D.S.; Orlova, E.G.; Paushkina, K.K. Ignition and Combustion Characteristics of Coal-Water-Oil Slurry Placed on Modified Metal Surface at Mixed Heat Transfer. Fuel Process. Technol. 2022, 233, 107291. [Google Scholar] [CrossRef]


| Liquid | Chemical Formula/Boiling Temperature, °C | Manufacturer | Reference Data | |||
|---|---|---|---|---|---|---|
| , mN/m | , mN/m | , mN/m | Ref. | |||
| Water | H2O/100.0 | Mill-Q water treatment system, Sigma-Aldrich, St. Louis, MO, USA | 72.8 | 51.0 | 21.8 | [28] |
| Monoethanolamine | C2H7NO/170.0 | Ekos-1, Moscow, Russia | 48.2 | 29.4 | 18.8 | [29] |
| Glycerol | C3H8O3/290.0 | Tula Pharm Factory, Tula, Russia | 63.4 | 26.4 | 37.0 | [28] |
| Ethylene glycol | C2H6O2/197.3 | Ekos-1, Moscow, Russia | 47.7 | 16.8 | 30.9 | [28] |
| Acetone | C3H6O/56.0 | Ekos-1, Moscow, Russia | 25.2 | 3.1 | 22.1 | [30] |
| Ethyl alcohol 95% | C2H6O/78.3 | Rosbio, St. Petersburg, Russia | 22.1 | 4.6 | 17.5 | [31] |
| Diiodomethane | CH2I2/182.1 | Alfa Aesar, Heysham, UK | 50.8 | 0.0 | 50.8 | [28] |
| Dodecane | C12H26/216.3 | Ekos-1, Moscow, Russia | 25.4 | 0.0 | 25.4 | [32] |
| Synthetic engine oil | –/190.4 | Gazpromneft, St. Petersburg, Russia | 33.4 | 1.4 | 32.0 | [25] |
| Compressor oil | –/190.5 | Gazpromneft, St. Petersburg, Russia | 28.01 | 0.01 | 28.0 | [25] |
| Oil TEDEX TU 32 | –/208.0 | Gazpromneft, St. Petersburg, Russia | 36.1 | 1.1 | 35.0 | [25] |
| Surface | , mN/m | , mN/m | , mN/m |
|---|---|---|---|
| AMG-6 | 29.8 | 3.5 | 26.3 |
| PTFE | 19.5 | 0.9 | 18.6 |
| Liquid | OWRK Method | , mN/m (Du Nouy/Wilhelmy Methods) | |
|---|---|---|---|
| , mN/m | , mN/m | ||
| First Group (Polar Liquids) | |||
| Water * | 51.0/21.8 | 72.80 | 72.56 ± 0.03/72.78 ± 0.01 |
| Monoethanolamine | 28.8/18.0 | 46.80 | 45.77 ± 0.02/46.00 ± 0.01 |
| Second Group (Dispersive Liquids with a High Value of the Polar Part) | |||
| Glycerol | 26.0/35.0 | 61.00 | 59.92 ± 0.06/60.88 ± 0.15 |
| Ethylene glycol | 17.6/26.4 | 44.00 | 43.52 ± 0.02/43.49 ± 0.01 |
| Third group (Dispersive Liquids with a Low Value of the Polar Part) | |||
| Acetone | 2.4/24.1 | 26.50 | 26.12 ± 0.09/25.88 ± 0.02 |
| Ethyl alcohol 95% | 3.4/19.0 | 22.40 | 22.08 ± 0.04/22.40 ± 0.01 |
| Fourth Group (Dispersive Liquids) | |||
| Diiodomethane * | 0.0/50.8 | 50.80 | 49.71 ± 0.02/49.79 ± 0.01 |
| Dodecane | 0.01/26.8 | 26.81 | 25.78 ± 0.03/26.10 ± 0.02 |
| Synthetic engine oil | 1.2/30.2 | 31.40 | 30.78 ± 0.05/31.50 ± 0.06 |
| Compressor oil | 0.01/29.5 | 29.51 | 28.12 ± 0.19/29.7 ± 0.09 |
| Oil TEDEX TU 32 | 0.8/32.1 | 32.90 | 32.85 ± 0.09/32.84 ± 0.05 |
| Composition of Binary Mixture | Recorded Process (Evaporation/Boiling/ Puffing/Microexplosion) | |
|---|---|---|
| Belonging to Groups 1–4 (Table 3) of the First Component * | Belonging to Groups 1–4 (Table 3) of the Second Component * | |
| 1st group | 1st group | Boiling |
| 2nd group | 2nd group | Boiling |
| 3rd group | 3rd group | Evaporation/Boiling ** |
| 4th group | 4th group | Boiling |
| 1st group | 2nd group | Boiling/Puffing ** |
| 1st group | 3rd group | Boiling |
| 1st group | 4th group | Microexplosion/Puffing ** |
| 2nd group | 3rd group | Boiling |
| 2nd group | 4th group | Puffing/Boiling ** |
| 3rd group | 4th group | Boiling |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feoktistov, D.; Orlova, E.; Glushkov, D.; Abedtazehabadi, A.; Belyaev, S. Conditions for and Characteristics of the Dispersion of Gel Fuel Droplets during Ignition. Appl. Sci. 2023, 13, 1072. https://doi.org/10.3390/app13021072
Feoktistov D, Orlova E, Glushkov D, Abedtazehabadi A, Belyaev S. Conditions for and Characteristics of the Dispersion of Gel Fuel Droplets during Ignition. Applied Sciences. 2023; 13(2):1072. https://doi.org/10.3390/app13021072
Chicago/Turabian StyleFeoktistov, Dmitriy, Evgeniya Orlova, Dmitriy Glushkov, Akram Abedtazehabadi, and Saveliy Belyaev. 2023. "Conditions for and Characteristics of the Dispersion of Gel Fuel Droplets during Ignition" Applied Sciences 13, no. 2: 1072. https://doi.org/10.3390/app13021072





