Robust Full-Screen Wavelength Calibration Algorithm
Abstract
:1. Introduction
- 1.
- At present, calibration methods are mostly used for spectrometers with a fixed grating. This type of spectrometer is commonly characterized by the small line-pairs grating and linear-array CCD. Spectrometers with this structure tend to have a lower wavelength calibration accuracy and a lower spectral resolution.
- 2.
- For the grating rotational spectrometer, a single-element detector and large line-pairs grating are usually used.
- 1.
- At the central pixels, we use the Levenberg–Marquardt algorithm to correct the function relationship between wavelength and feedback value and obtain a sinusoidal function.
- 2.
- We creatively propose converting the feedback values of the non-central pixels into its corresponding feedback values at the central pixels, and then calculate the wavelength using the formula in the previous step. Based on the linear relationship between wavelengths and feedback values, the Huber regression is employed to fit a robust model to better overcome the inherent instrument errors and operation mistakes.
- 3.
- By integrating the formulas obtained in step 1 and step 2, we obtain a wavelength calibration formula that can accurately calibrate all pixels. Experiments show that the novel calibration method has good continuity and high wavelength calibration accuracy.
2. Spectrometer Construction and Related Principles
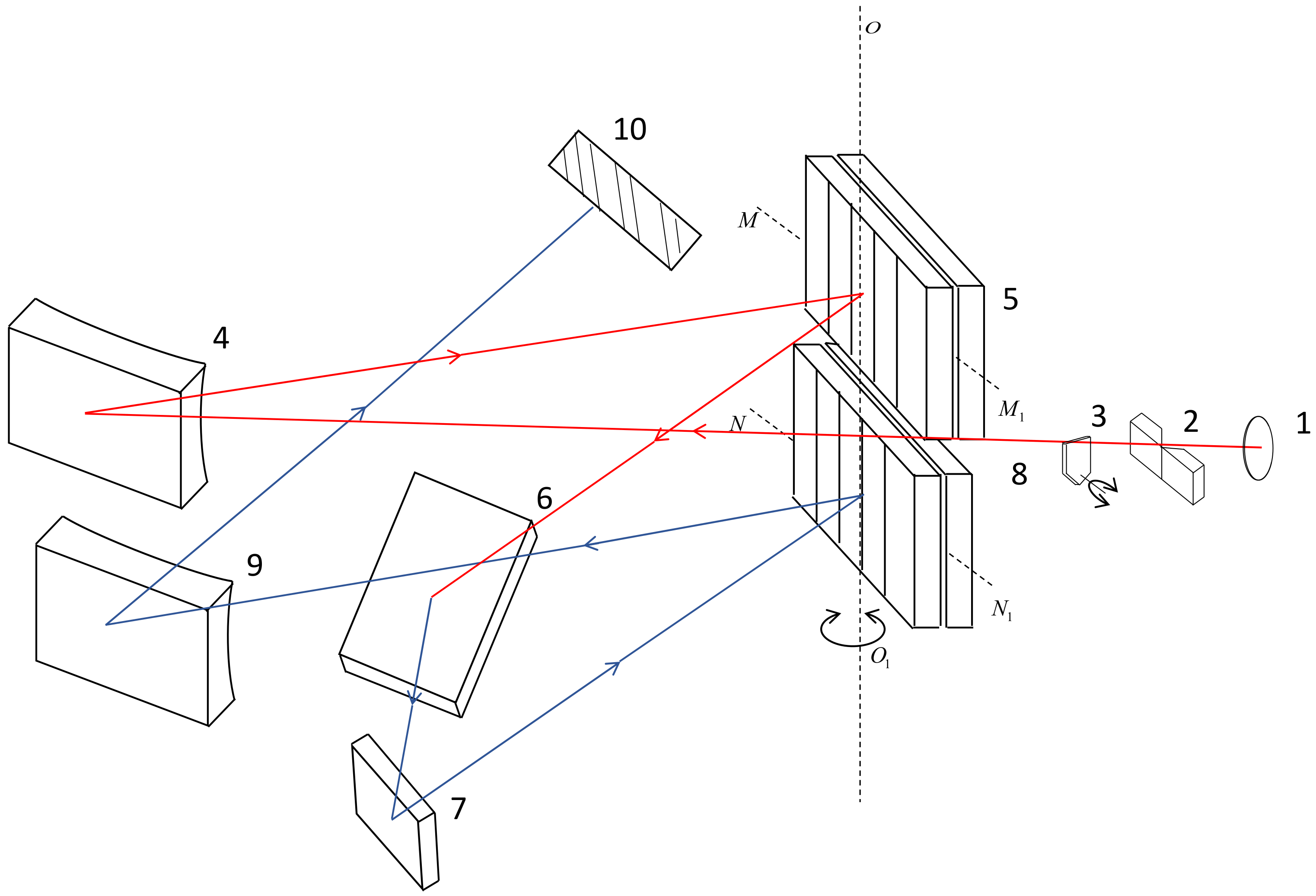
2.1. Construction of the Scanning, Double-Layer, Secondary Diffraction, Linear-Array CCD Spectrometer
2.2. Theoretical Background
3. The Proposed Calibration Method
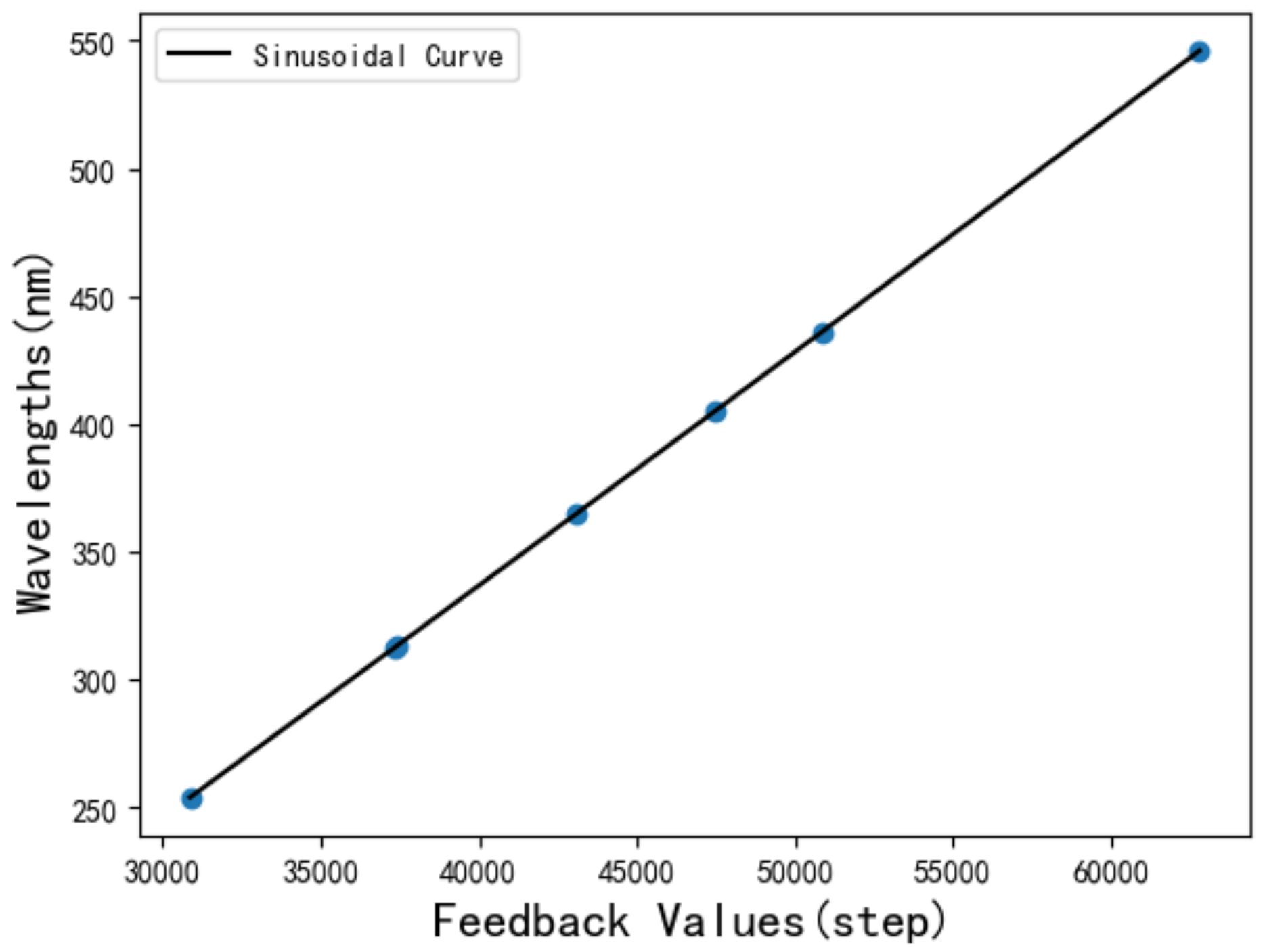
3.1. Spectral Wavelength Calibration Algorithm at Central Pixels
The Levenberg–Marquardt Algorithm to Fit the Sinusoidal Function
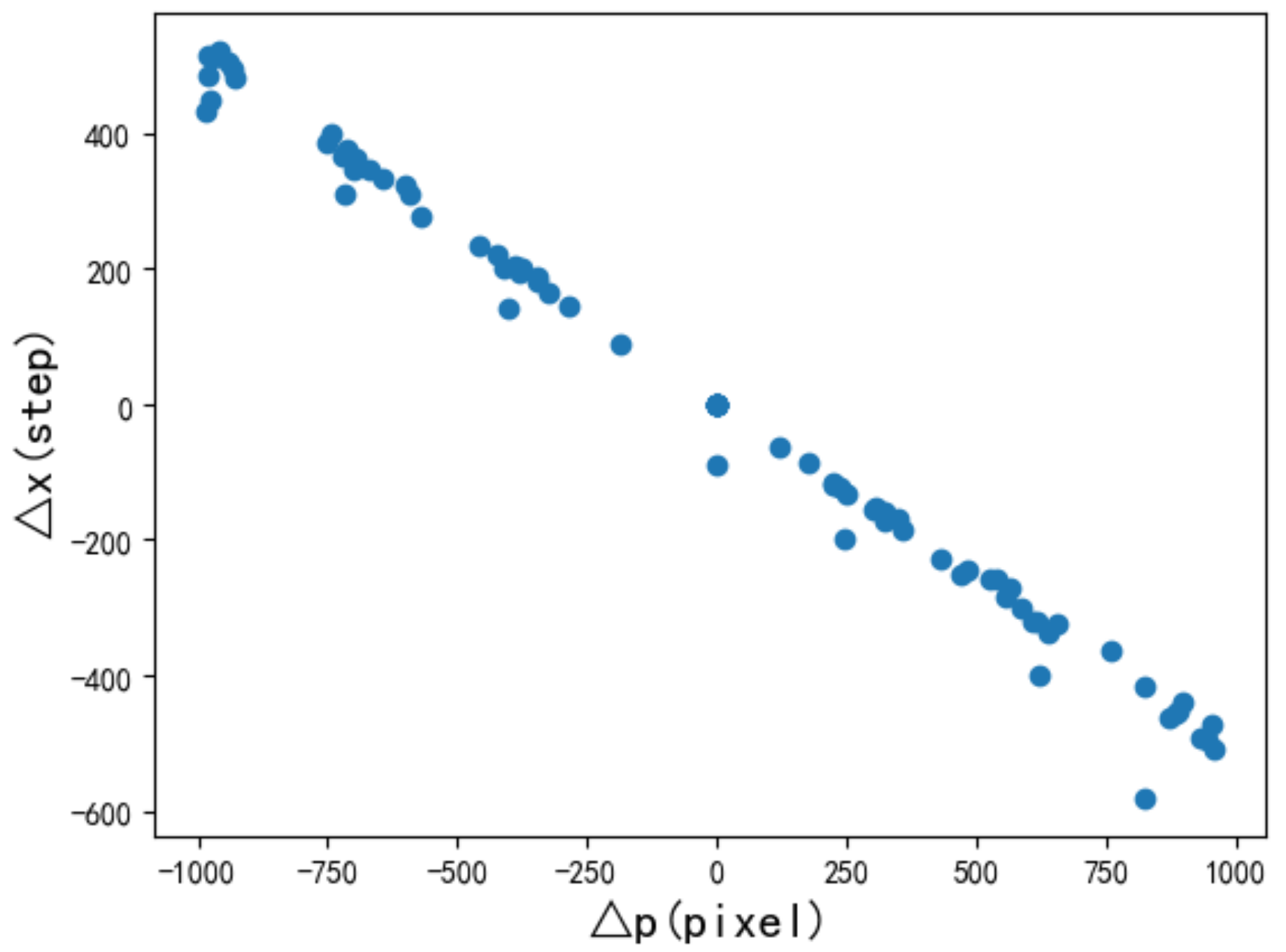
3.2. Functional Relation at Non-Central Pixels
| Algorithm 1 The Levenberg–Marquardt method used to fit the sinusoidal function at central pixels |
| Input:n datapoints (), ⋯, (), the initial weight , and the initial optimization radius . Output: The optimal .
|
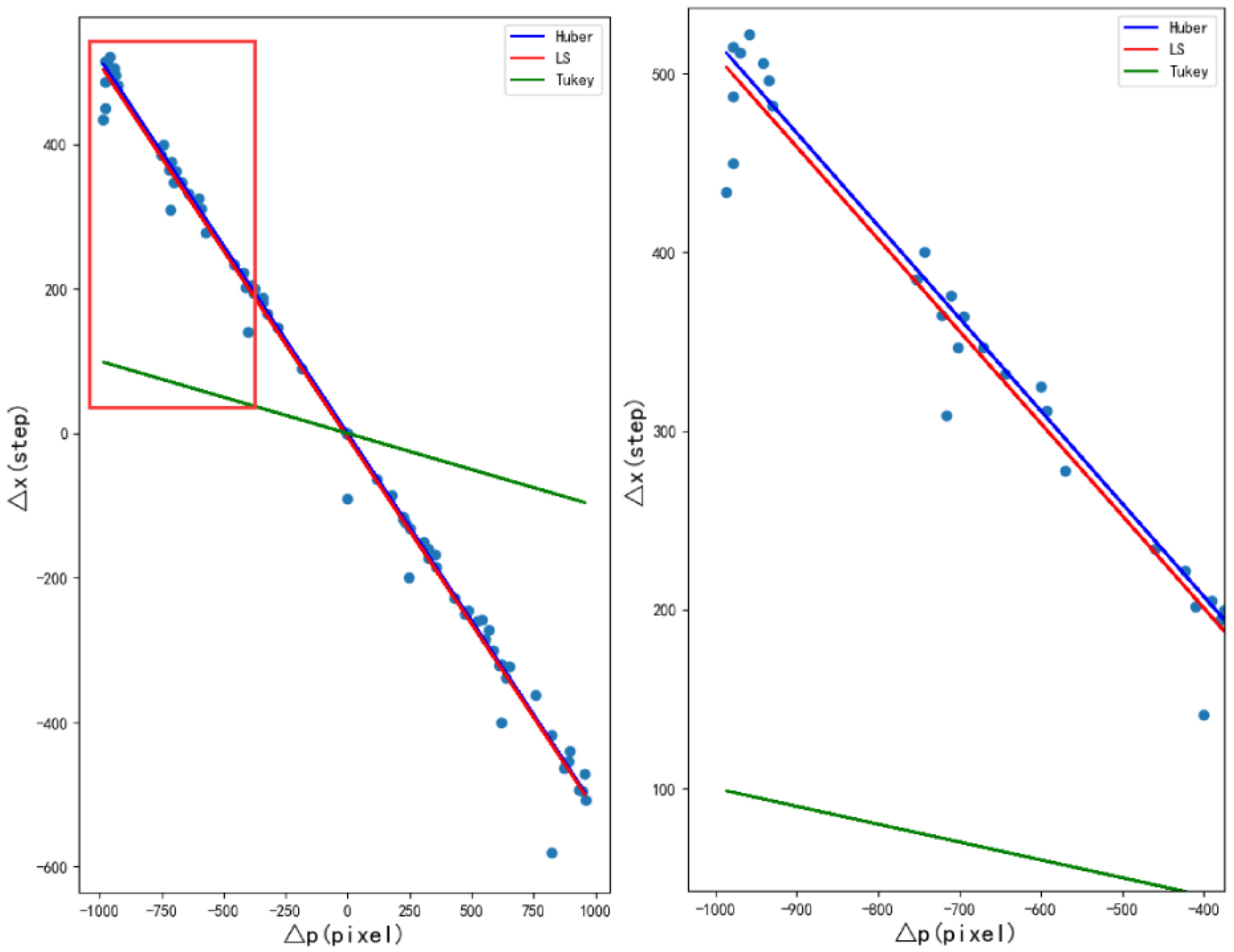
3.2.1. Huber Regression
| Algorithm 2 Spectral wavelength calibration algorithm at noncentral pixels |
| Input: The step size , the initial weight vector , the hyperparameter , the number of iterations E, the initial value of the first-order differential , the data pairs Output: The final estimated parametric vector
|
3.2.2. Tukey Regression
3.3. Full-Screen Spectral Wavelength Calibration Algorithm
| Algorithm 3 Full-screen spectral wavelength calibration algorithm |
| Input: (, , , , , , the initial weight , , the step size , the hyperparameter , the number of iterations E, the initial value of first-order differential . Output: All parameters of Equation (15)
|
4. Experimental Studies
4.1. Simulated Experiments
4.2. Validation on the Instrument
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. A Rough Calibration
Appendix A.2. Functional Relation at Non-Central Pixels
Appendix A.2.1. Acquisition of Calibration Data of Non-Central Pixels
Appendix A.2.2. Two Loss Functions of Linear Regression
Appendix A.3. Parameter Setting
References
- Sun, S.; Sun, B.; Gu, Y. Research on the Embedded Control System of Automatic Grating Concolorous Apparatus. China Instrum. 2005, 11, 45–49. [Google Scholar] [CrossRef]
- Huang, J.Q. Research on a Quick and High Accuracy Wavelength Setting Method for Grating Spectrometer. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2010. [Google Scholar]
- Chen, S.; Ke, F.; Le, Y. Calibration of grating spectrometer. Phys. Exp. 2012, 32, 44–46. [Google Scholar] [CrossRef]
- XU, Z.; Yu, B. Wavelength calibration for PC2000-PC/104spectrometer. Phys. Exp. 2004, 12, 11–14. [Google Scholar] [CrossRef]
- Zhang, Q.; Chang, J.; Wang, F.; Wang, Z.; Xie, Y.; Gong, W. Improvement in QEPAS system utilizing a second harmonic based wavelength calibration technique. Opt. Commun. 2018, 415, 25–30. [Google Scholar] [CrossRef]
- Sun, C.; Wang, M.; Cui, J.; Yao, X.; Chen, J. Comparison and analysis of wavelength calibration methods for prism–Grating imaging spectrometer. Results Phys. 2019, 12, 143–146. [Google Scholar] [CrossRef]
- Yuan, L.; Qiu, L. Wavelength calibration methods in laser wavelength measurement. Appl. Opt. 2021, 60, 4315–4324. [Google Scholar] [CrossRef] [PubMed]
- Mark, H.; Workman, J. A new approach to generating transferable calibrations for quantitative near-infrared spectroscopy. Spectroscopy 1988, 3, 28–36. [Google Scholar]
- Swierenga, H.; de Groot, P.; de Weijer, A.; Derksen, M.; Buydens, L. Improvement of PLS model transferability by robust wavelength selection. Chemom. Intell. Lab. Syst. 1998, 41, 237–248. [Google Scholar] [CrossRef]
- Qiao, D.; Gu, Y.; Xu, X. Wavelength Calibration Algorithm in Grating Spectrometer. Acta Photonica Sin. 2009, 38, 2283–2287. [Google Scholar]
- Wu, K.; Xue, S.; Lu, Q.; Peng, Z. Simulation analysis and measurement of rotation angle repeatability for grating sine mechanism of SX-700 monochromator. Opt. Precis. Eng. 2010, 18, 46–49. [Google Scholar]
- Baselga, S. Global optimization solution of robust estimation. J. Surv. Eng. 2007, 133, 123–128. [Google Scholar] [CrossRef]
- Zhu, B.; Chang, L.; Xu, J.; Zha, F.; Li, J. Huber-Based Adaptive Unscented Kalman Filter with Non-Gaussian Measurement Noise. Circuits Syst. Signal Process. 2018, 37, 3842–3861. [Google Scholar] [CrossRef]
- Pennacchi, P. Robust estimation of excitations in mechanical systems using M-estimators—Experimental applications. J. Sound Vib. 2009, 319, 140–162. [Google Scholar] [CrossRef] [Green Version]
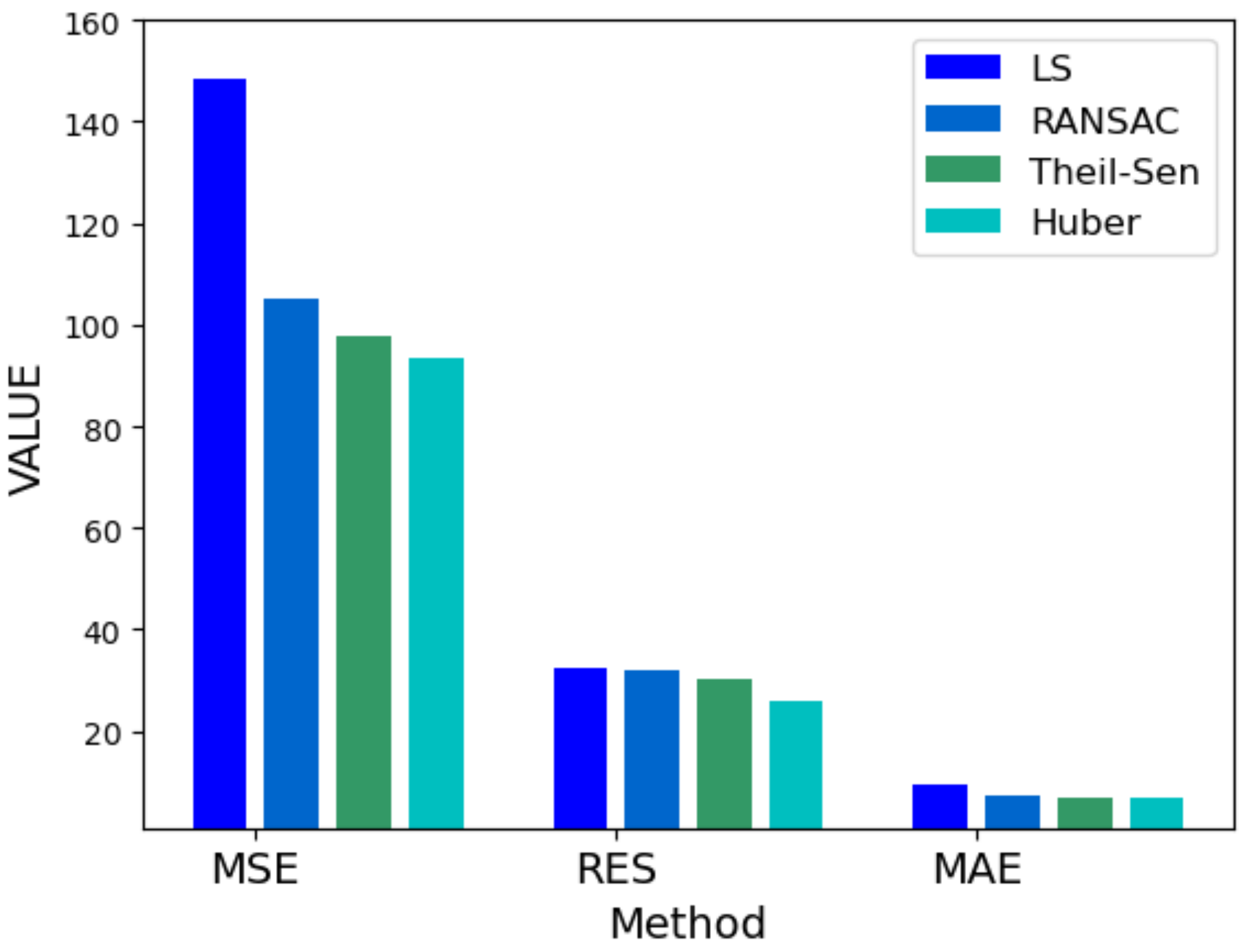

| Parameter | ||||
|---|---|---|---|---|
| Initial value | 0 |
| Parameter () | a | b | c | d |
|---|---|---|---|---|
| Fitting results | −1993.820 | 4.65 | 2.773 | 699.383 |
| Hyperparameter | E | ||||
|---|---|---|---|---|---|
| Value | 0.0001 | [−0.1, −0.1] | 0.001 | 150 | [0, 0] |
| Parameter () | e | f |
|---|---|---|
| Fitting results | −0.519 | −0.0981 |
| Spectrometer Number | Standard Value/nm | Mean Value/nm | Accuracy/nm | Repeated Measurement Accuracy/nm |
|---|---|---|---|---|
| 01 | 253.65 | 253.63 | −0.02 | 0.003 |
| 365.02 | 365.04 | 0.02 | ±0.002 | |
| 404.65 | 404.66 | 0.01 | −0.003 | |
| 546.07 | 546.08 | 0.01 | −0.004 | |
| 579.07 | 579.04 | −0.03 | ±0.002 | |
| 02 | 253.65 | 253.62 | −0.03 | −0.004 |
| 365.02 | 365.03 | 0.01 | −0.004 | |
| 404.65 | 404.67 | 0.02 | −0.002 | |
| 546.07 | 546.05 | −0.02 | −0.003 | |
| 579.07 | 579.02 | −0.05 | 0.003 | |
| 03 | 253.65 | 253.61 | −0.04 | −0.003 |
| 365.02 | 365.04 | 0.02 | 0.002 | |
| 404.65 | 404.63 | −0.02 | ±0.003 | |
| 546.07 | 546.11 | 0.04 | −0.002 | |
| 579.07 | 579.05 | −0.02 | −0.003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, B.; Zhang, C.; Zhao, N.; Li, H.; Yuan, L.; Chen, J.; Bai, H.; Wang, L. Robust Full-Screen Wavelength Calibration Algorithm. Appl. Sci. 2023, 13, 1100. https://doi.org/10.3390/app13021100
Jiang B, Zhang C, Zhao N, Li H, Yuan L, Chen J, Bai H, Wang L. Robust Full-Screen Wavelength Calibration Algorithm. Applied Sciences. 2023; 13(2):1100. https://doi.org/10.3390/app13021100
Chicago/Turabian StyleJiang, Baisong, Chunxia Zhang, Nanqi Zhao, Hongguang Li, Liang Yuan, Juan Chen, Haowen Bai, and Le Wang. 2023. "Robust Full-Screen Wavelength Calibration Algorithm" Applied Sciences 13, no. 2: 1100. https://doi.org/10.3390/app13021100







