Research on Safe Following Distance on an Expressway Based on Braking Process Analysis

Abstract

As an important part of the vehicle active collision avoidance system, improvement of the minimum safe following distance model has aroused the interest of researchers at home and abroad. According to the characteristics of the safe driving of vehicles on expressways, the braking process of vehicles is analyzed using the principle of kinematics. According to the requirements of the safe following distance between vehicles, the safe following distance of different braking system structures, different following states, different speeds and different slope sections on expressways is quantitatively analyzed. Three different safe following distance calculation methods based on braking deceleration under different slope conditions are established. Matlab software was used for simulation analysis. The simulation results show that the calculation method of the safe following distance meets the requirements of keeping safe distance in the Implementation Regulations of Road Traffic Safety Law of the People’s Republic of China and provides a more specific reference basis for speed limit used on expressways. This study provides a theoretical basis for the application and interpretation of the parking sight distance value stipulated in the Design Specification for Highway Alignment, and has certain practical guiding significance for improving the density and transportation efficiency of expressway vehicles and reducing the incidence of rear-end traffic accidents.

1. Introduction

As a fast, flexible and economical means of transportation, cars are generally favored by people over other forms of transportation. Although cars bring convenience to people, the following problems are also obvious: with the increase of vehicles, traffic accidents happen more frequently, causing an alarming number of casualties and property losses. Rear-end collisions caused by inaccurate spacing and improper control between vehicles traveling at high speed on expressways has become one of the main forms of traffic accidents in China in recent years. The analysis of highway rear-end collisions shows that more than 80% of the accidents are caused by the driver’s slow response, and more than 65% of the car collisions are rear-end collisions. The main reason for this kind of accident is that the speed of the driving vehicle is too high, and the driver fails to maintain the corresponding safe distance. According to the research of Mercedes-Benz on various traffic accidents, if drivers can realize the danger of accidents in advance and take appropriate measures, the vast majority of traffic accidents can still be avoided [1]. In the same direction of the highway, there are complete following, incomplete following and other driving conditions. As far as driving safety is concerned, different following states have different requirements for safe driving distance. If the distance between vehicles in longitudinal alignment on the expressway is kept completely in line with the requirements of stopping sight distance, rear-end collision accidents can be completely avoided, but road capacity will be greatly reduced, resulting in a serious waste of road capacity. As an important part of the vehicle active collision avoidance system, improvement of the minimum safe following distance model has aroused the interest of researchers at home and abroad. In the collision avoidance system, the determination of safe following distance completely depends on the safety distance model adopted. Therefore, whether the safe following distance model is reasonable is of great significance to improve the reliability and effectiveness of the collision avoidance system. In order to ensure traffic safety between vehicles on the expressway and bring the road capacity into play, it is particularly important to discuss the determination and internal relationship of the appropriate value of the safe distance between vehicles running in the same direction on the expressway in different following states, different speeds and different slope sections. Study into the highway safety following distance has far-reaching significance for improving traffic safety level and service quality.

2. Related Work

There are many reasons for causing traffic accidents, among which, the failure to maintain a safe following distance accounts for a large proportion. Peng et al. analyzed 1521 expressway traffic accidents in mountainous areas from 2012 to 2017 and found that one of the most common factors involved in serious accidents in the daytime was the failure to maintain a safe distance [2]. He et al. analyzed the causes of road traffic accidents on foggy days and believed that the main reason was that the drivers failed to allow a sufficient following distance [3].

There are many reasons for having a dangerous following distance, such as driving speed, driver conditions and road conditions. The method of solving these problems and reducing the occurrence of traffic accidents is of particular importance. In 2012, Li et al. designed a rear-end collision warning system based on Zigbee technology, which can compare the actual distance measured by radar with the safe distance and provide early warning information for drivers [4]. In 2013, Wang et al. proposed an improved safety distance model (SDM) based on vehicle-to-vehicle communication technology, which realized real-time data acquisition and real-time workshop communication and could effectively improve the efficiency of a vehicle anti-collision system [5]. In 2014, Wang et al. proposed a self-optimizing PID model based on fuzzy control which could assist a car in following another car at a safe distance, and this model was established on a wireless sensor network sharing information for perceiving different statuses of the traffic stream [6]. Cao et al. established a practical calculation model for safe gaps. In addition, they used Matlab to simulate three different safe gaps under dry pavement [7]. In 2018, Gargoum pointed out in his paper that if the available sight distance is less than the required sight distance, the possibility of the driver completing a certain action will be reduced [8]. In the article, he also proposed a process through which the sight distance of the highway can be evaluated. In 2013, He et al. designed an effective, intelligent traffic safety distance control system for foggy days [3]. In 2022, Sroczyński et al. proposed a new design method for a recommendation system which can suggest the safe speed on the road, and the system can suggest the safe speed for overtaking vehicles to prevent collisions by taking into account the distance from the previous vehicle [9].The rational design of roads is also of great significance to the safe driving of vehicles. Zhang et al. discussed the safe driving conditions on the highway and obtained the relationship among the design length of the vertical curve, the stopping sight distance and the slope algebra, and gave treatment suggestions [10]. If the conditions of a section of road cannot meet the requirements of safe sight distance, traffic engineering control measures can be taken to ensure traffic safety as much as possible. Fambro et al. established a parking sight distance calculation model based on driver and vehicle performance and recommended the parking sight distance of different models through actual data verification [11]. Hassan et al. established the line-of-sight calculation model by analyzing drivers’ characteristics and road alignment and other factors [12]. Crisman et al. for the first time, used the friction coefficient between the tire and the ground instead of the vehicle speed reduction in an emergency as the main calculation parameter in the calculation of sight distance [13]. Nehate et al. established a new parking sight distance model based on GPS data [14]. Hassan et al. proposed the mathematical model and calculation method of 3D sight distance through parametric analysis of road section [15]. According to the coordinate equation and cross section parameters of road median line, Zhang et al. put forward the highway 3D sight distance test technology [16]. Jiang et al. reclassified the braking process and established the stopping sight distance model under different road conditions [17]. Yang corrected the stopping sight distance by running speed and braking speed reduction [18]. Xun established the parking sight distance test model and used the simulation platform to test and evaluate the sight distance on the highway in mountainous areas [19]. Yang et al. revised the parking sight distance model from three aspects and put forward suggestions to ensure the parking sight distance from the angle of the height of the target [20].

According to the characteristics of the safe driving of vehicles on an expressway, this paper analyzes the braking process of vehicles with regard to the kinematic principle and establishes three different safe following distance calculation methods based on braking deceleration under different slope conditions. We used Matlab software for simulation analysis. The results of the simulation can be a specific and clear reference for the limited speeds used on expressways. This study has certain practical guiding significance for improving the vehicle density and transportation efficiency of expressways and reducing the incidence of rear-end traffic accidents.

3. Modeling

3.1. Analysis and Assessment of Braking Distance

3.1.1. Running Status of Automobiles

Let car A (the front car) and car B (the following car), which are arranged longitudinally and separated by distance “D” (unit: m), drive successively in the same direction on the same road. This is shown in Figure 1. The two cars drive at the speeds of V_A and V_B, respectively.

It is assumed that the driver of car A starts to brake after finding obstacles in the front of the road. When the speed of car A decreases to V’_A, the distance driven by car A is D_A. At the same time, the driver of car B starts to brake after observing car A’s braking, and the distance traveled by car B when its speed decreases to V’_B is D_B. The symbol d (m) is the actual distance between car A and car B when car A and car B reach the post-braking speed, V’_A and V’_B, respectively, as required by design.

3.1.2. Analysis of the Automobile Braking Process

In order to establish a reasonable minimum following distance model, it is necessary to have a comprehensive understanding of the braking process [21]. Assuming that the front car, A, suddenly appears in some emergency situation (sudden deceleration and stopping or cargo scattering), the curves of the following car’s brake-pedal force, braking deceleration and braking time are as shown in Figure 2, when the driver of the following car enacts emergency braking. In Figure 2, F_p is brake-pedal force and j is brake deceleration.

According to Figure 2, the driver needs to finish five periods in the actual braking process, and the specific analysis is as follows.

(1)

The driver’s reaction time t₁: the time required for the driver to move the right foot to the brake pedal after the driver detects a dangerous situation and begins to react.

(2)

The brake coordination time t₂: the time required from starting to step down on the brake pedal to eliminate the brake pedal clearance, clearance of various hinges and bearings and drum brake clearance.

(3)

The braking force growth time t₃. At this stage, the braking force gradually increases from zero to the maximum; that is, the braking deceleration increases from zero to the maximum, and the car moves through variable deceleration.

(4)

The continuous braking time t₄. At this stage, the braking force is basically maintained at a stable value; that is, the brake deceleration remains unchanged, and the car goes through uniform deceleration until stopping.

(5)

The braking relaxation time t₅, that is, the time that is required after stopping until the automatic elimination of braking force.

3.1.3. Problem Simplification

In order to obtain the critical safe distance between two cars and carry out theoretical analysis, it is necessary to perform a specific analysis of driving on an expressway and make some simplifications [22].

(1)

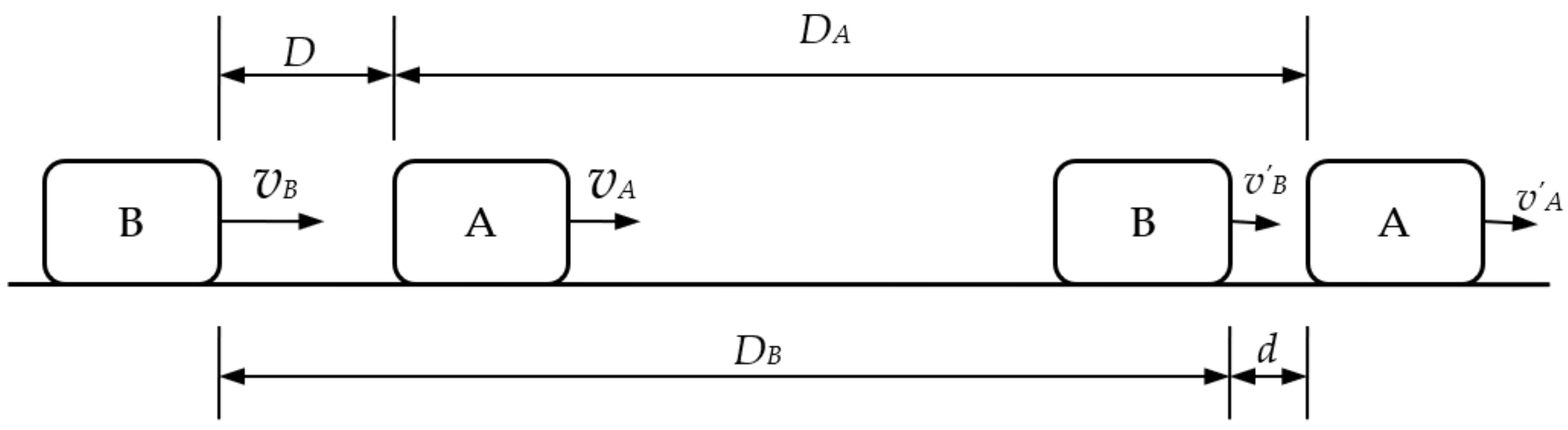
The car movement in a short time on the expressway is simplified to a uniform movement. Assume that at a certain moment on the expressway, the front car (A) is moving at the speed of V_A and the following car (B) is moving at the speed of V_B. In this case, the distance between car A and car B is “D”. This is shown in Figure 1.

(2)

With the passage of time, the distance between the front car (A) and the following car (B) has two possible changing trends. One is that the distance between the two cars is getting larger and larger, which obviously eliminates the problem of safe following distance between the two cars, so this situation is not the process to be discussed. We are concerned about the other situation, where the distance between the two cars gets smaller and smaller, and if no action is taken, there will be a rear-end collision. Among the possible situations, the most dangerous is that either the front car brakes and the following car accelerates, or the front car brakes and the following car still moves at its original speed. However, those two scenarios are not what the article is talking about here, as, in them, the following car is likely trying to overtake the front car, the two cars are not in the same lane, or the crash is intentional. Obviously, the situation in question is that on the expressway, the front car and the following car are moving in the same direction in the same lane, and the following car does not intend to pass the car in front, but just follows the front car. At a certain moment, car A suddenly brakes. The driver of car B will discover that the distance between the two cars is decreasing, so the following car immediately brakes to avoid a collision between the two cars (assuming that there is no possibility or possible behavior of steering to avoid the crash). In this case, when the following car adopts braking, the front car and the following car will not collide. We define the minimum distance that the two cars must keep at the moment before the front car brakes as the critical safe distance.

(3)

We assume that the driving conditions of the two cars are the same and the drivers are in the same condition. That is, it is assumed that the braking parameters of the two cars are the same and the drivers’ abilities to respond are the same.

3.1.4. Braking Distance

(1)

Analysis of braking deceleration process of the following car

The driver of the following car completes the whole braking process after receiving the braking signal. According to the above braking process analysis, in the whole braking process, the actual distance traveled by the following car includes four periods: the driver’s reaction time t₁, the brake braking coordination time t₂, the braking force growth time t₃ and the continuous braking time t₄.

As the brakes do not have an effect during t₁ and t₂, the distance (D_B1) traveled by car B in times t₁ and t₂ is

D_B1 = V_B × (t₁ + t₂)

(1)

The distance traveled by car B in time t₃ is

$$D_{B2}={\displaystyle {\int }_0^{t_3}(V_B-\frac{j_{B\max }}{2t_3}{t}^2)}dt=V_B{t}_3-\frac{j_{B\max }}{6}{t}_3^2$$

(2)

Meanwhile, at the end of time t₃, the speed V₃ of car B is as follows.

$$V_3=V_B-\frac{j_{B\max }}{2}{t}_3$$

(3)

The distance traveled by car B during t₄ is

$$D_{B3}=\frac{V_3^2-V_B^{\prime }{}^2}{2j_{B\max }}=\frac{V_B^2-V_B^{\prime }{}^2}{2j_{B\max }}-\frac{V_B{t}_3}{2}+\frac{1}{8}{j}_{B\max }{t}_3^2$$

(4)

The total braking distance of car B is as follows:

$$D_B=D_{B1}+D_{B2}+D_{B3}=V_B(t_1+{\mathrm{t}}_2+\frac{t_3}{2})+\frac{V_B^2-V_B^{\prime }{}^2}{2j_{B\max }}-\frac{j_{B\max }}{24}{t}_3^2$$

(5)

(2)

Braking distance analysis of the front car

Theoretically, the front car should also undergo the same deceleration process as the following car. Therefore, in theory, the braking distance $D^{\prime }{}_A$ of the front car is similar to that of the following car.

$$D^{\prime }{}_A=D_{A1}+D_{A2}+D_{A3}=V_A(t_1+t_2+\frac{t_3}{2})+\frac{V_A^2-V_A^{\prime }{}^2}{2j_{A\max }}-\frac{j_{A\max }}{24}{t}_3^2$$

(6)

During actual driving, the driver of car B is sure that the front car has implemented braking after the brake lights of car A come on. Therefore, the distance covered by car A during the braking process should only be the distance driven by the car in the braking force growth stage and the continuous braking stage. Therefore, the braking distance $D_A$ of car A during t₂ and t₃ can be obtained as follows:

$$D_A=D_{A2}+D_{A3}=V_A\frac{t_3}{2}+\frac{V_A^2-V_A^{\prime }{}^2}{2j_{A\max }}-\frac{j_{A\max }}{24}{t}_3^2$$

(7)

3.2. Establishment of a Mathematical Model of Minimum Safe Distance

3.2.1. Analysis of Safe Distance

If the front car and the following car do not collide, from the perspective of driving speed, the ideal situation is that the final speeds of car A and car B are equal; that is, V’_B = V’_A (including a requirement that the final speed of car A and car B is zero). Otherwise, the two cars will collide (if V’_B > V’_A) or the calculated result is not the critical distance (V’_B < V’_A). In addition, if the front car and the following car do not collide, it can be seen in Figure 1 that the driving distance must align with the following formula:

D_A + D ≥ D_B + d

(8)

Therefore, the distance “D” between the front car and the following car before braking must align with the following formula:

D ≥ D_B + d − D_A

(9)

Therefore, in order to avoid collision between car A and car B, the critical safe distance D* must align with the following formula:

D* = D_B + d − D_A

(10)

According to the above analysis, it can be seen that the required distance between car A and car B in the longitudinal arrangement varies with speed, braking performance, the value of “d” and other factors. In practice, “d” can be viewed as a certain value. Therefore, when the driving speed and braking performance are different for car A and car B, the required safe following distance will also be different.

3.2.2. Discussion of Safe Distance

According to the analysis of the braking distance of the front car, three different safety distances were obtained.

(1)

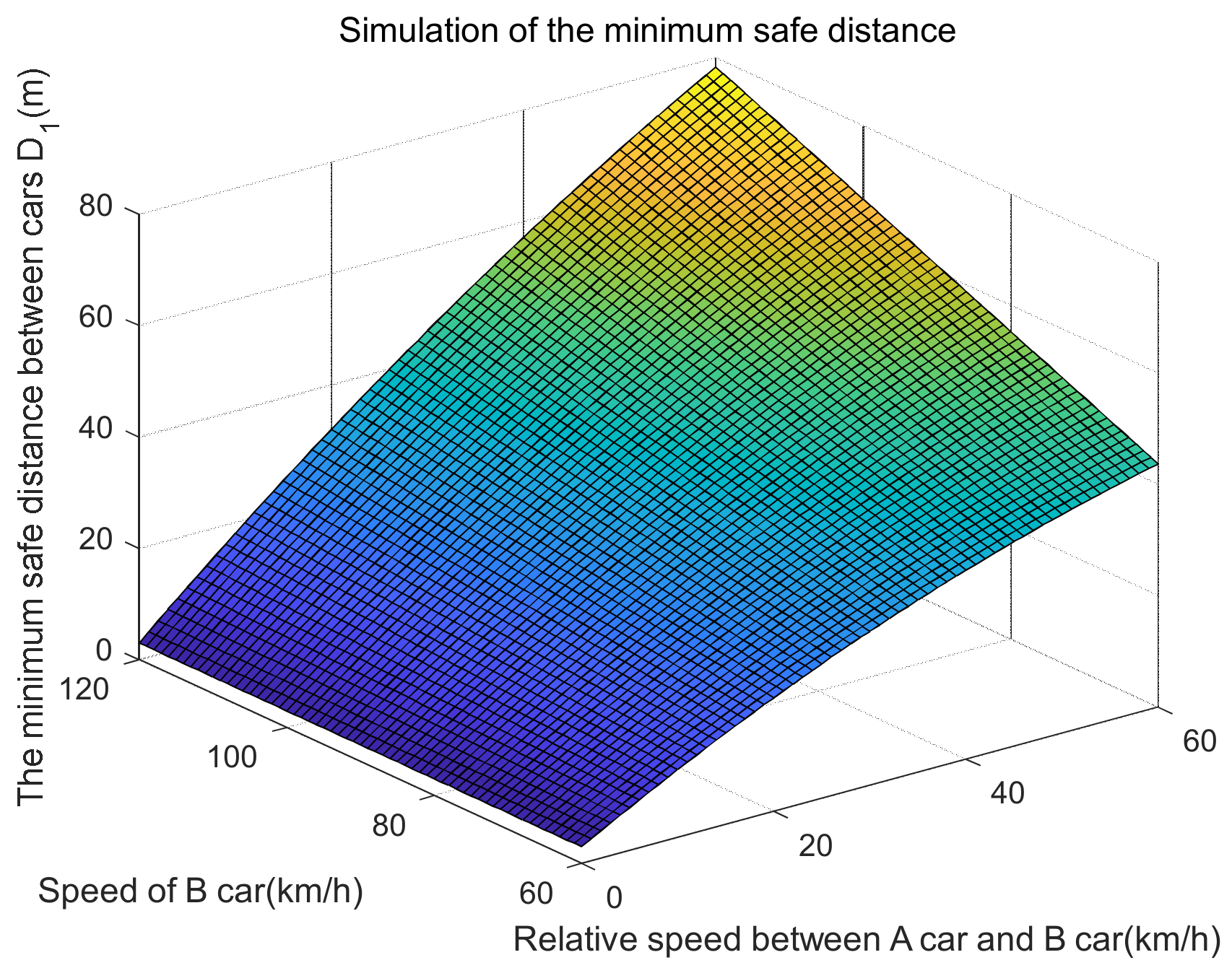
Minimum safe distance D₁

Obviously, the critical safe distance is calculated by considering the response of the driver of car A and the braking time.

$$\begin{gathered} D_1=D_{\mathrm{B}}+d-{D^{\prime }}_A\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \\ \hspace{1em}=V_B({\mathrm{t}}_1+t_2+\frac{t_3}{2})+\frac{V_B^2-V_B^{\prime }{}^2}{2j_{B\max }}-\frac{j_{B\max }}{24}{t}_3^2-(V_A({\mathrm{t}}_1+t_2+\frac{t_3}{2})+\frac{V_A^2-V_A^{\prime }{}^2}{2j_{A\max }}-\frac{j_{A\max }}{24}{t}_3^2)+d \\ =({\mathrm{t}}_1+t_2+\frac{t_3}{2})(V_B-V_A)+\frac{V_B^2-V_B^{\prime }{}^2}{2j_{B\max }}-\frac{V_A^2-V_A^{\prime }{}^2}{2j_{A\max }}-\frac{j_{B\max }}{24}{t}_3^2+\frac{j_{A\max }}{24}{t}_3^2+d\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \end{gathered}$$

(11)

This formula reflects the minimum distance between car A and car B before the two cars brake if the two cars want to avoid a collision. It is called the minimum following distance.

(2)

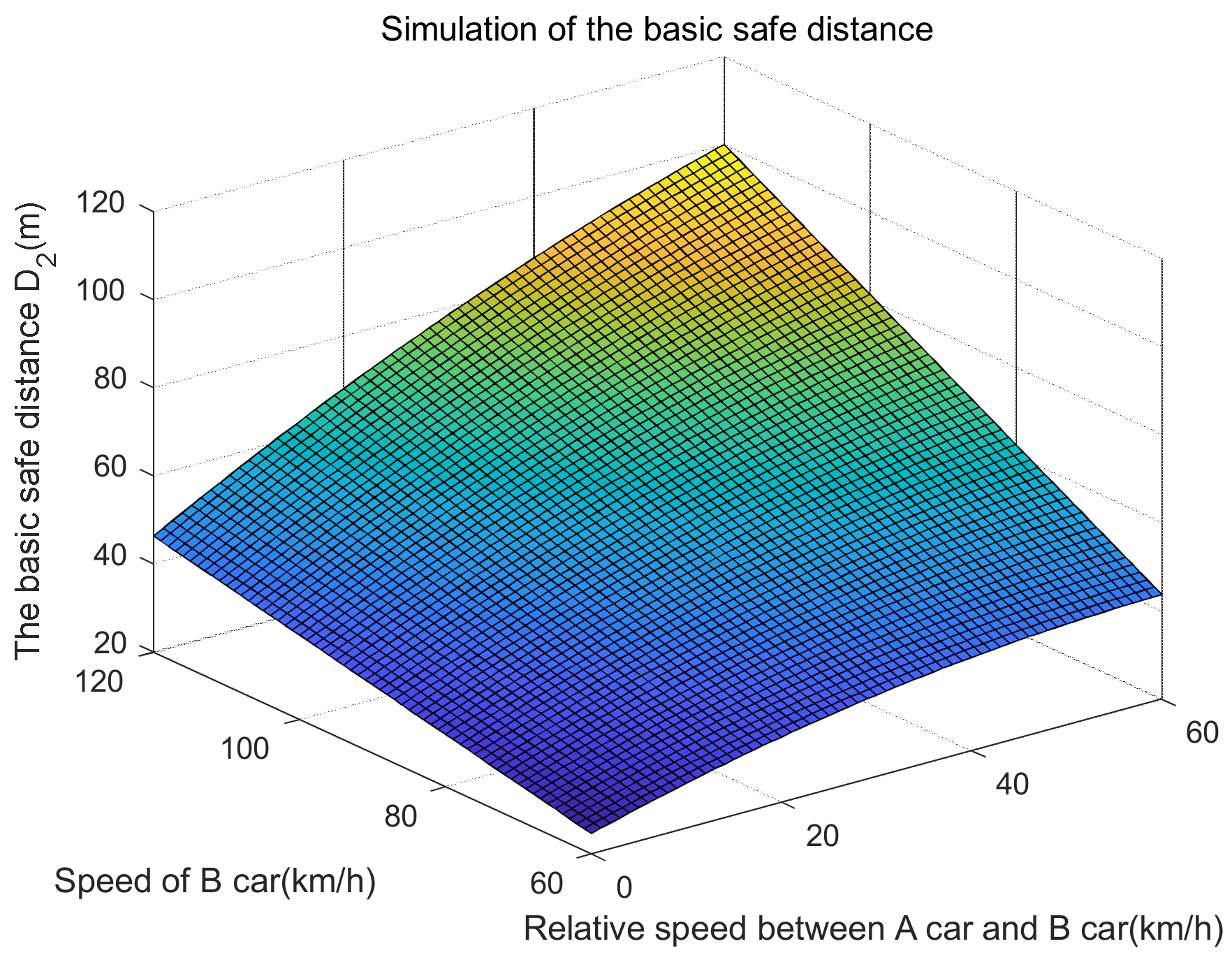
Basic safe distance D₂

In the actual expressway driving process, the driver of the following car (car B) will implement braking only after identifying the front car’s brake lights. Therefore, this reduces the distance that car A moves before the driver reacts. Therefore, this distance requirement is the general distance requirement. Hence, the basic following distance D₂ can be obtained.

$$\begin{gathered} D_2=D_{\mathrm{B}}+d-D_A\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \\ =V_B({\mathrm{t}}_1+t_2+\frac{t_3}{2})+\frac{V_B^2-V_B^{\prime }{}^2}{2j_{B\max }}-\frac{j_{B\max }}{24}{t}_3^2-(V_A\frac{t_3}{2}+\frac{V_A^2-V_A^{\prime }{}^2}{2j_{A\max }}-\frac{j_{A\max }}{24}{t}_3^2)+\mathrm{d}\hspace{1em}\hspace{1em} \\ =V_B({\mathrm{t}}_1+{\mathrm{t}}_2)+(V_B-V_A)\frac{t_3}{2}+\frac{V_B^2-V_B^{\prime }{}^2}{2j_{B\max }}-\frac{V_A^2-V_A^{\prime }{}^2}{2j_{A\max }}-\frac{j_{B\max }}{24}{t}_3^2+\frac{j_{A\max }}{24}{t}_3^2+\mathrm{d}\hspace{1em}\hspace{1em} \end{gathered}$$

(12)

This formula reflects the distance between car A and car B that should be maintained when the following car can see the front car’s brake lights (assuming they function). It is called the basic following distance.

(3)

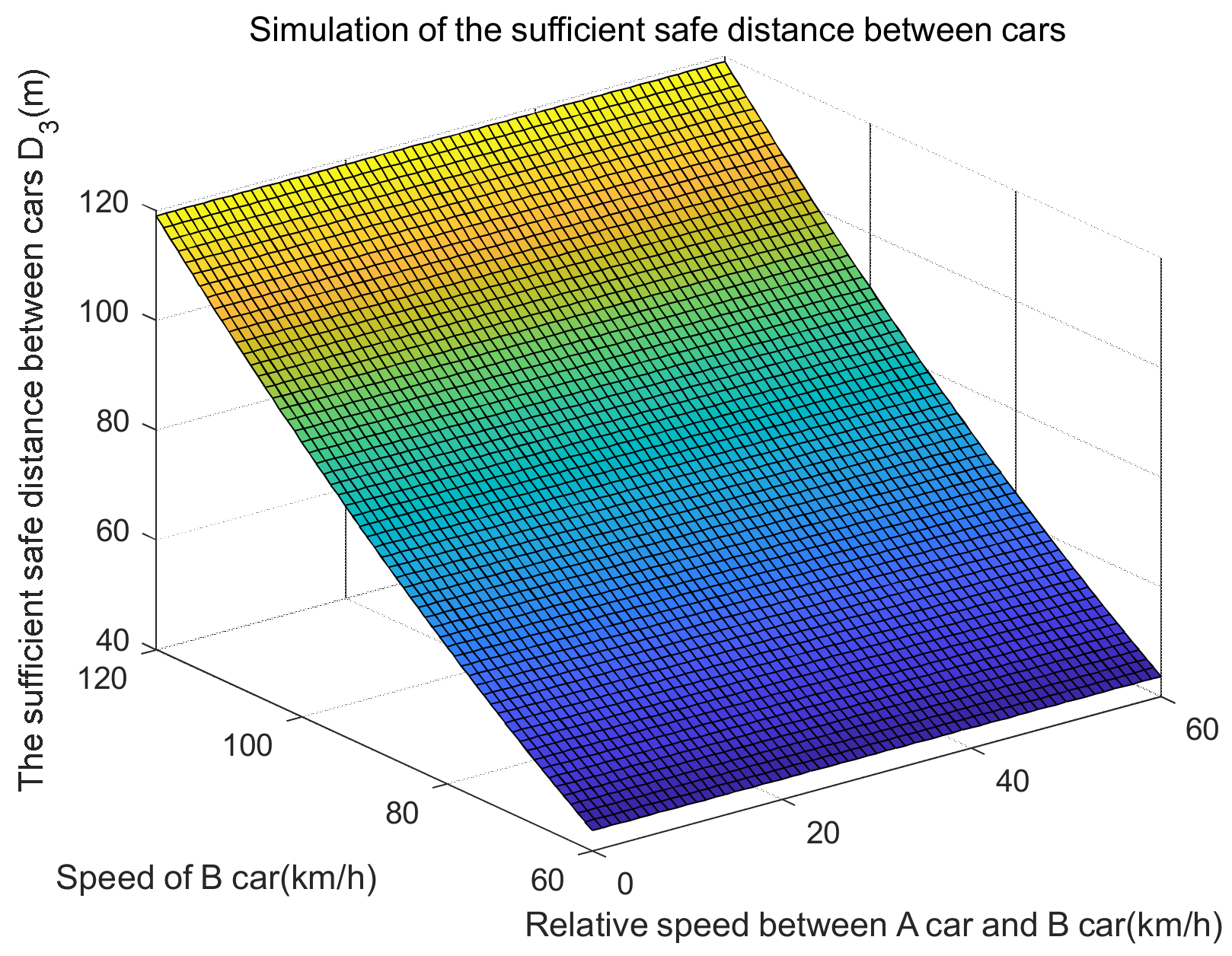
Sufficient safe distance D₃

The front car’s deceleration j_Amax can tend toward ∞—that is, j_Amax = ∞. (This can happen, for example, if the front car crashes, or if it has very powerful brakes). As a result, the initial velocity V_A of car A can be considered to become 0 instantaneously [23]. In this case, D_A ≈ 0, so the safe spacing D₃ can be obtained.

$$D_3 =V_B(t_1+t_2+\frac{t_3}{2})+\frac{V_B^2-V_B^{\prime }{}^2}{2j_{B\max }}-\frac{j_{B\max }}{24}{t}_3^2+d$$

(13)

This reflects the safe distance requirement when car B must brake in the most unfavorable conditions (such as the front vehicle suddenly happening to crash). This is called the sufficient following distance.

Obviously, from the above analysis, the following formula can be obtained: D₁ < D₂ < D_3.

3.3. Determination of Parameter Values in the Model

Before the simulation of the model, it is necessary to determine the value of each parameter in the model. In the model, the speed of the following car V_B, the speed of the front car V_A and the relative speed V_r are to be measured. The speed of the following car V_B is measured by the vehicle speed sensor in real time. The relative speed V_r is measured by the vehicle-mounted radar in the collision avoidance system, and the speed “V_A” of car A can be calculated by the formula V_r = V_B − V_A. The value of each other parameter in the model needs to be set in advance.

3.3.1. Determination of Parameters t₁, t₂ and t₃

According to the analysis of the braking process, the driver’s reaction time t₁ is generally 0.3–1.0 s, and the value of the reaction time is related to the driver’s driving experience, proficiency and fatigue. In this paper, t₁ = 1.0 s. The braking coordination time t₂ is generally 0.2–0.4 s, and the value of the braking coordination time is mainly related to the structural form of the braking system. In this paper, t₂ = 0.3 s. According to relevant statistical analysis, in the actual braking process, the braking force growth time t₃ is generally considered to be 0.1–0.2 s. In this paper, t₃ = 0.2 s [24].

3.3.2. Determination of Parameters j_Amax and j_Bmax

During the braking process, the braking deceleration produced by a car reflects the value of the ground braking force, which is not only related to the brake force when the wheel is rolling, but is also related to the adhesion provided by the road when the anti-lock system drags or slips. Specifically, the braking deceleration is related to the type of brakes, wheel load, road adhesion coefficient and road slope. In general, the road adhesion condition is the key factor affecting the braking deceleration. Due to different road conditions and a different adhesion coefficient, the car’s ground braking force varies, so the time the car takes to achieve the maximum braking deceleration differs.

According to car theory [25], j_max = φg. Obviously, the maximum braking deceleration varies with the road adhesion coefficient. However, if the car is driving on a sloped section of road, the gravity of the car is decomposed along the longitudinal slope, and the direction of the supporting force is perpendicular to the road. In an uphill section, the gravity component along the longitudinal slope and the ground braking force jointly provide braking force for the vehicle. In a downhill section, gravity along the longitudinal slope of the component force will offset part of the vehicle’s braking force, which is not conducive to vehicle braking. According to JTG B01-2014 Highway Engineering and Technical Standards, the maximum longitudinal slope of an expressway shall not exceed 5%. Therefore, the maximum braking acceleration j_max under different slopes can be obtained by the formula j_max = (φ + i)g by simplification. When the slip rate is in the range of 15–30%, the wheel–road adhesion coefficient is at the maximum value, and the braking force can reach the maximum value. Asphalt and cement are widely used as the pavement materials in China [26]. The values of the wheel–road adhesion coefficient φ are shown in

Table 1. Wheel–road adhesion coefficient (φ) values.

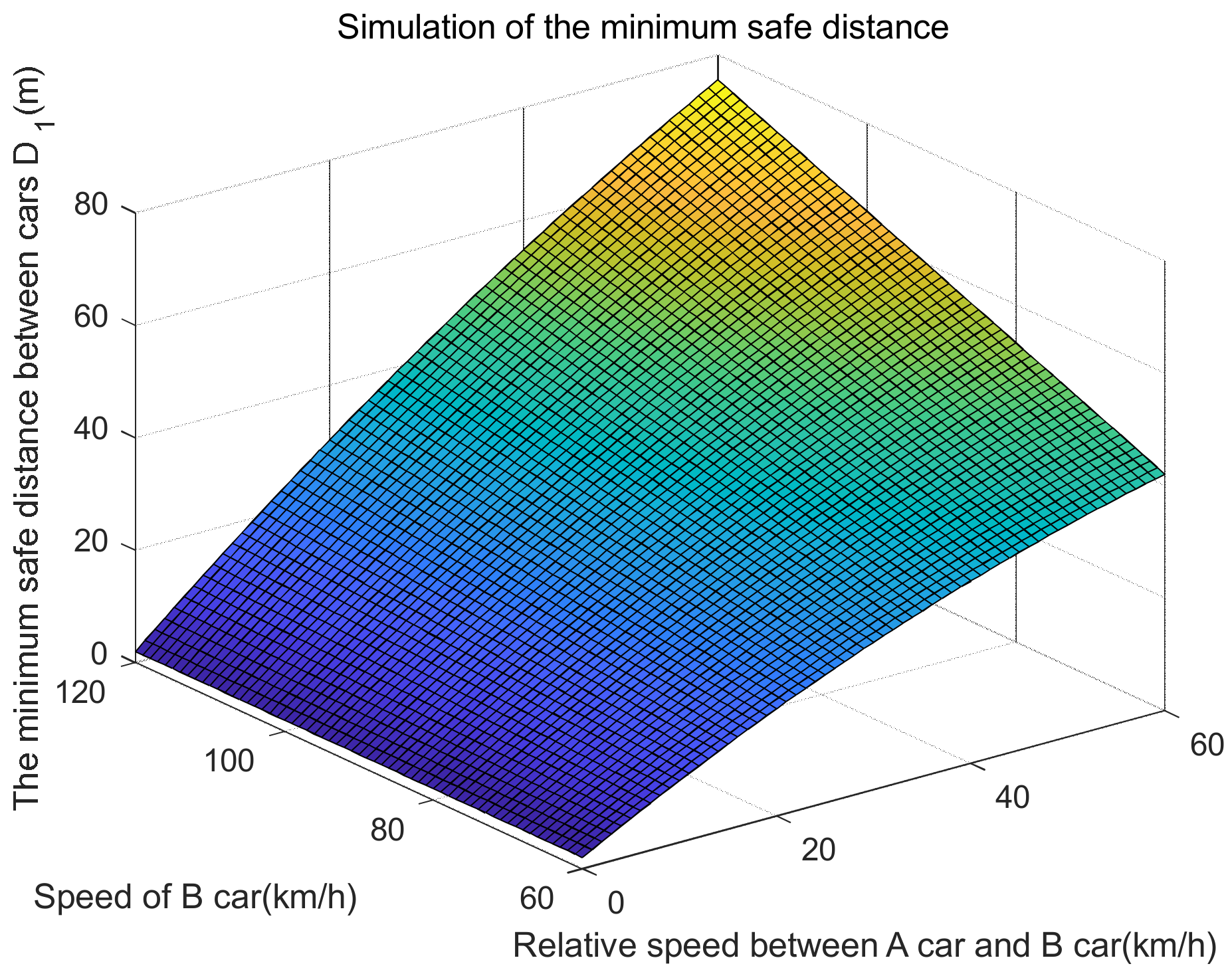
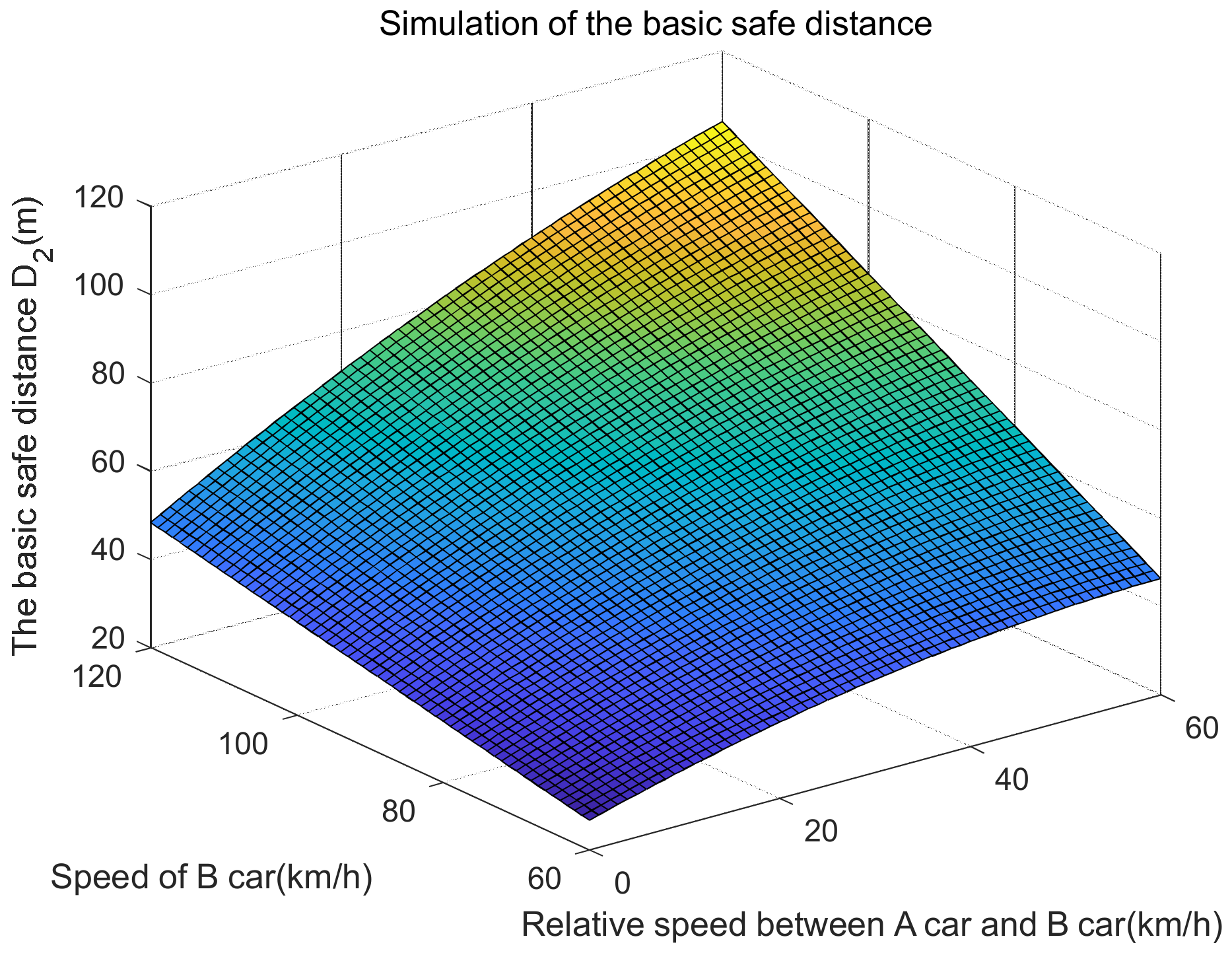
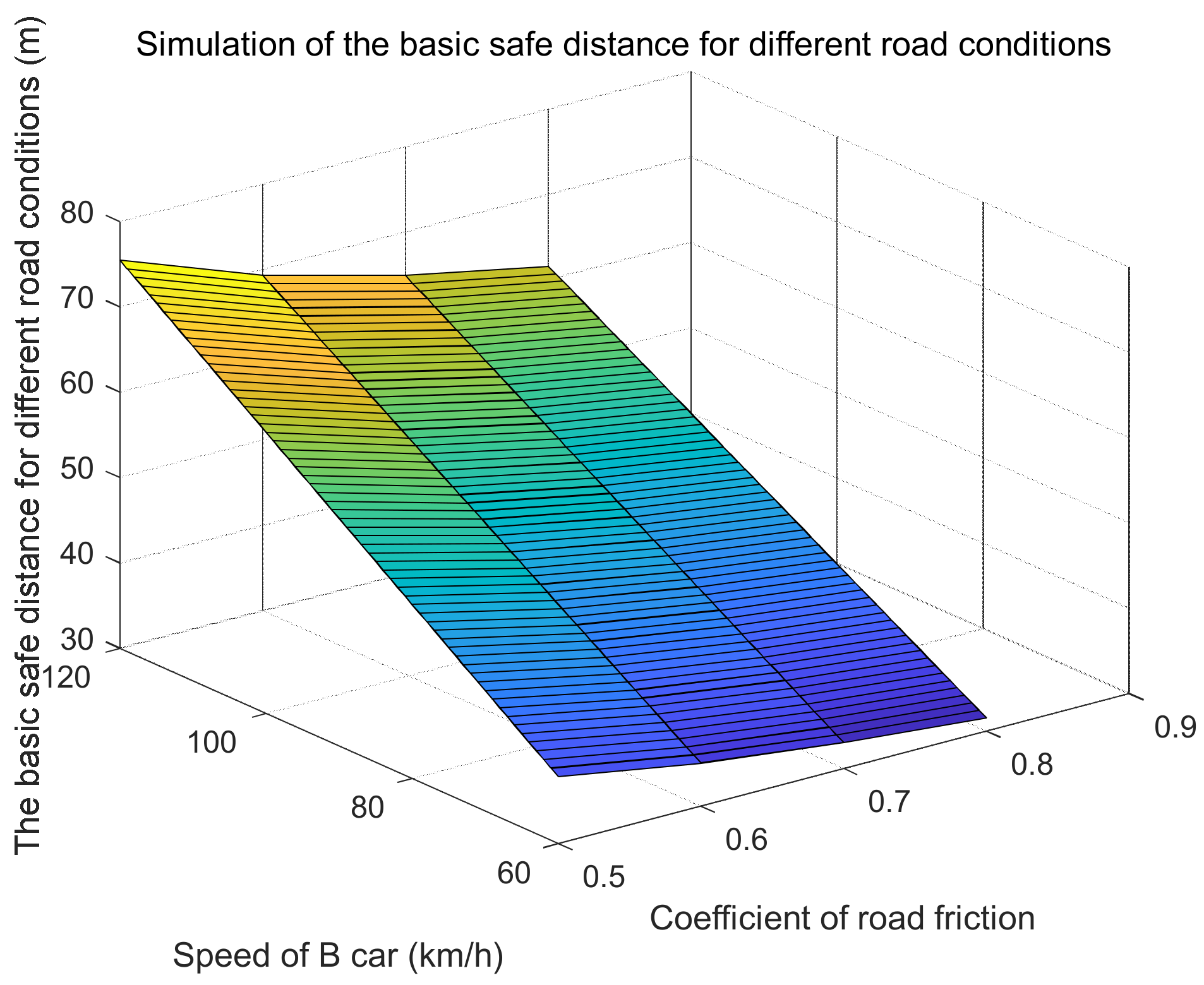
Pavement Condition	Asphalt, Concrete Pavement (Dry)	Asphalt, Concrete Pavement (Wet)	Dirt Road, Gravel Road (Snow)	Ice Road
The adhesion coefficient φ value	0.8	0.7	0.6	0.15

.

3.3.3. Determination of the Value of Parameter “d”

There should be distance “d” between the front car and the following car. In order to ensure that the distance after stopping is not severely distressing, the value of “d” can be based on people’s individual responses. Generally, the value of “d” is 2–5 m. The value is affected by the driver’s experience, the conditions on the road and the psychological resilience the driver has that day. In this paper, it is defined that the value of “d” is 2 m for ascending roads, 3 m for flat roads and 5 m for downhill roads.

4. Simulation Analysis and Application

4.1. Calculations of Three Safe Distances for Different Road Conditions and Slopes

Since only the deceleration during braking is involved in the minimum following distance model, and the front car and the following car are driving on the same road (making the road conditions the same), the maximum deceleration during braking is taken as j_Amax = j_Bmax in this paper. We take the braking deceleration of both cars to be the same. On the one hand, this simplifies the calculations. On the other hand, in actual scenarios, the deceleration of the following car is generally greater than that of the front car. If they are equal, greater safety is implied. At the same time, we can assume that V’_A = V’_B after car A and car B finish braking (including a requirement that both cars have stopped after the end of braking). If V’_A is less than V’_B, obviously both cars are not in the safe state, and if V’_A is greater than V’_B, then obviously both cars are in the safe state.

(1)

For i = 0 and d = 3, the simulations of the three safe distances are shown in Figure 3, Figure 4 and Figure 5. The results of

Table 2. The minimum safe distance D₁ based on V_B between 60 and 120 km/h when i = 0 and d = 3.

i = 0, d = 3	Relative Velocity Vr (km/h) (Vr = VB − VA)							VB (km/h)
	0	10	20	30	40	50	60
The minimum safe distance D1 (m)	3.0000							60
	3.0000	14.1227	24.2809					80
	3.0000	16.0517	28.1389	39.2616	49.4198			100
	3.0000	17.9807	31.9969	45.0486	57.1358	68.2585	78.4167	120

,

Table 3. The basic safe distance D₂ based on V_B between 60 and 120 km/h when i = 0 and d = 3.

i = 0, d = 3	Relative Velocity Vr (km/h) (Vr = VB − VA)							VB (km/h)
	0	10	20	30	40	50	60
The basic safe distance D2 (m)	24.6667							60
	31.8889	39.4005	45.9475					80
	39.1111	48.5517	57.0278	64.5394	71.0864			100
	46.3333	57.7029	68.1080	77.5486	86.0247	93.5363	100.0833	120

and

Table 4. The sufficient safe distance D₃ based on V_B between 60 and 120 km/h when i = 0 and d = 3.

i = 0, d = 3	Relative Velocity Vr (km/h) (Vr = VB − VA)				VB (km/h)
	60	80	100	120
The sufficient safe distance between cars D3 (m)	43.6844				60
		64.9653			80
			90.1042		100
				119.1011	120

can be obtained from Figure 3, Figure 4 and Figure 5, respectively.

(2)

For i = 0.3 and d = 2 on the uphill road, the simulations of three kinds of safe distance are shown in Figure 6, Figure 7 and Figure 8. The results of

Table 5. The minimum safe distance D₁ based on V_B between 60 and 120 km/h when i = 0.3 and d = 2.

i = 0.3, d = 2	Relative Velocity Vr (km/h) (Vr = VB − VA)							VB (km/h)
	0	10	20	30	40	50	60
The minimum safe distance D1 (m)	2.0000							60
	2.0000	12.8612	22.7928					80
	2.0000	14.7205	26.5114	37.3726	47.3042			100
	2.0000	16.5798	30.2300	42.9505	54.7413	65.6026	75.5341	120

,

Table 6. The basic safe distance D₂ based on V_B between 60 and 120 km/h when i = 0.3 and d = 2.

i = 0.3, d = 2	Relative Velocity Vr (km/h) (Vr = VB − VA)							VB (km/h)
	0	10	20	30	40	50	60
The basic safe distance D2 (m)	23.6667							60
	30.8889	38.1390	44.4595					80
	38.1111	47.2205	55.4003	62.6504	68.9708			100
	45.3333	56.3020	66.3411	75.4505	83.6302	90.8803	97.2008	120

and

Table 7. The sufficient safe distance D₃ based on V_B between 60 and 120 km/h when i = 0.3 and d = 2.

i = 0.3, d = 2	Relative Velocity Vr (km/h) (Vr = VB − VA)				VB (km/h)
	60	80	100	120
The sufficient safe distance between cars D3 (m)	42.0569				60
		62.8497			80
			87.3611		100
				115.5911	120

can be obtained from Figure 6, Figure 7 and Figure 8, respectively

(3)

For i = −0.3 and d = 5 on the downhill road, the simulations of three kinds of safe distance are shown in Figure 9, Figure 10 and Figure 11. The results of

Table 8. The minimum safe distance D₁ based on V_B between 60 and 120 km/h when i = −0.3 and d = 5.

i = −0.3, d = 5	Relative Velocity Vr (km/h) (Vr = VB − VA)							VB (km/h)
	0	10	20	30	40	50	60
The minimum safe distance D1 (m)	5.0000							60
	5.0000	16.4045	26.8070					80
	5.0000	18.4087	30.8153	42.2198	52.6223			100
	5.0000	20.4129	34.8236	48.2323	60.6389	72.0435	82.4459	120

,

Table 9. The basic safe distance D₂ based on V_B between 60 and 120 km/h when i = −0.3 and d = 5.

i = −0.3, d = 5	Relative Velocity Vr (km/h) (Vr = VB − VA)							VB (km/h)
	0	10	20	30	40	50	60
The basic safe distance D2 (m)	26.6667							60
	33.8889	41.6823	48.4736					80
	41.1111	50.9087	59.7042	67.4976	74.2889			100
	48.3333	60.1351	70.9347	80.7323	89.5278	97.3212	104.1126	120

and

Table 10. The sufficient safe distance D₃ based on V_B between 60 and 120 km/h when i = −0.3 and d = 5.

i = −0.3, d = 5	Relative Velocity Vr (km/h) (Vr = VB − VA)				VB (km/h)
	60	80	100	120
The sufficient safe distance between cars D3 (m)	46.3609				60
		68.1678			80
			93.9831		100
				123.8067	120

can be obtained from Figure 9, Figure 10 and Figure 11, respectively.

According to the implementation of Article 80 of the Road Traffic Safety Law of the People’s Republic of China, when a car is being driven on an expressway at a speed of more than 100 km per hour, the driver shall keep a distance of more than 100 m from any vehicle that is in front and in the same lane. When the vehicle speed is lower than 100 km per hour, the distance between the vehicle and the vehicle in front in the same lane may be shortened appropriately, but the minimum distance shall not be less than 50 m.

As can be seen in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 and Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10, the numerical simulation results meet the highway speed limit requirements stipulated in Article 80 of the Implementation Regulations of the Road Traffic Safety Law of the People’s Republic of China. According to the detailed analysis in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 and Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10, under the same slope section, the minimum safe distance D₁ is the minimum, the basic safe distance D₂ is the second and the sufficient safe distance D₃ is the maximum. Under the same driving conditions, such as the same speed V_B of car B, relative speed V_r and the same road adhesion, all kinds of safety distances required by the downhill section are the largest, followed by the corresponding flat section, and the smallest on the uphill section. The results of this study can provide a more specific reference value for the safe following distance at different vehicle speeds and provide a theoretical basis for the traffic management department to formulate relevant policies.

4.2. Application of Three Kinds of Safe Distance on Expressways

In practical cases, it is assumed that a selection switch is set on the dashboard of the cab. The driver can put the button in an appropriate position according to the actual road conditions during the day of driving, and the alarm system can select the road adhesion coefficient for the data processing unit to calculate.

Here, the relative speed was set as V_r = V_B − V_A = 20 km/h, and V_B ranged from 80 to 120 km/h. The basic following distance between car A and car B on different roads was simulated, and the results shown in Figure 12 were obtained. The specific parameters are shown in

Table 11. The basic following distance based on V_B between 60 and 120 km/h when i = 0, V_r = 20 km/h.

Vr = VB − VA = 20 km/h	Coefficient of Road Adhesion φ				VB (km/h)
	0.5	0.6	0.7	0.8
The basic safety distance between cars D2 (m)	54.5361	50.8616	48.2369	46.2684	80
	68.0576	63.3332	59.9586	57.4276	100
	81.5790	75.8047	71.6802	68.5869	120

.

As we considered the safety distance under three different driving conditions, we can consider providing an impact factor according to the needs of practical operation and feasibility. As the minimum following distance expects perfection from the following car’s driver’s reaction time, and the sufficient following distance accounts for an extreme case, the basic following distance reflects most real scenarios. Thus, we set three factors influencing safe following distance (which can be analyzed using probability statistics according to actual driving conditions). The influencing factor of the minimum following distance D₁ is ω₁, the influencing factor of the basic following distance D₂ is ω₂, and the influencing factor of the sufficient following distance D₃ is ω₃; and ω₁ + ω₂ + ω₃ = 1. Therefore, it is finally provided to the warning system as the warning critical safe distance S:

S = ω₁D₁ + ω₂D₂ + ω₃D₃

(14)

5. Conclusions

In this study, according to the characteristics of safe driving and rear-end accidents on expressways, the safe following distance on an expressway is studied from the angle of vehicle braking deceleration based on kinematic principles. Based on the characteristics of the vehicle braking process, three kinds of highway safe following distance models based on braking deceleration were constructed. Based on the investigation of the road section and the study of the calculation model and parameters of the safe following distance, the key parameters of the safe following distance model, such as the driving speed and the deceleration speed and different slope values, were discussed in depth, and the recommended values of the safe following distance of the vehicles on plain and longitudinal slopes were put forward. The research results show that the calculation results of the safe following distance conform to the requirements of safe following distance in the Implementation Regulations of the Road Traffic Safety Law of the People’s Republic of China. The calculation of three kinds of safe following distance can provide a theoretical basis and practical examples for the traffic police department to formulate different traffic management policies. The results of this study have practical guiding significance for improving the vehicle density and transportation efficiency of expressways and reducing the incidence of rear-end traffic accidents on expressways. The next step of this study is to carry out the following research contents:

(1)

Construct the calculation model of expressway parking sight distance based on braking deceleration and study the relationship between safe following distance and stopping sight distance.

(2)

Propose the suggested value of expressway stopping sight distance based on braking deceleration under different longitudinal slopes and study different design speeds.

(3)

Carry out the vehicle braking deceleration test, to further improve the parameter value of the model and enhance the application value of the research.