Stability Analysis of Equilibrium Point and Limit Cycle of Two-Dimensional Nonlinear Dynamical Systems—A Tutorial
Abstract
1. Introduction
2. Stability of the Equilibrium Point
2.1. Stability Analysis by Lyapunov–LaSalle Energy-Based Approach
2.2. Stability Analysis by Graphical Phase Plane Approach
2.3. Stability Analysis by Linearizing around an Equilibrium Point
3. Stability of Limit Cycle
3.1. Stability of Limit Cycle by Invariant Set Theorem
3.2. Stability of Limit Cycle by Poincaré–Bendixson (PB) Theorem
“If we have the following conditions satisfied: (1) if we can find a closed and bounded region, (2) and there is no equilibrium point in the region, (3) and there exists a trapped trajectory that lies in the region from the beginning and stays in the region for all future times, then the trajectory is either a closed trajectory itself or it spirals toward a closed trajectory as time goes on”.
4. Comparison among Different Approaches
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tocino, A.; Rey, A. Local stochastic stability of SIRS models without Lyapunov functions. Commun. Nonlinear Sci. Numer. Simul. 2021, 103, 105956. [Google Scholar] [CrossRef]
- Zhou, G.; Liao, X.; Xu, B.; Yu, P.; Chen, G. Simple algebraic necessary and sufficient conditions for Lyapunov stability of a Chen system and their applications. Trans. Inst. Meas. Control 2018, 40, 2200–2210. [Google Scholar] [CrossRef]
- Bernstein, D.S.; Bhat, S.P. Lyapunov stability, semistability, and asymptotic stability of matrix second-order systems. In Proceedings of the 1994 American Control Conference—ACC ‘94, Baltimore, MD, USA, 29 June–1 July 1994; Volume 2, pp. 2355–2359. [Google Scholar]
- Phat, V.N.; Nam, P.T. Exponential stability and stabilization of uncertain linear time-varying systems using parameter dependent Lyapunov function. Int. J. Control 2007, 80, 1333–1341. [Google Scholar] [CrossRef]
- Ansari, M.; Meigoli, V.; Razminia, A. Stability analysis of the homogeneous nonlinear dynamical systems using Lyapunov function generation based on the basic functions. SN Appl. Sci. 2020, 2, 219. [Google Scholar] [CrossRef]
- Choi, J. Connections between local stability in Lyapunov and input/output senses. IEEE Trans. Autom. Control 1995, 40, 2139–2143. [Google Scholar] [CrossRef]
- Elkaranshawy, H.; Ezzat, H.; Ibrahim, N. Lyapunov function and global asymptotic stability for a new multiscale viral dynamics model incorporating the immune system response: Implemented upon HCV. PLoS ONE 2021, 16, e0257975. [Google Scholar] [CrossRef]
- Korobeinikov, A.; Wake, G. Lyapunov functions and global stability for SIR, SIRS, and SIS epidemiological models. Appl. Math. Lett. 2002, 15, 955–960. [Google Scholar] [CrossRef]
- Shuai, Z.; Driessche, P. Global Stability of Infectious Disease Models Using Lyapunov Functions. SIAM J. Appl. Math. 2013, 73, 1513–1532. [Google Scholar] [CrossRef]
- Mancilla-Aguilar, J.L.; Haimovich, H.; García, R.A. Global Stability Results for Switched Systems Based on Weak Lyapunov Functions. IEEE Trans. Autom. Control 2017, 62, 2764–2777. [Google Scholar] [CrossRef]
- Kuniya, T.; Wang, J. Lyapunov functions and global stability for a spatially diffusive SIR epidemic model. Appl. Anal. 2017, 96, 1935–1960. [Google Scholar] [CrossRef]
- Wang, X.; Ma, H. A Lyapunov Function and Global Stability for a Class of Predator-Prey Models. Discret. Dyn. Nat. Soc. 2012, 2012, 218785. [Google Scholar] [CrossRef]
- Cao, J. Global stability conditions for delayed CNNs. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 1330–1333. [Google Scholar]
- Su, H.; Li, W.; Wang, K. Global stability analysis of discrete-time coupled systems on networks and its applications. Chaos 2012, 22, 033135. [Google Scholar] [CrossRef] [PubMed]
- Masoumnezhad, M.; Rajabi, M.; Chapnevis, A. An Approach for the Global Stability of Mathematical Model of an Infectious Disease. Symmetry 2020, 12, 1778. [Google Scholar] [CrossRef]
- Taieb, N. Indefinite derivative for stability of time-varying nonlinear systems. IMA J. Math. Control Inf. 2021, 38, 534–551. [Google Scholar] [CrossRef]
- Gómez, M.; Mondragon, E.; Molano, P. Global stability analysis for a model with carriers and non-linear incidence rate. J. Biol. Dyn. 2020, 14, 409–420. [Google Scholar] [CrossRef]
- Wei, B. A Tutorial on Robust Control, Adaptive Control and Robust Adaptive Control—Application to Robotic Manipulators. Inventions 2019, 4, 49. [Google Scholar] [CrossRef]
- Esterhuizen, W.; Aschenbruck, T.; Streif, S. On maximal robust positively invariant sets in constrained nonlinear systems. Automatica 2020, 119. [Google Scholar] [CrossRef]
- Chellaboina, V.; Leonessa, A.; Haddad, W. Generalized Lyapunov and invariant set theorems for nonlinear dynamical systems. Syst. Control. Lett. 1999, 38, 289–295. [Google Scholar] [CrossRef]
- Naoya, T.; Yoshinobu, K. Learning Dynamics Models with Stable Invariant Sets. Proc. AAAI Conf. Artif. Intell. 2021, 35, 9782–9790. [Google Scholar]
- Hakimi, A.R.; Binazadeh, T. Generation of stable oscillations in uncertain nonlinear systems with matched and unmatched uncertainties. Int. J. Control 2019, 92, 163–174. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, D. Extensions of LaSalle’s Invariance Principle for Switched Nonlinear Systems. IFAC Proc. Vol. 2008, 41, 14397–14402. [Google Scholar] [CrossRef]
- Willems, J. Dissipative dynamical systems part I: General theory. Arch. Ration. Mech. Anal. 1972, 45, 321–351. [Google Scholar] [CrossRef]
- Matthieu, B.; Sophie, T.; Frédéric, G. Lyapunov Stability Analysis of a Mass Spring system subject to Friction. Syst. Control Lett. 2021, 150, 104910. [Google Scholar]
- Giesl, P.; Hafstein, S. Review on computational methods for Lyapunov functions. Discret. Contin. Dyn. Syst. Ser. B 2015, 20, 2291–2331. [Google Scholar]
- Neumann, K.; Lemme, A. Neural learning of stable dynamical systems based on data-driven Lyapunov candidates. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1216–1222. [Google Scholar]
- Bhatia, N.; Szego, G. Stability Theory of Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Fischer, N.; Kamalapurkar, R.; Dixon, W. LaSalle-Yoshizawa Corollaries for Nonsmooth Systems. IEEE Trans. Autom. Control 2013, 58, 2333–2338. [Google Scholar] [CrossRef]
- Shevitz, D.; Paden, B. Lyapunov Stability Theory of Nonsmooth Systems. IEEE Trans. Autom. Control 1994, 39, 1910–1914. [Google Scholar] [CrossRef]
- Ahmadi, A.; Krstic, M.; Parrilo, P. A globally asymptotically stable polynomial vector field with no polynomial Lyapunov function. In Proceedings of the 50th IEEE Conference on Decision and Control, Orlando, FL, USA, 12–15 December 2011; pp. 7579–7580. [Google Scholar]
- Mancilla-Aguilar, J.; García, R. An extension of LaSalle’s invariance principle for switched systems. Syst. Control Lett. 2006, 55, 376–384. [Google Scholar] [CrossRef]
- Ahmadi, M.; Michalska, H.; Buehler, M. Control and Stability Analysis of Limit Cycles in a Hopping Robot. IEEE Trans. Robot. 2007, 23, 553–563. [Google Scholar] [CrossRef]
- Naiwert, L.; Spindler, K. Phase portraits, Lyapunov functions, and projective geometry. Math. Semesterber. 2021, 68, 143–161. [Google Scholar] [CrossRef]
- Malisoff, M.; Mazenc, F. Constructions of Strict Lyapunov Functions; Springer: London, UK, 2009. [Google Scholar]
- Ravanbakhsh, H.; Sankaranarayanan, S. Learning control Lyapunov functions from counterexamples and demonstrations. Auton. Robot. 2019, 43, 275–307. [Google Scholar] [CrossRef]
- Chen, Z. LaSalle–Yoshizawa Theorem for nonlinear systems with external inputs: A counter-example. Automatica 2022, 147, 110636. [Google Scholar] [CrossRef]
- Hsiung, Y. Phase-Plane Methods. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 1969. [Google Scholar]
- He, R.; Jing, Z.; Shen, X. Stability Analysis of Combined Braking System of Tractor-Semitrailer Based on Phase-Plane Method. SAE Int. J. Commer. Veh. 2018, 11, 151–160. [Google Scholar] [CrossRef]
- Han, Z.; Xu, N.; Chen, H.; Huang, Y.; Zhao, B. Energy-efficient control of electric vehicles based on linear quadratic regulator and phase plane analysis. Appl. Energy 2018, 213, 639–657. [Google Scholar] [CrossRef]
- Aksjonov, A.; Ricciardi, V.; Vodovozov, V.; Augsburg, K. Trajectory Phase-Plane Method—Based Analysis of Stability and Performance of a Fuzzy Logic Controller for an Anti-Lock Braking System. In Proceedings of the 2019 IEEE International Conference on Mechatronics (ICM), Ilmenau, Germany, 18–20 March 2019; pp. 602–607. [Google Scholar]
- Hao, Z.; Xian, L.; Shu, S.; Hong, L.; Rachel, G.; Li, L. Phase Plane Analysis for Vehicle Handling and Stability. Int. J. Comput. Intell. Syst. 2011, 4, 1179–1186. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y.; Gardner, M.R. Transient stability analysis with phase plane of high-order derivatives of angle dynamics. In Proceedings of the 2014 IEEE PES T&D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014; pp. 1–5. [Google Scholar]
- Jhangeer, A.; Muddassar, M.; Awrejcewicz, J.; Naz, Z.; Riaz, M.B. Phase portrait, multi-stability, sensitivity and chaotic analysis of Gardner’s equation with their wave turbulence and solitons solutions. Results Phys. 2022, 32, 104981. [Google Scholar] [CrossRef]
- Xing, X.; Jiang, S. The application of LabVIEW in control system phase plane analysis. In Proceedings of the 2010 3rd International Conference on Computer Science and Information Technology, Chengdu, China, 9–11 July 2010; pp. 243–246. [Google Scholar]
- Rahmouni, W.; Benasla, L. Phase-Plane Methods to Analyse Power System Transient Stability. In Advanced Control Engineering Methods in Electrical Engineering Systems; Chadli, M., Bououden, S., Ziani, S., Zelinka, I., Eds.; ICEECA 2017; Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2019; Volume 522. [Google Scholar]
- Chou, K.Y.; Chen, Y.P. Energy based swing-up controller design using phase plane method for rotary inverted pendulum. In Proceedings of the 2014 13th International Conference on Control Automation Robotics & Vision (ICARCV), Singapore, 10–12 December 2014; pp. 975–979. [Google Scholar]
- Li, X.; Xu, N.; Xu, J. A novel envelope stability control scheme based on phase plane with enhanced overshoot dynamics of vehicle. In Proceedings of the 2020 4th CAA International Conference on Vehicular Control and Intelligence (CVCI), Hangzhou, China, 18–20 December 2020; pp. 436–441. [Google Scholar]
- Ghaffari, A.; Lasemi, N. New method to examine the stability of equilibrium points for a class of nonlinear dynamical systems. Nonlinear Dyn. 2015, 79, 2271–2277. [Google Scholar] [CrossRef]
- Yang, T.; Chua, L. Piecewise-linear chaotic systems with a single equilibrium point. Int. J. Bifurc. Chaos 2000, 10, 2015–2060. [Google Scholar] [CrossRef]
- Kurtz, M.; Henson, M. Stability analysis of a feedback linearizing control strategy for constrained nonlinear systems. In Proceedings of the 1997 American Control Conference, Albuquerque, NM, USA, 4–6 June 1997; Volume 5, pp. 3480–3484. [Google Scholar]
- Lobo, F.; Garattini, R. Linearized stability analysis of gravastars in noncommutative geometry. J. High Energy Phys. 2013, 2013, 65. [Google Scholar] [CrossRef]
- García-Agúndez, A.; García-Vallejo, D.; Freire, E. Linearization approaches for general multibody systems validated through stability analysis of a benchmark bicycle model. Nonlinear Dyn. 2021, 103, 557–580. [Google Scholar] [CrossRef]
- Freidovich, L.; Shiriaev, A.; Manchester, I. Stability Analysis and Control Design for an Underactuated Walking Robot via Computation of a Transverse Linearization. IFAC Proc. Vol. 2008, 41, 10166–10171. [Google Scholar] [CrossRef]
- Rice, J.; Platt, D. Stability and localization of rapid shear in fluid-saturated fault gouge: 1. Linearized stability analysis. J. Geophys. Res. Solid Earth 2014, 119, 4311–4333. [Google Scholar] [CrossRef]
- Park, C. LMI-based robust stability analysis for fuzzy feedback linearization regulators with its applications. Inf. Sci. 2003, 152, 287–301. [Google Scholar] [CrossRef]
- Garcke, H.; Kohsaka, Y. Linearized Stability Analysis of Stationary Solutions for Surface Diffusion with Boundary Conditions. SIAM J. Math. Anal. 2005, 36, 1031–1056. [Google Scholar] [CrossRef]
- Li, L.; Chen, Y.; Zhou, B.; Liu, H.; Liu, Y. Linearization threshold condition and stability analysis of a stochastic dynamic model of one-machine infinite-bus (OMIB) power systems. Prot. Control Mod. Power Syst. 2021, 6, 19. [Google Scholar] [CrossRef]
- Song, Y.; Baker, C. Linearized stability analysis of discrete Volterra equations. J. Math. Anal. Appl. 2004, 294, 310–333. [Google Scholar] [CrossRef]
- Asano, F. Stability analysis of underactuated compass gait based on linearization of motion. Multibody Syst. Dyn. 2015, 33, 93–111. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Jiang, F.; Shi, J.; Wang, Q. On the existence and uniqueness of a limit cycle for a lienard system with a discontinuity line. Commun. Pure Appl. Anal. 2016, 15, 2509–2526. [Google Scholar]
- Volchenkov, D. Nonlinear Dynamics, Chaos, and Complexity; Springer Higher Education Press: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Slotine, J.; Li, W.P. Applied Nonlinear Control; Pearson Education Press: New York, NY, USA, 1991. [Google Scholar]
- Isidori, A. Nonlinear Control Systems, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Karlheinz, O. A comprehensive analytical solution of the nonlinear pendulum. Eur. J. Phys. 2011, 32, 479–490. [Google Scholar]
- Lozano, R.; Fantoni, I.; Block, D. Stabilization of the inverted pendulum around its homoclinic orbit. Syst. Control Lett. 2000, 40, 197–204. [Google Scholar] [CrossRef]
- Lima, F.; Arun, P. An accurate formula for the period of a simple pendulum oscillating beyond the small-angle regime. Am. J. Phys. 2006, 74, 892. [Google Scholar] [CrossRef]
- Wei, B. Adaptive Control Design and Stability Analysis of Robotic Manipulators. Actuators 2018, 7, 89. [Google Scholar] [CrossRef]
- Robert, M. Linearization and Stability Analysis of Nonlinear Problems. Rose-Hulman Undergrad. Math. J. 2015, 16, 5. [Google Scholar]
- Moatimid, G.; Amer, T. Analytical Approximate Solutions of a Magnetic Spherical Pendulum: Stability Analysis. J. Vib. Eng. Technol. 2022, 1–11. [Google Scholar] [CrossRef]
- Rubensson, M.; Lennartson, B. Stability of limit cycles in hybrid systems using discrete-time Lyapunov techniques. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, NSW, Australia, 12–15 December 2000; Volume 2, pp. 1397–1402. [Google Scholar]
- Simic, S.; Sastry, S.; Johansson, K. Hybrid limit cycles and hybrid Poincare-Bendixson. In Proceedings of the 15th IFAC World Congress, Barcelona, Spain, 21–26 July 2002; Volume 35, pp. 197–202. [Google Scholar]
- Armengol, G.; Héctor, G.; Maite, G. Effective construction of Poincaré-Bendixson regions. J. Appl. Anal. Comput. 2017, 7, 1549–1569. [Google Scholar]
- Ciesielski, K. The Poincaré-Bendixson Theorem: From Poincaré to the XXIst century. Cent. Eur. J. Math. 2012, 10, 2110–2128. [Google Scholar] [CrossRef]
- Alsholm, P. Existence of limit cycles for generalized Li’enard equations. J. Math. Anal. Appl. 1992, 171, 242–255. [Google Scholar] [CrossRef]
- Meng, F.; Shi, S.; Zhang, B.; Bai, M.; Lin, N. Analysis for global characteristics of Lyapunov exponents in vehicle plane motion system. Sci. Rep. 2022, 12, 9300. [Google Scholar] [CrossRef]
- Sadri, S.; Wu, C. Stability analysis of a nonlinear vehicle model in plane motion using the concept of Lyapunov exponents. Int. J. Veh. Mech. Mobil. 2013, 51, 906–924. [Google Scholar] [CrossRef]
- Chesi, G. Rational Lyapunov functions for estimating and controlling the robust domain of attraction. Automatica 2013, 49, 1051–1057. [Google Scholar] [CrossRef]
- Tan, W. Stability region analysis using polynomial and composite polynomial Lyapunov functions and sum-of-squares programming. IEEE Trans. Autom. Control 2008, 53, 565–571. [Google Scholar] [CrossRef]
- Yajima, T.; Yamasaki, K. Jacobi stability for dynamical systems of two-dimensional second-order differential equations and application to overhead crane system. Int. J. Geom. Methods Mod. Phys. 2016, 13, 1650045. [Google Scholar] [CrossRef]
- Valmorbida, G.; Anderson, J. Region of attraction analysis via invariant sets. In Proceedings of the American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014; pp. 3591–3596. [Google Scholar]
- Mazenc, F.; Niculescu, S. Lyapunov stability analysis for nonlinear delay systems. Syst. Control Lett. 2001, 42, 245–251. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, W.; Li, X.; Zhou, X. Lyapunov stability analysis of fractional nonlinear systems. Appl. Math. Lett. 2016, 51, 13–19. [Google Scholar] [CrossRef]
- Barreau, M.; Seuret, A.; Gouaisbaut, F.; Baudouin, L. Lyapunov Stability Analysis of a String Equation Coupled With an Ordinary Differential System. IEEE Trans. Autom. Control 2018, 63, 3850–3857. [Google Scholar] [CrossRef]
- Li, X.; Yang, X. Lyapunov stability analysis for nonlinear systems with state-dependent state delay. Automatica 2020, 112, 108674. [Google Scholar] [CrossRef]
- Huang, R.; Harinath, E.; Biegler, L. Lyapunov stability of economically oriented NMPC for cyclic processes. J. Process Control 2011, 21, 501–509. [Google Scholar] [CrossRef]
- Kojima, C.; Rapisarda, P.; Takaba, K. Lyapunov stability analysis of higher-order 2-D systems. Multidimens. Syst. Signal Process. 2011, 22, 287–302. [Google Scholar] [CrossRef]
- Owens, D.H.; Li, L.M. Multi-periodic repetitive control system: A Lyapunov stability analysis for MIMO systems. Int. J. Control 2004, 77, 504–515. [Google Scholar] [CrossRef]
- Chen, Z.; Xie, Y.; Guo, Y.; Guo, J.; Zhang, K.; Liu, W.; Li, Y.; Li, G.; Zhou, Z. Stability Analysis of Spacecraft Phase Plane Control Systems: A Brief Overview and Some Problems. In 2020 Chinese Automation Congress (CAC); IEEE: Piscataway, NJ, USA, 2020; pp. 6465–6470. [Google Scholar]
- Chen, Z.; Xie, Y. Stability Analysis of the Closed-Loop System of a Phase-Plane Controlled Rigid Satellite. Aerosp. Control Appl. Chin. 2018, 44, 1–14. [Google Scholar]
- Penchuk, A.; Hattis, P. A Frequency Domain Stability Analysis of a Phase Plane Control System. J. Guid. Control Dyn. 1985, 81, 50–55. [Google Scholar] [CrossRef]
- Bobiti, R.; Lazar, M. A sampling approach to finding Lyapunov functions for nonlinear discrete-time systems. In Proceedings of the 2016 European Control Conference (ECC), Bucharest, Romania, 13–16 June 2023; pp. 561–566. [Google Scholar]
- Hernández-Solano, Y.; Atencia, M. Numerical methods that preserve a Lyapunov function for ordinary differential equations. Mathematics 2023, 11, 71. [Google Scholar] [CrossRef]
- Papachristodoulou, A.; Prajna, S. On the construction of Lyapunov functions using the sum of squares decomposition. In Proceedings of the 41st IEEE Conference on on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; Volume 3, pp. 3482–3487. [Google Scholar]
- Gritli, H. Poincaré maps design for the stabilization of limit cycles in non-autonomous nonlinear systems via time-piecewise-constant feedback controllers with application to the chaotic Duffing oscillator. Chaos Solitons Fractals 2019, 127, 127–145. [Google Scholar] [CrossRef]
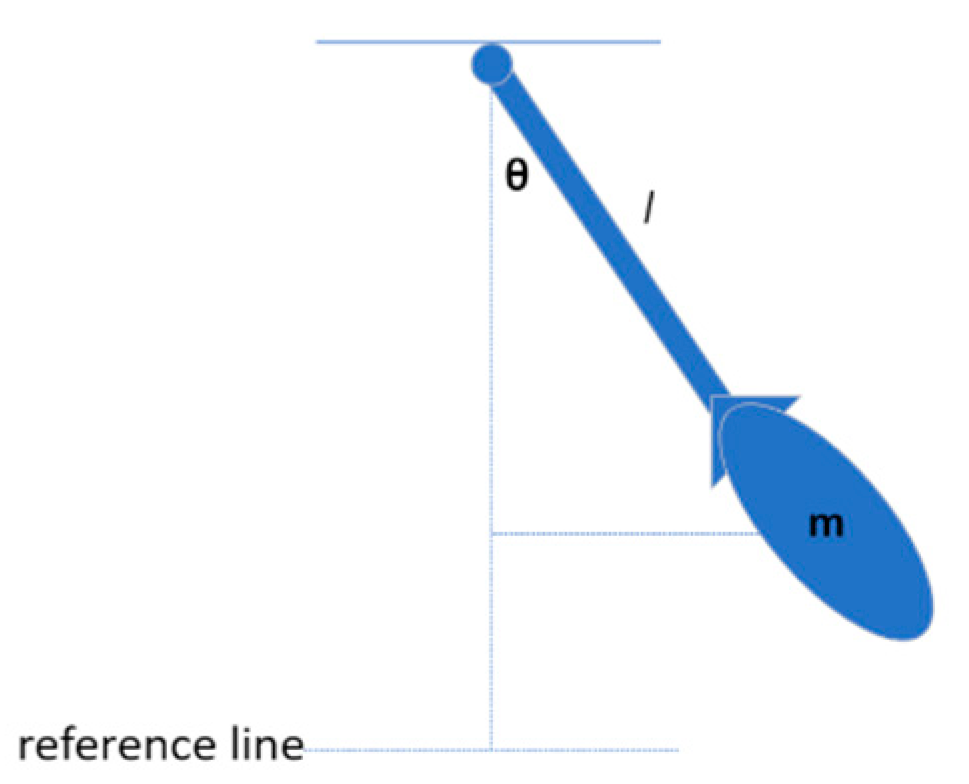





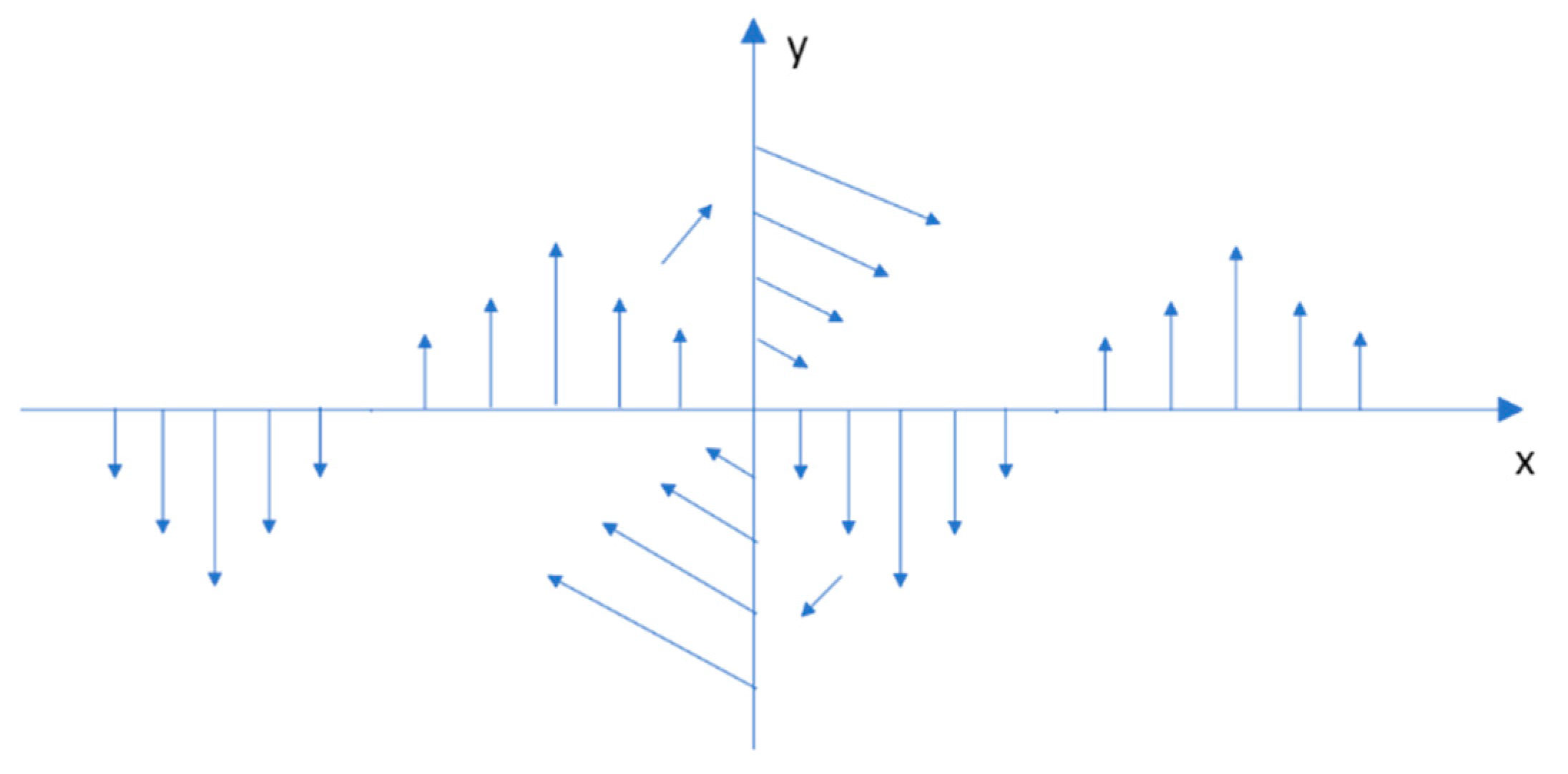




| Approaches for Stability Analysis of an Equilibrium Point | Advantages | Disadvantages |
|---|---|---|
| Lyapunov–LaSalle energy-based approach | 1. This analytical method can give quantitative result based on the Lyapunov and LaSalle theorems; 2. The Lyapunov–LaSalle energy-based approach is applicable to all dynamical systems | 1. It is difficult to choose the right Lyapunov candidate function, if one did not manage finding one, it does not mean the equilibrium point being analyzed is unstable, it could be stable or it could be unstable; 2. It involves with large calculations when we calculate the time derivative of the chosen Lyapunov function |
| Graphical phase plane approach | 1. It is a visualization method, which can give the conclusion without being getting into calculation; 2. This method is faster than the Lyapunov method when determining the stability of an equilibrium point | 1. This method most of the time is limited to the two-dimensional systems; 2. As it is visualization method, it cannot give us the quantitative result, only the qualitative result; 3. This method can only be applied to autonomous systems, not non-autonomous systems |
| Linearizing-around-an-equilibrium-point approach | 1. It involves with very simple calculation as the nonlinear system has been linearized; 2. this analytical method can give us the qualitatively correct dynamics information fast near the equilibrium point | 1. This method has limitations, it is not applicable to all dynamical systems. It can only give us the correct dynamics information fast near the equilibrium point when the equilibrium point is saddle, node, or focus/spiral. It could give us the false information when the equilibrium point is other than saddle, node, or focus. |
| Approaches for stability analysis of a limit cycle | - | - |
| Poincaré–Bendixson theorem | 1. The theorem is intuitive, and it is one of the few theorems that can prove whether there exists a limit cycle | 1. In order to use this theorem we need to construct a closed region, and it is difficult to construct a closed region that there exists a limit cycle in the region; 2. It is only valid for two-dimensional systems |
| LaSalle Local Invariant Set theorem | 1. It is obvious and easy to determine if there exist a limit cycle once we determined the time derivative of the chosen Lyapunov function | 1. It is difficult to choose the right Lyapunov candidate function. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, B. Stability Analysis of Equilibrium Point and Limit Cycle of Two-Dimensional Nonlinear Dynamical Systems—A Tutorial. Appl. Sci. 2023, 13, 1136. https://doi.org/10.3390/app13021136
Wei B. Stability Analysis of Equilibrium Point and Limit Cycle of Two-Dimensional Nonlinear Dynamical Systems—A Tutorial. Applied Sciences. 2023; 13(2):1136. https://doi.org/10.3390/app13021136
Chicago/Turabian StyleWei, Bin. 2023. "Stability Analysis of Equilibrium Point and Limit Cycle of Two-Dimensional Nonlinear Dynamical Systems—A Tutorial" Applied Sciences 13, no. 2: 1136. https://doi.org/10.3390/app13021136
APA StyleWei, B. (2023). Stability Analysis of Equilibrium Point and Limit Cycle of Two-Dimensional Nonlinear Dynamical Systems—A Tutorial. Applied Sciences, 13(2), 1136. https://doi.org/10.3390/app13021136












