Fault Location Method of Multi-Terminal Transmission Line Based on Fault Branch Judgment Matrix
Abstract
:1. Introduction
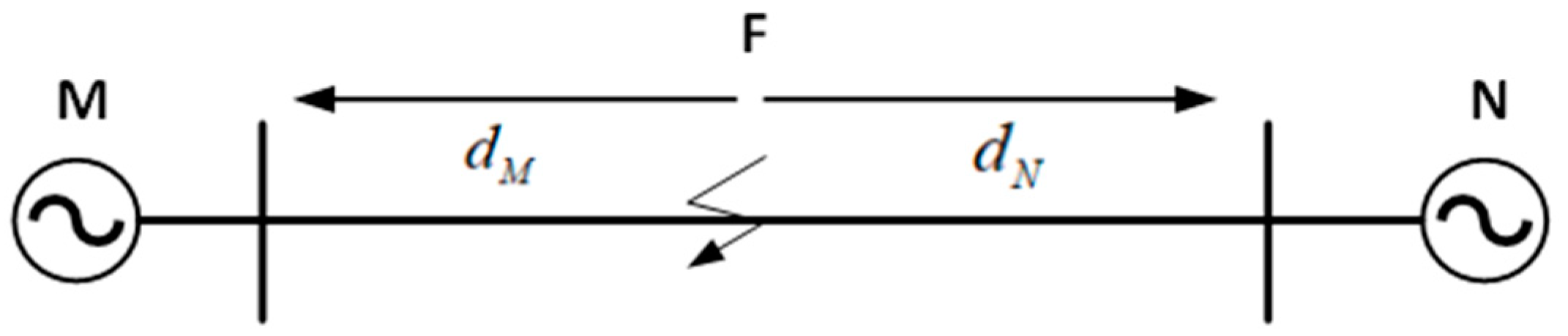
2. Improved Double-Ended Traveling Wave Localization Method Based on Line Mode Component
2.1. Decoupling of Three-Phase Transmission Lines
2.2. Main Errors of Double-Ended Traveling Wave Ranging
- Traveling wave velocity: In actual working conditions, the transmission line environment affects line parameters, making it difficult to determine the wave speed. Therefore, wave speed cannot be accurately calculated in practical applications, leading to large-ranging errors.
- Wave head capture accuracy: First arrival time of fault traveling wave at both ends of the line is a primary factor affecting the positioning accuracy. The error mainly consists of the synchronization error of the sampling clock and the extraction error of the faulty traveling wave head.
- Arc sag, ambient temperature, load current, and other factors on the line length.
2.3. Improved Double-Ended Traveling Wave Ranging Method Based on the Line Mode Component
3. Traveling Wave Head Detection Algorithm Based on CEEMDAN-TEO
3.1. Selection of IMFs
3.2. Demodulation of TEO
3.3. Simulation Verification
3.4. Algorithm Adaptation Analysis
3.4.1. Different Transition Resistance
3.4.2. Different Fault Types
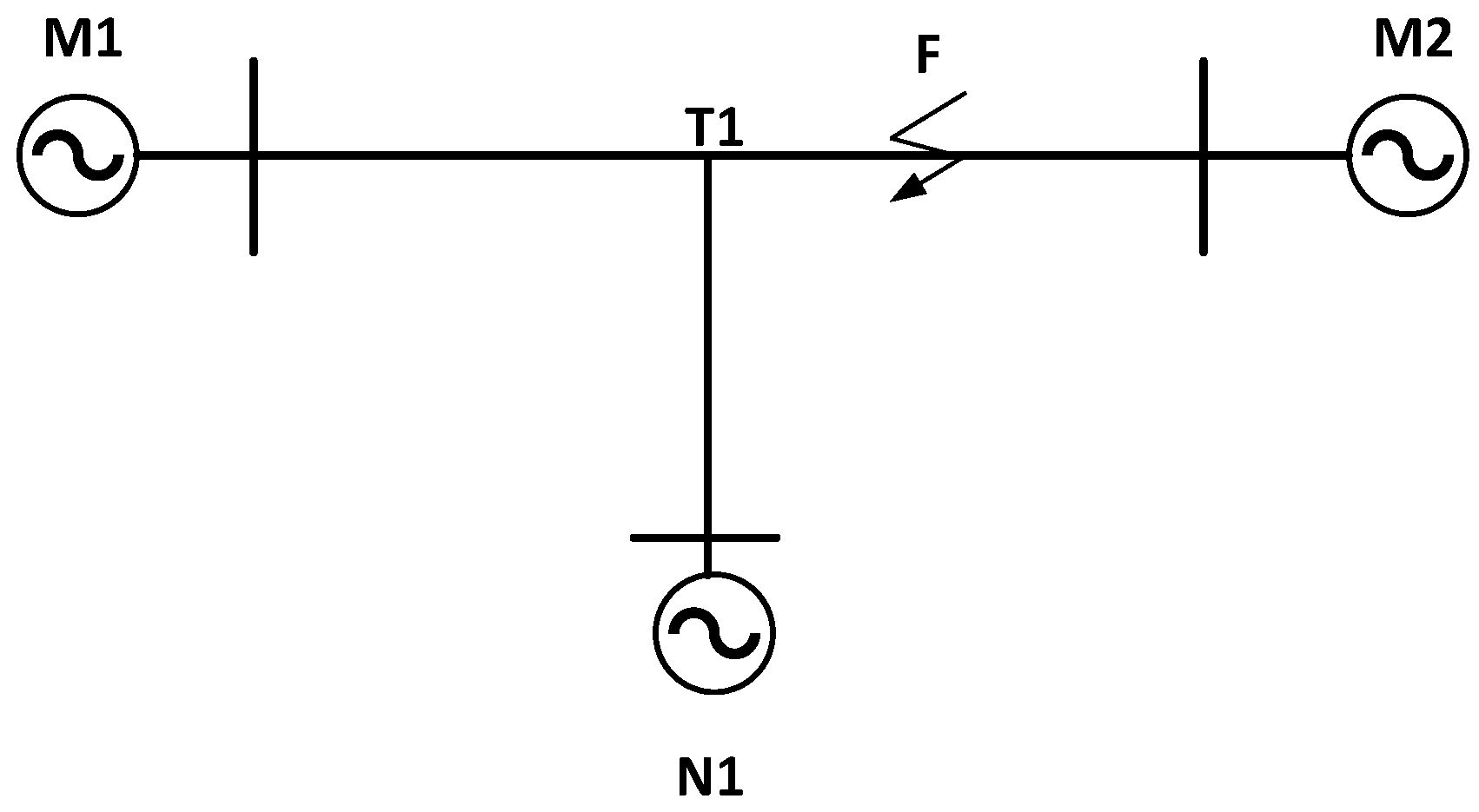
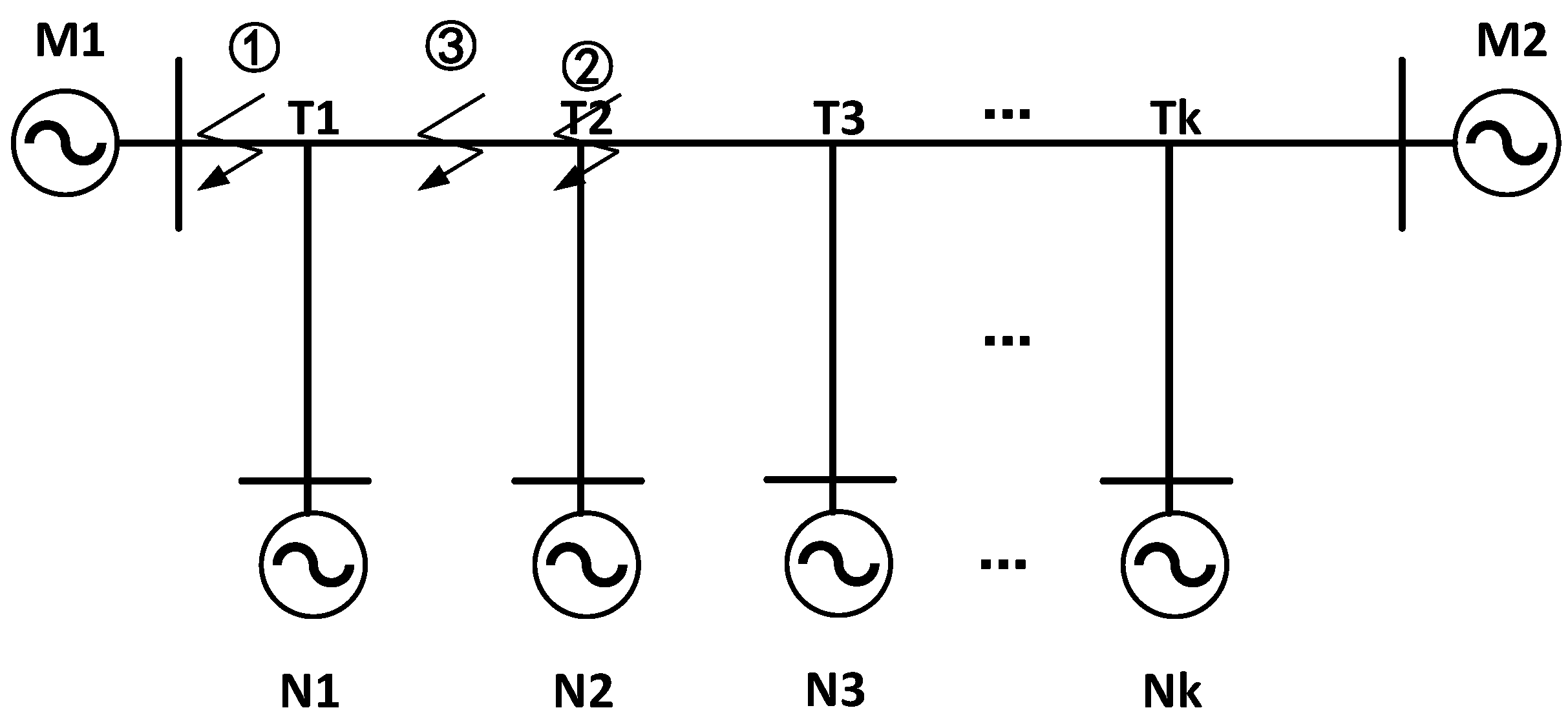
4. Research on Multi-Branch Line Fault Ranging Technology Based on Fault Branch Judgment Matrix
4.1. T-Type Transmission Line Fault Branch Judgment Method
4.1.1. Fault Occurred on The Branch Line
4.1.2. T-Node Failure
4.2. Multi-Terminal Transmission Line Fault Location Method
4.2.1. Branch Line Failure
4.2.2. T-Node Failure
4.2.3. T-T Inter-Node Failure
4.3. Fault Distance Calculation
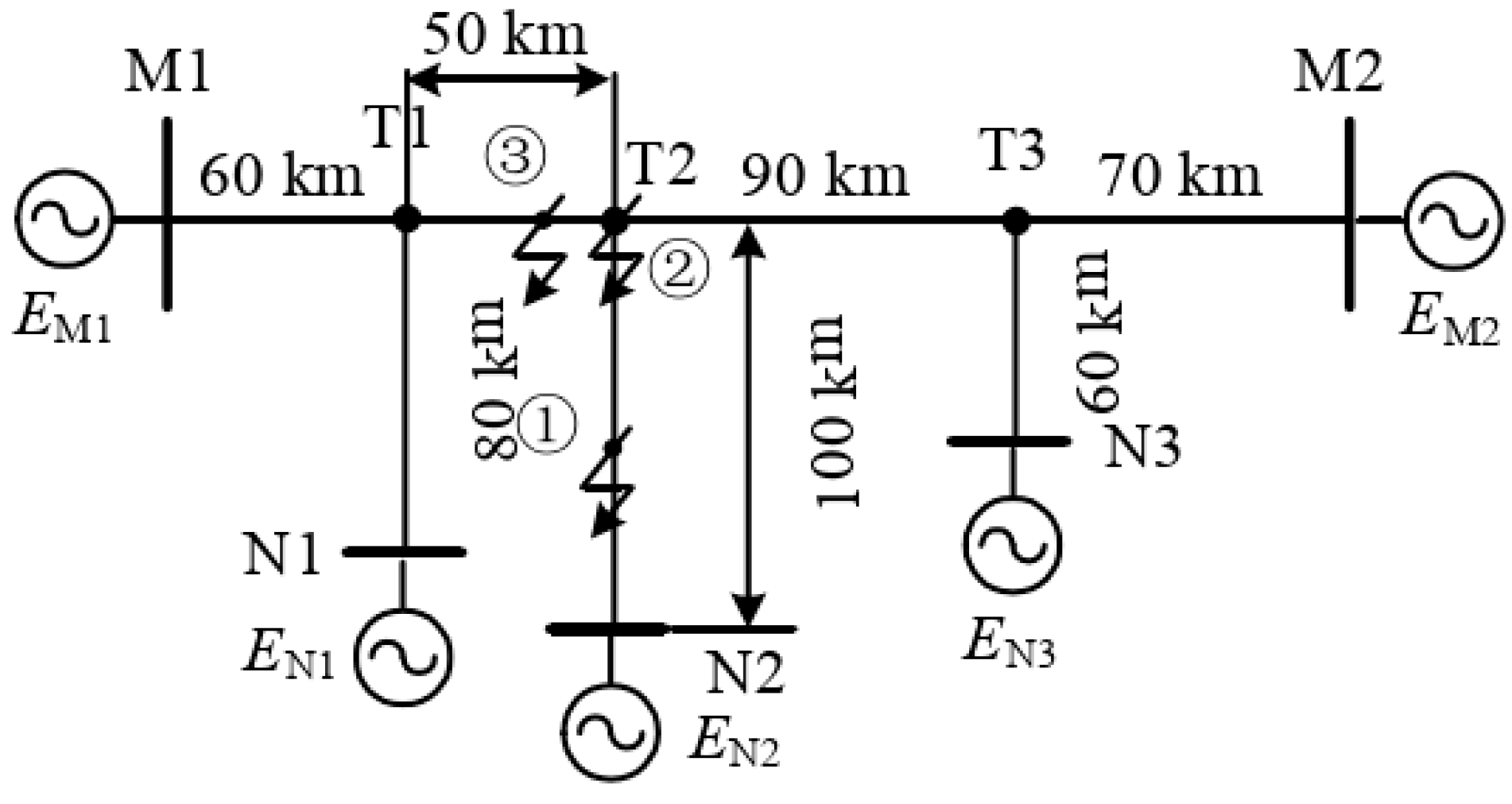
4.4. Simulation Verification
4.4.1. Branch Line Failure
4.4.2. T-Node Failure
4.4.3. T-T Failure
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khoshbouy, M.; Yazdaninejadi, A.; Bolandi, T.G. Transmission line adaptive protection scheme: A new fault detection approach based on pilot superimposed impedance. Int. J. Electr. Power Energy Syst. 2022, 137, 107826. [Google Scholar] [CrossRef]
- Ortega, J.S.; Tavares, M.C. Fault impedance analysis and non-conventional distance protection settings for half-wavelength transmission line applications. Electr. Power Syst. Res. 2021, 198, 107361. [Google Scholar] [CrossRef]
- Dai, F.; Zeng, D.; Liu, S.; Wang, G. A practical impedance modeling method of MMC-HVDC transmission system for medium-and high-frequency resonance analysis. Electr. Power Syst. Res. 2022, 212, 108636. [Google Scholar] [CrossRef]
- Wang, D.; Cheng, D.; Sun, X.; Chen, W.; Qiao, F.; Liu, X.; Hou, M. Novel travelling wave directional pilot protection approach for LCC-MMC-MTDC overhead transmission line. Int. J. Electr. Power Energy Syst. 2023, 144, 108553. [Google Scholar] [CrossRef]
- Chen, W.; Wang, D.; Cheng, D.; Liu, X. Travelling wave fault location approach for MMC-HVDC transmission line based on frequency modification algorithm. Int. J. Electr. Power Energy Syst. 2022, 143, 108507. [Google Scholar] [CrossRef]
- Banafer, M.; Mohanty, S.R. A travelling wave based primary and backup protection for MMC-MTDC transmission system using morphological un-decimated wavelet scheme. Electr. Power Syst. Res. 2022, 212, 108367. [Google Scholar] [CrossRef]
- Mousaviyan, I.; Seifossadat, S.G.; Saniei, M. Traveling Wave-based Algorithm for Fault Detection, Classification, and Location in STATCOM-Compensated Parallel Transmission Lines. Electr. Power Syst. Res. 2022, 210, 108118. [Google Scholar] [CrossRef]
- Parsi, M.; Crossley, P.; Dragotti, P.L.; Cole, D. Wavelet based fault location on power transmission lines using real-world travelling wave data. Electr. Power Syst. Res. 2020, 186, 106261. [Google Scholar] [CrossRef]
- Ravesh, N.R.; Ramezani, N.; Ahmadi, I.; Nouri, H. A hybrid artificial neural network and wavelet packet transform approach for fault location in hybrid transmission lines. Electr. Power Syst. Res. 2022, 204, 107721. [Google Scholar] [CrossRef]
- Rezaei, D.; Gholipour, M.; Parvaresh, F. A single-ended traveling-wave-based fault location for a hybrid transmission line using detected arrival times and TW′ s polarity. Electr. Power Syst. Res. 2022, 210, 108058. [Google Scholar] [CrossRef]
- Chen, W.; Wang, D.; Cheng, D.; Qiao, F.; Liu, X.; Hou, M. Novel travelling wave fault location principle based on frequency modification algorithm. Int. J. Electr. Power Energy Syst. 2022, 141, 108155. [Google Scholar] [CrossRef]
- Malik, H.; Fatema, N.; Iqbal, A. Intelligent Data-Analytics for Condition Monitoring: Smart Grid Applications; Academic Press: Cambridge, MA, USA, 2021; pp. 115–140. ISBN 9780323855105. [Google Scholar]
- Xie, L.; Luo, L.; Ma, J.; Li, Y.; Zhang, M.; Zeng, X.; Cao, Y. A novel fault location method for hybrid lines based on traveling wave. Int. J. Electr. Power Energy Syst. 2019, 141, 108102. [Google Scholar] [CrossRef]
- Abbasi, F.; Abdoos, A.A.; Hosseini, S.M.; Sanaye-Pasand, M. New ground fault location approach for partially coupled transmission lines. Electr. Power Syst. Res. 2023, 216, 109054. [Google Scholar] [CrossRef]
- Khalili, M.; Namdari, F.; Rokrok, E. Traveling wave-based protection for SVC connected transmission lines using game theory. Int. J. Electr. Power Energy Syst. 2020, 123, 106276. [Google Scholar] [CrossRef]
- Jamali, S.; Mirhosseini, S.S. Protection of transmission lines in multi-terminal HVDC grids using travelling waves morphological gradient. Int. J. Electr. Power Energy Syst. 2019, 108, 125–134. [Google Scholar] [CrossRef]
- Anane, P.O.K.; Huang, Q.; Bamisile, O.; Ayimbire, P.N. Fault location in overhead transmission line: A novel non-contact measurement approach for traveling wave-based scheme. Int. J. Electr. Power Energy Syst. 2021, 133, 107233. [Google Scholar] [CrossRef]
- Wang, D.; Hou, M. Travelling wave fault location principle for hybrid multi-terminal LCC-VSC-HVDC transmission line based on R-ECT. Int. J. Electr. Power Energy Syst. 2020, 117, 105627. [Google Scholar] [CrossRef]
- Reis, R.L.; Lopes, F.V. Correlation-based single-ended traveling wave fault location methods: A key settings parametric sensitivity analysis. Electr. Power Syst. Res. 2022, 213, 108363. [Google Scholar] [CrossRef]
- Zeng, R.; Wu, Q.; Zhang, L. Two-terminal traveling wave fault location based on successive variational mode decomposition and frequency-dependent propagation velocity. Electr. Power Syst. Res. 2022, 213, 108768. [Google Scholar] [CrossRef]
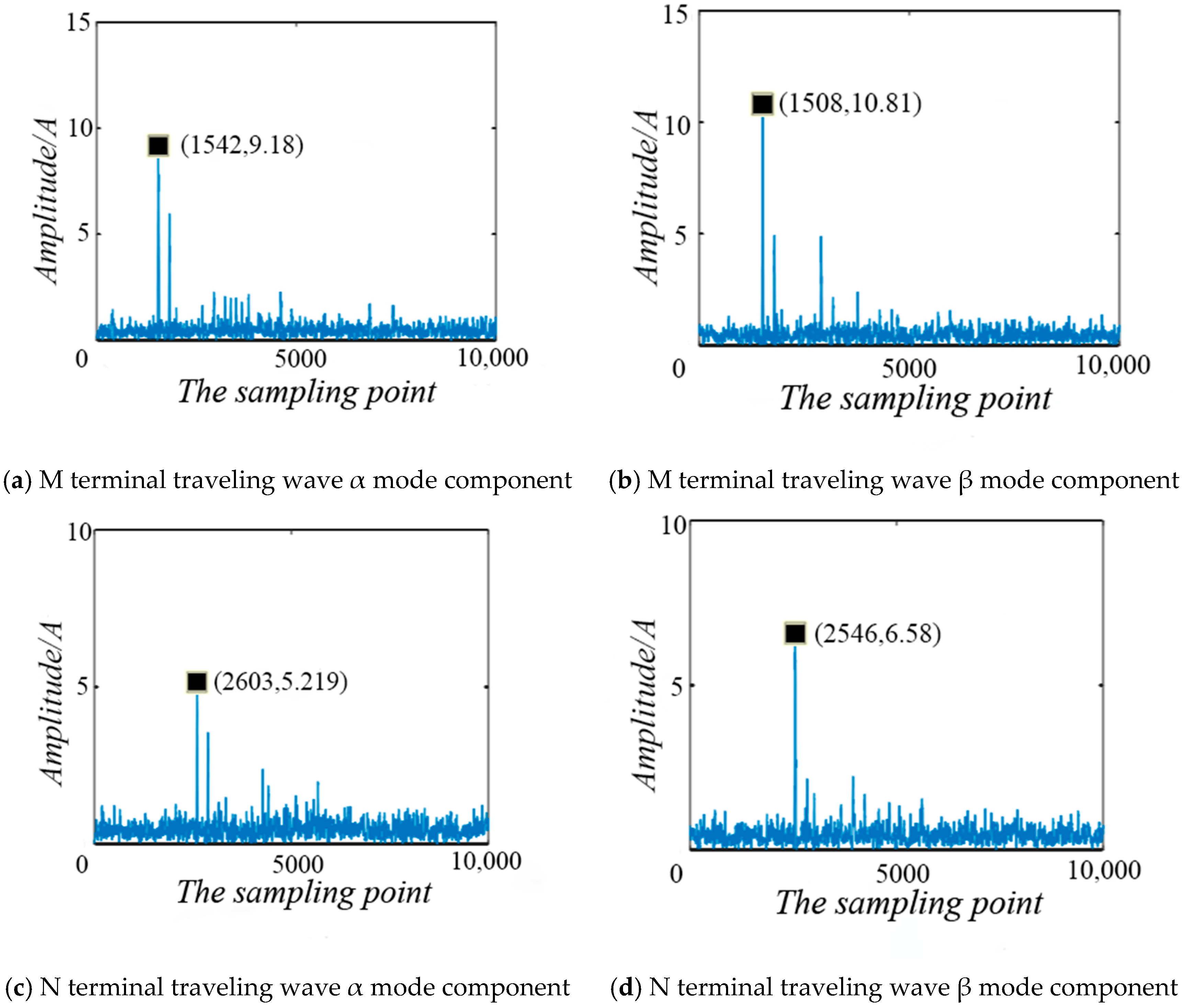
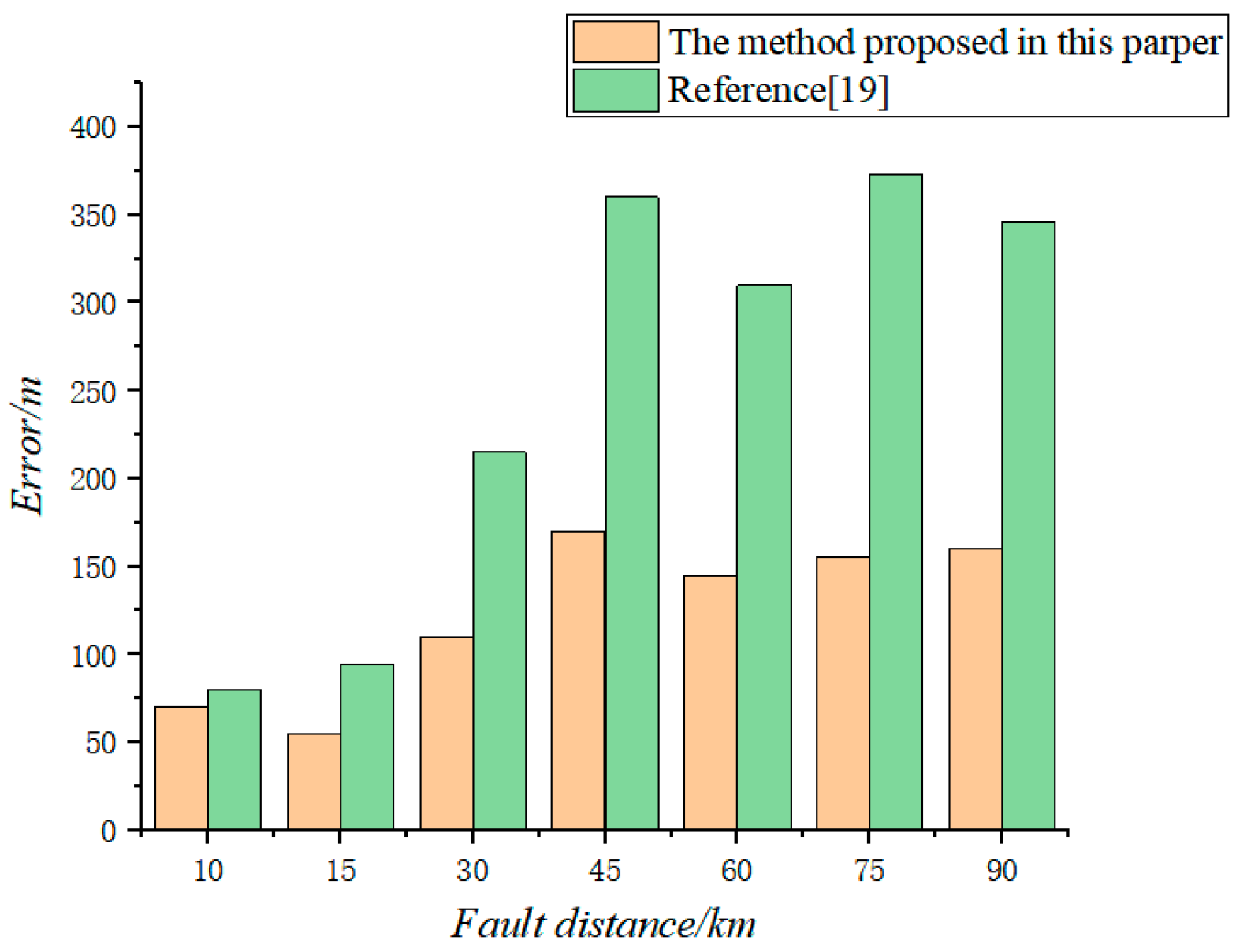
| Transition Resistance /Ω | In This Paper Positioning Results/km | Positioning Error/m | Relative Error/% | Reference [19] Positioning Results/km | Positioning Error/m | Relative Error/% |
|---|---|---|---|---|---|---|
| 0 | 49.921 | 79 | 0.158 | 49.837 | 163 | 0.326 |
| 10 | 49.912 | 88 | 0.176 | 50.198 | 198 | 0.396 |
| 50 | 50.096 | 96 | 0.192 | 50.241 | 241 | 0.482 |
| 200 | 50.111 | 111 | 0.222 | 49.764 | 236 | 0.472 |
| 500 | 49.846 | 154 | 0.308 | 49.743 | 257 | 0.514 |
| 1000 | 49.824 | 176 | 0.352 | 50.346 | 346 | 0.692 |
| 2000 | 50.251 | 251 | 0.502 | 50.428 | 428 | 0.856 |
| Fault Type | In This Paper Positioning Results/km | Positioning Error/m | Relative Error/% | Reference [19] Positioning Results/km | Positioning Error/m | Relative Error/% |
|---|---|---|---|---|---|---|
| Ag | 80.124 | 124 | 0.155 | 79.703 | 297 | 0.371 |
| AB | 79.824 | 176 | 0.220 | 80.367 | 367 | 0.459 |
| BC | 80.192 | 192 | 0.240 | 80.344 | 344 | 0.430 |
| ABg | 80.137 | 137 | 0.171 | 79.641 | 359 | 0.449 |
| BCg | 79.845 | 155 | 0.194 | 79.639 | 361 | 0.451 |
| ABC | 80.131 | 131 | 0.163 | 80.369 | 369 | 0.461 |
| Line Parameters | r/(Ω/km) | r/(Ω/km) | g/(S/km) |
|---|---|---|---|
| Positive sequence parameters | 0.035 | 0.43 | 1 × 10−7 |
| Zero sequence parameters | 0.3 | 1.21 | 1 × 10−7 |
| Measurement Point Name | M1 | N1 | N2 | N3 | M2 |
|---|---|---|---|---|---|
| α-mode | 1120 | 1437 | 1273 | 276 | 1405 |
| β-mode | 1023 | 1356 | 1103 | 291 | 1312 |
| Measurement Point Name | M1 | N1 | N2 | N3 | M2 |
|---|---|---|---|---|---|
| α-mode | 720 | 1054 | 903 | 710 | 1056 |
| β-mode | 687 | 984 | 921 | 690 | 1145 |
| Measurement Point Name | M1 | N1 | N2 | N3 | M2 |
|---|---|---|---|---|---|
| α-mode | 864 | 956 | 1047 | 1123 | 1187 |
| β-mode | 793 | 902 | 1103 | 1082 | 1097 |
| Fault Point | Fault Type | Beginning | Actual Failure Distance/km | Calculation of Faults Distance/km | Positioning Error/m |
|---|---|---|---|---|---|
| N2-T2 | Bg | N2 | 40 | 40.134 | 134 |
| ABg | N2 | 40 | 40.087 | 87 | |
| BC | N2 | 40 | 39.921 | 79 | |
| ABC | N2 | 40 | 40.104 | 104 | |
| T2 node | Bg | N2 | 100 | 100.094 | 94 |
| ABg | N2 | 100 | 99.961 | 39 | |
| BC | N2 | 100 | 100.145 | 145 | |
| ABC | N2 | 100 | 100.109 | 109 | |
| T1-T2 | Bg | N2 | 110 | 110.036 | 36 |
| 1 | ABg | N2 | 110 | 110.127 | 127 |
| BC | N2 | 110 | 109.934 | 66 | |
| ABC | N2 | 110 | 109.947 | 53 |
| Fault Point | Fault Type | Beginning | Actual Failure Distance/km | Calculation of Faults Distance/km | Positioning Error/m |
|---|---|---|---|---|---|
| N2-T2 | Bg | N2 | 40 | 40.376 | 376 |
| ABg | N2 | 40 | 40.341 | 341 | |
| BC | N2 | 40 | 39.795 | 205 | |
| ABC | N2 | 40 | 40.267 | 267 | |
| T2 node | Bg | N2 | 100 | 100.401 | 401 |
| ABg | N2 | 100 | 99.654 | 346 | |
| BC | N2 | 100 | 100.317 | 317 | |
| ABC | N2 | 100 | 100.397 | 397 | |
| T1-T2 | Bg | N2 | 110 | 110.295 | 295 |
| 1 | ABg | N2 | 110 | 110.364 | 364 |
| BC | N2 | 110 | 109.629 | 371 | |
| ABC | N2 | 110 | 109.713 | 287 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Zhang, Q.; Wang, M.; Wang, X.; Qi, E. Fault Location Method of Multi-Terminal Transmission Line Based on Fault Branch Judgment Matrix. Appl. Sci. 2023, 13, 1174. https://doi.org/10.3390/app13021174
Yang Y, Zhang Q, Wang M, Wang X, Qi E. Fault Location Method of Multi-Terminal Transmission Line Based on Fault Branch Judgment Matrix. Applied Sciences. 2023; 13(2):1174. https://doi.org/10.3390/app13021174
Chicago/Turabian StyleYang, Yongsheng, Qi Zhang, Minzhen Wang, Xinheng Wang, and Entie Qi. 2023. "Fault Location Method of Multi-Terminal Transmission Line Based on Fault Branch Judgment Matrix" Applied Sciences 13, no. 2: 1174. https://doi.org/10.3390/app13021174
APA StyleYang, Y., Zhang, Q., Wang, M., Wang, X., & Qi, E. (2023). Fault Location Method of Multi-Terminal Transmission Line Based on Fault Branch Judgment Matrix. Applied Sciences, 13(2), 1174. https://doi.org/10.3390/app13021174






