An Inversion Algorithm for the Dynamic Modulus of Concrete Pavement Structures Based on a Convolutional Neural Network

Abstract

Based on the spectral element method (SEM) and a convolutional neural network (CNN), an inversion algorithm for the dynamic modulus of concrete pavement structures is proposed in this paper. In order to evaluate the service performance of pavement structures more systematically and accurately via the existing testing techniques using a falling weight deflectometer (FWD), it is necessary to obtain accurate dynamic modulus parameters of the structures. In this work, an inversion algorithm for predicting the dynamic modulus is established by using a CNN which is trained with the dynamic response samples of a multi-layered concrete pavement structure obtained through SEM. The gradient descent method is used to adjust the weight parameters in the network layer by layer in reverse. As a result, the accuracy of the CNN can be improved via iterative training. With the proposed algorithm, more accurate results of the dynamic modulus of pavement structures are obtained. The accuracy and numerical stability of the proposed algorithm are verified by several numerical examples. The dynamic modulus and thickness of concrete pavement structure layers can be accurately predicted by the CNN trained with a certain number of training samples based on the displacement curve of the deflection basin from the falling weight deflectometer. The proposed method can provide a reliable testing tool for the FWD technique of pavement structures.

1. Introduction

In recent years, with the vigorous development of nondestructive testing techniques for pavements, falling weight deflectometer (FWD) has been widely applied. Simultaneously, the inversion analysis of the dynamic modulus of pavement structures has also become one of the most critical techniques used in their service performance evaluation [1]. The method for solving the dynamic responses of a multi-layered pavement under impact loads is limited by the boundary conditions and computational efficiency; thus, in the early development stage of FWD instruments, most inversion software was based on the quasi-static analysis method [2]. However, this method cannot simulate the dynamic effect of vehicle loads. Moreover, the static inversion method is prone to causing the phenomenon of “modulus transferring”, which leads to the failure of the inversion results [3]. Although the dynamic effect of loads can be considered in the dynamic response analysis of the pavement structure system by the finite element method (FEM), its solution process requires meshing the pavement structures, which greatly reduces its solution efficiency and seriously affects its application in the inversion of the dynamic modulus of the pavement structures [4,5]. In recent years, with the deepening of research on the dynamic responses of layered semi-infinite media, increasingly more dynamic response algorithms have emerged, most notably the integral equation transformation method [6,7,8,9]. These algorithms can obtain the dynamic displacement and stress responses of layered soil under dynamic load in the frequency domain and can reveal the dynamic characteristics of the layered soil. However, when solving the displacement responses of road surfaces under FWD loads, it is necessary to solve the infinite integral problem; thus, the solution efficiency is greatly reduced. As an algorithm for solving the dynamic responses of layered soil under axisymmetric loads, the spectral element method (SEM) not only can consider the dynamic effect of FWD loads to obtain accurate calculation results, but also has high solution efficiency [10,11]. Thus, it has been successfully applied to the back-calculation of the dynamic modulus of pavement structures [3,12,13,14,15,16,17].

With the development of forward algorithms for the dynamic responses of layered pavement structures, a variety of dynamic modulus inversion software has been developed based on nondestructive testing techniques using FWD equipment. However, most existing inversion software is based on the peak deflection of the road surface, which only reflects the overall bearing capacity of the pavement structure. The deflection basin displacement time–history curve obtained by FWD testing equipment contains comprehensive pavement structure information, which cannot be completely reflected by its peak deflection. In the inversion process, the insufficient input conditions usually lead to the non-unique problem of parameter inversion. It is thus difficult for the inversion results to objectively characterize the actual performance of each structural layer of the pavement [13,14,15]. Zhang et al. [13] used SEM as the forward model, and used the backpropagation neural network (BPNN) and real-coded multi-population genetic algorithm to predict the structural parameters of pavements. While the input conditions of the pavement mechanical model were increased (the interlayer contact conditions and transverse isotropic properties of materials), the non-unique problem could not be solved by relying only on the maximum deflection of the road surface. Cao et al. [3] also used SEM as a forward analysis method, constructed an optimization objective function using the measured deflection time–history curve and theoretical calculation results, and carried out the dynamic inversion of the mechanical parameters of a pavement via numerical optimization methods. Compared with traditional static methods, better inversion results were achieved, and the phenomenon of “modulus transferring” was effectively avoided, but the inversion is not efficient and the results are not accurate. Li et al. [18] overcame the low search efficiency and heavy calculation workload by applying the conventional particle swarm optimization (PSO) [19] algorithm to the inversion of geotechnical engineering parameters, and proposed an improved PSO algorithm. However, the inversion based on peak deflection was still characterized by the problem of non-unique solutions, while the inversion based on the time–history curve involved a large calculation workload. Moreover, a single objective function cannot reflect the complex nonlinear function optimization problem.

The existing inversion algorithms are restricted by various factors. To solve the current challenges, an accurate and effective inversion method is needed. The convolutional neural network (CNN) has a strong feature extraction ability [20,21]. It is a potential scheme to realize pavement detection based on vibration signals, and can effectively solve the challenges faced by the above research. Due to its unique mechanism of partial connection and weight sharing, the CNN has exceptional advantages in processing massive data. In the field of damage detection based on vibration signals, Teng et al. [22] used a CNN to determine the damage location of a steel structure. Furthermore, Teng et al. [23] presented a novel and efficient approach for detection of structural damage from real-time vibration signals via a CNN. In terms of the prediction of the mechanical properties of materials by CNNs, Hu et al. [24] carried out research on the mechanical properties of hot-rolled steel. To further improve the computational efficiency of the CNN, Zheng et al. [25] established a fault diagnosis method for cylindrical roller bearing cages based on vibration signals and a 1-D CNN. These applications all confirm the unique advantages of CNNs in the field of diagnosis and prediction, as well as their potential application prospects for the task of processing pavement vibration signals and the inversion of pavement structural parameters.

For this reason, this study develops an accurate and effective inversion algorithm for the parameter identification of multi-layered pavement structures based on a CNN with SEM as the forward calculation model. As an algorithm for solving the dynamic responses of pavement structures, SEM can accurately simulate the dynamic effect of FWD loads and avoid the phenomenon of “modulus transferring”. In addition, most of the inversion calculations use the maximum value of the deflection as the training samples, which do not reflect the overall dynamic characteristics of the pavement structures. As a result, the inversion results suffer from the non-unique problem, and the calculation accuracy cannot be guaranteed. In this paper, the deflection curves are used to replace the peak values of the deflection curves as the training samples, which can reflect the dynamic characteristics of the pavement structure more comprehensively. The CNN model is used to predict the dynamic modulus and thickness of the pavement structure layers. The proposed inversion algorithm is verified by the assumed numerical model of pavement structures, and relevant parameters in the algorithm are analyzed.

2. Forward Modeling of Pavement Structures

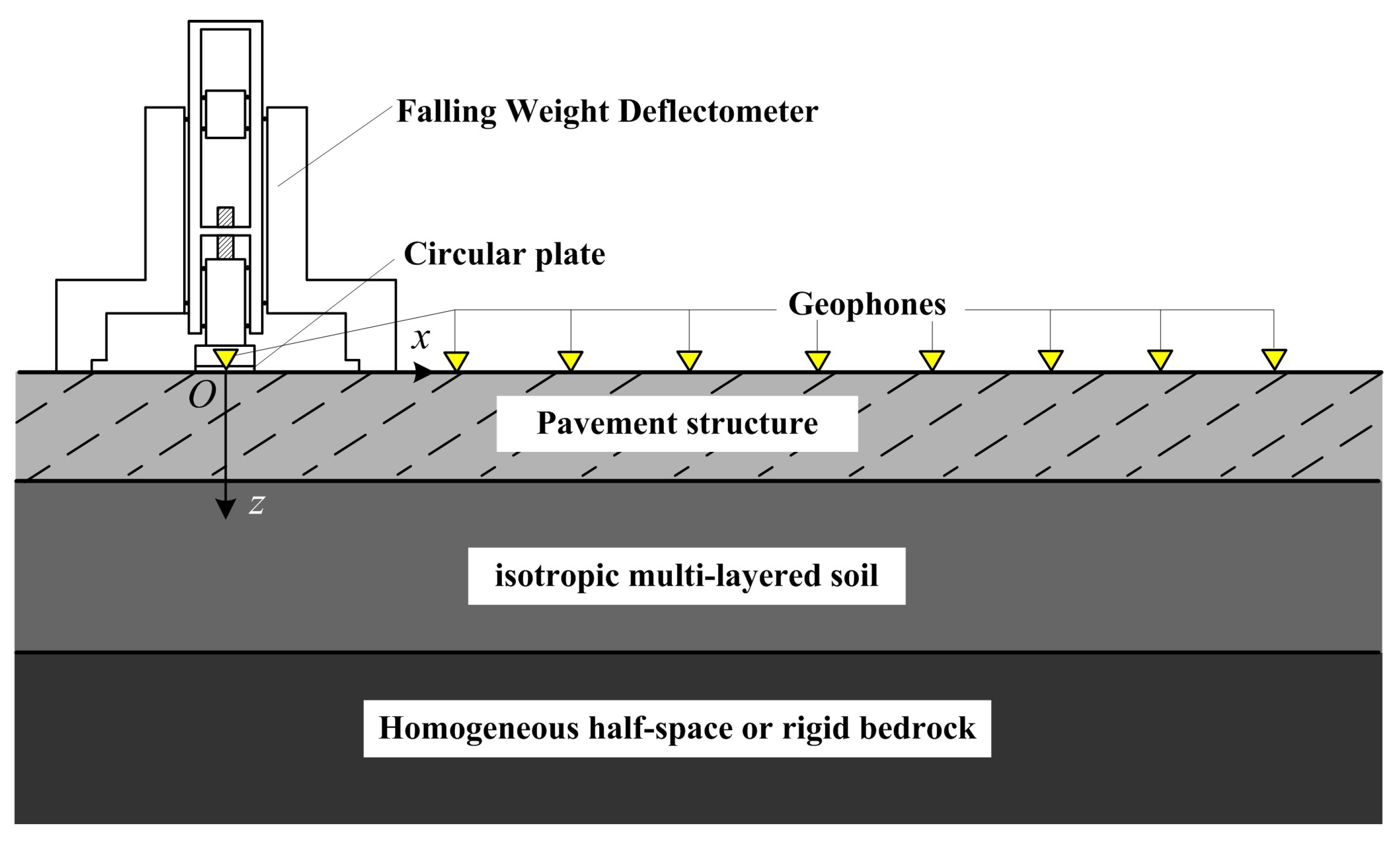
2.1. Pavement Structure System

It is assumed that a layered pavement structure is placed on a layered semi-infinite soil (Figure 1), both of which are isotropic and homogeneous, and the bottom soil can be an elastic or rigid bedrock. As displayed in Figure 1, a rectangular coordinate system is established. The coordinate origin O is set on the surface of the layered pavement structure, with the z-axis vertically downward and the x-axis in the horizontal direction. An FWD load is applied to a disc with a radius of ∆, and the center of the disk is at the origin of the coordinate system. The load is axisymmetric and expressed as $P\left(r, t\right)=S\left(r\right)F\left(t\right)$, where S(r) represents the spatial distribution of the load and F(t) represents its change with time. As the wave propagation under the load is axisymmetric, a cylindrical coordinate system is then established in Figure 2. In this study, SEM is used to solve the displacement responses of the deflection basin under FWD loads and provide an efficient and accurate forward model for the inversion calculation of the dynamic modulus and thickness of the layered pavement structure.

2.2. Spectral Element Method

For the axisymmetric wave problem, only the radial and vertical displacements are considered. The wave propagation formula of the continuous medium in the time–spatial domain under the cylindrical coordinate system is

$$\begin{array}{l}\frac{\partial {\sigma }_r}{\partial r}+\frac{\partial {\tau }_{zr}}{\partial z}+\frac{{\sigma }_r-{\sigma }_{\theta }}{r}=\rho \frac{{\partial }^2{u}_r}{\partial t^2},\hfill \\ \frac{\partial {\tau }_{zr}}{\partial r}+\frac{\partial {\sigma }_z}{\partial z}+\frac{{\tau }_{zr}}{r}=\rho \frac{{\partial }^2{u}_z}{\partial t^2},\hfill \end{array}$$

(1)

where ${\sigma }_i \left(i=r,\theta ,z\right)$ is the normal stress in the subscript direction, ${\tau }_{zr}$ is the shear stress in the z-r plane, $\rho$ represents the mass density of the medium, and $u_r$ and $u_z$ represent the radial and vertical displacements of the medium, respectively.

In Helmholtz decomposition, the displacement field of the medium can be expressed as the gradient of scalar potential $\alpha$ and the curl of vector potential $\mathit{\beta },$ i.e.,

$$u=\nabla \alpha +\nabla \times \mathit{\beta },$$

(2)

where $\nabla$ represents a partial differential operator. In the axisymmetric wave problem, vector potential $\mathit{\beta }$ has only one component ${\beta }_{\theta }$, so the problem to be solved can be simplified as a scalar potential problem. For simplicity, $\beta$ is used to represent ${\beta }_{\theta }$. As it is an axisymmetric problem, the displacement of the medium in the circumferential direction $\theta$ is zero, and the radial and vertical displacement can be expressed as follows [10]:

$$u_r=\frac{\partial \alpha }{\partial r}-\frac{\partial \beta }{\partial z}, u_z=\frac{\partial \alpha }{\partial z}+\frac{1}{r}\frac{\partial \left(r\beta \right)}{\partial r}.$$

(3)

The relationship between stress and displacement in the cylindrical coordinate system is

$$\begin{array}{l}\begin{array}{c}{\sigma }_r=\left(\lambda +2\mu \right)\frac{\partial u_r}{\partial r}+\mu \left(\frac{u_r}{r}+\frac{\partial u_z}{\partial z}\right),\\ {\sigma }_{\theta }=\left(\lambda +2\mu \right)\frac{u_r}{r}+\mu \left(\frac{\partial u_r}{\partial r}+\frac{\partial u_z}{\partial z}\right),\end{array}\hfill \\ \begin{array}{l}{\sigma }_z=\left(\lambda +2\mu \right)\frac{\partial u_z}{\partial z}+\mu \left(\frac{\partial u_r}{\partial r}+\frac{u_r}{r}\right),\hfill \\ {\tau }_{zr}=\mu \left(\frac{\partial u_z}{\partial r}+\frac{\partial u_r}{\partial z}\right),\hfill \end{array}\hfill \end{array}$$

(4)

where λ and μ are the Lamé constants, and

$$\lambda =\frac{\nu E}{\left(1+\nu \right)\left(1-2\nu \right)}, \mu =\frac{E}{2\left(1+\nu \right)},$$

(5)

where E is the Young’s modulus and ν is the Poisson’s ratio.

Equation (4) is substituted into Equation (1) and the displacement is expressed by the scalar potential in Equation (3). After algebraic simplification, the following equations are satisfied:

$$\left(\lambda +2\mu \right)\left(\frac{{\partial }^2\alpha }{\partial r^2}+\frac{{\partial }^2\alpha }{\partial z^2}+\frac{\partial \alpha }{r\partial r}\right)=\rho \frac{{\partial }^2\alpha }{\partial t^2}$$

(6)

$$\mu \left(\frac{{\partial }^2\beta }{\partial z^2}+\frac{{\partial }^2\beta }{\partial r^2}+\frac{\partial \beta }{r\partial r}-\frac{\beta }{r^2}\right)=\rho \frac{{\partial }^2\beta }{\partial t^2}$$

(7)

It is evident that Equations (6) and (7) represent two forms of waves, namely P and SH waves, respectively, the wave velocities of which are $c_P=\sqrt{\frac{\left(\lambda +2\mu \right)}{\rho }}$ and $c_{SH}=\sqrt{\frac{\mu }{\rho }}$, respectively. For isotropic layered media, the two waves can be decoupled and solved separately. The potential function α in Equation (6) in the frequency–wavenumber domain can be obtained by using the variable separation method:

$$\widehat{\alpha }\left(r,z\right)=A_n{e}^{-i{k}_{pz}z}{J}_0\left(kr\right),$$

(8)

where superscript “ˆ” represents the function of the frequency–wavenumber domain, A_n represents an unknown constant which is determined by the boundary conditions, J₀ is the first kind of Bessel function, and k is the wavenumber. The expression of k_pz is

$$k_{pz}={\left(\frac{{\omega }_n^2}{c_P^2}-k^2\right)}^{\frac{1}{2}},$$

(9)

where ω_n is the frequency.

To introduce the boundary conditions in the radial direction, the amplitude of the oscillation at the radial boundary r = R (far away from the load source) is considered to vanish. That requires the item J₀(kR) to be equal to 0. This condition can be satisfied at the infinite positive roots k_mR of the J₀ function. Hence, the m functions,

$${\widehat{\alpha }}_{mn}\left(r,z\right)=A_{mn}{e}^{-i{k}_{pz}z}{J}_0\left(k_{m}r\right),$$

(10)

In the same way, the solution of the potential function β in the frequency–wavenumber domain in Equation (7) is

$${\widehat{\beta }}_{mn}\left(r,z\right)=B_{mn}{e}^{-i{k}_{sz}z}{J}_1\left(k_{m}r\right),$$

(11)

where B_mn is a constant determined by the boundary conditions and J₁ is the first kind of Bessel function. Moreover, k_sz represents the vertical shear wavenumber, and is expressed as

$$k_{sz}={\left(\frac{{\omega }_n^2}{c_{SH}^2}-k_m{}^2\right)}^{\frac{1}{2}}$$

(12)

Because Equations (6) and (7) are linear homogeneous formulas, the superposition principle is applicable, i.e., the solutions of the potential functions $\alpha$ and $\beta$ can be obtained by the superposition of the infinitely many solutions of ${\widehat{\alpha }}_{mn}$ and ${\widehat{\beta }}_{mn}$. The inversion of the integral transformation is usually solved using infinite numerical integration [6,26]. A high number of wavenumbers must be calculated to approximate the infinite integration. In order to obtain an accurate result, the step of the integration needs to be divided very small, which can reduce the computational efficiency significantly. In SEM, the double-sum of the discrete angular frequency ${\omega }_n \left(n=1, 2, \dots , N\right)$ and wavenumber $k_m \left(m=1,2,\dots ,M\right)$ is used to obtain all arrays of the whole system dissipated at r = R (R is a large finite value). The summation over the wave numbers in SEM is discontinuous, and the wave number is finite. Therefore, the general solution of the wave formula of an axisymmetric system can be obtained by superimposing the special solution [10], as follows.

$$\alpha \left(r,z,t\right)={\displaystyle \sum }_N{\displaystyle \sum }_M{A}_{mn}{e}^{-i{k}_{pz}z}{J}_0\left(k_{m}r\right)e^{-i{\omega }_{n}t}$$

(13)

$$\beta \left(r,z,t\right)={\displaystyle \sum }_N{\displaystyle \sum }_M{B}_{mn}{e}^{-i{k}_{sz}z}{J}_1\left(k_{m}r\right)e^{-i{\omega }_{n}t}$$

(14)

The finite values N and M in the general solution Equations (13) and (14) can be determined by the time and spatial amplitude spectra of the excitation load. The sum of N frequencies can be obtained by using the fast Fourier transform (FFT), and the sum of M wavenumbers can be obtained by using the Fourier–Bessel series. The sum of wavenumbers replaces the integral from 0 to infinity in the conventional numerical integration method, which is crucial to improving the efficiency of the algorithm. For the infinite integral, when the damping ratio of the medium is zero, the integrand has singular points, which makes its integral calculation more expensive. The sum of the wavenumbers in double-sum form can effectively avoid this problem.

The general solutions of the potential functions $\alpha$ and $\beta$ (Equations (13) and (14)) are substituted into Equation (3) to obtain the displacements of the axisymmetric problem, as follows:

$$\left\{\begin{array}{c}{u}_r\left(r,z,t\right)\\ u_z\left(r,z,t\right)\end{array}\right\}={\displaystyle \sum }_n{\displaystyle \sum }_m\left\{\begin{array}{c}{\widehat{G}}_{rz}\left(k_m,z\right)J_1\left(k_{m}r\right)\\ {\widehat{G}}_{zz}\left(k_m,z\right)J_0\left(k_{m}r\right)\end{array}\right\}{\widehat{F}}_m{\widehat{F}}_n{e}^{i{\omega }_{n}t},$$

(15)

where $\widehat{G}\left(k_m,z\right)$ represents the flexibility coefficient of the medium in the conversion domain, and its solution is evident [10], and ${\widehat{F}}_m$ is the Fourier–Bessel transformation coefficient of the excitation load $S\left(r\right)$, which can be obtained by the Fourier–Bessel transformation of the excitation load $S\left(r\right)$. For the contact boundary condition at the interface between the adjacent layers, the displacements and stresses meet the continuous conditions. If the layered soil is underlain by an elastic semi-infinite space, the radiation condition should be considered. Two spectral elements were developed in the literature [10] to illustrate the solution of $\widehat{G}\left(k_m,z\right)$ as well as the contact boundary condition and radiation condition.

Assuming that the FWD load is applied to the disc with radius $\mathsf{\Delta }$, $S\left(r\right)$ can be expressed as follows:

$$S\left(r\right)=\{\begin{array}{cc}q& \mathrm{for} 0⩽r⩽\mathsf{\Delta }\\ 0& \mathrm{for} r>\mathsf{\Delta }\end{array},$$

(16)

The Fourier–Bessel transformation of $S\left(r\right)$ is

$$S\left(r\right)={\displaystyle \sum }_M{\widehat{F}}_m{J}_0\left(k_{m}r\right),$$

(17)

where ${\widehat{F}}_m$ can be parsed as

$${\widehat{F}}_m=\frac{2}{R^2{J}_1^2\left({\alpha }_m\right)}{{\displaystyle \int }}_0^{a}r{J}_0\left(\frac{{\alpha }_m}{R}r\right)dr=\frac{2\mathsf{\Delta }}{{\alpha }_{m}R{J}_1^2\left({\alpha }_m\right)}{J}_1\left(\frac{{\alpha }_m}{R}\Delta \right),$$

(18)

where ${\alpha }_m=\frac{k_m}{R}$, and ${\widehat{F}}_n$ is the Fourier transform coefficient of excitation load $F\left(t\right)$, which can be obtained by FFT. Under the discrete Fourier transform state, the relationship between $F\left(t\right)$ and ${\widehat{F}}_n$ is

$$\begin{array}{c}F\left(j\Delta t\right)=\frac{1}{N}{\displaystyle {\displaystyle \sum }_n}{\widehat{F}}_n\left(\frac{n}{N\cdot \Delta t}\right)e^{\frac{i2\pi nj}{N}}\left(n=1,2,\dots ,N-1\right),\\ {\widehat{F}}_n\left(\frac{n}{N\cdot \Delta t}\right)={\displaystyle {\displaystyle \sum }_j}F\left(j\Delta t\right)e^{-\frac{i2\pi nj}{N}}\left(j=1,2,\dots ,N-1\right),\end{array}$$

(19)

where $\mathsf{\Delta }t$ is the load time step.

2.3. Forward Model Validation

First, the accuracy of SEM was verified by selecting a three-layer pavement structure model placed on a homogeneous semi-infinite soil. Grenier et al. [27] studied a general pavement in Quebec, Canada, including a 150 mm thick asphalt layer, a 300 mm thick granular material base course, and a 600 mm thick subbase sand layer set on the semi-infinite soil, as shown in Figure 3. The generic pavement was isotropic, and its material parameters, including its Young’s modulus, Poisson’s ratio, mass density, and damping ratio, are reported in

Table 1. The properties of the generic pavement.

Layers	h (m)	E (MPa)	μ	ρ (kg/m3)	ζ (%)
Asphalt	0.15	3000	0.35	2400	5
Base course	0.30	300	0.35	2300	2
Subbase	0.60	150	0.35	1900	2
Subgrade	-	75	0.35	1800	2

.

The FWD load applied on the pavement is shown in Figure 4; the load amplitude was 40 kN, the duration was 30 ms, the number of Fourier transform samples N = 2048, and the number of wavenumber samples M = 200. The load acted within a circle of radius 0.15 m, i.e., the radius of the drop hammer was 0.15 m. The displacement of the deflection point was calculated at the radial distances from the load center point r = 0, 0.25, 0.375, 0.50, 0.625, 0.75, 1.00, 1.25, 1.50, and 2.00 m. The oscillation dissipation distance was assumed to be R = 150 m. The calculated displacement time–history curve is shown in Figure 5a, and the calculated maximum displacement curve at the deflection point is shown in Figure 5b. The calculation results were compared with the published results in the reference [27]. The figure reveals that the two results were basically completely matched, thus verifying the accuracy of the calculation results of the proposed algorithm in the time domain.

3. Inversion Method for the Dynamic Modulus of Pavement Structures

3.1. Convolutional Neural Network

A CNN can effectively reduce the number of network parameters, alleviate the model overfitting problem, and reduce the memory occupied by deep networks. A standard fitting CNN is usually composed of convolution layers, pooling layers, activation layers, fully connected layers, and regression layers. In practical applications, the convolution and activation layers are often referred to together as convolution layers. The data input (network input) transmits through a series of layers, and is finally mapped to the fitting value corresponding to the original data through regression layers. In particular, the input of a 1-D CNN is a 1 × N or N × 1 matrix. Figure 6 presents the basic structure of the CNN. The feature extraction is carried out through the convolution layer and the pooling layer, and the fitting value (parameter value of soil layers 1–3) is finally obtained in the regression layer.

A 1-D CNN is often used in sequence models. Figure 7a presents a typical 1-D CNN operation, in which the original data of the convolution layer are an input matrix whose size is 1 × 6, and the convolution kernel is a matrix whose size is 1 × 3. The convolution operation process is to multiply each element in the convolution kernel with the corresponding element in a sub-region (e.g., orange box or purple dotted box) of the original data of the convolution layers, and then add the results to obtain an element in the feature vector. Each time the convolution operation is performed, the convolution kernel moves down with a certain step size (the step size is 1 in Figure 7a), and the operation process is repeated until all elements of the original data are traversed. Finally, after the convolution operation, a new array is formed (for example, the feature vector [8 23 6 29]).

The pooling operation is a down sampling technique. By reducing the characteristic dimensions of the output after convolution, the network parameters can be effectively reduced, thus accelerating the calculation process. This can greatly improve the computational speed of the CNN and effectively prevent overfitting. During pooling, the input matrix is divided into several regions, and the maximum value is output for each sub-region. There are usually two different pooling methods, namely maximum pooling and average pooling. For the purposes of this study, maximum pooling is superior to average pooling. Figure 7b shows the maximum pooling operation.

The activation function introduces nonlinear factors into the neural network and improves its fitting ability to learn complex features. Thus, the neural network can approximate any nonlinear function, and the convergence of the network can also be accelerated. Common activation functions include the Sigmoid, Tanh, ReLU, and Leaky ReLU. The activation function used in this study is Leaky ReLU, which is similar to ReLU and helps to expand the applicability of the ReLU function. This function retains the characteristic information that the negative values may contain. It has greater application significance than the ReLU function. Its form is

$$\mathrm{Leaky} \mathrm{ReLU}\left(x\right)=\{\begin{array}{c}x,\\ \alpha x,\end{array}\begin{array}{c}x\ge 0\\ x<0\end{array}$$

(20)

where x is the input value of the network, and $\alpha$ is 0.01 by default.

3.2. Inversion Process

The training process of the CNN is divided into two stages, namely forward propagation and backward propagation. In this study, the time–history curve of pavement deflection obtained by using SEM is used as the CNN input, and the parameter value of the dynamic modulus of the three-layer pavement structure is used as the CNN output. In the forward propagation process, the pavement deflection time–history curve is calculated via a series of convolution–activation–pooling to obtain the dynamic modulus of the three-layer pavement structures, i.e., the parameters of the soil layers are predicted through the response. By comparing the difference between the predicted and exact values, the training error of the CNN is obtained. When the error is greater than the expected value, the backward propagation process is carried out, the error is sent back to the network to readjust the weight, and the training is continued to reduce the error. When the error is equal to or less than the expected value (close to 0, reaching convergence), the network ends the training.

The data set of the CNN prediction model used in this study consisted of a training set, a validation set, and a testing set. The training set was used to train the parameters in the neural network, and the validation set was used to verify the performance of the training model. Whether the network training reached convergence was judged according to the root mean square error (RMSE) and the loss function of the validation set. The testing set was used to evaluate the performance of the trained neural network.

To ensure the accuracy of the inversion results, two groups of comparative training were conducted. According to the elastic modulus E of the three-layer pavement structure (as shown in Figure 3), different values were selected to establish the sample set. The value range of E₁ of the first layer was selected as 1500–4500 MPa, the value range of E₂ of the second layer was 150–450 MPa, and the value range of E₃ of the third layer was 75–225 MPa. The elastic modulus of each layer was considered to be 11 different values at equal intervals. Therefore, 1331 samples were established as the data set of the neural network. A certain number of samples were randomly selected from the 1331 samples for training and testing.

To avoid random and accidental errors in the experiment process, both the testing and validation sets are 100 randomly selected discrete samples from the 1331 samples.

The first group of comparative training aimed to find the optimal sample input dimension. The specific division of the training data set is shown in

Table 2. The division of the first group of comparative training data sets.

Project	Training Set	Validation Set	Testing Set	Total
Quantity	950	100	100	1150

. The first sampling method was to take the peak values of the 10 FWD deflection basin curves, and the second sampling method was to take the entire curves. The sample input and output dimensions are reported in

Table 3. The input and output dimensions of the first group of comparative training.

Sampling Method	Input Dimension	Output Dimension
Peak value of 10 deflection curves	10	3
All values of 10 deflection time history curves	20,480	3

.

The purpose of the second group of comparative training was to determine the optimal number of training samples and carry out a comparative test in which the number of training samples in eight groups varied from 600 to 950. The specific division of the second group of comparative training data sets is exhibited in

Table 4. The division of the second group of comparative training data sets.

The Best Training Sample Quantity Comparison Training	Training Set	Validation Set	Testing Set	Total
➀	600	100	100	800
➁	650	100	100	850
➂	700	100	100	900
➃	750	100	100	950
➄	800	100	100	1000
➅	850	100	100	1050
➆	900	100	100	1100
➇	950	100	100	1150

.

Based on the divided data set, the specific parameter settings of the convolution layer after CNN model optimization are presented in

Table 5. The parameter settings of the convolution layer.

Convolution Layer	Size	Step	Number of Convolution Kernels	Padding
1	1 × 2	1	60	0

. The pooled window size of a pooled layer was 1 × 2, and the pooled window moved in two steps. The activation function used by the activation layer was the Leaky ReLU function.

The performance evaluation indicators of common regression models mainly include the RMSE, mean absolute error (MAE), mean square error (MSE), and R² value. Among them, the RMSE is a typical evaluation indicator of regression models, and is used to represent the size of the error generated in the model prediction process. In this study, the RMSE and relative error were used as the evaluation indicators of the CNN model, and their expressions are

$$\mathrm{RMSE}=\sqrt{\frac{1}{N}{\displaystyle \sum }_{t=1}^N{\left(observe{d}_t-predicte{d}_t\right)}^2},$$

(21)

$$\mathrm{Relative} \mathrm{error}=\frac{observe{d}_t-predicte{d}_t}{observe{d}_t}\ast 100\%$$

(22)

where N is the number of samples.

4. Analysis of the Inversion Results

4.1. Influence of Different Input Dimensions on the Inversion Results

The trained CNN was used to predict the validation sample, and the RMSE values are reported in

Table 6. The comparison of the training effects of CNN models with two kinds of input data.

Sampling Method	Peak Values of 10 Deflection Curves	All Values of 10 Deflection Curves
RMSE of validation samples	0.1564	0.0417

. The RMSE obtained by the first input condition (peak value of 10 deflection curves in Table 3) was found to be far greater than that obtained by the second input condition (all values of 10 deflection time history curves in Table 3). Therefore, the inversion of the entire deflection curves was more accurate than their peak values. The first input condition does not reflect the overall dynamic characteristics of the pavement structures. As a result, the inversion results have a non-unique problem. In this example, the deflection curves are used to replace the maximum values of the deflection curves as the training samples, which can reflect the dynamic characteristics of the pavement structure more comprehensively. The calculation results also show the high accuracy of the algorithm. The main reason why existing algorithms seldom use the entire deflection time–history curve for inversion is that they cannot cope with huge data sets. The CNN inversion model used in this study has better regression performance and can overcome this problem more effectively.

4.2. Influence of Different Sample Numbers on the Inversion Results

The final calculation results of the second comparison group are exhibited in Figure 8. With the increase in the number of training samples, the RMSE of the validation samples decreased gradually. Figure 8 shows that when the number of training samples was 950, the RMSE of the validation samples reached the minimum value of 0.0417, and the validation accuracy of the CNN model reached about 96%. To further illustrate the accuracy of this algorithm for the inversion of the dynamic modulus of the pavement structure, the evaluation metrics (RMSE, R² value, MAPE (mean absolute percentage error), and MAE) of the algorithm in this paper are shown in

Table 7. Training result.

Training Set	RMSE	R2	MAPE	MAE
950	0.0417	0.9809	[4.11% 3.18% 3.34%]	[101.0193 8.6192 4.5244]

when the training set samples are taken as 950.

4.3. The Inversion Calculation Results of the Dynamic Modulus for Pavement Structures

To further illustrate the accuracy of the proposed algorithm for the inversion of the dynamic modulus of the pavement structure, the 950 training samples used in Section 3.2 were used for exploration. The resulting changes in the RMSE and training loss curve of the training samples predicted by the CNN model are shown in Figure 9. During the first 300 iterations of the CNN training, the loss curve showed a downward trend with the improvement of prediction accuracy. After 3000 iterations at a certain stage of training, the loss value reached the minimum, the loss curve tended to be stable, and the CNN model converged. The changing trend of the RMSE curve of the training samples decreased greatly at first and then tended to be stable.

To reflect the prediction effect of the proposed inversion model more intuitively for the dynamic moduli of the pavement structure layers, the inversion results of the validation samples were compared with the exact values, as exhibited in Figure 10. Figure 10a–c represent the comparison results of the dynamic elastic moduli E₁, E₂, and E₃ of the pavement structure layers, respectively. The predicted and exact values of the dynamic elastic modulus of the first layer of the pavement were found to be basically completely matched. Furthermore, the dynamic elastic moduli of the second and third layers were also well-matched, with only a few samples having certain errors. As the FWD load is applied on the road surface, the deflection curves obtained contain more information on the dynamic characteristics of the surface layer than that of the deep pavement layers. That is, with the increase in the depth, the correlation of the pavement structure properties to the displacement of the road surface decreases; thus, the relative error of its dynamic modulus gradually increases. The relative errors of the inversion results of the dynamic elastic moduli E₁, E₂, and E₃ of the three-layer pavement structure are shown in Figure 11. The MAPE of the first layer was 4.11%, and the maximum relative error was 9.53%. The MAPE of the second and third layers were basically within 3.34%, and their maximum relative errors were 11.33% and 11.91%, respectively. It is worth noting that only 950 samples were selected for training in this example. More accurate inversion results can be achieved if the number of training samples is increased.

4.4. The Inversion Calculation of the Dynamic Modulus and Depth for Pavement Structures

As with the dynamic modulus, the thickness of the pavement structures also has a significant effect on the pavement deflection. In this example, the same pavement profile as in Section 4.3 was used with the assumption that, in addition to the dynamic modulus, the thicknesses of the three pavement structure layers were also unknown. Hence, the number of the unknown inversion variables is twice as large as the example in Section 4.3. In order to obtain an accurate result, more samples are needed for the training than the previous example. A total of 3000 samples are calculated, of which 2400 samples were used for training, 300 samples for validation, and 300 samples for testing. The dynamic modulus and thickness are randomly generated in these 3000 samples. The value ranges of these inversion variables are shown in

Table 8. The value range of the inversion variables.

Inversion Variables	E1 (MPa)	E2 (MPa)	E3 (MPa)	h1(m)	h2(m)	h3(m)
Value range	1500–4500	150–450	75–225	0.075–0.225	0.15–0.45	0.30–0.90
average relative error	7.96%	3.52%	6.90%	10.58%	8.51%	11.97%

.

The inversion results of the validation samples were compared with the exact values, as exhibited in Figure 12 and Figure 13. Figure 12a–c represent the comparison results of the dynamic elastic moduli E₁, E₂, and E₃ of the pavement structure layers, respectively. Figure 13a–c represent the comparison results of the dynamic elastic moduli h₁, h₂, and h₃ of the pavement structure layers, respectively. The average relative error of the six inversion variables is listed in Table 8. As the figures show, the predicted modulus and depth obtained by the presented inversion algorithm have a good agreement with exact modulus and depth. The non-unique problem in the inversion calculation of the pavement structure parameters is solved by the proposed algorithm in engineering accuracy requirements.

5. Conclusions

In this study, an algorithm for parameter identification of concrete pavement structures has been presented. SEM was used as the forward algorithm for the dynamic responses of layered pavement structures, and the time–history curve of the pavement deflection basin displacement responses under FWD loads was obtained. The accuracy of the forward algorithm was verified via a comparison with the existing literature. Based on this, the CNN was adopted, and the deflection basin displacement time–history curves were taken as the input condition to establish a numerical model for the parameter identification of layered pavement structures. The main conclusions of this research are as follows.

• Compared with inversion using the peak values of the pavement deflection basin displacement as the input condition, more accurate inversion results can be obtained by using the entire time–history curves of the pavement deflection basin displacement as the input condition. The phenomenon of “modulus transferring” is avoided, as well as the non-unique problem.
• With the increase in the number of samples, the accuracy of the inversion results increases gradually. For the inversion model of the dynamic modulus of the three-layer pavement structure, when the number of training samples reached 950, the RMSE was only 0.0417, which proves the high accuracy of the proposed inversion algorithm. For the inversion of the dynamic modulus of the pavement structure, the MAPE of the inversion results was found to be basically controlled within 4.11%, and the MAPE of the inversion results of the base and subbase layers were also basically controlled within 3.34%. Thus, inversion results were found to have adequate numerical stability.
• The algorithm can also be used for the inversion of the thickness and dynamic modulus of the pavement structure layer. As the number of inversion variables increases, the inversion accuracy will decline to a certain extent. The algorithm in this paper is of a high solution accuracy for the inversion of the dynamic elastic modulus of the pavement structure surface. The average relative error of the inversion results is basically controlled within 8%, while the inversion accuracy for the thickness is relatively low. The average relative error of the inversion results is basically controlled within 12%, and the inversion results have adequate numerical stability.
• The limitation of this study is that the contact boundary conditions between the pavement structure and the subgrade are not considered, and all the results obtained are purely simulation results without considering the impact of noise. Previous research shows that the interface between the pavement structure and the subgrade will have a certain degree of relative slip, which has a certain impact on the dynamic response of the pavement surface. Therefore, the inversion accuracy of pavement structure dynamic modulus will also be affected. The contact boundary conditions will be considered in future research, and the proposed algorithm will be applied to the actual tests and engineering practice.