Analysis of Efficient and Fast Prediction Method for the Kinematics Solution of the Steel Bar Grinding Robot

Abstract

Aiming at the robotization of the grinding process in the steel bar finishing process, the steel bar grinding robot can achieve the goal of fast, efficient, and accurate online grinding operation, a multi-layer forward propagating deep neural network (DNN) method is proposed to efficiently predict the kinematic solution of grinding robot. The process and kinematics model of the grinding robot are introduced. Based on the proposed method, simulations of the end position and orientation, and joint angle of the grinding robot are given. Three different methods, including SGD + tanh, Nadam + tanh, Nadam + ELU, are used to test the DNN calculation process results show that the method combining Nadam with ELU function has the fastest solution speed and higher accuracy can be obtained with the increase in iteration times. Finally, the Nadam optimizer is used to optimize the calculation results of the example. The optimization results show that this method accelerates the convergence rate of trajectory prediction error and improves the accuracy of trajectory prediction. Thus, the proposed method in this paper is an effective method to predict the kinematic solution when the grinding robot works online.

1. Introduction

Modern society is featured with the rapid advance of industrialization, the replacement of manual labor by robots is accelerated due to the existence of heavy manual labor and potential safety risks. More and more manipulators have assumed the responsibility of assisting or even replacing human beings to complete tasks in industrial automation, equipment manufacturing, medical assistance, aerospace, etc. [1,2].

As we all know, the steel industry is one of the process industries with a high degree of automation. However, there are some problems in the finishing area of the special steel bar, such as frequent operation, harsh environment, heavy labor, and high safety risk, which have been a great threat and hidden danger to the life safety of workers for a long time. In view of this, the traditional steel industry urgently needs to be promoted to robotic operation, in order to meet the requirements of unmanned positions and finishing processes of high quality and efficiency. The bar finishing process consists of straightening, shot blasting, chamfering, polishing, and other processes (the finishing process is shown in Figure 1), grinding as one of the most important processes is given more and more attention by producers. In order to achieve the goal of fast, efficient, and accurate online grinding operation of the grinding robot, it is very necessary to efficiently predict the kinematic solution of the grinding robot before working [3,4,5].

Kinematics analysis of robots is an important field of robot studies. Kinematics analysis of grinding robots (6-DOF articulated industrial robots) is actually the study of the mapping relationship of position vector and orientation vector between the joint space of the manipulator and Cartesian coordinate space [6,7,8]. Kinematics analysis can provide some reference value for the motion control of the robot. In reference [9], the forward kinematics of the 6-DOF parallel robot was solved based on BP neural network, and the nonlinear vector mapping from joint space to workspace was realized by the L-M method. In reference [10], linear interpolation and circular interpolation were used to optimize the spatial interpolation points, and the trajectory optimization was solved. In reference [11], the BP and RBF neural networks were applied to solve the inverse kinematics of the 6-DOF manipulator, and the proposed algorithm was faster than the traditional method, with less computation time. In reference [12], a sliding mode trajectory tracking control method based on a convolution neural network was proposed, the convergence rate of trajectory tracking error was accelerated, and the trajectory tracking accuracy was effectively improved. In reference [13], a scale optimization GEMM optimization method was proposed to further optimize convolution. In reference [14], a special acceleration structure for graph neural network application is proposed. In reference [15], a robust zeroing neural network (RZNN) model for real-time kinematic analysis of manipulators was proposed. In reference [16], a new motion controller based on a recursive neural network (RNN) was proposed, which had good model adaptive ability. In reference [17], a neural network method for residual positioning and positioning error compensation was proposed. In reference [18], a visual analysis tool for solving forward and inverse kinematics of 7-DOF robots based on artificial neural networks was developed. In reference [19], an artificial neural network (ANN) approach to the reliable calculation of direct kinematics problem (DKP) was presented. In reference [20], BNN is proposed to establish a highly nonlinear kinematic and dynamic model of a tendon-driven surgical robot to ensure the accuracy and safety of robotic surgery. In reference [21], two novel loss functions are proposed to train the feed-forward artificial neural network (ANN), and the differential relationship between position and velocity mapping is incorporated into the forward kinematics model of the robot structure, the study shows that the introduction of velocity mapping can improve the adaptability of the learning model to the control task. In reference [22], a novel feed-forward artificial neural network (ANN) structure is proposed to learn the complete pose of the robot in SE (3), and the difference relation is introduced into the learning process. The research shows that the proposed method can correctly model the pose of the robot. In reference [23], the authors do not consider reinforcement learning or trial and error methods. Reinforcement learning is to apply these mapped actions, get a series of feedback reward values, and then select the action with the largest reward value. When the degree of freedom of the robot increases, the convergence performance of the controller will be significantly worse. As you get more and more degrees of freedom, it takes longer and longer to converge. In reference [24], the transfer learning method was applied to train neural networks, which greatly reduced the number of training images required. In reference [25], a new robust return to zero neural networks (RZNN) model was proposed to study the timing trajectory tracking control of wheeled mobile robots in a noise pollution environment. Neural networks have many other applications as well. In reference [26], The finite-time stabilization problem of complex-valued neural networks with proportional delays and inertia terms is studied. In reference [27], an improved convolutional neural network (CNN) was developed for fault feature extraction and classification of hydraulic piston pumps. The DNN method proposed in this paper is a deep learning method included in ANN. In this paper, literature [19] is introduced to better understand the feasibility of the DNN method proposed. DNN is more capable of modeling or abstracting things and can simulate more complex models. The problem of inverse kinematics of grinding robots is characterized by high computational complexity and time consumption. Hence, it is necessary to introduce DNN into the inverse kinematics of grinding robots.

In order to more effectively control the trajectory of the grinding robot and correctly solve the forward and inverse kinematics parameters of the robot, and to avoid the complicated process of solving kinematics equations and the un-uniqueness of inverse kinematics solutions, to achieve fast and efficient online grinding operation of bar grinding robot, in this paper a method based on the multi-layer forward propagation deep neural network is proposed. The proposed method is used to solve the forward and inverse kinematics and realize the kinematics calculation and is compared with the traditional analytical calculation method. It is demonstrated that not only the complicated mathematical theoretical derivation calculation process can be avoided, but results with higher accuracies can also be achieved, it can achieve the goal of fast, efficient, and accurate online grinding operation of bar grinding robot.

This paper takes KUKA KR series industrial robot (grinding robot) as the research object, the main structure of the article is arranged as follows: in Section 2, the basic concepts and related theories of the grinding robot process and kinematics are introduced. A strategy for solving grinding robot kinematics equations based on a multi-layer forward propagation deep neural network is proposed in Section 3. In Section 4, the experimental scheme is stated, and the main simulation experiments and optimization are described in detail. In Section 5 some conclusions are drawn.

2. Grinding Robot Process Introduction and Kinematics Model

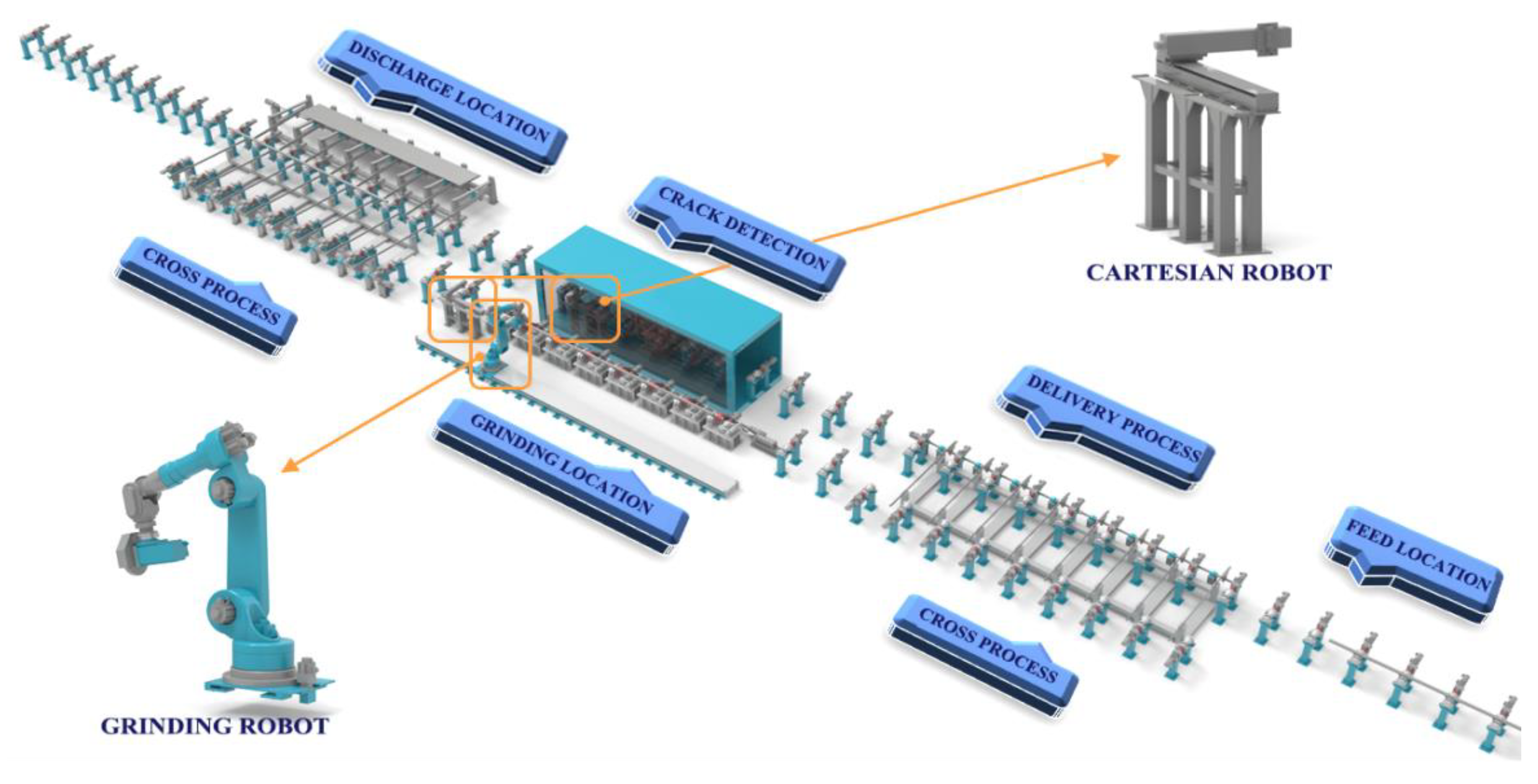
2.1. Grinding Robot Process Introduction

Finishing is the last process of quality control of special steel products, and it is animportant means to ensure the quality of steel products, improve the grade of products and create fine products. It is through the special steel products shot blasting, straightening, chamfering, flaw detection, grinding, labeling, baling, weighing, heat treatment, surface peeling and other processing, to eliminate surface and internal defects of the special steel bar, so that special steel products can meet the factory standards and user requirements, but also can greatly improve the added value of products. The finishing process includes online finishing and offline finishing. The online finishing process is shown in Figure 2.

Online finishing generally refers to the product in the rolling line completing the relevant finishing process. The offline finishing is independent of the rolling production line, which is a process route for the advanced finishing treatment of steel. There are different offline processing processes according to different steel products. As an important part of the finishing process, grinding is paid more and more attention by scientific and technical workers. Grinding robots are mainly used for polishing sanitary porcelain, tables, chairs, and body and deburring castings, these are floating flexible polish. Special steel bar grinding belongs to rigid grinding, grinding material is hard, compared with manual grinding existing problems of uncontrollable depth, and surface quality is not high, it is necessary to realize the special steel bar grinding robotization. Therefore, it is necessary to efficiently predict the kinematic solution of the grinding robot before the online grinding of the special steel bar.

Before the grinding robot is used to grind the defects of the special steel bar, the robot grinding system needs to recognize the bar defect data provided by the crack detection device, then the program in the robot database is called to command the grinding robot to realize the grinding of bar defects. According to the actual working conditions provided parameters, the parameters of bar defect are depth greater than 0.2 mm and length greater than 0.5 mm. The defect location and sample diagram of the bar are shown in Figure 3. According to the requirements of the grinding compliance rate of the production line, the compliance rate of the bar after the robot grinding should be greater than or equal to 95%. The actual transfer speed of the special steel bar production line is 1~2 m per s.

Special steel bar grinding belongs to rigid grinding, grinding material is hard, compared with the traditional manual grinding, there are problems of uncontrollable depth, and surface quality is not high. The kinematics control of the robot must be considered to realize the robotic operation of the grinding process. The efficiency and accuracy of the robot grinding steel bar depend on whether the robot can accurately reach the target grinding point. The motion trajectory and drive control of the robot have a great influence on the grinding, so it is necessary to effectively predict the robot’s kinematic solution in advance. In the process of robot grinding, there will be kinematic problems such as rotation of each joint, trajectory planning, position, and attitude of the end-effector. Considering the timeliness of robot motion control by the robot grinding strategy program, it is necessary and effective to predict the robot kinematic solution to improve the grinding efficiency and precision. In order to accurately control the robot to reach the grinding target point, it must be able to accurately predict the actual state displacement of the robot in the moving space.

In this paper, the deep neural network proposed instead of the traditional D-H kinematics calculation method is aimed at the specific practical application field of robot grinding special steel bar defects. When the robot is used to grind the steel bar, the grinding wheel installed at the end of the robot will wear off its own abrasive particles with friction contact with the steel bar, resulting in the reduction of the diameter of the grinding wheel. Therefore, the diameter change in the grinding wheel becomes an uncertain parameter in the actual robot grinding process. It is well known that the traditional D-H kinematics calculation method can accurately obtain the parameter information of robot kinematics. However, in view of the fact that the uncertainty caused by the change in grinding wheel diameter in the actual grinding process will affect the efficiency and accuracy of robot grinding. In this paper, the deep neural network is proposed to predict the robot kinematics in advance, which can effectively avoid the above problems. The robot kinematics solution of was predicted to eliminate the uncertainty of grinding caused by the change of grinding wheel diameter in the actual grinding process. Some compensation and correction are given to the robot before grinding so that the robot can adjust in real time when grinding the steel bar, so as to complete the grinding task more efficiently and accurately.

As mentioned above, when the grinding wheel is grinding the steel bar, the abrasive particles will be worn off and the diameter of the grinding wheel will become smaller. Therefore, the uncertainty caused by the change of grinding wheel diameter becomes a factor affecting the efficiency and precision of robot grinding. The reduction of grinding precision and the change of surface morphology of steel bar defects, which leads to the secondary inspection of the steel bar. As shown in Figure 2, bar finishing process flow chart. It can be seen that if secondary inspection of steel bar defects is carried out, the “detecting-distributing-grinding” cycle process will be re-implemented. As a result, steel bar accumulation occurred in the storage area, and the efficiency of the whole finishing operation will be significantly reduced, thus greatly reducing the overall grinding efficiency. Therefore, it is necessary to predict the robot kinematics of the steel bar before the robot grinding, which can fully ensure the efficiency and accuracy of the robot grinding.

To sum up, it is necessary to effectively predict the kinematic solution of the grinding robot before the grinding robot is used to repair the defects of the special steel bar, in order to achieve the fast, efficient and accurate online grinding operation goal of the grinding robot.

2.2. Grinding Robot Kinematics Model

This paper takes the KUKA KR series robot (grinding robot) as the research object, which is composed of a base frame, rotating column, link arm, in-line wrist, arm, and other parts. The main purpose is to install a grinding wheel at the end of the robot manipulator to grind the special steel bar with surface defects, the existing robot manipulator, and the steel bar grinding system (the work of this paper is to provide motion support for the realization of robot grinding steel bar) in the laboratory are shown in Figure 4.

The essence of the kinematic analysis of the grinding robot is the process of matrix transformation between two adjacent coordinate systems, and then the transformed matrices are multiplied successively, and finally, the kinematic equation of the robot is obtained. The solution of the kinematics equation consists of two parts, forward kinematics solution, and inverse kinematics solution. The forward kinematics solution is based on the known angle of each joint variable to solve the position and orientation of the end-effector. The inverse kinematics is based on the known position and orientation of the end-effector to solve the angle of each joint variable [28]. The specific solution process is described in detail in the literature [8], which will not be described here. In order to obtain higher calculation accuracy and simplify the calculation process, a method based on a multi-layer forward propagation deep neural network was proposed to solve the kinematics equation of the robot.

According to D-H model parameter method, the coordinate system of each link of grinding robot is established, as shown in Figure 5. The grinding robot is revolute joint, the end is connected with an actuator. No matter how the revolute joint 0 connecting the base frame and the rotating column rotates, its length has no influence on the movement of grinding robot, so the reference coordinate system 0 and coordinate system 1 are coaxial. According to the right-hand rule, the coordinate axes direction of remaining joints are determined [28,29].

When the coordinate system of grinding robot manipulator is established, the corresponding kinematics analysis and calculation can be carried out according to the given parameters of each link of grinding robot. The variation range of D-H model parameters and related variables of each link is shown in

Table 1. Basic parameters of grinding robot.

i	ai−1	αi−1	di	θi	θi Scope
1	0	0	0	θ1	+/−185°
2	a1	−90°	0	θ2	−5~−140°
3	a2	0	0	θ3	+155~−120°
4	a3	−90°	d4	θ4	+/−350°
5	0	90°	0	θ5	+/−122.5°
6	0	−90°	0	θ6	+/−350°

.

Where $a_{i-1}$ is the length of the link and represents the common perpendicular of two adjacent joints axes connecting link $i-1$, ${\alpha }_{i-1}$ is the angle of the link and represents the angle between two adjacent joints, $d_i$ is the offset of the link and represents the distance from the point where $a_{i-1}$ intersects axis $i$ to the point where $a_i$ intersects axis $i$, ${\theta }_i$ is the angular displacement between adjacent joints and represents the angle between the extension of $a_{i-1}$ and the extension of $a_i$.

The transformation matrix ${}_i{}^{i-1}T$ of coordinate system $\left\{i\right\}$ with respect to coordinate system $\{i-1\}$ is as follows.

$${}_i{}^{i-1}T=Rot\left(x,{\alpha }_{i-1}\right)Trans\left(x,a_{i-1}\right)Rot\left(z,{\theta }_i\right)Trans\left(z,d_i\right)$$

(1)

$${}_i{}^{i-1}T=Screw\left(x,a_{i-1},{\alpha }_{i-1}\right)Screw\left(z,d_i,{\theta }_i\right)$$

(2)

where $Screw\left(L,r,\phi \right)$ is translating $r$ along axis $L$ and rotating $\phi$ around axis $L$.

The general expression of transformation matrix ${}_i{}^{i-1}T$ between links is as follows.

$${}_i{}^{i-1}T=\left[\begin{array}{cccc}\cos {\theta }_i& -\sin {\theta }_i& 0& a_{i-1}\\ \sin {\theta }_i\cos {\alpha }_{i-1}& \cos {\theta }_i\cos {\alpha }_{i-1}& -\sin {\alpha }_{i-1}& -d_i\sin {\alpha }_{i-1}\\ \sin {\theta }_i\sin {\alpha }_{i-1}& \cos {\theta }_i\sin {\alpha }_{i-1}& \cos {\alpha }_{i-1}& d_i\cos {\alpha }_{i-1}\\ 0& 0& 0& 1\end{array}\right]$$

(3)

The position vector $P$ represents the position of the terminal link, the rotation matrix $R=\left[\begin{array}{ccc}n& o& a\end{array}\right]$ represents the orientation of the terminal link. The kinematics equation of manipulator is as follows.

$$\left[\begin{array}{cc}{}_n{}^{0}R& {}_n{}^{0}p\\ 0& 1\end{array}\right]=\left[\begin{array}{cccc}{n}_x& o_x& a_x& p_x\\ n_y& o_y& a_y& p_y\\ n_z& o_z& a_z& p_z\\ 0& 0& 0& 1\end{array}\right]={}_1{}^{0}T\left({\theta }_1\right){}_2{}^{1}T\left({\theta }_2\right)\dots {}_n{}^{\mathrm{n}-1}T\left({\theta }_n\right)$$

(4)

where the equation represents the relationship between the position and orientation of the terminal link $(n,o,a,p)$ and the joint variables ${\theta }_1,{\theta }_2,\cdots ,{\theta }_n$.

The robot kinematics model is the core technology of robot application, especially the inverse kinematics model of series robots and the forward kinematics model of parallel robots. The solution process is complicated, and most of them even do not have analytical solutions. All these problems bring difficulties for the application of robots. The solution of the robot kinematics model based on a neural network is the process of generating data fitting the forward kinematics model according to the inverse kinematics model, or generating data fitting the inverse kinematics model according to the forward kinematics model. When solving the kinematics of the 6-DOF robot, selecting solutions and missing solutions to problems will arise. Deep neural networks can deal with many complex underfitting problems. It is possible to solve some complex problems by increasing the depth of the network and improving learning ability. In view of the deep learning algorithm has the advantages of automatic learning, automatic optimization, and incremental learning of advanced functions from data. Therefore, the deep neural net is introduced in this paper to solve and predict the kinematics model of the robot.

The fast prediction method proposed in this paper is different from the traditional robot kinematics analysis method. The deep neural network is applied to solve the robot kinematics, and a large amount of data drive and mapping relationship between parameters are used to solve and analyze the robot kinematics, so as to replace the traditional analytical method to realize the application of the robot.

3. DNN Based Grinding Robot Kinematics Solution

3.1. DNN Overview

Deep neural network (DNN) is a technique in the field of machine learning, it refers to a neural network containing multiple hidden layers. According to the position of different levels, the neural network layer inside DNN can be divided into three categories, including the input layer, hidden layer, and output layer, and the layers are fully connected [30,31]. By using DNN to make a prediction, the accuracy will get better as the number of training sessions increases. The application of a deep learning model to grinding robots for trajectory tracking and predictive control is the current research direction of the industry [32,33].

3.2. DNN Model

In this paper, a deep neural network (DNN) method is proposed to solve the kinematic problems of grinding robot, the problem of solving robot kinematics is transformed into a weight coefficient matrix, bias vector, and input vector of training a neural network, and a series of linear operations and activation operations are carried out.

This paper takes the KUKA KR300 R2500 6-DOF series robot (grinding robot) as an example. The essence of a forward kinematics solution is to solve the position and orientation ($X$,$Y$,$Z$,$A$,$B$,$C$) of the end-effector of the manipulator under the condition of known joint variables (${\theta }_1$,${\theta }_2$,${\theta }_3$,${\theta }_4$,${\theta }_5$,${\theta }_6$). Similarly, the inverse kinematic solution is to solve the angle of each joint in the case of known terminal position and orientation. Therefore, the six joint angles of the manipulator are taken as the input of the whole neural network, the input vector is $J=\left[{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5,{\theta }_6\right]$, the position and orientation of the end-effector are taken as the output of the whole neural network, and the output is $W=\left[X,Y,Z,A,B,C\right]$. On the contrary, the inverse kinematics is solved by taking the terminal position and orientation as input and the joint angle as output.

For the analysis of grinding robot kinematics, according to the topological structure type of neural network [34,35], a forward propagation neural network structure with six dimensions of input, six dimensions of output, and multiple hidden layers is established (as shown in Figure 6) to realize the desired mapping vector relationship from input space to output space.

According to the classification of DNN’s internal neural network layers, the layers are fully connected, any neuron in layer $i$ must be connected to any neuron in layer $i+1$, it is a linear relationship $z={\displaystyle \sum c_i{x}_i+b}$ plus an activation function $\sigma (z)$.

If the activation function is $\sigma \left(z\right)$ and the output value of the hidden layer and output layer is $w$, then the output of the second layer is available. The expression is as follows:

$$\begin{array}{c}{w}_1^2=\sigma (z_1^2)=\sigma (c_{11}^2{x}_1+c_{12}^2{x}_2+\cdots +c_{1k}^2{x}_k+b_1^2)\\ w_2^2=\sigma (z_2^2)=\sigma (c_{21}^2{x}_1+c_{22}^2{x}_2+\cdots +c_{2k}^2{x}_k+b_2^2)\\ ⋮\hspace{1em}\hspace{1em}\hspace{1em}⋮\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ w_k^2=\sigma (z_k^2)=\sigma (c_{k1}^2{x}_1+c_{k2}^2{x}_2+\cdots +c_{kk}^2{x}_k+b_k^2)\end{array}$$

(5)

The output of the third layer is $w_1^3$, the expression is as follows:

$$w_1^3=\sigma (z_1^3)=\sigma (c_{11}^3{w}_1^2+c_{12}^3{w}_2^2+\cdots +c_{1k}^3{w}_k^2+b_1^3)$$

(6)

Assuming that layer $i-1$ has a total of $m$ neurons, then the output of the $j$ neuron of layer $i$ is $w_j^i$, the algebraic expression is as follows:

$$w_j^i=\sigma (z_j^i)=\sigma ({\displaystyle \sum _{k=1}^m{c}_{jk}^i{w}_k^{i-1}+b_j^i})$$

(7)

Assuming that the layer $i-1$ has a total of $m$ neurons, the layer $i$ has a total of $n$ neurons, then the layer $i$ has coefficient matrix $C^i$ of the order $n\times m$, the bias vector for layer $i$ has vector $b^i$ of the order $n\times 1$, the output of layer $i-1$ has vector $w^{i-1}$ of the order $m\times 1$, the output of the inactive parameter at layer $i$ has vector $z^i$ of the order $n\times 1$, the output of layer $i$ has vector $w^i$ of the order $n\times 1$, the matrix expression is as follows:

$$w^i=\sigma (z^i)=\sigma (C^i{w}^{i-1}+b^i)$$

(8)

where $C$ refers to the matrix corresponding to the hidden layer and the output layer, $b$ is the bias vector, $z$ refers to the parameters contained in the activation function, $w$ refers to the matrix corresponding to the output layer.

3.3. Complexity

In order to better prove the effectiveness of the method proposed in this paper, the space complexity and time complexity of DNN method are explained, which meet the conditions of increasing relationship between execution efficiency and data volume. Time complexity refers to the number of operations of the model, which measures how fast or slow the model runs. Time complexity refers to the number of operations of the model, which is an indicator to measure hardware performance and determines the training and prediction time of the model. If the complexity is too high, the model training and prediction will consume a lot of time, which can neither verify the idea and improve the model quickly nor make fast prediction. Space complexity refers to the number of model parameters and determines the number of model parameters. Due to the limitation of curse of dimensionality, the more parameters of the model, the greater the amount of data required to train the model, while the data set in real life is usually not too large, which will lead to the training of the model is easier to overfit.

The time complexity is calculated as follows: suppose the input sequence is of dimension $n$, each element has dimension $d$, and the number of neurons is $x$ The big $O$ is used to simplify time complexity. The number of repetitions of the basic operation of the algorithm is a function $f\left(n\right)$ of module $n$. Therefore, the time complexity of the algorithm is denoted as $T\left(n\right)=O\left(f\left(n\right)\right)$. Less complexity means better code. Space complexity is a measure of the amount of storage space temporarily occupied by an algorithm during its operation. The calculation rule of space complexity is basically similar to that of time complexity, which can be denoted as $S\left(n\right)=S\left(f\left(n\right)\right)$.

(1)

Forward kinematics solution

Table 2. Forward kinematics complexity calculation.

i	Layer	Input Dimension n	Element Dimension d	Neuron x	Time Complexity	Space Complexity
1	Fully Connected	6	1	64	O (n * d * x)	S (n * d * x)
2	Activation	64	1	N/A	O (n * d)	S (n)
3	Fully Connected	64	1	64	O (n * d * x)	S (n * d * x)
4	Activation	64	1	N/A	O (n * d)	S (n)
5	Fully Connected	64	1	64	O (n * d * x)	S (n * d * x)
6	Activation	64	1	N/A	O (n * d)	S (n)
7	Fully Connected	64	1	32	O (n * d * x)	S (n * d * x)
8	Activation	32	1	N/A	O (n * d)	S (n)
9	Fully Connected	32	1	16	O (n * d * x)	S (n * d * x)
10	Activation	16	1	N/A	O (n * d)	S (n)
11	Fully Connected	16	1	6	O (n * d * x)	S (n * d * x)

shows the calculation process of time complexity and space complexity of forward kinematics.

The number of times a statement is executed in an algorithm is called the statement frequency or time–frequency, which can be denoted as $T\left(n\right)$. In the time–frequency $T\left(n\right)$, $n$ is called the scale of the problem. When $n$ keeps changing, the time–frequency $T\left(n\right)$ will also keep changing. Space complexity is a measure of the amount of storage space temporarily occupied by an algorithm during its run, also reflecting a trend. The amount of storage space required by an algorithm is expressed as $f\left(n\right)$. In Table 2, $T\left(n\right)=O\left(f\left(n\right)\right)$ indicates that with the increase of problem size $n$, the growth rate of algorithm execution time is the same as that of $f\left(n\right)$. $S\left(n\right)=S\left(f\left(n\right)\right)$ indicates that when the space complexity of an algorithm is linearly proportional to $n$, it can be expressed as $S\left(n\right)$.

The layers of the deep neural network structure are connected in series, fully connected, and gradually descend during deep learning. Space complexity is a measure of the amount of storage space temporarily occupied by an algorithm during running, not the number of bytes occupied by a program, so space complexity is the number of variables.

(2)

Inverse kinematics solution

Table 3. Inverse kinematics complexity calculation.

i	Layer	Input Dimension n	Element Dimension d	Neuron x	Time Complexity	Space Complexity
1	Fully Connected	6	1	128	O (n * d * x)	S (n * d * x)
2	Activation	128	1	N/A	O (n * d)	S (n)
3	Fully Connected	128	1	128	O (n * d * x)	S (n * d * x)
4	Activation	128	1	N/A	O (n * d)	S (n)
5	Fully Connected	128	1	128	O (n * d * x)	S (n * d * x)
6	Activation	128	1	N/A	O (n * d)	S (n)
7	Fully Connected	128	1	128	O (n * d * x)	S (n * d * x)
8	Activation	128	1	N/A	O (n * d)	S (n)
9	Fully Connected	128	1	128	O (n * d * x)	S (n * d * x)
10	Activation	128	1	N/A	O (n * d)	S (n)
11	Fully Connected	128	1	128	O (n * d * x)	S (n * d * x)
12	Activation	128	1	N/A	O (n * d)	S (n)
13	Fully Connected	128	1	64	O (n * d * x)	S (n * d * x)
14	Activation	64	1	N/A	O (n * d)	S (n)
15	Fully Connected	64	1	32	O (n * d * x)	S (n * d * x)
16	Activation	32	1	N/A	O (n * d)	S (n)
17	Fully Connected	32	1	16	O (n * d * x)	S (n * d * x)
18	Activation	16	1	N/A	O (n * d)	S (n)
19	Fully Connected	16	1	6	O (n * d * x)	S (n * d * x)

shows the calculation process of time complexity and space complexity of inverse kinematics.

The number of times a statement is executed in an algorithm is called the statement frequency or time–frequency, which can be denoted as $T\left(n\right)$. In the time–frequency $T\left(n\right)$, $n$ is called the scale of the problem. When $n$ keeps changing, the time–frequency $T\left(n\right)$ will also keep changing. Space complexity is a measure of the amount of storage space temporarily occupied by an algorithm during its run, also reflecting a trend. The amount of storage space required by an algorithm is expressed as $f\left(n\right)$. In Table 2, $T\left(n\right)=O\left(f\left(n\right)\right)$ indicates that with the increase of problem size $n$, the growth rate of algorithm execution time is the same as that of $f\left(n\right)$. $S\left(n\right)=S\left(f\left(n\right)\right)$ indicates that when the space complexity of an algorithm is linearly proportional to $n$, it can be expressed as $S\left(n\right)$.

The layers of the deep neural network structure are connected in series, fully connected, and gradually descend during deep learning. Space complexity is a measure of the amount of storage space temporarily occupied by an algorithm during running, not the number of bytes occupied by a program, so space complexity is the number of variables.

4. Simulation Experiments and Optimization

4.1. Experimental Scheme

This paper takes the KUKA KR300 R2500 6-DOF series robot (grinding robot) as an example, the parameters are given as follows: a₁ = 350 mm, a₂ = 1150 mm, a₃ = 41 mm, d₄ = 1000 mm.

Based on the above theories, 550 training samples are selected in this paper, the data used to train the deep neural network in this paper are extracted from the existing Leica-AT960-SR laser tracker in the laboratory, and the data acquisition platform is shown in Figure 7. The KUKA robot model was selected in RoboDyn software, and parameters such as the D-H parameter table and motion range of each joint were imported into the software, and the operating workspace boundary was set. Multiple sets of data were automatically generated by the software and then a simulation was carried out. The corresponding inverse kinematic joint angle is derived by software, excluding the data generated by the irregular running trajectory when coupling occurs. The simulation data were input into the robot demonstrator, the software and the laser tracker were connected to the same subnet, and the T-Mac sensor was installed at the end of the robot. After confirming the accuracy of the calibration, the final data was obtained through the laser tracker. Joint angle sample data are shown in

Table 4. Joint angles sample data. The row represents joint angles, the column represents the sample number.

i	θ1	θ2	θ3	θ4	θ5	θ6
1	169.152	−74.474	100.077	−250.680	−19.168	291.015
2	108.117	−10.469	60.329	−325.002	85.537	303.795
3	66.132	−37.705	84.361	−75.441	38.092	−230.169
4	76.237	−135.703	−43.846	−317.680	−98.703	226.420
5	−140.971	−72.721	143.930	−111.730	20.891	−193.332
6	−92.969	−105.562	19.138	139.354	95.771	321.504
7	17.470	−121.286	−78.944	−169.744	83.476	−172.002
8	116.285	−107.124	135.547	−105.011	−74.334	−174.241
9	42.937	−76.106	−23.294	231.580	20.890	34.807
10	154.362	−101.412	88.230	177.610	−29.291	47.475
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$

.

The training method of DNN is adopted to set the network structure as 6-128-128-…-128-128-64-32-16-6, let every 100 iterations be an epoch, batch size for each iteration is set to 550, so one epoch is equivalent to 55,000 training samples, represented by the number of sessions per hour on the server as the number of training epochs. Use Python to execute code programs.

4.2. Simulation Experiments

(1)

Conventional stochastic gradient optimization is solved by using an activation function combining stochastic gradient descent (SGD) and hyperbolic tangent (tanh). The curves of the Sigmoid function and tanh function are shown in Figure 8. The advantage is that it is smooth and easy to derivate and can map a real number to the interval [0, 1]. The disadvantage is that the exponential operation has a large amount of calculation, slow descent speed, and there is division in the derivation when the backpropagation is solving the error gradient. In the process of backpropagation, saturated neurons will lead to the disappearance of the gradient, so that the training of the deep network cannot be completed. The fitting situation of SGD plus tanh solution is shown in Figure 9 and Figure 10.

(2)

The activation function combining Nesterov adaptive moment estimation (Nadam) and hyperbolic tangent (tanh) is used to complete the experiment. Nadam has a stronger constraint on the learning rate and a more direct influence on the gradient update. In this case, the gradient disappearance still exists. The main advantage of Nadam over Adam is better performance in the case of disappearing gradients. In general, where you want to use RMSprop or Adaptive Moment Estimation (Adam), most can use Nadam for better results. The fitting situation of the Nadam plus tanh solution is shown in Figure 11 and Figure 12.

(3)

The activation function combining Nesterov adaptive moment estimation (Nadam) and improved ReLU function (ELU) is used to complete the experiment. The curve of the ELU function is shown in Figure 13. Compared with the ReLU function, there is a certain number of outputs in the case of negative input, and this part of the output has a certain anti-interference ability, which can eliminate the problem of ReLU dying. However, there are still problems with gradient saturation and exponential operation, and the calculation intensity is high. The fitting situation of the Nadam plus ELU solution is shown in Figure 14 and Figure 15.

The loss function used in this paper is mean_squared_error function, which is the mean square error loss function. This function can accurately describe the angle difference when calculating the joint angles, which is equivalent to the accuracy difference of the FK.

The experiment results of the above three solution methods are shown in Figure 16 and

Table 5. The partial test results of three solution methods.

Method + Iteration	2000	10,000	100,000	400,000
SGD + Tanh	80.9%	80.9%	80.9%	80.9%
Nadam + Tanh	87.1%	88.3%	88.3%	88.3%
Nadam + ELU	90.9%	93.4%	97.8%	98.5%

. According to the analysis of data results, the Nadam solver plus ELU function has the fastest solution speed. A higher accuracy is obtained with the increasing number of iterations.

Different methods consume different times when reaching different iteration times. With the increase in iteration times, different methods consume more and more time. The time consumed by different methods during iteration is shown in

Table 6. The time consumed by different methods during iteration.

Method + Iteration + Consumption Time	SGD + Tanh	Nadam + Tanh	Nadam + ELU
2000	80.9%	87.1%	90.9%
Single iteration time consumption	20 ms	22 ms	22 ms
Total time consumption	40 s	45 s	45 s
10,000	80.9%	88.3%	93.4%
Single iteration time consumption	20 ms	22 ms	22 ms
Total time consumption	3 min 21 s	3 min 47 s	3 min 44 s
100,000	80.9%	88.3%	97.8%
Single iteration time consumption	20 ms	22 ms	22 ms
Total time consumption	33 min 16 s	33 min 51 s	33 min 57 s
400,000	80.9%	88.3%	98.5%
Single iteration time consumption	20 ms	22 ms	22 ms
Total time consumption	2 h 14 min 26 s	2 h 27 min 06 s	2 h 28 min 25 s

.

4.3. Nadam Optimization

Nadam optimizer is used to optimize the processing results of DNN. The optimization strategy for Nadam (Nesterov accelerated adaptive moment estimation) is to update model parameters according to the following formula [36,37].

$$g_t={\nabla }_{{\theta }_{t-1}}f\left({\theta }_{t-1}\right)$$

(9)

$$\stackrel{\wedge }{g_t}=\frac{g_t}{1-{\displaystyle {\prod }_{i=1}^t{\alpha }_i}}$$

(10)

$$m_t={\alpha }_t{m}_{t-1}+\left(1-{\alpha }_t\right)g_t$$

(11)

$$\stackrel{\wedge }{m_t}=\frac{m_t}{1-{\displaystyle {\prod }_{i=1}^{t+1}{\alpha }_i}}$$

(12)

$$n_t=\beta n_{t-1}+\left(1-\beta \right)g_t^2$$

(13)

$$\stackrel{\wedge }{n_t}=\frac{n_t}{1-{\beta }^t}$$

(14)

$$\stackrel{\_}{m_t}=\left(1-{\alpha }_t\right)\stackrel{\wedge }{g_t}+{\alpha }_{t+1}\stackrel{\wedge }{m_t}$$

(15)

$${\theta }_t-{\theta }_{t-1}=\Delta {\theta }_t=-\eta \frac{\stackrel{\_}{m_t}}{\sqrt{\stackrel{\wedge }{n_t}}+\epsilon }$$

(16)

where $g_t$ refers to gradient, $\theta$ refers to Initial parameters, $\alpha$ refers to momentum factor, $m_t$ refers to first order moment estimation, $n_t$ refers to second order moment estimation, $\beta$ refers to gradient cumulant factor, $\eta$ refers to learning rate, $\epsilon$ refers to learning speed rate and make sure the denominator is not 0.

The obtained experimental results after optimization of the Nadam optimizer, the training time required by the corresponding method to achieve the corresponding accuracy is significantly reduced compared with that before optimization. The results show that the proposed method can greatly improve the accuracy and efficiency of the robot kinematics solution. The optimized time results and efficiency are shown in

Table 7. The optimized time results and efficiency.

Method + Accuracy	Time Required for 80% Accuracy	Time Required for 85% Accuracy	Time Required for 90% Accuracy	Time Required for 95% Accuracy
SGD + Tanh	About 30 s	N/A	N/A	N/A
Nadam + Tanh	About 20 s	About 30 s	N/A	N/A
Nadam + ELU	About 20 s	About 30 s	About 45 s	About 10 min

.

(1)

The relationship between joint angle and terminal position and orientation can be understood as nonlinear regression of $x$ and $y$, the nonlinear fitting is carried out by the full connection of layer to layer of DNN, represented as $y=f(x)$. After running the program, the predicted result of terminal position and orientation can be obtained, and then compared with the theoretical analytical value, the absolute mean error of orientation forward kinematics solution is about 0.02°, the absolute mean error of position forward kinematics solution is about 0.3 mm, they are all within the margin of error. It shows that there is little difference between the predicted value and the analytical solution, which can meet the precision requirement of engineering applications. The comparison curves between the analytic solution and the predicted solution of forward kinematics are shown in Figure 17, the selected sample data is shown in

Table 8. Comparison of analytic and predictive solutions of forward kinematics.

1	Joint angle actual value	103.157	−82.834	−95.024	−163.470	−84.854	−153.296
	Position and orientation actual value	51.512	519.156	2124.172	−130.236	4.834	16.073
	Position and orientation predicted value	52.048	519.625	2124.669	−130.266	4.825	16.080
2	Joint angle actual value	88.812	−108.298	82.113	329.419	89.898	−289.636
	Position and orientation actual value	142.725	−993.218	1986.104	174.860	35.362	−161.150
	Position and orientation predicted value	143.089	−993.617	1986.581	174.353	35.718	−161.664
3	Joint angle actual value	−69.850	−68.648	−74.447	71.387	−58.072	107.855369
	Position and orientation actual value	−231.802	−71.347	2403.578	−87.774	66.774	75.165
	Position and orientation predicted value	−232.019	−71.836	2403.117	−88.013	66.384	75.881
4	Joint angle actual value	−155.081	−35.073	128.912	23.640	−95.757	228.066
	Position and orientation actual value	−278.397	−988.946	2562.402	171.416	12.991	−55.852
	Position and orientation predicted value	−278.662	−989.034	2562.831	171.956	12.448	−55.725

.

(2)

Similarly, the relationship between terminal position and orientation and joint angle can be understood as nonlinear regression of $y$ and $x$. The deep neural network is combined with the inverse kinematics solving program, and the unique inverse kinematics solution of the robot is determined by filtering and limiting conditions. After running the program, the predicted result of joint angle can be obtained and then compared with the theoretical analytical value, the absolute mean error of orientation inverse kinematics solution is about 10⁻⁵, and it is almost close to 0. It shows that there is little difference between the predicted value and the analytical solution (negligible), which can meet the precision requirement of engineering applications. The comparison curves between the analytic solution and the predicted solution of inverse kinematics are shown in Figure 18, the selected sample data is shown in

Table 9. Comparison of analytic and predictive solutions of inverse kinematics.

1	Position and orientation actual value	1131.414	−7.778	124.19	−11.456	−55.673	−93.113
	Joint angle actual value	12.630900	−20.476474	127.226347	88.156338	−88.722097	−197.538884
	Joint angle predicted value	12.630894	−20.476461	127.226353	88.156347	−88.722106	−197.538896
2	Position and orientation actual value	835.82	−16.01	614.392	−47.505	−11.666	−170.864
	Joint angle actual value	0.474678	−81.717642	154.329096	218.121807	−3.515341	276.113429
	Joint angle predicted value	0.474703	−81.717651	154.329104	218.121796	−3.515348	276.113437
3	Position and orientation actual value	−380.804	−2003.691	815.821	−76.990	−10.079	−87.533
	Joint angle actual value	106.601969	−34.660064	63.840859	−256.547298	−117.218808	41.888494
	Joint angle predicted value	106.602017	−34.660035	63.840873	−256.547304	−117.218824	41.888486
4	Position and orientation actual value	−1613.768	−765.244	2298.126	48.712	20.206	−90.383
	Joint angle actual value	147.210303	−59.896149	18.556023	78.966712	78.258449	22.322419
	Joint angle predicted value	147.210309	−59.896154	18.556041	78.966708	78.258453	22.322422

.

Table 8 shows the prediction results of forward kinematics, reflecting the terminal pose obtained by giving six joint angles, which is represented as $\left[{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5,{\theta }_6\right]\to \left[X,Y,Z,A,B,C\right]$. Table 9 shows the prediction results of inverse kinematics, reflecting the six joint angles obtained by the given position and orientation, which is represented as $\left[X,Y,Z,A,B,C\right]\to \left[{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5,{\theta }_6\right]$, where $\left[X,Y,Z\right]$ represents position (first three columns) and $\left[A,B,C\right]$ represents orientation (last three columns).

The Nesterov momentum included in the Nadam optimizer is capable of producing a better gradient update than classical momentum (Adam). Take advantage of this and train the model with RMSProp (Root Mean Square Prop algorithm, which can adjust the running distance of the model in this direction according to each parameter to accommodate different depths.) containing Nesterov momentum. It can produce a significant effect of consistent dimensions in the training process along the gradient direction, the next accuracy is predicted in advance and accelerating gradient descent learning.

As can be seen from the results in Figure 17 and Figure 18, Table 8 and Table 9, the Nadam optimizer is used to optimize the processing results of DNN, and more accurate solutions can be obtained. It can be shown that this method can accelerate the convergence rate of trajectory prediction error, improve the accuracy of trajectory prediction, and realize the process of deep learning.

DNN can be used to enhance robots’ ability to carry out human commands, it is particularly good at acquiring representations of linguistic expressions, often requiring training them on large data sets that include robot movements, verbal descriptions, and information about different environments. Therefore, efficient prediction and real-time motion control of robot kinematics can be realized.

5. Conclusions

In this paper, a method based on a multi-layer forward propagation deep neural network is proposed to solve the kinematics equation of a grinding robot, to achieve the goal of fast, efficient, and accurate online grinding operation. The working process and kinematics model of grinding robots are introduced. Based on the proposed method, simulations of the end position and orientation, and joint angle of the grinding robot are given. The calculation examples and simulation shows that the proposed method can meet the requirements of trajectory predictive control and efficient grinding. Compared with the traditional method, the proposed method can obtain higher computational efficiency when solving the end-effector pose of the grinding robot. Finally, the Nadam optimizer is used to optimize the processing results of DNN. The results show that the mean absolute errors of forward and inverse kinematics are in a reasonable range. The optimization results show that this method can accelerate the convergence rate of trajectory prediction error and improve the trajectory prediction accuracy. Compared with the traditional analytical method, this method has a shorter training time, stronger replaceable ability, and shorter response time to solve faults. If the hardware configuration of the computer is higher, the processing speed of this method is faster, and the advantage is more obvious. The actual response time of this method is much shorter than the decision time of mechanical motion. The method proposed in this paper can achieve the goal of fast, efficient, and accurate online grinding operation of the grinding robot. In the future, the author will use DNN to conduct in-depth research on real-time trajectory tracking and visual recognition of grinding robots.