An Anomaly Detection Method for Wireless Sensor Networks Based on the Improved Isolation Forest
Abstract
:1. Introduction
2. Related Work
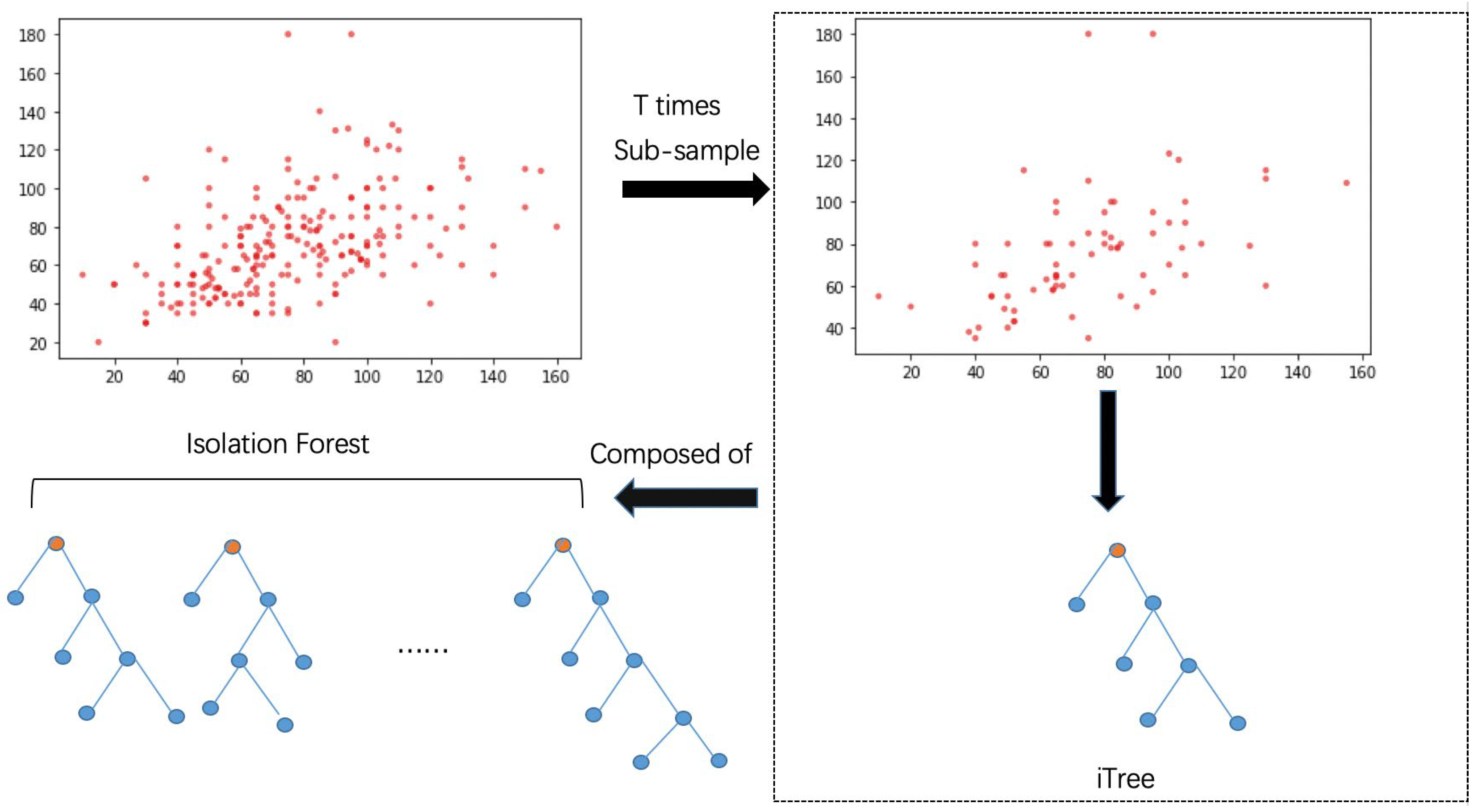
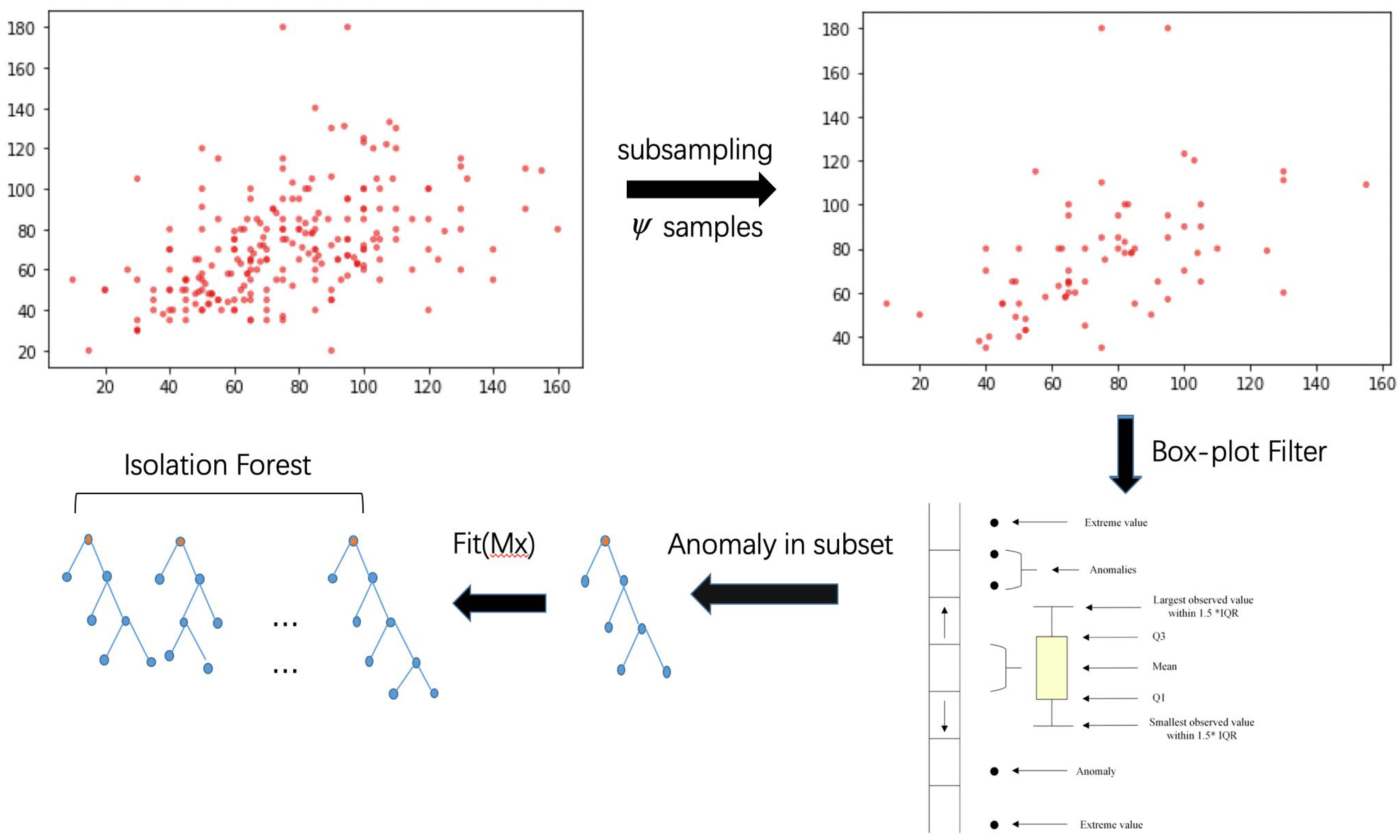
3. Improved Anomaly Detection Based on Isolation Forest
| Algorithm 1: BS-iForest(X,t,) |
| Inputs: X—input data, t—number of trees, —sub-sampling size Output: a set of BS-iForest trees 1: intialize Forest 2: set height limit l = ceiling() 3: i = 1 4: while i <= t { 5: X’sample(X,){ 6: if(box-plot-filter(X’)) 7: ForestForest iTree(X’,0,l) 8: i = i + 1 } 9: else continue 10:} 11: for j = 1 to iTrees_num in Forest 12: compute(fit(iTree[j]) 13: end for 14: select top k iTrees for BS_iForest //k < t 15: return BS-iForest |
4. Discussion
4.1. Dataset
4.2. Experimental Parameter Setting
4.3. Performance Metrics
4.4. Analysis of Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ayadi, A.; Ghorbel, O.; Obeid, A.M.; Abid, M. Outlier detection approaches for wireless sensor networks: A survey. Comput. Netw. 2017, 129, 319–333. [Google Scholar] [CrossRef]
- Garcia-Font, V.; Garrigues, C.; Rifà-Pous, H. Difficulties and Challenges of Anomaly Detection in Smart Cities: A Laboratory Analysis. Sensors 2018, 18, 3198. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation-based anomaly detection. ACM Trans. Knowl. Discov. Data (TKDD) 2012, 6, 1–39. [Google Scholar] [CrossRef]
- Hariri, S.; Kind, M.C.; Brunner, R.J. Extended Isolation Forest. IEEE Trans. Knowl. Data Eng. 2021, 33, 1479–1489. [Google Scholar] [CrossRef] [Green Version]
- Zivkovic, Z. Improved adaptive Gaussian mixture model for background subtraction. In Proceedings of the 17th International Conference on Pattern Recognition (ICPR), Cambridge, UK, 23–26 August 2004; Volume 22, pp. 28–31. [Google Scholar]
- Karczmarek, P.; Kiersztyn, A.; Pedrycz, W.; Al, E. K-Means-based isolation forest. Knowl.-Based Syst. 2020, 195, 105659. [Google Scholar] [CrossRef]
- Laksono, M.A.T.; Purwanto, Y.; Novianty, A. DDoS detection using CURE clustering algorithm with outlier removal clustering for handling outliers. In Proceedings of the 2015 International Conference on Control, Electronics, Renewable Energy and Communications (ICCEREC), Bandung, Indonesia, 27–29 August 2015; pp. 12–18. [Google Scholar]
- Guha, S.; Rastogi, R.; Shim, K. Rock: A robust clustering algorithm for categorical attributes. Inf. Syst. 2000, 25, 345–366. [Google Scholar] [CrossRef]
- Saeedi Emadi, H.; Mazinani, S.M. A Novel Anomaly Detection Algorithm Using DBSCAN and SVM in Wireless Sensor Networks. Wirel. Pers. Commun. 2018, 98, 2025–2035. [Google Scholar] [CrossRef]
- Prodanoff, Z.G.; Penkunas, A.; Kreidl, P. Anomaly Detection in RFID Networks Using Bayesian Blocks and DBSCAN. In Proceedings of the 2020 SoutheastCon, Raleigh, NC, USA, 28–29 March 2020; pp. 1–7. [Google Scholar]
- Yin, C.; Zhang, S. Parallel implementing improved k-means applied for image retrieval and anomaly detection. Multimed. Tools Appl. 2017, 76, 16911–16927. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, Y.; Li, G. Anomaly Detection by Using Streaming K-Means and Batch K-Means. In Proceedings of the 2020 5th IEEE International Conference on Big Data Analytics (ICBDA), Xiamen, China, 8–11 May 2020; pp. 11–17. [Google Scholar]
- Ying, S.; Wang, B.; Wang, L.; Li, Q.; Zhao, Y.; Shang, J.; Huang, H.; Cheng, G.; Yang, Z.; Geng, J. An Improved KNN-Based Efficient Log Anomaly Detection Method with Automatically Labeled Samples. ACM Trans. Knowl. Discov. Data 2021, 15, 34. [Google Scholar] [CrossRef]
- Wang, B.; Ying, S.; Cheng, G.; Wang, R.; Yang, Z.; Dong, B. Log-based anomaly detection with the improved K-nearest neighbor. Int. J. Softw. Eng. Knowl. Eng. 2020, 30, 239–262. [Google Scholar] [CrossRef]
- Xu, S.; Liu, H.; Duan, L.; Wu, W. An Improved LOF Outlier Detection Algorithm. In Proceedings of the 2021 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 28–30 June 2021; pp. 113–117. [Google Scholar]
- Kriegel, H.-P.; Kröger, P.; Schubert, E.; Zimek, A. LoOP: Local outlier probabilities. In Proceedings of the 18th ACM conference on Information and Knowledge Management, Hong Kong, China, 2–6 November 2009; pp. 1649–1652. [Google Scholar]
- Tan, R.; Ottewill, J.R.; Thornhill, N.F. Monitoring statistics and tuning of kernel principal component analysis with radial basis function kernels. IEEE Access 2020, 8, 198328–198342. [Google Scholar] [CrossRef]
- Yokkampon, U.; Chumkamon, S.; Mowshowitz, A.; Hayashi, E. Anomaly Detection in Time Series Data Using Support Vector Machines. In Proceedings of the International Conference on Artificial Life & Robotics (ICAROB2021), Online, 21–24 January 2021; pp. 581–587. [Google Scholar]
- Choi, Y.-S. Least squares one-class support vector machine. Pattern Recognit. Lett. 2009, 30, 1236–1240. [Google Scholar] [CrossRef]
- Yu, Q.; Jibin, L.; Jiang, L. An improved ARIMA-based traffic anomaly detection algorithm for wireless sensor networks. Int. J. Distrib. Sens. Netw. 2016, 12, 9653230. [Google Scholar] [CrossRef] [Green Version]
- Ghorbel, O.; Ayedi, W.; Snoussi, H.; Abid, M. Fast and Efficient Outlier Detection Method in Wireless Sensor Networks. IEEE Sens. J. 2015, 15, 3403–3411. [Google Scholar] [CrossRef]
- Li, Q.; Li, R.; Ji, K.; Dai, W. Kalman filter and its application. In Proceedings of the 2015 8th International Conference on Intelligent Networks and Intelligent Systems (ICINIS), Tianjin, China, 1–3 November 2015; pp. 74–77. [Google Scholar]
- Li, H.; Achim, A.; Bull, D. Unsupervised video anomaly detection using feature clustering. IET Signal Process. 2012, 6, 521–533. [Google Scholar] [CrossRef]
- Amidi, A. Arima based value estimation in wireless sensor networks. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 41. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, F.; Suri-Payer, F.; Gulenko, A.; Wallschläger, M.; Acker, A.; Kao, O. Unsupervised anomaly event detection for cloud monitoring using online arima. In Proceedings of the 2018 IEEE/ACM International Conference on Utility and Cloud Computing Companion (UCC Companion), Zurich, Switzerland, 17–20 December 2018; pp. 71–76. [Google Scholar]
- Ren, H.; Ye, Z.; Li, Z. Anomaly detection based on a dynamic Markov model. Inf. Sci. 2017, 411, 52–65. [Google Scholar] [CrossRef]
- Honghao, W.; Yunfeng, J.; Lei, W. Spectrum anomalies autonomous detection in cognitive radio using hidden markov models. In Proceedings of the 2015 IEEE Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 19–20 December 2015; pp. 388–392. [Google Scholar]
- Yuanyang, P.; Guanghui, L.; Yongjun, X.; software. Abnormal data detection method for environmental sensor networks based on DBSCAN. Comput. Appl. Softw. 2012, 29, 69–72+111. [Google Scholar]
- Wazid, M.; Das, A.K. An efficient hybrid anomaly detection scheme using K-means clustering for wireless sensor networks. Wirel. Pers. Commun. 2016, 90, 1971–2000. [Google Scholar] [CrossRef]
- Duan, D.; Li, Y.; Li, R.; Lu, Z. Incremental K-clique clustering in dynamic social networks. Artif. Intell. Rev. 2012, 38, 129–147. [Google Scholar] [CrossRef]
- Zhang, K.; Hutter, M.; Jin, H. A new local distance-based outlier detection approach for scattered real-world data. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Bangkok, Thailand, 27–30 April 2009; pp. 813–822. [Google Scholar]
- Breunig, M.M.; Kriegel, H.-P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 93–104. [Google Scholar]
- Abid, A.; Kachouri, A.; Mahfoudhi, A. Anomaly detection through outlier and neighborhood data in Wireless Sensor Networks. In Proceedings of the 2016 2nd International Conference on Advanced Technologies for Signal and Image Processing (ATSIP), Monastir, Tunisia, 21–23 March 2016; pp. 26–30. [Google Scholar]
- Bosman, H.H.W.J.; Iacca, G.; Tejada, A.; Wörtche, H.J.; Liotta, A. Spatial anomaly detection in sensor networks using neighborhood information. Inf. Fusion 2017, 33, 41–56. [Google Scholar] [CrossRef]
- Xie, M.; Hu, J.; Han, S.; Chen, H.H. Scalable Hypergrid k-NN-Based Online Anomaly Detection in Wireless Sensor Networks. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 1661–1670. [Google Scholar] [CrossRef]
- Luo, Z.; Shafait, F.; Mian, A. Localized forgery detection in hyperspectral document images. In Proceedings of the 2015 13th International Conference on Document Analysis and Recognition (ICDAR), Nancy, France, 23–26 August 2015; pp. 496–500. [Google Scholar]
- Xu, D.; Wang, Y.; Meng, Y.; Zhang, Z. An improved data anomaly detection method based on isolation forest. In Proceedings of the 2017 10th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 9–10 December 2017; pp. 287–291. [Google Scholar]
- Xuxiang, W.L.Q.H.B. Multidimensional Data Anomaly Detection Method Based on Fuzzy Isolated Forest Algorithm. Comput. Digit. Eng. 2020, 48, 862–866. [Google Scholar]
- Zhou, J.C. Satellite Anomaly Detection Based on Unsupervised Algorithm. Master’s Thesis, Wuhan University, Wuhan, China, May 2020. [Google Scholar]










| Type | Classical Algorithms | Advantages | Disadvantages |
|---|---|---|---|
| Statistics-based methods | Gaussian model [6], regression model, histogram | Applicable to low dimensional data and high efficiency | Data distribution, probability model, and parameters are difficult to determine |
| Clustering-based methods | CURE [7], ROCK [8], DBSCAN [9,10], K-means [11] | Low time complexity and can be applied to real-time monitoring | High cost for large datasets |
| Proximity-based methods | KNN [12,13], LOF [14,15], LOOP [16], RBF [17,18] | No need to assume data distribution | Not applicable to high-dimensional data and requires manual parameter adjustment |
| Classification-based methods | OCSVM [19], C4.5, decision tree | High accuracy and short training time | Difficult model selection and parameter setting |
| Method | Advantages | Disadvantages |
|---|---|---|
| Kalman filtering [22,23] | Being widely applied and less computation consumption | Only being applied to linearly distributed data |
| ARIMA [24,25] | extremely simple | The dataset is required to be stable or stable after differentiation |
| Markov [26,27] | High accuracy | High computational cost of training and detection |
| Method | Advantages | Disadvantages |
|---|---|---|
| K-means [29] | simple, fast convergence and excellent performance for large-scale datasets | converges to the local optimal, sensitive to the selection of initial cluster center |
| DBSCAN [10,11] | Dense clusters of arbitrary shapes can be clustered to seek outliers | difficult to process high-dimensional data, poor performance on datasets with long distances between clusters |
| SOM [28] | Mapping data to two-dimensional plane to achieve visualization and better clustering results | highly complex and depends on experience |
| CURE [8] | Clusters that can handle complex spaces | many parameters, sensitive to spatial data density difference |
| CLIQUE [30] | Good at dealing with high-dimensional data and large datasets | low clustering accuracy results in the low accuracy of whole algorithm |
| Method | Advantages | Disadvantages |
|---|---|---|
| RBF neural network | dealing with complex nonlinear data, fast convergence speed during model learning process | Highly dependent on training data, complex network structure |
| KNN | Simple model, produces better performance without too much adjustment | low efficiency, highly dependent on training data, poor effect on high-dimensional data |
| LOF | sensitive to local outliers, excellent effect on data clusters with different densities | difficult to determine the minimum neighborhood, the data dimension increases, the computational complexity and time complexity increase greatly |
| INFLO [36] | suitable for clusters with slightly different densities | Low accuracy and efficiency |
| LOOP | Output abnormal probability instead of abnormal score; no need to input the threshold parameter based on experience | assume that the data conforms to Gaussian distribution and the scope of application area is small |
| Algorithm | Data Set Partition | Detector Diversity | Stability |
|---|---|---|---|
| iForest | Continuously divide the data set, calculate the abnormal score according to the number of divisions | Single type of detector | Random feature selection, poor stability |
| ex-iForest | Subsampling according to the Raida criteria | Increased classification ability | Strong stability |
| MRH-iForest | Partitioning datasets using Hyperplanes | Compared with iForest, the classification ability increased | Strong stability |
| BS-iForest | Use the box plot to divide the data set and use the fitness to select the data set | Increased diversity and classification ability | Perform joint judgment of similar samples in the boundary fuzzy area, strong stability |
| Attributes | Description |
|---|---|
| voltage | Current server cabinet input voltage |
| current | Current server cabinet input current |
| power | Current server cabinet power |
| energy | Current server cabinet electric energy |
| temperature | Current server cabinet temperature |
| humidity | Current server cabinet humidity |
| Attributes | Description |
|---|---|
| Sample-cn number | Sample code number (1–10) |
| Clump | Clump thickness (1–10) |
| Cell size | Uniformity of cell size (1–10) |
| Cell shape | Uniformity of cell shape (1–10) |
| MA | Marginal adhesion (1–10) |
| SECS | Single epithelial cell size (1–10) |
| Bare nuclei | Bare nuclei (1–10) |
| Bland-ch | Bland chromatin (1–10) |
| Normal-nuc | Normal nucleoli (1–10) |
| Mitoses | Mitoses (1–10) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Zhang, J.; Qian, R.; Yuan, J.; Ren, Y. An Anomaly Detection Method for Wireless Sensor Networks Based on the Improved Isolation Forest. Appl. Sci. 2023, 13, 702. https://doi.org/10.3390/app13020702
Chen J, Zhang J, Qian R, Yuan J, Ren Y. An Anomaly Detection Method for Wireless Sensor Networks Based on the Improved Isolation Forest. Applied Sciences. 2023; 13(2):702. https://doi.org/10.3390/app13020702
Chicago/Turabian StyleChen, Junxiang, Jilin Zhang, Ruixiang Qian, Junfeng Yuan, and Yongjian Ren. 2023. "An Anomaly Detection Method for Wireless Sensor Networks Based on the Improved Isolation Forest" Applied Sciences 13, no. 2: 702. https://doi.org/10.3390/app13020702
APA StyleChen, J., Zhang, J., Qian, R., Yuan, J., & Ren, Y. (2023). An Anomaly Detection Method for Wireless Sensor Networks Based on the Improved Isolation Forest. Applied Sciences, 13(2), 702. https://doi.org/10.3390/app13020702





