The Definition of Perennial Streams Based on a Wet Channel Network Extracted from LiDAR Data
Abstract
:1. Introduction
2. Data and Methodology
3. Results and Discussion
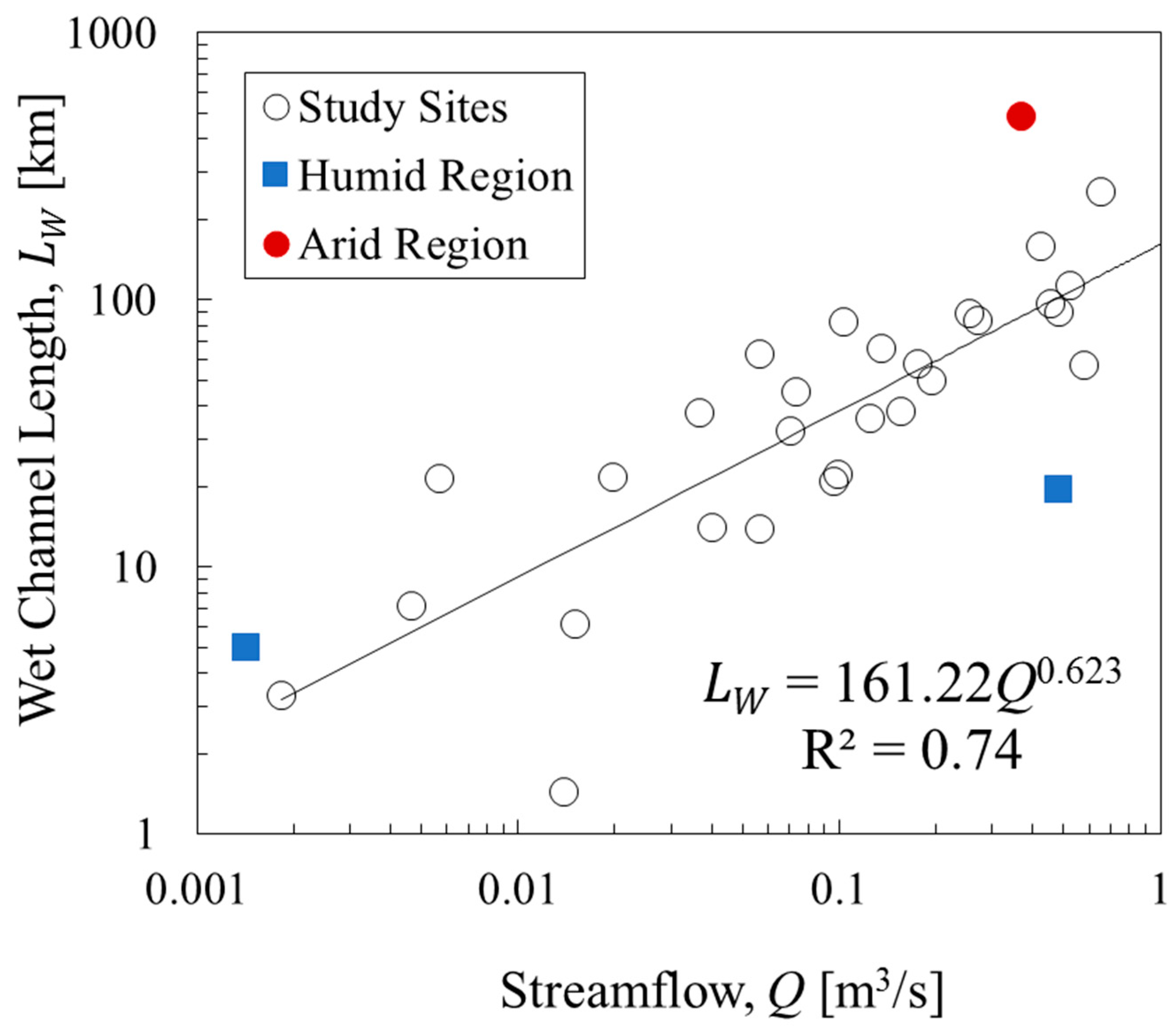
3.1. The Relationship between the Wet Channel Length and Streamflow
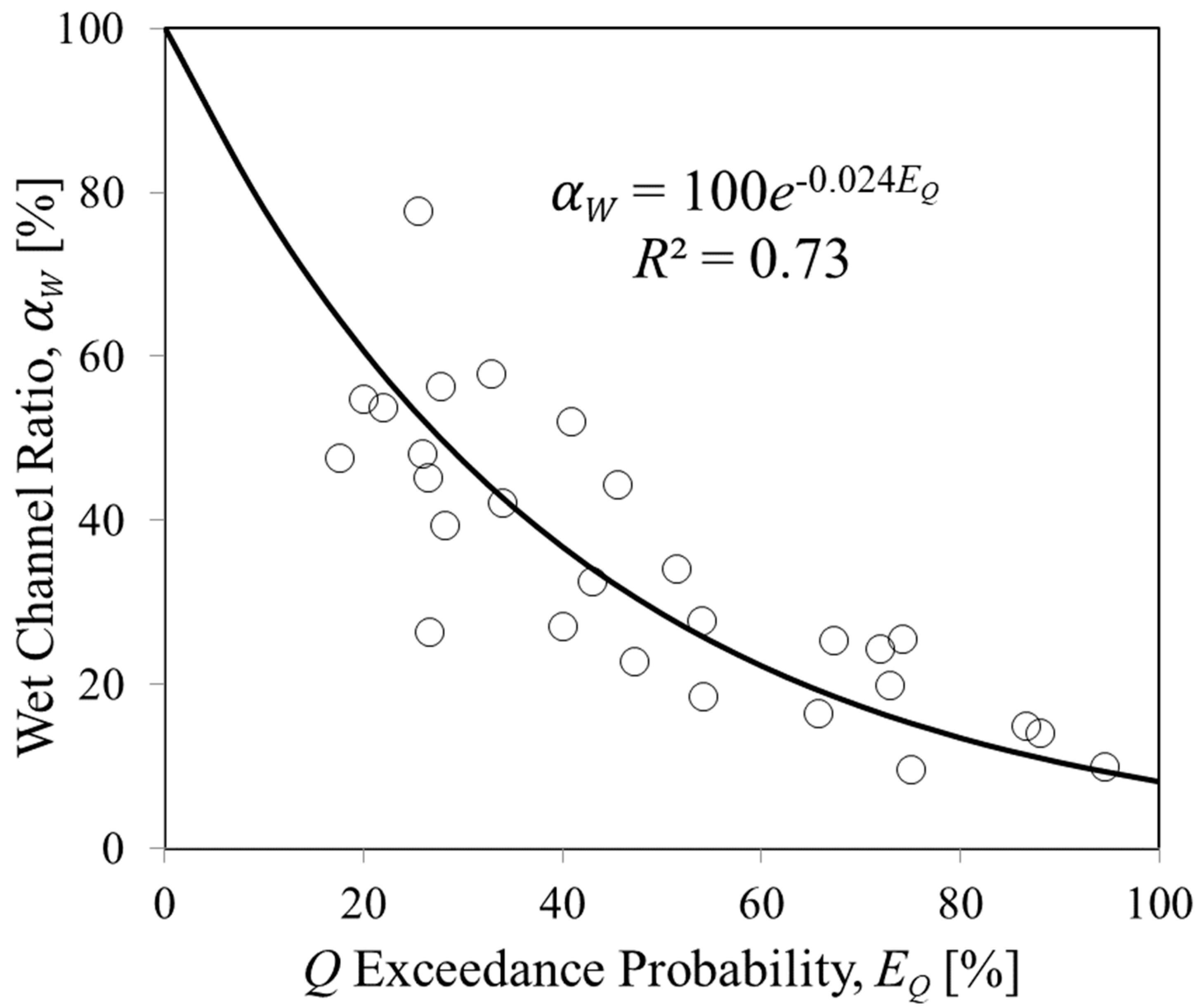
3.2. The Relationship between the Wet Channel Ratio and Streamflow Exccedance Probability
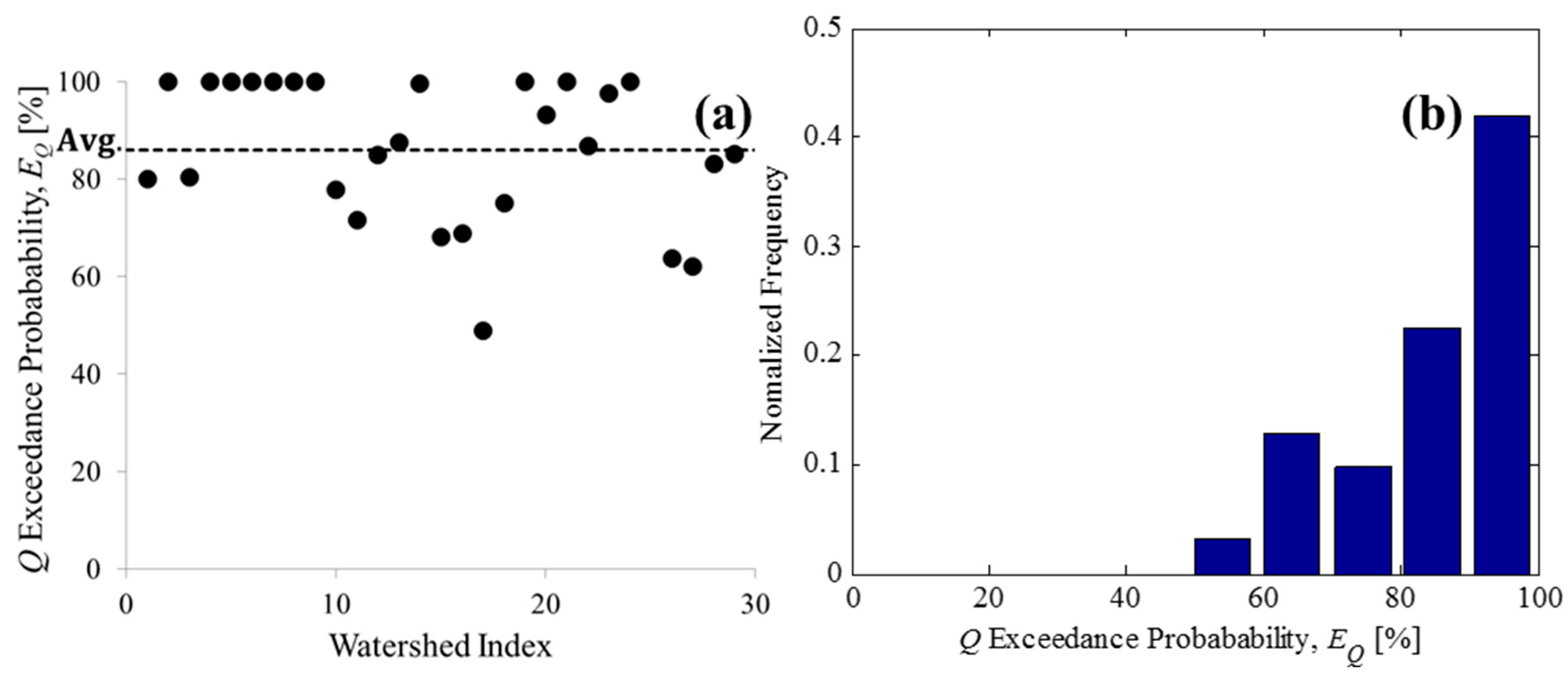
3.3. Temporal Variability
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meinzer, O.E. Outline of ground-water hydrology, with definitions. US Govt. Print. Off. 1923, 494, 1–68. [Google Scholar]
- Von Schiller, D.; Acuña, V.; Sabater, S. Wetlands and Habitats, 2nd ed.; Streams: Perennial and seasonal; CRC Press: Boca Raton, FL, USA, 2020; ISBN 978-04-2944-550-7. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw Hill: New York, NY, USA, 1988. [Google Scholar]
- Blasch, K.W.; Ferré, T.; Christensen, A.H.; Hoffmann, J.P. New field method to determine streamflow timing using electrical resistance sensors. Vadose Zone J. 2002, 1, 289–299. [Google Scholar] [CrossRef]
- Levick, L.R.; Goodrich, D.C.; Hernandez, M.; Fonseca, J.; Semmens, D.J.; Stromberg, J.C.; Tluczek, M.; Leidy, R.A.; Scianni, M.; Guertin, D.P. The Ecological and Hydrological Significance of Ephemeral and Intermittent Streams in the Arid and Semi-Arid American Southwest; US Environmental Protection Agency, Office of Research and Development: Washington, DC, USA, 2008.
- NC Division of Water Quality. Methodology for Identification of Intermittent and Perennial Streams and Their Origins, Version 4.11; North Carolina Department of Environment and Natural Resources, Division of Water Quality: Raleigh, NC, USA, 2010. [Google Scholar]
- Hedman, E.; Osterkamp, W. Streamflow Characteristics Related to Channel Geometry of Streams in Western United States; Water Supply Paper 2193; US Geological Survey: Alexandria, VA, USA, 1982.
- Hewlett, J.D. Principles of Forest Hydrology; University of Georgia Press: Athens, GA, USA, 1982. [Google Scholar]
- Texas Forest Service. Texas Forestry Best Management Practices. Online Report. 2000. Available online: https://tfsweb.tamu.edu/uploadedFiles/TFSMain/Manage_Forest_and_Land/Water_Resources_and_BMPs/Stewardship(1)/BMP%20Handbook_clean%20copy,%20Aug%202017.pdf (accessed on 3 January 2023).
- Schumm, S.A. Evolution of drainage systems and slopes in badlands at Perth Amboy, New Jersey. Geol. Soc. Am. Bull. 1956, 67, 597–646. [Google Scholar] [CrossRef]
- Howard, A.D.; Kerby, G. Channel changes in badlands. Geol. Soc. Am. Bull. 1983, 94, 739–752. [Google Scholar] [CrossRef]
- Simley, J. National Hydrography Dataset Newsletter. US Geol. Surv. Rep. 2003, 2. Available online: http://nhd.usgs.gov/newsletterlist.html (accessed on 3 January 2023).
- Svec, J.R.; Kolka, R.; Stringer, J. Defining perennial, intermittent, and ephemeral channels in eastern Kentucky: Application to forestry best management practices. For. Ecol. Manag. 2005, 214, 170–182. [Google Scholar] [CrossRef]
- Jaeger, K.L.; Sando, R.; McShane, R.R.; Dunham, J.B.; Hockman-Wert, D.P.; Kaiser, K.E.; Hafen, K.; Risley, J.C.; Blasch, K.W. Probability of Streamflow Permanence Model (PROSPER): A spatially continuous model of annual streamflow permanence throughout the Pacific Northwest. J. Hydrol. X 2019, 2, 100005. [Google Scholar] [CrossRef]
- Marks, K.; Bates, P. Integration of high-resolution topographic data with floodplain flow models. Hydrol. Process. 2000, 14, 2109–2122. [Google Scholar] [CrossRef]
- Bowen, Z.H.; Waltermire, R.G. Evaluation of light detection and ranging (LIDAR) for measuring river corridor topography. J. Am. Water Resour. Assoc. 2002, 38, 33–41. [Google Scholar] [CrossRef]
- Lashermes, B.; Foufoula-Georgiou, E.; Dietrich, W.E. Channel network extraction from high resolution topography using wavelets. Geophys. Res. Lett. 2007, 34, L23S04. [Google Scholar] [CrossRef] [Green Version]
- Orlandini, S.; Moretti, G. Determination of surface flow paths from gridded elevation data. Water Resour. Res. 2009, 45, W03417. [Google Scholar] [CrossRef] [Green Version]
- Orlandini, S.; Tarolli, P.; Moretti, G.; Dalla Fontana, G. On the prediction of channel heads in a complex alpine terrain using gridded elevation data. Water Resour. Res. 2011, 47, W02538. [Google Scholar] [CrossRef]
- Sofia, G.; Tarolli, P.; Cazorzi, F.; Dalla Fontana, G. An objective approach for feature extraction: Distribution analysis and statistical descriptors for scale choice and channel network identification. Hydrol. Earth Syst. Sci. 2011, 15, 1387–1402. [Google Scholar] [CrossRef] [Green Version]
- Pelletier, J.D. A robust, two-parameter method for the extraction of drainage networks from high-resolution digital elevation models (DEMs): Evaluation using synthetic and real-world DEMs. Water Resour. Res. 2013, 49, 75–89. [Google Scholar] [CrossRef] [Green Version]
- Clubb, F.J.; Mudd, S.M.; Milodowski, D.T.; Hurst, M.D.; Slater, L.J. Objective extraction of channel heads from high-resolution topographic data. Water Resour. Res. 2014, 50, 4283–4304. [Google Scholar] [CrossRef] [Green Version]
- Metes, M.J.; Jones, D.K.; Baker, M.E.; Miller, A.J.; Hogan, D.M.; Loperfido, J.V.; Hopkins, K.G. Ephemeral stream network extraction from Lidar-derived elevation and topographic attributes in urban and forested landscapes. J. Am. Water Resour. Assoc. 2022, 58, 547–565. [Google Scholar] [CrossRef]
- Genc, L.; Smith, S.E.; Dewitt, B.A. Using satellite imagery and lidar data to corroborate an adjudicated ordinary high water line. Int. J. Remote Sens. 2005, 26, 3683–3693. [Google Scholar] [CrossRef]
- Höfle, B.; Vetter, M.; Pfeifer, N.; Mandlburger, G.; Stötter, J. Water surface mapping from airborne laser scanning using signal intensity and elevation data. Earth Surf. Process. Landf. 2009, 34, 1635–1649. [Google Scholar] [CrossRef]
- Smeeckaert, J.; Mallet, C.; David, N.; Chehata, N.; Ferraz, A. Large-scale classification of water areas using airborne topographic lidar data. Remote Sens. Environ. 2013, 138, 134–148. [Google Scholar] [CrossRef]
- Wu, H.; Liu, C.; Zhang, Y.; Sun, W.; Li, W. Building a water feature extraction model by integrating aerial image and lidar point clouds. Int. J. Remote Sens. 2013, 34, 7691–7705. [Google Scholar] [CrossRef]
- Hooshyar, M.; Kim, S.; Wang, D.; Medeiros, S.C. Wet channel network extraction by integrating LiDAR intensity and elevation data. Water Resour. Res. 2015, 51, 10029–10046. [Google Scholar] [CrossRef]
- Liu, C.; Wang, L.; Xin, Z.; Li, Y. Comparative study of wet channel network extracted from LiDAR data under different climate conditions. Hydrol. Res. 2018, 49, 1101–1119. [Google Scholar] [CrossRef]
- Zambory, L.C.; Ellis, H.; Pierce, L.C.; Roe, J.K.; Weber, J.M.; Schilling, E.K.; Young, C.N. The Development of a GIS Methodology to Identify Oxbows and Former Stream Meanders from LiDAR-Derived Digital Elevation Models. Remote Sens. 2019, 11, 12. [Google Scholar] [CrossRef] [Green Version]
- Budyko, M.I. The Heat Balance of the Earth’s Surface; US Department of Commerce: Washington, DC, USA, 1958.
- Heidemann, H.K. Lidar Base Specification (ver. 1.3, February 2018): U.S. Geological Survey Techniques and Methods; U.S. Geological Survey: Sioux Falls, SD, USA, 2018; Book 11; Chapter B4; 101p. [CrossRef] [Green Version]
- National Hydrography Dataset Homepage. Available online: https://www.usgs.gov/national-hydrography/national-hydrography-dataset (accessed on 6 November 2022).
- Wolfe, W.L.; Zissis, G.J. The Infrared Handbook; ERIM: Rotterdam, The Netherlands, 1989; pp. 1124–1127. [Google Scholar]
- Rasmussen, C.E. The infinite Gaussian mixture model. In Advances in Neutral Information Processing Systems 12; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Canny, J. A Computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI–8, 679–698. [Google Scholar] [CrossRef]
- Blyth, K.; Rodda, J. A stream length study. Water Resour. Res. 1973, 9, 1454–1461. [Google Scholar] [CrossRef]
- Godsey, S.; Kirchner, J. Dynamic, discontinuous stream networks: Hydrologically driven variations in active drainage density, flowing channels and stream order. Hydrol. Process. 2014, 28, 5791–5803. [Google Scholar] [CrossRef]
- Whiting, J.A.; Godsey, S.E. Discontinuous headwater stream networks with stable flowheads, salmon river basin, Idaho. Hydrol. Process. 2016, 30, 2305–2316. [Google Scholar] [CrossRef]
- Wigington, P.; Moser, T.; Lindeman, D. Stream network expansion: A riparian water quality factor. Hydrol. Process. 2005, 19, 1715–1721. [Google Scholar] [CrossRef]
- Roberts, M.C.; Archibold, O. Variation of Drainage Density in a Small British Columbia Watershed; Wiley Online Library: Hoboken, NJ, USA, 1978. [Google Scholar]
- Morgan, R.P.C. Observations on factors affecting the behaviour of a first-order stream. Trans. Ins. Brit. Geogr. 1972, 56, 171–185. [Google Scholar] [CrossRef]
- Day, D.G. Drainage density changes during rainfall. Earth Surf. Process. 1978, 3, 319–326. [Google Scholar] [CrossRef]
- Gurnell, A.M. The dynamics of a drainage network. Nord. Hydrol. 1978, 9, 293–306. [Google Scholar] [CrossRef]
- Goulsbra, C.; Evans, M.; Lindsay, J. Temporary streams in a peatland catchment: Pattern, timing, and controls on stream network expansion and contraction. Process. Landf. 2014, 39, 790–803. [Google Scholar] [CrossRef]
- Wang, D.; Wu, L. Similarity of climate control on base flow and perennial stream density in the Budyko framework. Hydrol. Earth Syst. Sci. 2013, 17, 315–324. [Google Scholar] [CrossRef]
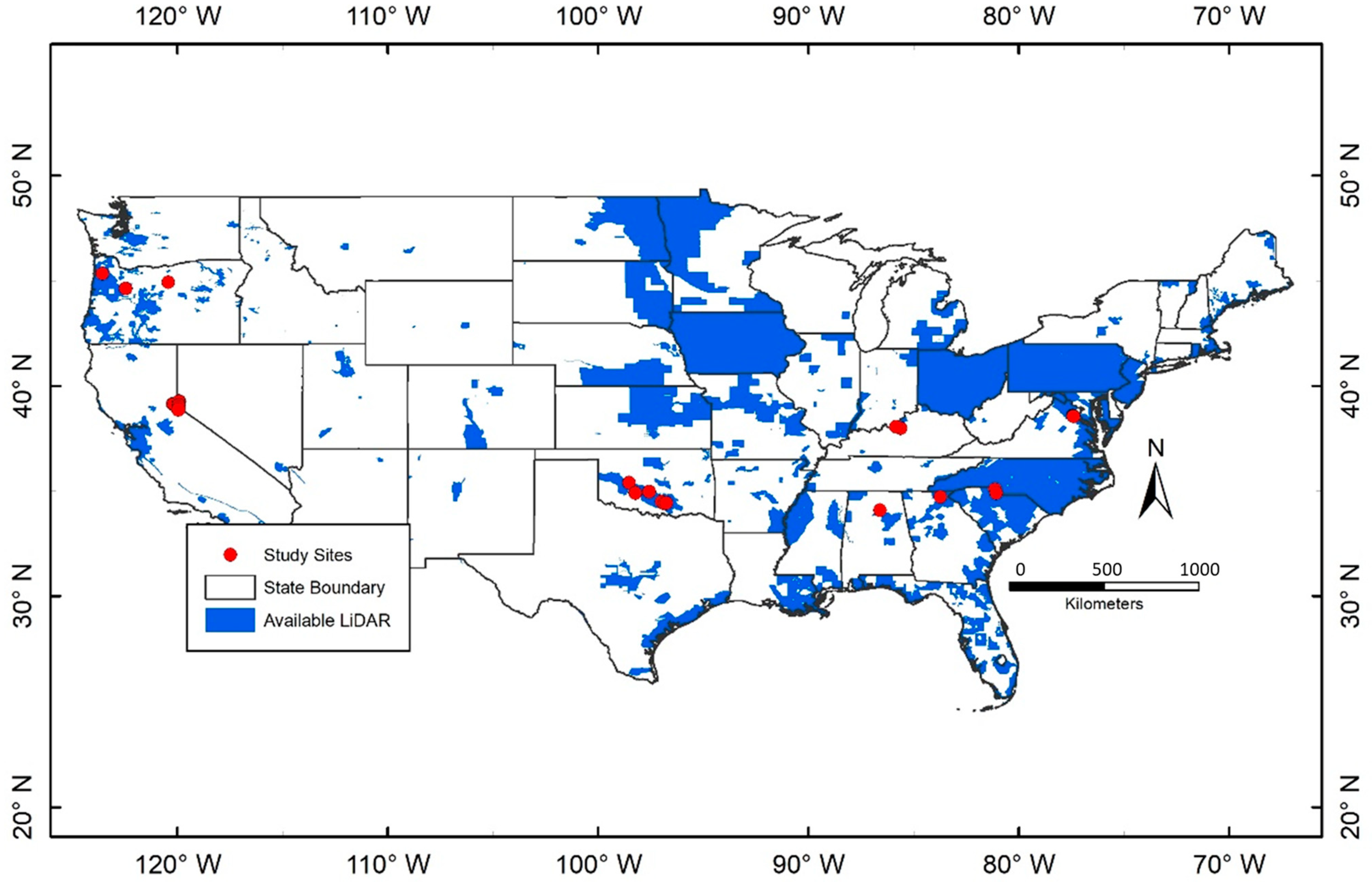

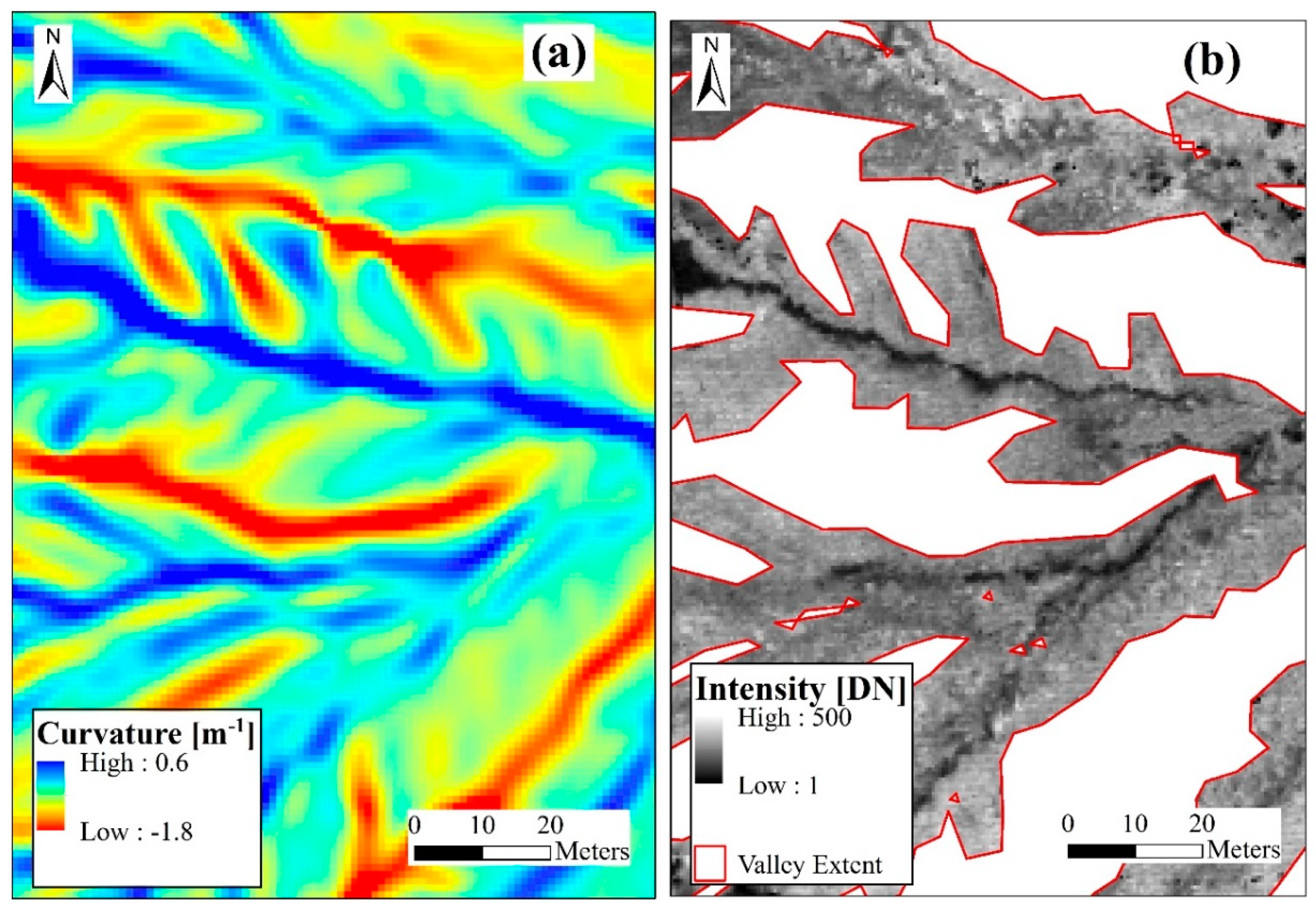

| Watershed | USGS Gage | Drainage Area (km2) | LiDAR Acquisition Date | Streamflow (m3/s) | (%) | |
|---|---|---|---|---|---|---|
| Tucca Creek, OR | 14303200 | 6.0 | 0.3 | 9 May 2010 ~13 May2010 | 0.481 ± 0.11 | 28 |
| Schafer Creek, OR | 14188610 | 5.5 | 0.4 | 9 October 2012 | 0.001 | 98 |
| Chattahoochee River, GA | 02330450 | 116.2 | 0.8 | 30 March 2010 | 4.474 | 27 |
| Ward Creek, CA (Upstream) | 10336674 | 12.0 | 0.9 | 14 August 2010 | 0.074 | 54 |
| Blue Springs Creek, AL | 02449882 | 31.4 | 0.9 | 26 February 2010 | 0.481 | 26 |
| Cedar Creek, KY | 03297800 | 31.2 | 1.0 | 21 March 2009 | 0.136 | 51 |
| Brier Creek, KY | 03302050 | 10.5 | 1.0 | 20 March 2009 | 0.037 | 47 |
| Blackwood Creek, CA | 10336660 | 28.9 | 1.0 | 20 August 2010 ~23 August 2010 | 0.103 ± 0.01 | 73 |
| 20 June 2012 ~21 June 2012 | 0.524 ± 0.01 | 40 | ||||
| Ward Creek, CA | 10336676 | 24.9 | 1.0 | 14 August 2010 | 0.057 | 72 |
| 20 June 2012 ~21 June2012 | 0.27 ± 0.01 | 43 | ||||
| South Fork Quantico Creek, VA | 01658500 | 19.4 | 1.0 | 7 April 2011 ~14 April 2011 | 0.194 ± 0.03 | 22 |
| Middle Branch Chopawamsic Creek, VA | 01659500 | 11.4 | 1.1 | 7 April 2011 | 0.096 | 28 |
| North Branch Chopawamsic Creek, VA | 01659000 | 15.0 | 1.1 | 7 April 2011 | 0.125 | 26 |
| South Branch Chopawamsic Creek, VA | 01660000 | 6.5 | 1.1 | 6 April 2011 ~7 April2011 | 0.057 ± 0.01 | 45 |
| General Creek, CA | 10336645 | 19.2 | 1.1 | 20 August 2010 ~23 August 2010 | 0.020 | 95 |
| Allison Creek, SC | 021457492 | 104.0 | 1.1 | 12 March 2012 | 0.425 | 34 |
| Wildcat Creek, SC | 021473428 | 76.6 | 1.1 | 8 March 2011 | 0.453 | 20 |
| Pennington Creek, OK | 07331295 | 85.2 | 1.3 | 22 December 2009 ~26 December 2009 | 0.580 ± 0.04 | 28 |
| Mill Creek, OK | 07331200 | 120.9 | 1.3 | 22 December 2009 | 0.255 | 26 |
| Rock Creek, OK | 07329852 | 114.3 | 1.3 | 22 December 2009 | 0.651 | 33 |
| Incline Creek, NV (Upstream) | 103366993 | 7.4 | 1.4 | 12 August 2010 | 0.040 | 74 |
| North Criner Creek, OK | 07328180 | 18.6 | 1.5 | 20 December 2009 | 0.006 | 67 |
| Incline Creek, NV | 10336700 | 17.3 | 1.5 | 12 August 2010 | 0.099 | 66 |
| Trout Creek, CA | 10336770 | 19.1 | 1.6 | 23 August 2010 | 0.156 | 54 |
| Little Washita River, OK | 07327442 | 36.5 | 1.6 | 17 December 2009 | 0.071 | 41 |
| Little Washita River, OK (Upstream) | 073274406 | 9.3 | 1.6 | 17 December 2009 | 0.015 | 45 |
| Lake Creek, OK | 07325840 | 49.4 | 1.7 | 13 December 2009 | 0.176 | 18 |
| Logan House Creek, NV | 10336740 | 5.3 | 1.9 | 16 August 2010 ~17 August 2010 | 0.002 | 87 |
| Glenbrook Creek, NV | 10336730 | 10.3 | 2.1 | 16 August 2010 ~18 August 2010 | 0.005 | 88 |
| Eagle Rock Creek, NV | 103367592 | 1.5 | 2.1 | 16 August 2010 ~17 August 2010 | 0.014 | 75 |
| Pine Creek near Clarno, OR | 14046890 | 336.9 | 2.7 | 19 May 2011 ~20 May 2011 | 0.368 | 7 |
| Watershed. | NHD Perennial Stream Length (km) | Perennial Stream Ratio (%) | Perennial Streamflow (m3/s) | (i) of Perennial Streamflow (%) | (ii) of Perennial Streamflow (%) |
|---|---|---|---|---|---|
| Chattahoochee River, GA | 167.5 | 13.50 | 1.1541 | 80 | 90 |
| Ward Creek, CA (Upstream) | 5.5 | 3.33 | 0.0037 | 100 | 97 |
| Blue Springs Creek, AL | 25.2 | 13.40 | 0.0478 | 80 | 78 |
| Cedar Creek, KY | 2.3 | 1.22 | 0.0009 | 100 | 100 |
| Brier Creek, KY | 7.1 | 4.27 | 0.0056 | 100 | 72 |
| Blackwood Creek, CA (2010) | 24.8 | 5.96 | 0.0466 | 100 | 95 |
| Blackwood Creek, CA (2012) | 24.8 | 5.95 | 0.0466 | 100 | 95 |
| Ward Creek, CA (2010) | 15.0 | 5.81 | 0.0199 | 100 | 90 |
| Ward Creek, CA (2012) | 15.0 | 5.81 | 0.0199 | 100 | 90 |
| South Fork Quantico Creek, VA | 13.2 | 14.27 | 0.0161 | 78 | 80 |
| Middle Branch Chopawamsic Creek, VA | 8.8 | 16.69 | 0.0082 | 72 | 90 |
| North Branch Chopawamsic Creek, VA | 9.5 | 11.95 | 0.0092 | 85 | 87 |
| South Branch Chopawamsic Creek, VA | 3.5 | 11.18 | 0.0017 | 88 | 99 |
| General Creek, CA | 18.1 | 8.27 | 0.0272 | 100 | 84 |
| Allison Creek, SC | 68.3 | 18.16 | 0.2551 | 68 | 51 |
| Wildcat Creek, SC | 31.6 | 17.87 | 0.0698 | 69 | 72 |
| Pennington Creek, OK | 29.9 | 29.38 | 0.0636 | 49 | 96 |
| Mill Creek, OK | 17.5 | 15.25 | 0.0259 | 75 | 96 |
| Rock Creek, OK | 9.9 | 2.26 | 0.0099 | 100 | 100 |
| Incline Creek, NV (Upstream) | 5.4 | 9.70 | 0.0036 | 93 | 100 |
| North Criner Creek, OK | 3.8 | 4.46 | 0.0020 | 100 | 77 |
| Incline Creek, NV | 15.3 | 11.42 | 0.0207 | 87 | 100 |
| Trout Creek, CA | 18.1 | 8.68 | 0.0273 | 98 | 100 |
| Little Washita River, OK | 1.6 | 2.51 | 0.0004 | 100 | 95 |
| Lake Creek, OK | 24.5 | 20.28 | 0.0455 | 64 | 59 |
| Logan House Creek, NV | 4.7 | 21.18 | 0.0028 | 62 | 73 |
| Glenbrook Creek, NV | 6.4 | 12.49 | 0.0047 | 83 | 88 |
| Eagle Rock Creek, NV | 1.8 | 11.86 | 0.0005 | 85 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Yoon, S.-K.; Choi, N. The Definition of Perennial Streams Based on a Wet Channel Network Extracted from LiDAR Data. Appl. Sci. 2023, 13, 704. https://doi.org/10.3390/app13020704
Kim S, Yoon S-K, Choi N. The Definition of Perennial Streams Based on a Wet Channel Network Extracted from LiDAR Data. Applied Sciences. 2023; 13(2):704. https://doi.org/10.3390/app13020704
Chicago/Turabian StyleKim, Seoyoung, Sun-Kwon Yoon, and Namjeong Choi. 2023. "The Definition of Perennial Streams Based on a Wet Channel Network Extracted from LiDAR Data" Applied Sciences 13, no. 2: 704. https://doi.org/10.3390/app13020704
APA StyleKim, S., Yoon, S. -K., & Choi, N. (2023). The Definition of Perennial Streams Based on a Wet Channel Network Extracted from LiDAR Data. Applied Sciences, 13(2), 704. https://doi.org/10.3390/app13020704







