Understanding the Distributions of Benthic Foraminifera in the Adriatic Sea with Gradient Forest and Structural Equation Models
Abstract
1. Introduction
2. Study Area
3. Materials and Methods
3.1. Sample Collection
3.2. Grain-Size and Geochemical Analyses
3.3. Benthic Foraminifera
3.4. Data Visualization and Analysis
3.4.1. Gradient Forest
3.4.2. Structural Equation Models
4. Results
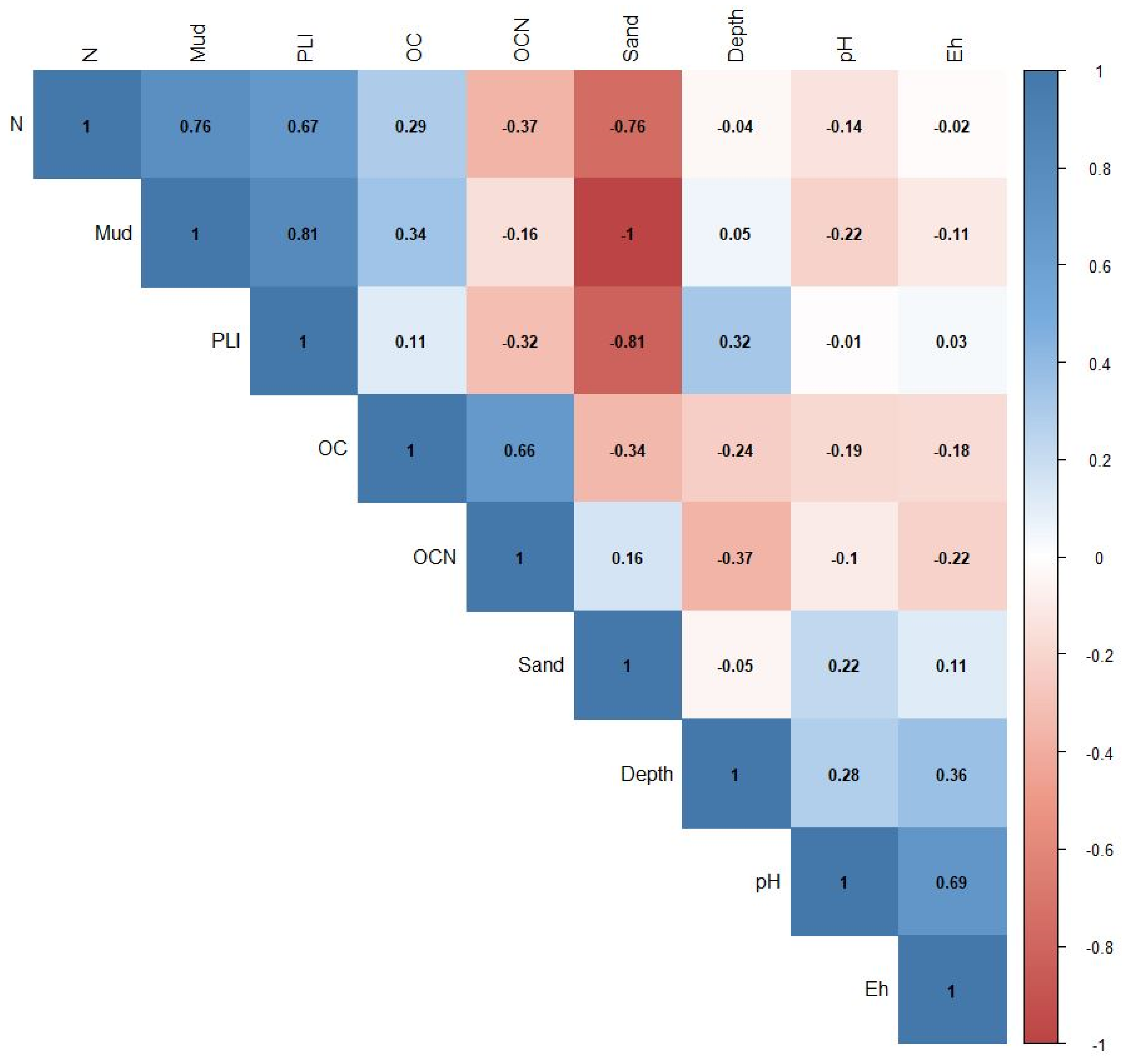
4.1. Grain-Size, Organic Matter, and Geochemistry
4.2. Benthic Foraminifera
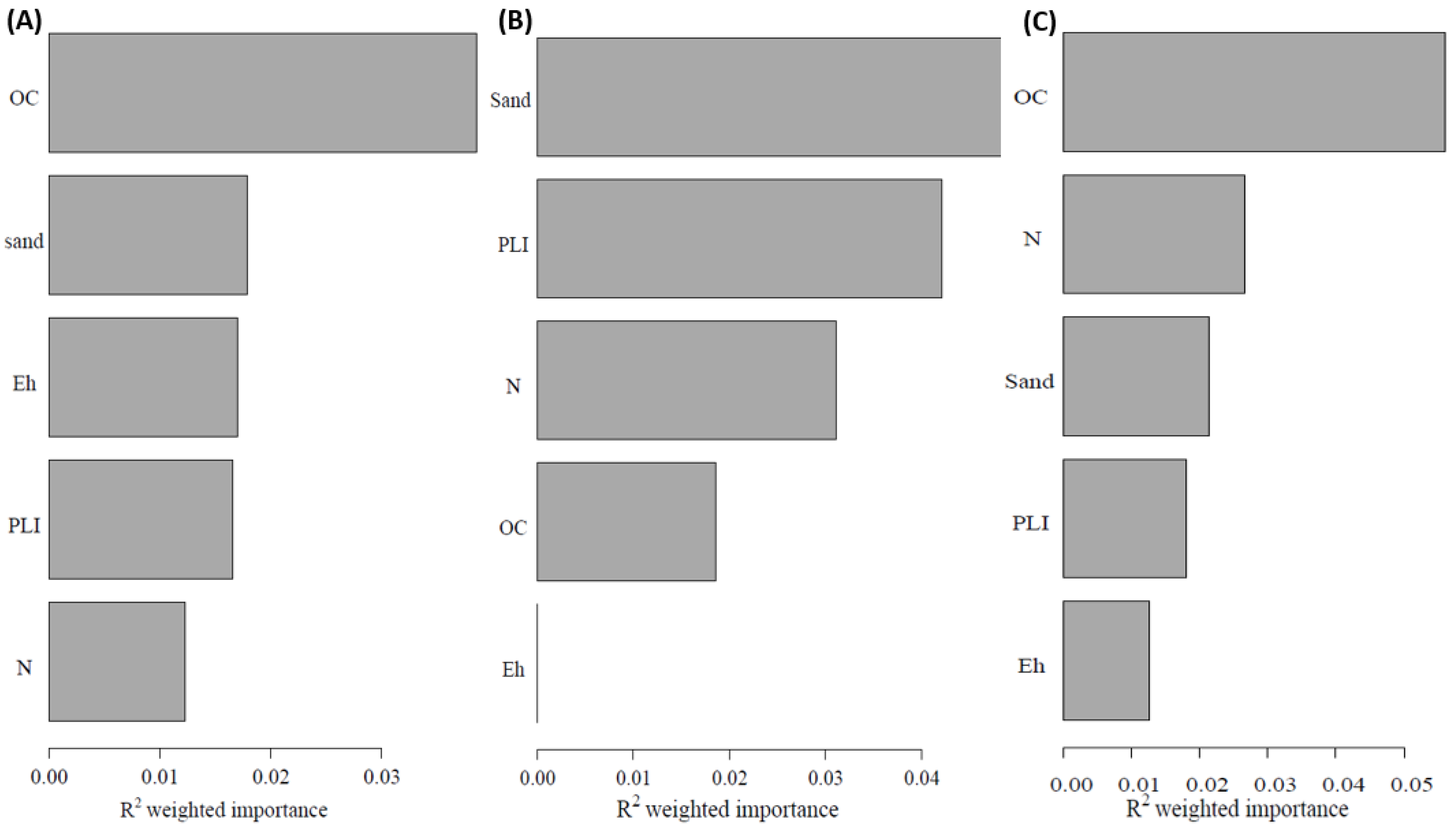
4.3. Models
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Martins, V.; Isabel, A.; Grangeia, G.; Paula, M.; Nagai, R.; Sousa, S.H.M.; Laut, L.L.M.; Dias, J.M.A.; Ferreira da Silva, E.; Rocha, F. Records of sedimentary dynamics in the continental shelf and upper slope between Aveiro–Espinho (N Portugal). J. Mar. Syst. 2012, 96, 48–60. [Google Scholar] [CrossRef]
- Martins, V.M.; Pinto, A.F.S.; Frontalini, F.; da Fonseca, M.C.M.; Terroso, D.L.; Laut, L.L.M.; Zaaboub, N.; Rodrigues, M.A.; Rocha, F. Can benthic foraminifera be used as bio-indicators of pollution in areas with a wide range of physiochemical variability? Estuar. Coast. Shelf Sci. 2016, 182, 211–225. [Google Scholar] [CrossRef]
- Raposo, D.; Clemente, I.; Figueiredo, M.; Vilar, A.; Lorini, M.L.; Frontalini, F.; Martins, M.V.A.; Belart, P.; Fontana, L.; Habib, R.; et al. Benthic foraminiferal and organic matter compounds as proxies of environmental quality in a tropical coastal lagoon: The Itaipu lagoon (Brazil). Mar. Pollut. Bull. 2018, 129, 114–125. [Google Scholar] [CrossRef] [PubMed]
- Förderer, E.M.; Rödder, D.; Langer, M.R. Global diversity patterns of larger benthic foraminifera under future climate change. Glob. Chang. Biol. 2022; 1–13, Online ahead of print. [Google Scholar]
- Reymond, C.E.; Roff, G.; Chivas, A.R.; Zhao, J.; Pandolfi, J.M. Millennium-scale records of benthic foraminiferal communities from the central Great Barrier Reef reveal spatial differences and temporal consistency. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2013, 374, 52–61. [Google Scholar] [CrossRef]
- Narayan, Y.R.; Lybolt, M.; Zhao, J.; Feng, Y.; Pandolfi, J.M. Holocene benthic foraminiferal assemblages indicate long-term marginality of reef habitats from Moreton Bay, Australia. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2015, 420, 49–64. [Google Scholar] [CrossRef]
- Bouchet, V.M.P.; Goberville, E.; Frontalini, F. Benthic foraminifera to assess the Ecological Quality Status of Italian transitional waters. Ecol. Indic. 2018, 84, 130–139. [Google Scholar] [CrossRef]
- Reymond, C.E.; Bode, M.; Renema, W.; Pandolfi, J.M. Ecological incumbency impedes stochastic community assembly in Holocene foraminifera from the Huon Peninsula, Papua New Guinea. Paleobiology 2011, 37, 670–685. [Google Scholar] [CrossRef]
- Reymond, C.E.; Uthicke, S.; Pandolfi, J.M. Tropical Foraminifera as indicators of water quality and temperature. In Proceedings of the 12th International Coral Reef Symposium, Cairns, Australia, 9–13 July 2012. [Google Scholar]
- Narayan, Y.R.; Pandolfi, J.M. Benthic foraminiferal assemblages from Moreton Bay, South-East Queensland, Australia: Applications in monitoring water and substrate quality in subtropical estuarine environments. Mar. Pollut. Bull. 2010, 60, 2062–2078. [Google Scholar] [CrossRef]
- Murray, J.W. Ecology and Applications of Benthic Foraminifera; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Frontalini, F.; Greco, M.; Di Bella, L.; Lejzerowicz, F.; Reo, E.; Caruso, A.; Cosentino, C.; Maccotta, A.; Scopelliti, G.; Nardelli, M.P.; et al. Assessing the effect of mercury pollution on cultured benthic foraminifera community using morphological and eDNA meta-barcoding approaches. Mar. Pollut. Bull. 2018, 129, 512–524. [Google Scholar] [CrossRef]
- Rostami, M.A.; Frontalini, F.; Giordano, P.; Francescangeli, F.; Martins, M.V.A.; Dyer, L.; Spagnoli, F. Testing the applicability of random forest modeling to examine benthic foraminiferal responses to multiple environmental parameters. Mar. Environ. Res. 2021, 172, 105502. [Google Scholar] [CrossRef]
- Armynot du Châtelet, E.; Francescangeli, F.; Bouchet, V.M.P.; Frontalini, F. Benthic foraminifera on transitional environments in the English Channel and the southern North Sea: A proxy for regional scale environmental and paleo-environmental characterizations. Mar. Environ. Res. 2018, 137, 37–48. [Google Scholar] [CrossRef] [PubMed]
- Armynot du Châtelet, E.A.; Francescangeli, F.; Frontalini, F. Definition of benthic foraminiferal bioprovinces in transitional environments of the Eastern English Channel and the Southern North Sea. Rev. Micropaléontologie 2018, 61, 223–234. [Google Scholar] [CrossRef]
- Narayan, G.R.; Herrán, N.; Reymond, C.E.; Shaghude, Y.W.; Westphal, H. Local Persistence of Large Benthic Foraminifera (LBF) under Increasing Urban Development: A Case Study from Zanzibar (Unguja), East Africa. J. Earth Sci. 2022, 33, 1434–1450. [Google Scholar] [CrossRef]
- Alve, E. Benthic foraminifera response to estuarine pollution. A review. J. Foraminifer. Res. 1995, 25, 190–203. [Google Scholar] [CrossRef]
- Armynot du Châtelet, E.A.; Frontalini, F.; Francescangeli, F. Significance of replicates: Environmental and paleoenvironmental studies on benthic foraminifera and testate amoebae. Micropaleontology 2017, 63, 257–274. [Google Scholar]
- Francescangeli, F.; Bouchet, V.M.P.; Trentesaux, A.; Armynot du Châtelet, E. Does elevation matter? Living foraminiferal distribution in a hyper tidal salt marsh (Canche Estuary, Northern France). Estuar. Coast. Shelf Sci. 2017, 194, 192–204. [Google Scholar] [CrossRef]
- Reymond, C.E.; Mateu-Vicens, G.; Westphal, H. Foraminiferal assemblages from a transitional tropical upwelling zone in the Golfe d’Arguin, Mauritania. Estuar. Coast. Shelf Sci. 2014, 148, 70–84. [Google Scholar] [CrossRef]
- Humphreys, A.F.; Halfar, J.; Ingle, J.C.; Manzello, D.; Reymond, C.E.; Westphal, H. Effect of seawater temperature, pH, and nutrients on the distribution and character of low abundance shallow water benthic foraminifera in the Galápagos. PLoS ONE 2018, 13, e0202746. [Google Scholar] [CrossRef]
- Francescangeli, F.; Portela, M.; Armynot du Chatelet, E.; Billon, G.; Andersen, T.J.; Bouchet, V.M.P.; Trentesaux, A. Infilling of the Canche Estuary (eastern English Channel, France): Insight from benthic foraminifera and historical pictures. Mar. Micropaleontol. 2018, 142, 1–12. [Google Scholar] [CrossRef]
- Narayan, G.R.; Reymond, C.E.; Stuhr, M.; Doo, S.; Schmidt, C.; Mann, T.; Westphal, H. Response of large benthic foraminifera to climate and local changes: Implications for future carbonate production. Sedimentology 2021, 69, 121–161. [Google Scholar] [CrossRef]
- Mojtahid, M.; Geslin, E.; Coynel, A.; Gorse, L.; Vella, C.; Davranche, A.; Zozzolo, L.; Blanchet, L.; Bénéteau, E.; Maillet, G. Spatial distribution of living (Rose Bengal stained) benthic foraminifera in the Loire estuary (western France). J. Sea Res. 2016, 118, 1–16. [Google Scholar] [CrossRef]
- Francescangeli, F.; Milker, Y.; Bunzel, D.; Thomas, H.; Norbisrath, M.; Schönfeld, J.; Schmiedl, G. Recent benthic foraminiferal distribution in the Elbe Estuary (North Sea, Germany): A response to environmental stressors. Estuar. Coast. Shelf Sci. 2021, 251, 107198. [Google Scholar] [CrossRef]
- Jorissen, F.J.; De Stigter, H.C.; Widmark, J.G.V.A. Conceptual model explaining benthic foraminiferal microhabitats. Mar. Micropaleontol. 1995, 26, 3–15. [Google Scholar] [CrossRef]
- Bouchet, V.M.P.; Frontalini, F.; Francescangeli, F.; Geslin, E.; Martins, V.; Almogi-Labin, A.; Avnaim-Katav, S.; Di Bella, L.; Cearreta, A.; Coccioni, R.; et al. Indicative value of benthic foraminifera for biomonitoring: Assignment to ecological groups of sensitivity to total organic carbon of species from European intertidal areas and transitional waters. Mar. Pollut. Bull. 2021, 164, 112071. [Google Scholar] [CrossRef]
- Murray, J.W. The niche of benthic foraminifera, critical thresholds and proxies. Mar. Micropaleontol. 2001, 41, 1–7. [Google Scholar] [CrossRef]
- Lucas, T.C.D. A translucent box: Interpretable machine learning in ecology. Ecol. Monogr. 2020, 90, e01422. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R. Species distribution models: Ecological explanation and prediction across space and time. Annu. Rev. Ecol. Evol. Syst. 2009, 40, 677–697. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Series in Statistics: Heidelberg, Germany, 2001. [Google Scholar]
- Ellis, N.; Smith, S.J.; Pitcher, C.R. Gradient Forests: Calculating importance gradients on physical predictors. Ecology 2012, 93, 156–168. [Google Scholar] [CrossRef]
- Shipley, B. Cause and Correlation in Biology: A User’s Guide to Path Analysis, Structural Equations and Causal Inference; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Jorissen, F. Benthic foraminifera from the Adriatic Sea; Principles of phenotypic variation. Utrecht Micropaleontol. Bull. 1988, 37, 174. [Google Scholar]
- Spagnoli, F.; De Marco, R.; Dinelli, E.; Frapiccini, E.; Frontalini, F.; Giordano, P. Sources and Metal Pollution of Sediments from a Coastal Area of the Central Western Adriatic Sea (Southern Marche Region, Italy). Appl. Sci 2021, 11, 1118. [Google Scholar] [CrossRef]
- Artegiani, A.; Bregant, D.; Paschini, E.; Pinardi, N.; Raicich, F.; Russo, A. The Adriatic Sea General Circulation. Part I: Air–Sea Interactions and Water Mass Structure. J. Phys. Oceanogr. 1997, 27, 1492–1514. [Google Scholar] [CrossRef]
- Vilibic, I.; Supic, N. Dense water generation on a shelf: The case of the Adriatic Sea. Ocean Dyn. 2005, 55, 403–415. [Google Scholar] [CrossRef]
- Civitarese, G.; Gacic, M.; Lipizer, M.; Eusebi Borzelli, G.L. On the impact of the Bimodal Oscillating System (BiOS) on the biogeochemistry and biology of the Adriatic and Ionian Seas (Eastern Mediterranean). Biogeosciences 2010, 7, 3987–3997. [Google Scholar] [CrossRef]
- Frascari, F.; Spagnoli, F.; Marcaccio, M.; Giordano, P. Anomalous Po river flood event effects on sediments and water column of the Northwestern Adriatic Sea. Clim. Res. 2006, 31, 151–165. [Google Scholar] [CrossRef]
- Cavaleri, L.; Stefanon, A. Bottom features due to extreme meteorological events in the North Adriatic Sea. Mar. Geol. 1980, 79, 159–170. [Google Scholar]
- Spagnoli, F.; Dinelli, E.; Giordano, P.; Marcaccio, M.; Zaffagnini, F.; Frascari, F. Sedimentological biogeochemical mineralogical facies of Northern and Central Western Adriatic Sea. J. Mar. Syst. 2014, 139, 183–203. [Google Scholar] [CrossRef]
- Syvitski, J.P.M.; Kettner, A.J. On the flux of water and sediment into the Northern Adriatic Sea. Cont. Shelf Res. 2007, 27, 296–308. [Google Scholar] [CrossRef]
- Frignani, M.; Langone, L.; Ravaioli, M.; Sorgente, D.; Alvisi, F.; Albertazzi, S. Fine sediment mass balance in the western Adriatic continental shelf over a century time scale. Mar. Geol. 2005, 222–223, 113–133. [Google Scholar] [CrossRef]
- Cattaneo, A.; Correggiari, A.; Langone, L.; Trincardi, F. The Late-Holocene Gargano subaqueous delta, Adriatic shelf: Sediment pathways and supply fluctuations. Mar. Geol. 2003, 193, 61–91. [Google Scholar] [CrossRef]
- Trincardi, F.; Asioli, A.; Cattaneo, A.; Correggiari, A.; Vigliotti, L.; Accorsi, C.A. Transgressive offshore deposits on the Central Adriatic Shelf: Architecture complexity and the record of the younger Dyas short-term event. Il Quaternario. Ital. J. Quat. Sci. 1996, 9, 753–762. [Google Scholar]
- Correggiari, A.; Trincardi, F.; Langone, L.; Roveri, M. Styles of failure in heavily sedimented highstand prodelta wedges on the Adriatic shelf. J. Sediment. Res. 2001, 71, 218–236. [Google Scholar] [CrossRef]
- Colantoni, P.; Asioli, A.; Borsetti, A.M. Evoluzione morfo-sedimentaria recente del Mare Adriatico. Atti del 9° Congresso. AIOL 1990, LM-75, 17–24. [Google Scholar]
- Colantoni, P.; Gallignani, P.; Lenaz, R. Late Pleistocene and Holocene evolution of the north Adriatic continental shelf Italy. Mar. Geol. 1979, 33, 41–50. [Google Scholar] [CrossRef]
- Cattaneo, A.; Trincardi, F. The late-Quaternary transgressive record in the Adriatic Epicontinental Sea: Basin widening and facies partitioning. In Isolated Shallow Marine Sand Bodies: Sequence Stratigraphic Analysis and Sedimentologic Interpretation; Bergman, K.M., Snedden, Eds.; SEPM SpecialPubllication: Tulsa, OK, USA, 1999; Volume 64, pp. 127–146. [Google Scholar]
- Loizeau, J.L.; Arbouille, D.; Santiago, S.; Vernet, J.P. Evaluation of a wide range laser diffraction grain size analyser for use with sediments. Sedimentology 1994, 41, 353–361. [Google Scholar] [CrossRef]
- Trentesaux, A.; Recourt, P.; Bout-Roumazeilles, V.; Tribovillard, N. Carbonate grain-size distribution in hemipelagic sediments from a laser particle sizer. J. Sediment. Res. 2001, 71, 858–862. [Google Scholar] [CrossRef]
- Leoni, L.; Menichini, M.; Saitta, M. Determination of S, Cl and F in silicate rocks by X-ray fluorescence analyses. X-ray Spectrom. 1982, 11, 156–158. [Google Scholar] [CrossRef]
- Tomlinson, D.L.; Wilson, J.G.; Harris, C.R.; Jeffrey, D.W. Problems in the assessment of heavy metal level in eastuaries and the formation of a pollution index. Helol. Meeresunters. 1980, 33, 566–575. [Google Scholar] [CrossRef]
- Surricchio, G.; Pompilio, L.; Arizzi Novelli, A.; Scamosci, E.; Marinangeli, L.; Tonucci, L.; d’Alessandro, N.; Tangari, A.C. Evaluation of heavy metals background in the Adriatic Sea sediments of Abruzzo region, Italy. Sci. Total Environ. 2019, 684, 445–457. [Google Scholar] [CrossRef]
- Loeblich, A.R.; Tappan, H. Foraminiferal Genera and Their Classification; Van Nostrand, Reinhold Co.: New York, NY, USA, 1987; Volume 2, p. 2047. [Google Scholar]
- Cimerman, F.; Langer, M.R. Mediterranean Foraminifera. In Academia Scientarium et Aritium Slovenica, Dela, Opera 30, Classis IV: Historia Naturalis; Academia Scientiarum et Artium Slovenica: Ljubljana, Slovenia, 1991. [Google Scholar]
- Fiorini, F.; Vaiani, S.C. Benthic foraminifers and transgressive-regressive cycles in the Late Quaternary subsurface sediments of the Po Plain near Ravenna (Northern Italy). Boll. Soc. Paleontol. Ital. 2001, 40, 357–403. [Google Scholar]
- Smith, P.F.; Ganesh, S.; Liu, P.A. Comparison of random forest regression and multiple linear regression for prediction in neuroscience. J. Neurosci. Methods 2013, 220, 85–91. [Google Scholar] [CrossRef]
- Grace, J.B.; Anderson, T.M.; Olff, H.; Scheiner, S.M. On the specification of structural equation models for ecological systems. Ecol. Monogr. 2010, 80, 67–87. [Google Scholar] [CrossRef]
- Pearl, J. The causal foundations of structural equation modeling. In Handbook of Structural Equation Modeling; Hoyle, R.H., Ed.; Guilford: New York, NY, USA, 2012; pp. 68–91. [Google Scholar]
- Rosseel, Y. lavaan: An R Package for Structural Equation Modeling. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef]
- van Morkhoven, F.P.C.M.; Berggren, W.A.; Edwards, A.S. Cenozoic cosmopolitan deep-water benthic foraminifera. In Bull. Cent. Rech. Explor.; Prod. Elf-Aquitaine, Mem.: Courbevoie, France, 1986; Volume 11, p. 421. [Google Scholar]
- Berggren, W.A.; Miller, K.G. Cenozoic bathyal and abyssal calcareous benthic foraminiferal zonations. Micropaleontology 1989, 35, 308–320. [Google Scholar] [CrossRef]
- Pérès, J.M.; Picard, J. Nouveau manuel de bionomie benthique de la Méditerranée. In Rec. Trav. Stat. Mar.; Endoume: Marseille, France, 1964; Volume 31, pp. 1–37. [Google Scholar]
- Sgarrella, F.; Moncharmont Zei, M. Benthic Foraminifera of the Gulf of Naples (Italy): Systematics and autoecology. Bollettino Soc. Paleontol. Ital. 1993, 32, 145–264. [Google Scholar]
- De Rijk, S.; Hayes, A.; Rohling, E.J. Eastern Mediterranean sapropel S1 interruption: An expression of the onset of climatic deterioration around 7 ka BP. Mar. Geol. 1999, 153, 337–343. [Google Scholar] [CrossRef]
- Gooday, A.J.; Lambshead, P.J.D. Influence of seasonally deposited phytodetritus on benthic foraminferal populations in the bathyal northeast Atlantic the species response. Mar. Ecol. Prog. Ser. 1989, 58, 53–67. [Google Scholar] [CrossRef]
- Gooday, A.J. Benthic foraminifera (Protista) as tools in deep-water palaeoceanography: Environmental influences on faunal characteristics. Adv. Mar. Biol. 2003, 46, 1–90. [Google Scholar]
- De Rijk, S.; Jorissen, F.; Rohling, E.J.; Troelstra, S.R. Organic flux control on bathymetric zonation of Mediterranean benthic foraminifera. Mar. Micropaleontol. 2000, 40, 151–166. [Google Scholar] [CrossRef]
- Koho, K.A.; Langezaal, A.M.; van Lith, Y.A.; Duijnstee, I.A.P.; Van der Zwaan, G.J. The influence of a simulated diatom bloom on deep-sea benthic foraminifera and the activity of bacteria: A mesocosm study. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2008, 55, 696–719. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
A. Rostami, M.; Frontalini, F.; Armynot du Châtelet, E.; Francescangeli, F.; Alves Martins, M.V.; De Marco, R.; Dinelli, E.; Tramontana, M.; Dyer, L.A.; Abraham, R.; et al. Understanding the Distributions of Benthic Foraminifera in the Adriatic Sea with Gradient Forest and Structural Equation Models. Appl. Sci. 2023, 13, 794. https://doi.org/10.3390/app13020794
A. Rostami M, Frontalini F, Armynot du Châtelet E, Francescangeli F, Alves Martins MV, De Marco R, Dinelli E, Tramontana M, Dyer LA, Abraham R, et al. Understanding the Distributions of Benthic Foraminifera in the Adriatic Sea with Gradient Forest and Structural Equation Models. Applied Sciences. 2023; 13(2):794. https://doi.org/10.3390/app13020794
Chicago/Turabian StyleA. Rostami, Masoud, Fabrizio Frontalini, Eric Armynot du Châtelet, Fabio Francescangeli, Maria Virginia Alves Martins, Rocco De Marco, Enrico Dinelli, Mario Tramontana, Lee A. Dyer, Romain Abraham, and et al. 2023. "Understanding the Distributions of Benthic Foraminifera in the Adriatic Sea with Gradient Forest and Structural Equation Models" Applied Sciences 13, no. 2: 794. https://doi.org/10.3390/app13020794
APA StyleA. Rostami, M., Frontalini, F., Armynot du Châtelet, E., Francescangeli, F., Alves Martins, M. V., De Marco, R., Dinelli, E., Tramontana, M., Dyer, L. A., Abraham, R., Bout-Roumazeilles, V., Delattre, M., & Spagnoli, F. (2023). Understanding the Distributions of Benthic Foraminifera in the Adriatic Sea with Gradient Forest and Structural Equation Models. Applied Sciences, 13(2), 794. https://doi.org/10.3390/app13020794









