Adaptive Fault-Tolerant Control of Hypersonic Vehicles with Unknown Model Inertia Matrix and System Induced by Centroid Shift
Abstract
:1. Introduction
- The topic of pose system modeling of rigid HSV with unexpected centroid shifts and actuator faults is explored in detail. In contrast to the common practice in the FTC literature for actuator failures, the challenge of the proposed FTC design manifests itself in the simultaneous variation of the system inertia matrix, the moment of eccentricity and the strong system uncertainty.
- Due to the above-mentioned coupling and unknown adverse effects, a higher-order sliding mode observer in slow-loop and the adaptive estimators are designed by the nature of eccentric moments and system uncertainties and the actuator faults instead of merging them into one item to improve the control performance of the system.
- The algorithm uses an adaptive observer and estimator, combined with adaptive feedback control, and can achieve attitude tracking without knowing the inertia matrix J, despite the existence of system inertia matrix, eccentric moment and actuator failures. In addition, the developed FTC scheme has fixed control structure and few design parameters, which is an effective method to solve similar problems.
2. Problem Formulation
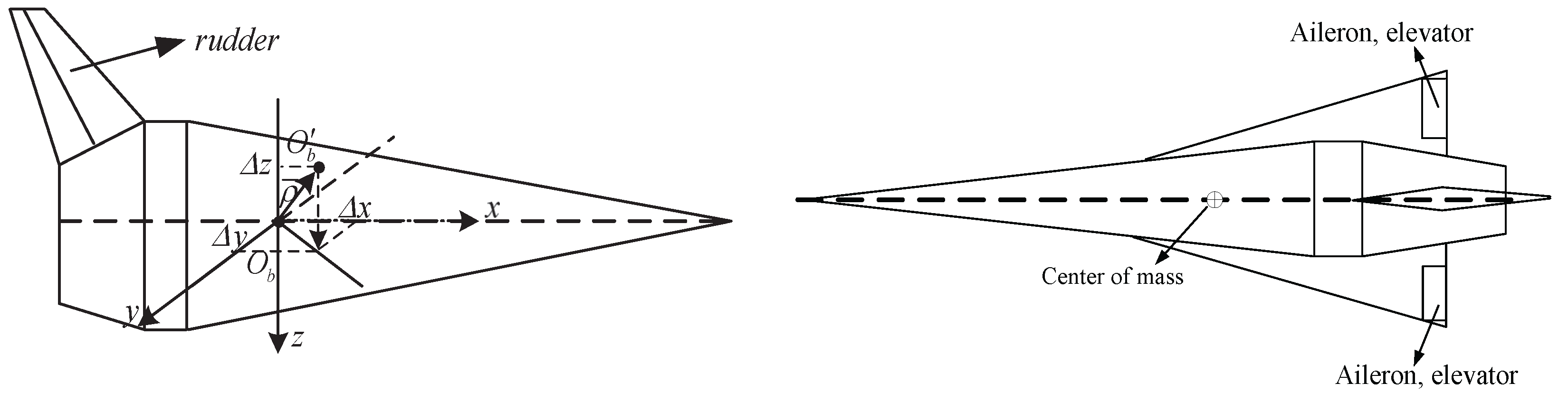
2.1. Nonlinear Attitude Model of HSV with Unexpected Centroid Shift
2.1.1. Attitude Angles Affine Nonlinear Equations of HSV with Centroid Shift
2.1.2. Attitude Angular Rates Affine Nonlinear Equations of HSV with Centroid Shift
2.2. Analysis of the Influence of the Centroid Shift on HSV Motion
2.2.1. Variation of Inertial Matrix
2.2.2. Eccentric Moment
2.2.3. The Uncertainty of the System
2.3. Actuator Faults
- Stuck or lock in place (LIP) fault: is a constant, and denotes the disturbance moment;
- Loss of effectiveness (LOE) fault: , with being a positive constant.
2.4. Control Objective
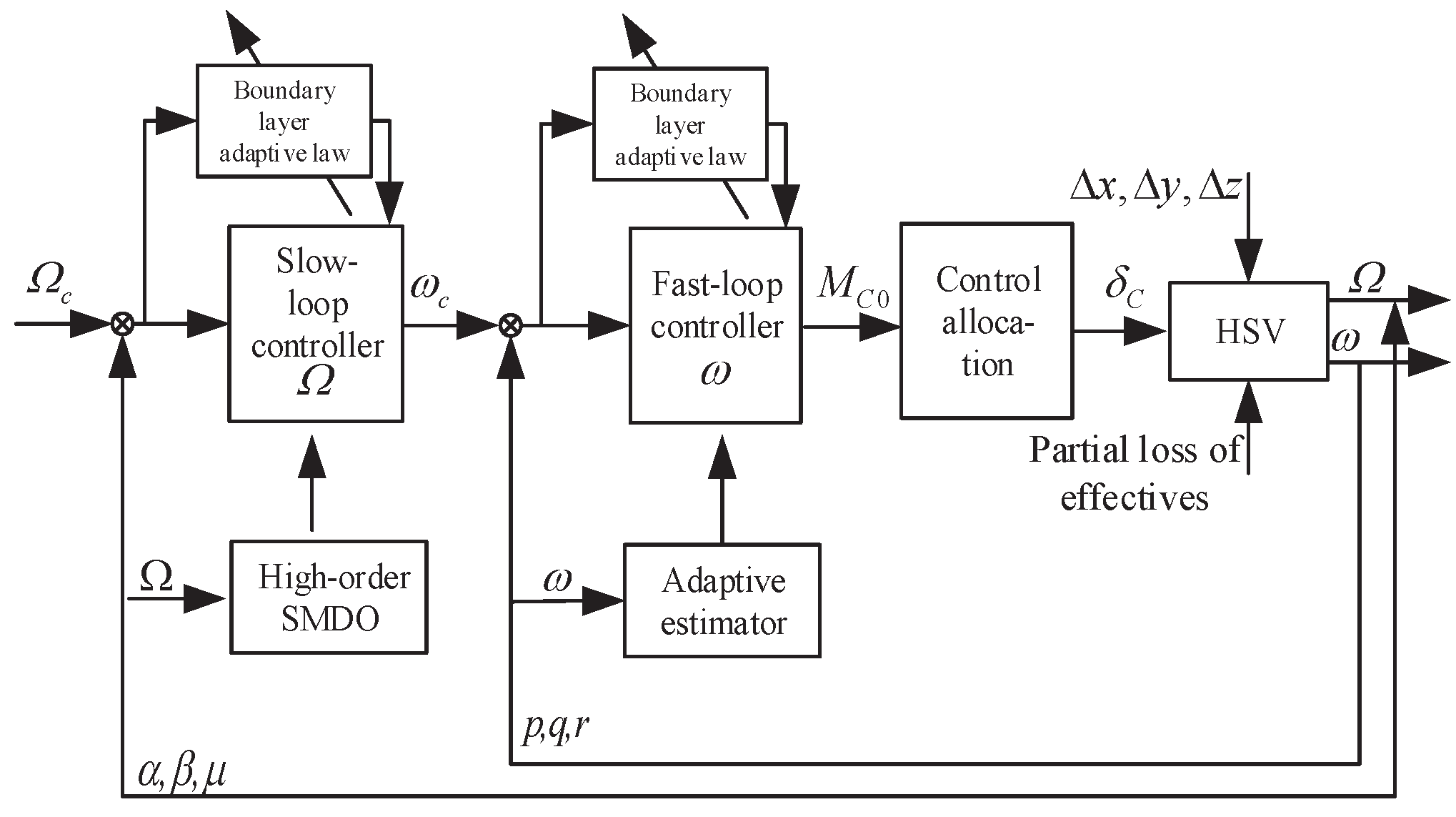
3. Fault-Tolerant Control Design for the Attitude System of HSV
3.1. Fault-Tolerant Control Design for Slow-Loop of HSV
3.1.1. Baseline Controller under Nominal Condition
- Obtaining future behaviors. To this aim, by resorting to the Taylor series expansion, the future behavior of can be predicted bywhere , , , , as shown in (A6), where is the relative degree corresponding to the system output, and r is the control order [22]. Then, the index signal is also predicted bywhere , seen in (A6). From this, the tracking error associated with the predicted behavior is derived asMoreover, by some algebraic manipulations and rearrangements of the resulting formulas, the prediction error in the performance index (15) is rewritten asFor analysis purpose, is defined as and its matrix blocks are split by
- Minimizing performance index. In order to minimize the performance index (20) through the proper , the optimal is solved by the following partial differential equation.Based on the assumption that and are reversible, it is obtained thatBy invoking (A6), the front m rows of (24) can be described as followswhere K represents the front m rows of ..Eventually, the optimal control law can be obtained as [33]
3.1.2. Fault-Tolerant Controller Design under Unexpected Centroid Shift and System Fault
- High-order sliding mode observer design. To estimate the complex perturbation , a top-order sliding mode observer is designed as follows [21]where and are the designed sliding mode surfaces based on the terminal sliding mode trick, and z denote the state of the designed observer. and are the designed system matrix, satisfying and . In addition, p and q are odd positive integers, satisfying . Furthermore, and are also the designed positive constants to regulate the estimation effect of . Finally, is the estimation of the adaptive parameter .Before analyzing the stability of the disturbance estimate error , combined with (4) and (28), the derivative of is deduced asFurthermore, by keeping the exponential reaching law and (29) in mind, can be obtained asIn what follows, the stability of the designed observer is analyzed through the following Lyapunov functionwhere is a designed parameter, satisfying , and we define that .Evaluating the time derivative of along (28) and (30) leads towhere . Furthermore, invoking , (32) can be further deduced asThe differential term in the designed higher-order sliding-mode observer is not directly obtained by using the derivative method. Moreover, according to Lemma 1, applying a higher-order sliding mode differentiator yields the corresponding derivative. Then, the states z converge to in finite time .
- According to (31), if at time , the states will arrive at the sliding mode in finite time , namelyExamining (34), it is straightforward to show that the sliding mode can be reached within the finite time .
- When the sliding mode is arrived, the convergence time of the system is up to the terminal sliding mode equationwhere denotes a terminal attractor of the system of (35). According to [21], the convergence time from when to when satisfiesIn a similar way, from the time point when move to the time point when , the convergence time is obtained as .
From this, we can obtain that the estimated value be approximated by an external perturbation in finite time . Combined with Assumption 3, we can conclude that the disturbance estimation error is bounded and can be defined as , where is a positive unknown constant. - Fault-tolerant controller design of slow-loop. Recall that Assumption 3, together with the estimate of complex disturbance from observer (28) and the baseline controller (27), the final control law and adaptive law are synthesized aswhere is applied to suppress uncertainties due to unexpected centroid shifts, external perturbations, etc. As for the adaptive term , it is applied to handle the estimation error of , where represents the estimation of .
3.2. Fault-Tolerant Control Design for Fast Loop of HSV
3.2.1. Fault-Tolerant Controller without Exact Knowledge of Inertial Matrix under Nominal Condition
- Step 1, a linear operator acting on is introduced byThen, based on (8), an intermediate vector is introduced to obtain the following transformation.
- Step 3, combined with Assumption 2, an adaptive feedback control law and its adaptive law are synthesized aswhere is a designed as positive definite symmetric matric, and represents the designed parameter, satisfying .
3.2.2. Adaptive Fault-Tolerant Controller without Exact Knowledge of Inertial Matrix
- System uncertainty. By means of the Jacobi identity of the cross product, , where are the vectors. In view of (11), we havewhere , remarked as . From this it follows thatSubsequently, its adaptation law was developed aswhere is a designed adaptive variable to estimate the unexpected effects of system uncertainties caused by centroid shift. Further, represents a designed positive definite symmetric parameter matrix, and stands for a constant coefficient, satisfying .
- Eccentric moment. For clarity, the effect of the eccentricity moment is rewritten as follows.and the corresponding adaptation law is developed aswhere is also an adaptive state to obtain the effect of the eccentricity moment. represents a design with positive definite symmetric coefficient matrix, and is also a positive parameter.
- LOE fault of actuator and external disturbance. For actuator faults and external perturbations , the complex perturbation is defined aswhere stands for the failure factor of the actuator fault, as shown in (12). Furthermore, combined with Assumption 3, the bounds of are introduced as , satisfying , where . Furthermore, an adaptive estimator is introduced aswhere is also utilized to estimate the influence of disturbance and LOE fault of actuator. and are both positive constants.
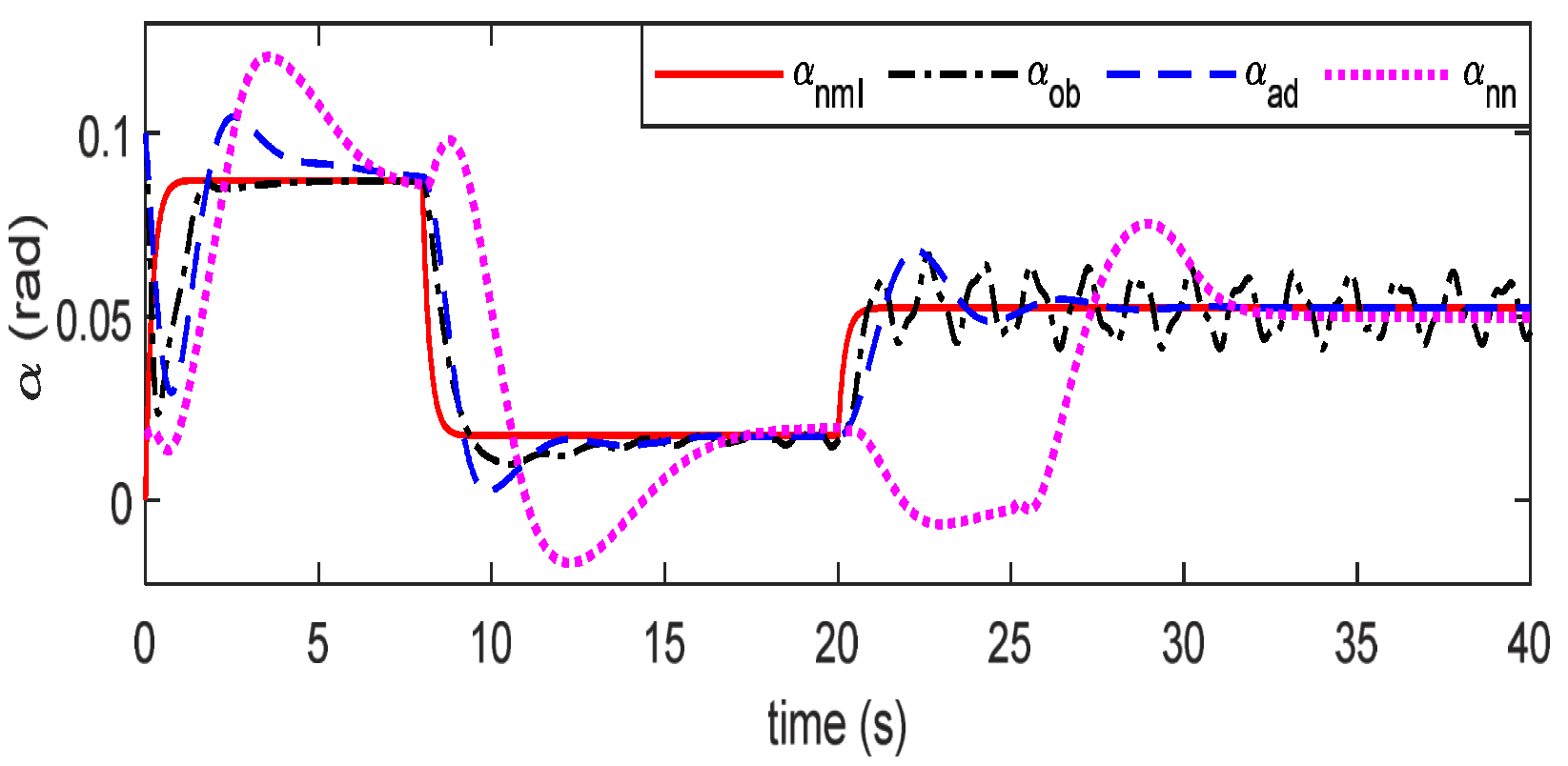
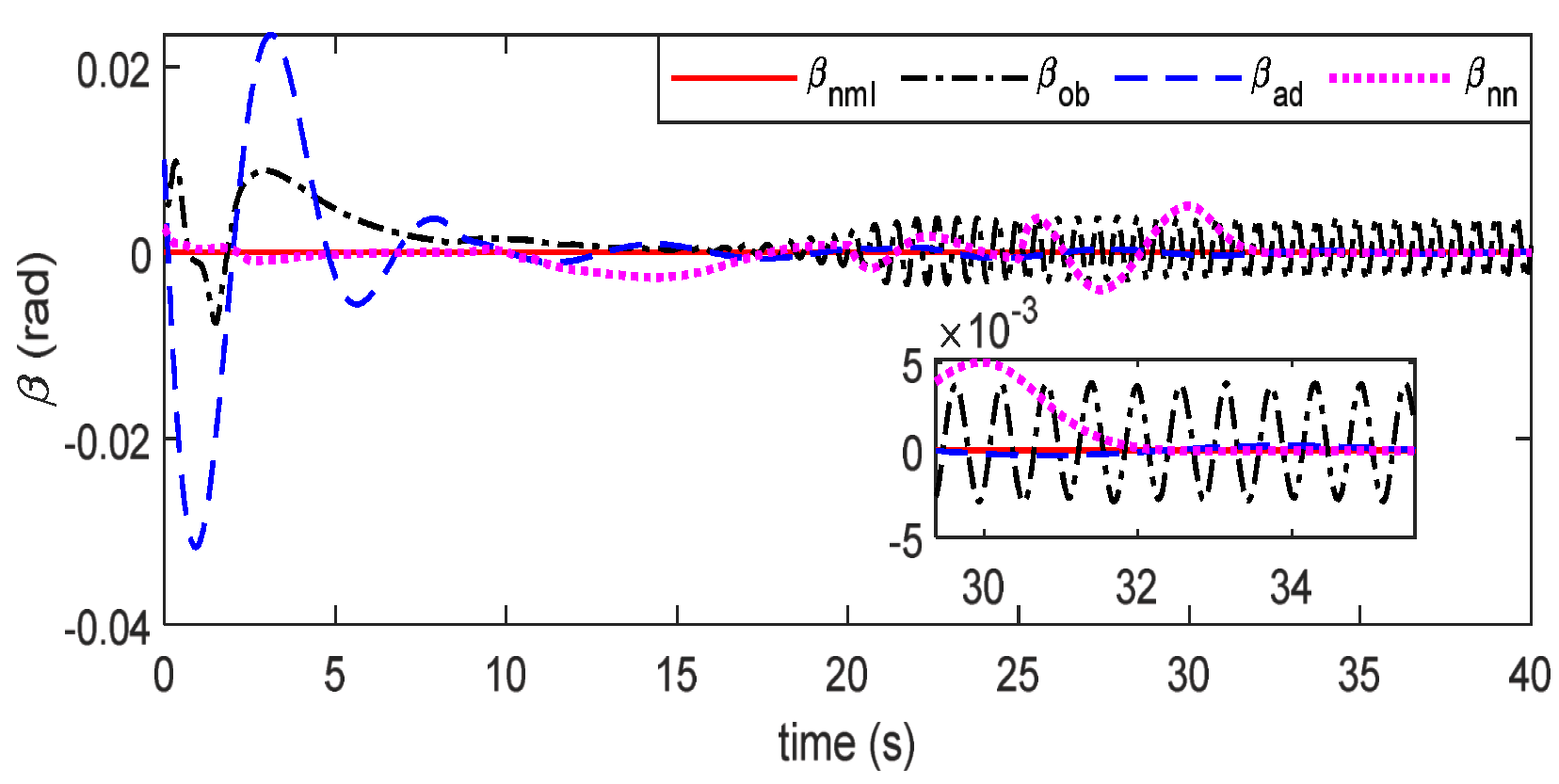
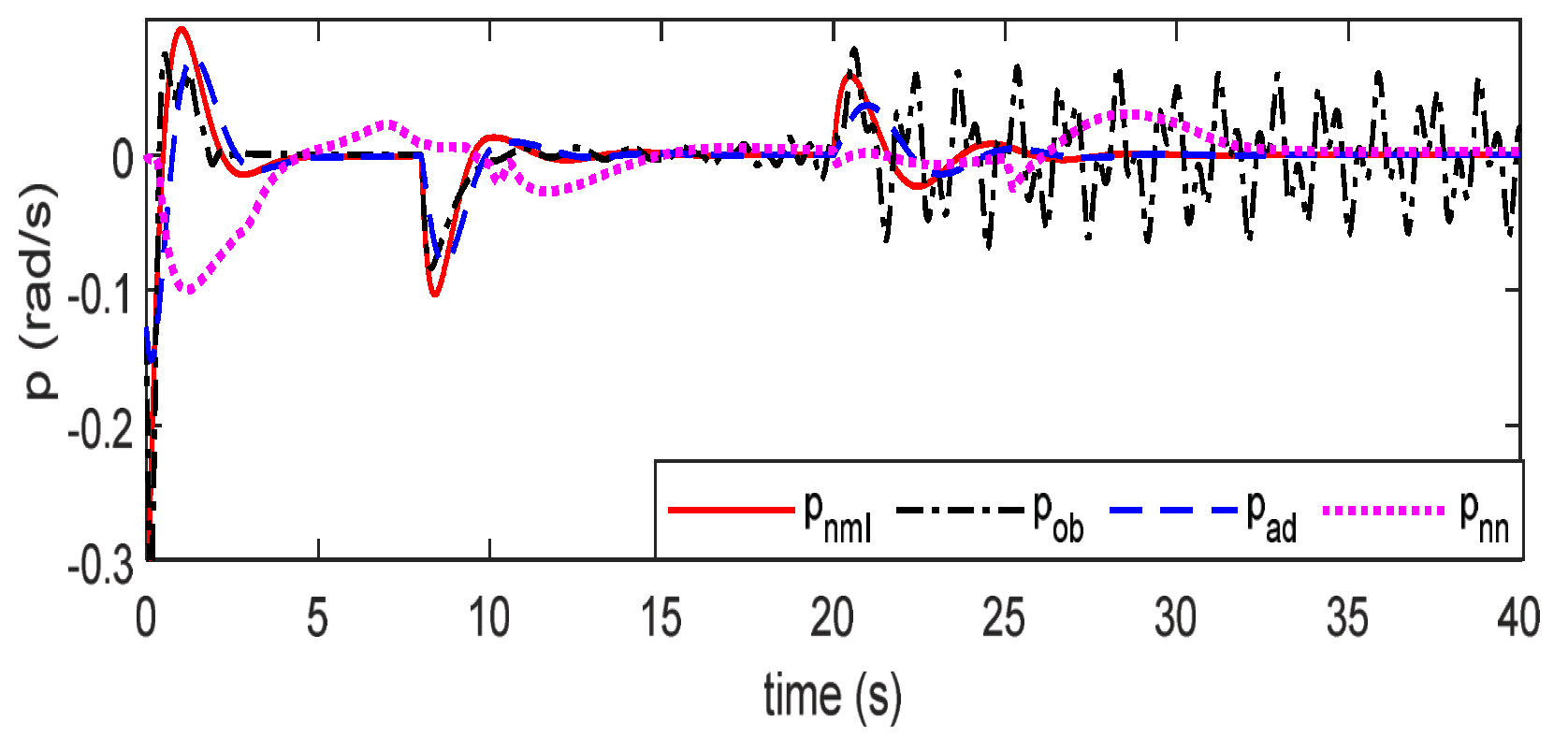
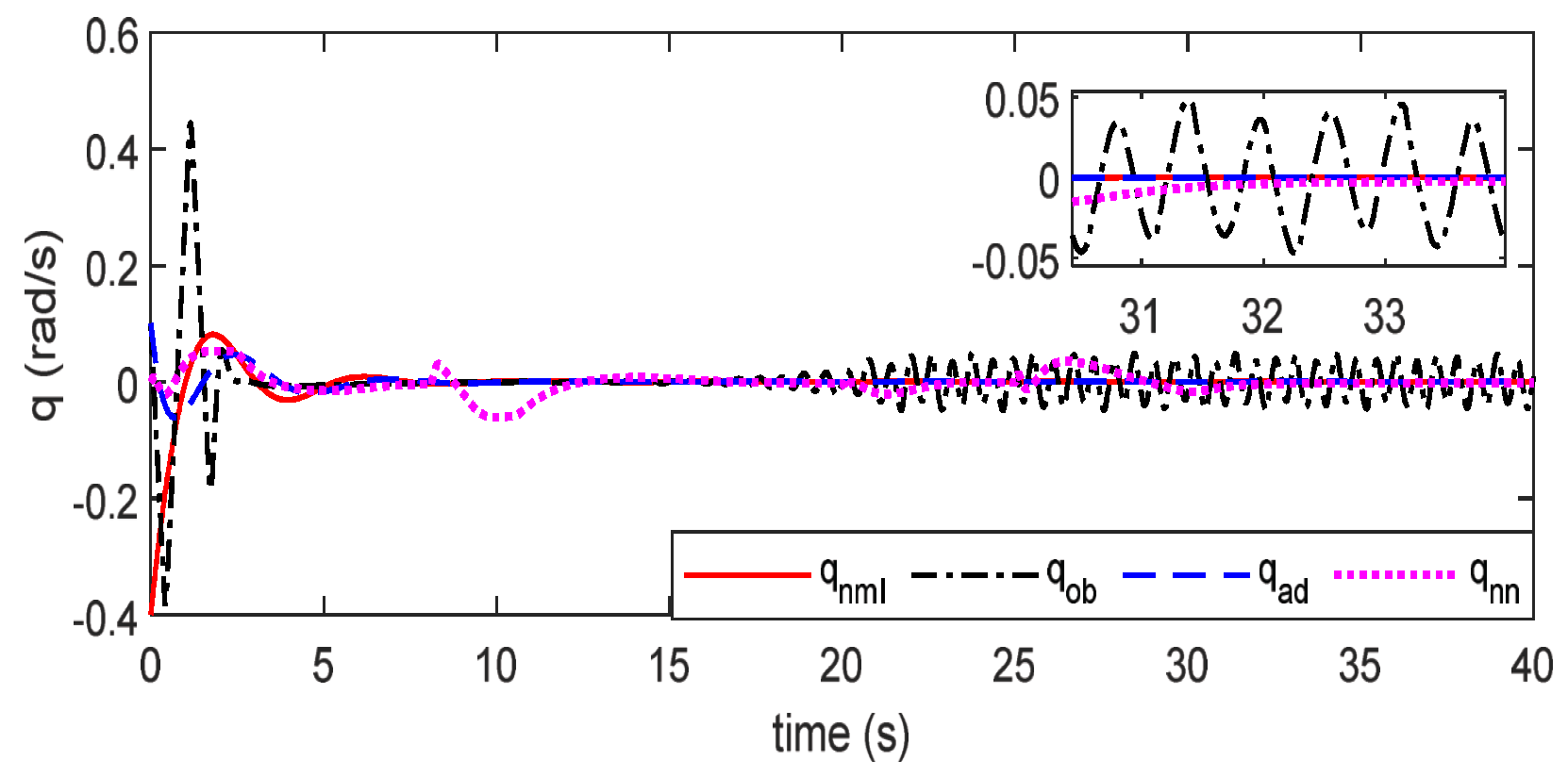
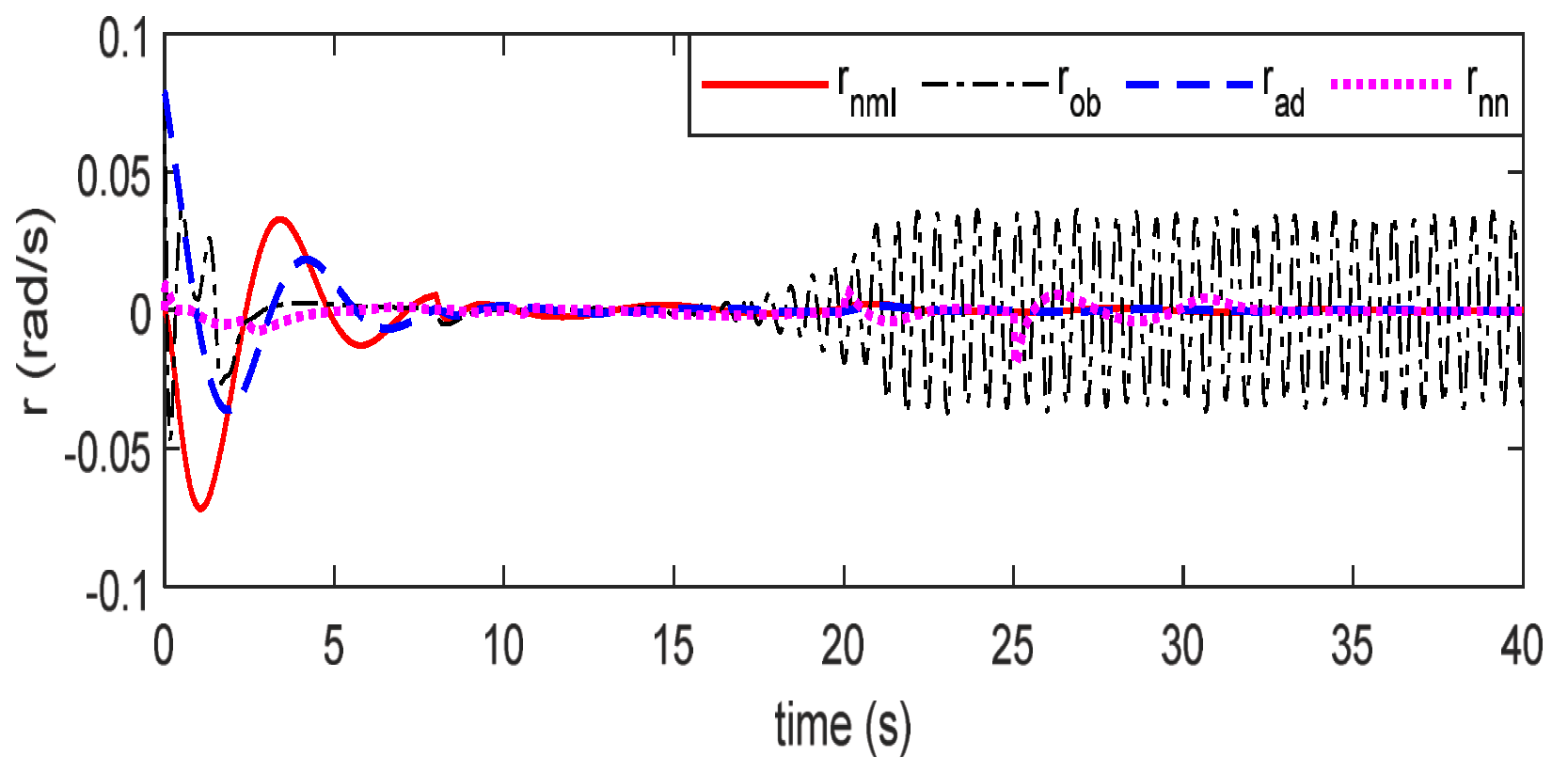
4. Simulation
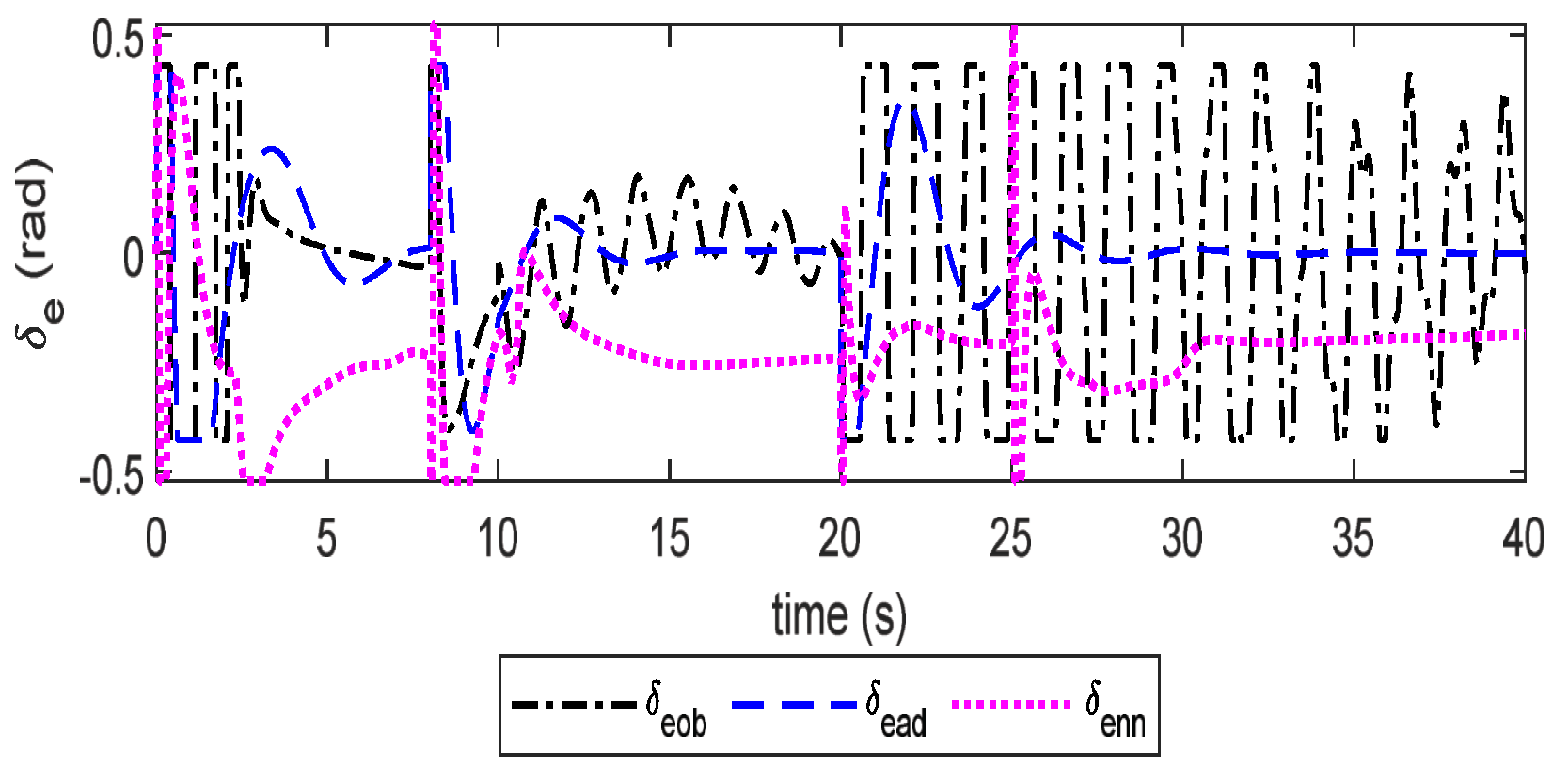


5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Tang, T.; Qi, R.Y.; Jiang, B. Adaptive nonlinear generalized predictive control for hypersonic vehicle with unknown parameters and control constraints. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 233, 510–532. [Google Scholar] [CrossRef]
- Yu, X.; Li, P.; Zhang, Y.M. The design of fixed-Time observer and finite-time fault-tolerant control for hypersonic gliding vehicles. IEEE Trans. Ind. Electron. 2018, 65, 4135–4144. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, N.; Krishnakumar, K.; Kaneshige, J.; Nespeca, P. Dynamics and adaptive control for stability recovery of damaged asymmetric aircraft. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, CO, USA, 21 August 2006; p. 6049. [Google Scholar]
- Li, J.; Gao, C.; Jing, W.; Wei, P. Dynamic analysis and control of novel moving mass flight vehicle. Acta Astronaut. 2017, 131, 36–44. [Google Scholar] [CrossRef]
- Li, J.Q.; Gao, C.S.; Li, C.Y. A survey on moving mass control technology. Aerosp. Sci. Technol. 2018, 82, 594–606. [Google Scholar] [CrossRef]
- Gasbarri, P.; Sabatini, M.; Pisculli, A. Dynamic modelling and stability parametric analysis of a flexible spacecraft with fuel slosh. Acta Astronaut. 2016, 127, 141–159. [Google Scholar] [CrossRef]
- Bacon, B.J.; Gregory, I.M. General equations of motion for a damaged asymmetric aircraft. AIAA Paper 2007-6306. In Proceedings of the 2007 AIAA Guidance, Navigation, and Control Conference, Hilton Head, SC, USA, 20 August 2007. [Google Scholar]
- Nguyen, N.; Krishnakumar, K.; Kaneshige, J.; Nespeca, P. Flight dynamics modeling and hybrid adaptive control of damaged asymmetric aircraft. J. Guid. Control. Dyn. 2008, 31, 171–186. [Google Scholar]
- Liu, Y.; Tao, G.; Joshi, S.M. Modeling and model reference adaptive control of aircraft with asymmetric damage. J. Guid. Control. Dyn. 2012, 33, 1500–1517. [Google Scholar] [CrossRef]
- Meng, Y.Z.; Jiang, B.; Qi, R.Y. Adaptive non-singular fault-tolerant control for hypersonic vehicle with unexpected centroid shift. IET Control Theory Appl. 2019, 13, 1773–1785. [Google Scholar] [CrossRef]
- Lee, T. Robust adaptive attitude tracking on SO(3) with an application to a quadrotor UAV. J. Guid. Control. Dyn. 2013, 21, 1924–1930. [Google Scholar]
- Yin, S.; Ding, S.X.; Xie, X.; Luo, H. A review on basic data-driven approaches for industrial process monitoring. IEEE Trans. Ind. Electron. 2014, 61, 6418–6428. [Google Scholar] [CrossRef]
- Xiao, B.; Yin, S.; Hao, H. Reconfigurable tolerant control of uncertain mechanical systems with actuator faults: A sliding mode observer-based approach. IEEE Trans. Control Syst. Technol. 2018, 26, 1249–1258. [Google Scholar] [CrossRef]
- Bounemeur, A.; Chemachema, M.; Essounbouli, N. Indirect adaptive fuzzy fault-tolerant tracking control for MIMO nonlinear systems with actuator and sensor failures. ISA Trans. 2018, 79, 45–61. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.; Niu, G.; Wang, C. Spacecraft attitude fault-tolerant control based on iterative learning observer and control allocation. Aerosp. Sci. Technol. 2018, 75, 245–253. [Google Scholar] [CrossRef]
- Xu, D.Z.; Jiang, B.; Shi, P. Robust NSV fault-tolerant control system design against actuator faults and control surface damage under actuator dynamics. IEEE Trans. Ind. Electron. 2015, 62, 5919–5928. [Google Scholar] [CrossRef]
- Jiang, B.; Gao, Z.; Shi, P.; Xu, Y. Adaptive fault-tolerant tracking control of near-space vehicle using takagi-sugeno fuzzy models. IEEE Trans. Fuzzy Syst. 2010, 18, 1000–1007. [Google Scholar] [CrossRef]
- Yin, S.; Yang, H.; Gao, H.; Qiu, J.; Kaynak, O. An adaptive NN-based approach for fault-tolerant control of nonlinear time-varying delay systems with unmodeled dynamics. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 1902–1913. [Google Scholar] [CrossRef]
- He, J.; Qi, R.; Jiang, B.; Qian, J. Adaptive output feedback fault-tolerant control design for hypersonic flight vehicles. J. Frankl. Inst. 2015, 352, 1811–1835. [Google Scholar] [CrossRef]
- Zhang, A.; Hu, Q.L.; Friswell, M.I. Finite-time fault tolerant attitude control for over-activated spacecraft subject to actuator misalignment and faults. Iet Control Theory Appl. 2013, 7, 2007–2020. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Yu, J. Disturbance observer-based adaptive sliding mode control for near-space vehicles. Nonlinear Dyn. 2015, 82, 1671–1682. [Google Scholar] [CrossRef]
- Chen, W.H.; Ballance, D.J.; Gawthrop, P.J. Brief optimal control of nonlinear systems: A predictive control approach. Automatica 2003, 39, 633–641. [Google Scholar] [CrossRef] [Green Version]
- Chaturvedi, N.A.; Bernstein, D.S.; Ahmed, J.; Bacconi, F.; McClamroch, N.H. Globally convergent adaptive tracking of angular velocity and inertia identification for a 3-DOF rigid body. IEEE Trans. Control. Syst. Technol. 2006, 14, 841–853. [Google Scholar] [CrossRef] [Green Version]
- Hu, Q.; Shao, X.; Guo, L. Adaptive fault-tolerant attitude tracking control of spacecraft with prescribed performance. IEEE/ASME Trans. Mechatron. 2018, 23, 331–341. [Google Scholar] [CrossRef]
- Meng, Y.Z.; Jiang, B.; Qi, R.Y. Modeling and control of hypersonic vehicle dynamic under centroid shift. Adv. Mech. Eng. 2018, 10, 1–21. [Google Scholar] [CrossRef]
- Zong, Q.; Zeng, F.L.; Zhang, B.X.; You, M. Modeling and Model Verification of Hypersonic Vehicle; Science China Press: Beijing, China, 2016. [Google Scholar]
- Yang, H.; Jiang, B.; Liu, H.H.; Yang, H.; Zhang, Q. Attitude synchronization for multiple 3-DOF helicopters with actuator faults. IEEE/ASME Trans. Mechatron. 2019, 24, 597–608. [Google Scholar] [CrossRef]
- Shaughnessy, J.D.; Pinckney, S.Z.; McMinn, J.D. Hypersonic Vehicle Simulation Model: Winged-Cone Configuration; NASA TM-102610; NASA Langley Reserch Center: Hamption, VA, USA, 1990; pp. 1–140.
- Xu, B.; Qi, R.; Jiang, B. Adaptive fault-tolerant control for HSV with unknown control direction. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 2743–2758. [Google Scholar] [CrossRef]
- Liu, Y.H.; Huang, L.; Xiao, D. Adaptive dynamic surface control for uncertain nonaffine nonlinear systems. Int. J. Robust Nonlinear Control 2017, 27, 535–546. [Google Scholar] [CrossRef]
- Xian, B.; Zhang, Y. Continuous asymptotically tracking control for a class of nonaffine-in-input system with non-vanishing disturbance. IEEE Trans. Autom. Control 2017, 62, 6019–6025. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Du, Y.L. Study of Nonlinear Adaptive Attitude and Trajectory Control for Near Space Vehicles; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2010. [Google Scholar]
- Lai, G.; Liu, Z.; Zhang, Y.; Chen, C.P. Adaptive position/attitude tracking control of aerial robot with unknown inertial matrix based on a new robust neural identifier. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 18–31. [Google Scholar] [CrossRef]
- Lee, D. Nonlinear disturbance observer-based robust control for spacecraft formation flying. Aerosp. Sci. Technol. 2018, 76, 82–90. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, H.; Meng, Y. Adaptive Fault-Tolerant Control of Hypersonic Vehicles with Unknown Model Inertia Matrix and System Induced by Centroid Shift. Appl. Sci. 2023, 13, 830. https://doi.org/10.3390/app13020830
Ye H, Meng Y. Adaptive Fault-Tolerant Control of Hypersonic Vehicles with Unknown Model Inertia Matrix and System Induced by Centroid Shift. Applied Sciences. 2023; 13(2):830. https://doi.org/10.3390/app13020830
Chicago/Turabian StyleYe, Hui, and Yizhen Meng. 2023. "Adaptive Fault-Tolerant Control of Hypersonic Vehicles with Unknown Model Inertia Matrix and System Induced by Centroid Shift" Applied Sciences 13, no. 2: 830. https://doi.org/10.3390/app13020830
APA StyleYe, H., & Meng, Y. (2023). Adaptive Fault-Tolerant Control of Hypersonic Vehicles with Unknown Model Inertia Matrix and System Induced by Centroid Shift. Applied Sciences, 13(2), 830. https://doi.org/10.3390/app13020830





