Study on the Median Opening Length of a Freeway Work Zone Based on a Naturalistic Driving Experiment
Abstract
:1. Introduction
2. Methodology
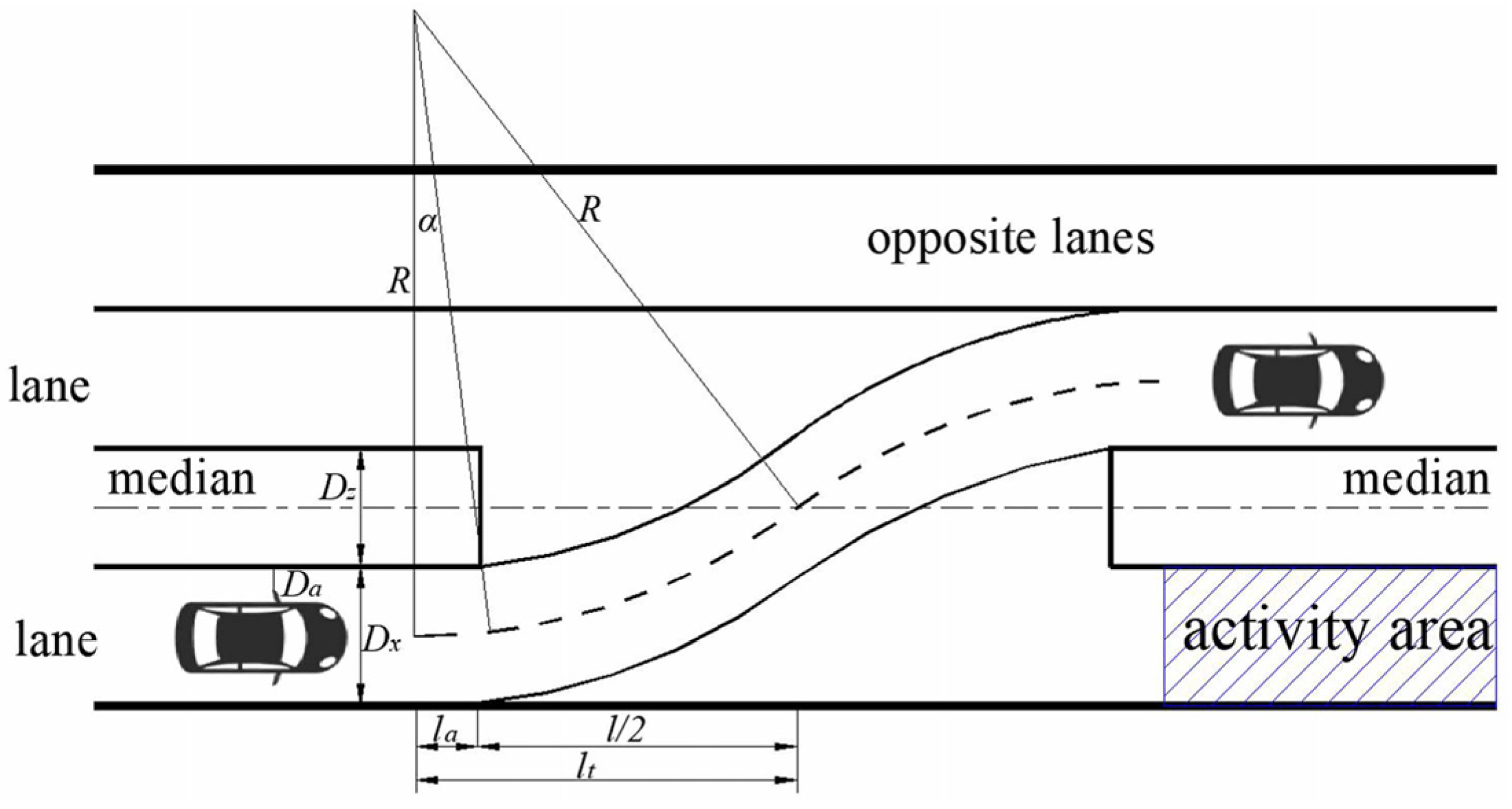
2.1. Length of Median Opening and Its Influencing Factors
2.2. Calculation of Driving Workload
3. Experiment
3.1. Participants and Vehicles
3.2. Instruments and Equipment
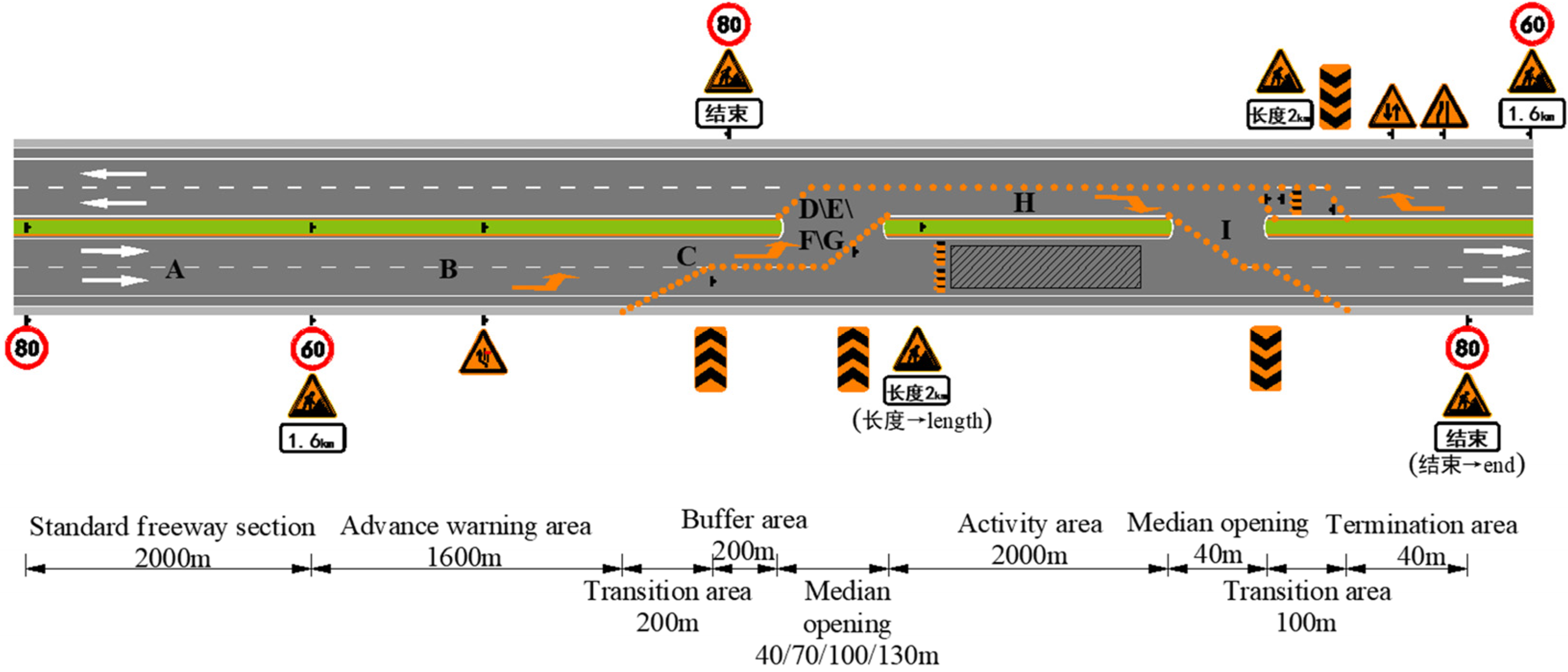
3.3. Experimental Road
- Advance warning area (1600 m), composed of two lanes in one direction with a lane width of 3.75 m.
- Upstream transition area (200 m), transitioning from two lanes to one lane.
- Buffer area (200 m), composed of one lane in one direction with a lane width of 4.25 m.
- Median opening: According to the calculation results, the median opening length should be 40~130 m. Combined with the actual crossover work area of the freeway expansion project, the commonly used lengths of 40 m, 70 m, 100 m and 130 m were selected as the median opening lengths of the experimental road, with an interval length of 30 m; this area was composed of one lane in one direction, with a lane width of 4.25 m.
- Activity area (2000 m), composed of one lane in one direction with a lane width of 4.25 m, separated from the opposite lane using traffic cones.
- The downstream median opening was 40 m long, the downstream transition area was 100 m long and the termination area was 40 m long; after the vehicle crosses through the work zone, the two-lane speed limit of 80 km/h is restored.
3.4. Experimental Procedures
3.5. Data Analysis
4. Results and Descriptive Analysis
4.1. Speed
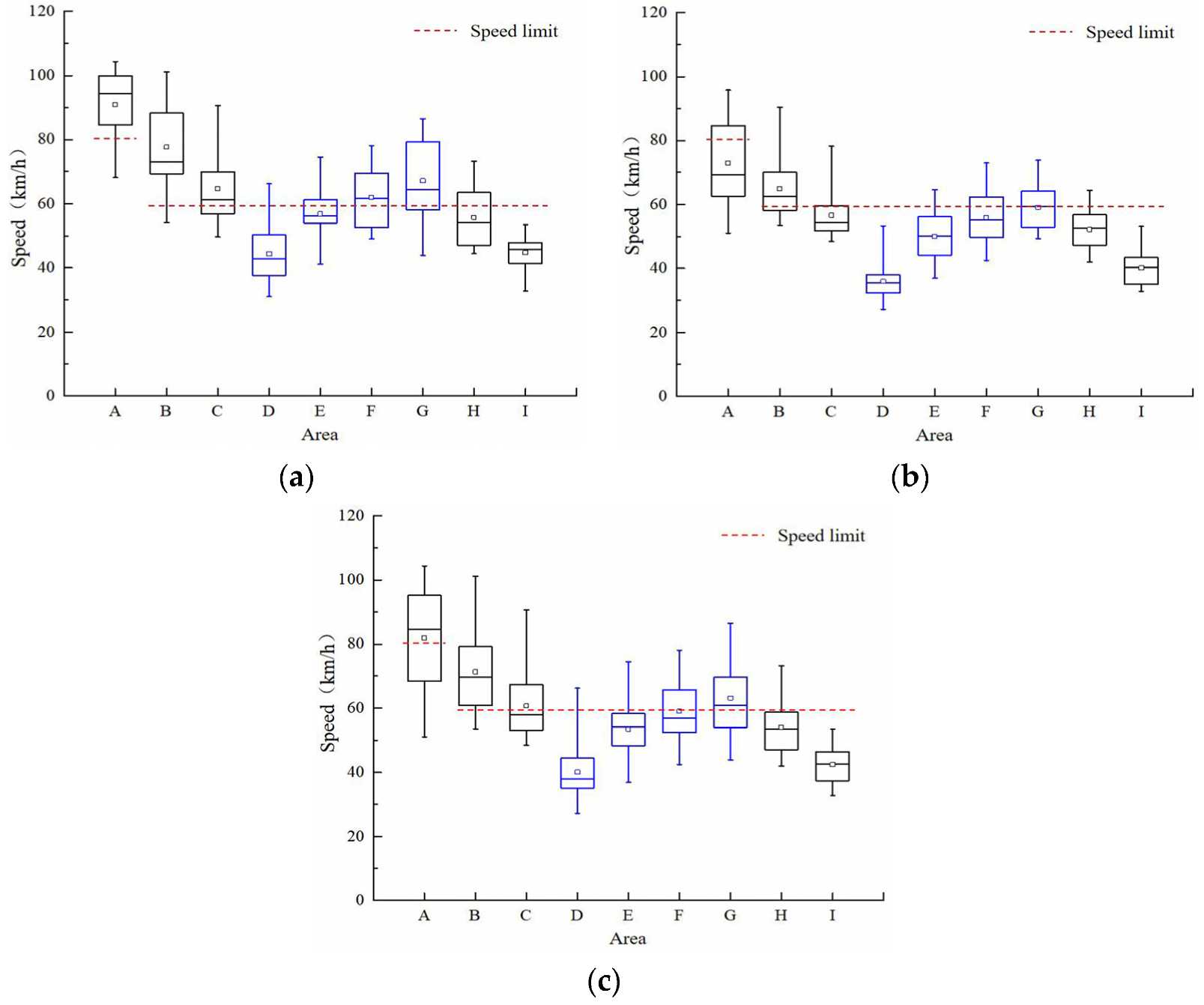
4.1.1. Speed Distribution in the Work Zone
4.1.2. Influence of Median Opening Length on Speed
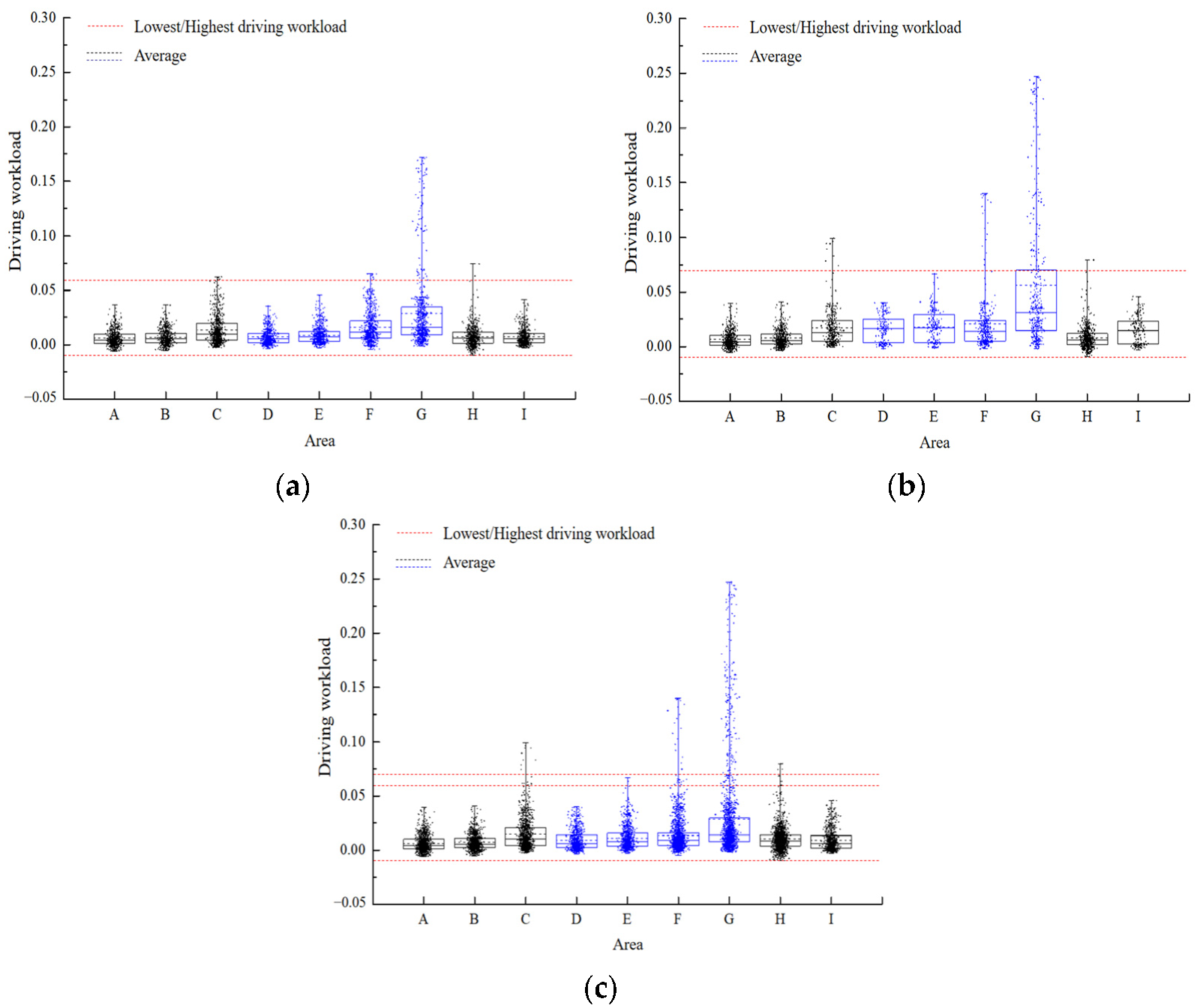
4.2. Driving Workload
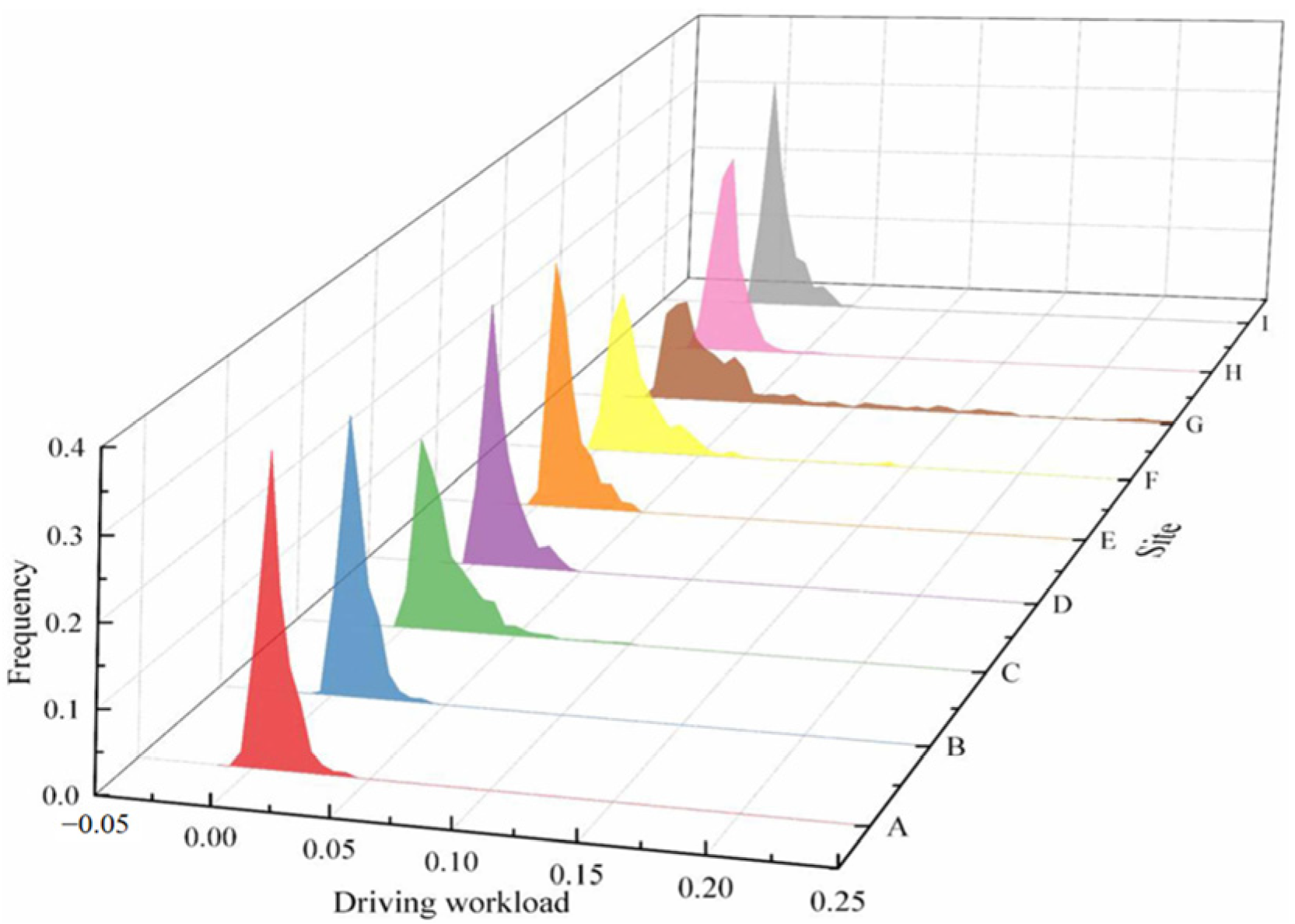
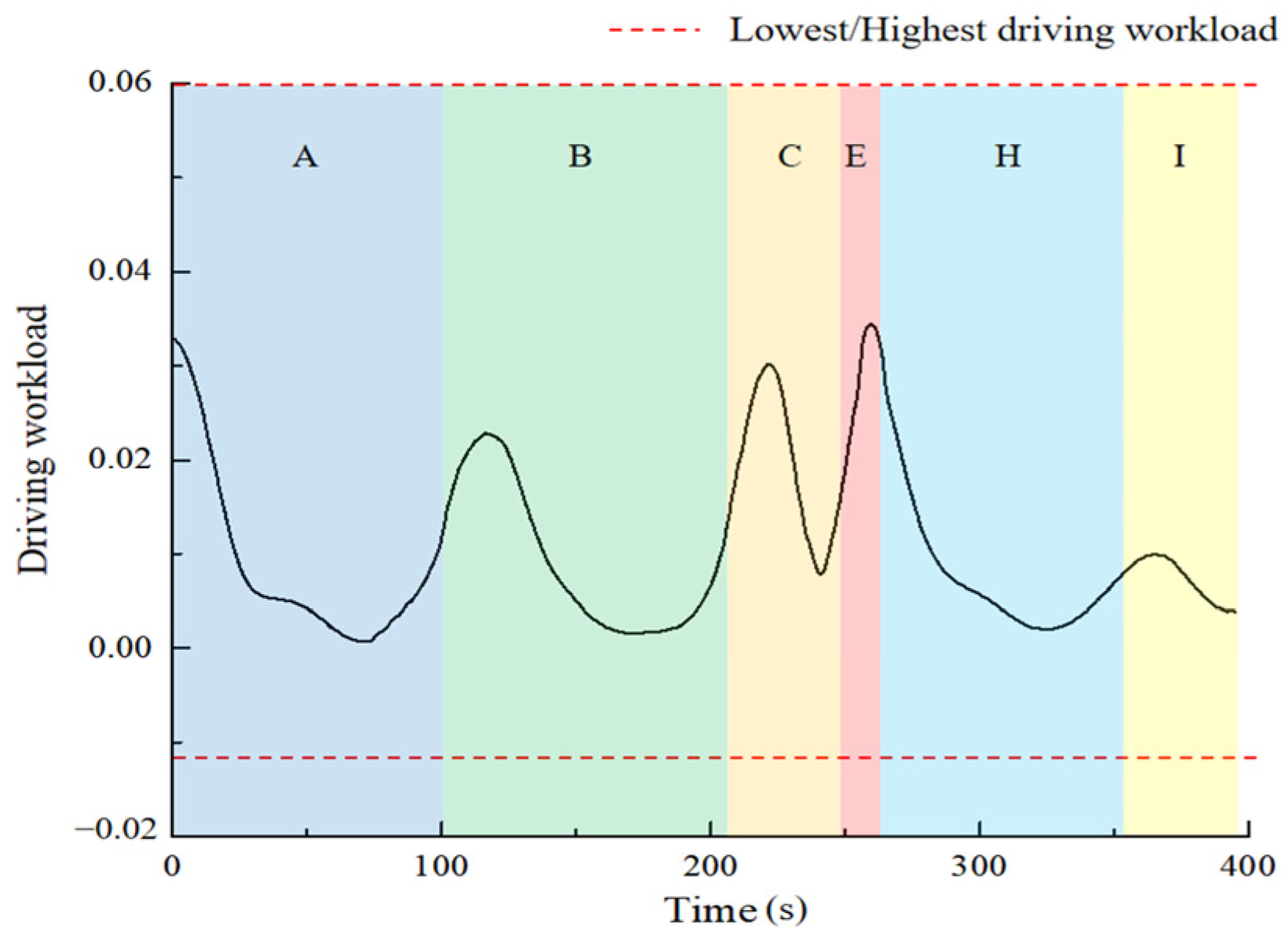
4.2.1. Driving Workload Distribution in the Work Zone
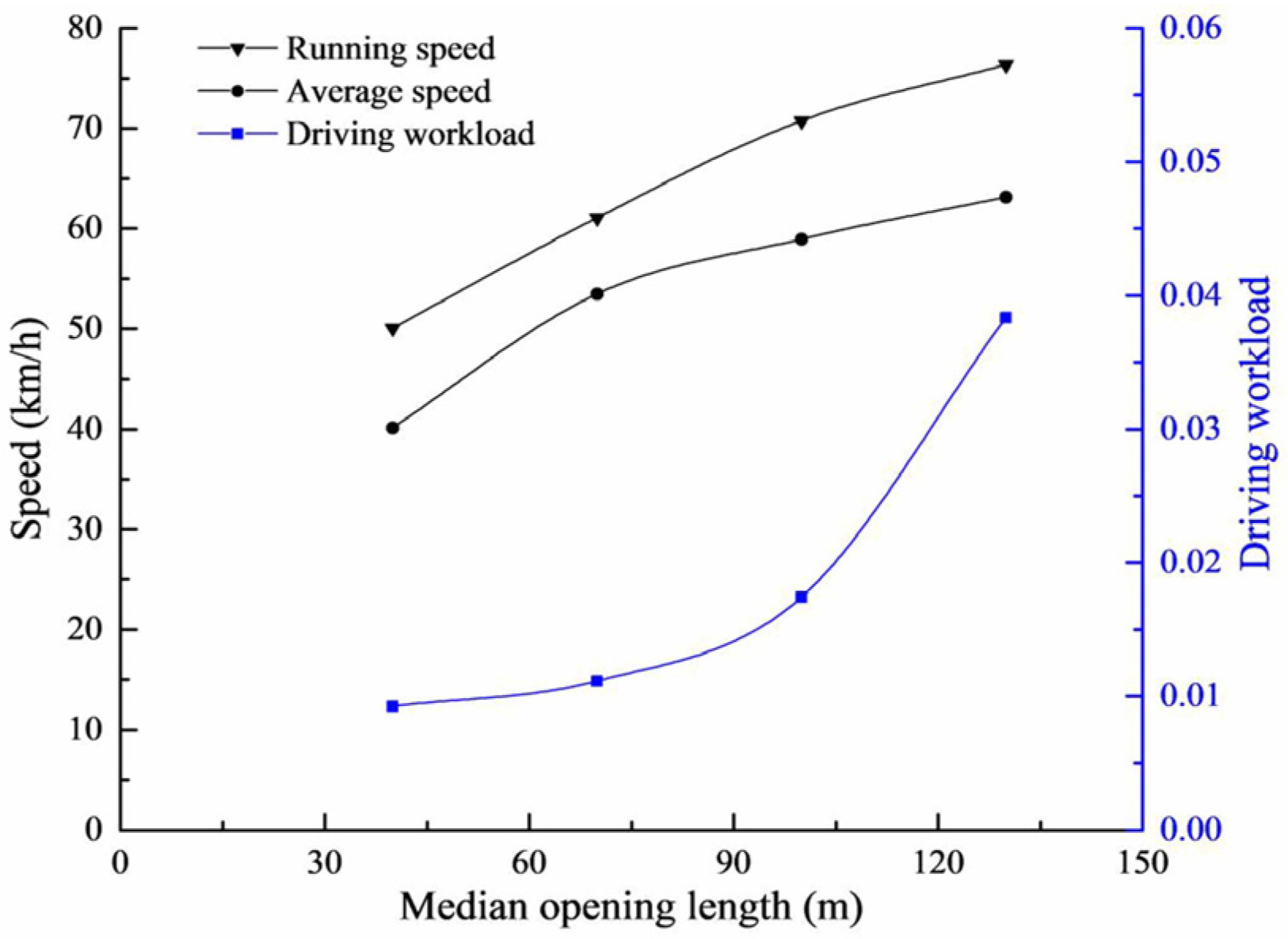
4.2.2. Influence of the Median Opening Length on the Driving Workload
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thapa, R.; Codjoe, J.; Osafo, A. Survey of work zone practices and validation of highway capacity manual work zone capacity model. Transp. Res. Rec. 2021, 2675, 1083–1091. [Google Scholar] [CrossRef]
- Weng, J.; Qiang, M. Estimating capacity and traffic delay in work zones: An overview. Transp. Res. C-Emer. 2013, 35, 34–45. [Google Scholar] [CrossRef]
- Khattak, A.J.; Khattak, A.J.; Council, F.M. Effects of work zone presence on injury and non-injury crashes. Accident Anal. Prev. 2002, 34, 19–29. [Google Scholar] [CrossRef]
- Cheng, Y.; Parker, S.T.; Ran, B.; Noyce, D.A. Enhanced analysis of work zone safety through integration of statewide crash and lane closure system data. Transp. Res. Rec. 2012, 2291, 17–25. [Google Scholar] [CrossRef] [Green Version]
- Work Zone Facts and Statistics Retrieved. Available online: https://ops.fhwa.dot.gov/wz/resources/factsstats.htm (accessed on 20 October 2022).
- Chen, E.; Tarko, A.P. Modeling safety of highway work zones with random parameters and random effects models. Anal. Methods Accid. R. 2014, 1, 86–95. [Google Scholar] [CrossRef]
- Zhang, K.; Hassan, M.; Yahaya, M.; Yang, S. Analysis of work-zone crashes using the ordered probit model with factor analysis in Egypt. J. Adv. Transp. 2018, 2018, 1784. [Google Scholar] [CrossRef]
- Kummetha, V.C.; Kondyli, A.; Chrysikou, E.G.; Schrock, S.D. Safety analysis of work zone complexity with respect to driver characteristics—A simulator study employing performance and gaze measures. Accident Anal. Prev. 2020, 142, 105566. [Google Scholar] [CrossRef]
- Nasrollahzadeh, A.A.; Sof, A.R.; Ravani, B. Identifying factors associated with roadside work zone collisions using machine learning techniques. Accident Anal. Prev. 2021, 158, 106203. [Google Scholar] [CrossRef]
- Osman, M.; Paleti, R.; Mishra, S. Analysis of passenger-car crash injury severity in different work zone configurations. Accident Anal. Prev. 2018, 111, 161–172. [Google Scholar] [CrossRef]
- Torre, F.L.; Domenichini, L.; Nocentini, A. Effects of stationary work zones on motorway crashes. Saf. Sci. 2017, 92, 148–159. [Google Scholar] [CrossRef]
- Meng, Q.; Weng, J. Evaluation of rear-end crash risk at work zone using work zone traffic data. Accident Anal. Prev. 2010, 43, 1291–1300. [Google Scholar] [CrossRef]
- Hou, G.; Chen, S. An improved cellular automaton model for work zone traffic simulation considering realistic driving behavior. J. Phys. Soc. Jpn. 2019, 88, 084001. [Google Scholar] [CrossRef]
- Lu, C.; Dong, J.; Sharma, A.; Huang, T.; Knickerbocker, S. Predicting freeway work zone capacity distribution based on logistic speed-density models. J. Adv. Transp. 2018, 1442, 9614501. [Google Scholar] [CrossRef]
- Migletz, J.; Graham, J.L.; Harwood, D.W. Procedure for Determining Work Zone Speed Limits, National Cooperative Highway Research Program, Project 3-41; Transportation Research Board: Washington, DC, USA, 1993; pp. 214–218. [Google Scholar]
- Salem, O.M.; Genaidy, A.M.; Wei, H.; Deshpande, N. Spatial distribution and characteristics of accident crashes at work zones of interstate freeways in Ohio. In Proceedings of the IEEE Intelligent Transportation Systems Conference, Toronto, Canada, 17–20 September 2006; pp. 1642–1647. [Google Scholar]
- Fhwa, U.S. Department of Transportation. In Manual on Uniform Traffic Control Devices, 2009; FHWA: Washington, DC, USA, 2009; pp. 547–559. [Google Scholar]
- Finley, M.D.; Jenkins, J.; McAvoy, D.S. Motorists’ speed response to non-variable and variable work zone speed limits and other work zone conditions. Transp. Res. Rec. 2015, 2485, 70–77. [Google Scholar] [CrossRef]
- Wang, Z.; He, W.; Zhang, X.; Wang, Y.; Wu, B.; Wang, Y. Lane-based vehicular speed characteristics analysis for freeway work zones using aerial videos. Can. J. Civil Eng. 2021, 48, 274–283. [Google Scholar] [CrossRef]
- Porter, R.J.; Mahoney, K.M.; Mason, J.M. Seemingly unrelated regression model of car speeds and speed deviations in freeway work zones. Transp. Res. Rec. 2018, 2023, 44–51. [Google Scholar] [CrossRef]
- Ishak, S.; Qi, Y.; Rayaprolu, P. Safety evaluation of joint and conventional lane merge configurations for freeway work zones. Traffic Inj. Prev. 2012, 13, 199–208. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, B.; Yang, S.; Zhang, M.; Gong, Q.; Zhang, H. The driving risk analysis and evaluation in rightward zone of expressway reconstruction and extension engineering. J. Adv. Transp. 2020, 1, 8943463. [Google Scholar] [CrossRef]
- Li, Y.X.; Ding, Q.; Kong, Y.Y. Modeling and analysis of the impact of urban and rural road reconstruction construction on vehicle capacity. Adv. Transp. Stud. 2019, 1, 97–110. [Google Scholar] [CrossRef]
- Pan, B.; Wu, M.; Wang, Z. Development of road surface inspection system based on computer vision with improved neural network. Highway 2012, 9, 214–217. [Google Scholar]
- Ge, T. Study on Traffic Organization of Expressway Expansion Engineering during Construction. Master’s Thesis, South China University of Technology, Guangzhou, China, 2012. [Google Scholar]
- Liu, X.F. Study on the Key Technologies of Traffic Organization in Freeway Reconstruction and Project Implementation. Master’s Thesis, Chang’an University, Xi’an, China, 2017. [Google Scholar]
- Wang, W. Study on Key Technologies in Expressway Maintenance Work-Zone Traffic Organization Optimization. Master’s Thesis, Chang’an University, Xi’an, China, 2014. [Google Scholar]
- Wei, Y.; Zhao, L.; Yuan, C.; Xu, M. Traffic organization simulation of expressway rebuilding project. J. Chang. Univ. Nat. Sci. Ed. 2012, 32, 38–43. [Google Scholar]
- Shao, C.; Ma, S.; Luo, K.; Qin, Y. Study on the length of median opening in expressway reconstruction and extension work zones. In Proceedings of the CICTP 2020: Advanced Transportation Technologies and Development-Enhancing Connections, Xi’an, China, 14–16 August 2020. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, J.; Easa, S.M.; Zheng, X.; Lin, W.; Peng, Y. Driving simulator study of the comparative effectiveness of monolingual and bilingual guide signs on Chinese highways. Transp. Res. F-Traf. 2019, 68, 67–78. [Google Scholar] [CrossRef]
- Domenichini, L.; Torre, F.L.; Branzi, V.; Nocentini, A. Speed behaviour in work zone crossovers. A driving simulator study. Accident Anal. Prev. 2017, 98, 10–24. [Google Scholar] [CrossRef]
- Bella, F. Validation of a driving simulator for work zone design. Transp. Res. Rec. 2005, 1937, 136–144. [Google Scholar] [CrossRef]
- Jing, D.; Song, C.; Guo, Z.; Li, R. Influence of the median opening length on driving behaviors in the crossover work zone-A driving simulation study. Transp. Res. F-Traf. 2021, 82, 333–347. [Google Scholar] [CrossRef]
- Pawar, N.M.; Velaga, N.R.; Sharmila, R.B. Exploring behavioral validity of driving simulator under time pressure driving conditions of professional drivers. Transp. Res. F-Traf. 2022, 89, 67–78. [Google Scholar] [CrossRef]
- Hu, J.; Gao, X.; Wang, R.; Sun, S. Research on comfort and safety threshold of pavement roughness. Transp. Res. Rec. 2017, 2641, 149–155. [Google Scholar] [CrossRef]
- American Association of State Highway and Transportation Officials. A Policy on Geometric Design of Highways and Streets, 7th ed.; AASHTO: Washington, DC, USA, 2018. [Google Scholar]
- JTG H30-2015; Safety Work Rules for Highway Maintenance. China Communications Press: Beijing, China, 2015.
- Lee, Y.M.; Chong, S.Y.; Goonting, K.; Sheppard, E. The effect of speed limit credibility on drivers’ speed choice. Transp. Res. F-Traf. 2017, 45, 43–53. [Google Scholar] [CrossRef]
- Weng, J.; Qiang, M. Analysis of driver casualty risk for different work zone types. Accident Anal. Prev. 2011, 43, 1811–1817. [Google Scholar] [CrossRef]
- Nes, N.; Brandenburg, S.; Twisk, D. Improving homogeneity by dynamic speed limit systems. Accident Anal. Prev. 2010, 42, 944–952. [Google Scholar] [CrossRef]
- Du, S.; Razavi, S. Variable speed limit for freeway work zone with capacity drop using discrete-time sliding mode control. J. Comput. Civil Eng. 2019, 33, 04019001.1–04019001.15. [Google Scholar] [CrossRef]
- Sarasua, W.A.; Davis, W.J.; Clarke, D.B.; Kottapally, J.; Mulukutla, P. Evaluation of interstate highway capacity for short-term work zone lane closures. Transp. Res. Rec. 2004, 1877, 85–94. [Google Scholar] [CrossRef]
- Cassidy, M.J.; Bertini, R.L. Some traffic features at freeway bottleneck. Transp. Res. F-Meth. 1999, 33, 25–42. [Google Scholar] [CrossRef] [Green Version]
- Al-Kaisy, A.; Hall, F. Guidelines for estimating capacity at freeway reconstruction zones. J. Transp. Eng. 2003, 129, 572–577. [Google Scholar] [CrossRef]
- Kianfar, J.; Abdoli, S. Deterministic and stochastic capacity in work zones: Findings from a long-term work zone. J. Transp. Eng. A-Syst. 2021, 147, 04020141. [Google Scholar] [CrossRef]



| Research Methods | Applicability | Advantage | Disadvantage |
|---|---|---|---|
| Traffic simulation | Traffic flow theory Road design Traffic safety Intelligent transportation | Risk-free Flexible Repeatable Comparable Cost-efficient | Difficulty in model calibration Results differ greatly |
| Driving simulation | Driving behavior Traffic safety Vehicle research | Risk-free Cost-efficient Ease of data collection Repeatability | Low degree of simulation Relative validity Simulator sickness |
| Naturalistic driving | Driving behavior Traffic safety Vehicle research Driver’s psychophysiological indicators | Real Reliable data Long-term observation | Expensive Harsh test conditions |
| Cross Slope (%) | −2.0 | −3.0 | −4.0 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Median Width (m) | 2 | 3 | 3.5 | 4.5 | 2 | 3 | 3.5 | 4.5 | 2 | 3 | 3.5 | 4.5 | |
| Speed Limit (km/h) | 40 | 40 | 40 | 45 | 45 | 40 | 40 | 45 | 45 | 40 | 45 | 45 | 45 |
| 50 | 55 | 60 | 60 | 65 | 55 | 60 | 60 | 65 | 55 | 60 | 65 | 65 | |
| 60 | 70 | 75 | 75 | 80 | 70 | 75 | 80 | 80 | 75 | 80 | 80 | 85 | |
| 70 | 85 | 90 | 95 | 100 | 90 | 95 | 100 | 105 | 95 | 100 | 105 | 110 | |
| 80 | 105 | 110 | 115 | 120 | 105 | 115 | 120 | 125 | 110 | 120 | 125 | 130 | |
| Driving Workload Degree | Safety Level | Passenger Car | Truck |
|---|---|---|---|
| Highest | Highly risky (nervous) | K > 0.060 | K > 0.070 |
| Higher | Relatively risky (relatively nervous) | 0.030 < K ≤ 0.060 | 0.035 < K ≤ 0.070 |
| Normal | Safe | −0.001 < K ≤ 0.030 | −0.001 < K ≤ 0.035 |
| Lower | Relatively risky (relatively fatigued) | −0.012 < K ≤ −0.001 | −0.011 < K ≤ −0.001 |
| Lowest | Highly risky (fatigue) | K ≤ −0.012 | K ≤ −0.011 |
| Area | Maximum Speed (km/h) | Minimum Speed (km/h) | Running Speed/v85 (km/h) | Mean Speed/v (km/h) | SD | Speed Limit Compliance Rate |
|---|---|---|---|---|---|---|
| A (Car) | 104.39 | 68.13 | 101.53 | 90.96 | 10.78 | 16.67% |
| A (Truck) | 95.80 | 51.06 | 88.52 | 72.85 | 13.10 | 70.83% |
| A (All) | 104.39 | 51.06 | 98.23 | 81.90 | 15.03 | 43.75% |
| B (Car) | 101.15 | 54.19 | 91.13 | 77.59 | 12.58 | 8.33% |
| B (Truck) | 90.40 | 53.59 | 72.19 | 64.96 | 9.37 | 33.33% |
| B (All) | 101.15 | 53.59 | 87.39 | 71.27 | 12.76 | 20.83% |
| C (Car) | 90.68 | 49.61 | 74.44 | 64.69 | 10.44 | 41.67% |
| C (Truck) | 78.15 | 48.44 | 61.06 | 56.64 | 6.92 | 75.00% |
| C (All) | 90.68 | 48.44 | 70.98 | 60.66 | 9.73 | 58.33% |
| D (Car) | 66.18 | 31.02 | 51.43 | 44.33 | 8.46 | 95.83% |
| D (Truck) | 53.38 | 27.19 | 39.14 | 35.89 | 5.48 | 100.00% |
| D (All) | 66.18 | 27.19 | 50.07 | 40.11 | 8.28 | 97.92% |
| E (Car) | 74.47 | 41.17 | 62.52 | 56.87 | 7.10 | 66.67% |
| E (Truck) | 64.60 | 36.88 | 56.97 | 50.06 | 7.21 | 95.83% |
| E (All) | 74.47 | 36.88 | 61.06 | 53.47 | 7.92 | 81.25% |
| F (Car) | 78.11 | 49.07 | 73.99 | 61.96 | 9.03 | 41.67% |
| F (Truck) | 72.94 | 42.44 | 65.64 | 55.88 | 8.15 | 70.83% |
| F (All) | 78.11 | 42.44 | 70.72 | 58.92 | 9.12 | 56.25% |
| G (Car) | 86.42 | 43.94 | 80.30 | 67.15 | 12.91 | 37.50% |
| G (Truck) | 73.82 | 49.34 | 65.18 | 59.05 | 6.84 | 54.17% |
| G (All) | 86.42 | 43.94 | 76.34 | 63.12 | 11.09 | 45.83% |
| H (Car) | 73.28 | 44.40 | 64.08 | 55.74 | 8.77 | 66.67% |
| H (Truck) | 64.36 | 42.04 | 57.16 | 52.19 | 5.67 | 95.83% |
| H (All) | 73.28 | 42.04 | 61.88 | 53.97 | 7.59 | 81.25% |
| I (Car) | 53.53 | 32.74 | 49.48 | 44.73 | 5.16 | 100.00% |
| I (Truck) | 53.25 | 32.82 | 44.52 | 40.12 | 5.38 | 100.00% |
| I (All) | 53.53 | 32.74 | 48.14 | 42.42 | 5.75 | 100.00% |
| Area | C | D | E * | F | G | H * |
|---|---|---|---|---|---|---|
| C | - | 20.55 # (v) 20.91 # (v85) | 7.19 # (v) 9.92 # (v85) | 1.74 (v) 0.62 (v85) | −2.46 # (v) −5.36 # (v85) | - |
| D | −20.55 # (v) −20.91 # (v85) | - | −13.36 # (v) −10.99 # (v85) | −18.81 # (v) −20.65 # (v85) | −23.01 # (v) −26.27 # (v85) | −13.86 # (v) −11.81 # (v85) |
| E * | −7.19 # (v) −9.92 # (v85) | 13.36 # (v) 10.99 # (v85) | - | −5.45 # (v) −9.66 # (v85) | −9.65 # (v) −15.28 # (v85) | −0.50 (v) −0.82 (v85) |
| F | −1.74 (v) −0.62 (v85) | 18.81 # (v) 20.65 # (v85) | 5.45 # (v) 9.66 # (v85) | - | −4.20 # (v) −5.62 # (v85) | 4.95 # (v) 8.84 # (v85) |
| G | 2.46 # (v) 5.36 # (v85) | 23.01 # (v) 26.27 # (v85) | 9.65 # (v) 15.28 # (v85) | 4.20 # (v) 5.62 # (v85) | - | 9.15 # (v) 14.46 # (v85) |
| H * | - | 13.86 # (v) 11.81 # (v85) | 0.50 (v) 0.82 (v85) | −4.95 # (v) −8.84 # (v85) | −9.15 # (v) −14.46 # (v85) | - |
| Area | Maximum | Minimum | Mean | SD | Higher Risk Ratio | High Risk Ratio |
|---|---|---|---|---|---|---|
| A (Car) | 0.03663 | −0.00613 | 0.00600 | 0.00716 | 13.73% | 0.00% |
| A (Truck) | 0.03950 | −0.00563 | 0.00642 | 0.00754 | 12.46% | 0.00% |
| A (All) | 0.03950 | −0.00613 | 0.00622 | 0.00735 | 13.11% | 0.00% |
| B (Car) | 0.03628 | −0.00548 | 0.00663 | 0.00711 | 11.89% | 0.00% |
| B (Truck) | 0.04066 | −0.00393 | 0.00756 | 0.00760 | 8.12% | 0.00% |
| B * (All) | 0.04066 | −0.00548 | 0.00709 | 0.00736 | 10.04% | 0.00% |
| C (Car) | 0.06245 | −0.00259 | 0.01336 | 0.01294 | 14.29% | 0.58% |
| C (Truck) | 0.09918 | −0.00038 | 0.01704 | 0.01658 | 7.73% | 2.40% |
| C * (All) | 0.09918 | −0.00259 | 0.01466 | 0.01444 | 11.97% | 1.23% |
| D (Car) | 0.03565 | −0.00351 | 0.00695 | 0.00677 | 5.05% | 0.00% |
| D (Truck) | 0.04015 | −0.00183 | 0.01614 | 0.01222 | 8.25% | 0.00% |
| D * (All) | 0.04015 | −0.00351 | 0.00921 | 0.00933 | 5.84% | 0.00% |
| E (Car) | 0.04565 | −0.00288 | 0.00869 | 0.00770 | 3.87% | 0.00% |
| E (Truck) | 0.06668 | −0.00138 | 0.01803 | 0.01457 | 15.00% | 0.00% |
| E * (All) | 0.06668 | −0.00288 | 0.01114 | 0.01078 | 6.79% | 0.00% |
| F (Car) | 0.06538 | −0.00463 | 0.01553 | 0.01400 | 17.86% | 0.00% |
| F (Truck) | 0.13975 | −0.00150 | 0.02083 | 0.02641 | 10.97% | 5.24% |
| F * (All) | 0.13975 | −0.00463 | 0.01741 | 0.01951 | 15.41% | 1.86% |
| G (Car) | 0.17175 | −0.00138 | 0.02889 | 0.03545 | 19.44% | 10.99% |
| G (Truck) | 0.24712 | −0.00188 | 0.05611 | 0.06532 | 21.46% | 25.00% |
| G * (All) | 0.24712 | −0.00188 | 0.03833 | 0.04968 | 20.14% | 15.85% |
| H (Car) | 0.07432 | −0.00971 | 0.00745 | 0.00943 | 16.03% | 0.17% |
| H (Truck) | 0.07961 | −0.00915 | 0.00793 | 0.00989 | 14.48% | 0.17% |
| H (All) | 0.07961 | −0.00971 | 0.00769 | 0.00966 | 15.78% | 0.17% |
| I (Car) | 0.04151 | −0.00331 | 0.00695 | 0.00743 | 7.95% | 0.00% |
| I (Truck) | 0.04615 | 0.00280 | 0.01475 | 0.01241 | 9.69% | 0.00% |
| I * (All) | 0.04615 | −0.00331 | 0.00889 | 0.00955 | 8.39% | 0.00% |
| Independent Variable | Dependent Variable | Fitting Formula | Domain | Range |
|---|---|---|---|---|
| Opening length | Running speed | y = −1.673*10−5 × 3 + 0.003 × 2 + 0.217x + 38.032 | [40, 130] | [50.07, 76.34] |
| Mean speed | y = 4.111*10−8x5 − 0.013x2 + 1.496x − 1.519 | [40.11, 63.12] | ||
| Driving workload | y = 6.364*10−8x3 − 1.095*10−5x2 + 0.001x − 0.004 | [0.00921, 0.03833] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Hu, J.; Wang, R.; Qu, S. Study on the Median Opening Length of a Freeway Work Zone Based on a Naturalistic Driving Experiment. Appl. Sci. 2023, 13, 851. https://doi.org/10.3390/app13020851
Ma S, Hu J, Wang R, Qu S. Study on the Median Opening Length of a Freeway Work Zone Based on a Naturalistic Driving Experiment. Applied Sciences. 2023; 13(2):851. https://doi.org/10.3390/app13020851
Chicago/Turabian StyleMa, Sen, Jiangbi Hu, Ronghua Wang, and Shangwen Qu. 2023. "Study on the Median Opening Length of a Freeway Work Zone Based on a Naturalistic Driving Experiment" Applied Sciences 13, no. 2: 851. https://doi.org/10.3390/app13020851
APA StyleMa, S., Hu, J., Wang, R., & Qu, S. (2023). Study on the Median Opening Length of a Freeway Work Zone Based on a Naturalistic Driving Experiment. Applied Sciences, 13(2), 851. https://doi.org/10.3390/app13020851








