Abstract
To solve the problem of low classification accuracy caused by differences in object types, shapes, and scales in SAS images, an object classification method based on a deformable residual network and transfer learning is proposed. First, a lightweight deformable convolution module DSDCN was designed by adding offsets to a traditional convolution, to adapt to objects with different shapes in SAS images, and the depthwise separable convolution was used to optimize the module. Second, a deformable residual network was designed with the DSDCN, which combined the traditional depth features with deformable features for object representation and improved the robustness of the model. Furthermore, the network was trained by the transfer learning method to save training time and prevent model overfitting. The model was trained and validated on the acquired SAS images. Compared with other existing state-of-the art models, the classification accuracy in this study improved by an average of 6.83% and had an advantage in the amount of computation, which is 108 M. On the deformation dataset, this method improved the accuracy, recall, and F1 scores by an average of 5.3%, 5.6%, and 5.8%, respectively. In the ablation experiments of the DSDCN module, the classification accuracy of the model with the addition of the DSDCN module improved by 5.18%. In addition, the training method of transfer learning also led to an improvement in model classification performance, reflected in the classification accuracy, which increased by 7.4%.
1. Introduction
Automatic Target Recognition technology has been a research hotspot in recent years and has attracted great attention from scholars [1,2,3]. Sonar images are an effective means of expressing underwater objects. with the booming development of synthetic aperture imaging technology, the acquisition of high-resolution underwater images is guaranteed, and the study of object classification in sonar images has become an important topic in the intelligence of modern sonar systems [4,5,6]. However, the complexity of the underwater environment makes the sonar images subject to noise interference and unclear edges [7,8]. In addition, there are differences in object type, shape, and scale, which make feature extraction difficult.
Researchers have conducted extensive research on underwater object classification for a long time. In ref. [9], a template matching method is proposed, which uses the correlation of object echoes and shadow features to achieve the classification. In ref. [10], invariant moment features and support vector machines are used to implement the classification and recognition of objects in sonar images. In addition, the fusion of shape features and texture features of the object can effectively improve the accuracy of underwater object recognition [11]. While the above methods of manually designing and extracting features achieve certain results, they require high professional domain knowledge. Some key information may be lost during the feature extraction, and the robustness and generalization ability of the model is lacking.
In recent years, convolutional neural networks, as an important tool for image processing, have independently learned effective features from training data for different tasks and show great superiority in image feature extraction, object detection, and classification efficiency. Features of objects are extracted by the convolutional neural network, and the classification is realized by a support vector machine in [12]. In ref. [13], an automatic target recognition method is proposed, which combines a CNN-based detector with a probabilistic grid map to achieve the detection and recognition of objects in forward-looking sonar images. In ref. [14], the use of a feature pyramid network combined with multi-scale features to automatically detect underwater targets has high efficiency. In the field of object detection, researchers use YOLOV4 and YOLOV3 as the backbone networks to achieve object detection through the use of dense layers and spatial pyramid pooling, offering better performance compared to current popular methods [15,16,17].
However, the above convolutional neural networks use fixed-shape convolutional kernels, which are often sampled in regions of no interest to the image and have inherent drawbacks for modeling complex shapes. The deformable convolution proposed by [18] can solve this problem by adding the offset of sampling points on the regular convolution, but the calculation produces a large number of parameters [19,20,21]. When using deformable convolutional theory for object classification, it is important to exploit its advantages in feature extraction on the one hand, and to be aware of the problem of long training times due to the complex computational process on the other. Therefore, it is important to choose a suitable backbone network and optimize the network structure. In addition, the problem of small samples is also an important factor limiting the performance of object classification, for which many scholars use the theory of transfer learning for model optimization [22].
To address the above issues, based on existing research, an underwater object classification method for SAS images based on deformable residual network and transfer learning is proposed. The innovation is reflected in several aspects. (1) The method uses ResNet as the basic network and downsampling at the input layer, then extracts the depth features of objects through multiple residual blocks, and the average improvement in classification accuracy is over 6%, compared to other models. (2) The lightweight deformable convolution module DSDCN is designed to increase the sampling offset so that the sampling points of the convolution kernel can change adaptively according to the object shape, to be more adaptable to objects with different shapes. (3) During the calculation of the offset, the depthwise separable convolution is used to reduce the network parameters and computational complexity while enhancing the spatial sampling capability, and the computational complexity can be reduced to one ninth of the original, compared to standard convolution. (4) Then, the simulation datasets are constructed to reduce model overfitting using transfer learning, and the classification accuracy is improved by 7.4%. In summary, the method designed in this study can change the shape and location of the actual sampling points of SAS images according to the morphology of the object, so that the network can focus on the region of interest and improve the feature extraction ability and classification accuracy.
The remainder of this paper is organized as follows: In Section 2, we analyze the characteristics of SAS images. In Section 3, we design the deformable convolution module DSDCN that can perform deformable sampling. Then, the structure of the underwater object classification network DSDCN-ResNet is proposed in Section 4. The dataset description and experimental results for the classification tasks are demonstrated in Section 5. The conclusions of this work are highlighted in Section 6.
2. Analysis of SAS Image Characteristics
During the operation of a synthetic aperture sonar (SAS), the sonar moves at a uniform speed along the azimuth and emits signals at a certain pulse interval while receiving the echoes reflected from the object [23]. The acquired images are characterized as follows:
(1) Due to the influence of the imaging equipment and marine environment, there is speckle noise in sonar images, resulting in a low signal-to-noise ratio of images. The edge of the object in the image is blurred, and there is less detailed information, such as texture [24]. On the whole, the object is higher in energy and more complete in form but does not have a regular geometry.
(2) SAS adopts the principle of side-view imaging, which may lead to a large difference in the appearance of the same object at different angles, and the morphology of different objects at a certain angle may have a large similarity. The objects in the image have the problems of high inter-class similarity and high intra-class difference.
(3) The complexity of the underwater environment and the speed of the platform may lead to some geometric distortion in the sonar image. Under this influence, the object may also undergo certain geometric changes [25].
The sonar images of several different classes of objects are shown in Figure 1.

Figure 1.
Examples of sonar images of four different classes of objects: (a) Real object A. (b) Real object B. (c) Real object C. (d) Real object D.
3. DSDCN Module
Convolutional neural networks have powerful feature extraction capabilities and play an important role in sonar image processing. Deformable convolutions derived from convolutional neural networks are capable of deformable sampling and have irreplaceable advantages in underwater object classification. In this study, we optimized the structure of deformable convolution to reduce the deformable convolution.
3.1. Defects of Traditional Convolution and DCN Module
SAS images differ significantly from natural images in that SAS images do not have color information. Under noise interference, the object has no regular edges. The energy concentration region contains both object and background noise with an irregular shape, and the difference between object classes is not obvious. Since the shape of the traditional convolution kernel is fixed, only the local feature information extraction can be realized during the convolution calculation. Therefore, there are some drawbacks when using traditional convolutional neural networks for object classification, though they have high efficiency [26,27].
In Figure 2, differences in the shapes and sizes of objects in SAS images can be seen, and the morphology of the objects varies at different imaging angles. If the traditional convolution kernel is used for feature extraction, the pixel proportion of the effective information of the object becomes smaller than the background pixel, and the background information causes serious interference with feature extraction [28].

Figure 2.
Sampling position of traditional convolution on objects in SAS Image. (a) Real object A. (b) Real object B. (c) Real object C. (d) Real object D. The red point is the position of the sampling points of traditional convolution.
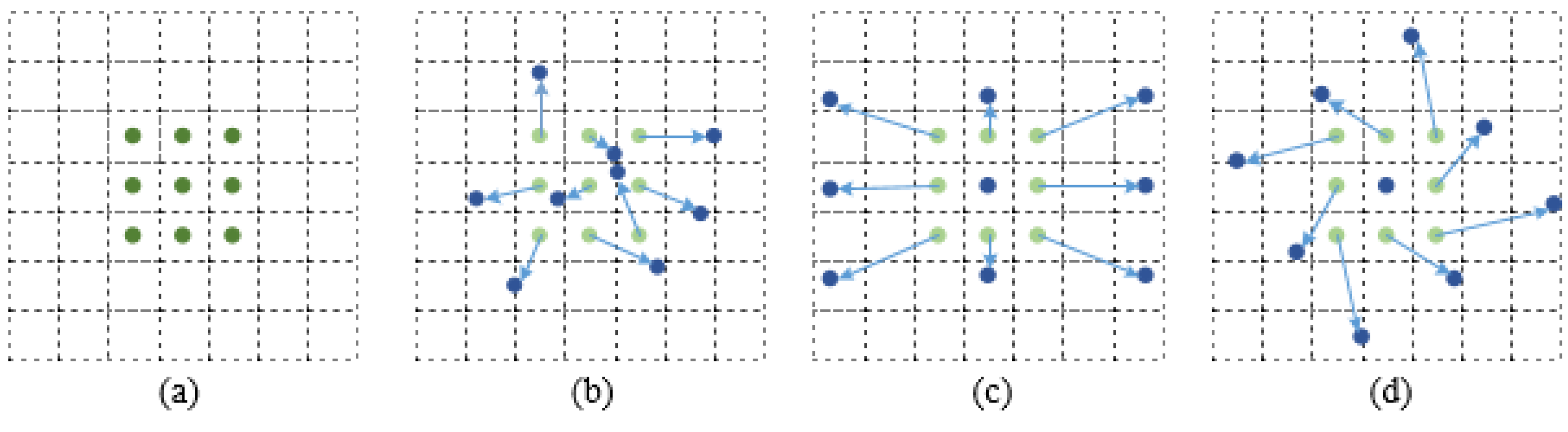
The deformable convolution allows the sampling grid to deform freely by adding a two-dimensional offset. with it, instead of traditional convolution, the model will enhance feature extraction capability and be adaptive to objects with different sizes and shapes [29,30]. The schematic diagram of a simple deformable convolutional network is shown in Figure 3.
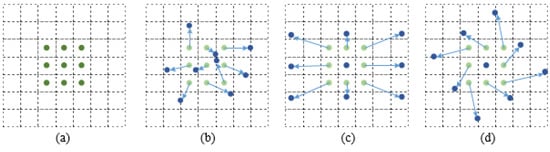
Figure 3.
Schematic diagram of a simple deformable convolutional network. (Green) Nine sampling points of traditional convolution. (Blue) Points of normal sampling points add offset. (a) Nine sampling points of traditional convolution. (b–d) Several examples of deformable convolutional. The arrows represent the direction and distance of the deformable convolution.
3.2. DSDCN Module
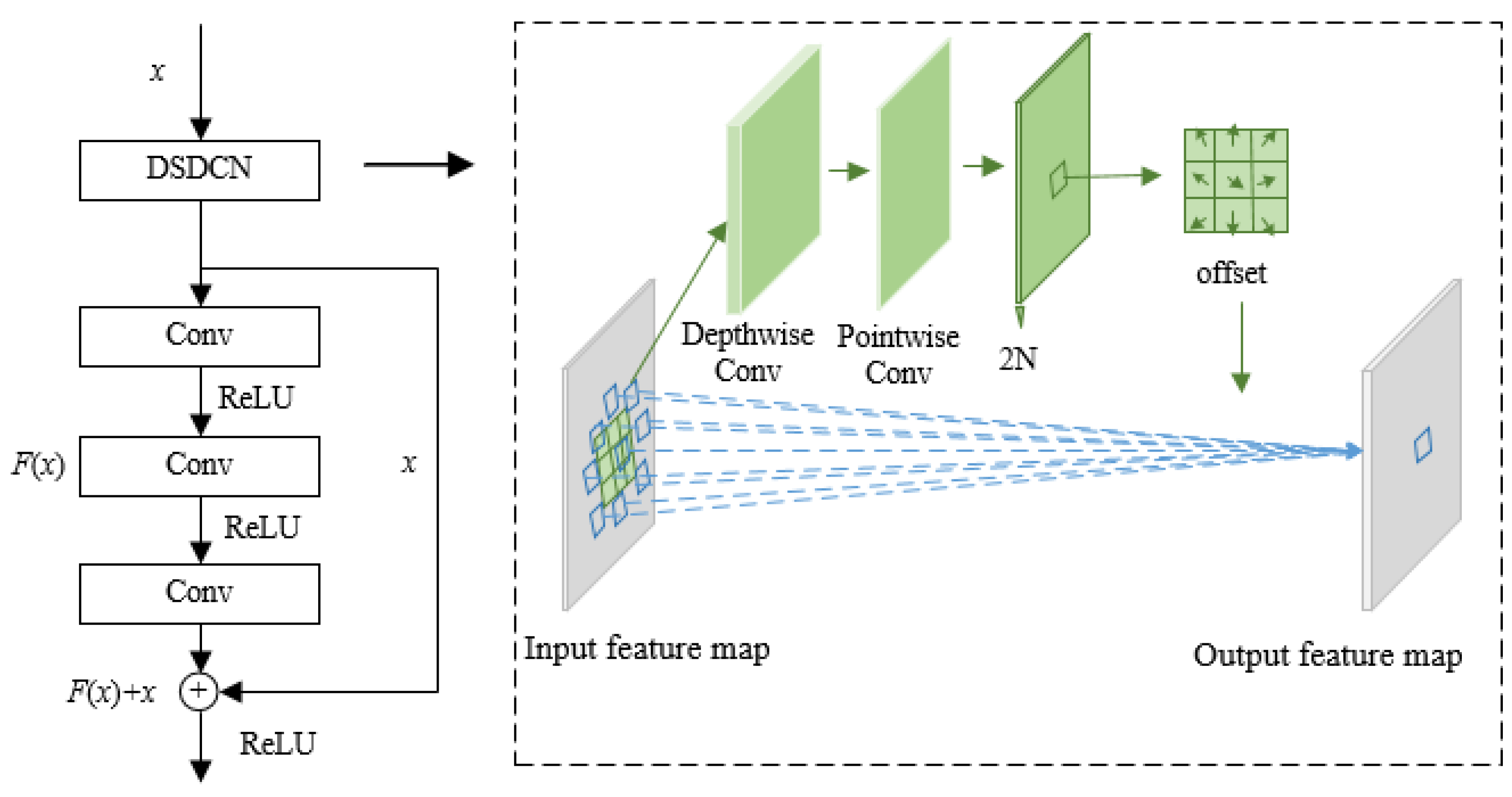
The traditional convolution kernel can realize “deformable learning” by adding offsets. However, the high computational cost of offsets increases the running time of the network, which is not suitable for feature extraction in complex scenes. According to the existing research, the depthwise separable convolution deposes traditional convolution into a depthwise convolution and a 1 × 1 pointwise convolution, which can reduce the model parameters and calculate consumption [31]. Therefore, the deformable convolution can be improved by the depthwise separable convolution to enhance the running speed of the network, which can obtain a depthwise separable deformable convolution network (DSDCN). The relevant theories of offset calculation are as follows:
The convolution kernel in traditional convolution is usually sampled as a sliding window within a regular grid on the input feature map [32]. For example, represents a sampling grid with a stride of 1 for a 3 × 3 convolution. For each position in the output feature map y, the feature value [33] can be calculated by
where is the convolution kernel weight of this sampling position, is the input feature value of the sampling position, is all sampling positions in the receptive field, and is the receptive field. In the DSDCN module, each point in the sampling grid is added by offset , which is
where is the input feature value of the sampling offset position, and is the offset of the sampling position.
The structure of DSDCN is shown in Figure 4. The implementation of the module is as follows:
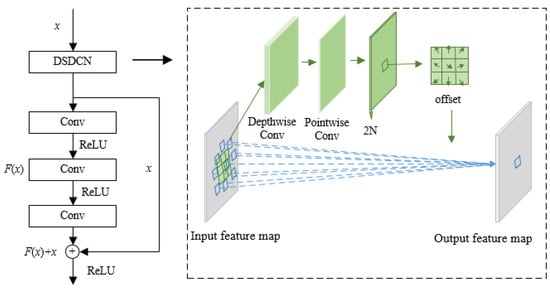
Figure 4.
Schematic diagram of DSDCN. The black and green arrows represent the procedure of the diagram, the blue arrows represent the change between the input and output feature map after the deformable convolution.
(1) Record the size of input feature map as , and ensure the feature map is sampled by depthwise separable convolution;
(2) After depthwise separable convolution, the size of the output feature map remains the same and is calculated as , where the represents the learned offset in two directions. Since the pixels have both horizontal and vertical directions, the number of offset channels is twice the number of ;
(3) The above offset represents the offset of the index of each pixel in the input feature map . By adding the index value of the pixel in the input feature map to the offset, the coordinates of the offset pixel in the original feature map can be obtained;
(4) Since the distribution of sampling points is not fixed, and the offset is generally not an integer, to obtain accurate pixel values and achieve backpropagation, a bilinear interpolation is used to obtain the pixels corresponding to the coordinate positions.
In DSDCN, both the size and direction of the offset need to be obtained through network training. Figure 5 shows the sampling points for the feature extraction of SAS images by the DSDCN proposed in this paper, with the red points being the actual sampling locations of the convolution kernels. Compared with the traditional convolution sampling points in Figure 2, the sampling position of the convolution kernel is changed, with the sampling points concentrated in the energy concentration region of the image. It can be seen that by training the network, the module can improve the feature extraction capability of the network by focusing the sampling points on the region of interest during the feature extraction.

Figure 5.
Sampling position of DSDCN on objects in SAS Image. (a) Real object A. (b) Real object B. (c) Real object C. (d) Real object D. The red point is the position of the sampling points of deformable convolution.
4. Object Classification Network DSDCN-ResNet
Aimed at addressing the shortcomings of conventional convolution neural networks in feature extraction, the object classification network DSDCN-ResNet was designed in this study. DSDCN-ResNet is based on ResNet and adds deformable convolution to optimize the model and to improve the classification performance of the model.
4.1. ResNet in SAS Image Classification
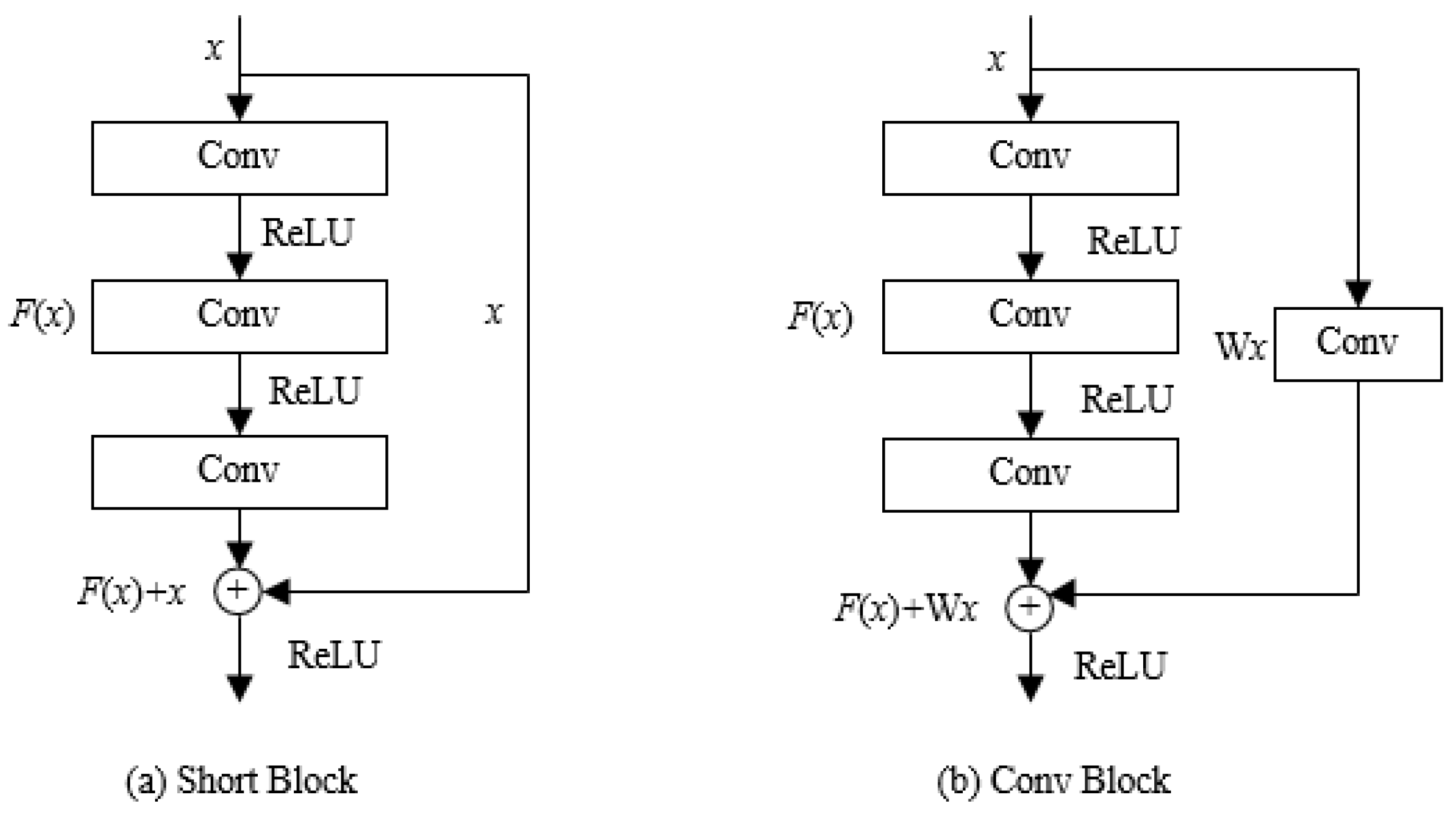
In recent years, convolutional neural networks have shown excellent performance in object classification tasks. Compared with shallow neural networks, deep neural networks have more nonlinear mapping structures, and with the deepening of network layers, their nonlinear expression ability is stronger, which is more beneficial for abstract feature acquisition. However, the increase of deep network layers brings the problem of gradient extinction. The residual module in ResNet networks allows for shortcut connections between convolutional layers, which can effectively avoid this problem in backpropagation [34]. The structure of the residual module is shown in Figure 6, where is the input and is the residual mapping. In Figure 6a, the output of the residual module is
when , and the residual module realizes identity mapping. The output of layer is:
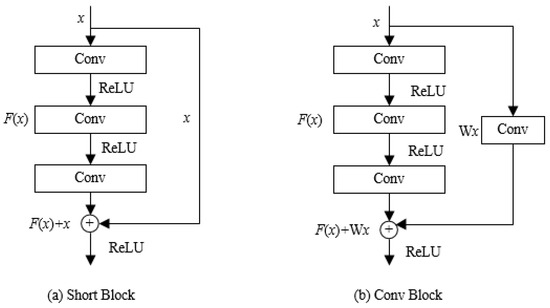
Figure 6.
Residual block in ResNet. (a) Short Block, (b) Conv Block.
In Figure 6b, when the input and output dimensions of the residual block are different, a convolutional layer is added to the shortcut connection to perform a linear transformation to obtain a valid output. The model learns only the input and output of the residual blocks during training and directly transfers the error to the upper layer through a shortcut connection, which has good performance in image feature extraction [35].
Since the residual blocks in ResNet use traditional convolution kernels with fixed sizes and shapes, which can only achieve the extraction of fixed local features, the original ResNet cannot be directly applied to the object classification of SAS images.
4.2. Structure of DSDCN-ResNet
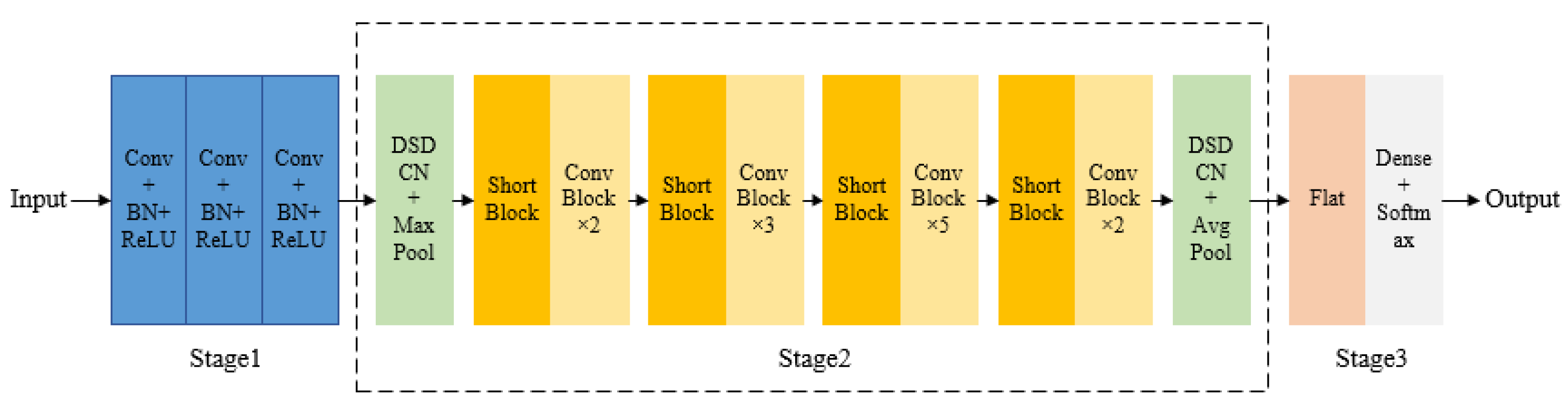
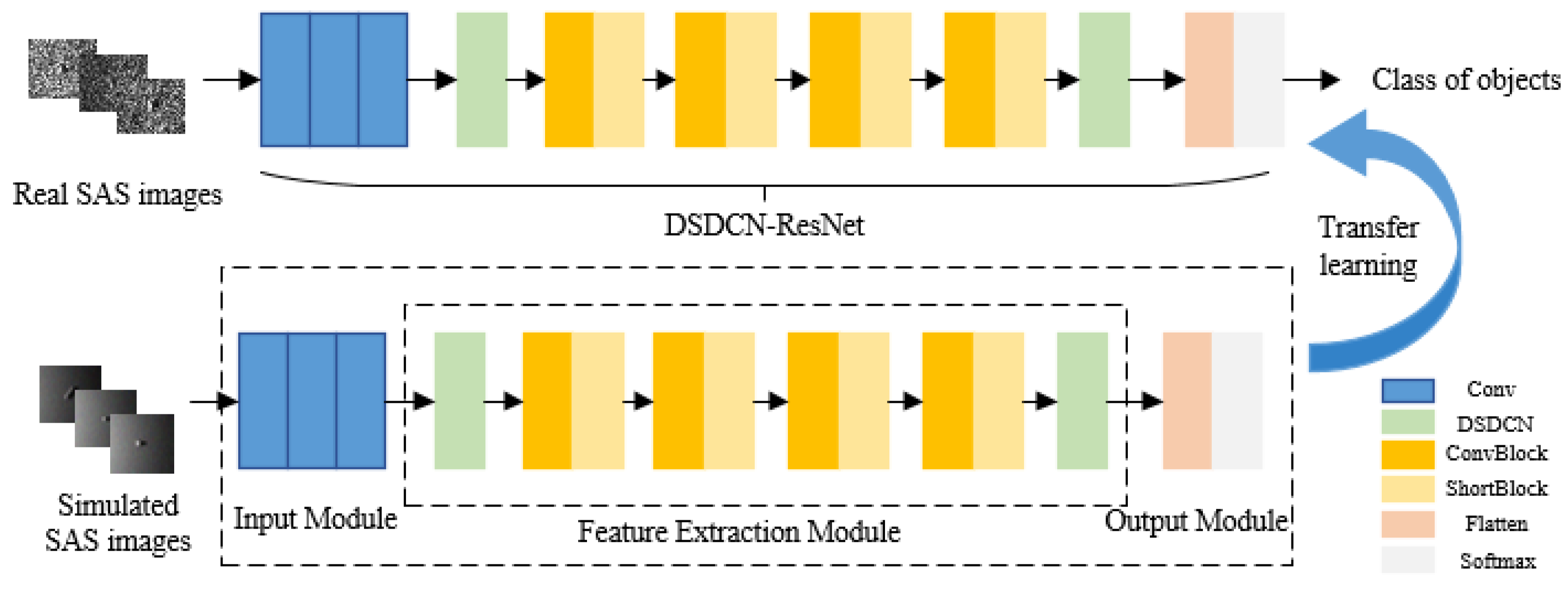
This section discusses the depthwise separable deformable residual classification network DSDCN-ResNet, designed based on ResNet with the DSDCN module. The network structure is shown in Figure 7, including the input convolution module, the feature extraction module, and the classification module.
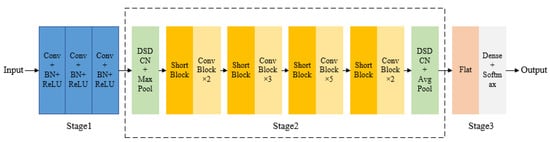
Figure 7.
Structure of DSDCN-ResNet. Every blue block represents the convolution layer and a batch normalization layer with ReLU nonlinear activation function. Every green block represents a DSDCN module and a maxpooling layer. Every dark yellow block represents the short block in the ResNet network. Every light yellow block represents the conv block in the ResNet network. The pink block represents the flatten layer and the gray block represents the dense layer and the softmax activation function.
Stage 1 was developing the input convolution module, which contained three convolution layers. The purpose was to downsample the input image before the residual blocks to avoid the computational explosion caused by the large input image. This operation first ensured that the improved network had the same receptive field as the original network, and then it could increase the network depth to further extract deep semantic information.
Stage 2 was the feature extraction module, which introduced the DSDCN module in Section 3.2 into the feature extraction of ResNet. This module could adaptively adjust the size and shape of the convolution kernel according to the characteristics of the object and realize the sampling of the offsets. Then, the bilinear interpolation algorithm was used to pool the sampling points to efficiently extract the robust features at different scales and enhance the discrimination of objects. DSDCN modules were added after the third convolutional layer and the residual blocks. The first DSDCN module extracted the shallow features of the object, followed by the depth residual features using Conv Block and Short Block. The second DSDCN module represented the object jointly with deformable and traditional depth features, to improve the robustness of the model and make it more applicable for underwater object classification [36].
Stage 3 was the classification module, which used Softmax to achieve the classification of objects in SAS images. In addition, the ReLU nonlinear activation functions were used in each convolutional layer and residual block during the network propagation to reduce model overfitting and enhance the nonlinear representation. The batch normalization layer was added before the activation function to increase the prediction accuracy of the model [37], which was calculated as follows:
Based on ResNet, the depthwise separable deformable residual classification network DSDCN-ResNet proposed in this paper was composed of convolutional layers, depthwise separable deformable convolution, residual blocks, global average pooling, and the Softmax classification layer. The network structure and parameters are shown in Table 1, where c represents the number of output channels of the current network layer, n represents the number of repetitions of the network layer, and s is the convolution stride.

Table 1.
Structure and parameters of DSDCN-ResNet.
4.3. Use of Transfer Learning
The complexity of the underwater environment and the cost of data acquisition result in a lack of sonar images, and training the network with a small amount of data may lead to serious overfitting problems [38]. Therefore, the method of transfer learning is introduced here to migrate the trained network parameters to the small sample network, thus reducing the network overfitting, saving training time, and improving classification accuracy. The existing public datasets, such as ImageNet, differ greatly in image types from SAS images, and they are not suitable as training sets. The transfer learning steps adopted in this study are as follows: First, the SAS image simulation dataset was constructed according to the sonar imaging characteristics and used as the training set of the model. Second, the network designed in Section 4.2 was trained on the simulation data, and the trained model was saved. Finally, the trained model was used for feature extraction and the classification of real SAS images. The framework of the network training and object classification algorithm is shown in Figure 8.
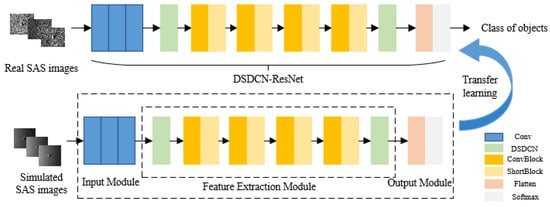
Figure 8.
Framework of the network training and object classification algorithm.
5. Experiments and Analysis
5.1. Dataset and Platform
The dataset used for the experiments included real sonar images, collected by lake and sea trials, and simulated images, obtained by three-dimensional modeling software, including a sphere, cylinder, truncated cone, and line. The number of each class of objects is shown in Table 2. The simulated images were used for auxiliary training of the model. During the simulation, the grazing angle between the sonar and the object was 30~45°, and the angle between the object axis and the incident acoustic wave was 0~180°. Some experimental images can be seen in Figure 9. During the experiments, 30% of the data were randomly selected to train the model, and the rest of the data were used to test the performance of the network. The GPU of the experiment computer was RTX2070 and the CPU was a 6-core i7-10750H.

Table 2.
Experimental dataset.

Figure 9.
Simulated Images of experimental dataset. (a) Simulated sphere object. (b) Simulated cylinder object. (c) Simulated truncated cone object. (d) Simulated line object.
5.2. Evaluation Metrics
To further validate the classification performance of the model proposed in this paper, experiments were conducted using different models, and the accuracy (), recall (), and similarity coefficient () were used as metrics to measure the classification effect. Each metric is defined as follows:
where is the true class of object , is the prediction class of object , is the true positive example, is the false negative example, is the false positive example, and is the true negative example. Here, is the case where the true class is the same as the prediction, and is the total probability of all cases [39].
In addition, as two important indicators, the parameters and calculate consumption of the model are usually used to evaluate the complexity of the network model. The parameters and calculate consumption mainly come from the convolution layer and full connection layer in the network. The calculation process can be expressed as
where and represent the parameters and calculate consumption of the model, respectively; and represent the size of the input image and the size of the convolution kernel used in the network, respectively; and are the numbers of channels of input and output feature maps in the convolution operation; and and represent the number of convolution layers and full connection layers in the network.
5.3. Model Validation and Results Analysis
When designing the network, the parameters of each layer were randomly initialized with Gaussian distribution. During the model training, it is usually necessary to use a suitable optimization algorithm to update the network parameters so that the error between the output image and the label converges to the best. The input was designed as (128, 128, 3) according to the size of the image, and the optimization algorithm adopted the Adam algorithm with the learning rate set to 0.0002. The Adam algorithm can maintain a high computing efficiency while occupying less memory, which is more suitable for the optimization of large-scale data. The batch size of images during training was 16 and the epoch was 100. The loss value was calculated using the categorical cross entropy, which is calculated as
where represents the number of samples in the training set, represents the number of classes, is the object class, and is the probability of prediction class.
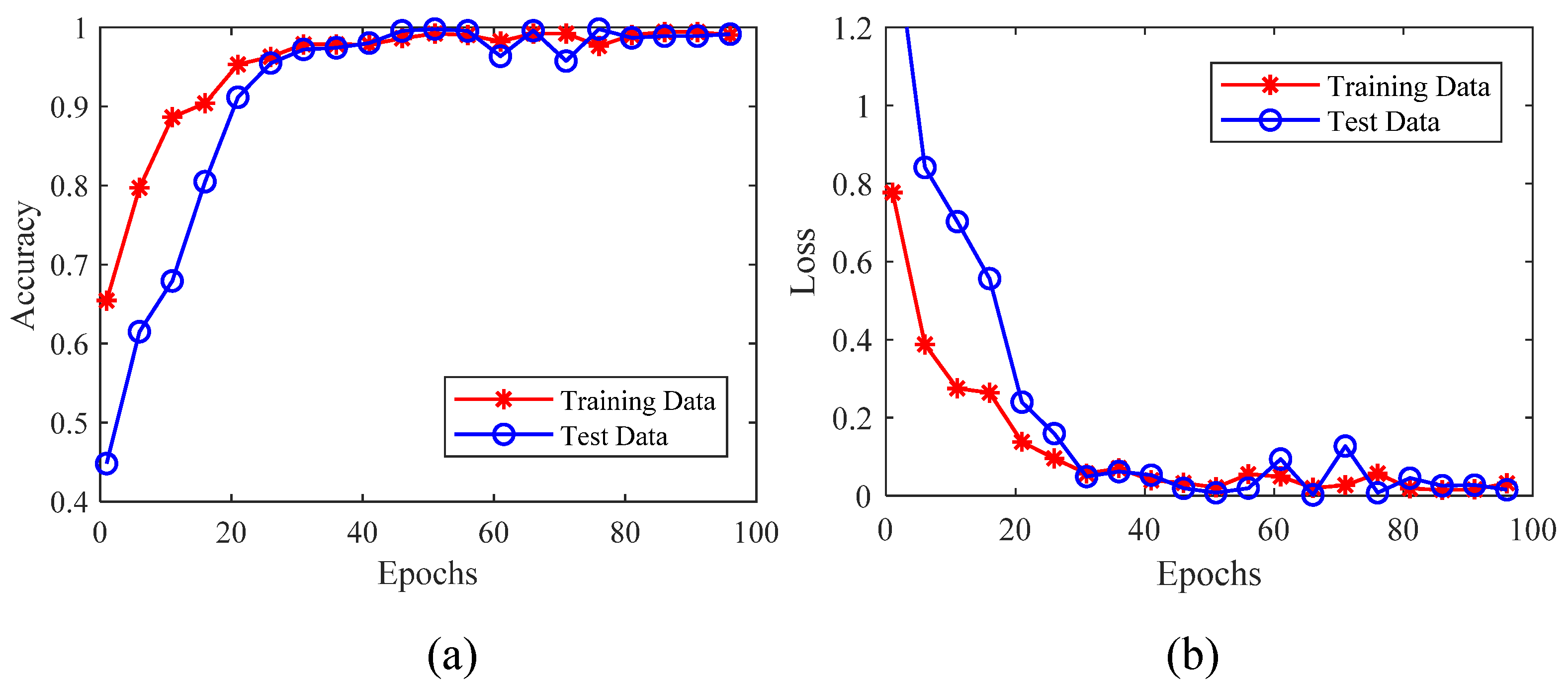
The curve of cost and accuracy of the model is shown in Figure 10. From Figure 10a, it can be seen that the cost curve decreased with the increase of epochs for both training and validation data, and it finally tended to reach a more stable value. The error remained below 0.1, indicating that the model kept the deviation within a reasonable range. The curve in Figure 10b shows that with the increase of epochs, the classification accuracy of the model could achieve a higher value.
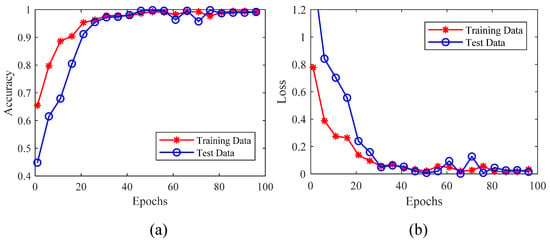
Figure 10.
Curve of accuracy and loss of the model. (a) Accuracy curve of the model. (b) Loss curve of the model.
5.3.1. Comparison of Experiments with Different Models
To further evaluate the classification performance of the model and verify its applicability to underwater object classification, the model in this study was compared with several representative models, including the baseline model ResNet_0, VGGNet, UNet, and Light-ResNet. Ten random experiments were conducted on the three networks separately, and the average values of the experimental results were calculated. Table 3 shows the classification accuracy and computational complexity of several models on the dataset in this paper.

Table 3.
Classification performance on different models.
From Table 3, it can be seen that there were differences in the classification effects of the convolutional network models with different structures for underwater objects, and the classification accuracy of the model proposed in this paper was higher than that of the others. The classification accuracy of VGGNet was as high as 94.5%, which is second only to the model proposed in this paper. However, the complexity of VGGNet was high due to its full connection layer with a large number of parameters. It can also be seen from the table that VGGNet had the largest number of parameters and floating point operations. The UNet connected the features from the shallow and deep convolution layers, which could make full use of the feature information with a small number of parameters. However, it had a large computational consumption with an accuracy rate of only 86.0%. The baseline model ResNet_0 was slightly less computationally intensive than the method in this study because the DSDCN module was not added; but similarly, its classification accuracy was reduced by 7.4%. The Light-ResNet was a lightweight residual network obtained by replacing the convolutional layer of the ResNet with a depthwise separable convolution. The number of parameters was reduced, compared to the original model, but the classification accuracy was also reduced, to a large extent. The above analysis shows that the method in this study was more advantageous in underwater object classification.
5.3.2. Ablation Experiment with DSDCN Module
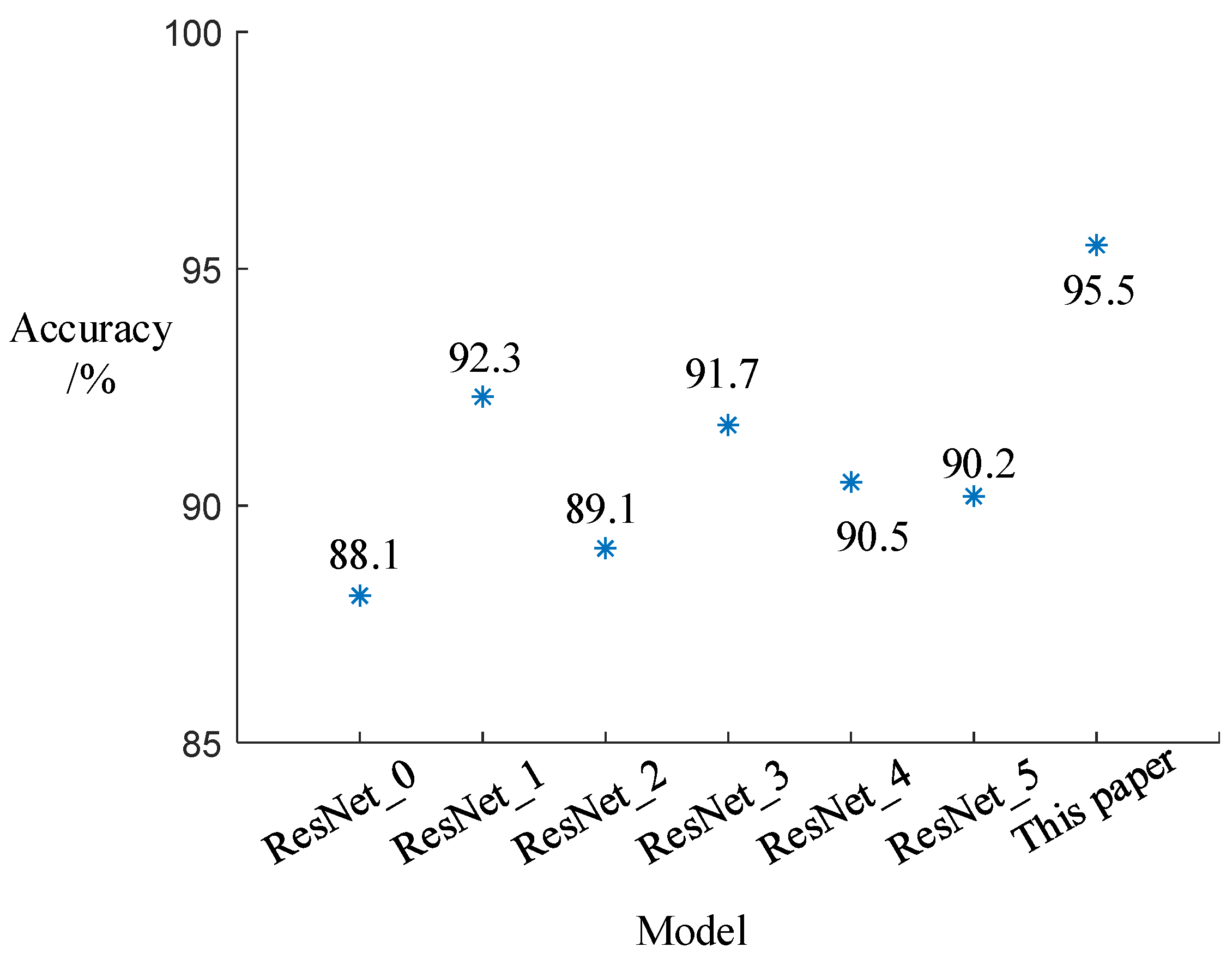
In this study, the DSDCN module was added to the network after the input layer and residual blocks to extract object features at the shallow and deep layers of the model. To verify the performance of the model with the DSDCN module at different positions, the model proposed in Section 4.2 and denoted as ResNet_0 was used without the addition of the DSDCN module. For ResNet_1, the DSDCN module was only added after the input layer. For ResNet_2, the DSDCN module was only added after the residual blocks input layer. For ResNet_3, ResNet_4, and ResNet_5, the DSDCN module was added between several residual blocks. The experiments were conducted using the above models under the same conditions as those described in Section 5.3.1, and the classification results were compared with the methods in this study, as shown in Figure 11. The results show that the addition of DSDCN at the positions designed in this study resulted in better classification of the objects, with an accuracy of 95.5%, an average improvement of 5.1% compared to others. The reason may be that the deformable convolution after the input layer extracts mostly shallow information about the object, and the deep information can be obtained by the residual blocks. The further use of deformable convolution after the residual blocks could make full use of the deep and shallow features of the object and improve the classification accuracy.
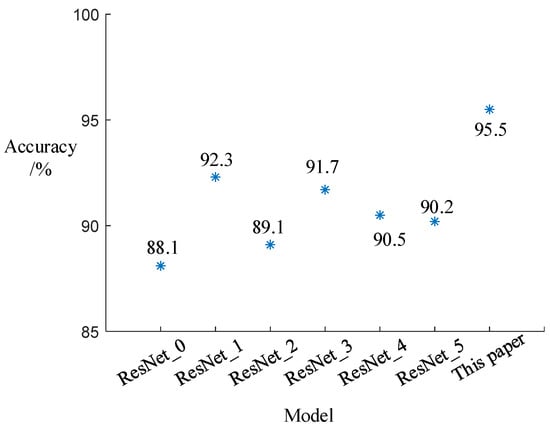
Figure 11.
Classification accuracy of the model with DSDCN at different positions. * is the accuracy of each model.
5.3.3. Comparison Experiments with Different Models on Deformable Images
To validate the classification performance of the model for deformable objects, data enhancement methods were used for the images. The deformable images were obtained through random rotation, stretching, translation, etc. These data were used for different models with the same experimental conditions as before, and the obtained results are shown in Table 4. From the data in the table, we can see that the classification accuracy of the method in this study was improved by 6.2% compared with the ResNet_0 without adding the DSDCN module. Results show that the deformable convolution had a good classification effect, which fully illustrates that the DSDCN module designed in this paper has excellent feature extraction performance for deformed objects. Compared with other models, the classification results of the DSDCN-ResNet in this study had improved in accuracy, recall, and F1 scores, with average increases of 5.3%, 5.6%, and 5.8%, respectively, which shows that the proposed method has better performance for underwater objects.

Table 4.
Performance of different models on deformable images.
5.3.4. Transfer Learning Validation Experiment
To verify the influence of the training method of transfer learning on the classification effect, the deformable residual network designed in Section 4.2 was used to train and classify the model on SAS images directly, which is denoted as ResNet_No, for comparison with the method trained using transfer learning in this study. The classification accuracy obtained by the two methods is shown in Table 5, and it can be seen that training the model through transfer learning under the condition of small samples was beneficial for improving the classification accuracy.

Table 5.
Accuracy of model with transfer learning.
6. Conclusions
In this paper, we focus on the underwater object classification in SAS images, and the structure of ResNet is optimized and redesigned to enhance the spatial sampling ability and improve the classification performance. The main contributions of the method in this study are as follows: (1) The DSDCN module can focus more on the position related to the object when extracting features, better adapt to different shapes of objects, and extract finer features than traditional convolution. (2) The depthwise separable convolution is used in the DSDCN module instead of standard convolution for the calculation of offsets, which has the advantage of being lightweight and improves the ability of feature extraction of the model. (3) The residual blocks in ResNet do not introduce additional parameters, so the complexity of the model is not affected, and the jump connection can realize information exchange between different layers. (4) By migrating the model parameters, the problem of insufficient data is effectively solved, and the classification accuracy is further improved.
Several experiments were conducted under different models, and the results were as follows: (1) The classification accuracy for sonar images with the method in this study was 95.5%, which was 6.83% better, on average, compared with the baseline model ResNet_0, VGGNet, UNet, and Light-ResNet. At the same time, it had a slight advantage in terms of computational consumption. (2) In the ablation experiment of DSDCN module, the classification accuracy of the model ResNet_0 without the DSDCN module was only 83.1%, and the classification accuracy of the other four models with DSDCN added at other positions was on average 5.1% lower than the model in this paper, and the classification performance of this model was better. (3) When using deformable images for underwater object classification, the classification results of the DSDCN-ResNet in this paper had improved in accuracy, recall, and F1 scores, with an average increase of 5.3%, 5.6%, and 5.8% respectively. (4) The classification accuracy of the model trained by the transfer learning method was higher than that without the method, about 7.4%.
In summary, the classification method proposed in this paper has high accuracy, compared with other models, and it has certain advantages in terms of parameters and computation. However, the study also had some limitations due to the high cost of acquiring sonar images, resulting in a small number of real images used in the experiments, and the deformable convolution module made the training time of the model longer. To solve the above problems, our future research will focus on the following: First, new data simulation methods will be studied to minimize the difference between the simulated and real images to obtain increasingly realistic simulated images. Second, the optimal feature set of the sonar images will be studied, and efficient feature extraction methods will be used to extract features; the classification accuracy of the model will be further improved for different scales and different types of objects. Finally, new model optimization methods will be investigated to reduce model training time and improve the model classification performance.
Author Contributions
J.T. gave academic guidance to this research work and put forward feasible suggestions for the research content. The manuscript has also been modified by J.L. in its content and structure. W.G. designed the core method proposed in this paper, wrote the program, carried out the relevant experimental verification, and drafted the manuscript. B.L. guided the general direction of the article research and provided a research framework for the subject. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Institute of Acoustics, Chinese Academy of Sciences, under a project entitled, “Intelligent Classification of Underwater Objects in Sonar Images”. The funding number is E151130101.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Karras, G.C.; Marantos, P.; Bechlioulis, C.P.; Kyriakopoulos, K.J. Unsupervised Online System Identification for Underwater Robotic Vehicles. IEEE J. Ocean. Eng. 2019, 44, 642–663. [Google Scholar] [CrossRef]
- Luo, X.W.; Feng, Y.L.; Zhang, M.H. An Underwater Acoustic Target Recognition Method Based on Combined Feature with Automatic Coding and Reconstruction. IEEE Access 2021, 9, 63841–63854. [Google Scholar] [CrossRef]
- Wilbur, J.; McDonald, R.J.; Stack, J. Contourlet detection and feature extraction for automatic target recognition. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 2734–2738. [Google Scholar]
- Liu, J.Y. Advancement of Synthetic Aperture Sonar Technique. Bull. Chin. Acad. Sci. 2019, 34, 283–288. [Google Scholar]
- Gerg, I.D.; Monga, V. Structural Prior Driven Regularized Deep Learning for Sonar Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4200416. [Google Scholar] [CrossRef]
- Williams, D.P.; Dugelay, S. Multi-view SAS image classification using deep learning. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey, Monterey, CA, USA, 19–23 September 2016; pp. 1–9. [Google Scholar]
- Courmontagne, P. A review on Stochastic Matched Filter based denoising methods for SAS images despeckling. In Proceedings of the OCEANS 2007 -Europe, Aberdeen, UK, 18–21 June 2007; pp. 1–6. [Google Scholar]
- Lopera, O.; Heremans, R.; Pizurica, A.; Dupont, Y. Filtering speckle noise in SAS images to improve detection and identification of seafloor targets. In Proceedings of the 2010 International WaterSide Security Conference, Carrara, Italy, 3–5 November 2010; pp. 1–4. [Google Scholar]
- Myers, V.; Fawcett, J. A Template Matching Procedure for Automatic Target Recognition in Synthetic Aperture Sonar Imagery. IEEE Signal Process. Lett. 2010, 17, 683–686. [Google Scholar] [CrossRef]
- Xu, W.H.; Xu, Y.J.; Dong, L.L.; Li, Y. Level-set and SVM based target recognition of image sonar. Chin. J. Sci. Instrum. 2012, 33, 49–55. [Google Scholar]
- Zhang, M.J.; Zhang, L.; Wan, Y.Y. Underwater target recognition based on feature fusion. J. Harbin Eng. Univ. 2011, 32, 1190–1195. [Google Scholar]
- Zhu, P.P.; Isaacs, J.; Fu, B.; Ferrari, S. Deep learning feature extraction for target recognition and classification in underwater sonar images. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 2724–2731. [Google Scholar]
- Palomeras, N.; Furfaro, T.; Williams, D.P.; Carreras, M.; Dugelay, S. Automatic Target Recognition for Mine Countermeasure Missions Using Forward-Looking Sonar Data. IEEE J. Ocean. Eng. 2021, 47, 141–161. [Google Scholar] [CrossRef]
- Le, H.T.; Phung, S.L.; Chapple, P.B.; Bouzerdoum, A.; Ritz, C.H. Deep Gabor Neural Network for Automatic Detection of Mine-Like Objects in Sonar Imagery. IEEE Access 2020, 8, 94126–94139. [Google Scholar]
- Lawal, M.O. Tomato detection based on modified YOLOv3 framework. Sci. Rep. 2021, 11, 1447. [Google Scholar] [CrossRef]
- Roy, A.M.; Bose, R.; Bhaduri, J. A fast accurate fine-grain object detection model based on YOLOv4 deep neural network. Neural Comput. Appl. 2022, 34, 3895–3921. [Google Scholar] [CrossRef]
- Roy, A.M.; Bhaduri, J.; Kumar, T.; Raj, K. WilDect-YOLO: An efficient and robust computer vision-based accurate object localization model for automated endangered wildlife detection. Ecol. Inform. 2022, 101919. [Google Scholar] [CrossRef]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. arXiv 2017, arXiv:1703.06211. [Google Scholar]
- Chen, Q.; Shen, F.; Ding, Y.; Gong, P.; Tao, Y.; Wang, J. Face Detection Using R-FCN Based Deformable Convolutional Networks. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 4165–4170. [Google Scholar]
- Cao, Z.Y.; Li, X.R.; Zhao, L.Y. Object Detection in VHR Image Using Transfer Learning with Deformable Convolution. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 326–329. [Google Scholar]
- Gao, X.; Li, H.; Zhang, Y. Vehicle Detection in Remote Sensing Images of Dense Areas Based on Deformable Convolution Neural Network. J. Electron. Inf. Technol. 2018, 40, 2812–2819. [Google Scholar]
- Roy, A.M. Adaptive transfer learning-based multiscale feature fused deep convolutional neural network for EEG MI multiclassification in brain–computer interface. Eng. Appl. Artif. Intell. 2022, 116, 105347. [Google Scholar] [CrossRef]
- Gough, P.T.; Hawkins, D.W. A short history of synthetic aperture sonar. IGARSS ’98. Sensing and Managing the Environment. In Proceedings of the 1998 IEEE International Geoscience and Remote Sensing. Symposium Proceedings. (Cat. No.98CH36174), Seattle, WA, USA, 6–10 July 1998; Volume 2, pp. 618–620. [Google Scholar]
- Xia, P.; Zhang, G.Y.; Lei, B.J.; Gong, G.Q.; Zou, Y.B.; Tang, T.L. Sonar image enhancement of digraph and Gaussian mixture model in complex contourlet domain. Acta Acust. 2021, 46, 529–539. [Google Scholar]
- Ban, D.X. Research and Application of Synthetic Aperture Sonar Image Preprocessing Technology. Master’s Thesis, Hangzhou Dianzi University, Hangzhou, China, 2020. [Google Scholar]
- Cao, X.; Zhang, X.M.; Yu, Y. Deep learning-based recognition of underwater target. In Proceedings of the IEEE International Conference on Digital Signal Processing (DSP), Beijing, China, 16–18 October 2016; pp. 89–93. [Google Scholar]
- Yuan, Y.Q.; Li, P.F. Research on Sonar Image Classification Algorithm Based on Deep Learning. In Proceedings of the 2021 2nd International Seminar on Artificial Intelligence, Networking and Information Technology (AINIT), Shanghai, China, 15–17 October 2021; pp. 12–15. [Google Scholar]
- Jin, L.L.; Liang, H.; Yang, C.S. Sonar image recognition of underwater target based on convolutional neural network. J. Northwestern Polytech. Univ. 2021, 39, 285–291. [Google Scholar] [CrossRef]
- Xi, W.; Sun, L.; Sun, J. Upgrade your network in-place with deformable convolution. In Proceedings of the 2020 19th International Symposium on Distributed Computing and Applications for Business Engineering and Science (DCABES), Xuzhou, China, 16–19 October 2020; pp. 239–242. [Google Scholar]
- Wang, Z.; Wang, C.; Pei, J.; Huang, Y.; Zhang, Y.; Yang, H. A Deformable Convolution Neural Network for SAR ATR. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2639–2642. [Google Scholar]
- Gong, W.; Tian, J.; Liu, J. Underwater Object Classification Method Based on Depthwise Separable Convolution Feature Fusion in Sonar Images. Appl. Sci. 2022, 12, 3268. [Google Scholar] [CrossRef]
- Ke, X.; Zhang, X.L.; Zhang, T.W. SAR Ship Detection Based on an Improved Faster R-CNN Using Deformable Convolution. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 3565–3568. [Google Scholar]
- Deng, S.Y.; Liu, C.Z.; Kang, Z.; Li, Z.W.; Liu, D.L.; Zhang, N.; Zhu, C.W.; Niu, B.L.; Chen, L.; Ding, Y.G. Automatic measurement of stellar atmospheric physical parameters based on deformable convolutional network. Sci. Technol. Eng. 2021, 21, 5223–5227. [Google Scholar]
- Mahajan, A.; Chaudhary, S. Categorical Image Classification Based on Representational Deep Network (RESNET). In Proceedings of the 2019 3rd International Conference on Electronics, Communication and Aerospace Technology (ICECA), online, 12–14 June 2019; pp. 327–330. [Google Scholar]
- Liu, F.L.; Li, W.H.; Gong, W.G. Deformable Feature Map Residual Network for Urban Sound Recognition. J. Comput.-Aided Des. Comput. Graph. 2020, 32, 1853–1862. [Google Scholar]
- Qiang, W.; He, Y.; Guo, Y.; Li, B.; He, L. Exploring Underwater Target Detection Algorithm Based on Improved SSD. J. Northwestern Polytech. Univ. 2020, 38, 747–754. [Google Scholar] [CrossRef]
- Gong, W.J.; Tian, J.; Li, B.Q.; Liu, J.Y. Acoustic-optical image fusion underwater target classification method based on improved MobilenetV2. J. Appl. Acoust. 2022, 3, 462–470. [Google Scholar]
- Shi, H.H.; Xu, Y.N.; Teng, W.X.; Wang, N. Scene classification of high-resolution remote sensing imagery based on deep transfer deformable convolutional neural networks. Acta Geod. Cartogr. Sin. 2021, 50, 652–663. [Google Scholar]
- Chen, M.; Mei, X.; Zhu, W.J.; Zhou, Y.; Zhang, M.Y.; Feng, L.H. A novel pulmonary nodule segmentation method using Mobile-Unet network. J. Nanjing Tech Univ. (Nat. Sci. Ed.) 2022, 44, 76–81+91. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).