Effect of Interatomic Potential on Simulation of Fracture Behavior of Cu/Graphene Composite: A Molecular Dynamics Study
Abstract
1. Introduction
2. Simulation Details
2.1. Interatomic Potential
2.1.1. AIREBO Potential
2.1.2. Morse Potential
2.1.3. EAM and Morse Potential
2.1.4. BOP Potential
2.2. Initial Structure
3. Results
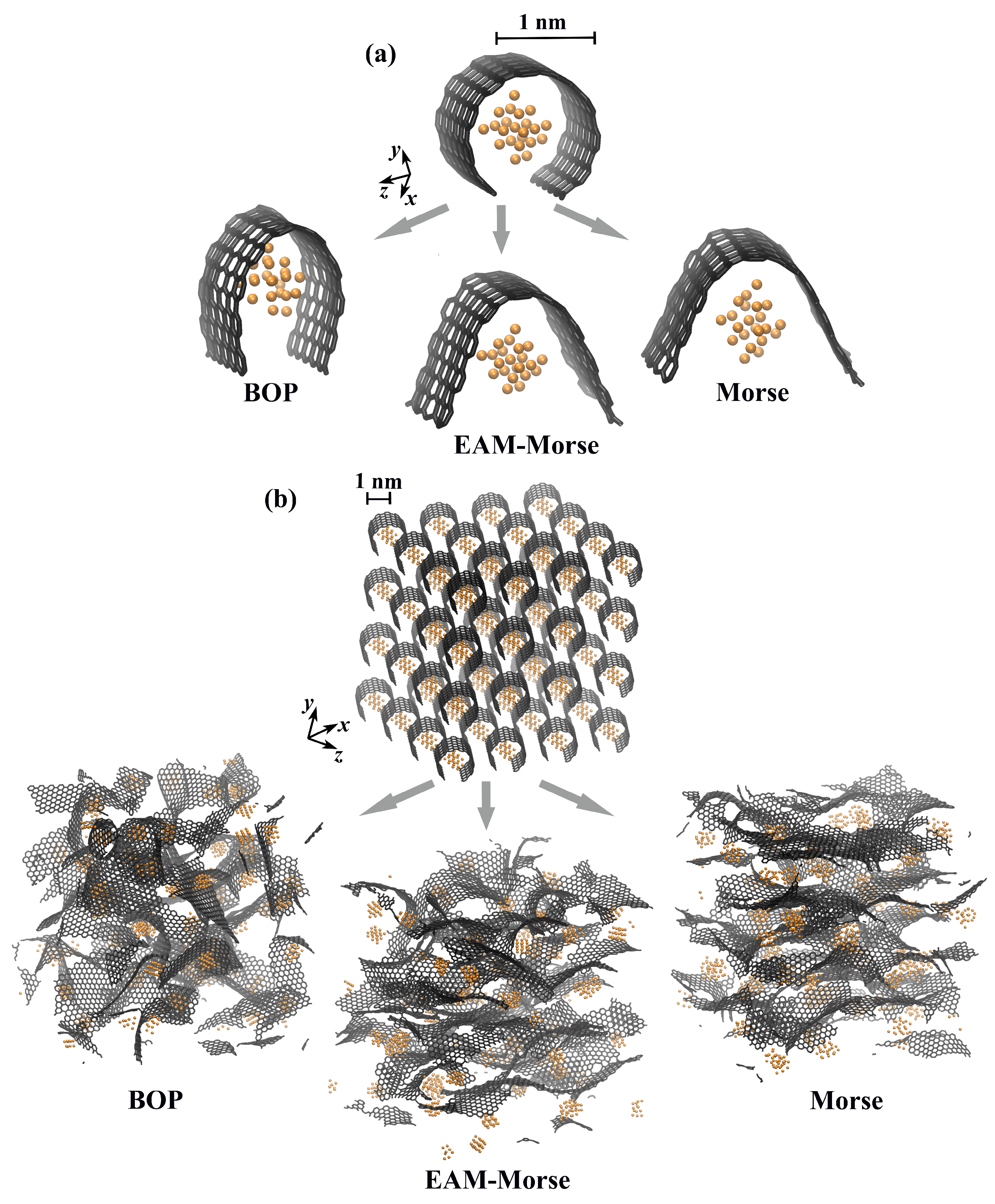
3.1. Exposure
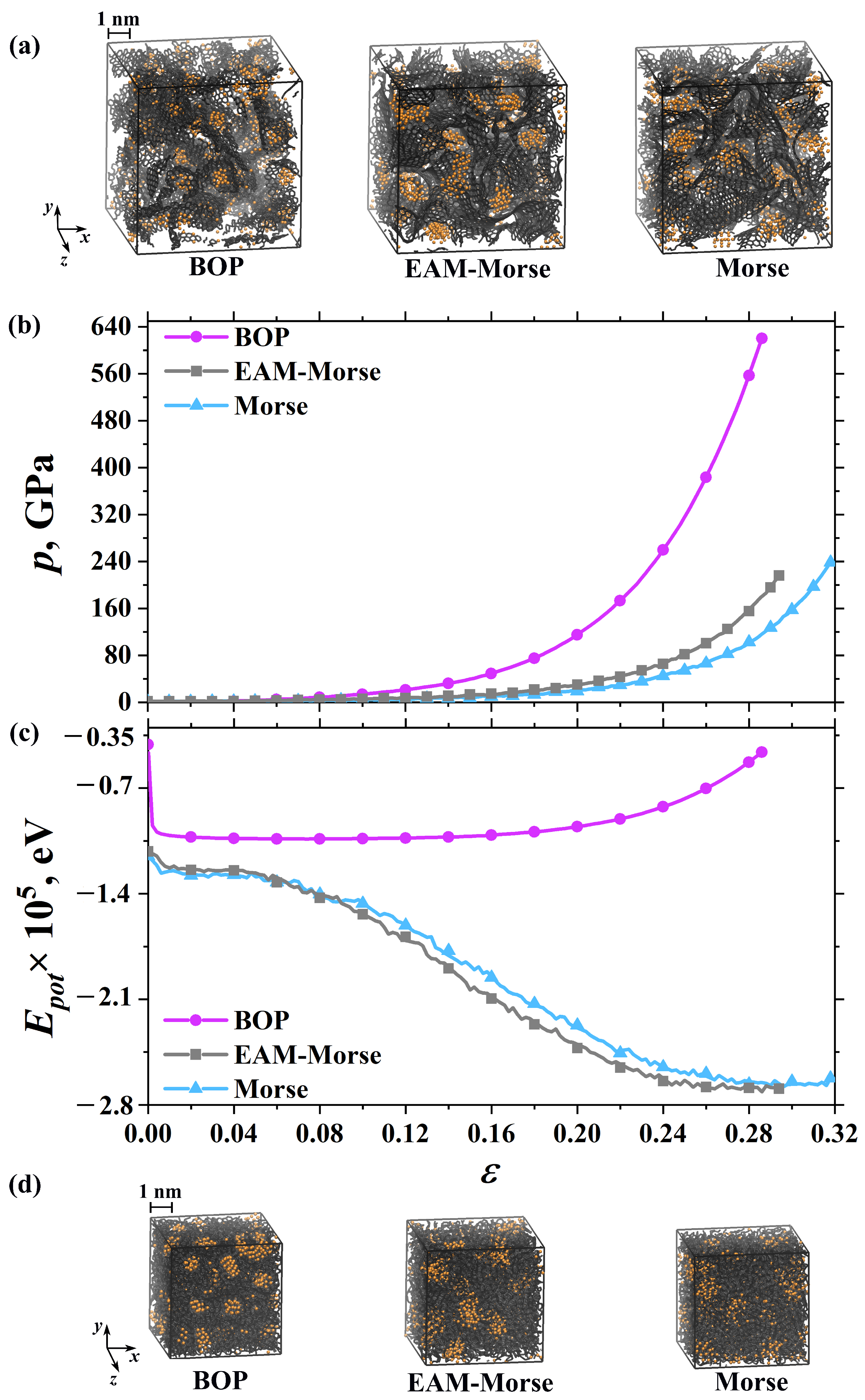
3.2. Hydrostatic Compression
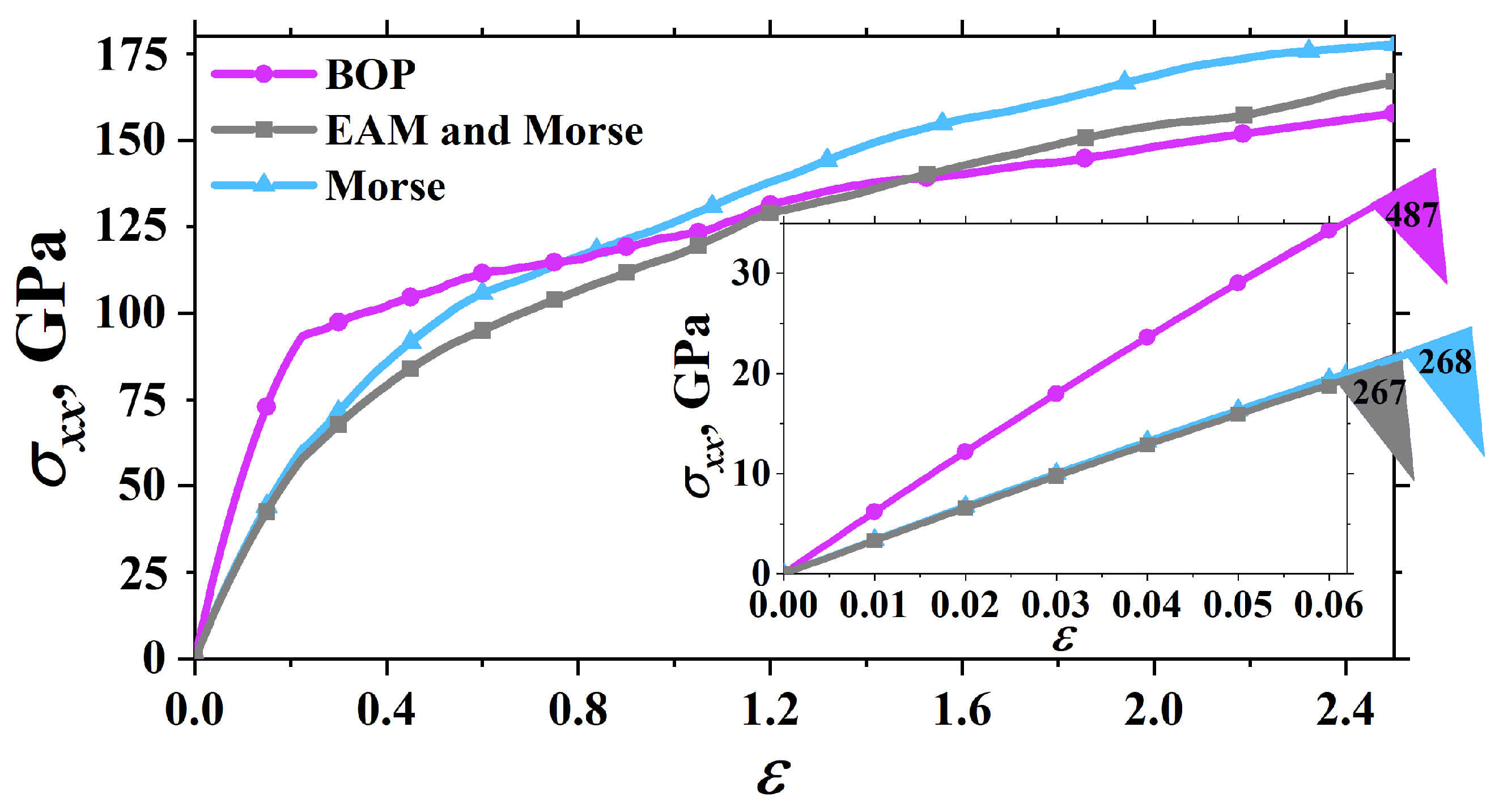
3.3. Uniaxial Tension
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Xiao, W.; Wang, J.; Sun, L.; Shi, J.; Guo, H.; Liu, Y.; Wang, L. Enhanced interfacial strength of graphene reinforced aluminum composites via X (Cu, Ni, Ti)-coating: Molecular-dynamics insights. Adv. Powder Technol. 2021, 32, 2585–2590. [Google Scholar] [CrossRef]
- Safina, L.R.; Baimova, J.A.; Krylova, K.A.; Murzaev, R.T.; Shcherbinin, S.A.; Mulyukov, R.R. Ni–Graphene Composite Obtained by Pressure–Temperature Treatment: Atomistic Simulations. Phys. Status Solidi (RRL)–Rapid Res. Lett. 2021, 15, 2100429. [Google Scholar] [CrossRef]
- Hou, B.; Liu, P.; Wang, A.; Xie, J. Interface optimization strategy for enhancing the mechanical and thermal properties of aligned graphene/Al composite. J. Alloys Compd. 2022, 900, 163555. [Google Scholar] [CrossRef]
- Wang, M.; Sheng, J.; Wang, L.D.; Wang, G.; Fei, W.D. Achieving high strength and electrical properties in drawn fine Cu matrix composite wire reinforced by in-situ grown graphene. J. Mater. Res. Technol. 2022, 17, 3205–3210. [Google Scholar] [CrossRef]
- Krylova, K.; Baimova, J.; Mulyukov, R. Effect of deformation on dehydrogenation mechanisms of crumpled graphene: Molecular dynamics simulation. Lett. Mater. 2019, 9, 81–85. [Google Scholar] [CrossRef]
- Mathew, E.E.; Balachandran, M. Crumpled and porous graphene for supercapacitor applications: A short review. Carbon Lett. 2021. [Google Scholar] [CrossRef]
- Qin, Z.; Jung, G.S.; Kang, M.J.; Buehler, M.J. The mechanics and design of a lightweight three-dimensional graphene assembly. Sci. Adv. 2017, 3, e1601536. [Google Scholar] [CrossRef]
- Wu, M.; Chen, Z.; Huang, C.; Huang, K.; Jiang, K.; Liu, J. Graphene platelet reinforced copper composites for improved tribological and thermal properties. RSC Adv. 2019, 9, 39883–39892. [Google Scholar] [CrossRef]
- Chen, D.; Feng, H.; Li, J. Graphene Oxide: Preparation, Functionalization, and Electrochemical Applications. Chem. Rev. 2012, 112, 6027–6053. [Google Scholar] [CrossRef]
- Wejrzanowski, T.; Grybczuk, M.; Chmielewski, M.; Pietrzak, K.; Kurzydlowski, K.; Strojny-Nedza, A. Thermal conductivity of metal-graphene composites. Mater. Des. 2016, 99, 163–173. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, X.; Shi, C.; Zhao, D.; Liu, E.; He, C.; Zhao, N. Comprehensive performance regulation of Cu matrix composites with graphene nanoplatelets in situ encapsulated Al2O3 nanoparticles as reinforcement. Carbon 2022, 188, 81–94. [Google Scholar] [CrossRef]
- Ali, S.; Ahmad, F.; Yusoff, P.S.M.M.; Muhamad, N.; Oñate, E.; Raza, M.R.; Malik, K. A review of graphene reinforced Cu matrix composites for thermal management of smart electronics. Compos. Part A Appl. Sci. Manuf. 2021, 144, 106357. [Google Scholar] [CrossRef]
- Zhai, W.; Lu, W.; Chen, Y.; Liu, X.; Zhou, L.; Lin, D. Gas-atomized copper-based particles encapsulated in graphene oxide for high wear-resistant composites. Compos. Part B Eng. 2019, 157, 131–139. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, Q.; Gao, L.; Ma, T.; Qiu, M.; Hu, Y.; Wang, H.; Luo, J. A molecular dynamics study of lubricating mechanism of graphene nanoflakes embedded in Cu-based nanocomposite. Appl. Surf. Sci. 2020, 511, 145620. [Google Scholar] [CrossRef]
- Lin, G.; Peng, Y.; Dong, Z.; Xiong, D.B. Tribology behavior of high-content graphene/nanograined Cu bulk composites from core/shell nanoparticles. Compos. Commun. 2021, 25, 100777. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Y.; Wang, M.; Liu, E.; Zhao, N.; Shi, C.; Lin, D.; Zhu, F.; He, C. A powder-metallurgy-based strategy toward three-dimensional graphene-like network for reinforcing copper matrix composites. Nat. Commun. 2020, 11, 2775. [Google Scholar] [CrossRef]
- Shi, L.; Liu, M.; Yang, Y.; Liu, R.; Zhang, W.; Zheng, Q.; Ren, Z. Achieving high strength and ductility in copper matrix composites with graphene network. Mater. Sci. Eng. A 2021, 828, 142107. [Google Scholar] [CrossRef]
- Shi, L.; Liu, M.; Zhang, W.; Ren, W.; Zhou, S.; Zhou, Q.; Yang, Y.; Ren, Z. Interfacial Design of Graphene Nanoplate Reinforced Copper Matrix Composites for High Mechanical Performance. JOM 2022, 74, 3082–3090. [Google Scholar] [CrossRef]
- Savin, A.V. Multistability of Carbon Nanotube Packings on Flat Substrate. Phys. Status Solidi (RRL)–Rapid Res. Lett. 2021, 16, 2100437. [Google Scholar] [CrossRef]
- Zhou, X.W.; Ward, D.K.; Foster, M.E. An analytical bond-order potential for carbon. J. Comput. Chem. 2015, 36, 1719–1735. [Google Scholar] [CrossRef]
- Yan, Y.; Lei, Y.; Liu, S. Tensile responses of carbon nanotubes-reinforced copper nanocomposites: Molecular dynamics simulation. Comput. Mater. Sci. 2018, 151, 273–277. [Google Scholar] [CrossRef]
- Safina, L.L.; Baimova, J.A. Molecular dynamics simulation of fabrication of Ni-graphene composite: Temperature effect. Micro Nano Lett. 2020, 15, 176–180. [Google Scholar] [CrossRef]
- Klaver, T.; Zhu, S.E.; Sluiter, M.; Janssen, G. Molecular dynamics simulation of graphene on Cu (1 0 0) and (1 1 1) surfaces. Carbon 2015, 82, 538–547. [Google Scholar] [CrossRef]
- Montazeri, A.; Panahi, B. MD-based estimates of enhanced load transfer in graphene/metal nanocomposites through Ni coating. Appl. Surf. Sci. 2018, 457, 1072–1080. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, C.; Pei, L.; Li, J.; Wang, R. The wrinkling and buckling of graphene induced by nanotwinned copper matrix: A molecular dynamics study. Nano Mater. Sci. 2021, 3, 95–103. [Google Scholar] [CrossRef]
- Shuang, F.; Aifantis, K.E. Dislocation-graphene interactions in Cu/graphene composites and the effect of boundary conditions: A molecular dynamics study. Carbon 2021, 172, 50–70. [Google Scholar] [CrossRef]
- Safina, L.R.; Krylova, K.A.; Baimova, J.A. Molecular dynamics study of the mechanical properties and deformation behavior of graphene/metal composites. Mater. Today Phys. 2022, 28, 100851. [Google Scholar] [CrossRef]
- De Tomas, C.; Suarez-Martinez, I.; Marks, N.A. Graphitization of amorphous carbons: A comparative study of interatomic potentials. Carbon 2016, 109, 681–693. [Google Scholar] [CrossRef]
- Rozhkov, M.; Abramenko, N.; Kolesnikova, A.; Romanov, A. Zero misorientation interfaces in graphene. Lett. Mater. 2020, 10, 551–557. [Google Scholar] [CrossRef]
- Hong, Y.; Li, L.; Zeng, X.C.; Zhang, J. Tuning thermal contact conductance at graphene–copper interface via surface nanoengineering. Nanoscale 2015, 7, 6286–6294. [Google Scholar] [CrossRef]
- Krylova, K.A.; Safina, L.R.; Murzaev, R.T.; Baimova, J.A.; Mulyukov, R.R. Effect of Nanoparticle Size on the Mechanical Strength of Ni–Graphene Composites. Materials 2021, 14, 3087. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Liu, M.; Du, J.; Zhang, W.; Zhou, S.; Ren, W.; Zhou, Q.; Shi, L. Construction of graphene network in Ni matrix composites: A molecular dynamics study of densification process. Carbon 2022, 191, 55–66. [Google Scholar] [CrossRef]
- Goh, B.; Choi, J. Mechanical evaluation of bidirectional surface deformation in contact between nanometer-sized carbon particle and copper substrate: A molecular dynamics approach. Surfaces Interfaces 2021, 26, 101388. [Google Scholar] [CrossRef]
- Baimova, Y.A.; Murzaev, R.T.; Dmitriev, S.V. Mechanical properties of bulk carbon nanomaterials. Phys. Solid State 2014, 56, 2010–2016. [Google Scholar] [CrossRef]
- Safina, L.; Baimova, J.; Krylova, K.; Murzaev, R.; Mulyukov, R. Simulation of metal-graphene composites by molecular dynamics: A review. Lett. Mater. 2020, 10, 351–360. [Google Scholar] [CrossRef]
- Wang, X.; Feng, S.; Qi, L.; Gao, W.; Zhang, S. Mechanical properties of Cu50Zr50 amorphous/B2-CuZr crystalline composites studied by molecular dynamic method. J. Non-Cryst. Solids 2021, 568, 120942. [Google Scholar] [CrossRef]
- Yang, Z.; Guo, Z.; Yuan, C.; Bai, X. Tribological behaviors of composites reinforced by different functionalized carbon nanotube using molecular dynamic simulation. Wear 2021, 476, 203669. [Google Scholar] [CrossRef]
- Savin, A.V.; Savina, O.I. Elastic and Plastic Deformations of Carbon Nanotubes Multilayer Packing on a Flat Substrate. J. Exp. Theor. Phys. 2022, 134, 60–68. [Google Scholar] [CrossRef]
- Zhou, K.; Liu, B.; Cai, Y.; Dmitriev, S.V.; Li, S. Modelling of Low-dimensional Functional Nanomaterials. Phys. Status Solidi (RRL)–Rapid Search Lett. 2022, 16, 2100654. [Google Scholar] [CrossRef]
- Morkina, A.Y.; Tuvalev, I.I.; Dmitriev, S.V.; Bebikhov, Y.V.; Semenov, A.S.; Sharapova, Y.R. The selection of interatomic potentials for simulation of extreme actions within the tungsten lattice. Front. Mater. Technol. 2022, 16–24. [Google Scholar] [CrossRef]
- Liang, T.; Devine, B.; Phillpot, S.R.; Sinnott, S.B. Variable Charge Reactive Potential for Hydrocarbons to Simulate Organic-Copper Interactions. J. Phys. Chem. A 2012, 116, 7976–7991. [Google Scholar] [CrossRef] [PubMed]
- Liang, T.; Shan, T.R.; Cheng, Y.T.; Devine, B.D.; Noordhoek, M.; Li, Y.; Lu, Z.; Phillpot, S.R.; Sinnott, S.B. Classical atomistic simulations of surfaces and heterogeneous interfaces with the charge-optimized many body (COMB) potentials. Mater. Sci. Eng. R Rep. 2013, 74, 255–279. [Google Scholar] [CrossRef]
- Devine, B.; Shan, T.R.; Cheng, Y.T.; McGaughey, A.J.H.; Lee, M.; Phillpot, S.R.; Sinnott, S.B. Atomistic simulations of copper oxidation and Cu/CuO interfaces using charge-optimized many-body potentials. Phys. Rev. B 2011, 84, 125308. [Google Scholar] [CrossRef]
- Elliott, J.A.; Shibuta, Y.; Amara, H.; Bichara, C.; Neyts, E.C. Atomistic modelling of CVD synthesis of carbon nanotubes and graphene. Nanoscale 2013, 5, 6662. [Google Scholar] [CrossRef]
- Yoon, S.M.; Choi, W.M.; Baik, H.; Shin, H.J.; Song, I.; Kwon, M.S.; Bae, J.J.; Kim, H.; Lee, Y.H.; Choi, J.Y. Synthesis of Multilayer Graphene Balls by Carbon Segregation from Nickel Nanoparticles. ACS Nano 2012, 6, 6803–6811. [Google Scholar] [CrossRef]
- Das, S.; Lahiri, D.; Lee, D.Y.; Agarwal, A.; Choi, W. Measurements of the adhesion energy of graphene to metallic substrates. Carbon 2013, 59, 121–129. [Google Scholar] [CrossRef]
- Xu, Z.; Buehler, M.J. Interface structure and mechanics between graphene and metal substrates: A first-principles study. J. Phys. Condens. Matter 2010, 22, 485301. [Google Scholar] [CrossRef] [PubMed]
- Lahiri, I.; Lahiri, D.; Jin, S.; Agarwal, A.; Choi, W. Carbon Nanotubes: How Strong Is Their Bond with the Substrate? ACS Nano 2011, 5, 780–787. [Google Scholar] [CrossRef]
- Moseler, M.; Cervantes-Sodi, F.; Hofmann, S.; Csányi, G.; Ferrari, A.C. Dynamic Catalyst Restructuring during Carbon Nanotube Growth. ACS Nano 2010, 4, 7587–7595. [Google Scholar] [CrossRef]
- Katin, K.P.; Prudkovskiy, V.S.; Maslov, M.M. Molecular dynamics simulation of nickel-coated graphene bending. Micro Nano Lett. 2018, 13, 160–164. [Google Scholar] [CrossRef]
- Sheinerman, A. Modeling of structure and interface controlled strength of laminated metal/graphene composites. Mech. Mater. 2021, 158, 103888. [Google Scholar] [CrossRef]
- Rezaei, R.; Deng, C.; Tavakoli-Anbaran, H.; Shariati, M. Deformation twinning-mediated pseudoelasticity in metal–graphene nanolayered membrane. Philos. Mag. Lett. 2016, 96, 322–329. [Google Scholar] [CrossRef]
- Poletaev, G.; Zorya, I.; Rakitin, R.; Iliina, M. Interatomic potentials for describing impurity atoms of light elements in fcc metals. Mater. Phys. Mech. 2019, 42. [Google Scholar] [CrossRef]
- Zalizniak, V.E.; Zolotov, O.A. Efficient embedded atom method interatomic potential for graphite and carbon nanostructures. Mol. Simul. 2017, 43, 1480–1484. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Brenner, D.W.; Shenderova, O.A.; Harrison, J.A.; Stuart, S.J.; Ni, B.; Sinnott, S.B. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J. Phys. Condens. Matter 2002, 14, 783–802. [Google Scholar] [CrossRef]
- Umeno, Y.; Yachi, Y.; Sato, M.; Shima, H. On the atomistic energetics of carbon nanotube collapse from AIREBO potential. Phys. E -Low-Dimens. Syst. Nanostruct. 2019, 106, 319–325. [Google Scholar] [CrossRef]
- Girifalco, L.A.; Weizer, V.G. Application of the Morse Potential Function to Cubic Metals. Phys. Rev. 1959, 114, 687–690. [Google Scholar] [CrossRef]
- Giovannetti, G.; Khomyakov, P.A.; Brocks, G.; Karpan, V.M.; van den Brink, J.; Kelly, P.J. Doping Graphene with Metal Contacts. Phys. Rev. Lett. 2008, 101, 026803. [Google Scholar] [CrossRef]
- He, R.; Zhao, L.; Petrone, N.; Kim, K.S.; Roth, M.; Hone, J.; Kim, P.; Pasupathy, A.; Pinczuk, A. Large Physisorption Strain in Chemical Vapor Deposition of Graphene on Copper Substrates. Nano Lett. 2012, 12, 2408–2413. [Google Scholar] [CrossRef]
- Nieto, A.; Bisht, A.; Lahiri, D.; Zhang, C.; Agarwal, A. Graphene reinforced metal and ceramic matrix composites: A review. Int. Mater. Rev. 2016, 62, 241–302. [Google Scholar] [CrossRef]
- Chen, F.; Gupta, N.; Behera, R.K.; Rohatgi, P.K. Graphene-Reinforced Aluminum Matrix Composites: A Review of Synthesis Methods and Properties. JOM 2018, 70, 837–845. [Google Scholar] [CrossRef]
- Bardotti, L.; Jensen, P.; Hoareau, A.; Treilleux, M.; Cabaud, B. Experimental Observation of Fast Diffusion of Large Antimony Clusters on Graphite Surfaces. Phys. Rev. Lett. 1995, 74, 4694–4697. [Google Scholar] [CrossRef] [PubMed]
- Galashev, A.Y.; Katin, K.P.; Maslov, M.M. Morse parameters for the interaction of metals with graphene and silicene. Phys. Lett. A 2019, 383, 252–258. [Google Scholar] [CrossRef]
- Verkhovtsev, A.V.; Schramm, S.; Solov’yov, A.V. Molecular dynamics study of the stability of a carbon nanotube atop a catalytic nanoparticle. Eur. Phys. J. D 2014, 68. [Google Scholar] [CrossRef]
- Sierra-Suarez, J.A.; Majumdar, S.; McGaughey, A.J.H.; Malen, J.A.; Higgs, C.F. Morse potential-based model for contacting composite rough surfaces: Application to self-assembled monolayer junctions. J. Appl. Phys. 2016, 119, 145306. [Google Scholar] [CrossRef]
- Krylova, K.A.; Baimova, J.A.; Lobzenko, I.P.; Rudskoy, A.I. Crumpled graphene as a hydrogen storage media: Atomistic simulation. Phys. B Condens. Matter 2020, 583, 412020. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, M.; Zhou, S.; Ren, W.; Zhou, Q.; Zhang, W. Strengthening behaviour of continuous graphene network in metal matrix composites. Carbon 2021, 182, 825–836. [Google Scholar] [CrossRef]
- Mendelev, M.; King, A. The interactions of self-interstitials with twin boundaries. Philos. Mag. 2013, 93, 1268–1278. [Google Scholar] [CrossRef]
- Daw, M.S.; Baskes, M.I. Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals. Phys. Rev. B 1984, 29, 6443–6453. [Google Scholar] [CrossRef]
- Mishin, Y.; Mehl, M.J.; Papaconstantopoulos, D.A.; Voter, A.F.; Kress, J.D. Structural stability and lattice defects in copper:Ab initio, tight-binding, and embedded-atom calculations. Phys. Rev. B 2001, 63, 224106. [Google Scholar] [CrossRef]
- Zhao, Y.; Peng, X.; Fu, T.; Sun, R.; Feng, C.; Wang, Z. MD simulation of nanoindentation on (001) and (111) surfaces of Ag–Ni multilayers. Phys. E-Low-Dimens. Syst. Nanostruct. 2015, 74, 481–488. [Google Scholar] [CrossRef]
- Weng, S.; Ning, H.; Hu, N.; Yan, C.; Fu, T.; Peng, X.; Fu, S.; Zhang, J.; Xu, C.; Sun, D.; et al. Strengthening effects of twin interface in Cu/Ni multilayer thin films—A molecular dynamics study. Mater. Des. 2016, 111, 1–8. [Google Scholar] [CrossRef]
- Weng, S.; Ning, H.; Fu, T.; Hu, N.; Zhao, Y.; Huang, C.; Peng, X. Molecular dynamics study of strengthening mechanism of nanolaminated graphene/Cu composites under compression. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef] [PubMed]
- Somlyai-Sipos, L.; Janovszky, D.; Sycheva, A.; Baumli, P. Investigation of the Melting Point Depression of Copper Nanoparticles. IOP Conf. Ser. Mater. Sci. Eng. 2020, 903, 012002. [Google Scholar] [CrossRef]
- Safina, L.R.; Murzaev, R.T. Size of Metal Nanoparticles as a Decisive Factor in the Formation of Nickel-Graphene Composite: Molecular Dynamics. J. Struct. Chem. 2021, 62, 794–801. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safina, L.R.; Rozhnova, E.A.; Murzaev, R.T.; Baimova, J.A. Effect of Interatomic Potential on Simulation of Fracture Behavior of Cu/Graphene Composite: A Molecular Dynamics Study. Appl. Sci. 2023, 13, 916. https://doi.org/10.3390/app13020916
Safina LR, Rozhnova EA, Murzaev RT, Baimova JA. Effect of Interatomic Potential on Simulation of Fracture Behavior of Cu/Graphene Composite: A Molecular Dynamics Study. Applied Sciences. 2023; 13(2):916. https://doi.org/10.3390/app13020916
Chicago/Turabian StyleSafina, Liliya R., Elizaveta A. Rozhnova, Ramil T. Murzaev, and Julia A. Baimova. 2023. "Effect of Interatomic Potential on Simulation of Fracture Behavior of Cu/Graphene Composite: A Molecular Dynamics Study" Applied Sciences 13, no. 2: 916. https://doi.org/10.3390/app13020916
APA StyleSafina, L. R., Rozhnova, E. A., Murzaev, R. T., & Baimova, J. A. (2023). Effect of Interatomic Potential on Simulation of Fracture Behavior of Cu/Graphene Composite: A Molecular Dynamics Study. Applied Sciences, 13(2), 916. https://doi.org/10.3390/app13020916








