Stiffening Cello Bridges with Design
Abstract
:1. Introduction
2. Materials and Methods
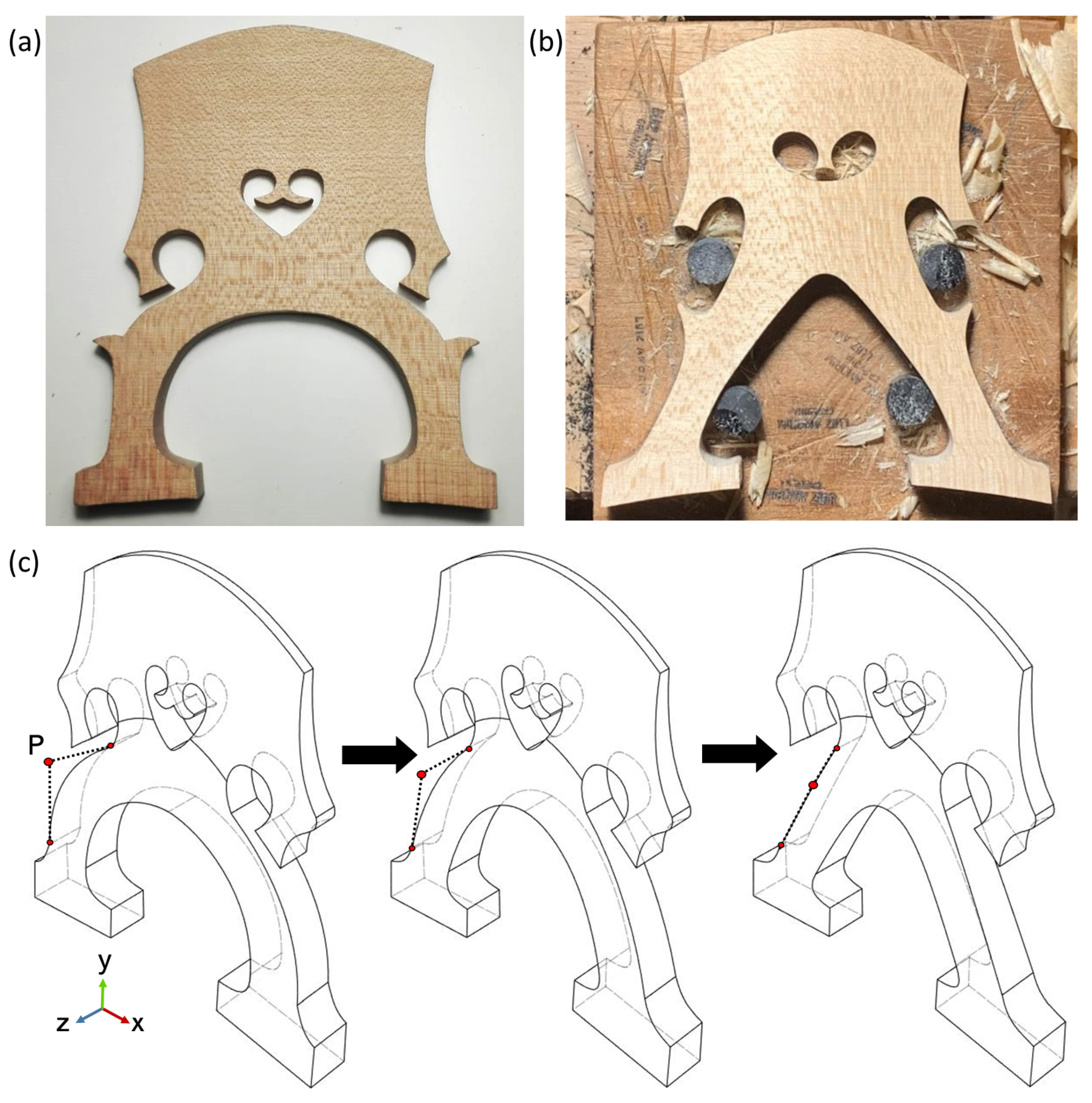
2.1. Modeling of the Bridge
2.2. Material Properties
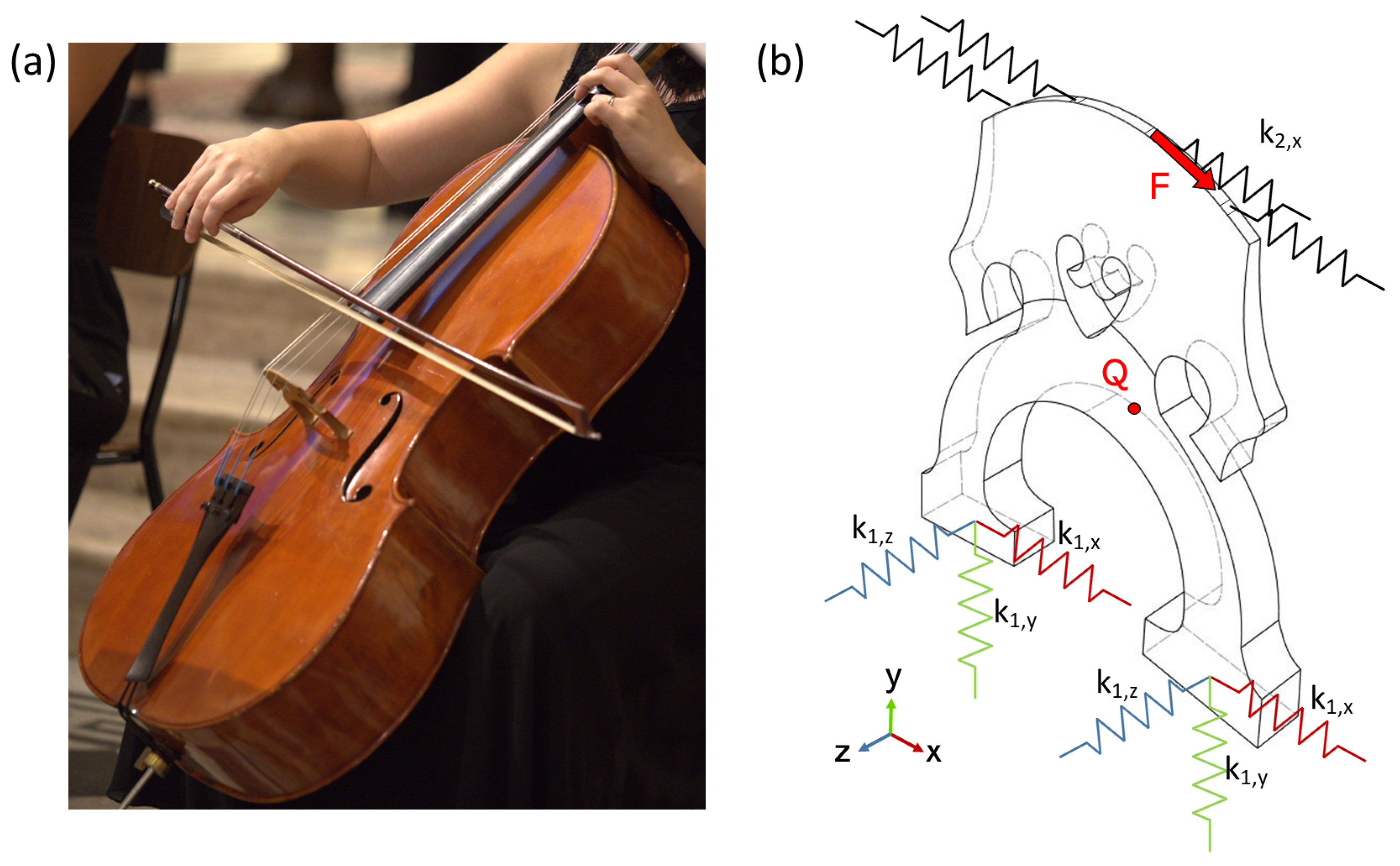
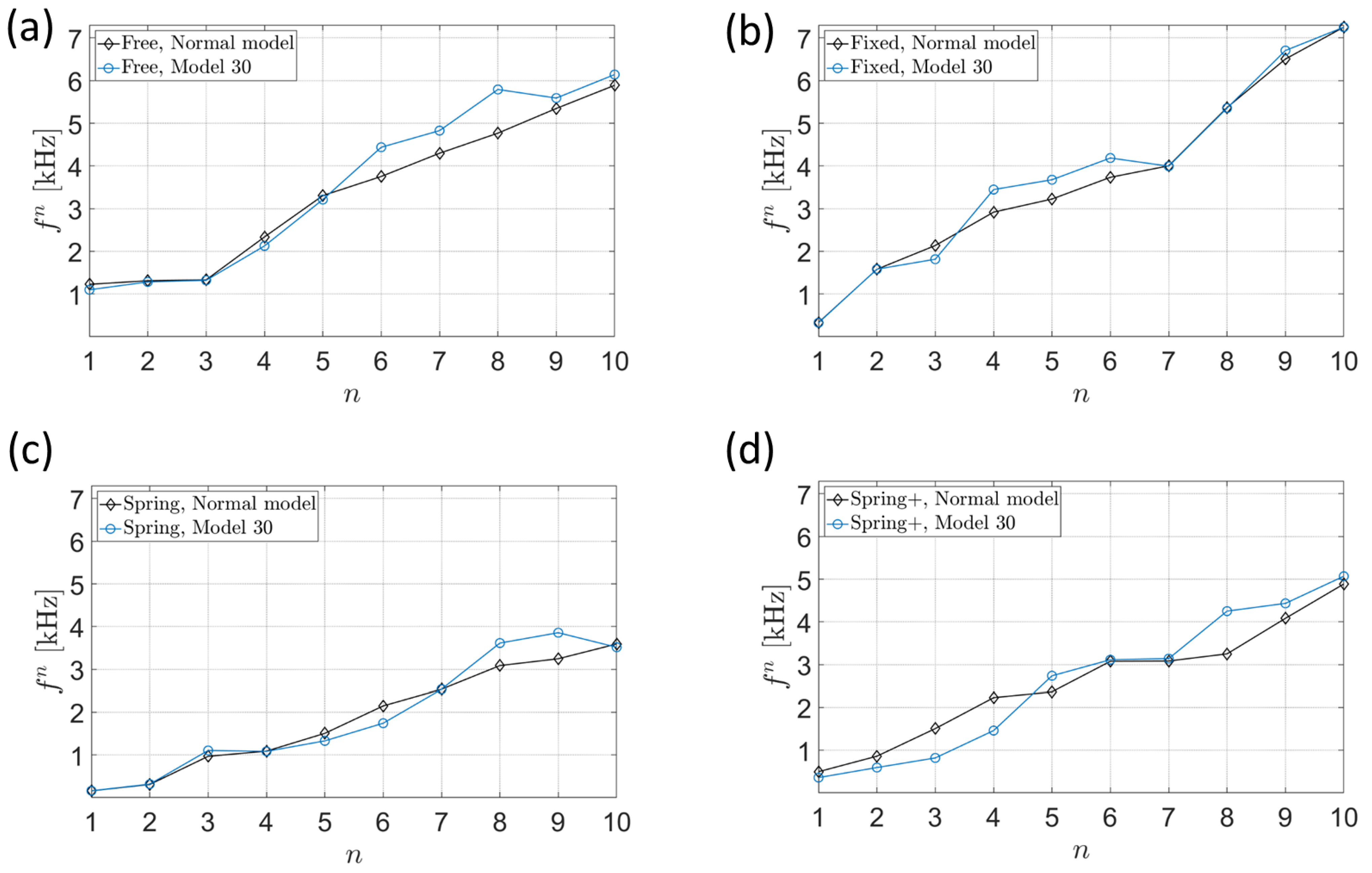
2.3. Boundary Conditions
2.4. Forcing Term and Measure Point
3. Results
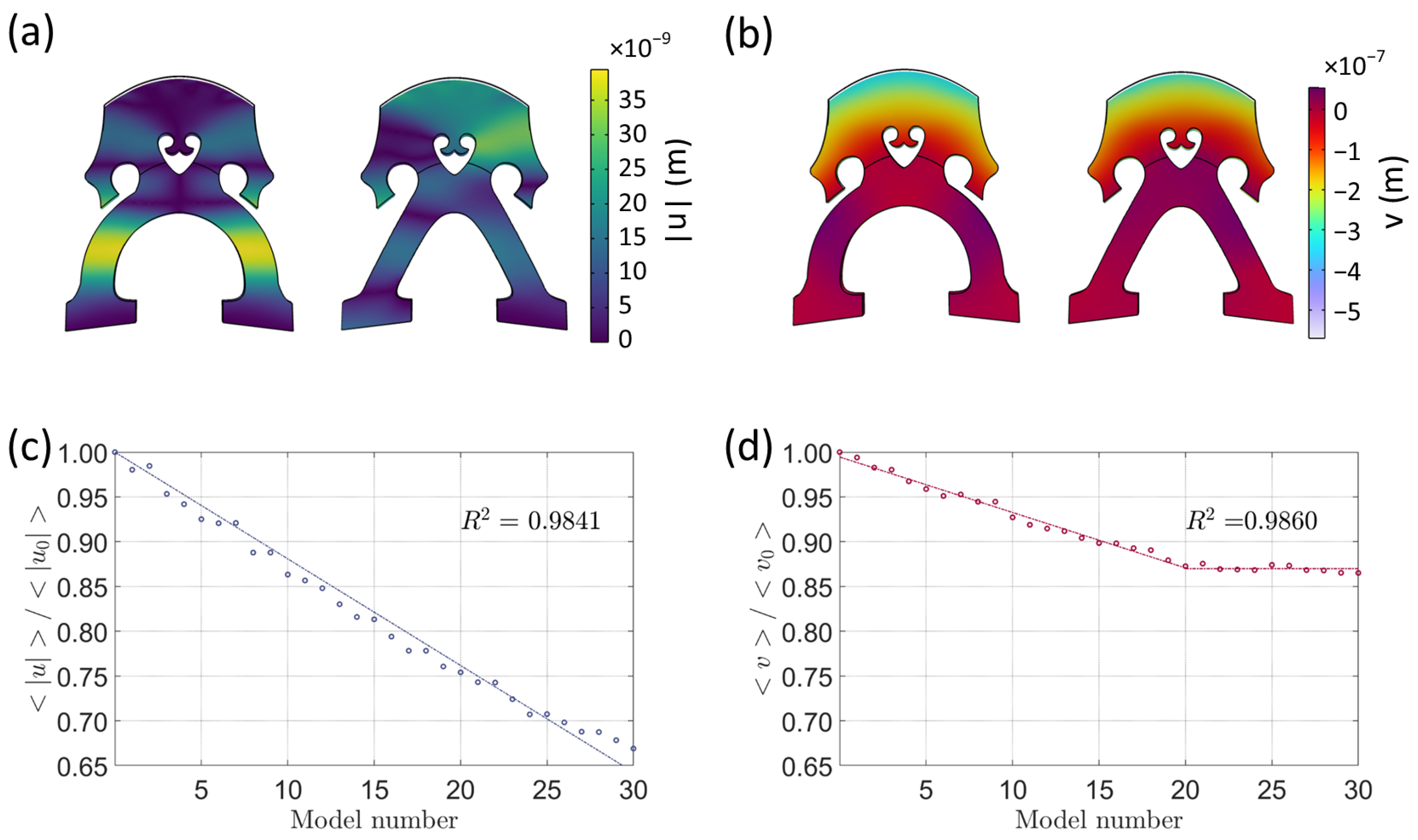
3.1. Static Behavior
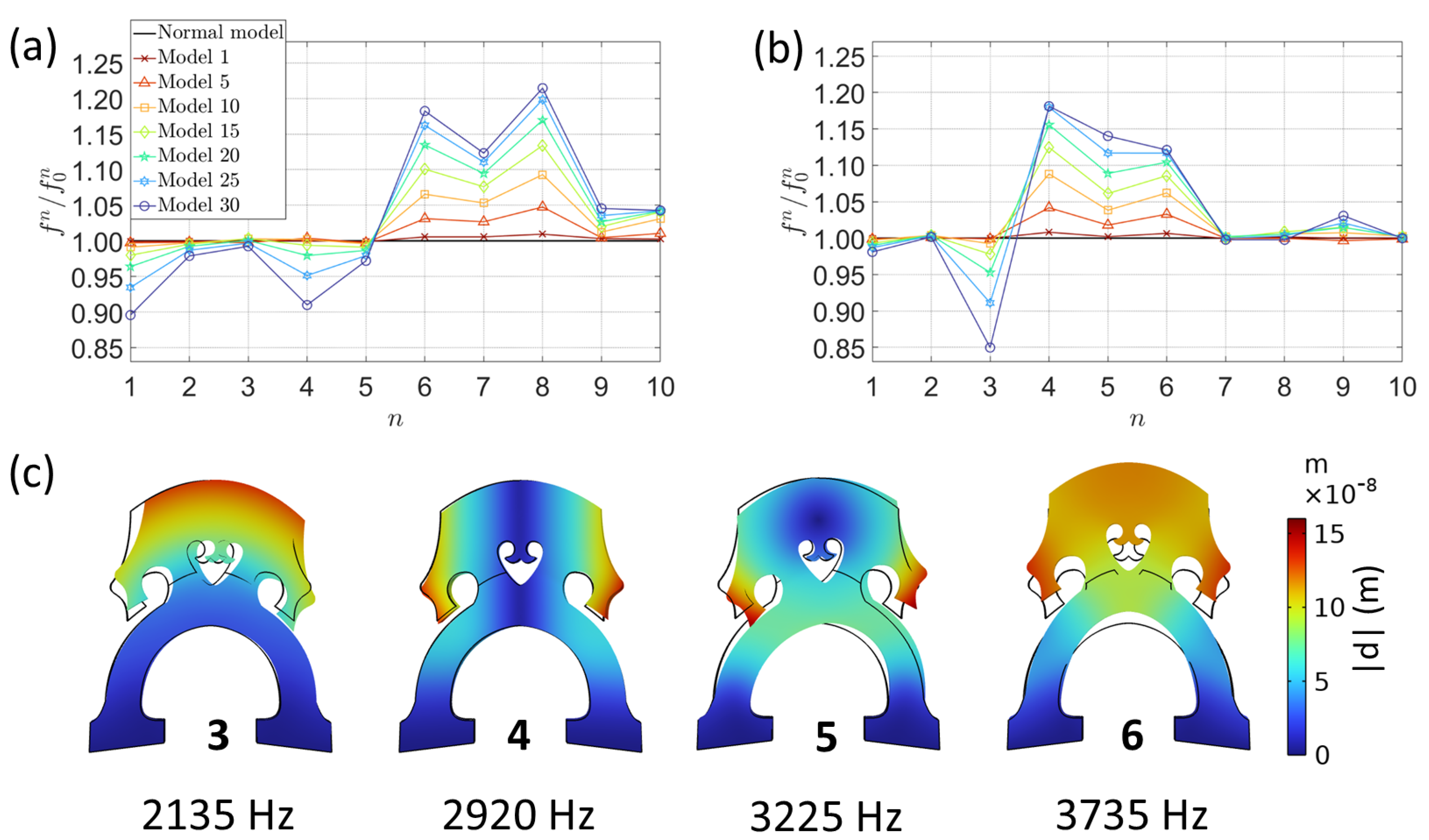
3.2. Eigenfrequency Study
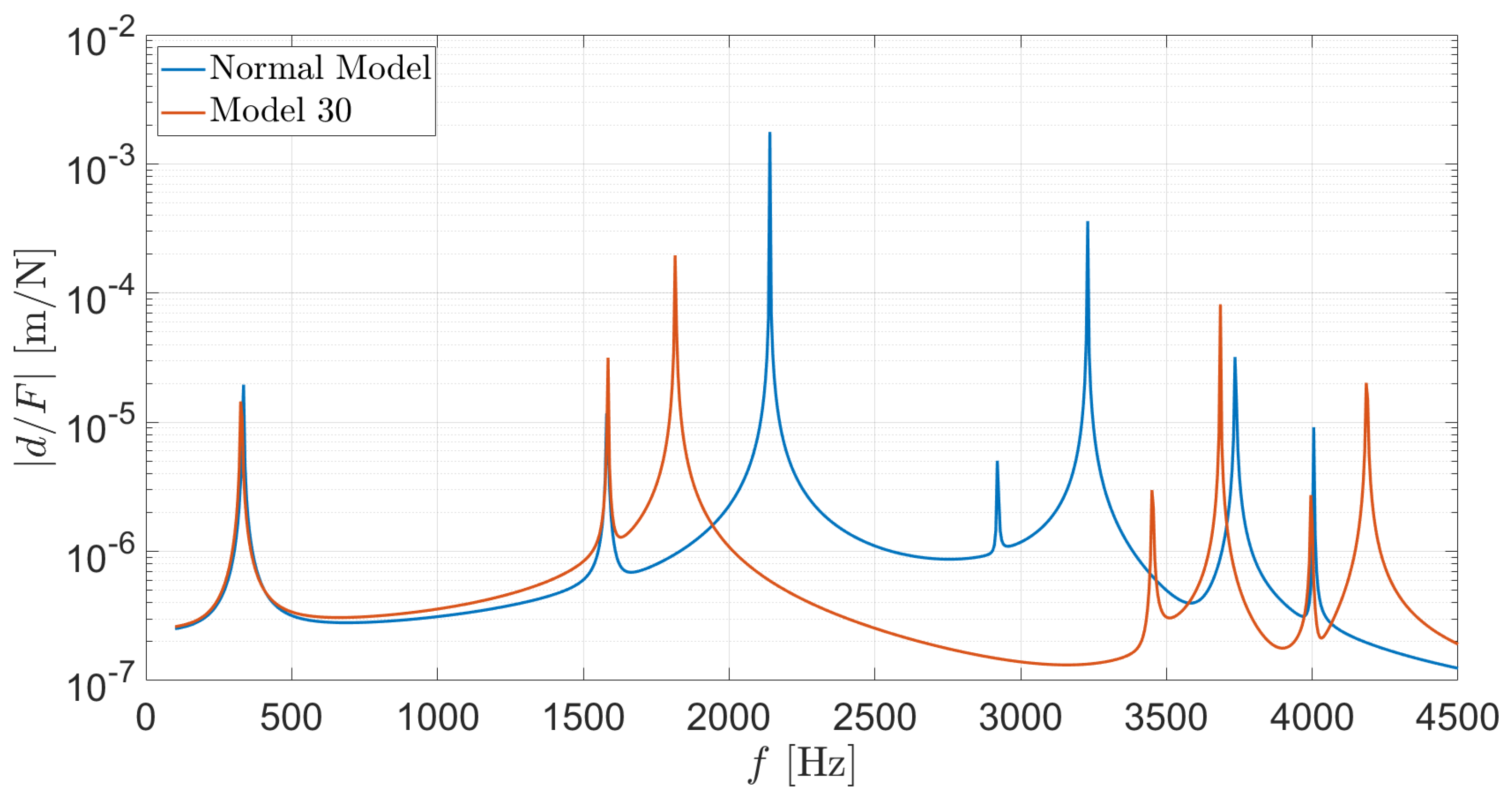
3.3. Frequency Response Function
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
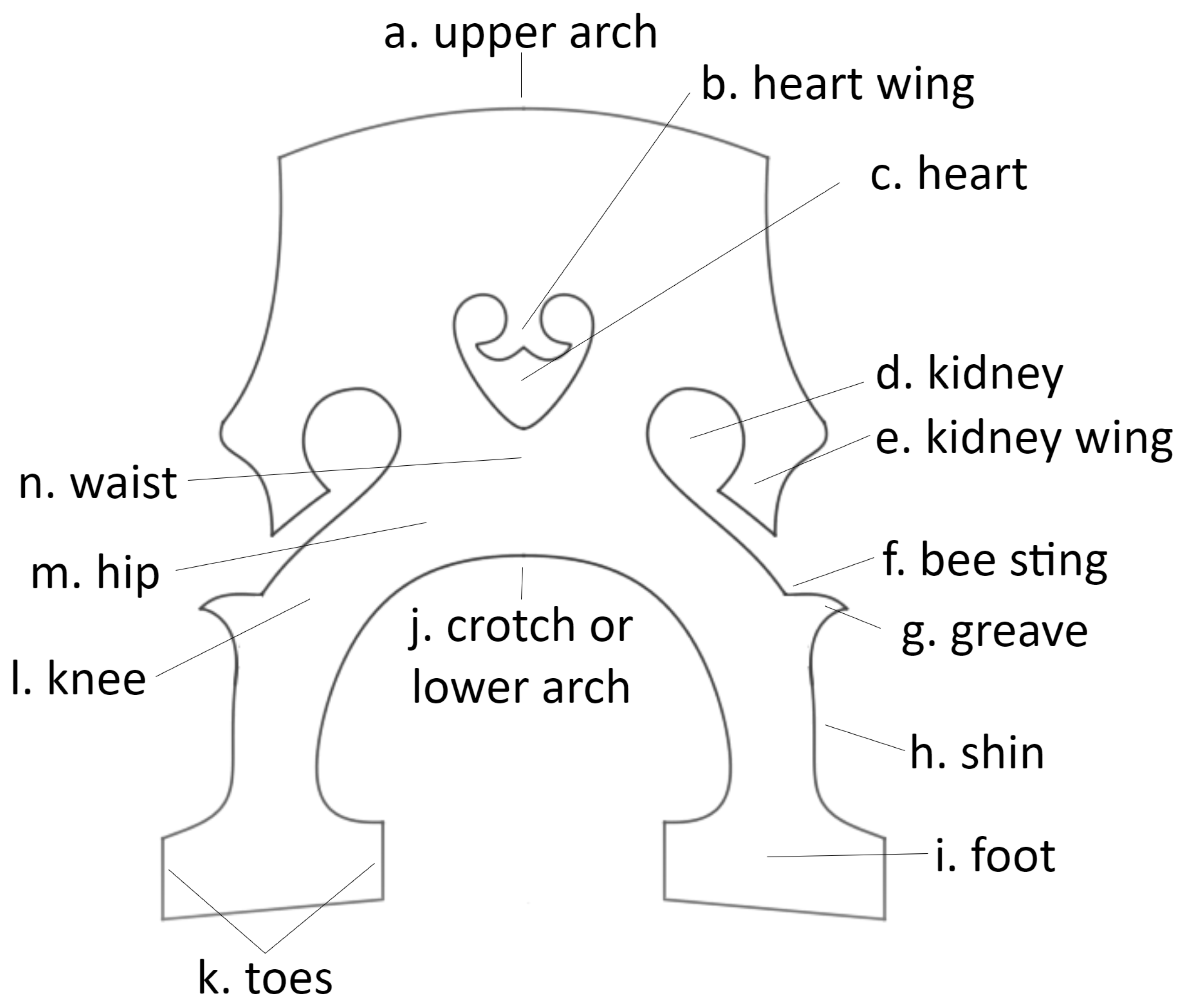
Appendix A.1. Terminology
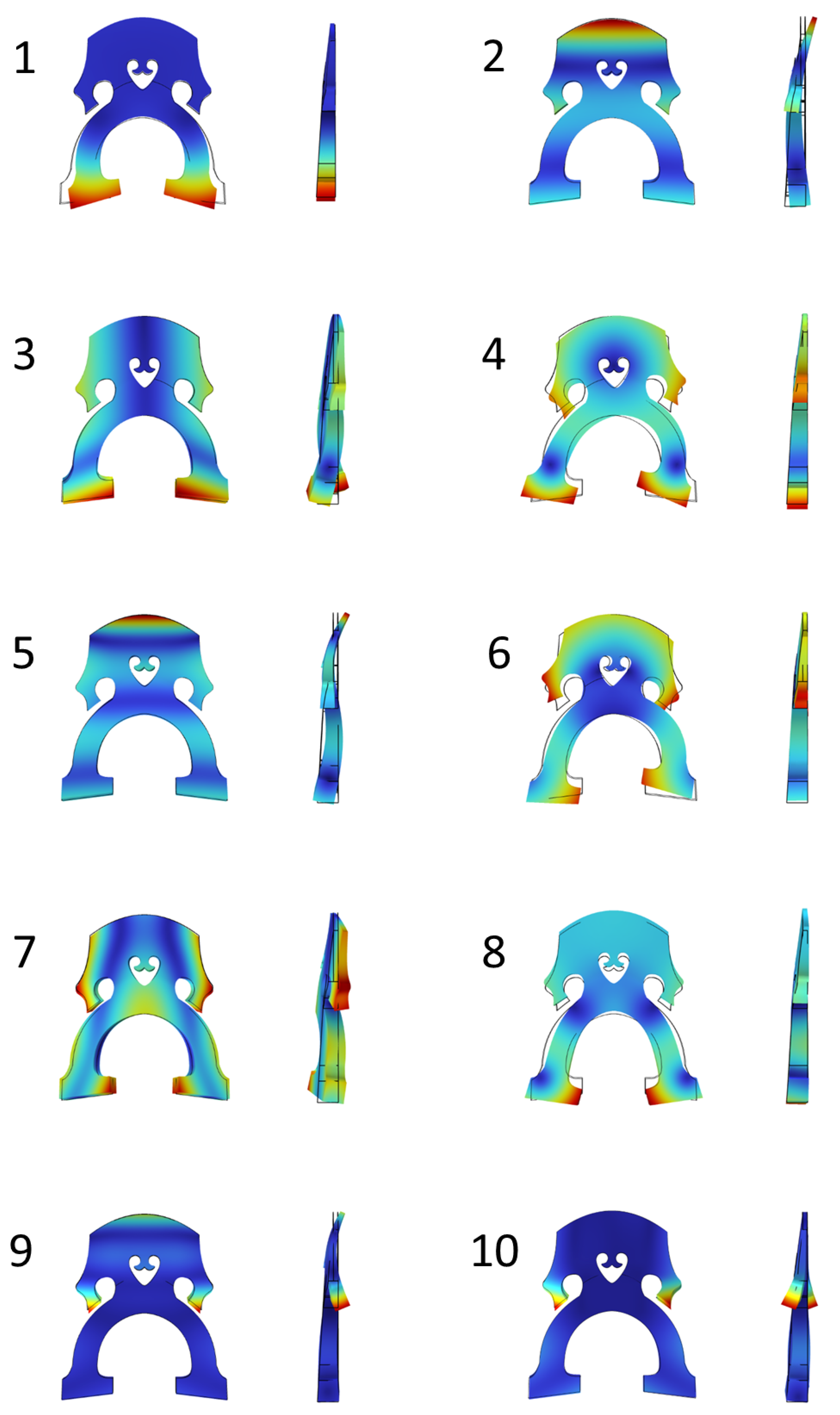
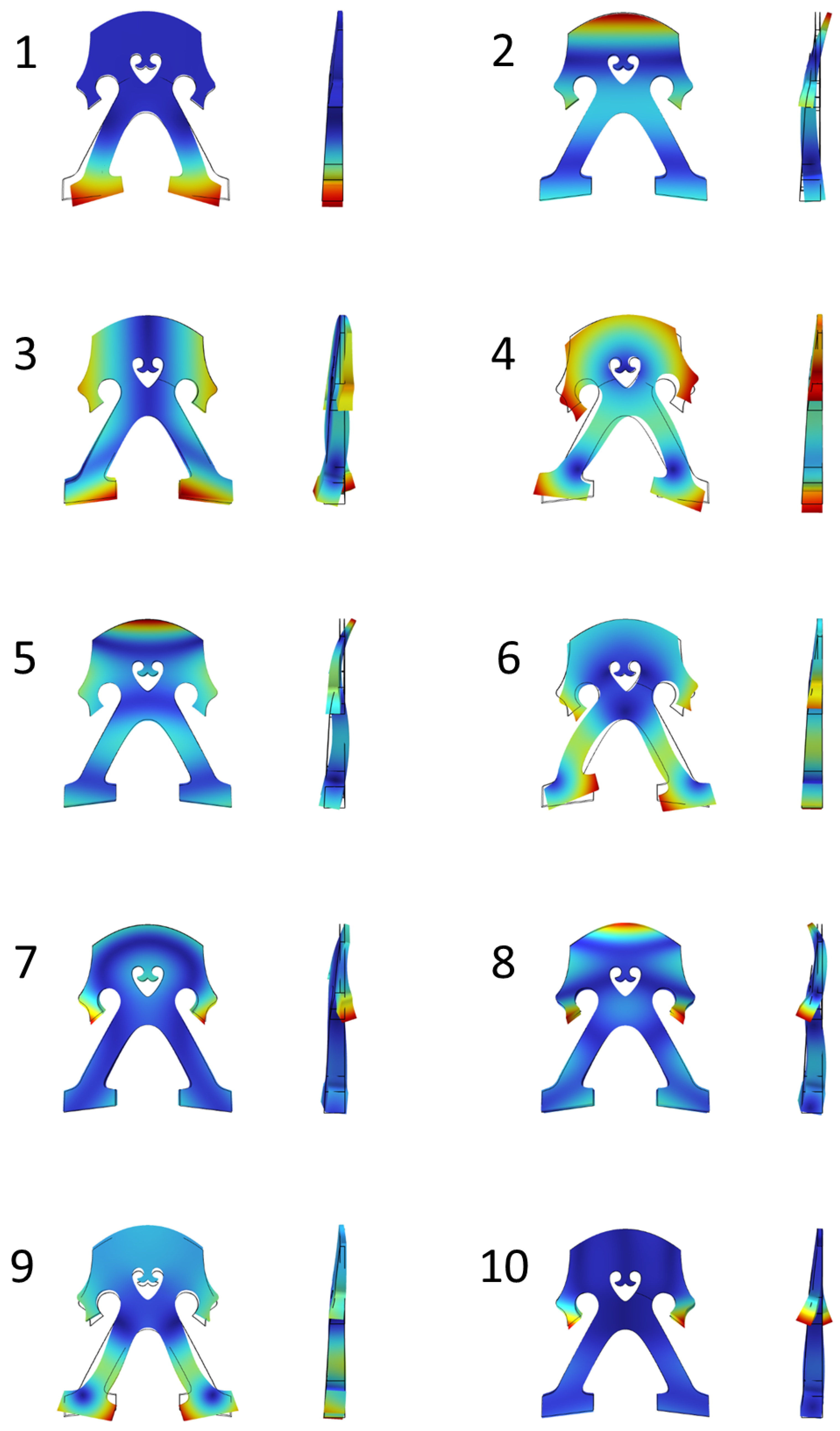
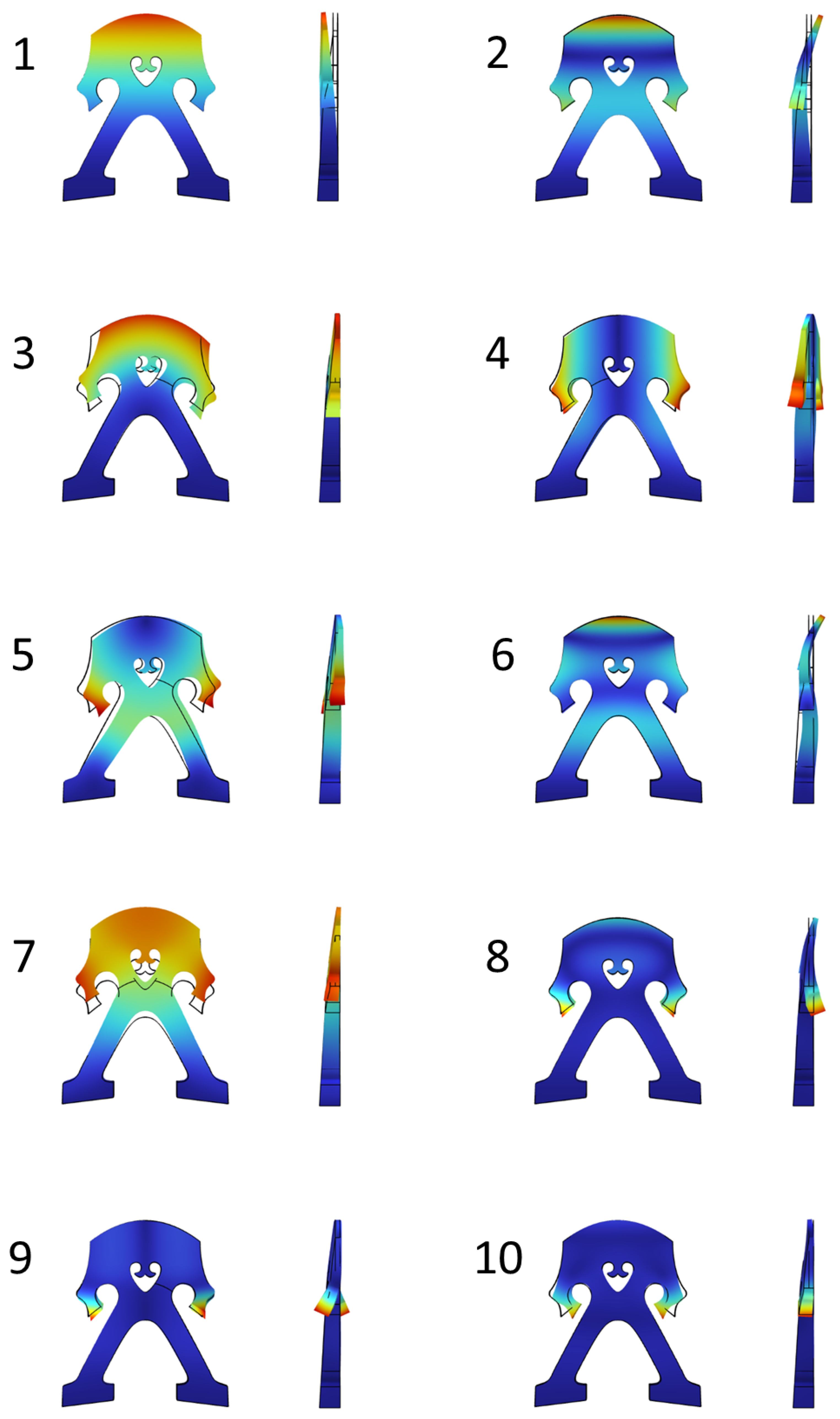
Appendix A.2. Mode Shapes




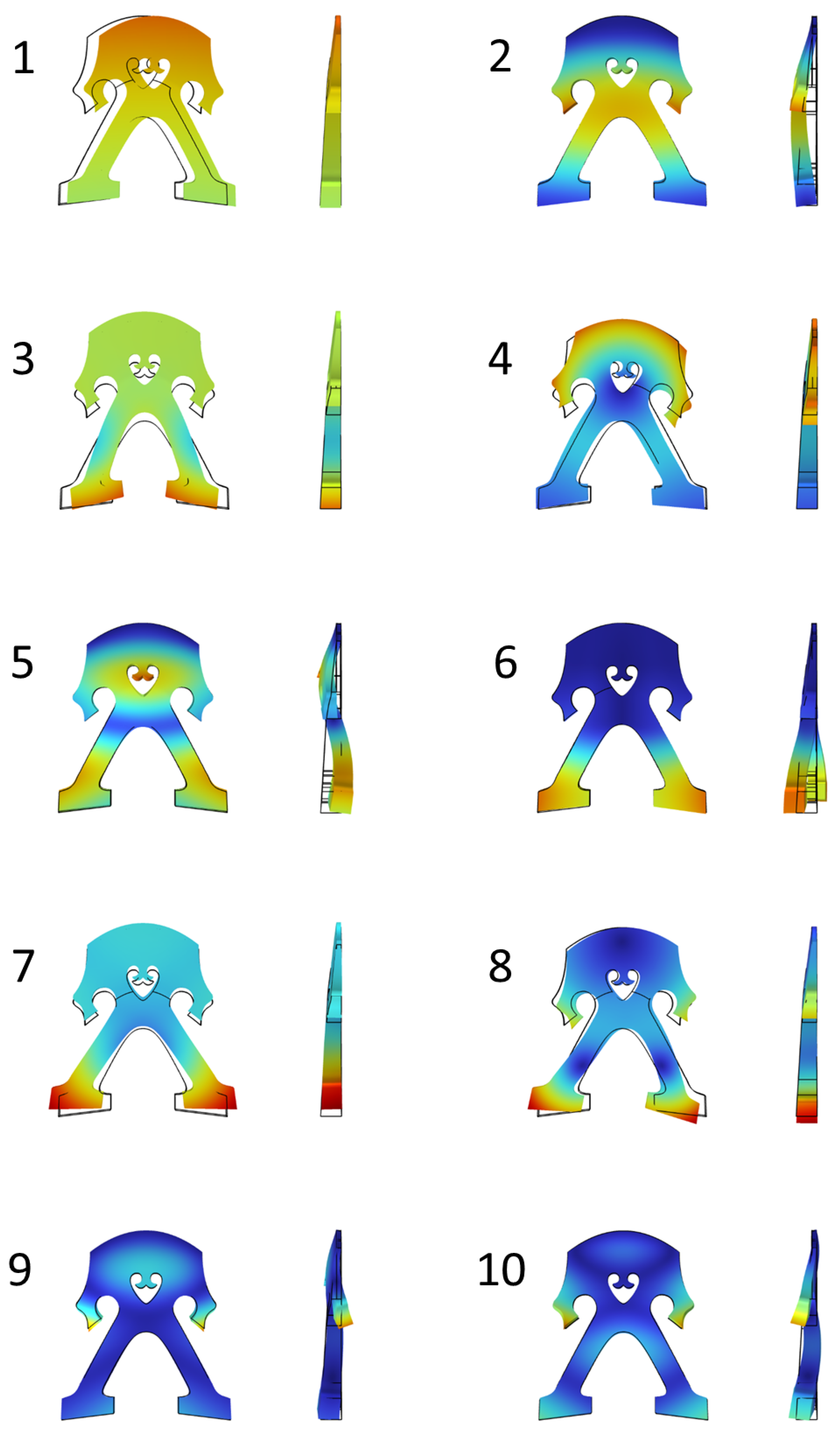
References
- Raymaekers, W. Bridge shapes of the violin and other bowed instruments, 1400–1900: The origin and evolution of their design. Early Music 2020, 48, 225–250. [Google Scholar] [CrossRef]
- Fletcher, N.H.; Rossing, T.D. The Physics of Musical Instruments; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Rossing, T.D. (Ed.) The Science of String Instruments; Springer: New York, NY, USA, 2010. [Google Scholar]
- Müller, H. The function of the violin bridge. Catgut Acoust. Soc. Newsl. 1979, 31, 19–22. [Google Scholar]
- Gough, C. Violin plate modes. J. Acoust. Soc. Am. 2015, 137, 139–153. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gonzalez, S.; Salvi, D.; Baeza, D.; Antonacci, F.; Sarti, A. A Data-driven Approach to Violin Making. Sci. Rep. 2021, 11, 9455. [Google Scholar] [CrossRef] [PubMed]
- Salvi, D.; Gonzalez, S.; Antonacci, F.; Sarti, A. Parametric optimization of violin top plates using machine learning. In Proceedings of the 27th International Congress on Sound and Vibration, ICSV 2021, Virtual, 11–16 July 2021. [Google Scholar]
- Marschke, S.; Wunderlich, L.; Ring, W.; Achterhold, K. An approach to construct a three-dimensional isogeometric model from µ-CT scan data with an application to the bridge of a violin. Comput. Aided Geom. Des. 2020, 78, 1–19. [Google Scholar] [CrossRef]
- Rodgers, O.; Masino, T. The effect of wood removal on bridge frequencies. Catgut Acoust Soc. J. 1990, 1, 6–10. [Google Scholar]
- Gonzalez, S.; Salvi, D.; Antonacci, F.; Sarti, A. Eigenfrequency Optimisation of Free Violin Plates. J. Acoust. Soc. Am. 2021, 149, 1400–1410. [Google Scholar] [CrossRef] [PubMed]
- Lercari, M.; Gonzalez, S.; Espinoza, C.; Longo, G.; Antonacci, F.; Sarti, A. Using Metamaterials in Guitar Top Plates: A Numerical Study. Appl. Sci. 2022, 12, 8619. [Google Scholar] [CrossRef]
- Gonzalez, S.; Chacra, E.; Carreño, C.; Espinoza, C. Wooden Mechanical Metamaterials: Towards tunable wood plates. Mater. Des. 2022, 221, 110952. [Google Scholar] [CrossRef]
- Kaselouris, E.; Bakarezos, M.; Tatarakis, M.; Papadogiannis, N.A.; Dimitriou, V. A Review of Finite Element Studies in String Musical Instruments. Acoustics 2022, 4, 183–202. [Google Scholar] [CrossRef]
- Kabała, A.; Niewczyk, B.K.; Gapiński, B. Violin bridge vibrations—FEM. Vib. Phys. Syst. 2018, 29, 1–7. [Google Scholar]
- Gi-Sang, C. Analysis of Vibration in Cello Bridge. J. Acoust. Soc. Korea 2006, 25, 197–206. [Google Scholar]
- Woodhouse, J. On the “bridge hill” of the violin. Acta Acust. United Acust. 2005, 91, 155–165. [Google Scholar]
- Mansour, H.; Woodhouse, J.; Scavone, G.P. On minimum bow force for bowed strings. Acta Acust. United Acust. 2017, 103, 317–330. [Google Scholar] [CrossRef]
| Young’s Modulus | Rigidity Modulus | Poisson’s Ratio |
|---|---|---|
| GPa | GPa | |
| GPa | GPa | |
| GPa | GPa |
| Mode Number | (a) Free | (b) Fixed | (c) Spring | (d) Spring+ |
|---|---|---|---|---|
| 1 | 1227 | 333 | 160 | 498 |
| 2 | 1311 | 1580 | 309 | 861 |
| 3 | 1331 | 2316 | 968 | 1597 |
| 4 | 2337 | 2918 | 1090 | 2231 |
| 5 | 3306 | 3224 | 1507 | 2364 |
| 6 | 3753 | 3734 | 2149 | 3076 |
| 7 | 4298 | 4003 | 2535 | 3083 |
| 8 | 4768 | 5369 | 3087 | 3250 |
| 9 | 5347 | 6504 | 3246 | 4082 |
| 10 | 5889 | 7252 | 3592 | 4887 |
| Mode Number | (a) Free | (b) Fixed | (c) Spring | (d) Spring+ |
|---|---|---|---|---|
| 1 | 1099 | 327 | 162 | 317 |
| 2 | 1283 | 1583 | 317 | 870 |
| 3 | 1320 | 1815 | 1106 | 1331 |
| 4 | 2126 | 3447 | 1085 | 1747 |
| 5 | 3212 | 3677 | 1330 | 2459 |
| 6 | 4437 | 4186 | 1744 | 3145 |
| 7 | 4827 | 3994 | 2536 | 3617 |
| 8 | 5590 | 5356 | 3856 | 3859 |
| 9 | 5791 | 6704 | 3516 | 4127 |
| 10 | 6140 | 7251 | 3614 | 4643 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lodetti, L.; Gonzalez, S.; Antonacci, F.; Sarti, A. Stiffening Cello Bridges with Design. Appl. Sci. 2023, 13, 928. https://doi.org/10.3390/app13020928
Lodetti L, Gonzalez S, Antonacci F, Sarti A. Stiffening Cello Bridges with Design. Applied Sciences. 2023; 13(2):928. https://doi.org/10.3390/app13020928
Chicago/Turabian StyleLodetti, Laura, Sebastian Gonzalez, Fabio Antonacci, and Augusto Sarti. 2023. "Stiffening Cello Bridges with Design" Applied Sciences 13, no. 2: 928. https://doi.org/10.3390/app13020928
APA StyleLodetti, L., Gonzalez, S., Antonacci, F., & Sarti, A. (2023). Stiffening Cello Bridges with Design. Applied Sciences, 13(2), 928. https://doi.org/10.3390/app13020928




