Numerical Assessment of Interacting Structural Units on the Seismic Damage: A Comparative Analysis with Different Modeling Approaches
Abstract
:1. Introduction
2. Materials and Methods
2.1. Historical Developments and Geometric Configuration
2.2. Damage Suffered Following the 2016–2017 Central Italy Earthquake
2.3. Numerical Models
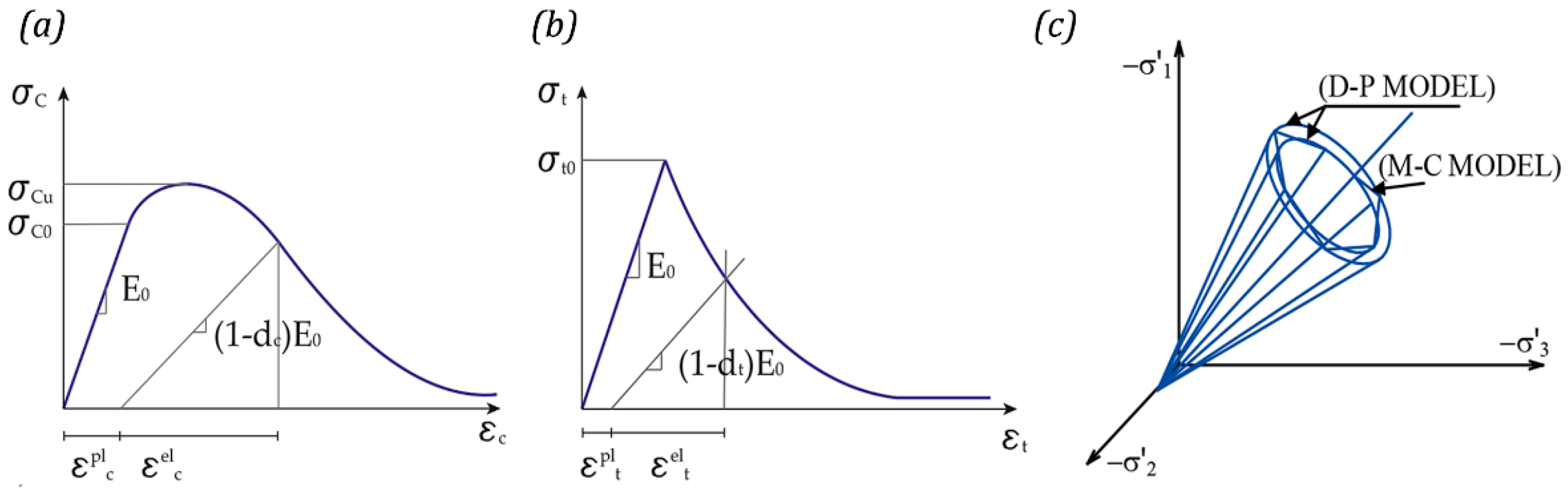
2.3.1. Concrete Damage Plasticity Model (CDP)
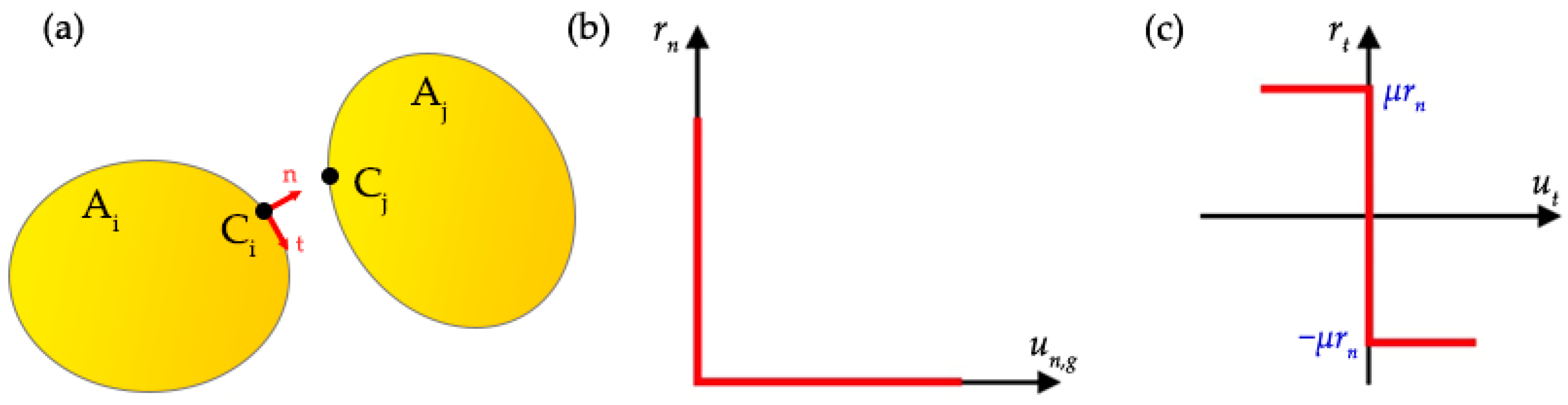
2.3.2. Non-Smooth Contact Dynamics Model (NSCD)
- 1.
- 2.
- The dry-friction Coulomb’s law (Figure 5c):where μ is the friction coefficient and λ is a positive real arbitrary number.
2.4. Numerical Model Characteristics
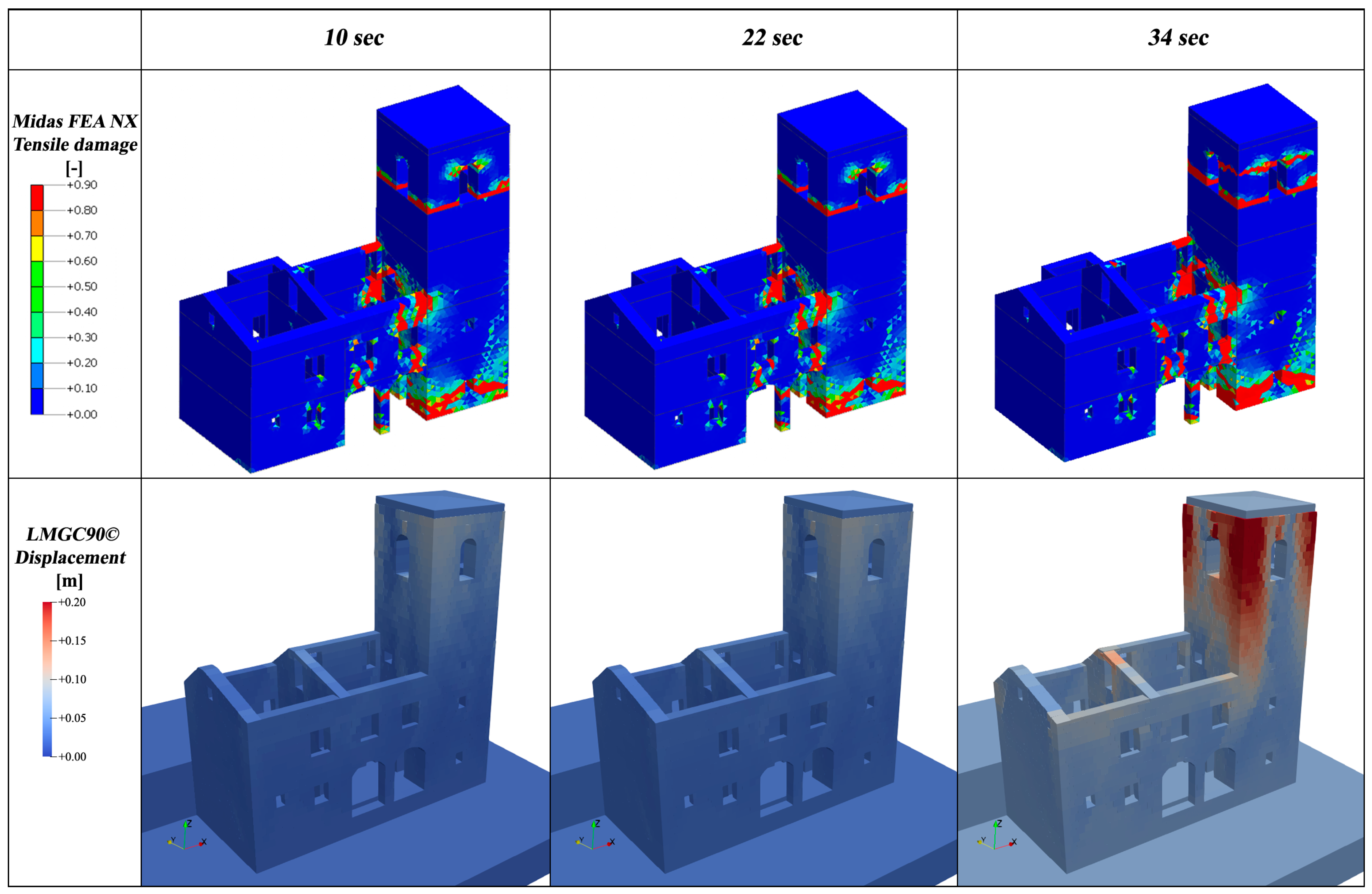
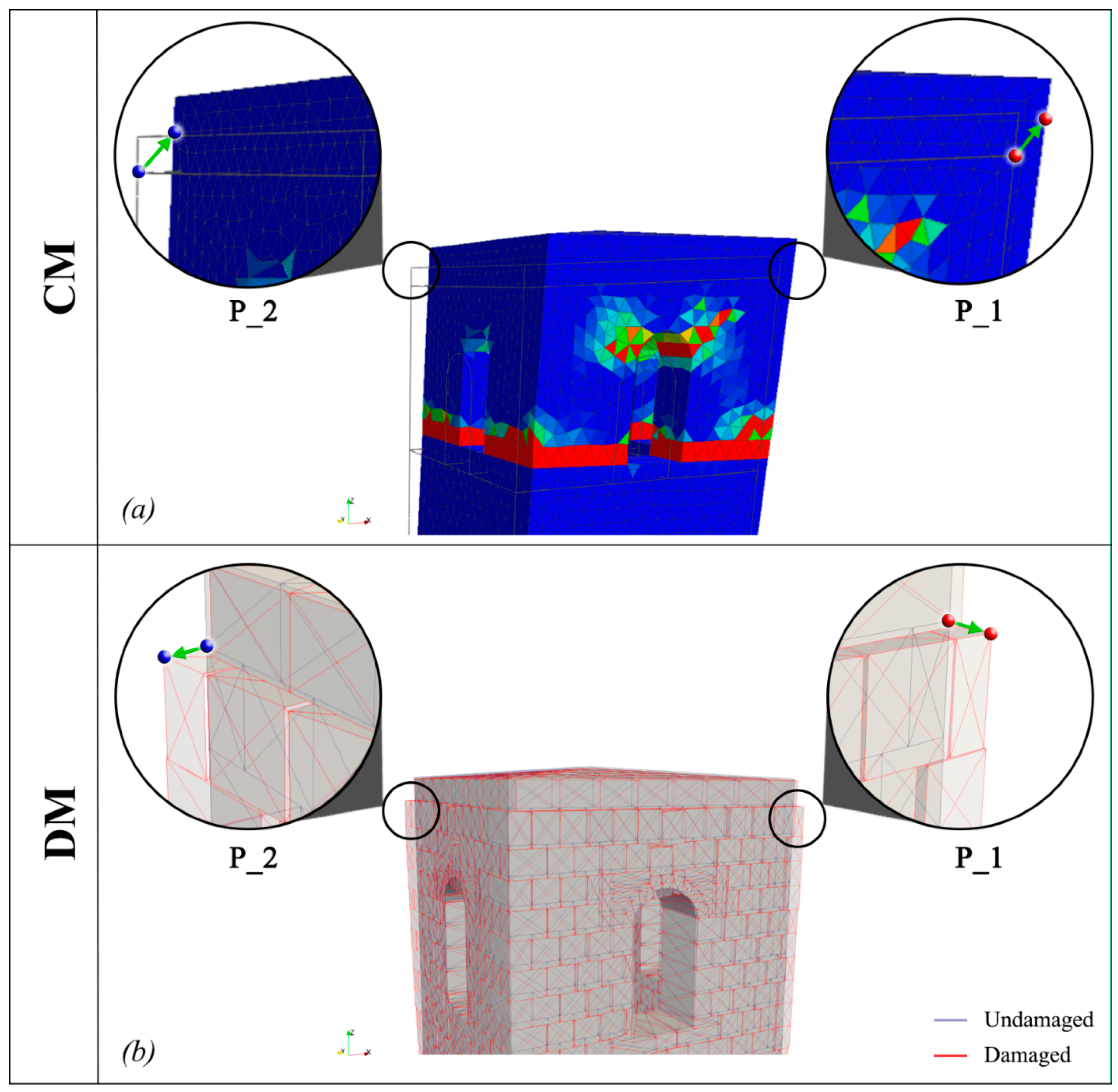
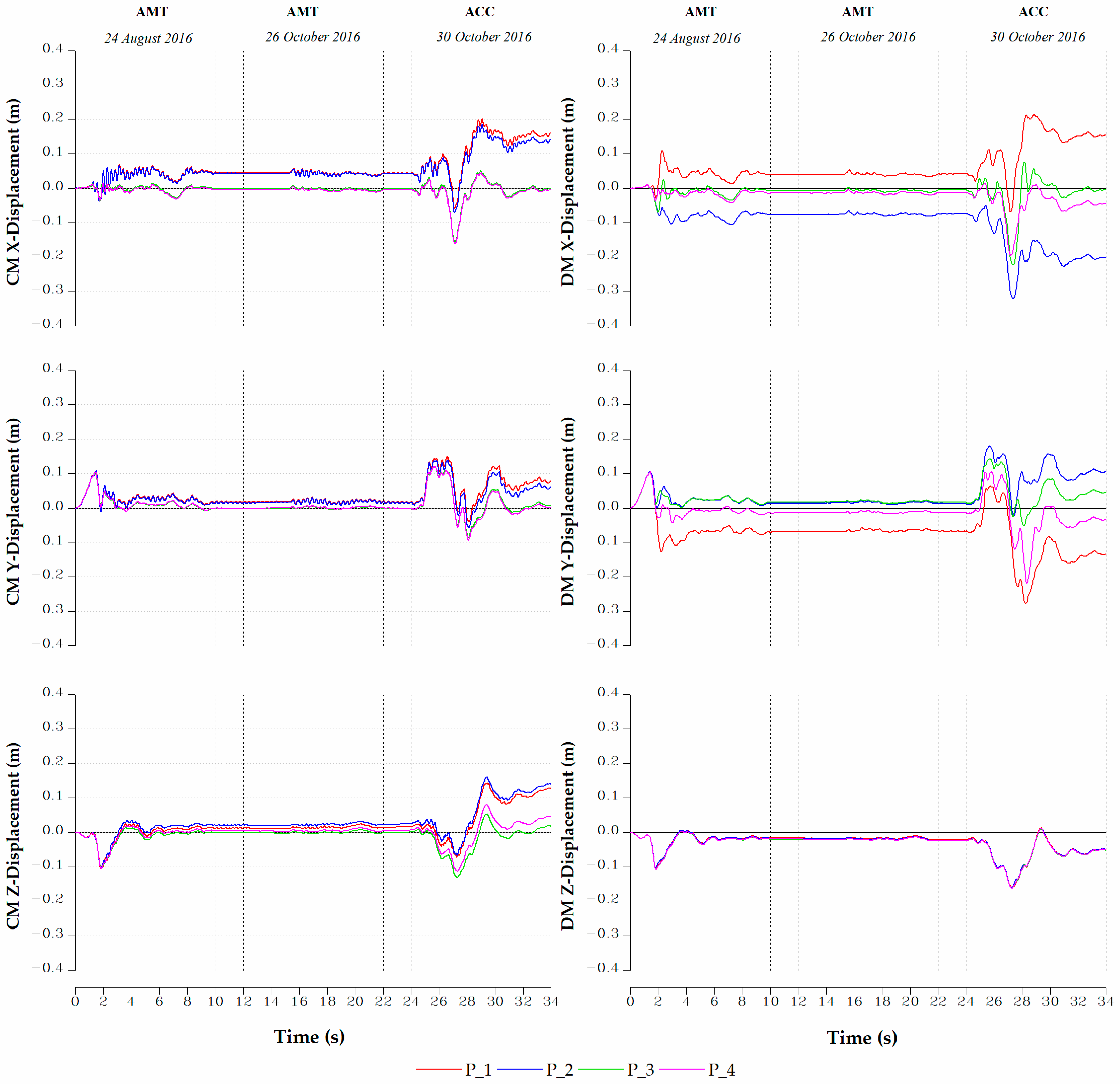
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sorrentino, L.; Cattari, S.; da Porto, F.; Magenes, G.; Penna, A. Seismic behaviour of ordinary masonry buildings during the 2016 central Italy earthquakes. Bull. Earthq. Eng. 2019, 17, 5583–5607. [Google Scholar] [CrossRef] [Green Version]
- Lagomarsino, S.; Penna, A.; Galasco, A.; Cattari, S. TREMURI program: An equivalent frame model for the nonlinear seismic analysis of masonry buildings. Eng. Struct. 2013, 56, 1787–1799. [Google Scholar] [CrossRef]
- Milani, G. Lesson learned after the Emilia-Romagna, Italy, 20-29 May 2012 earthquakes: A limit analysis insight on three masonry churches. Eng. Fail. Anal. 2013, 34, 761–778. [Google Scholar] [CrossRef]
- Mallardo, V.; Malvezzi, R.; Milani, E.; Milani, G. Seismic vulnerability of historical masonry buildings: A case study in Ferrara. Eng. Struct. 2008, 30, 2223–2241. [Google Scholar] [CrossRef]
- Malena, M.; Angelillo, M.; Fortunato, A.; de Felice, G.; Mascolo, I. Arch bridges subject to pier settlements: Continuous vs. piecewise rigid displacement methods. Meccanica 2021, 56, 2487–2505. [Google Scholar] [CrossRef]
- García-Macías, E.; Ubertini, F. Seismic interferometry for earthquake-induced damage identification in historic masonry towers. Mech. Syst. Signal Process. 2019, 132, 380–404. [Google Scholar] [CrossRef]
- Cavalagli, N.; Comanducci, G.; Ubertini, F. Earthquake-Induced Damage Detection in a Monumental Masonry Bell-Tower Using Long-Term Dynamic Monitoring Data. J. Earthq. Eng. 2018, 22, 96–119. [Google Scholar] [CrossRef]
- Bartoli, G.; Betti, M.; Vignoli, A. A numerical study on seismic risk assessment of historic masonry towers: A case study in San Gimignano. Bull. Earthq. Eng. 2016, 14, 1475–1518. [Google Scholar] [CrossRef]
- Clementi, F.; Milani, G.; Ferrante, A.; Valente, M.; Lenci, S. Crumbling of Amatrice clock tower during 2016 Central Italy seismic sequence: Advanced numerical insights. Frat. Integrità Strutt. 2019, 14, 313–335. [Google Scholar] [CrossRef] [Green Version]
- Ferrante, A.; Schiavoni, M.; Bianconi, F.; Milani, G.; Clementi, F. Influence of Stereotomy on Discrete Approaches Applied to an Ancient Church in Muccia, Italy. J. Eng. Mech. 2021, 147, 04021103. [Google Scholar] [CrossRef]
- Standoli, G.; Salachoris, G.P.; Masciotta, M.G.; Clementi, F. Modal-based FE model updating via genetic algorithms: Exploiting artificial intelligence to build realistic numerical models of historical structures. Constr. Build. Mater. 2021, 303, 124393. [Google Scholar] [CrossRef]
- D’Altri, A.M.; Sarhosis, V.; Milani, G.; Rots, J.; Cattari, S.; Lagomarsino, S.; Sacco, E.; Tralli, A.; Castellazzi, G.; de Miranda, S. Modeling Strategies for the Computational Analysis of Unreinforced Masonry Structures: Review and Classification. Arch. Comput. Methods Eng. 2020, 27, 1153–1185. [Google Scholar] [CrossRef]
- Lemos, J.V. Discrete Element Modeling of Masonry Structures. Int. J. Archit. Herit. 2007, 1, 190–213. [Google Scholar] [CrossRef]
- Sandoval, C.; Arnau, O. Experimental characterization and detailed micro-modeling of multi-perforated clay brick masonry structural response. Mater. Struct. 2017, 50, 34. [Google Scholar] [CrossRef]
- Calderón, S.; Sandoval, C.; Arnau, O. Shear response of partially-grouted reinforced masonry walls with a central opening: Testing and detailed micro-modelling. Mater. Des. 2017, 118, 122–137. [Google Scholar] [CrossRef]
- Ferrante, A.; Loverdos, D.; Clementi, F.; Milani, G.; Formisano, A.; Lenci, S.; Sarhosis, V. Discontinuous approaches for nonlinear dynamic analyses of an ancient masonry tower. Eng. Struct. 2021, 230, 111626. [Google Scholar] [CrossRef]
- Lourenço, P.B.; Rots, J.G. Multisurface Interface Model for Analysis of Masonry Structures. J. Eng. Mech. 1997, 123, 660–668. [Google Scholar] [CrossRef]
- Lourenço, P.B. Recent advances in masonry modelling: Micromodelling and homogenisation. In Multiscale Modeling in Solid Mechanics: Computational Approaches; Imperial College Press: London, UK, 2009; pp. 251–294. [Google Scholar]
- Bagnéris, M.; Cherblanc, F.; Bromblet, P.; Gattet, E.; Gügi, L.; Nony, N.; Mercurio, V.; Pamart, A. A complete methodology for the mechanical diagnosis of statue provided by innovative uses of 3D model. Application to the imperial marble statue of Alba-la-Romaine (France). J. Cult. Herit. 2017, 28, 109–116. [Google Scholar] [CrossRef] [Green Version]
- Reccia, E.; Cazzani, A.; Cecchi, A. FEM-DEM Modeling for Out-of-plane Loaded Masonry Panels: A Limit Analysis Approach. Open Civ. Eng. J. 2012, 6, 231–238. [Google Scholar] [CrossRef] [Green Version]
- Giordano, E.; Clementi, F.; Nespeca, A.; Lenci, S. Damage Assessment by Numerical Modeling of Sant’Agostino’s Sanctuary in Offida During the Central Italy 2016–2017 Seismic Sequence. Front. Built Environ. 2019, 4. [Google Scholar] [CrossRef]
- Facchini, L.; Betti, M.; Corazzi, R.; Kovacevic, V.C. Nonlinear seismic behavior of historical masonry towers by means of different numerical models. Procedia Eng. 2017, 199, 601–606. [Google Scholar] [CrossRef]
- Illampas, R.; Ioannou, I.; Lourenço, P.B. Seismic appraisal of heritage ruins: The case study of the St. Mary of Carmel church in Cyprus. Eng. Struct. 2020, 224, 111209. [Google Scholar] [CrossRef]
- Valente, M.; Milani, G. Seismic assessment of historical masonry structures through advanced nonlinear dynamic simulations: Applications to castles, churches, and palaces. In Numerical Modeling of Masonry and Historical Structures; Elsevier: Amsterdam, The Netherlands, 2019; pp. 163–200. [Google Scholar]
- Malena, M.; de Felice, G.; Marfia, S. AnMas: Anisotropic strength domain for masonry. Eng. Struct. 2022, 257, 114050. [Google Scholar] [CrossRef]
- Salachoris, G.P.; Magagnini, E.; Clementi, F. Mechanical characterization of “Scaglia Rossa” stone masonry through experimental and numerical analyses. Constr. Build. Mater. 2021, 303, 124572. [Google Scholar] [CrossRef]
- Valente, M.; Milani, G. Non-linear dynamic and static analyses on eight historical masonry towers in the North-East of Italy. Eng. Struct. 2016, 114, 241–270. [Google Scholar] [CrossRef]
- Ministero delle Infrastrutture e dei Trasporti Aggiornamento delle “Norme Tecniche per le Costruzioni”–NTC 2018; Gazzetta Ufficiale: Rome, Italy, 2018; pp. 1–198. (In Italian)
- Ministero delle Infrastrutture e dei Trasporti Circolare 21 Gennaio 2019 n. 7 C.S.LL.PP. In Istruzioni per L’applicazione Dell’aggiornamento delle “Norme Tecniche per le Costruzioni” di cui al D.M. 17/01/2018. Suppl. ord. alla G.U. n. 35 del 11/2/19; Gazzetta Ufficiale: Rome, Italy, 2019; pp. 1–338. (In Italian)
- Midas FEA NX Analysis Reference 2020. Available online: https://www.midasoft.com/ (accessed on 6 January 2023).
- Chetouane, B.; Dubois, F.; Vinches, M.; Bohatier, C. NSCD discrete element method for modelling masonry structures. Int. J. Numer. Methods Eng. 2005, 64, 65–94. [Google Scholar] [CrossRef] [Green Version]
- Dubois, F.; Acary, V.; Jean, M. The Contact Dynamics method: A nonsmooth story. Comptes Rendus Mécanique 2018, 346, 247–262. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Vasconcelos, G.; Lourenço, P.B. Experimental characterization of stone masonry in shear and compression. Constr. Build. Mater. 2009, 23, 3337–3345. [Google Scholar] [CrossRef]
- Ferrante, A.; Clementi, F.; Milani, G. Dynamic Behavior of an Inclined Existing Masonry Tower in Italy. Front. Built Environ. 2019, 5. [Google Scholar] [CrossRef]
- Ferrante, A.; Clementi, F.; Milani, G. Advanced numerical analyses by the Non-Smooth Contact Dynamics method of an ancient masonry bell tower. Math. Methods Appl. Sci. 2020, 43, 7706–7725. [Google Scholar] [CrossRef]
- Luzi, L.; Hailemikael, S.; Bindi, D.; Pacor, F.; Mele, F.; Sabetta, F. ITACA (ITalian ACcelerometric Archive): A Web Portal for the Dissemination of Italian Strong-motion Data. Seismol. Res. Lett. 2008, 79, 716–722. [Google Scholar] [CrossRef]




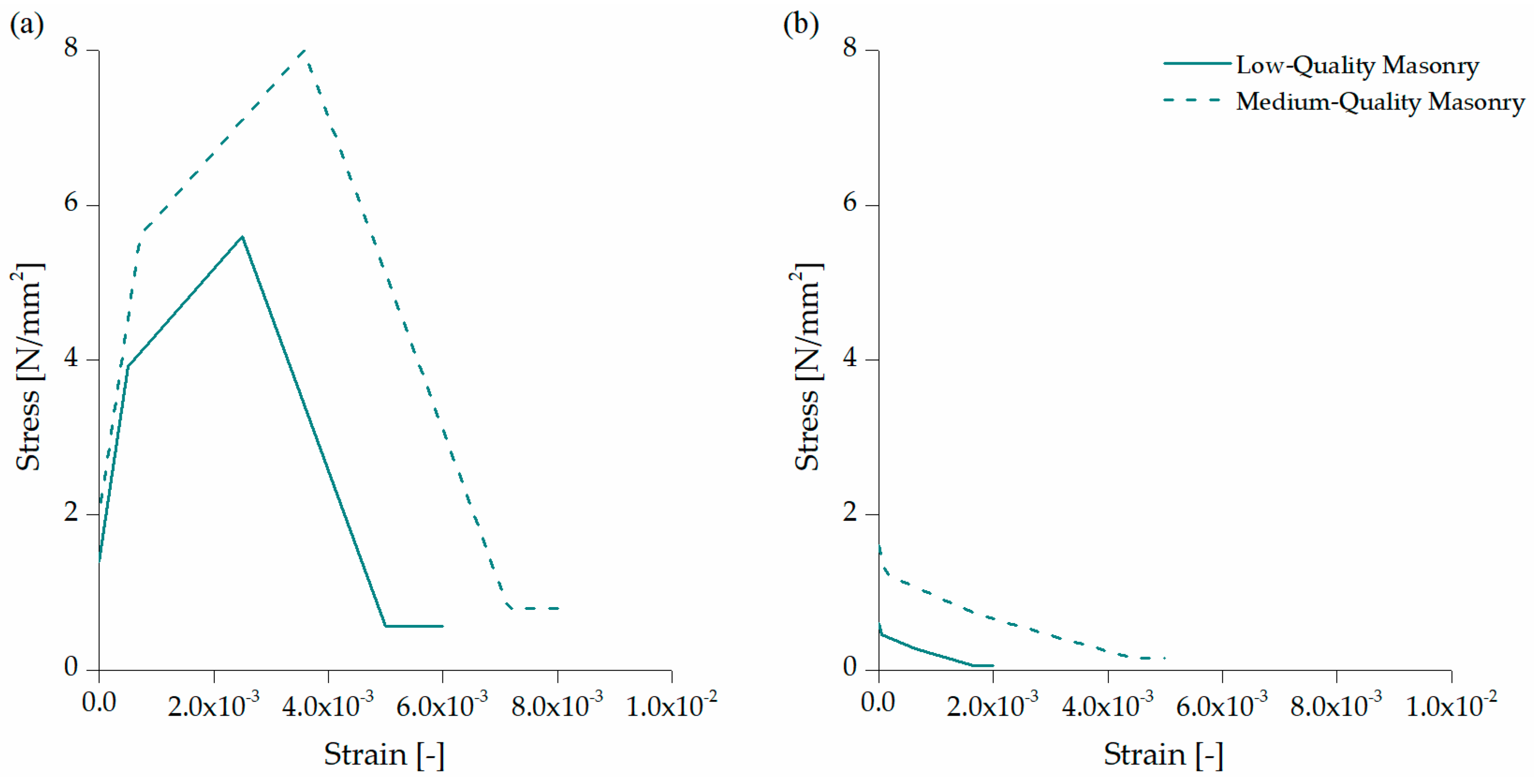

| Medium-Quality Masonry Properties | Low-Quality Masonry Properties | Concrete | |
|---|---|---|---|
| Young’s Module (MPa) | 2800 | 31,500 | |
| Poisson’s module (−) | 0.25 | 0.3 | |
| Mass (kN/m3) | 22 | 25 | |
| Strength in compression (MPa) | 8.0 | 5.6 | - |
| Strength in tension (MPa) | 1.6 | 0.46 | - |
| Parameters to define the CDP Yield surface | |||
| Dilatation angle, | 10° | - | |
| Correction parameter, | 0.666 | - | |
| Eccentricity, | 0.1 | - | |
| Biaxial strength ratio, | 1.16 | - | |
| Viscosity | 0.01 | - | |
| Non-Smooth Contact Dynamic Method | |||
| Friction masonry structure | 0.50 | ||
| Friction inner core | 0.30 | ||
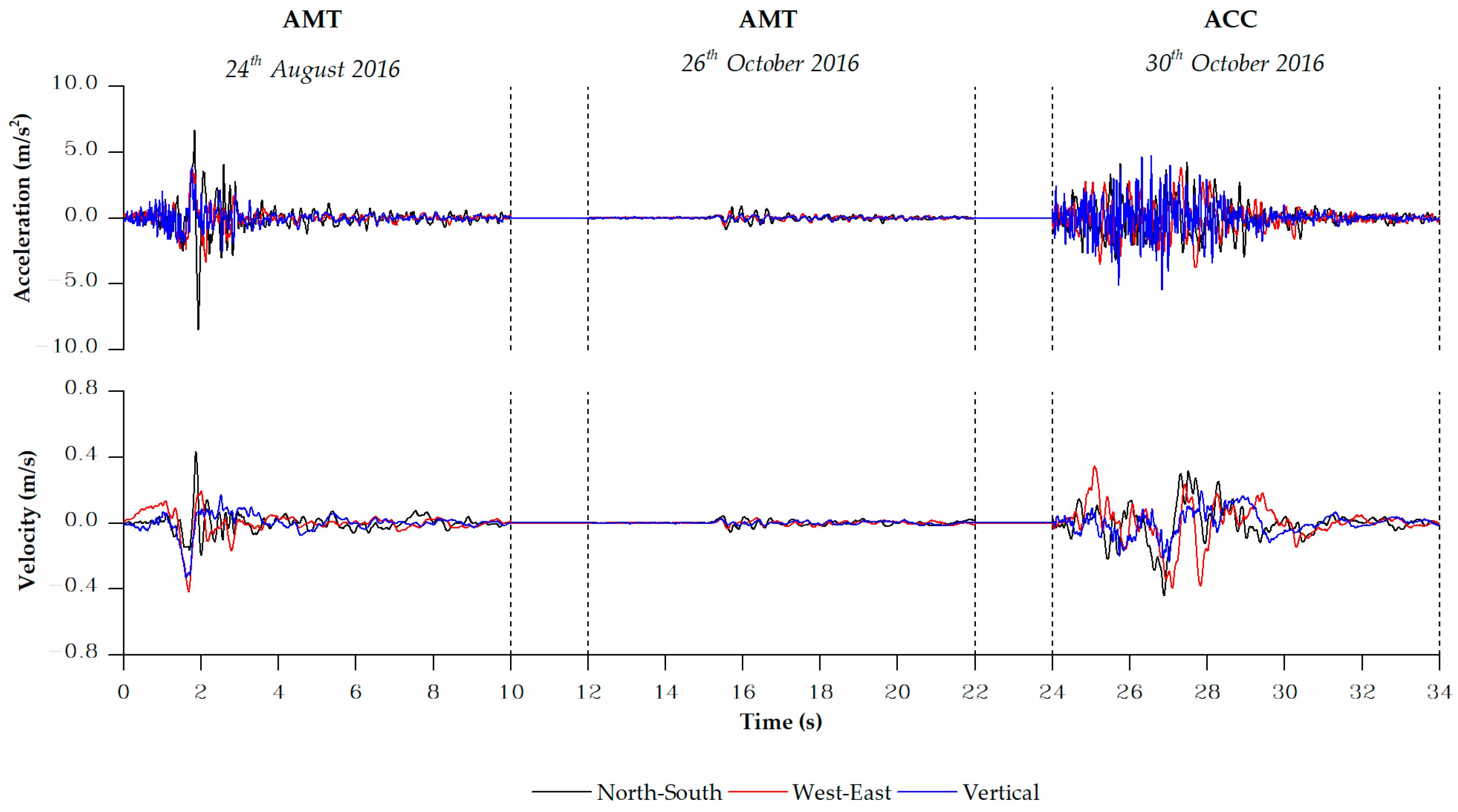
| Seismic Event | ML | Depth (km) | Station | Class EC8 | Rjb (km) | Rrup (km) | Repi (km) | N-S PGA (m/s2) | E-W PGA (m/s2) | Z PGA (m/s2) |
|---|---|---|---|---|---|---|---|---|---|---|
| 24 August 2016 | 6.0 | 8.1 | AMT | B * | 1.38 | 4.62 | 8.50 | 3.68 | −8.51 | 3.91 |
| 26 October 2016 | 5.9 | 7.5 | AMT | B * | 25.9 | 26.1 | 33.30 | −0.59 | 0.91 | 0.49 |
| 30 October 2016 | 6.1 | 9.2 | ACC | A * | 2.2 | 5.7 | 18.60 | −3.95 | 4.34 | −5.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schiavoni, M.; Giordano, E.; Roscini, F.; Clementi, F. Numerical Assessment of Interacting Structural Units on the Seismic Damage: A Comparative Analysis with Different Modeling Approaches. Appl. Sci. 2023, 13, 972. https://doi.org/10.3390/app13020972
Schiavoni M, Giordano E, Roscini F, Clementi F. Numerical Assessment of Interacting Structural Units on the Seismic Damage: A Comparative Analysis with Different Modeling Approaches. Applied Sciences. 2023; 13(2):972. https://doi.org/10.3390/app13020972
Chicago/Turabian StyleSchiavoni, Mattia, Ersilia Giordano, Francesca Roscini, and Francesco Clementi. 2023. "Numerical Assessment of Interacting Structural Units on the Seismic Damage: A Comparative Analysis with Different Modeling Approaches" Applied Sciences 13, no. 2: 972. https://doi.org/10.3390/app13020972
APA StyleSchiavoni, M., Giordano, E., Roscini, F., & Clementi, F. (2023). Numerical Assessment of Interacting Structural Units on the Seismic Damage: A Comparative Analysis with Different Modeling Approaches. Applied Sciences, 13(2), 972. https://doi.org/10.3390/app13020972








