Deadbeat Predictive Current Control for Surface-Mounted Permanent-Magnet Synchronous Motor Based on Weakened Integral Sliding Mode Compensation
Abstract
:1. Introduction
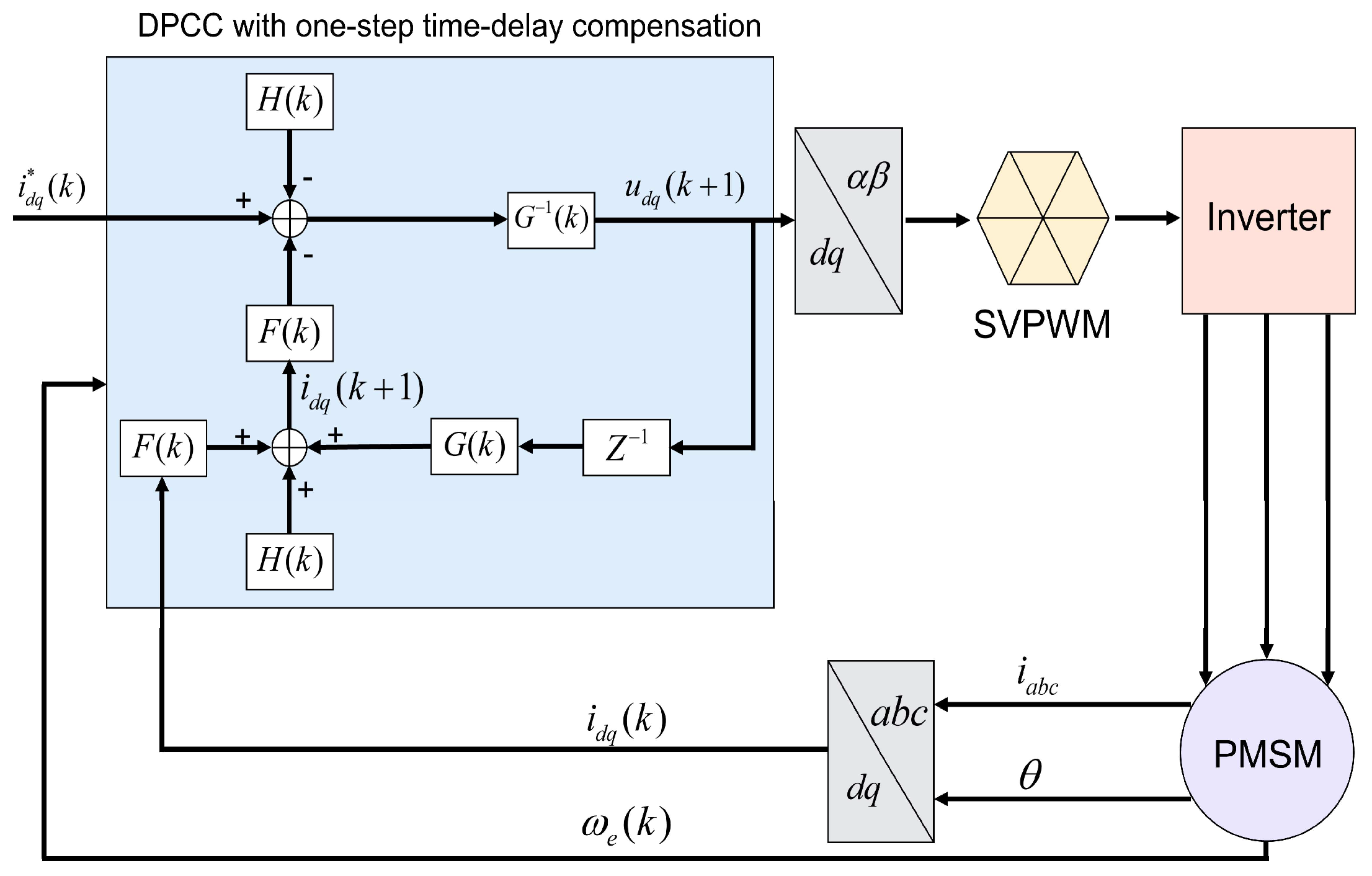
2. DPCC with Delay Compensation
2.1. The Principles of One-Step Delay Compensation DPCC
2.2. Parameter Mismatch Error Analysis
3. An Integral Sliding Mode Compensation Method with Weakened Integrals
3.1. Design of Sliding Mode Surface
3.2. Weakened Integral Sliding Mode Compensation Method
3.3. Stability Analysis
3.4. Adding Weight Factors to Optimize Feedback Currents and Solve the Inductance Mismatch Problem
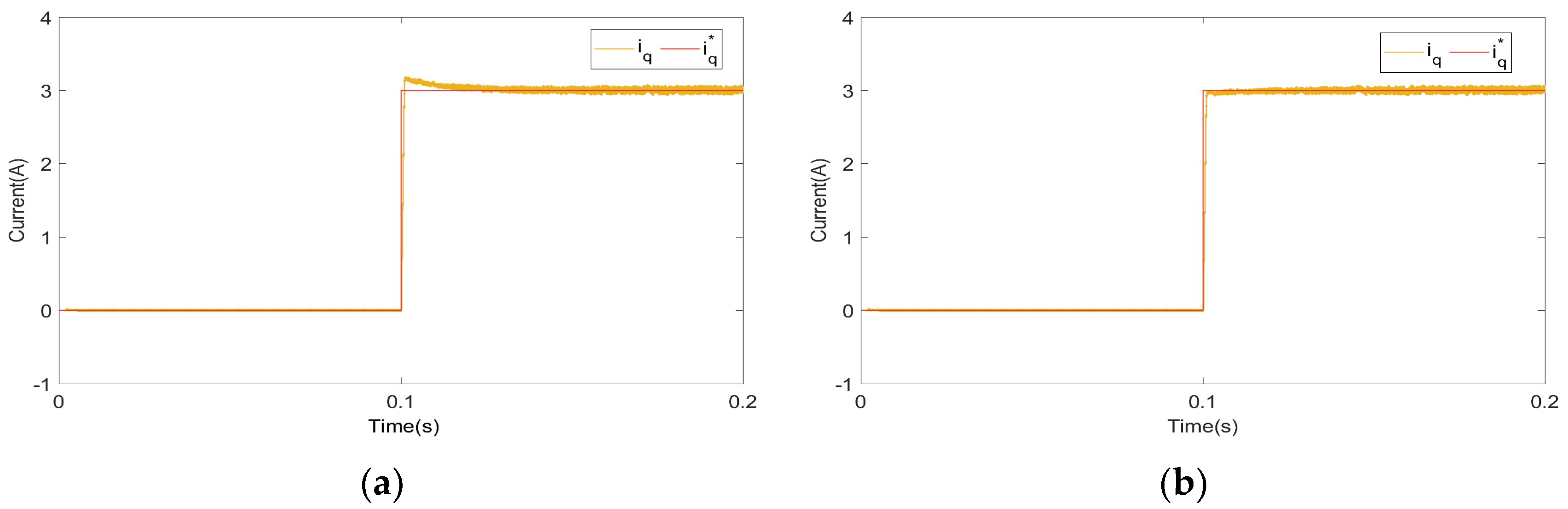
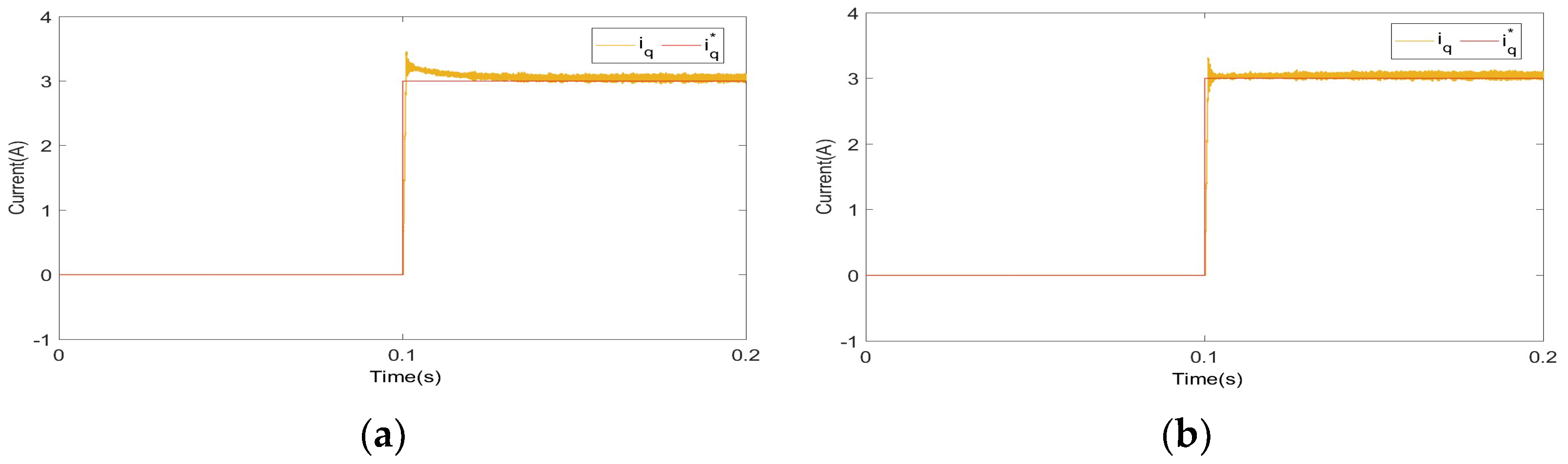
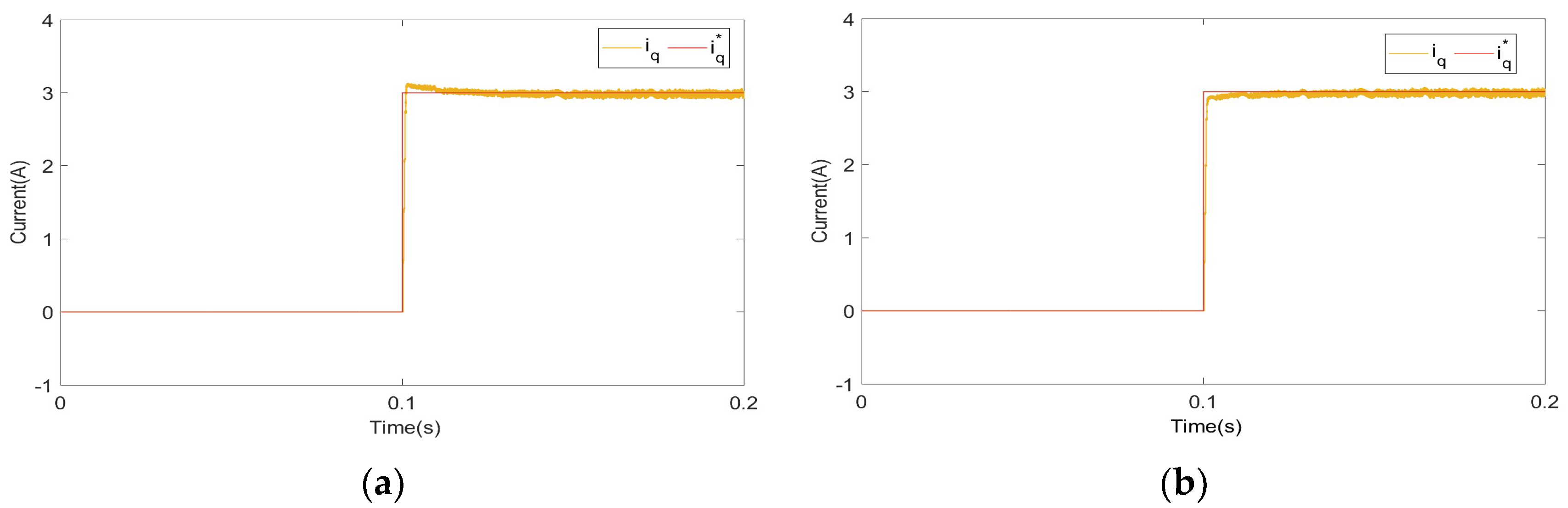
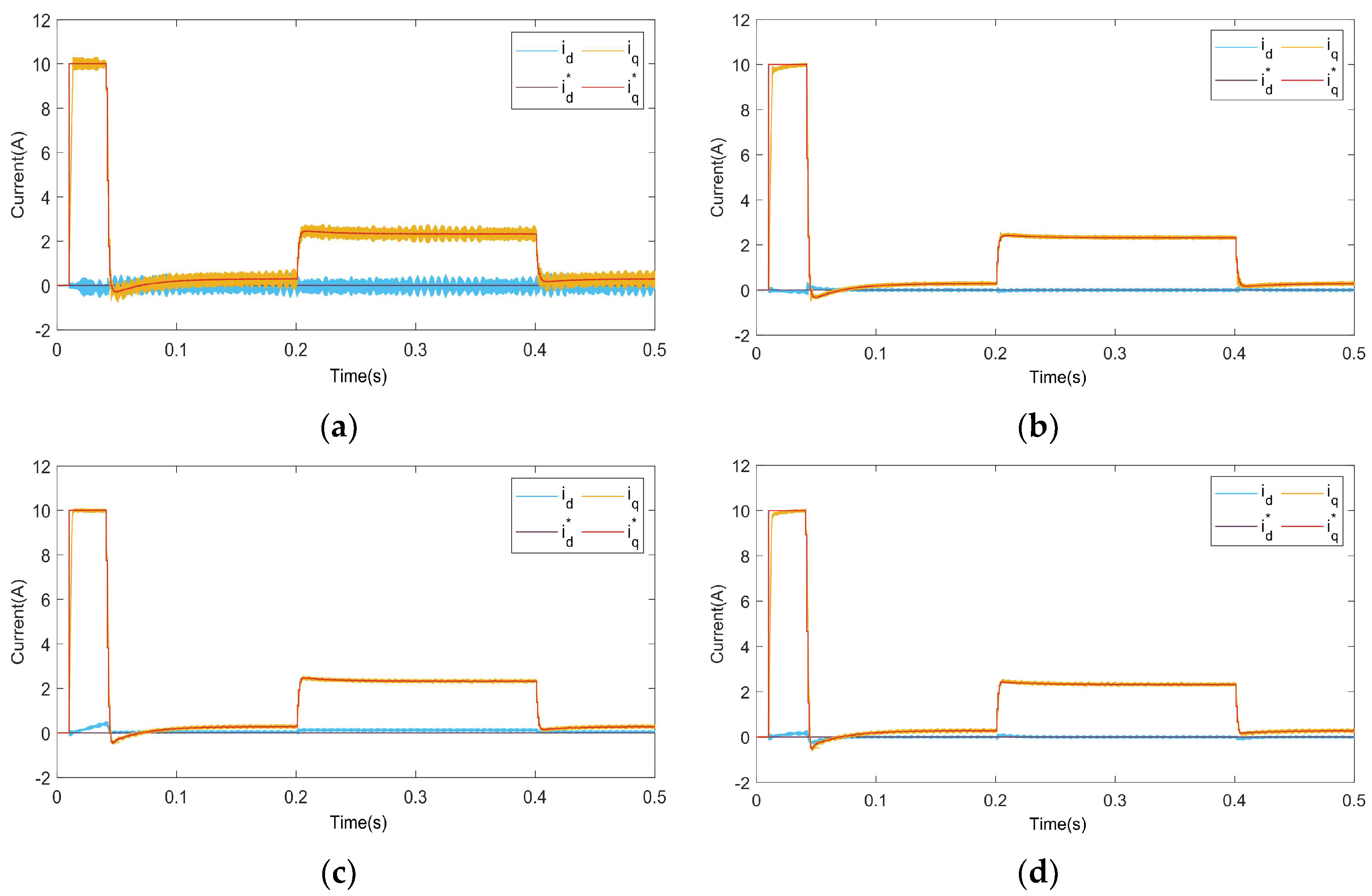
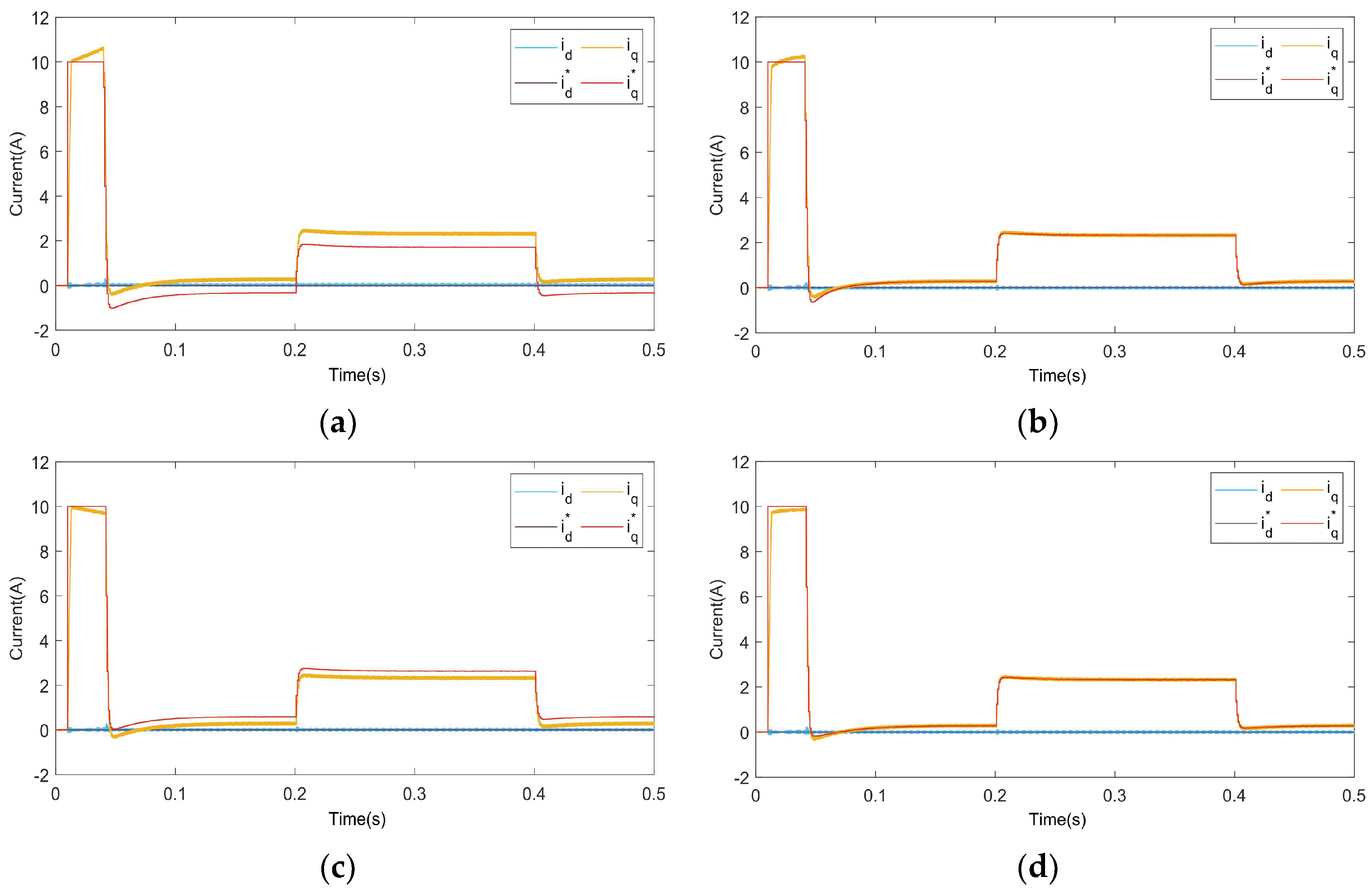
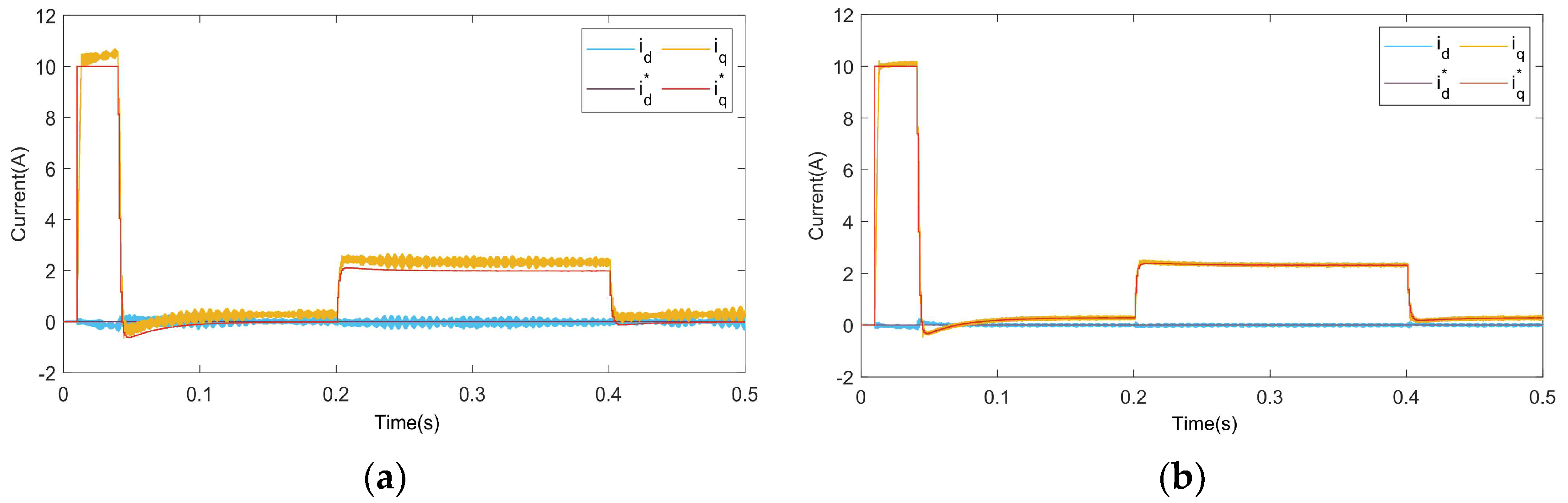
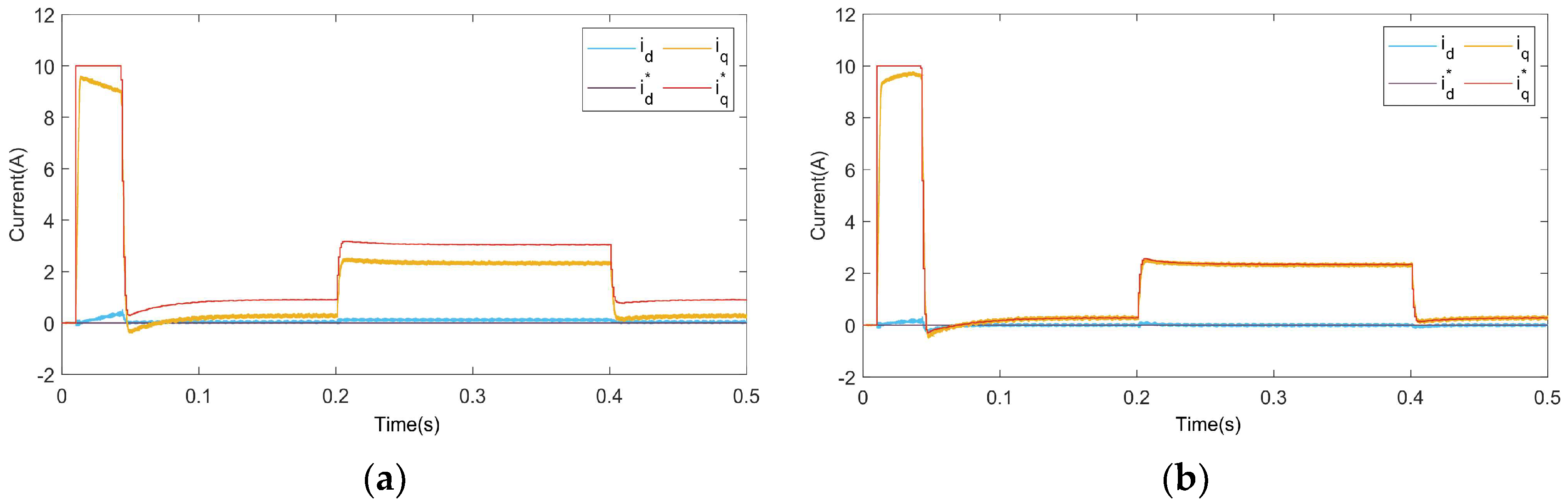
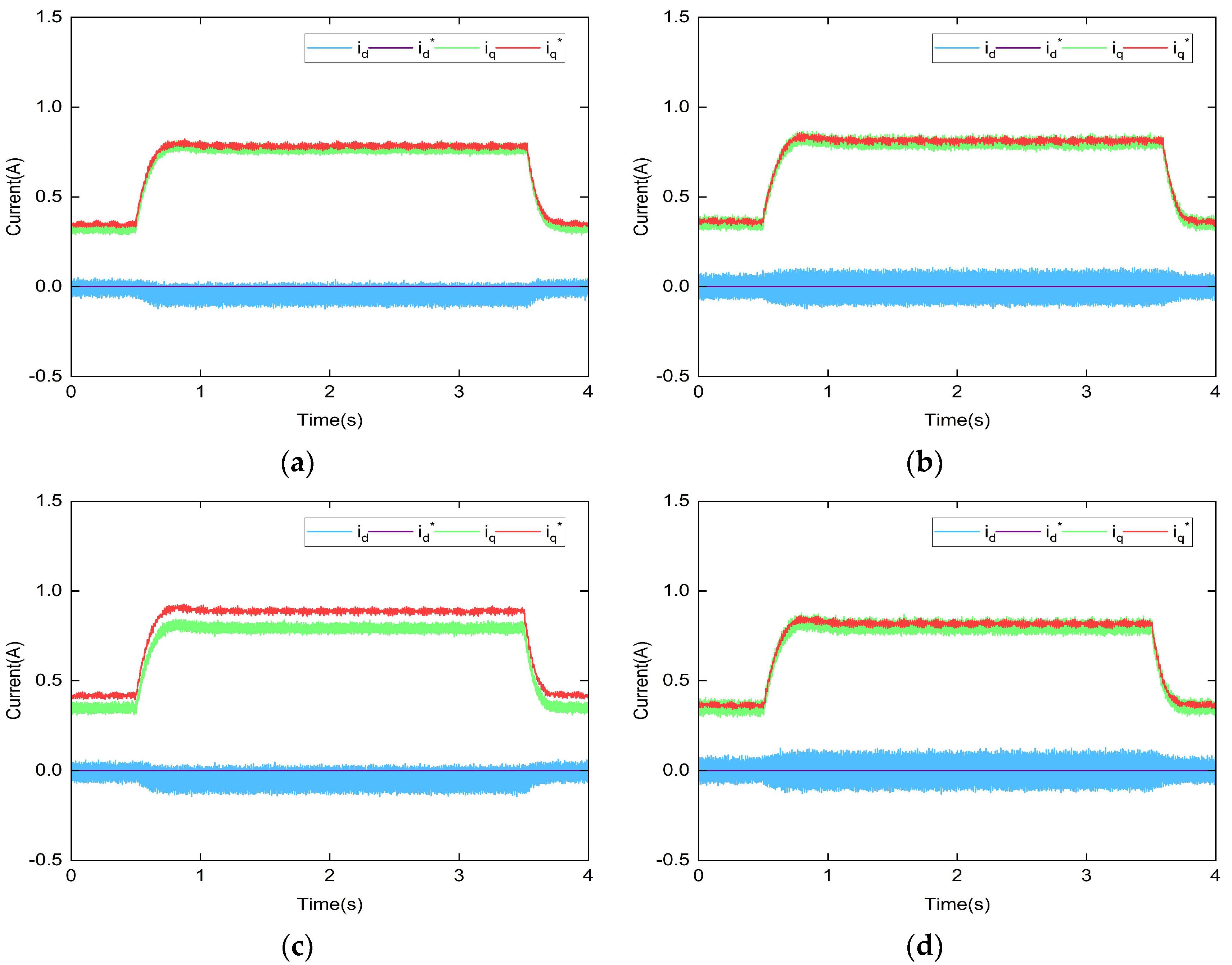
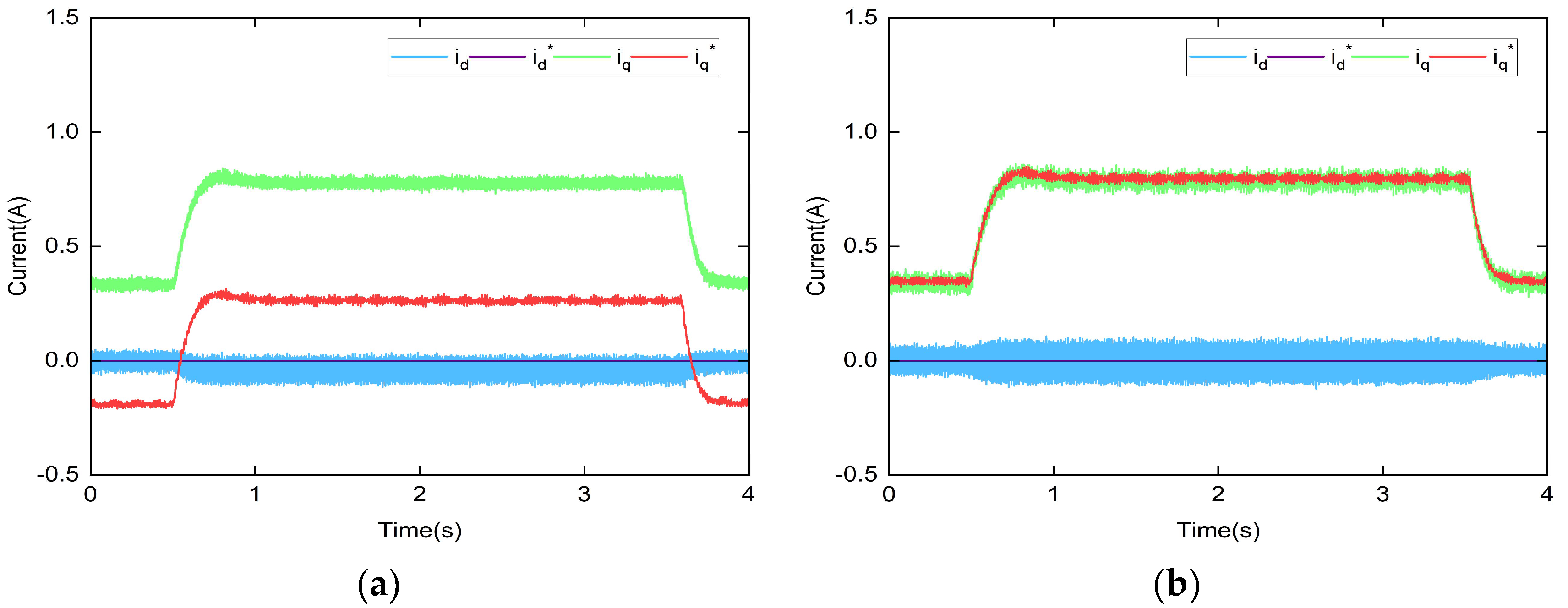
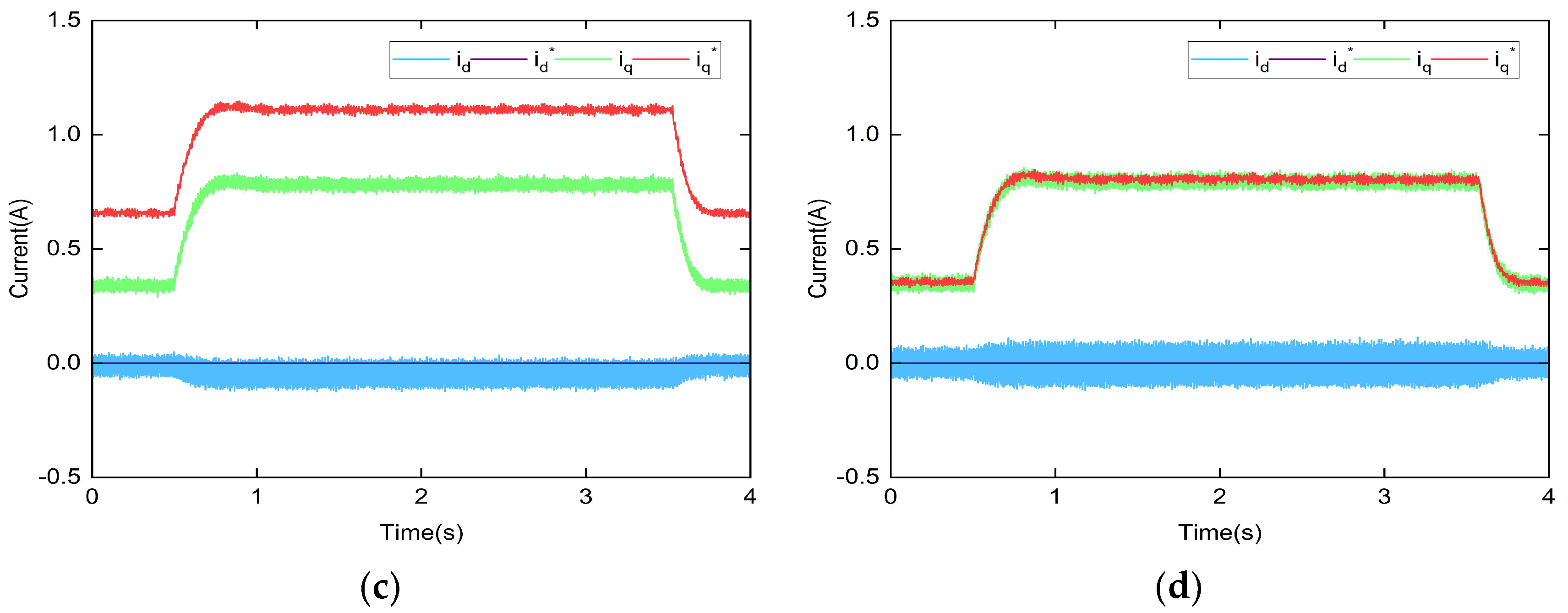
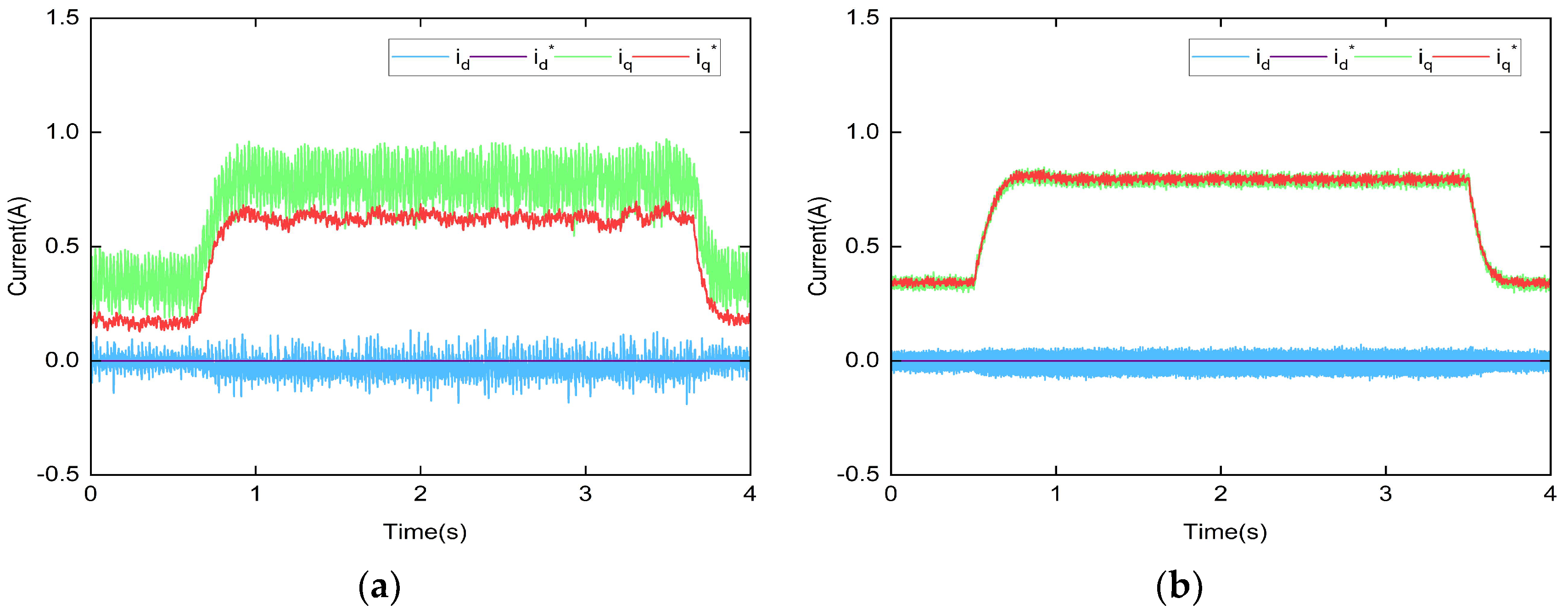
4. Simulation Study
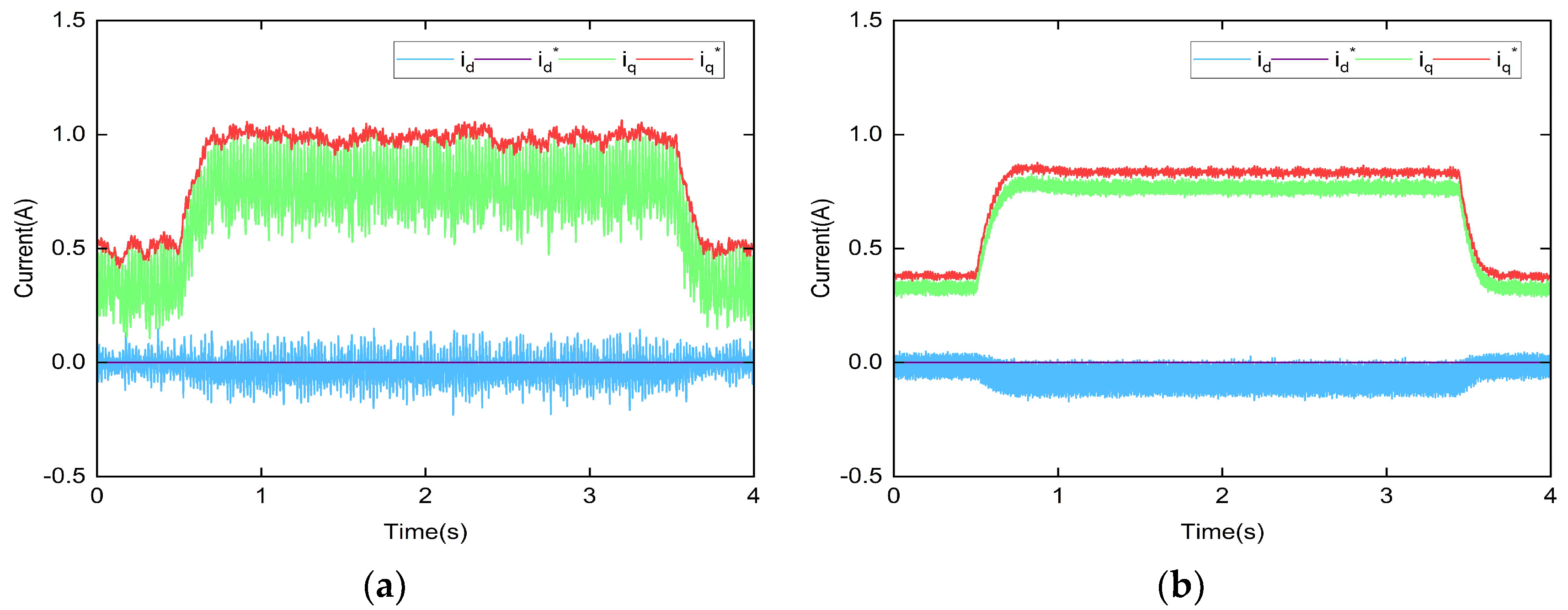
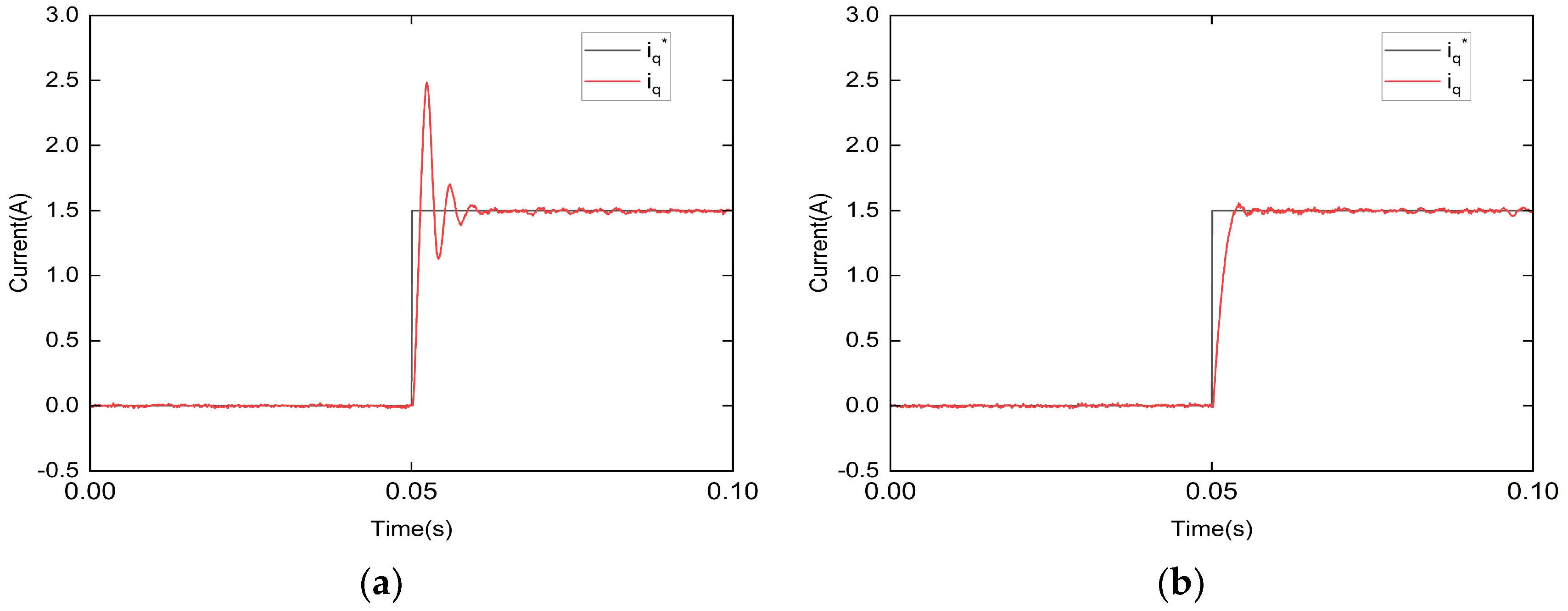
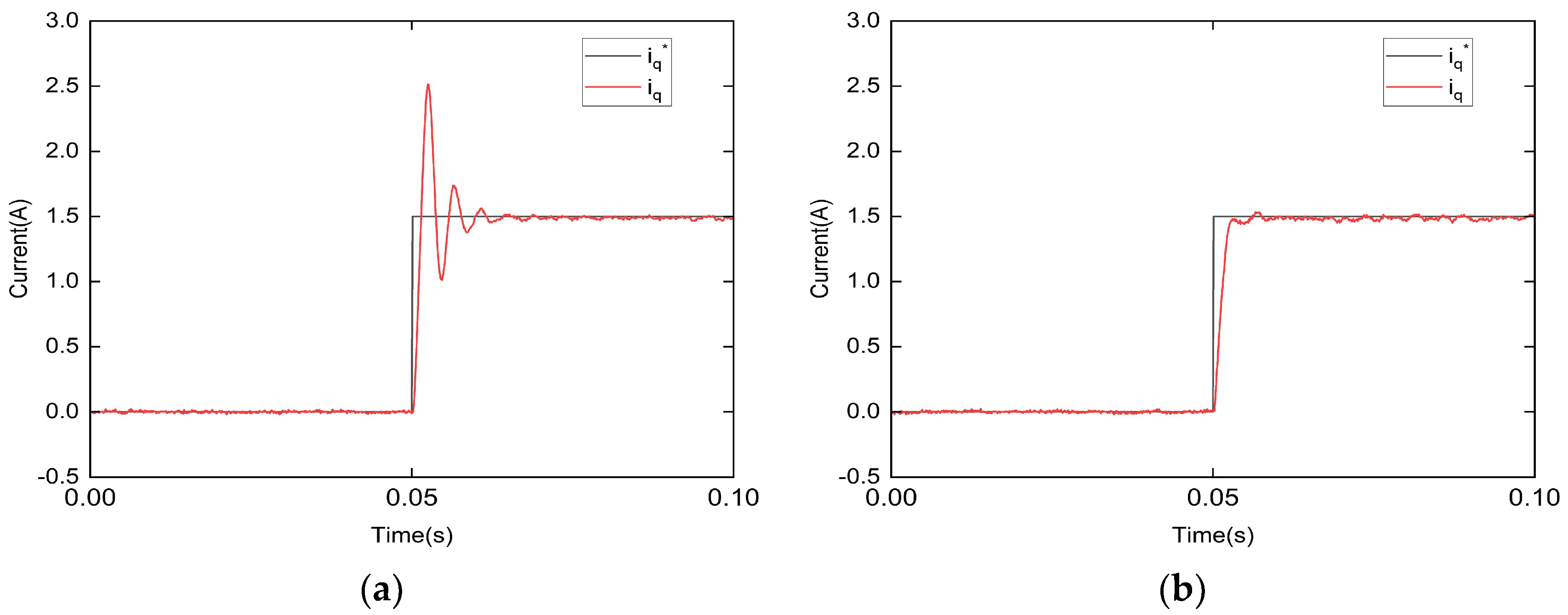
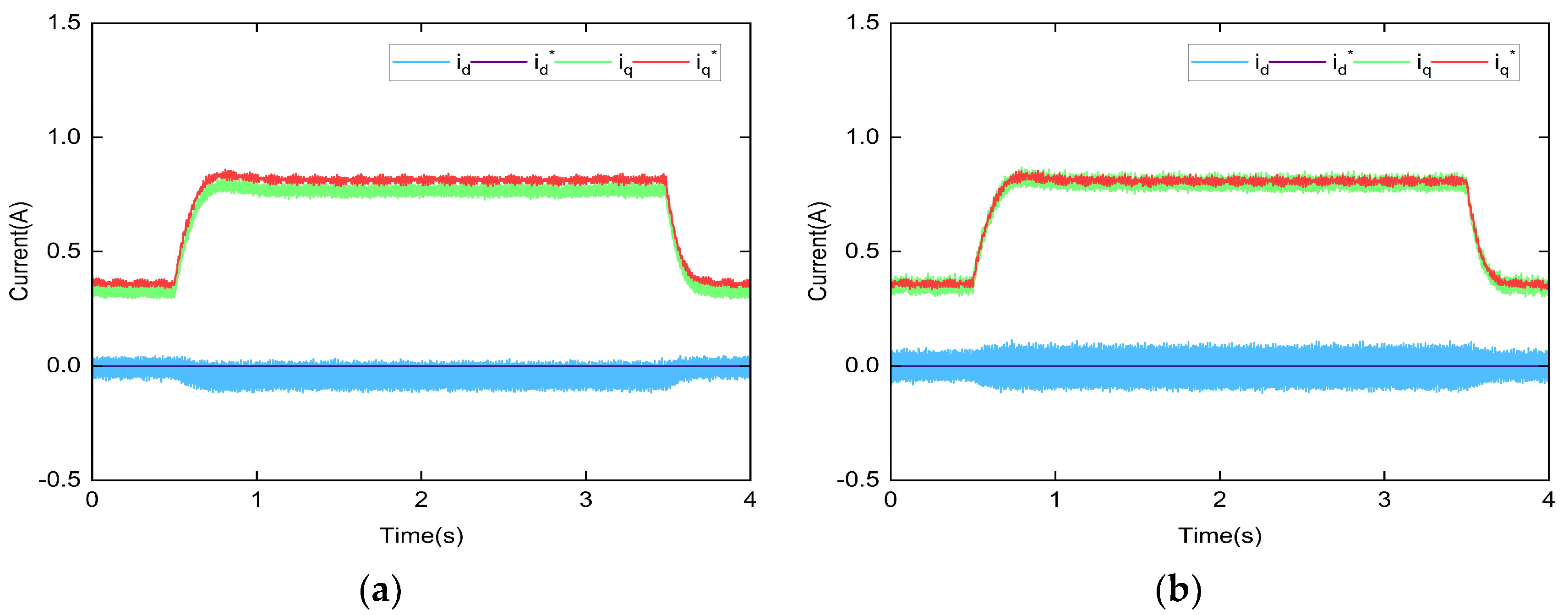
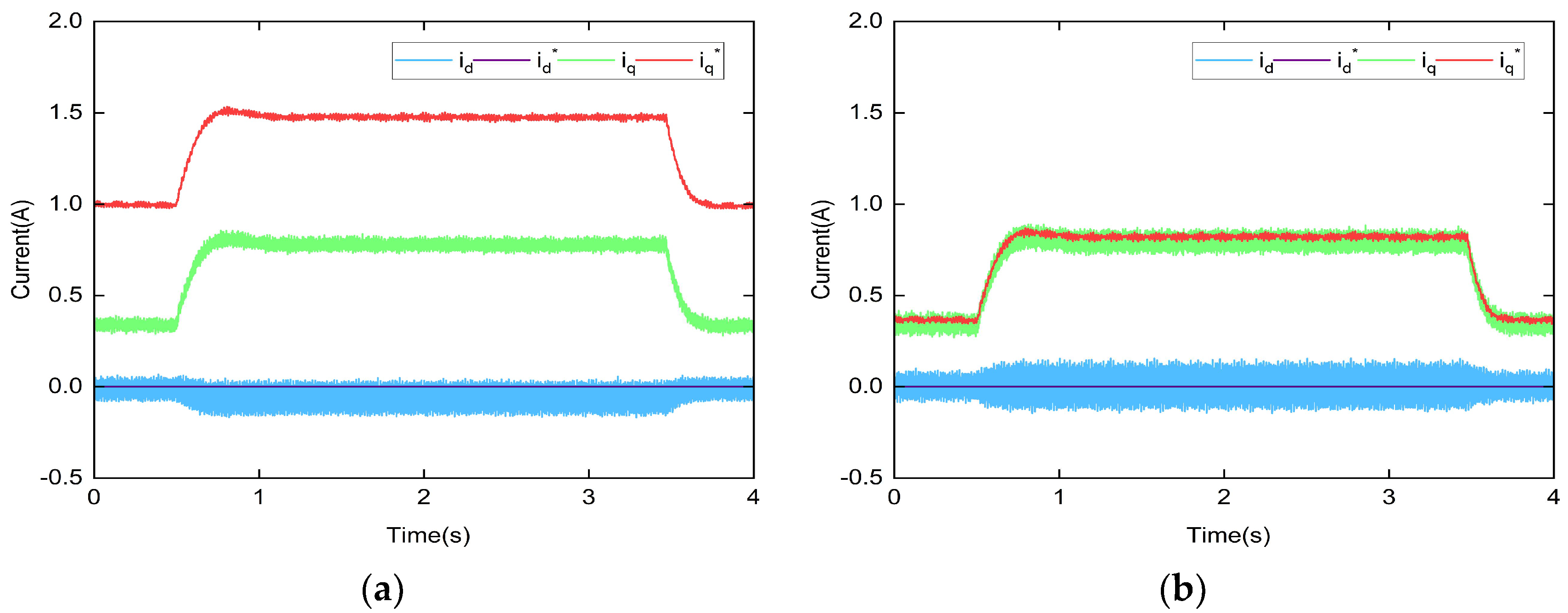
5. Experimental Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Orlowska-Kowalska, T.; Wolkiewicz, M.; Pietrzak, P.; Skowron, M.; Ewert, P.; Tarchala, G.; Krzysztofiak, M.; Kowalski, C.T. Fault Diagnosis and Fault-Tolerant Control of PMSM Drives–State of the Art and Future Challenges. IEEE Access 2022, 10, 59979–60024. [Google Scholar] [CrossRef]
- Loganayaki, A.; Kumar, R.B. Permanent Magnet Synchronous Motor for Electric Vehicle Applications. In Proceedings of the 2019 5th International Conference on Advanced Computing & Communication Systems (ICACCS), Coimbatore, India, 15–16 March 2019; pp. 1064–1069. [Google Scholar]
- Guo, Q.; Han, J.; Peng, W. PMSM Servo Control System Design Based on Fuzzy PID. In Proceedings of the 2017 2nd International Conference on Cybernetics, Robotics and Control (CRC), Chengdu, China, 21–23 July 2017; pp. 85–88. [Google Scholar]
- Gao, J.; Li, S.; Xu, Y.; Zou, J. Time-Delay Compensation Method in PMSM Servo System based on Predictive Current Control with Sensitivity Analysis. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–6. [Google Scholar]
- Wang, H.; Xu, S.; Hu, H. PID Controller for PMSM Speed Control Based on Improved Quantum Genetic Algorithm Optimization. IEEE Access 2023, 11, 61091–61102. [Google Scholar] [CrossRef]
- Lee, H.; Utkin, V.I. Chattering suppression methods in sliding mode control systems. Annu. Rev. Control 2007, 31, 179–188. [Google Scholar] [CrossRef]
- Peng, J.; Yao, M. Overview of Predictive Control Technology for Permanent Magnet Synchronous Motor Systems. Appl. Sci. 2023, 13, 6255. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, S.; Li, X.; Li, X. A New Model-Free Deadbeat Predictive Current Control for PMSM Using Parameter-Free Luenberger Disturbance Observer. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 407–417. [Google Scholar] [CrossRef]
- Yin, K.; Gao, L.; Chen, R.; Feng, Z.; Liu, S. Adaptive Deadbeat Predictive Current Control for PMSM with Feed Forward Method. IEEE Access 2021, 9, 101300–101310. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, S.; Zhang, C.; Li, X.; Li, X.; Yuan, X. Current Prediction Error Based Parameter Identification Method for SPMSM with Deadbeat Predictive Current Control. IEEE Trans. Energy Convers. 2021, 36, 1700–1710. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.; Cui, X.; Wang, Y.; Zhang, C.; Li, Z.; Zhou, Y. Novel Deadbeat Predictive Current Control for PMSM with Parameter Updating Scheme. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2065–2074. [Google Scholar] [CrossRef]
- Shen, W.; Liu, H.; Shao, L. Deadbeat Predictive Current Control of Permanent Magnet Synchronous Motors Based on Disturbance Compensation. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 4256–4263. [Google Scholar]
- Gong, Z.; Zhang, C.; Ba, X.; Guo, Y. Improved Deadbeat Predictive Current Control of Permanent Magnet Synchronous Motor Using a Novel Stator Current and Disturbance Observer. IEEE Access 2021, 9, 142815–142826. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Bai, H. Sliding-Mode-Based Deadbeat Predictive Current Control for PMSM Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 962–969. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, W.; Mu, C.; Liu, Y. Improved Deadbeat Predictive Current Control Combined Sliding Mode Strategy for PMSM Drive System. IEEE Trans. Veh. Technol. 2018, 67, 251–263. [Google Scholar] [CrossRef]
- Wang, G.; Yang, M.; Niu, L.; Gui, X.; Xu, D. A static current error elimination algorithm for PMSM predictive current control. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2015, 35, 2544–2551. [Google Scholar] [CrossRef]
- Xu, Y.; Li, S.; Zou, J. Integral Sliding Mode Control Based Deadbeat Predictive Current Control for PMSM Drives with Disturbance Rejection. IEEE Trans. Power Electron. 2022, 37, 2845–2856. [Google Scholar] [CrossRef]
- Hu, Z.; Ding, J.; Kang, J. Deadbeat Robust Current Predictive Control for PMSM with Sliding Mode Observer. In Proceedings of the 2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 20–22 November 2021; pp. 622–627. [Google Scholar]
- Zhang, X.; Hou, B.; Mei, Y. Deadbeat Predictive Current Control of Permanent-Magnet Synchronous Motors with Stator Current and Disturbance Observer. IEEE Trans. Power Electron. 2017, 32, 3818–3834. [Google Scholar] [CrossRef]
- Qi, L.; Bao, S.; Shi, H. Permanent-magnet synchronous motor velocity control based on second-order integral sliding mode control algorithm. Trans. Inst. Meas. Control 2015, 37, 875–882. [Google Scholar] [CrossRef]
- Li, P.; Sun, W.; Li, W. Application of improved integral sliding surface to flight control system. Control Eng. China 2010, 17, 269–271. [Google Scholar]
- Cao, X.; Ge, Q.; Zhu, J.; Sun, P.; Wang, X. Traction-System Research of High-Speed Maglev Train Based on Integral Sliding Mode Control. Diangong Jishu Xuebao/Trans. China Electrotech. Soc. 2022, 37, 3598–3607. [Google Scholar]
- Liu, J.; Hao, W.; Chen, A.; Tian, J. Research on Deadbeat Predictive Current Control of Permanent Magnet Synchronous Motor. Tiedao Xuebao/J. China Railw. Soc. 2021, 43, 62–72. [Google Scholar]






| Parameter | Value |
|---|---|
| Rated voltage (V) | 220 |
| Rated speed (rpm) | 3000 |
| Rated torque (Nm) | 2.4 |
| Number of pole pairs | 4 |
| -axis inductance (mH) | 5 |
| Stator resistance () | 1.08 |
| Flux linkage (Wb) | 0.0819 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Ji, C.; You, Q.; Sun, D.; Xie, Y. Deadbeat Predictive Current Control for Surface-Mounted Permanent-Magnet Synchronous Motor Based on Weakened Integral Sliding Mode Compensation. Appl. Sci. 2023, 13, 11678. https://doi.org/10.3390/app132111678
Zhang Y, Ji C, You Q, Sun D, Xie Y. Deadbeat Predictive Current Control for Surface-Mounted Permanent-Magnet Synchronous Motor Based on Weakened Integral Sliding Mode Compensation. Applied Sciences. 2023; 13(21):11678. https://doi.org/10.3390/app132111678
Chicago/Turabian StyleZhang, Yongkang, Chengsheng Ji, Qianliang You, Dexin Sun, and Yuee Xie. 2023. "Deadbeat Predictive Current Control for Surface-Mounted Permanent-Magnet Synchronous Motor Based on Weakened Integral Sliding Mode Compensation" Applied Sciences 13, no. 21: 11678. https://doi.org/10.3390/app132111678





