Flow-Induced Noise Characteristics Analysis of a Pipeline Structure in a Cabin Rigid Corner

Abstract

The acoustic radiation characteristics of pipeline structures caused by turbulent fluctuating pressure are among the most important acoustic radiation sources in vessel cabins. Studying the vibro-acoustic characteristics of pipeline structures is of great relevance to engineering. The turbulence fluctuation pressure of pipeline structures’ inner surfaces was numerically analyzed by using the large eddy simulation (LES) method. At first, the vibro-acoustic differential equation of the pipeline structure system was derived by defining the fluctuation pressure as the excitation loading. According to the acoustic radiation characteristic in the quarter-infinite space, which had a combination of two rigid wall interfaces at the same time for the pipeline structures in the vessel cabins, the double reflection method, mirror image method and elastic wave Graf addition principle were applied, and the analytical function of the acoustic radiation for the cylindrical shell was derived. For the pipeline structures in the quarter-infinite acoustic space, for example, the numerical calculation for the acoustic radiation of cylindrical shell was carried out, which was excited by the turbulent pulsating pressure. Finally, the influence of inner flow velocity, frequency, and pipeline installation position were compared using numerical analysis. The results can provide technical support for the acoustic design of pipeline structure systems with complex acoustic boundaries.

1. Introduction

Vessel cabins are equipped with a large number of pipeline structures to carry fluid media such as oil, gas and water. Aside from the structural strength problem, the structure dynamic response problem must be considered in designing pipeline structures. The common dynamic loading actions on the pipeline system include the excitation of the pump source, internal fluid turbulent excitation loading, and impact loading caused by the steep end face or valve elements. The cabin is a significant source of vibration and acoustic radiation caused by turbulent excitation loading in the pipeline structure, affecting the comfortable and concealment of the vessel and, as such, it is now a hot topic in pipeline research [1,2,3,4,5,6]. The vibro-acoustic characteristics of pipeline structures were investigated using theoretical analysis, numerical calculation, and experimental analysis. Three aspects of these studies are involved: the fluid turbulent characteristic problem, flow noise problem, and pipeline structure vibration and acoustic radiation problem [7,8,9,10]. For the turbulent pulsating pressure, Corcos proposed the frequency wave number spectral model to investigate the turbulent pulsating pressure of plate structure, which laid the groundwork for the quantitative analysis of turbulent pulse pressure theory [11]. In addition, the large eddy simulation (LES) method, the discrete eddy simulation method, and the Reynolds averaging method are the primary methods for numerical computation of the turbulent driving pressure, with the LES method being the most widely used [12,13,14]. The LES method and dynamic Smagorinsky sublattice vortex model are often combined to predict the vortex features induced by the complex fluid field, and the turbulent pulsating pressure distribution parameter of the fluid–solid surface are discussed [13,14,15]. On the other hand, turbulent pulse pressure is a random excitation loading and flow excitation loading is a random force. To analyze the acoustic radiation caused by turbulent pulse pressure, it is necessary to obtain the power spectrum of the turbulent pulsating pressure (the pulse pressure is defined as a virtual excitation force in the vibro-acoustic characteristics analysis) [16,17].

In structural dynamic analysis, the pipeline structure can be simplified as a cylindrical shell structure system, and the Flügge shell theory can be employed in dynamic response analysis. Applying the analytical solution of the acoustic Helmholtz equation to the cylinder shell structure is possible in free space. However, the acoustic boundary conditions may be irregular or complicated in many engineering domains, and these acoustic boundary conditions may affect the acoustic radiation characteristics. Thus, the influence of the acoustic boundary characteristics, particularly their effect on the control acoustic space, must be considered in the vibro-acoustic problem. Currently, the research result is more mature for the half-space acoustic radiation problem, including concerns with the free interface and rigid wall interface [18]. To solve the complex acoustic radiation problem, the mirror theory is broadened to the three-dimensional domain. Acoustic boundary characteristics have been studied extensively in order to analyze their influence. The double reflection method is presented to address multiple issues caused by the acoustic boundary [19,20]. Multiple boundary problems can be solved by combining the double reflection method with the elastic wave Graf addition principle and the research scope for vibro-acoustic problems to vibration power flow problems has been extended with the inclusion of the right-angle domain of the acoustic radiation from the cylindrical shell structure [21,22,23,24]. It is necessary and feasible to study the noise characteristics caused by a pipeline structure in a rigid corner of a cabin.

The main objectives of the present work were to analyze the influence of acoustic boundaries of quarter-infinite space on vibro-acoustic characteristics of the pipeline structure. The vibro-acoustic analytical function in the quarter-infinite space was derived using a combination of the double reflection method, mirror image method, and the Graf addition principle. According to the principles of numerical analysis, the influences of the acoustic radiation power on frequency, flow and velocity location were compared using fluctuation pressure. The main innovation of the present work is to propose a method to solve the flow-induced noise of the pipeline inside the cabin, taking into account the installation factors of the pipeline structure.

2. Flow Excitation Equation for Piping System

2.1. Pipeline Fluctuation Pressure

Discussion of the internal flow functions of the pipeline is necessary to obtain the turbulent pulsating pressure equation of the pipeline structure system. In the calculation of turbulent pulse pressure, the transient turbulent pulse motion decomposes into two parts according to the large eddy simulation method (LES): the Navier–Stokes equation for the resolvable scale (which can be solved directly to obtain the large-scale motion), and the subgrid scale model (which uses the filtering method to simulate the impact of small-scale motion on large-scale motion).

The LES method is implemented for parametric filtering of the motion in the flow field and the parametric analysis and the filtering process of the flow field is denoted by the equation:

$$\tilde{f}(x_i,t)={\displaystyle \underset{D}{\int }G(x_i,x_i^{\prime },\overrightarrow{\Delta })}f(x_i^{\prime },t)\mathrm{d}{x}_i^{\prime },$$

(1)

where $f=\tilde{f}+f^{″}$, $\tilde{f}$ is the resolvable large-scale quantity; $f^{″}$ is the intractable fluctuation quantity, and $f$ is the subgrid fraction. D is the computational domain of the flow field, and G is the filter function. $x_i^{\prime }$ and $x_i$ are the pre-and post-filtering vectors, respectively. According to the box filter theory, the filter function can be written as follows:

$$G(x_i,x_i^{\prime },\overrightarrow{\Delta })=\left\{\begin{array}{l}\frac{1}{\Delta x_1\Delta x_2\Delta x_3},\hspace{1em}\left|x_t^{\prime }-x_i\right|\le \frac{\Delta x_i}{2}\hspace{1em}i=1,2,3\hfill \\ 0,\hspace{1em}\left|x_t^{\prime }-x_i\right|\le \frac{\Delta x_i}{2}\hspace{1em}i=1\hspace{1em}\hspace{0.17em}\mathrm{or}\hspace{0.17em}2\hspace{0.17em},\hspace{0.17em}3\hfill \end{array}\right.$$

(2)

Applying the box filter to the Navier–Stokes equation (N–S equation), and the filtered N–S equation is obtained:

$$\left\{\begin{array}{l}\frac{\partial {\tilde{u}}_i}{\partial x_i}=0\hfill \\ \frac{\partial {\tilde{u}}_i}{\partial t}+\frac{\partial {\tilde{u}}_i{\tilde{u}}_j}{\partial x_j}=-\frac{1}{\rho }\frac{\partial \tilde{p}}{\partial x_i}+\nu \frac{{\partial }^2{\tilde{u}}_i}{\partial x_j\partial x_j}+\frac{\partial {\tau }_{ij}^{LES}}{\partial x_j}\hfill \\ {\tau }_{ij}^{LES}=-{\overline{u}}_i^{″}{u}_j^{″}\hfill \end{array}\right.$$

(3)

where $-{\overline{u}}_i^{″}{u}_j^{″}$ is the subgrid stress parameter, which can be expressed as $-{\overline{u}}_i^{″}{u}_j^{″}={\nu }_{SGS}\left(\frac{\partial {\tilde{u}}_i}{\partial x_j}+\frac{\partial {\tilde{u}}_j}{\partial x_i}\right)$, and ${\nu }_{SGS}$ is the vortex viscosity coefficient in the Smagorinsky vortex viscosity model [2,4].

2.2. Stochastic Acoustic Vibration Analysis of the Piping System

In order to solve the random vibration problem of the continuous elastic structure, the virtual excitation method is introduced. The motion equation of the elastic structure under the random excitation can be written as:

$$M\ddot{x}+C\dot{x}+Kx=Ry(t)$$

(4)

where M, C and K are the structural mass matrix, viscous damping matrix, and structural stiffness matrix, respectively. R is the specified constant matrix, which describes the distribution of the external excitation, and $y(t)$ is a smooth random vector of order N.

Based on the virtual excitation method, the power spectrum density of the dynamic response of the elastic structure can be written as follows:

$$S_{xx}(k)={\displaystyle \sum _{j=1}^r\{Y_j(k)}{\}}^{\ast }{\{Y_j(k)\}}^{\mathrm{T}}$$

(5)

where the power spectral density matrix $S_{xx}(k)$ is a determinate parameter of the determinate turbulence model and $Y_j(k)$ is the virtual displacement response of the structure under the j-th virtual excitation force after the spectral decomposition. According to Equation (5), the virtual acoustic radiation responses of the structure under random excitation are calculated by using the structural virtual response as the acoustic boundary condition.

3. The Acoustic Radiation Equation of the Pipeline Structure in a Rigid Corner

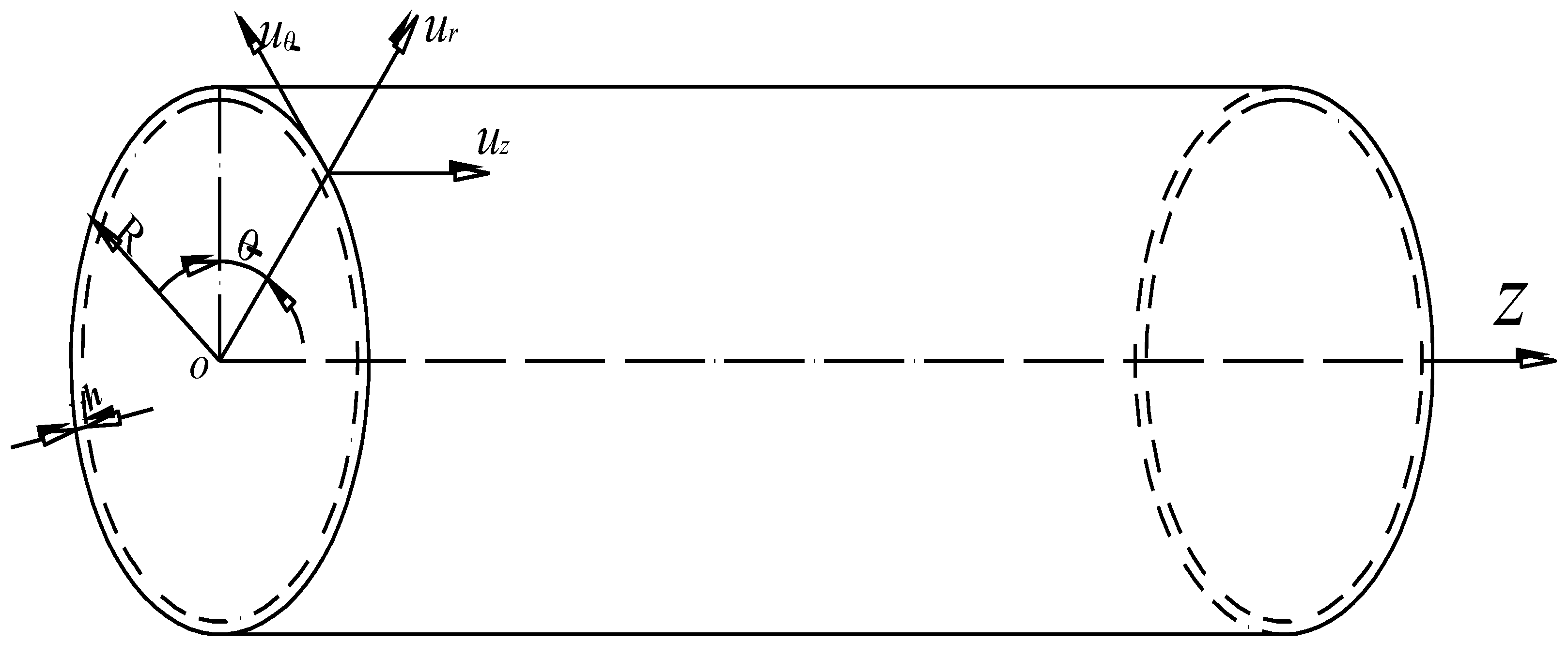
3.1. Cylindrical Shell Model

The vibration and acoustic radiation problem of a cylindrical shell structure is essentially the structural vibro-acoustic radiation problem of the pipeline structure in the acoustic field. To analyze the structural–acoustic radiation problem of cylindrical shell structures, it is necessary to propose a series of appropriate assumptions: the acoustic medium is inviscid and compressible; and the acoustic medium cannot withstand stress.

An infinite thin-walled cylindrical shell was submerged within a fluid with density ${\rho }_f$ and acoustic speed $c_f$, as shown in Figure 1. The definition of certain assumptions is as follows: the material used to make the cylindrical shell structure is both isotropic and linearly elastic; the cylindrical shell has slight deformation; and the cylindrical shell and fluid gravity force are not given sufficient attention.

The position of the fluid domains and cylindrical shell is determined by the cylindrical coordinate system (x₀, θ₀, r₀). The center of the cylindrical shell is where the ordinate origin of the coordinate system is located, as depicted in Figure 1.

In the cylindrical coordinate system, the centerline of the cylindrical shell was chosen as the coordinate axis z and the coordinate axes r and θ responded to the radial and circumferential directions, respectively. u_z, u_θ, and u_r are the orthogonal components of cylindrical shell displacement in the axial, circumferential, and radial directions, respectively. R is the mean radius of the cylindrical shell, and h is the cylindrical shell thickness. R and h satisfy $h/R<<1$.

According to the acoustic Helmholtz equation, in cylindrical coordinate systems, the associated form of the acoustic field in free space is expressed by solving the acoustic wave equation using the variable separation method. The far-field acoustic pressure of the cylindrical shell structure can be described as follows:

$$p_f={\displaystyle \sum _{\zeta =1}^{\infty }{\displaystyle \sum _{n=-\infty }^{\infty }}}{P}_{n,\zeta }\cos (n\theta )H_n^{(1)}(k_{r}r{)\mathrm{e}}^{-\mathrm{i}{k}_{n,\zeta }z},$$

(6)

where $P_{n,\zeta }$ is the acoustic pressure amplitude of every n and ζ, $H_n^{(1)}()$ is the nth order of the first-order Hankel function, and $H_n^{(1)}()=J_n()+\mathrm{i}{Y}_n()$, and $k_r$ are the radial and free wave numbers. The parameter $k_r$ depends on the free wave number $k_0$ and axial wave numbers $k_{n,\zeta }$ and the relationship between them can be written as follows: $\left\{\begin{array}{c}{k}_r=\sqrt{k_0^2-k_{n,\zeta }^2}\\ k_r=-\mathrm{i}\sqrt{k_0^2-k_{n,\zeta }^2}\end{array}\begin{array}{c},0<k_{n,\zeta }<k_0\\ \begin{array}{cc}& \end{array},k_0<k_{n,\zeta }\end{array}\right.$.

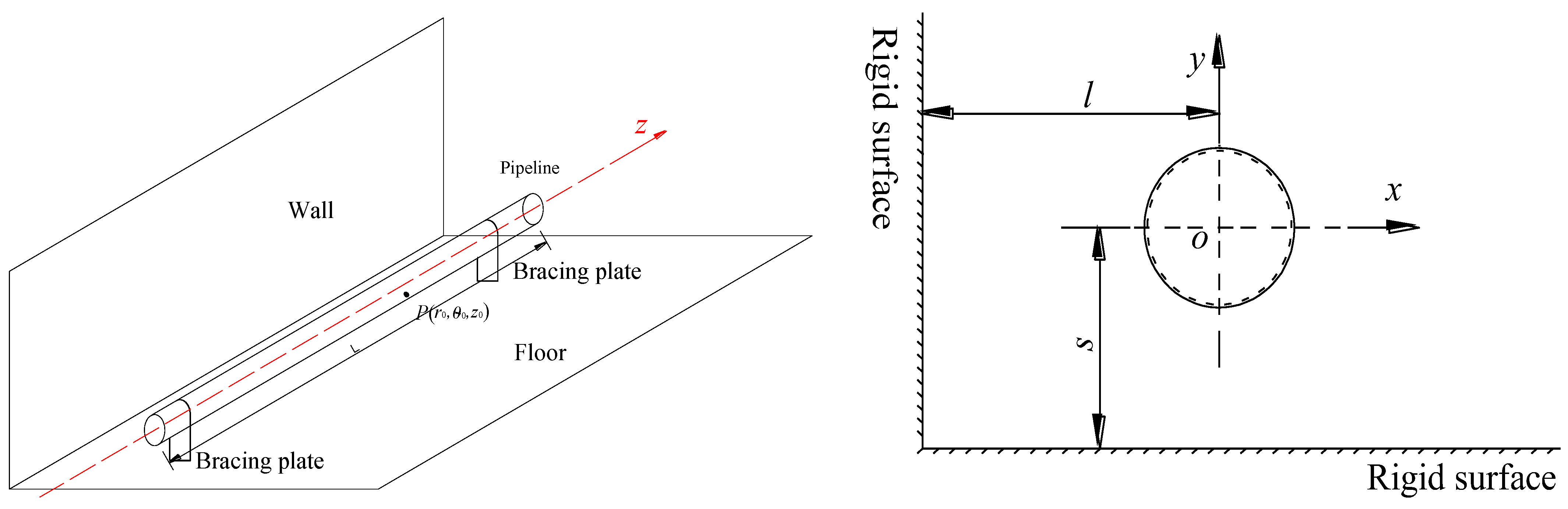
3.2. Corner Space Overview

Suppose the pipeline is arranged on the quarter-infinite space with two rigid acoustic boundaries (wall and floor) at the same time, as shown in Figure 2. In addition, suppose that the two ends of the pipeline structure are simple supports. If the factor of the axial coordinate z is ignored then the problem of the 3D quarter-infinite space can be transformed into a 2D plane problem. The z-direction is set to the axial direction of the pipeline, the x-axis is set to the right direction, and the y-axis is set to the top direction. The distances between the center of the pipeline structure and the rigid wall are l and s $(l>R,s>R)$, respectively, as shown in Figure 2.

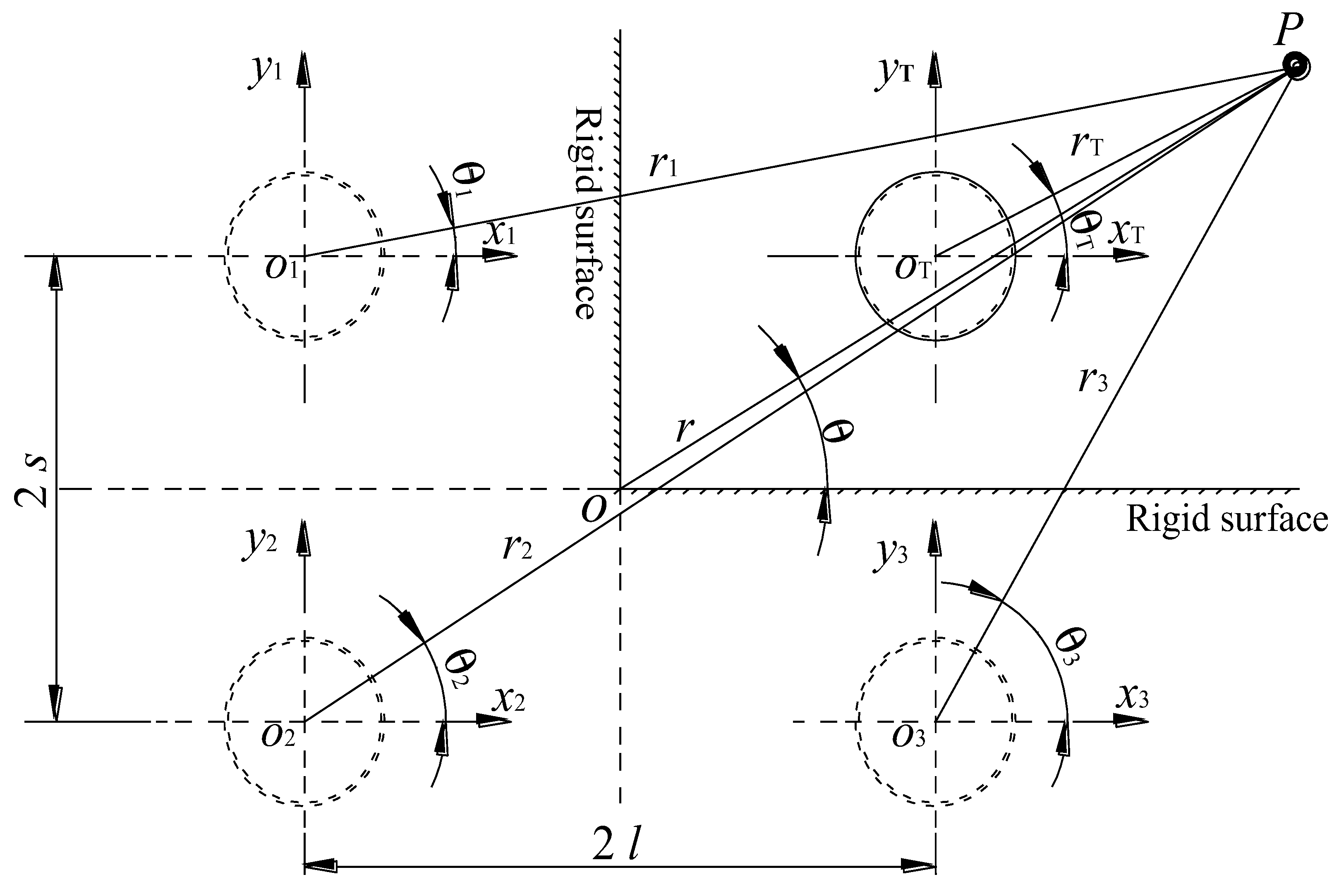
3.3. Double-Reflection Theory

According to the research results by Chan [20], Chen [21,22] and Guo [24], the double reflection method is highly effective to solve the acoustic radiation problem in the quarter-infinite acoustic space. The double reflection method states that the quarter-infinite space has four acoustic radiation sources, as shown in Figure 3.

In the 2D domain, resource O_T (the solid circle) is the actual cylindrical shell and the cylindrical shell O₁ (the dotted ring) and cylindrical shell O₂ (the dotted ring) are formed by the rigid wall, with cylindrical shell O₃ (the dotted ring) being formed by the double reflection mirrors. Since three images exist, the acoustic pressure $p(r,\theta ,z)$ of the acoustic field point P is superimposed by four parts:

$$p(r,\theta ,z)=p_1(r_1,{\theta }_1,z)+p_2(r_2,{\theta }_2,z)+p_3(r_3,{\theta }_3,z)+p_T(r_T,{\theta }_T,z),$$

(7)

where $p_T(r_T,{\theta }_T,z)$ is the acoustic radiation pressure of O_T, $p_1(r_1,{\theta }_1,z)$ is the acoustic radiation pressure of O₁, $p_2(r_2,{\theta }_2,z)$ is the acoustic radiation pressure of O₂, and $p_3(r_3,{\theta }_3,z)$ is the acoustic radiation pressure of O₃. $r_T$, $r_1$, $r_2$ and $r_3$ are the vector distances between the observer and the positions of the acoustic source, respectively. ${\theta }_T$, ${\theta }_1$, ${\theta }_2$ and ${\theta }_3$ are the angles between the observer and the positions of the acoustic source, respectively.

Based on the acoustic radiation function of the cylindrical shell in the free space of Equation (6), in the quarter-infinite acoustic space shown in Figure 3, the acoustic function of the actual cylindrical shell and the three images can be expressed as follows:

$$\left\{\begin{array}{c}{p}_T(r_T,{\theta }_T,z)={\displaystyle \sum _{\zeta =1}^{\infty }{\displaystyle \sum _{n=-\infty }^{\infty }}}{P}_{n,\zeta }^T{H}_n^{(1)}(k_r{r}_T){\mathrm{e}}^{-\mathrm{i}n{\theta }_T}\\ p_1(r_1,{\theta }_1,z)={\displaystyle \sum _{\zeta =1}^{\infty }{\displaystyle \sum _{n_1=-\infty }^{\infty }}}{P}_{n_1,\zeta }^1{H}_{n_1}^{(1)}(k_r{r}_1){\mathrm{e}}^{-\mathrm{i}{n}_1{\theta }_1}\\ p_2(r_2,{\theta }_2,z)={\displaystyle \sum _{\zeta =1}^{\infty }{\displaystyle \sum _{n_2=-\infty }^{\infty }}}{P}_{n_2,\zeta }^2{H}_{n_2}^{(1)}(k_r{r}_2){\mathrm{e}}^{-\mathrm{i}{n}_2{\theta }_2}\\ p_3(r_3,{\theta }_3,z)={\displaystyle \sum _{\zeta =1}^{\infty }{\displaystyle \sum _{n_3=-\infty }^{\infty }}}{P}_{n_3,\zeta }^3{H}_{n_3}^{(1)}(k_r{r}_3){\mathrm{e}}^{-\mathrm{i}{n}_3{\theta }_3}\end{array}\right.$$

(8)

where $P_{n,\zeta }^T$, $P_{n_1,\zeta }^1$, $P_{n_2,\zeta }^2$ and $P_{n_3,\zeta }^3$ correspond to acoustic pressure amplitudes, respectively. $H_n^{(1)}()$, $H_{n_1}^{(1)}()$, $H_{n_2}^{(1)}()$ and $H_{n_3}^{(1)}()$ correspond to the first kind of Hankel function, respectively. According to the literature [20,21,24], the acoustic boundary of the cylindrical shell structure can be determined using the orthogonality of Hankell’s function combined with Besser’s function (Graf addition principle), and acoustic radiation function in quarter-infinite acoustic space can be obtained.

In addition, the acoustic radiation field quantities are relevant to acoustic pressure and acoustic radiation power. The structural acoustic radiation powers of the cylindrical shell with quarter space and two rigid walls can be determined as follows:

$$W=\frac{1}{2}{\displaystyle {\int }_S\mathrm{Re}\{p(r)\cdot v_n^{\ast }(r)\}}\mathrm{d}S$$

(9)

where $p\left(r\right)$ is the acoustic pressure at the acoustic field point; Re represents the real part of a complex variable; ${\mathrm{v}}_{\mathrm{n}}^{\ast }\left(r\right)$ is the field point velocity of the normal complex conjugate operator of a fluid particle; and S is the integral surface of the acoustic calculation domain.

4. Numerical Calculation

To demonstrate the effect of the boundary on acoustic radiation for the pipeline structure in the quarter-infinite space, numerical analysis was performed.

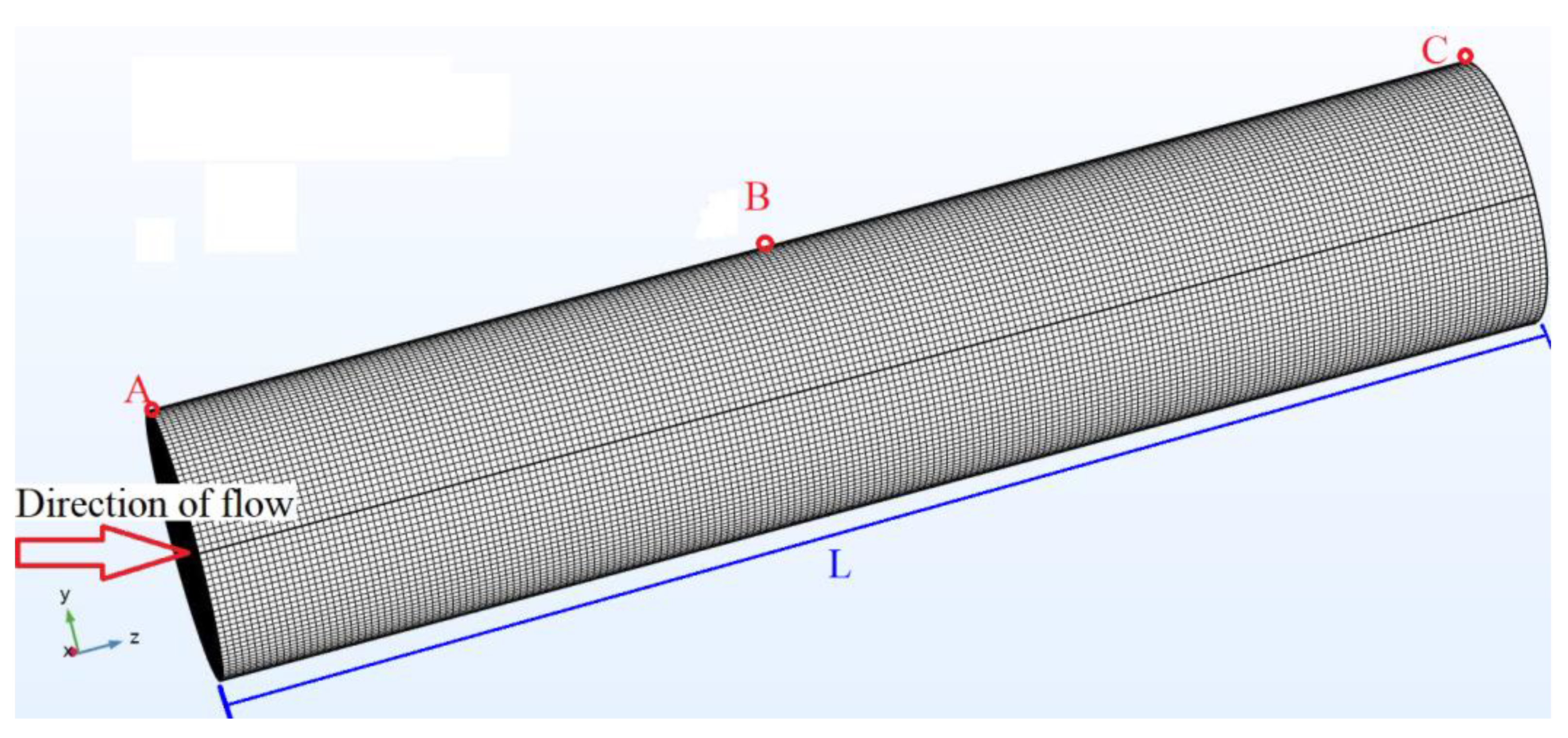
4.1. Model Description

In the analysis of the flow excitation noise of the pipeline structure, the pipeline ss assumed to be a cylindrical shell structure with an equal cross section. In order to determine the vibro-acoustic characteristic of the pipeline structure in the quasi-infinite space, the pipeline structure was defined as having an indefinite length. The analysis domain is defined as [−L/2, L/2] if the pipeline structure length is satisfied and $L>>l,s,r,R$ an acoustic baffle defining the two ends in the pipeline structure.

In the case of numerical calculations for the pipeline structure, the design parameters of the pipeline structure are defined as follows: pipeline diameter D = 0.2 m; pipeline length L = 5 m; and pipeline shell thickness h = 0.002 m. The internal flow is water with density ${\rho }_S$ =1000 kg/m³, and the dynamic viscosity coefficient is $v=1.05\times {10}^{-3}$ Pa·s.

4.2. Fluctuation Pressure Calculation

The fluid dynamics software platform OpenFOAM 5.5 was used to mesh the internal fluid domain of the pipeline. The fluid boundary conditions were defined for calculating the turbulent driving pressure and the fluid property assumptions were defined as follows: the fluid satisfies the no-slip condition in the fluid–solid interface; and the mean velocity of the flow is 2 and 5 m/s, satisfying the continuity condition at the fluid–solid interface. A dense FE mesh is applied to the fluid–solid interface to achieve high numerical accuracy, enhancing the numerical computation precision in the turbulent pulse pressure analysis. The computational domain mesh is shown in Figure 4.

Numerical analysis of the turbulent pulse pressure in the pipeline was based on LES theory. The Smagorinsky–Lilly sublattice model was applied to capture information regarding the vortex structure inside the pipeline structure. The turbulent pulse pressure was applied to the pipeline as an excitation loading action. In the numerical calculation, the calculation step was 10⁻⁶ s and the total calculation time was 2 s. The influence of the flow velocity on the turbulent fluctuation pressure inside the pipeline was analyzed. In the turbulent vortex distribution analysis, the Q criteria were used to evaluate the vortex characteristics and Q = 10 was chosen in the present work, as shown in Figure 5.

The turbulent pulse pressure at the inner surface of the pipeline structure was transformed from time domain to frequency domain. Three points previously identified in Figure 4 were used as reference points for the flow field to compare the influence of the flow velocity on the fluctuation pressure, as shown in Figure 6.

The turbulent pulse pressure was concentrated in the low-frequency band. With increasing flow velocity, the turbulent fluctuation pressure increased significantly, and the peak value of fluctuation pressure shifted towards the high-frequency direction. The fluctuation pressure at the exit point was significantly greater than at the entrance point, regardless of high flow velocity or low flow velocity.

4.3. Pipeline Acoustic Radiation Analysis

A finite element model of the pipeline structure was established. In pipeline structure dynamic numerical analysis, both ends of the pipeline structure were simply supported. The dynamic response of the pipeline structure was analyzed using the excitation force of the pulsating pressure on the inner wall surface of the pipeline structure. The finite element method (FEM) was employed to verify the dynamic response of the pipeline structure. Considering that the business software MSC.Patran/Nastran 2012.2 is a proven and widely used numerical tool for structural dynamic response analysis, the FEM predictions were calculated using MSC/Nastran 2012. The pipe material is steel with the following mechanical properties: density ${\rho }_S$ = 7800 kg/m³; modulus of elasticity E = 210 GPa; and Poisson’s ratio μ = 0.3.

The normal vibration velocity of the pipeline structure was defined as the acoustic boundary condition, the outer surface was defined as the acoustic radiation surface and the boundary element method (BEM) was applied to deal with the exterior acoustic radiation problem. In addition, the influence of the internal flow noise was neglected in the numerical calculations. In the numerical analysis for acoustic radiation, the acoustic parameters of the acoustic medium were as follows: density ρ = 1.225 kg/m³ and acoustic velocity c = 340 m/s. The reference value of acoustic power was W₀ = 1 × 10⁻¹² W.

In the numerical calculations, the calculated frequency range was between 1 Hz and 1000 Hz. The step size is 1 Hz in the 1–200 Hz frequency band and 2 Hz in the 200–1000 Hz frequency band.

Firstly, the influences of flow velocity on acoustic radiation power in the pipeline structure are discussed, in which the pipeline structure was defined as the free-space field. Figure 7 indicates the influence of the flow velocity, showing that the acoustic radiation power of the pipeline structure increased significantly when the flow velocity increased in the pipe.

4.4. Acoustic Boundary Condition Influence Analysis

According to Figure 2, the pipeline structure has four different locations; namely, the distance between the cylindrical shell and three kinds of acoustic boundary conditions were selected to compare the influence of location factor. Figure 3 shows the location position of the pipeline structure. Here, l = s = 0 m is defined as the free-space field.

Four different locations were selected for comparison, namely, the distance between the centers of the cylindrical shell to the rigid acoustic boundary. The influence of flow velocity, frequency, and location on acoustic radiation power were compared, as shown in Figure 8.

There is a clear distance influence of the center of pipeline to the rigid wall, and the maximum values of the difference were approximately 10 dB in low-frequency scenarios; when the frequency increased, the influence of the location factor gradually decreased, and the maximum value was approximately 2 dB; in addition, the localization factor on the acoustic radiation power also decreased.

The total level of acoustic radiation power corresponding to the different positions of the pipeline structure are shown in

Table 1. Comparison of total level of acoustic power with different flow velocities (dB).

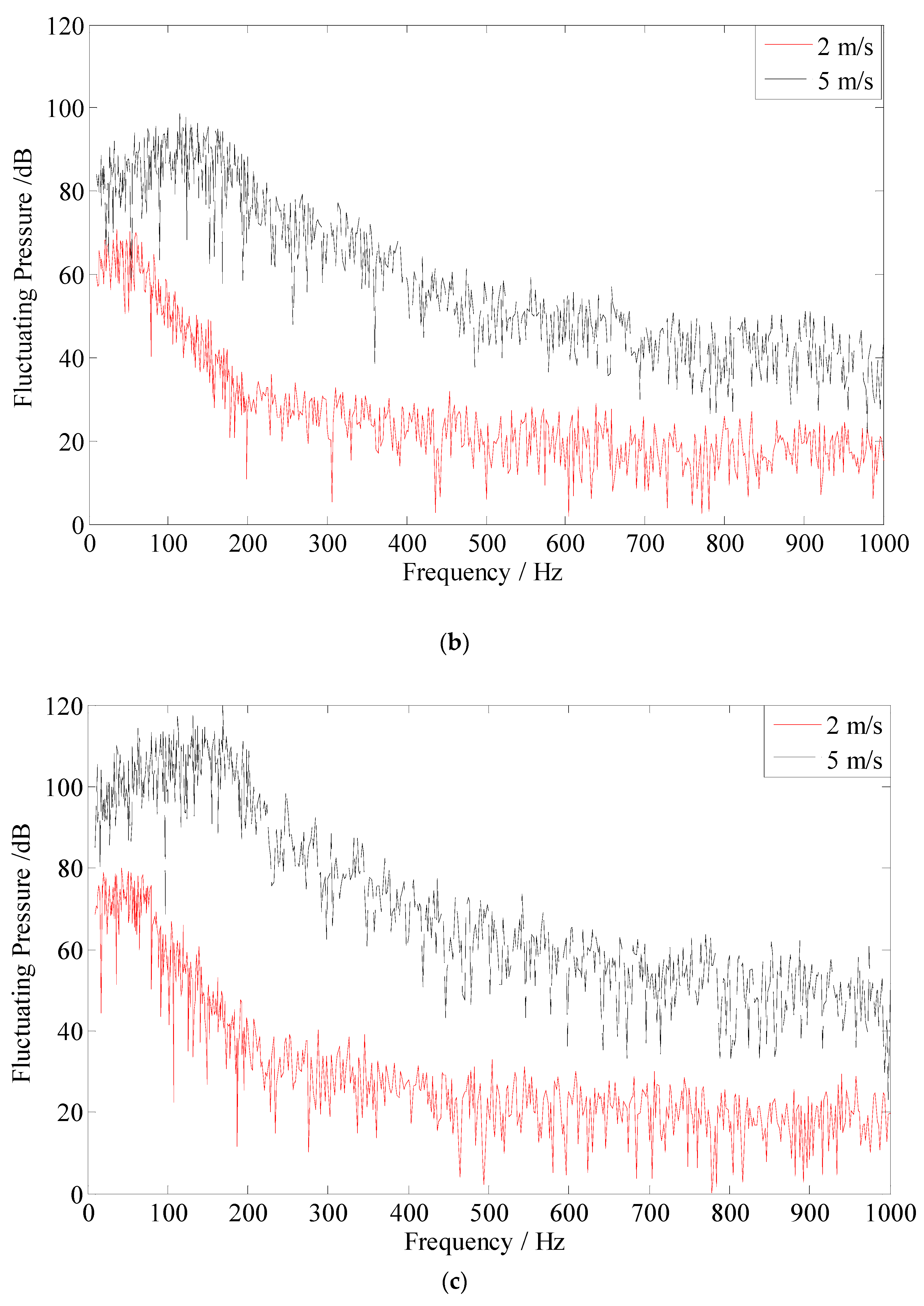
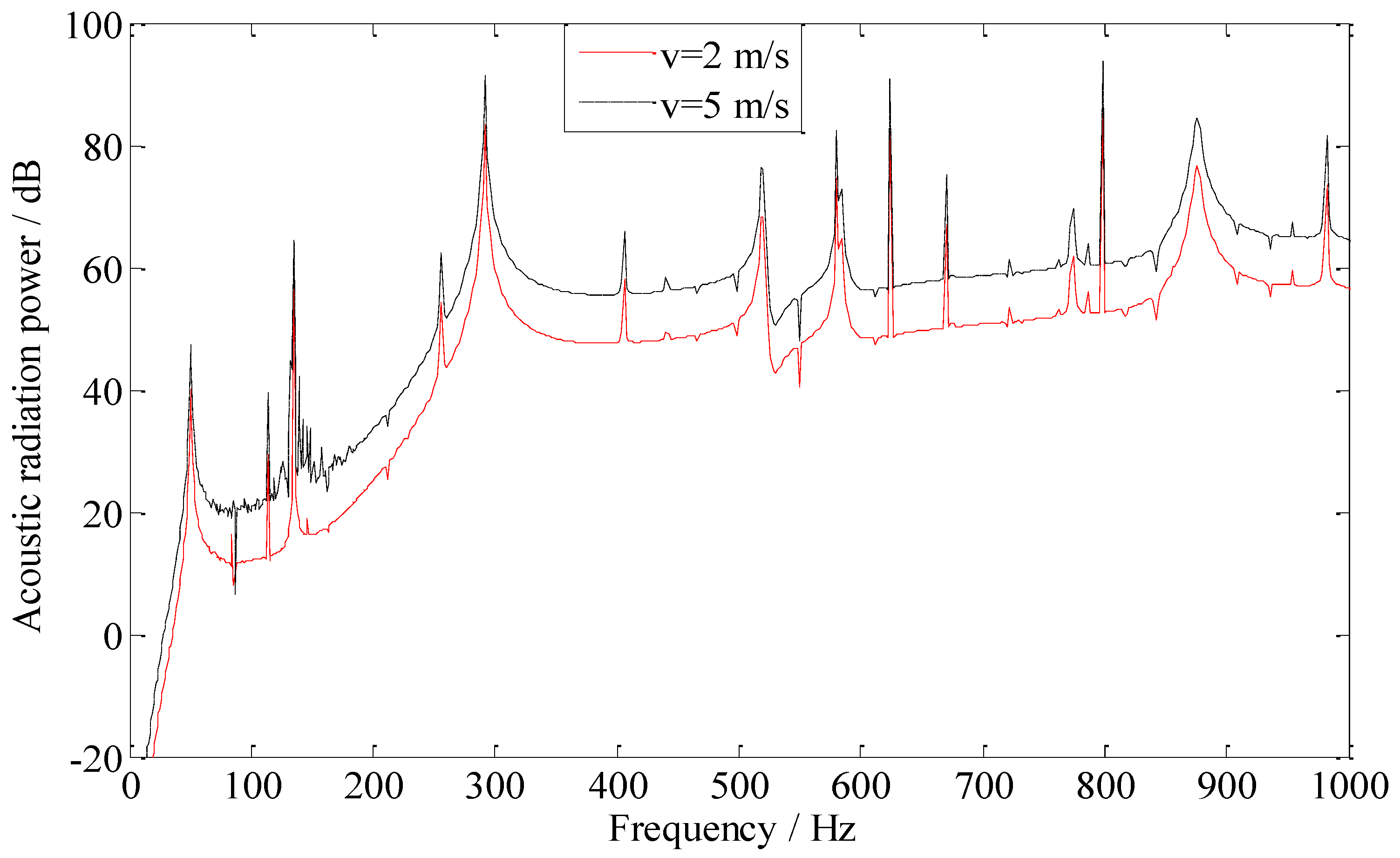
	2 (m/s)			5 (m/s)
	10–200 Hz	200–1000 Hz	10–1000 Hz	10–200 Hz	200–1000 Hz	10–1000 Hz
l = 0, s = 0	54.92	79.82	79.84	62.18	87.82	87.83
l = 0.25, s = 0.25	60.10	86.45	86.46	67.65	94.46	94.47
l = 0.25, s = 1.0	65.51	86.14	86.17	72.82	94.14	94.17
l = 1.0, s = 1.0	62.20	85.89	85.91	69.26	93.88	93.90

.

As shown in Table 1 and Figure 8, when comparing the frequency and location parameter effects on the acoustic radiation power of the cylindrical shell subject to turbulent fluctuating pressure, the following conclusions can be drawn: (1) In the low-frequency band, the distance parameter of the pipeline structure has a slight influence on the acoustic radiation power parameter. (2) In the low-frequency range, the existence of two rigid surface acoustic boundaries has a significant influence on the acoustic radiation power parameter, and the influence is more obvious at the peak value of the acoustic radiation power parameter; (3) The influence of the acoustic boundary condition decreases if the distance between the cylindrical shell and the acoustic boundary increases. In general, the acoustic boundary characteristics have a significant influence on the acoustic radiation power, especially in the low frequency band.

5. Conclusions

By using the acoustic phase theory, the double reflection method and the Graf addition theorem, the acoustic radiation function expression in the acoustic domain for vessel cabins with double rigid walls in quarter space was obtained. The acoustic radiation characteristic of the pipeline structure caused by flow excitation in the vessel cabins was performed. Through numerical calculation, the influence of the flow velocity, frequency and location in the vessel cabins was illustrated. The results of the research show that the distance from the rigid surface in the low-frequency band has undergone a significant enhancement effect. The presence of a rigid wall significantly increases the value of the acoustic radiation parameters of the cylindrical shell structure. As the distance between the centers of the pipeline structure to the rigid wall increases, the influence of the rigid wall decreases. In addition, with an increase in frequency, the influence of the rigid wall decreases. The results of present work can be used as a reference for in pipeline layout design for ships.