Segment Thickness Design and Bearing Performance Analysis of Large Inner-Diameter Shield Tunnel under Lateral Unloading
Abstract
:1. Introduction
2. The Numerical Model of Shield Tunnel with Stagger-Jointed Assembly
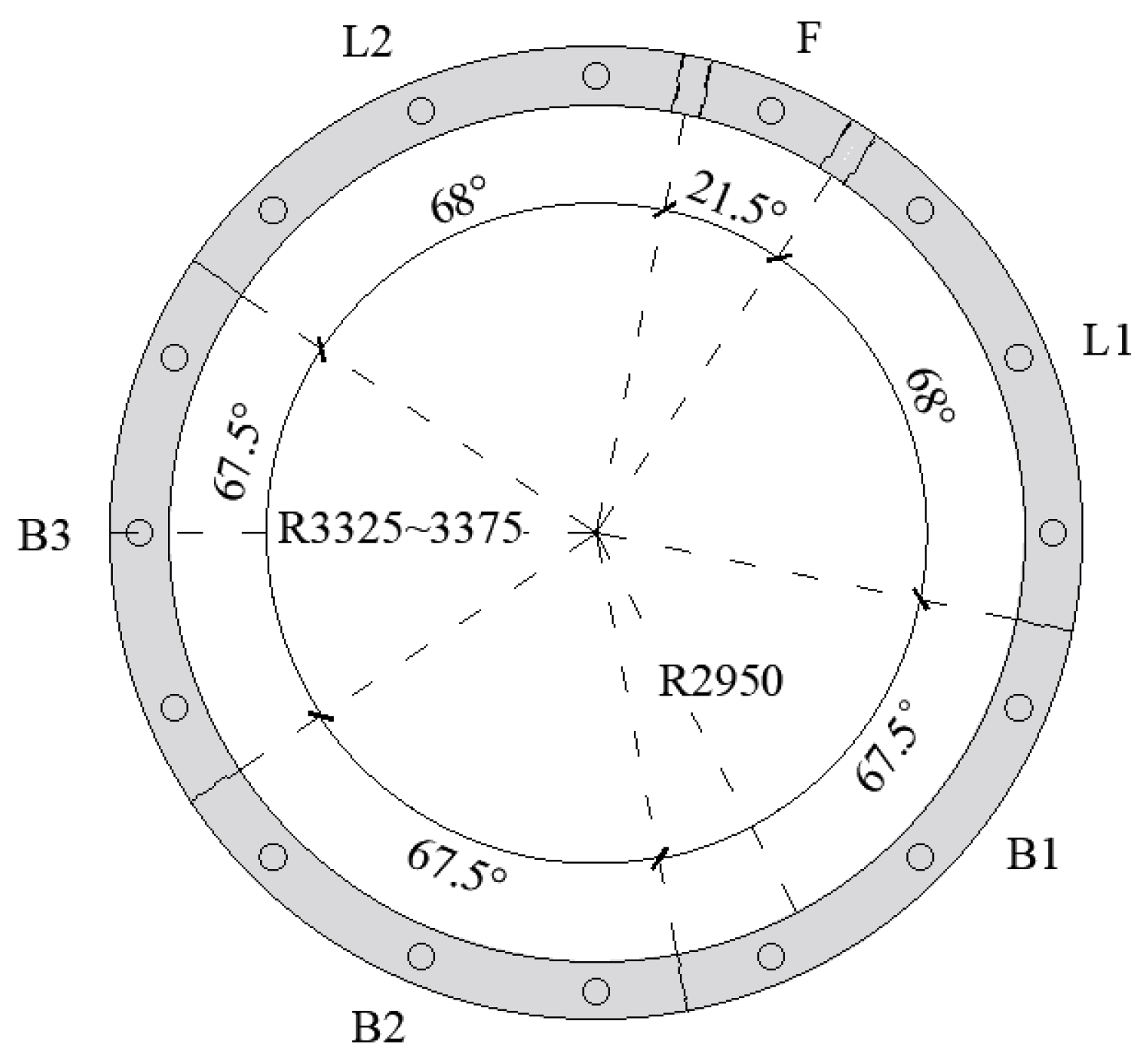
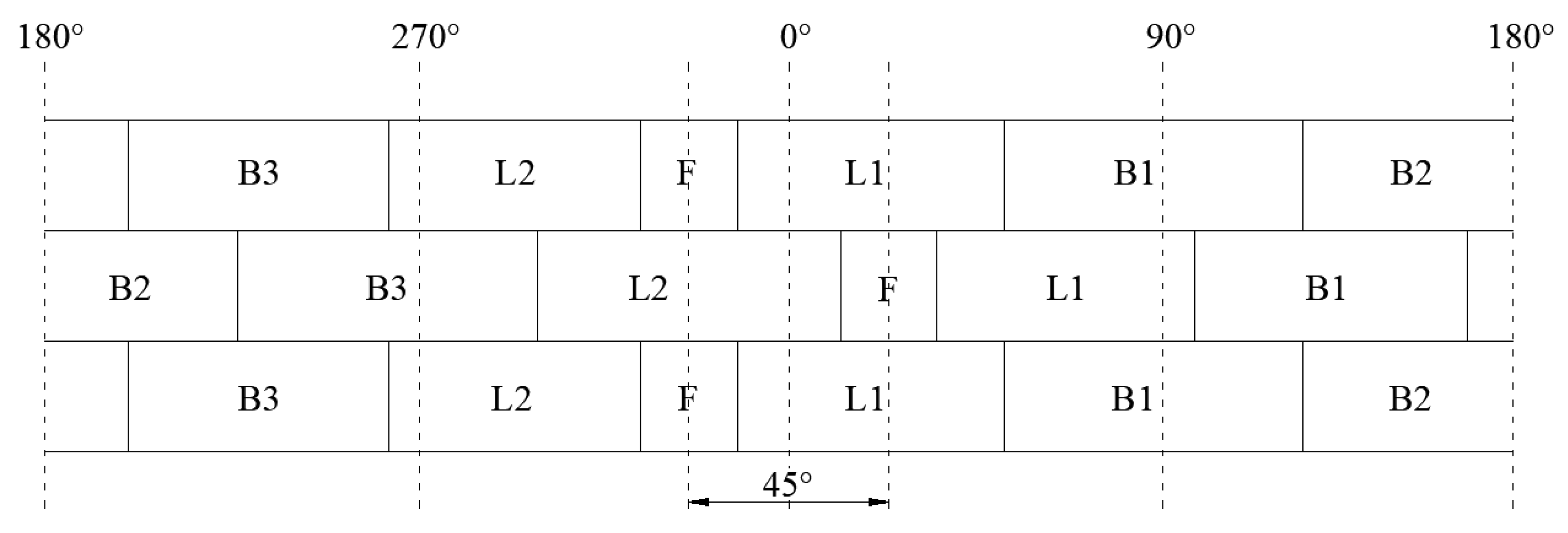
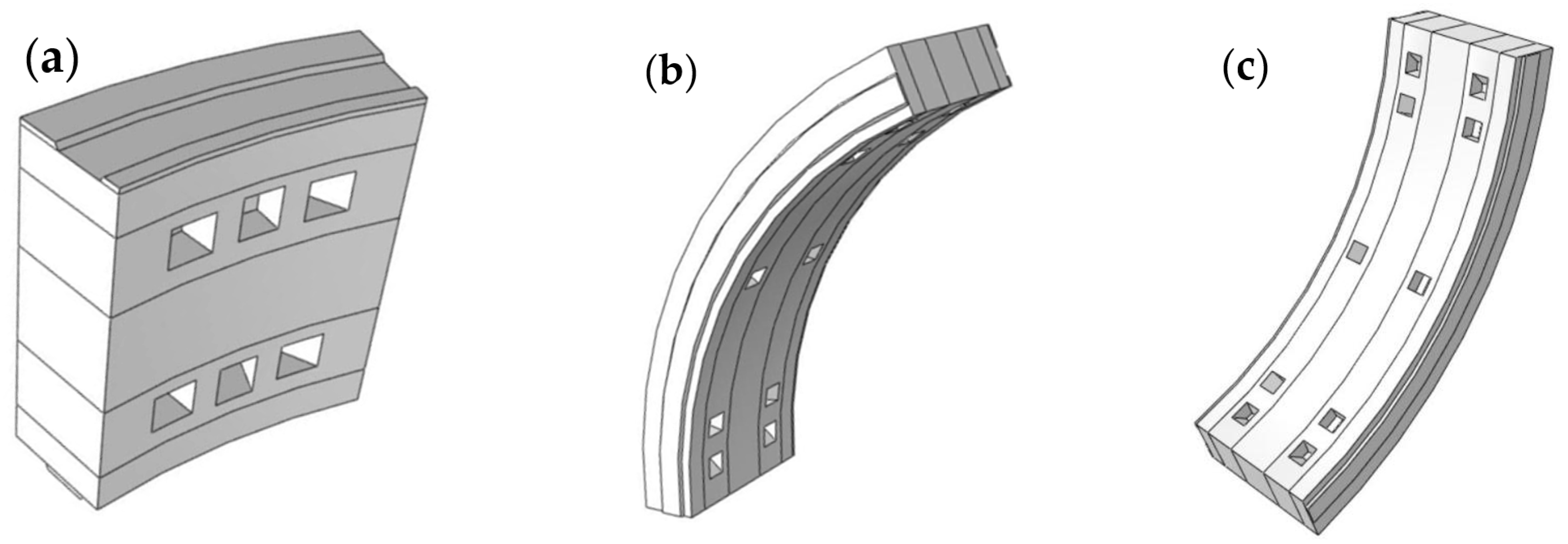
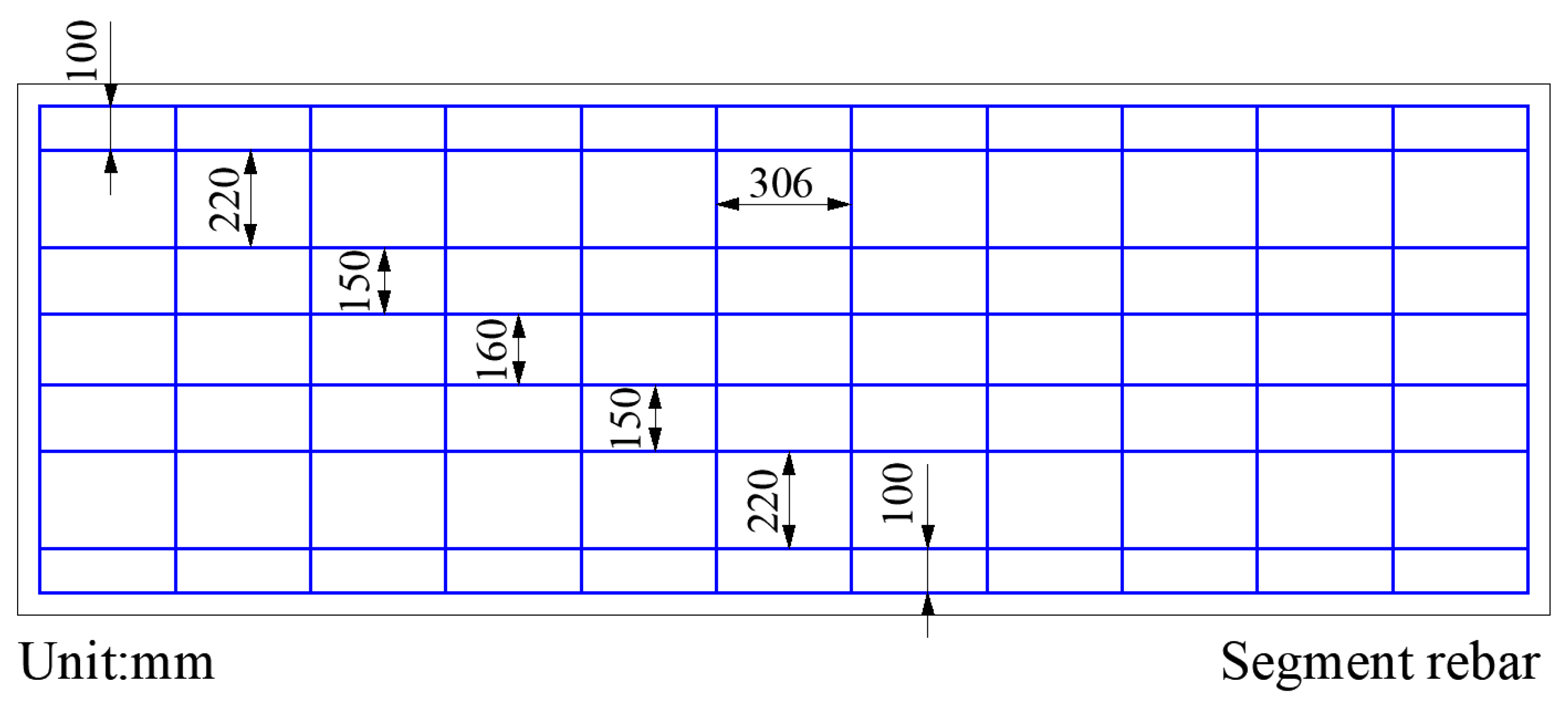
2.1. Geometry Detail of Shield Tunnel Numerical Model
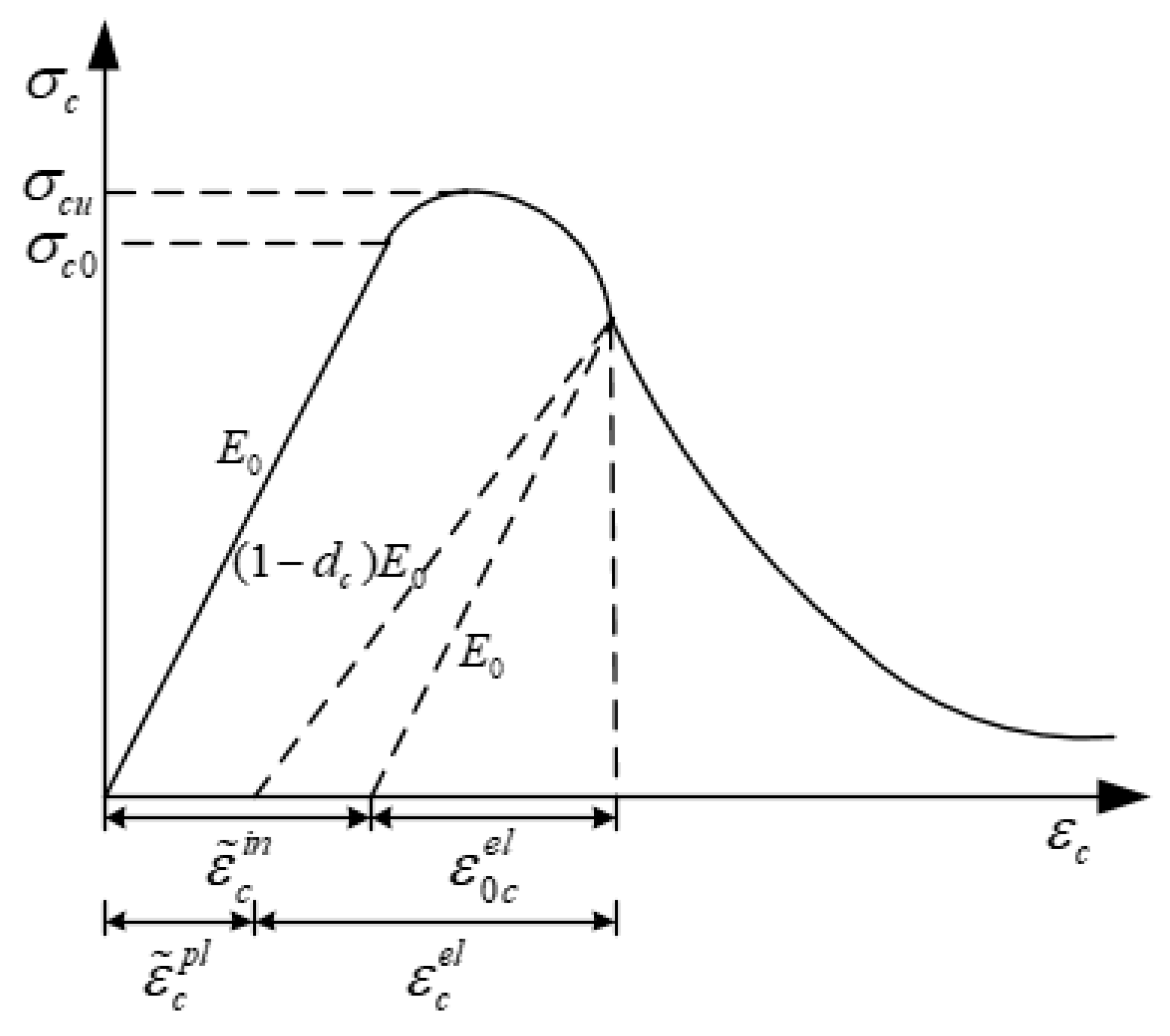
2.2. Material Properties
2.3. Load and Boundary Conditions
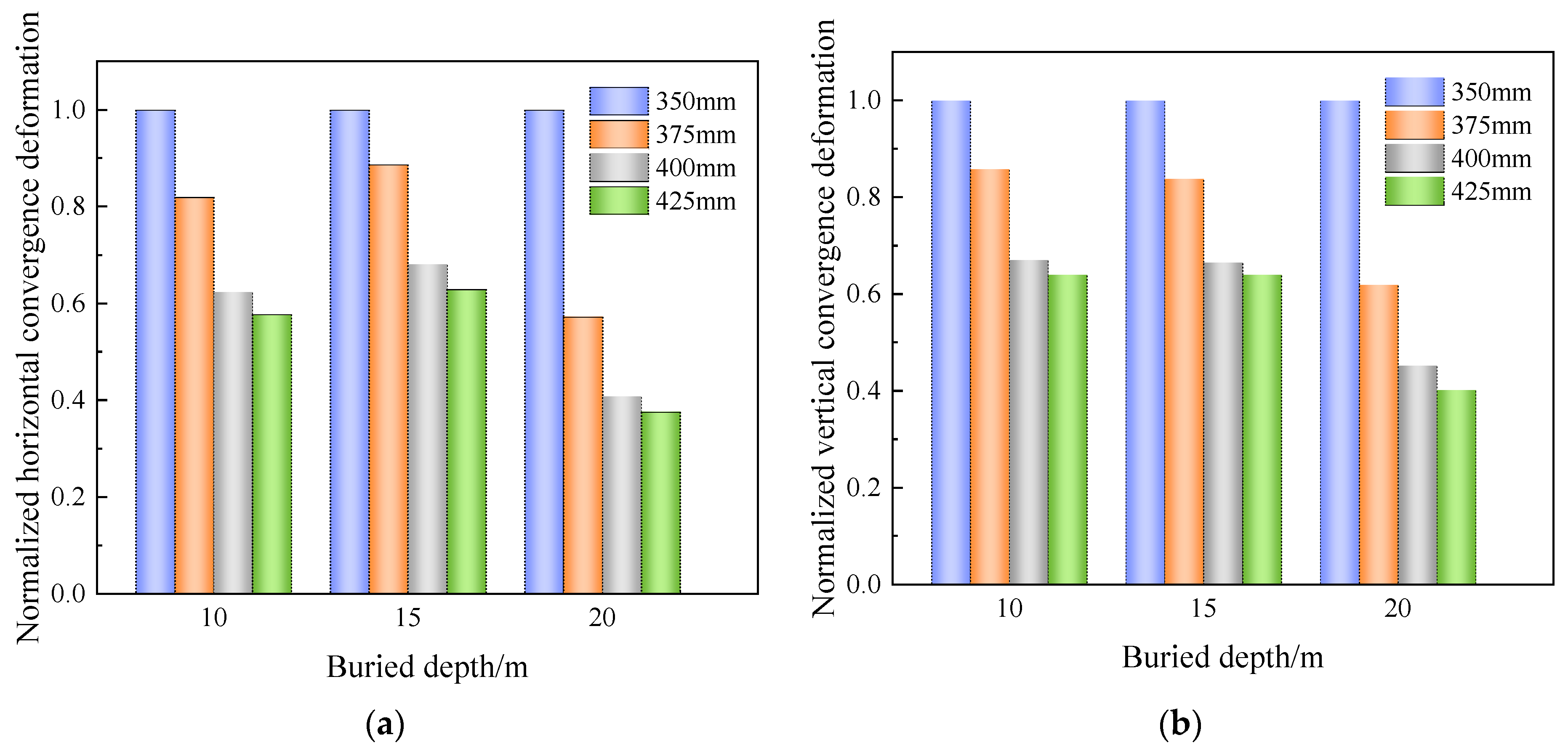
3. Analysis of Bearing Capacity of Shield Tunnels with Different Segment Thickness
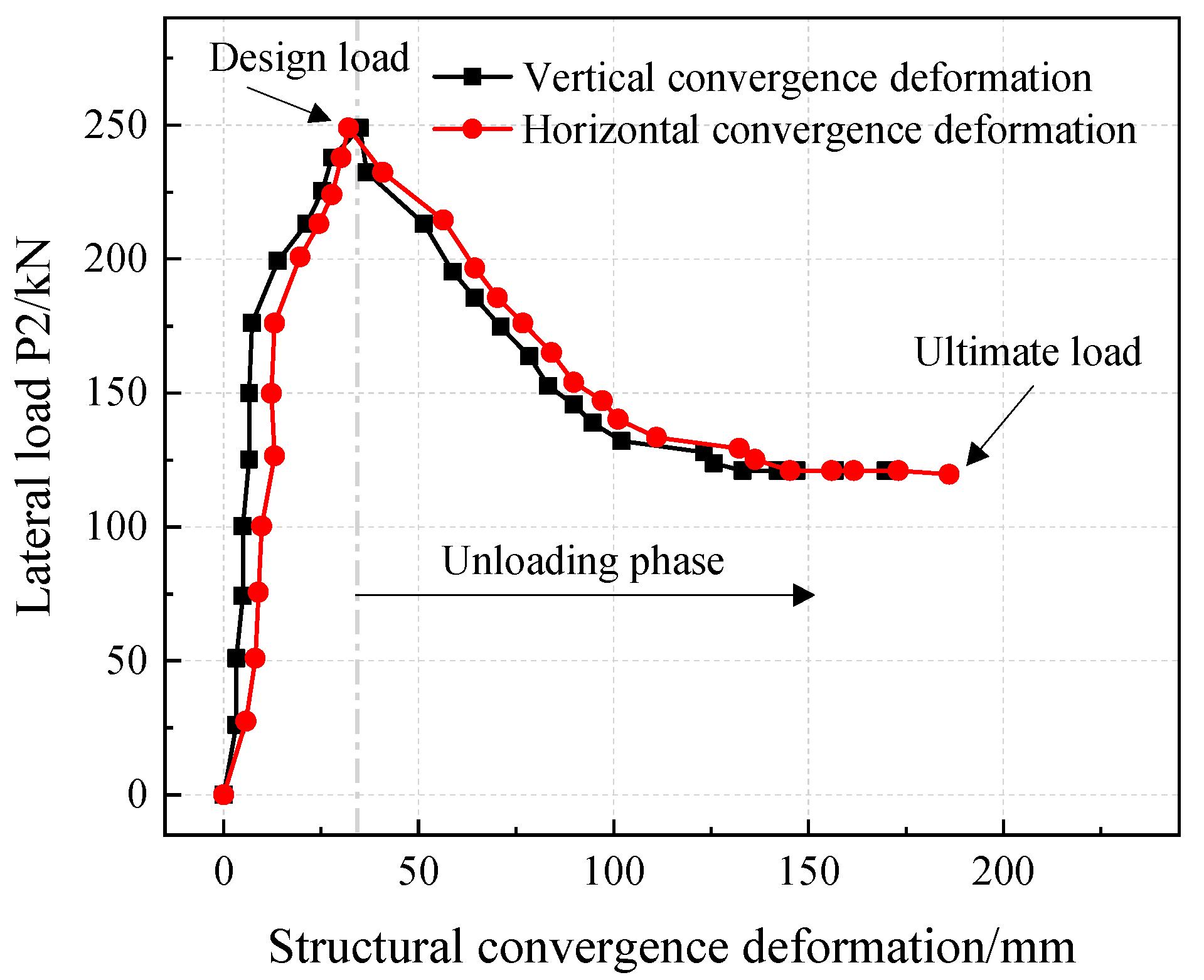
3.1. Structural Convergence Deformation under Normal Design Loading
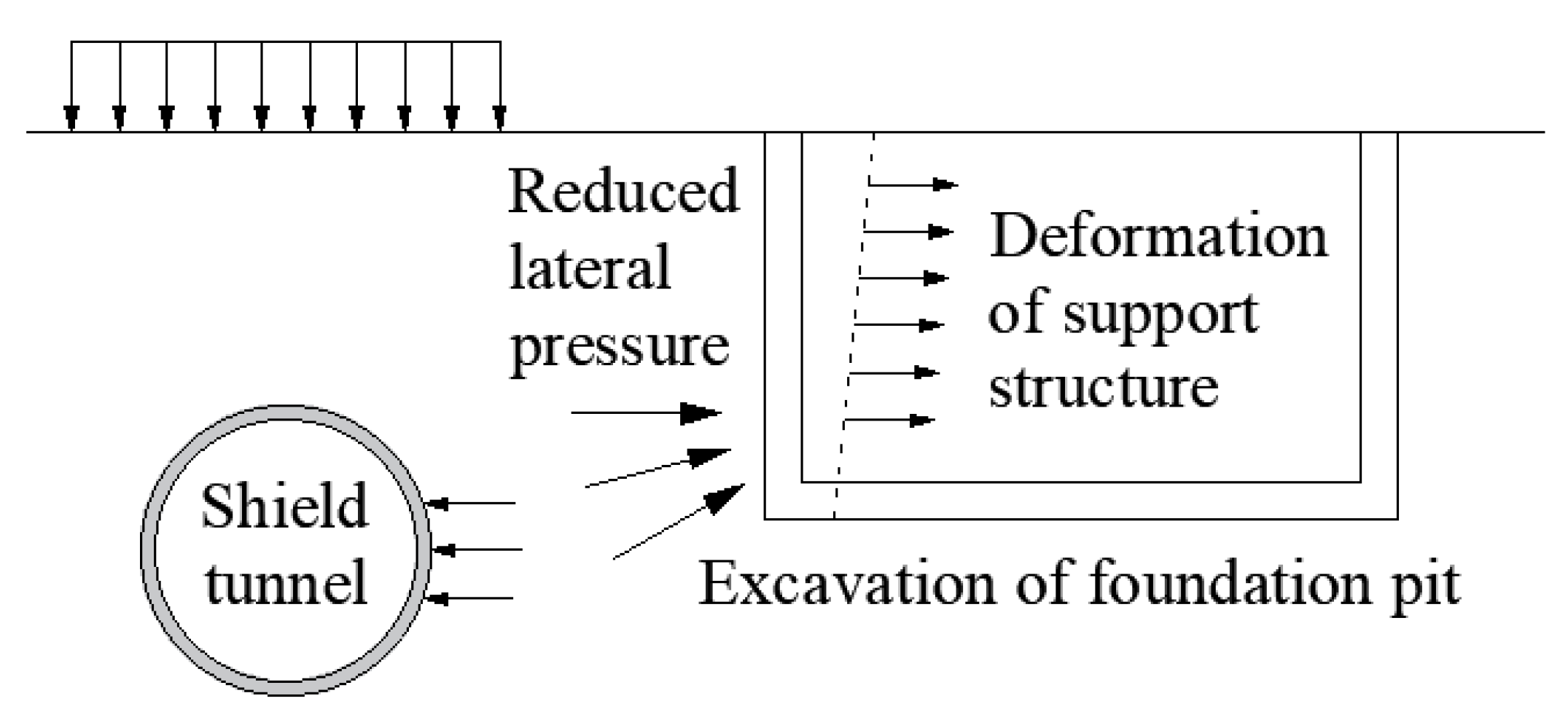
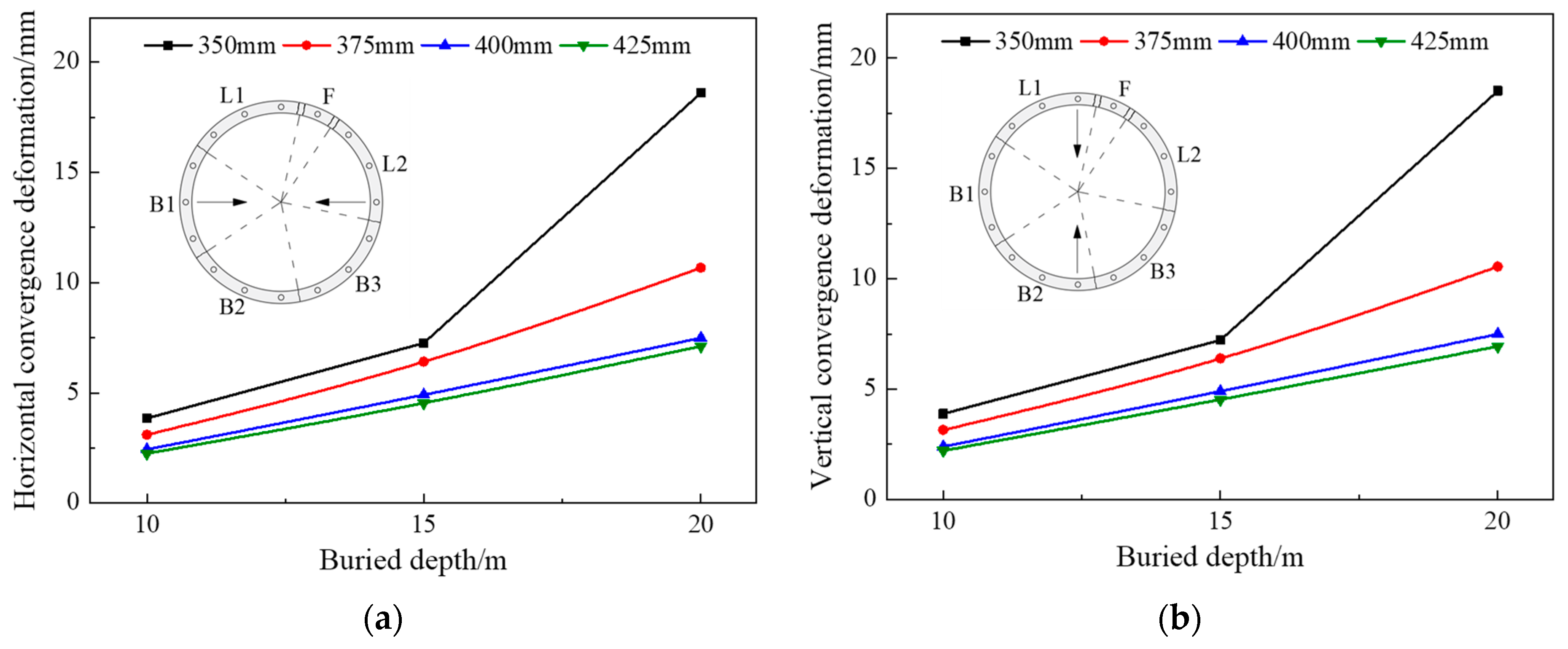
3.2. Structural Convergence Deformation under Excavation Unloading
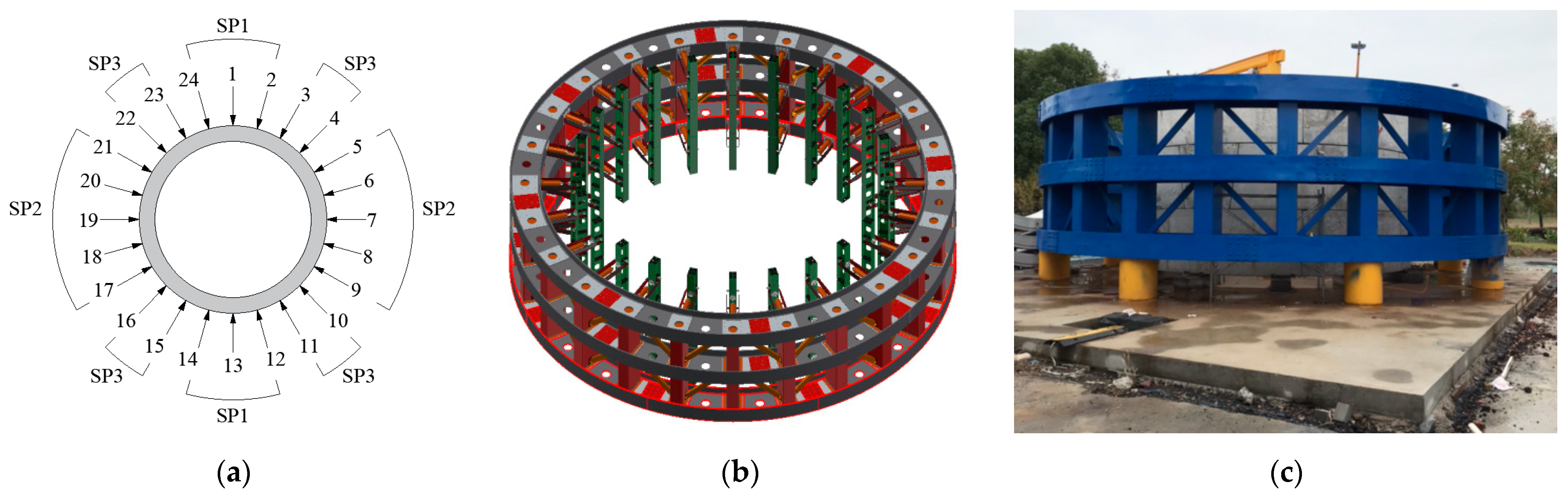
4. Shield Tunnel Load-Bearing Performance Analysis by Full-Scale Test
4.1. Loading Scheme of Test
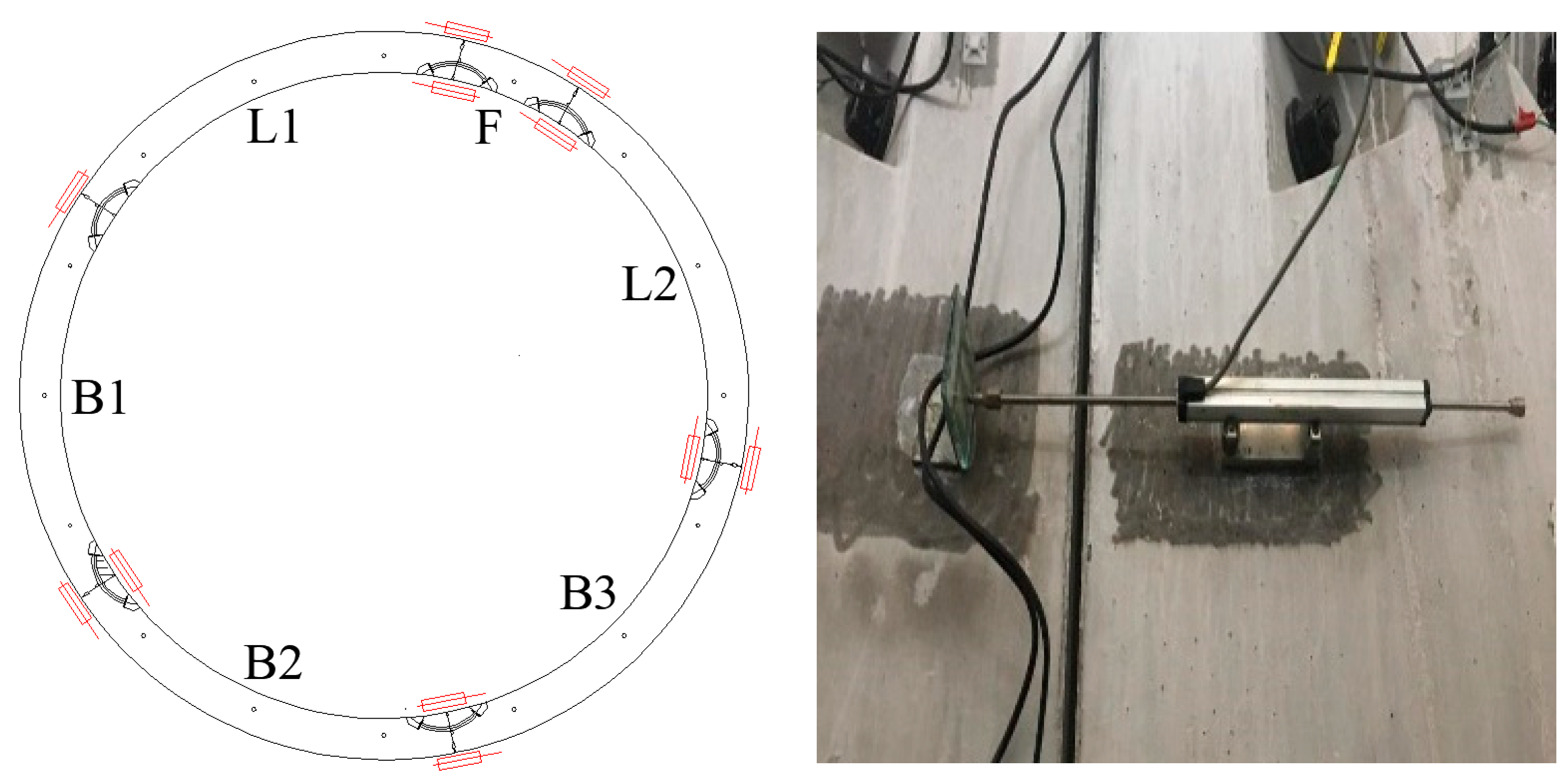
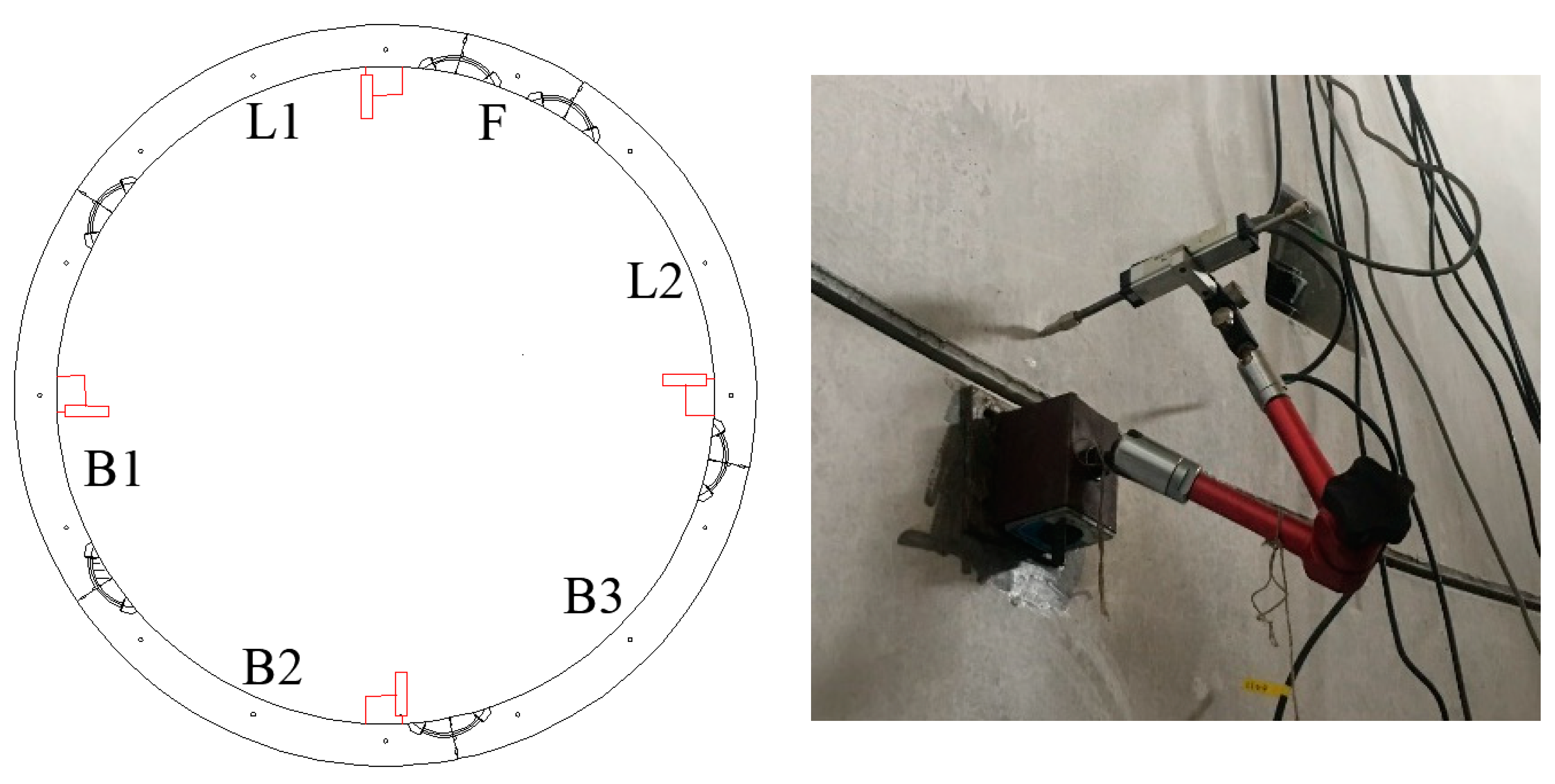
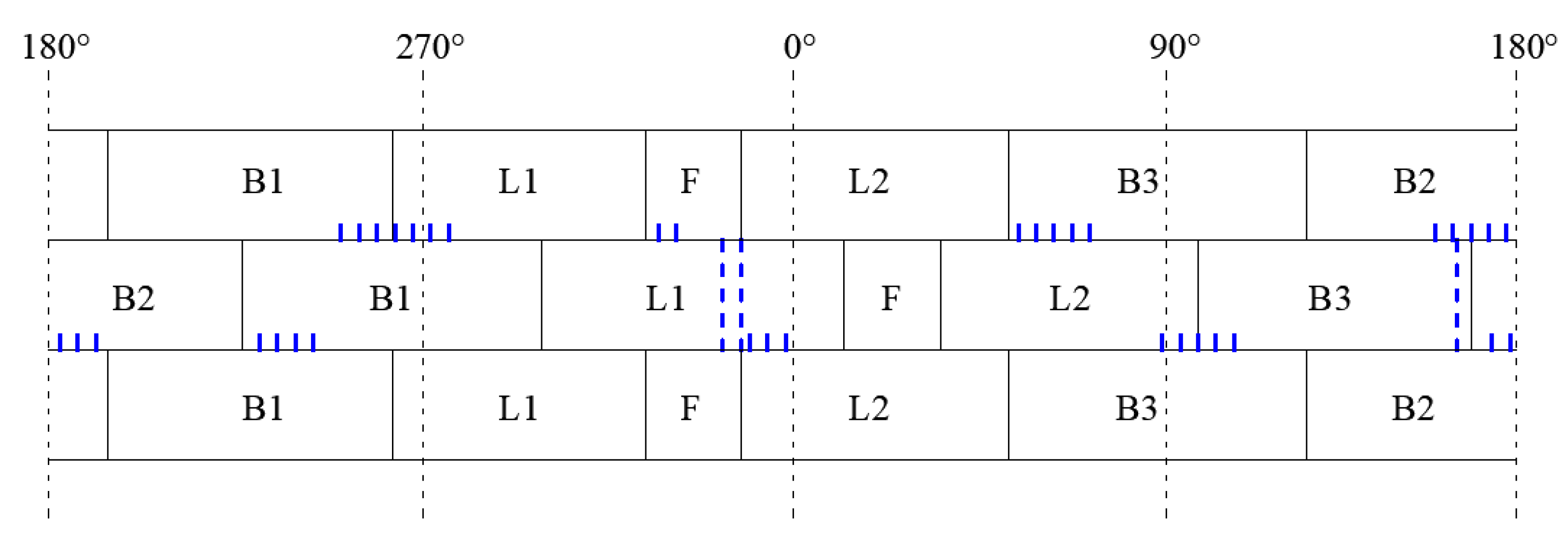
4.2. Measurement Point
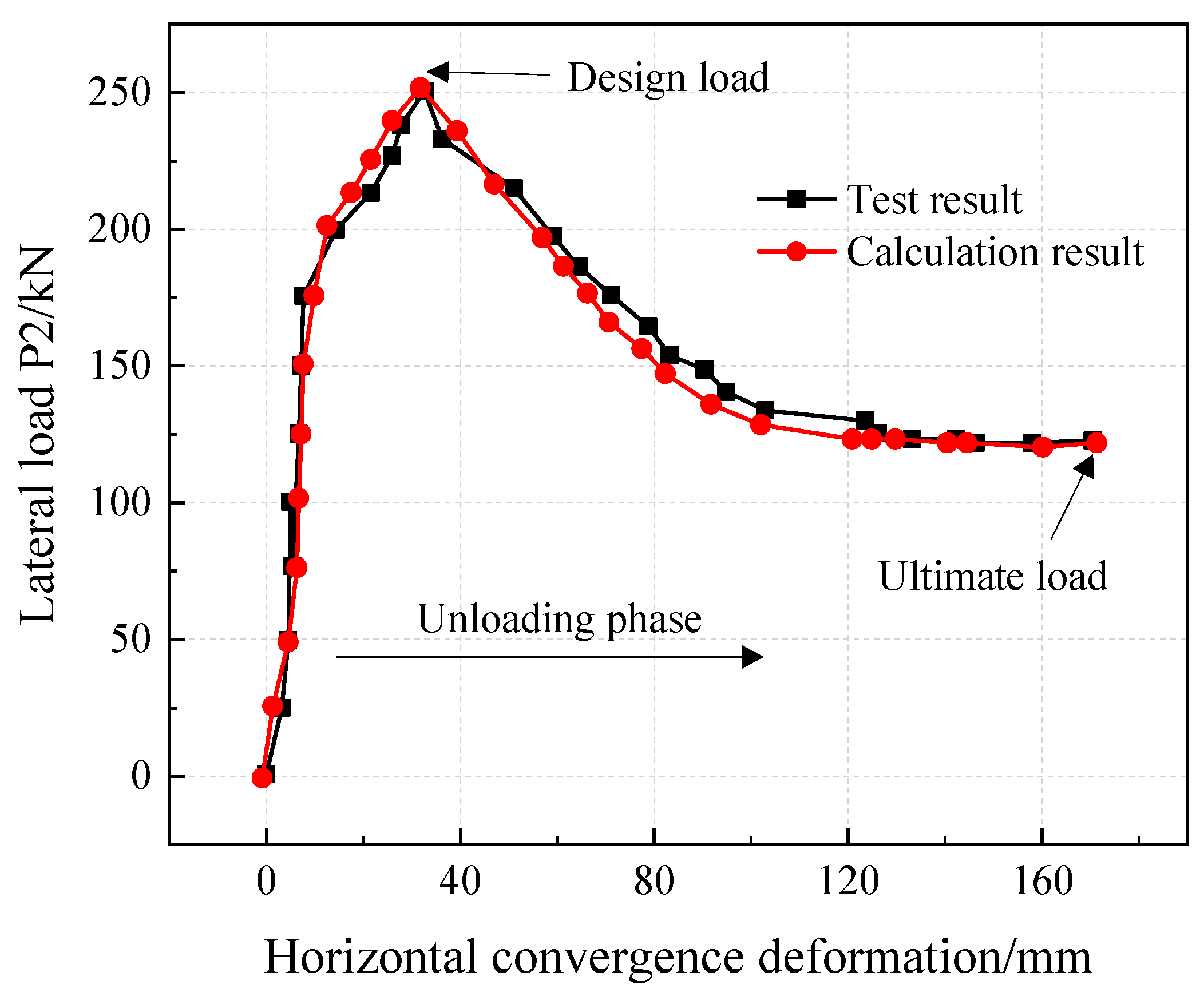
4.3. Test Result
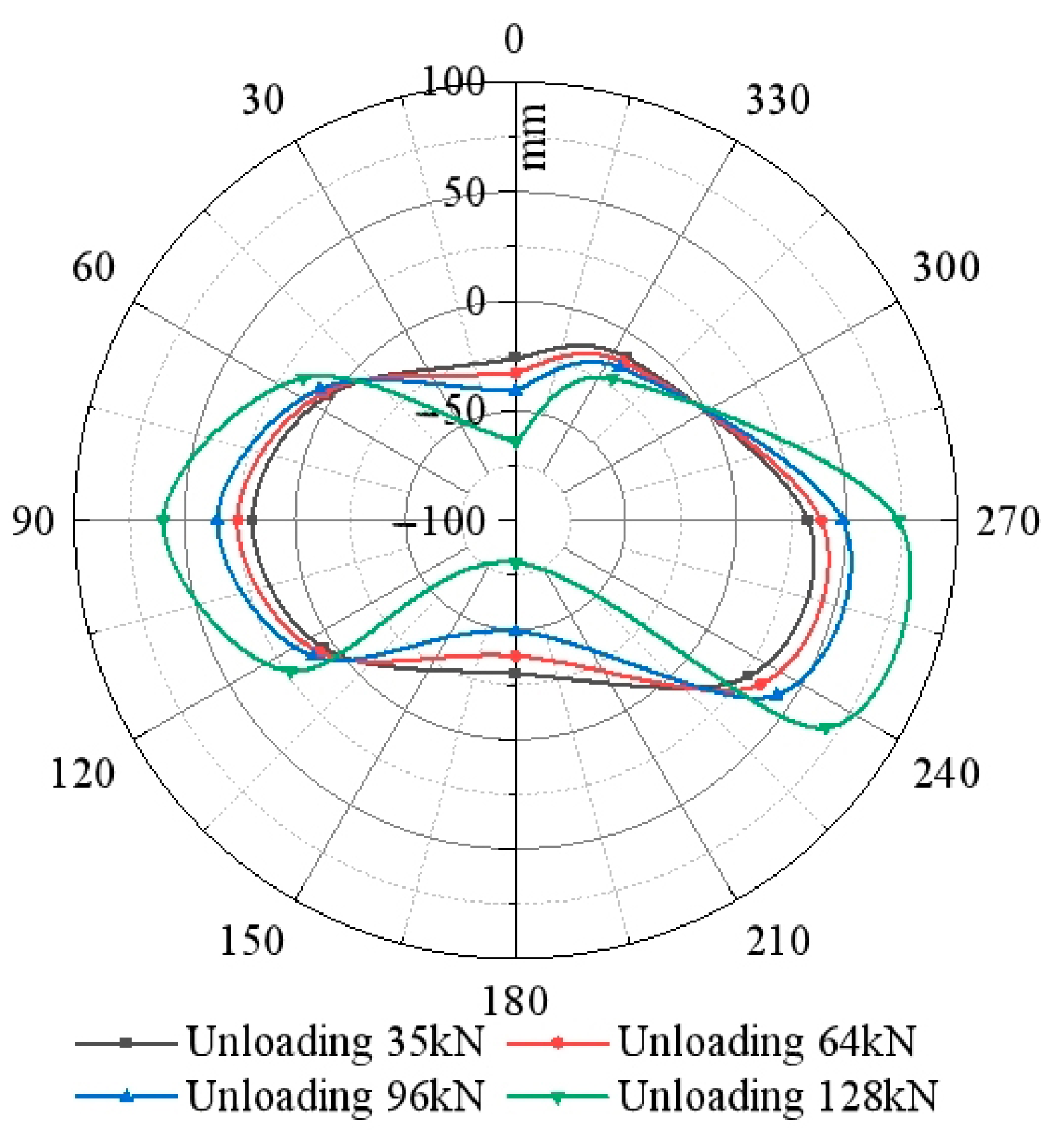
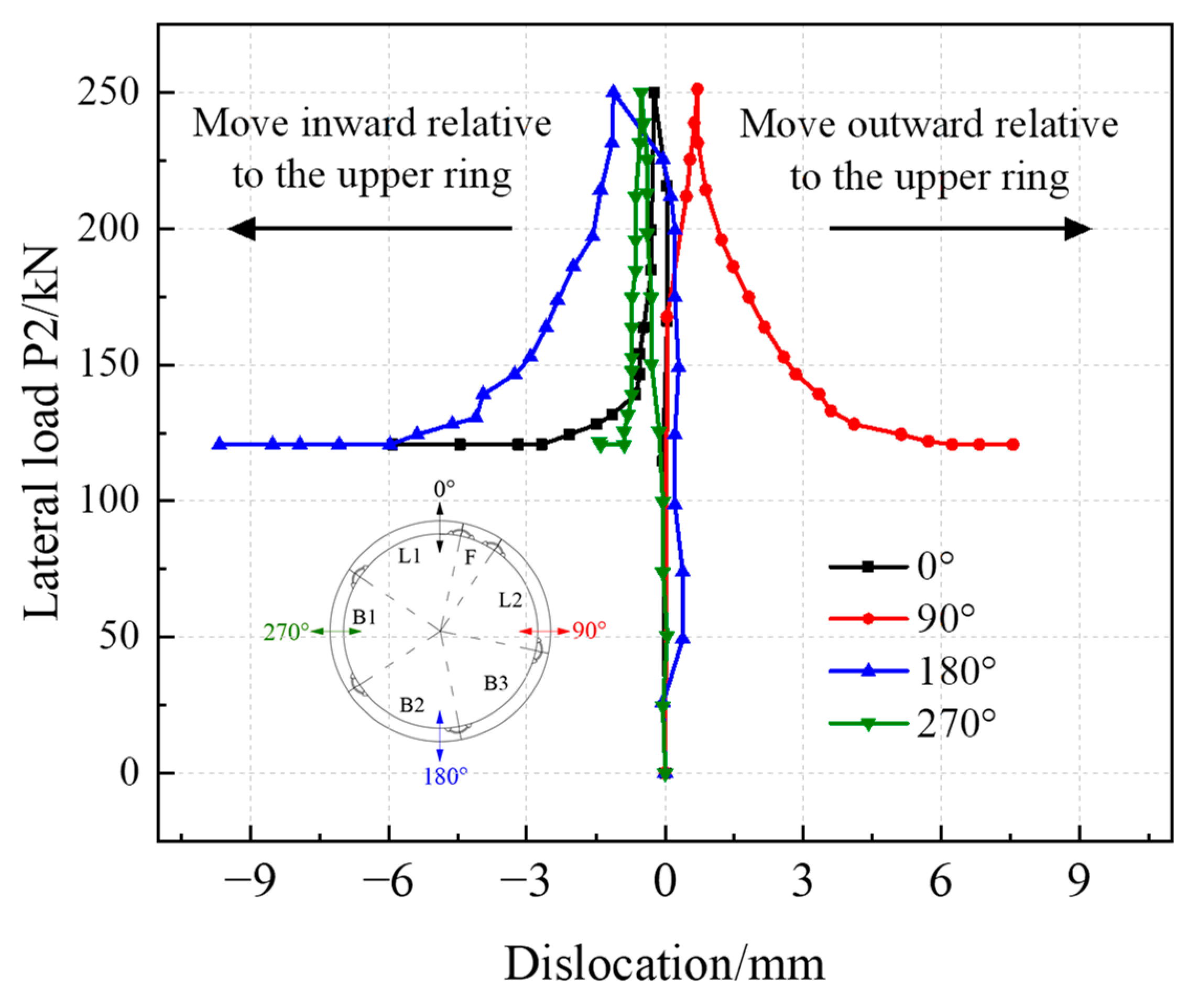
4.3.1. Convergence Deformation of Shield Tunnel Structure
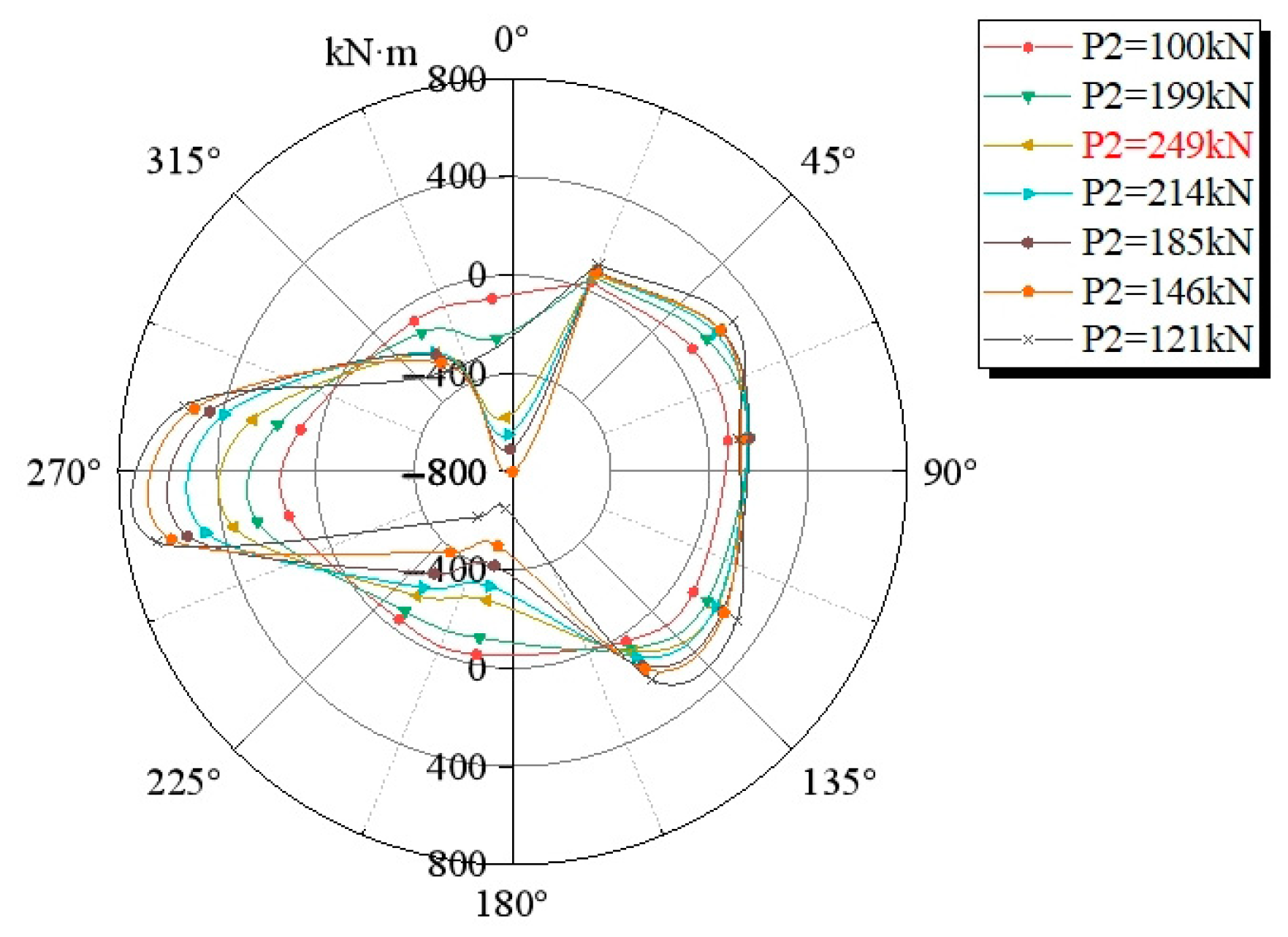
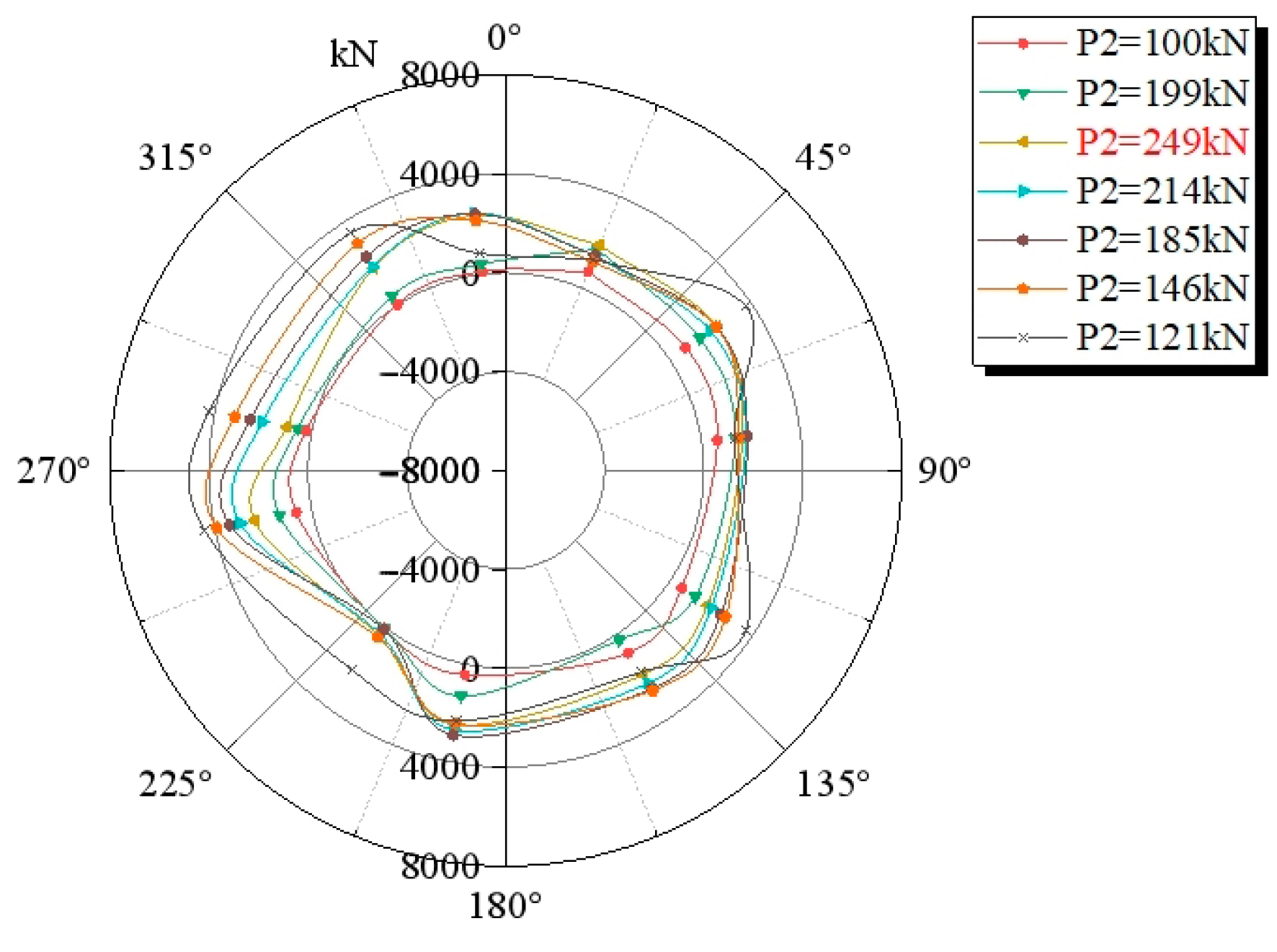
4.3.2. Internal Force of Shield Tunnel Structure
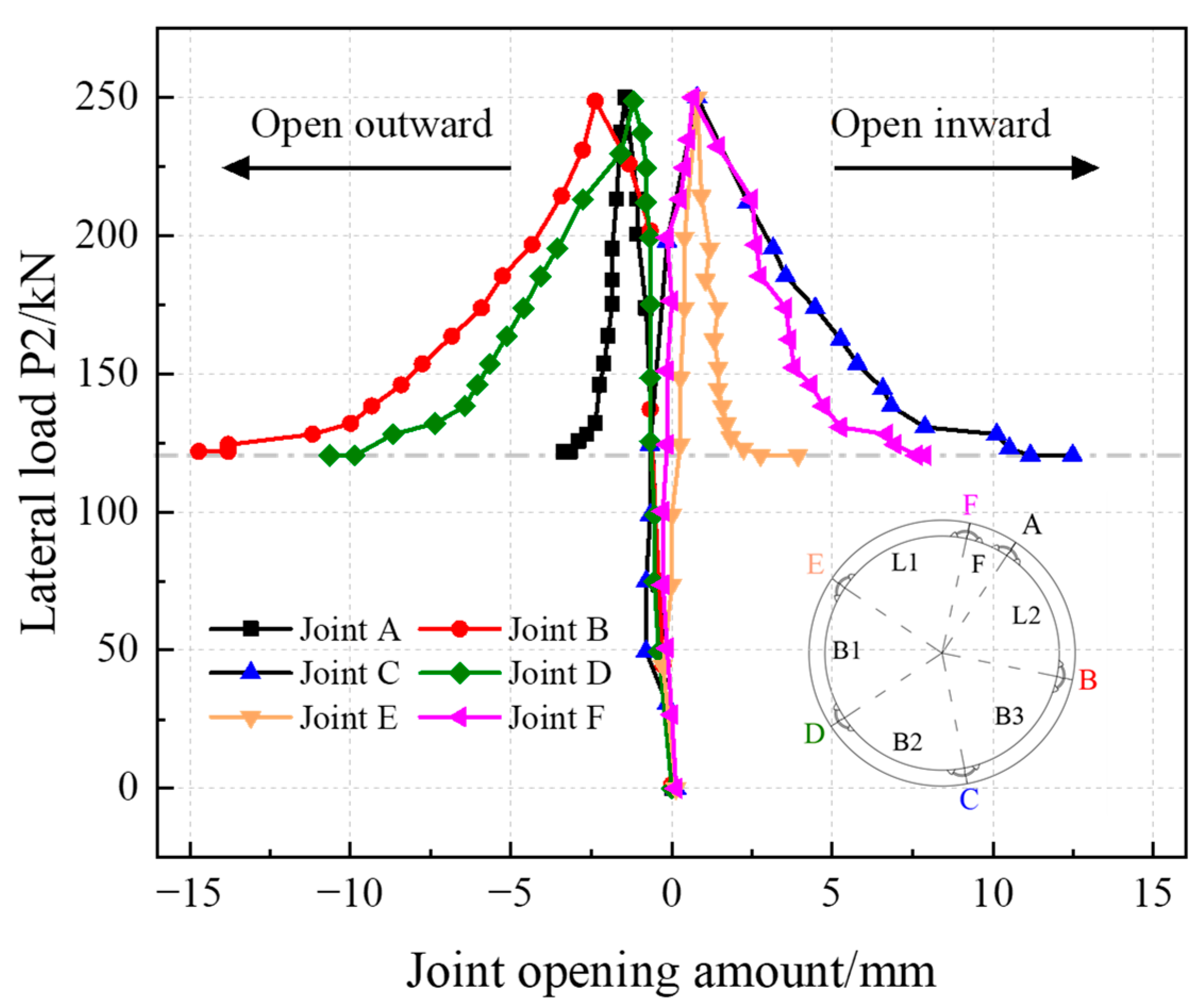
4.3.3. Joint Deformation
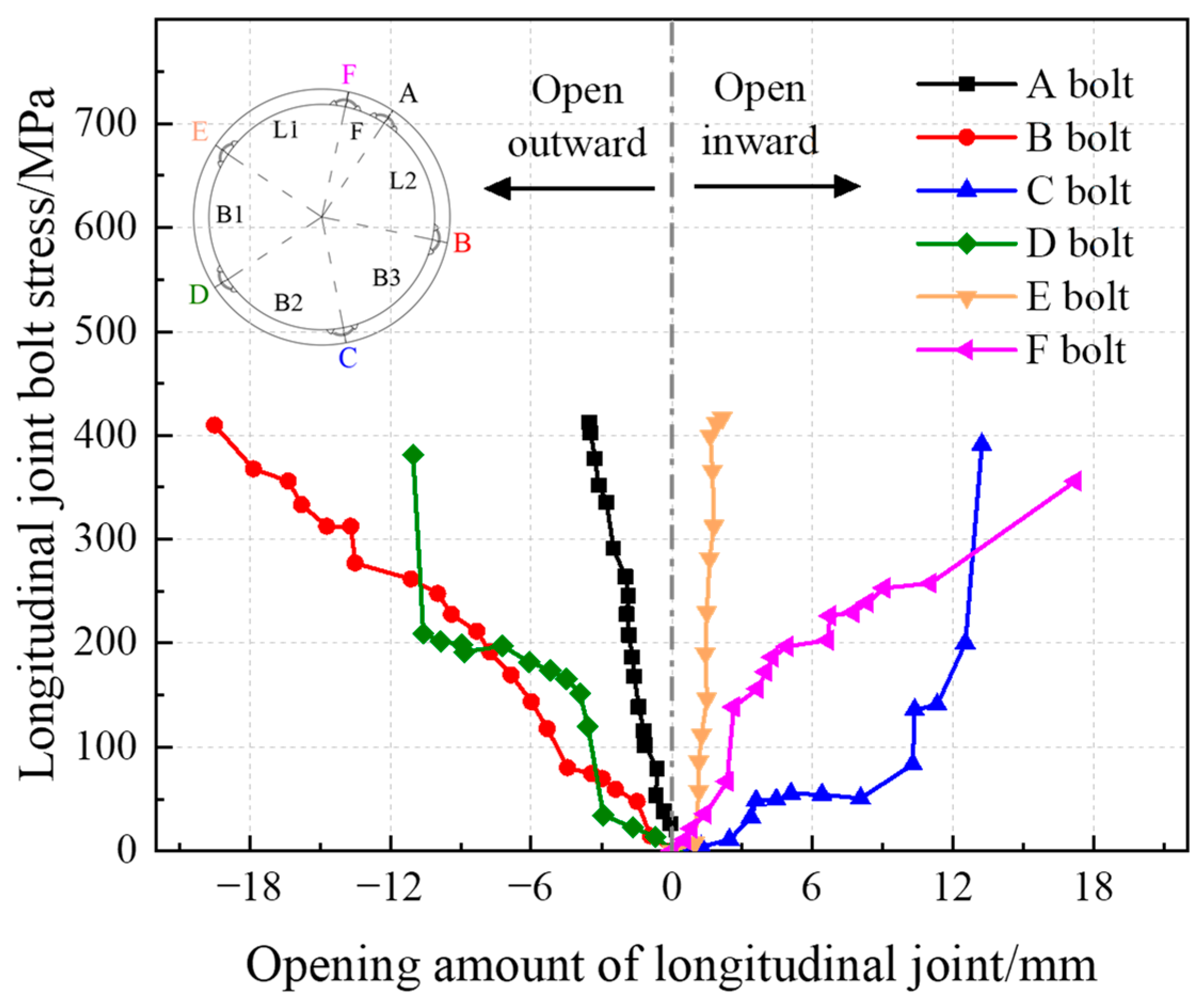
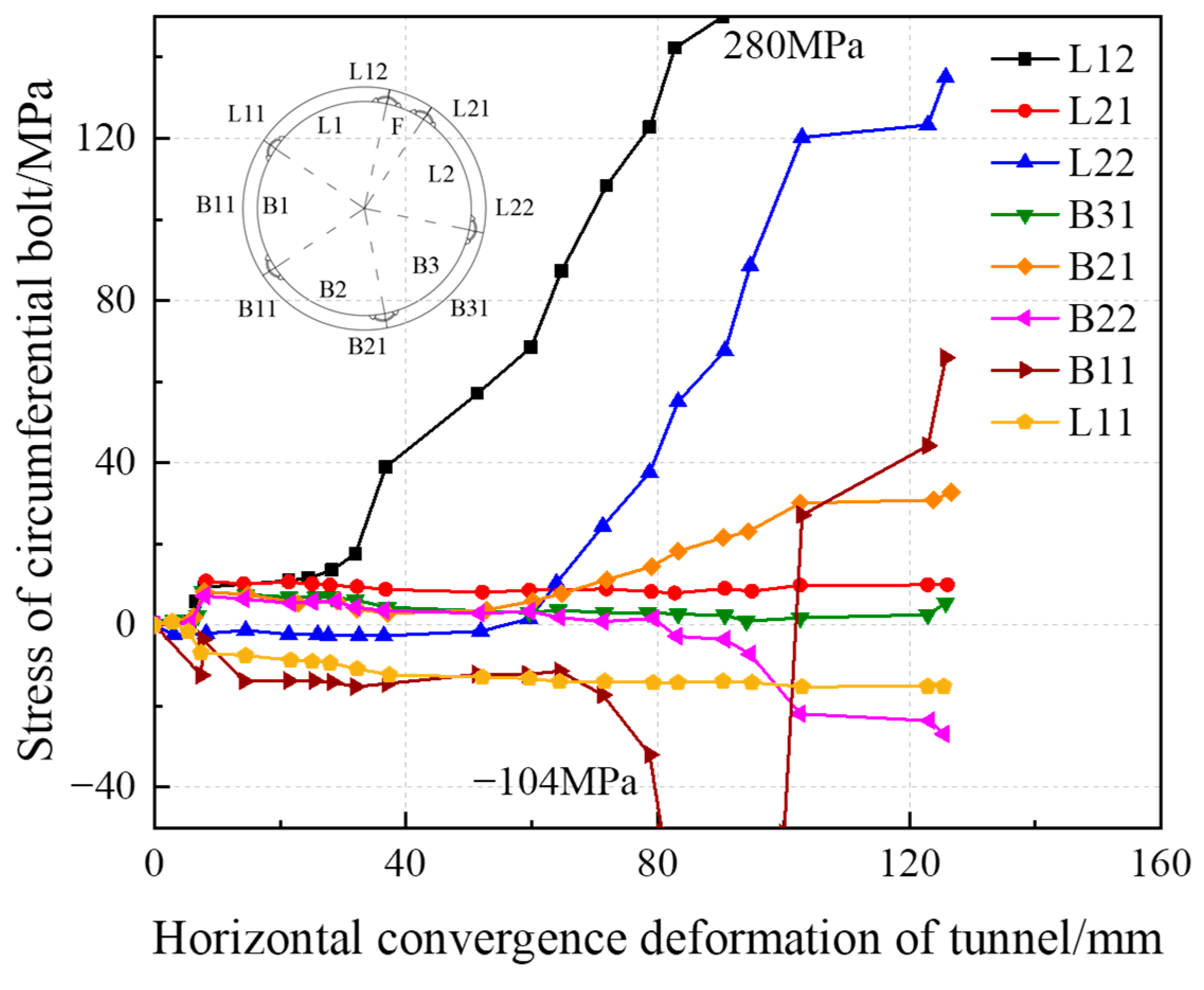
4.3.4. Bolt Stress
4.3.5. Distribution of Segment Crack
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mussa, M.H.; Mutalib, A.A.; Hamid, R.; Naidu, S.R.; Radzi, N.A.M.; Abedini, M. Assessment of damage to an underground box tunnel by a surface explosion. Tunn. Undergr. Space Technol. 2017, 66, 64–76. [Google Scholar] [CrossRef]
- Mussa, M.H.; Mutalib, A.A.; Hamid, R.; Raman, S.N. Blast damage assessment of symmetrical box-shaped underground tunnel according to peak particle velocity (PPV) and single degree of freedom (SDOF) criteria. Symmetry 2018, 10, 158. [Google Scholar] [CrossRef]
- Zeng, Y.; Njock, P.G.A.; Xiong, W.; Zhang, X.-L.; Shen, S.-L. Risks analysis of large diameter slurry shield tunneling in urban area. Undergr. Space 2023, 13, 281–300. [Google Scholar] [CrossRef]
- Zhao, Z.; Cui, J.; Liu, C.; Liu, H.; Rehman, M.U.; Chen, W.; Peng, Z. Seismic damage characteristics of large-diameter shield tunnel lining under extreme-intensity earthquake. Soil Dyn. Earthq. Eng. 2023, 171, 107958. [Google Scholar] [CrossRef]
- Su, D.; Song, Q.; Lin, X.; Li, Q.; Chen, X. Limit equilibrium models for active failures of large-diameter shield tunnel faces in soft clay reinforced with soil–cement walls. Comput. Geotech. 2023, 153, 105104. [Google Scholar] [CrossRef]
- Gao, F.; Ye, J.; Zhao, C.; Bian, X. Soil disturbance induced by shield tunnelling in sensitive clay: In Situ test and analyses. Transp. Geotech. 2023, 42, 101106. [Google Scholar] [CrossRef]
- Zheng, G.; Wang, R.; Lei, H.; Zhang, T.; Fan, Q. Load-transfer-associated settlements of a piled building during shield tunnelling in soft ground. Tunn. Undergr. Space Technol. 2023, 133, 104964. [Google Scholar] [CrossRef]
- Song, X.; Meng, F.-Y.; Chen, R.-P.; Wang, H.-L.; Wu, H.-N. Effect of seepage on soil arching effect in deep shield tunnel. Undergr. Space 2023, 12, 218–233. [Google Scholar] [CrossRef]
- Liu, C.; Peng, Z.; Cui, J.; Huang, X.; Li, Y.; Chen, W. Development of crack and damage in shield tunnel lining under seismic loading: Refined 3D finite element modeling and analyses. Thin-Walled Struct. 2023, 185, 110647. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, D.; Xue, Y.; Zhou, M.; Huang, H. A deep learning-based approach for refined crack evaluation from shield tunnel lining images. Autom. Constr. 2021, 132, 103934. [Google Scholar] [CrossRef]
- Zhang, Z.; Liang, R.; Li, Z.; Kang, C.; El Naggar, M.; Xiao, M.; Wu, W. Analytical solution for longitudinal deformation of shield tunnel induced by overcrossing tunnelling considering circumferential joints. J. Rock Mech. Geotech. Eng. 2023, 15, 2355–2374. [Google Scholar] [CrossRef]
- Zhang, J.; He, C.; Geng, P.; He, Y.; Wang, W. Improved longitudinal seismic deformation method of shield tunnels based on the iteration of the nonlinear stiffness of ring joints. Sustain. Cities Soc. 2019, 45, 105–116. [Google Scholar] [CrossRef]
- Li, R.; Lei, H.; Ma, C.; Liu, Y.; Liu, N. The development of sand erosion induced by shield-tunnel joint leakage. Eng. Fail. Anal. 2023, 148, 107068. [Google Scholar] [CrossRef]
- Shi, C.; Chao, C.; Lei, M.; Peng, L.; Ai, H. Effects of lateral unloading on the mechanical and deformation performance of shield tunnel segment joints. Tunn. Undergr. Space Technol. 2016, 51, 175–188. [Google Scholar] [CrossRef]
- Liu, J.; Shi, C.; Lei, M.; Wang, Z.; Cao, C.; Lin, Y. A study on damage mechanism modelling of shield tunnel under unloading based on damage–plasticity model of concrete. Eng. Fail. Anal. 2021, 123, 105261. [Google Scholar] [CrossRef]
- Wu, H.N.; Chen, S.; Chen, R.P.; Cheng, H.Z.; Feng, D.L. Deformation behaviors and failure mechanism of segmental RC lining under unloading condition. Tunn. Undergr. Space Technol. 2022, 130, 104687. [Google Scholar] [CrossRef]
- Guo, W.; Feng, K.; Lu, X.; Qi, M.; Liu, X.; Fang, Y.; He, C.; Xiao, M. Model test investigation on the longitudinal mechanical property of shield tunnels considering internal structure. Tunn. Undergr. Space Technol. 2023, 140, 105293. [Google Scholar] [CrossRef]
- Guo, R.; Zhang, M.; Xie, H.; He, C.; Fang, Y.; Wang, S. Model test study of the mechanical characteristics of the lining structure for an urban deep drainage shield tunnel. Tunn. Undergr. Space Technol. 2019, 9, 103014. [Google Scholar] [CrossRef]
- Zhang, J.-Z.; Huang, H.-W.; Zhang, D.-M.; Phoon, K.K. Experimental study of the coupling effect on segmental shield tunnel lining under surcharge loading and excavation unloading. Tunn. Undergr. Space Technol. 2023, 140, 105199. [Google Scholar] [CrossRef]
- Wei, G.; Feng, F.; Cui, Y.; Wang, X.; Diao, H.; Wu, Y. Research on the influence of foundation pit excavation on the lateral force and deformation of side shield tunnels based on full-scale experiments. Tunn. Undergr. Space Technol. 2023, 140, 105236. [Google Scholar] [CrossRef]
- Liang, K.; Feng, K.; Zhang, L.; He, C.; Su, A.; Guo, W. Failure mechanism of underwater shield tunnel: An experimental and theoretical study. Tunn. Undergr. Space Technol. 2023, 137, 105155. [Google Scholar] [CrossRef]
- Liu, X.; Dong, Z.; Bai, Y.; Zhu, Y. Investigation of the structural effect induced by stagger joints in segmental tunnel linings: First results from full-scale ring test. Tunn. Undergr. Space Technol. 2017, 66, 1–18. [Google Scholar] [CrossRef]
- Jin, H.; Yu, K.; Gong, Q.; Zhou, S. Load-carrying capability of shield tunnel damaged by shield shell squeezing action during construction. Thin-Walled Struct. 2018, 132, 69–78. [Google Scholar] [CrossRef]
- Jin, H.; Yu, K.; Zhou, S.; Gong, Q.; Yan, H. Performance assessment of shield tunnel damaged by shield shell extrusion during construction. Int. J. Civ. Eng. 2019, 17, 1015–1027. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, H.; Yu, S.; Bi, X.; Zhou, S. Analysis of bending deflection of tunnel segment under load- and corrosion-induced cracks by improved XFEM. Eng. Fail. Anal. 2022, 140, 106576. [Google Scholar] [CrossRef]
- Yu, S.; Jin, H.; Cao, M.; Liu, C. Effect of straight bolt corrosion on mechanical properties of shield tunnel under DC stray current. Structures 2022, 45, 1607–1620. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, S.; Di, H.; Wang, P.; Wang, J. Semi–analytical solution for ultimate bearing capacity of straight–jointed segmental tunnel lining. Tunn. Undergr. Space Technol. 2023, 138, 105160. [Google Scholar]

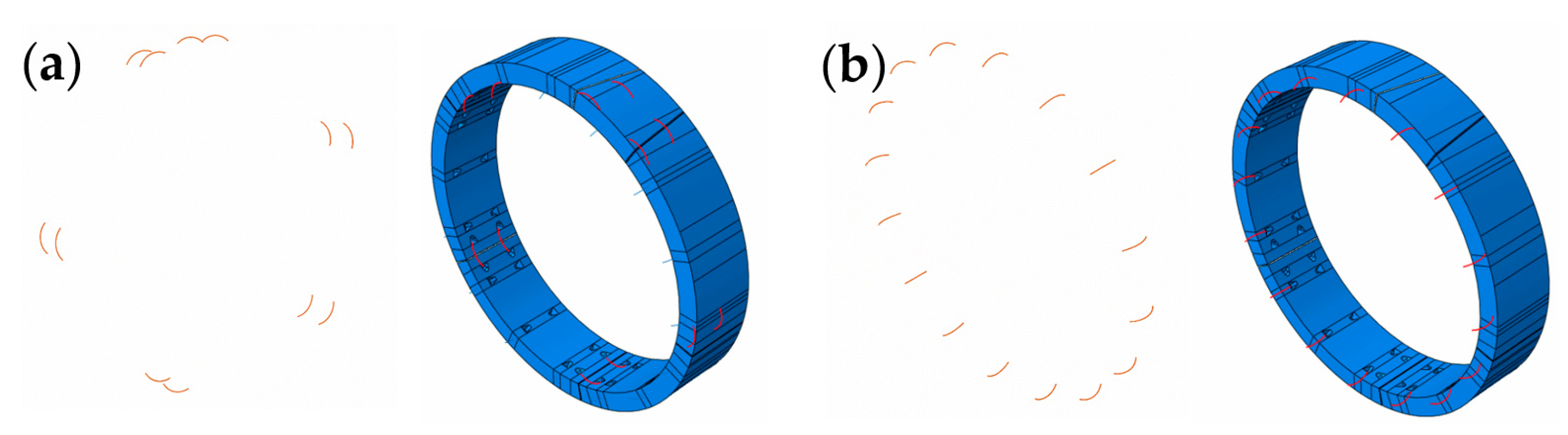
















| Ec/GPa | ν | ψ | κ | fb0/fc0 | Kc | μ |
|---|---|---|---|---|---|---|
| 20 | 0.2 | 38° | 0.1 | 1.16 | 0.667 | 0.001 |
| Compressive Behavior | Tensile Behavior | ||||
|---|---|---|---|---|---|
| Yield Stress/MPa | Inelastic Strain | Damage Parameter | Yield Stress/MPa | Cracking Strain | Damage Parameter |
| 22.663797 | 0 | 0 | 3.212006 | 0 | 0 |
| 32.407299 | 0.00062 | 0.207 | 2.647291 | 0.000024 | 0.115139 |
| 30.263324 | 0.00110 | 0.313 | 2.271104 | 0.000064 | 0.266938 |
| 26.187998 | 0.00164 | 0.415 | 1.827634 | 0.000105 | 0.399685 |
| 22.205742 | 0.00218 | 0.501 | 1.499156 | 0.000144 | 0.496630 |
| 18.884596 | 0.00269 | 0.569 | 1.264951 | 0.000179 | 0.567478 |
| 16.236637 | 0.00318 | 0.623 | 0.965578 | 0.000243 | 0.662001 |
| 14.139070 | 0.00366 | 0.666 | 0.667770 | 0.000363 | 0.762434 |
| 12.464749 | 0.00412 | 0.701 | 0.432369 | 0.000590 | 0.847499 |
| 10.530291 | 0.00479 | 0.742 | 0.271803 | 0.001035 | 0.907989 |
| 8.488588 | 0.00577 | 0.786 | 0.169277 | 0.001917 | 0.946488 |
| 6.534231 | 0.00720 | 0.831 | 0.105193 | 0.003673 | 0.969498 |
| 4.831139 | 0.00930 | 0.871 | 0.065376 | 0.007174 | 0.982788 |
| 2.836598 | 0.01480 | 0.921 | 0.040713 | 0.014137 | 0.990323 |
| Buried Depth/m | P1 | P2 | P3 | P4 |
|---|---|---|---|---|
| 10 | 255 | 281 | 179 | 244 |
| 15 | 267 | 298 | 187 | 261 |
| 20 | 356 | 383 | 249 | 325 |
| Load Ratios | P1/kN | P2/kN | P3/kN | P4/kN |
|---|---|---|---|---|
| 0.75 | 267 | 298 | 200 | 285 |
| 0.72 | 267 | 298 | 192 | 274 |
| 0.70 | 267 | 298 | 187 | 261 |
| 0.68 | 267 | 298 | 182 | 258 |
| 0.66 | 267 | 298 | 176 | 251 |
| 0.65 | 267 | 298 | 174 | 247 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, C.; Liu, C.; Zhang, X. Segment Thickness Design and Bearing Performance Analysis of Large Inner-Diameter Shield Tunnel under Lateral Unloading. Appl. Sci. 2023, 13, 11871. https://doi.org/10.3390/app132111871
Lu C, Liu C, Zhang X. Segment Thickness Design and Bearing Performance Analysis of Large Inner-Diameter Shield Tunnel under Lateral Unloading. Applied Sciences. 2023; 13(21):11871. https://doi.org/10.3390/app132111871
Chicago/Turabian StyleLu, Cirong, Changbao Liu, and Xiaohui Zhang. 2023. "Segment Thickness Design and Bearing Performance Analysis of Large Inner-Diameter Shield Tunnel under Lateral Unloading" Applied Sciences 13, no. 21: 11871. https://doi.org/10.3390/app132111871
APA StyleLu, C., Liu, C., & Zhang, X. (2023). Segment Thickness Design and Bearing Performance Analysis of Large Inner-Diameter Shield Tunnel under Lateral Unloading. Applied Sciences, 13(21), 11871. https://doi.org/10.3390/app132111871





