Inducing Optimality in Prescribed Performance Control for Uncertain Euler–Lagrange Systems
Abstract
:1. Introduction
2. State of the Art and Contributions
- An identification framework that is able to retrieve the unknown system dynamics even in the case of open-loop instability.
- A successive approximation algorithm that aims to obtain a near-optimal control law, while incorporating prescribed performance specifications.
- A method that guarantees the evolution of the system’s trajectories strictly within the set for which the approximation capabilities of the identification structure are sufficient.
3. Problem Formulation and Preliminaries
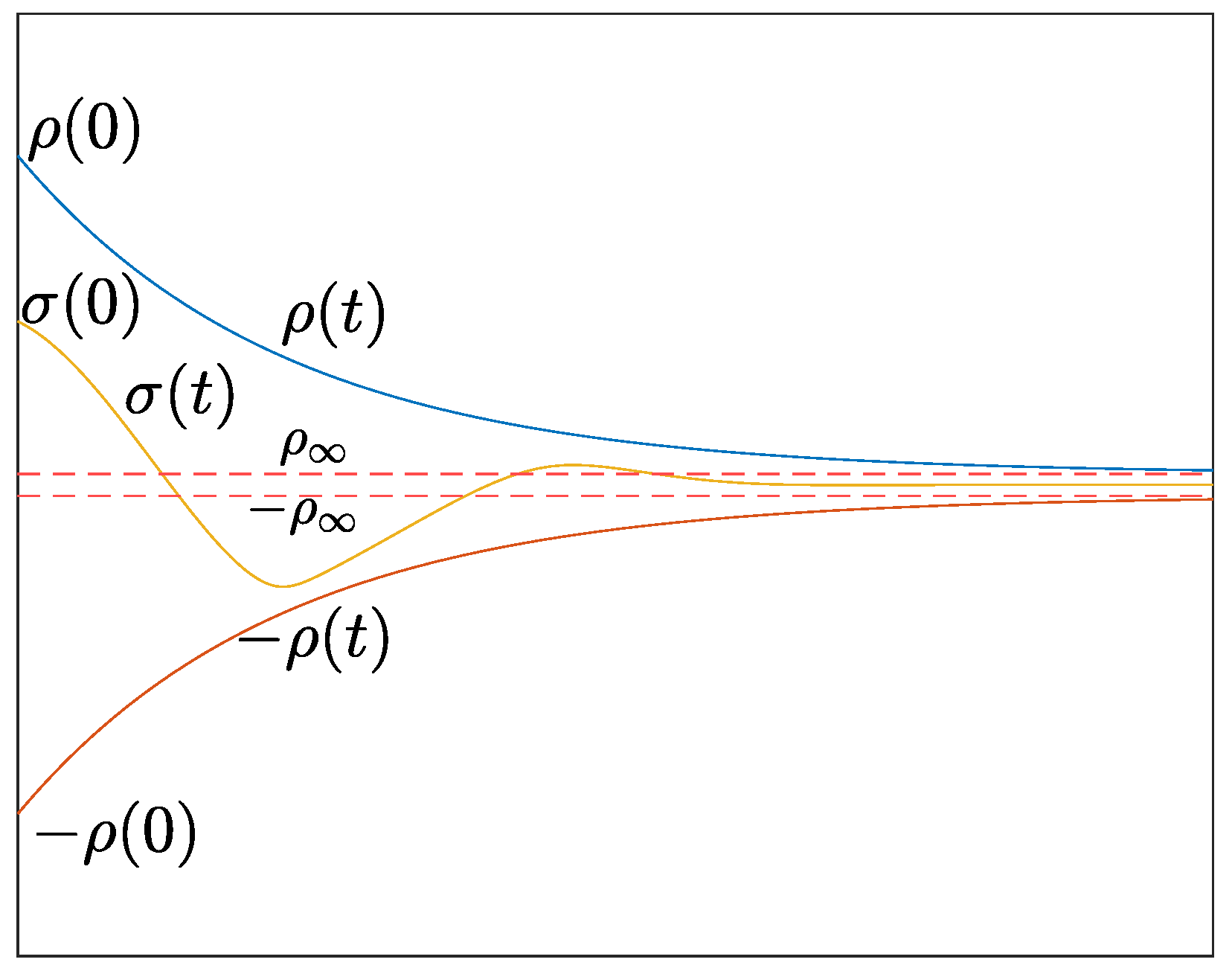
3.1. Prescribed Performance Control (PPC)
3.2. Optimal Control with Prescribed Performance
4. Methodology
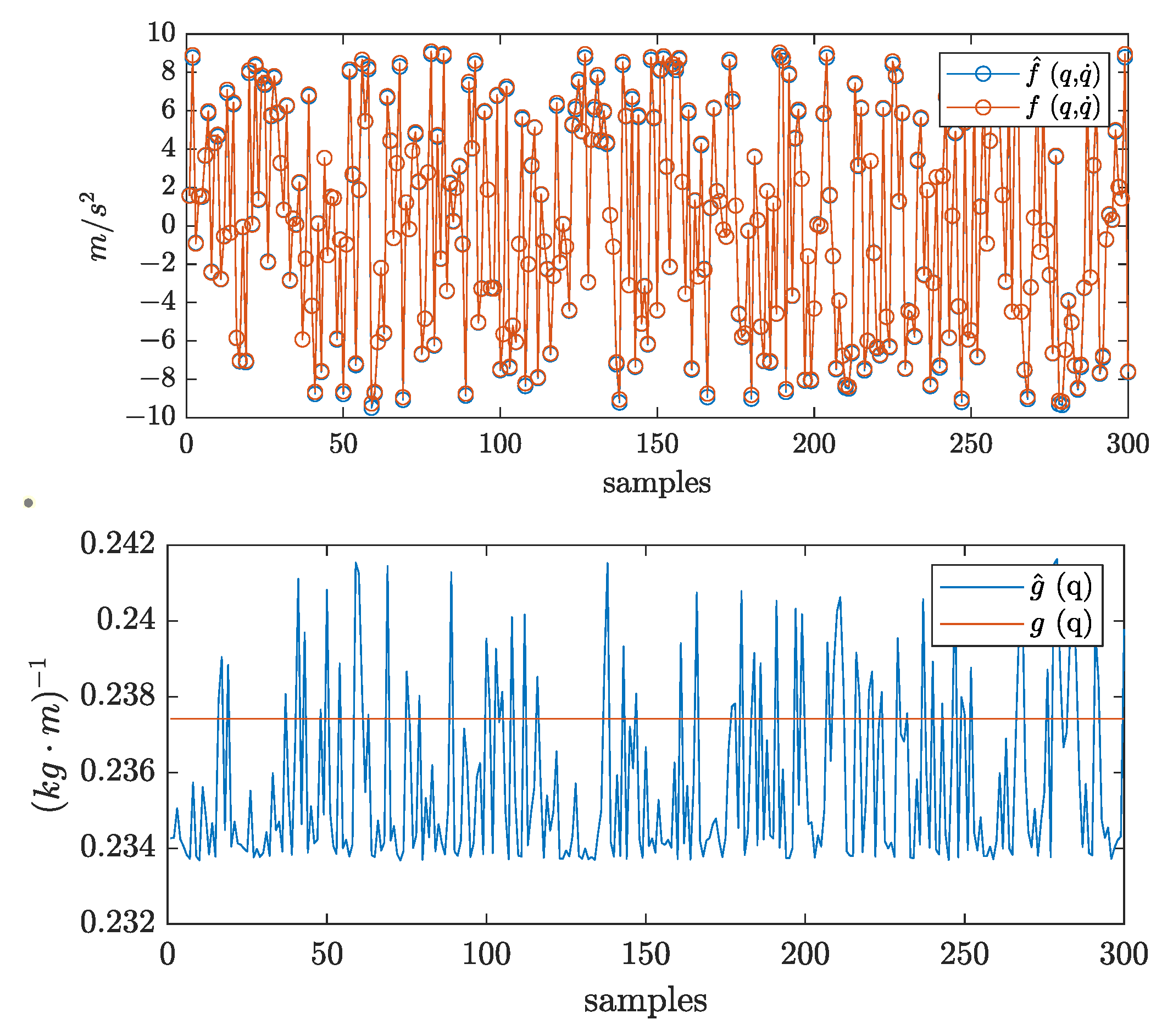
4.1. Identification of System Dynamics
4.2. Solving the Hamilton–Jacobi–Bellman Equation
| Algorithm 1: Cost function approximation algorithm |
|
5. Simulation Results
5.1. Case A: Pendulum
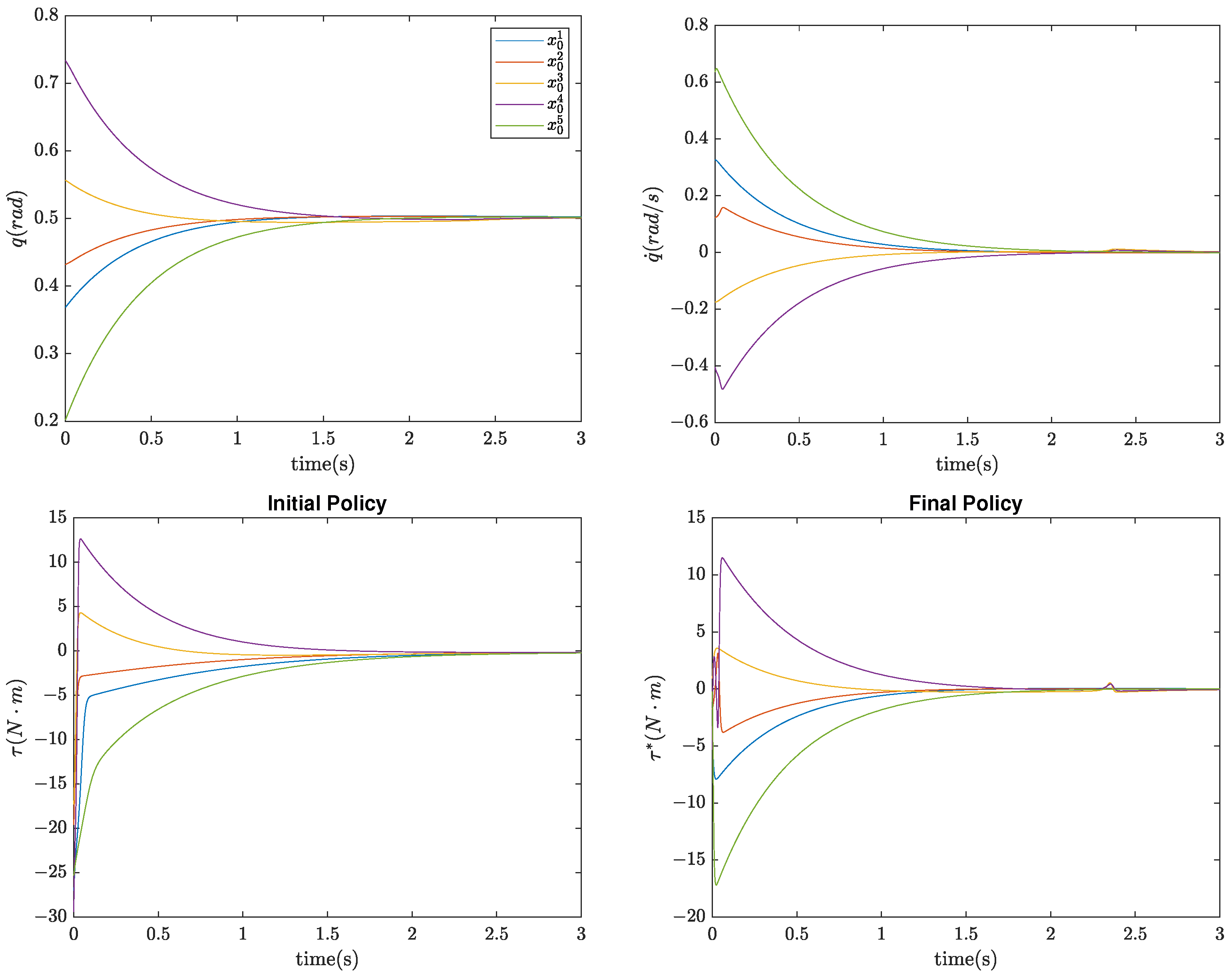
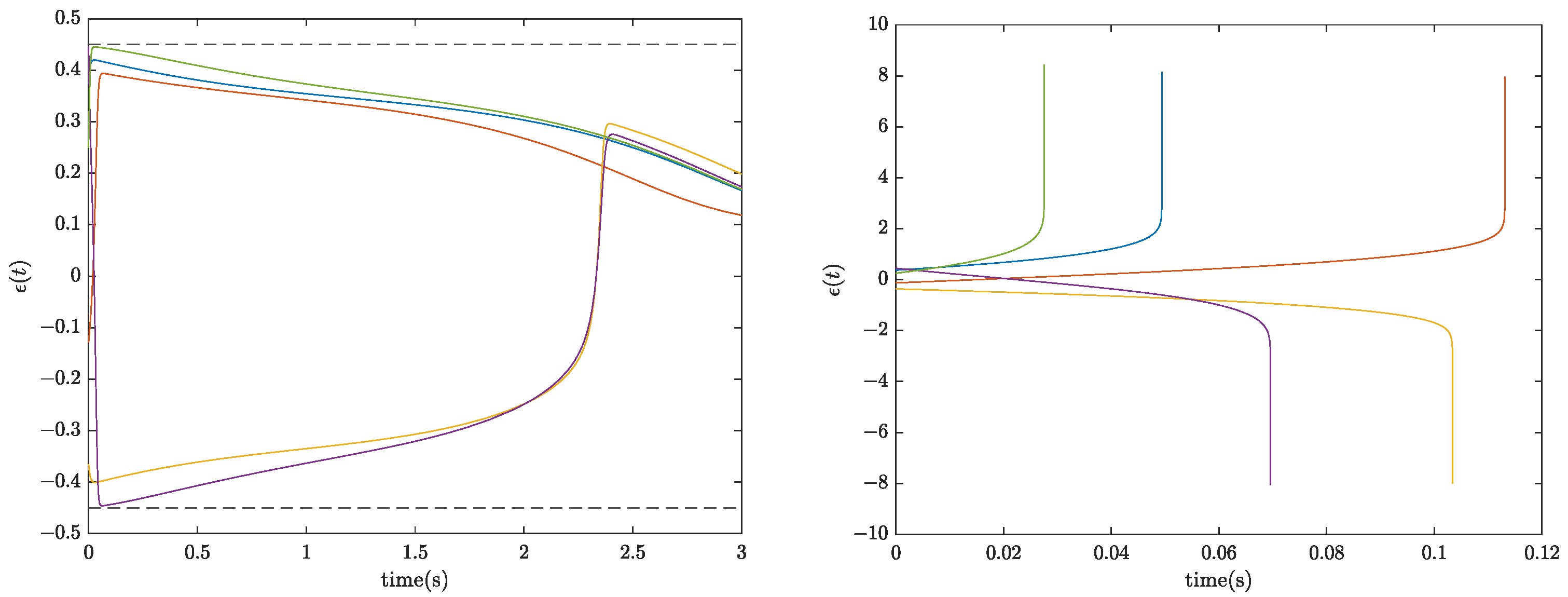
5.2. Case B: 2-DOF Robotic Manipulator
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Powell, W.B.; Ryzhov, I.O. Optimal Learning and Approximate Dynamic Programming. In Reinforcement Learning and Approximate Dynamic Programming for Feedback Control; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012; Chapter 18; pp. 410–431. [Google Scholar]
- Kirk, D. Optimal Control Theory: An Introduction; Dover Books on Electrical Engineering Series; Dover Publications: Mineola, NY, USA, 2004. [Google Scholar]
- Lewis, F.L.; Vrabie, D. Reinforcement learning and adaptive dynamic programming for feedback control. IEEE Circuits Syst. Mag. 2009, 9, 32–50. [Google Scholar] [CrossRef]
- Werbos, P. Elements of intelligence. Cybernetica 1968, 11, 131. [Google Scholar]
- Al-Tamimi, A.; Lewis, F.L.; Abu-Khalaf, M. Discrete-Time Nonlinear HJB Solution Using Approximate Dynamic Programming: Convergence Proof. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2008, 38, 943–949. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.Y.; Jin, N.; Liu, D.; Wei, Q. Adaptive Dynamic Programming for Finite-Horizon Optimal Control of Discrete-Time Nonlinear Systems with ε-Error Bound. IEEE Trans. Neural Netw. 2011, 22, 24–36. [Google Scholar] [CrossRef] [PubMed]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Jiang, Y.; Jiang, Z.P. Robust Adaptive Dynamic Programming and Feedback Stabilization of Nonlinear Systems. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 882–893. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Liu, D.; Luo, C. Reinforcement Learning-Based Optimal Stabilization for Unknown Nonlinear Systems Subject to Inputs with Uncertain Constraints. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4330–4340. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Jiang, Z.P. Learning-Based Adaptive Optimal Tracking Control of Strict-Feedback Nonlinear Systems. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2614–2624. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Gao, W.; Na, J.; Zhang, D.; Hämäläinen, T.T.; Stojanovic, V.; Lewis, F.L. Value iteration and adaptive optimal output regulation with assured convergence rate. Control Eng. Pract. 2022, 121, 105042. [Google Scholar] [CrossRef]
- Chen, C.; Modares, H.; Xie, K.; Lewis, F.L.; Wan, Y.; Xie, S. Reinforcement Learning-Based Adaptive Optimal Exponential Tracking Control of Linear Systems with Unknown Dynamics. IEEE Trans. Autom. Control 2019, 64, 4423–4438. [Google Scholar] [CrossRef]
- Kamalapurkar, R.; Dinh, H.; Bhasin, S.; Dixon, W.E. Approximate optimal trajectory tracking for continuous-time nonlinear systems. Automatica 2015, 51, 40–48. [Google Scholar] [CrossRef]
- Na, J.; Lv, Y.; Wu, X.; Guo, Y.; Chen, Q. Approximate optimal tracking control for continuous-time unknown nonlinear systems. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 8990–8995. [Google Scholar] [CrossRef]
- Na, J.; Lv, Y.; Zhang, K.; Zhao, J. Adaptive Identifier-Critic-Based Optimal Tracking Control for Nonlinear Systems with Experimental Validation. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 459–472. [Google Scholar] [CrossRef]
- Zhao, K.; Song, Y.; Ma, T.; He, L. Prescribed Performance Control of Uncertain Euler–Lagrange Systems Subject to Full-State Constraints. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3478–3489. [Google Scholar] [CrossRef]
- Bhasin, S.; Kamalapurkar, R.; Johnson, M.; Vamvoudakis, K.; Lewis, F.; Dixon, W. A novel actor–critic–identifier architecture for approximate optimal control of uncertain nonlinear systems. Automatica 2013, 49, 82–92. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Robust Adaptive Control of Feedback Linearizable MIMO Nonlinear Systems with Prescribed Performance. IEEE Trans. Autom. Control 2008, 53, 2090–2099. [Google Scholar] [CrossRef]
- Yin, Z.; Luo, J.; Wei, C. Robust prescribed performance control for Euler–Lagrange systems with practically finite-time stability. Eur. J. Control 2020, 52, 1–10. [Google Scholar] [CrossRef]
- Jabbari Asl, H.; Narikiyo, T.; Kawanishi, M. Bounded-input prescribed performance control of uncertain Euler–Lagrange systems. IET Control Theory Appl. 2019, 13, 17–26. [Google Scholar] [CrossRef]
- Dong, H.; Zhao, X.; Luo, B. Optimal Tracking Control for Uncertain Nonlinear Systems with Prescribed Performance via Critic-Only ADP. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 561–573. [Google Scholar] [CrossRef]
- Fortuna, L.; Frasca, M. Optimal and Robust Control: Advanced Topics with MATLAB®; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar] [CrossRef]
- Dimanidis, I.S.; Bechlioulis, C.P.; Rovithakis, G.A. Output Feedback Approximation-Free Prescribed Performance Tracking Control for Uncertain MIMO Nonlinear Systems. IEEE Trans. Autom. Control 2020, 65, 5058–5069. [Google Scholar] [CrossRef]
- Kosmatopoulos, E.B.; Ioannou, P.A. Robust switching adaptive control of multi-input nonlinear systems. IEEE Trans. Autom. Control 2002, 47, 610–624. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Prescribed Performance Adaptive Control for Multi-Input Multi-Output Affine in the Control Nonlinear Systems. IEEE Trans. Autom. Control 2010, 55, 1220–1226. [Google Scholar] [CrossRef]
- Lewis, F.L.; Vrabie, D.L.; Syrmos, V.L. Optimal Control; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Guo, B.Z.; Zhao, Z. On convergence of tracking differentiator. Int. J. Control 2011, 84, 693–701. [Google Scholar] [CrossRef]
- Rousseas, P.; Bechlioulis, C.; Kyriakopoulos, K.J. Harmonic-Based Optimal Motion Planning in Constrained Workspaces Using Reinforcement Learning. IEEE Robot. Autom. Lett. 2021, 6, 2005–2011. [Google Scholar] [CrossRef]
- Potra, F.A.; Wright, S.J. Interior-point methods. J. Comput. Appl. Math. 2000, 124, 281–302. [Google Scholar] [CrossRef]
- Abu-Khalaf, M.; Lewis, F.L. Nearly optimal control laws for nonlinear systems with saturating actuators using a neural network HJB approach. Automatica 2005, 41, 779–791. [Google Scholar] [CrossRef]


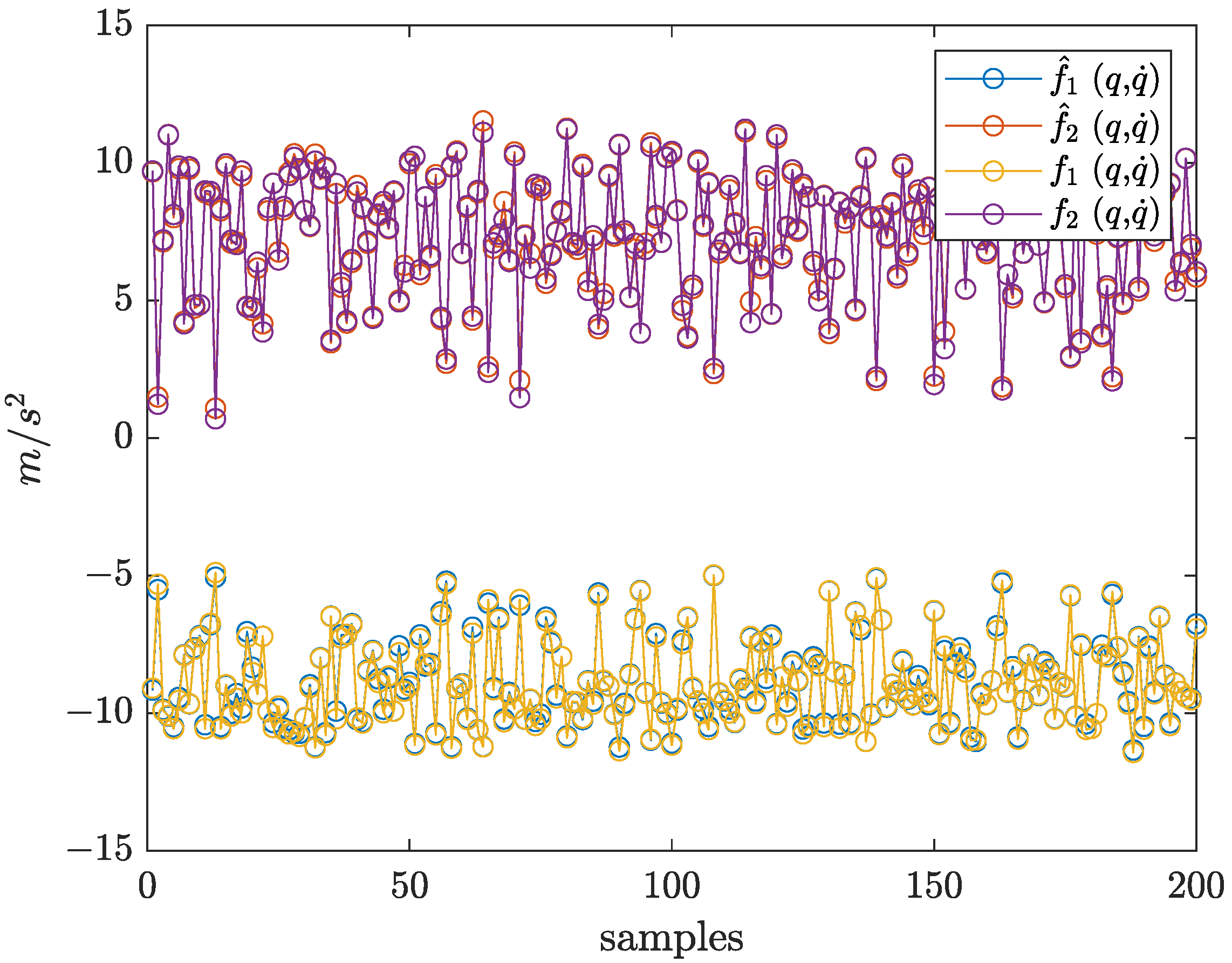
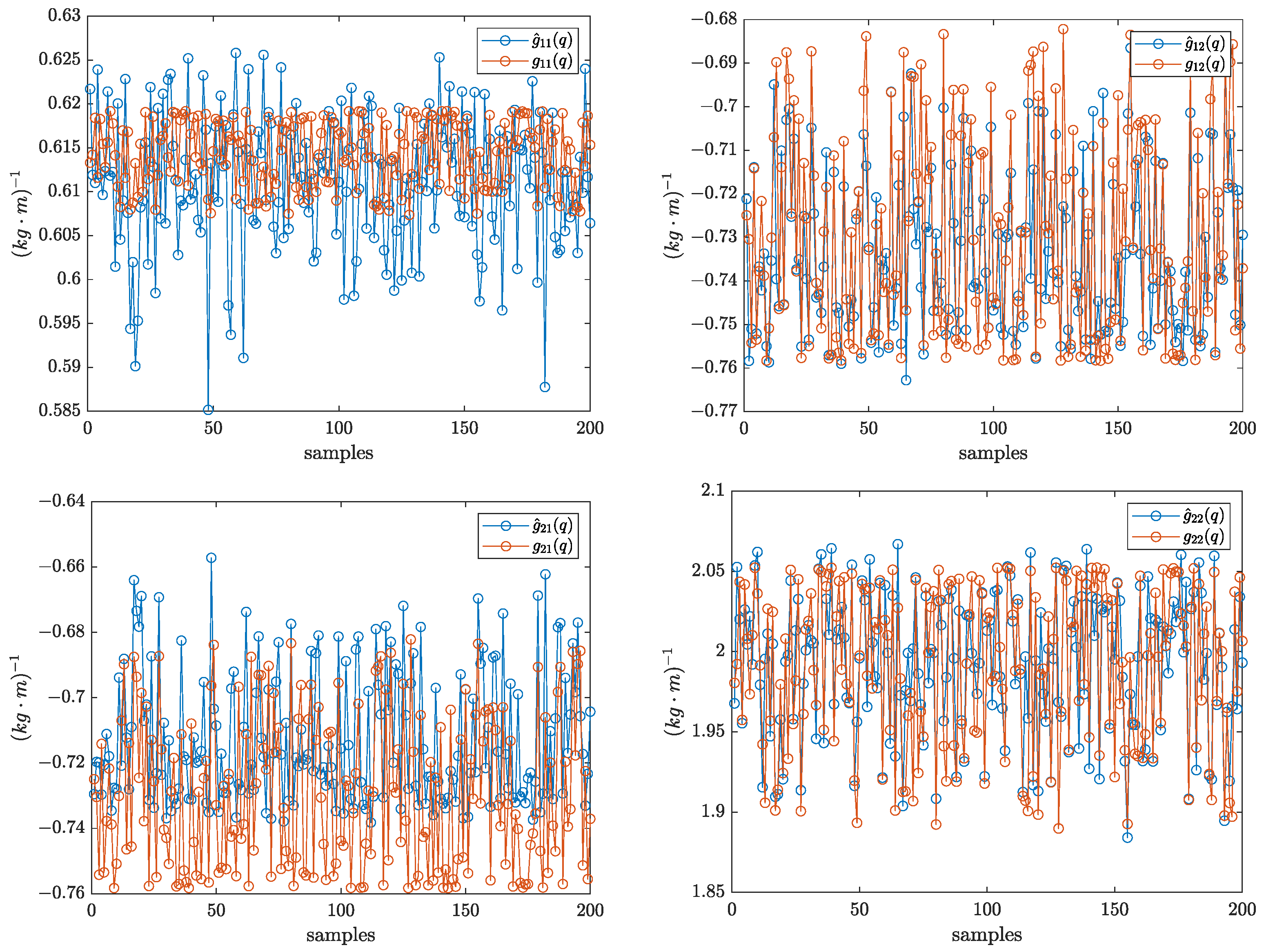
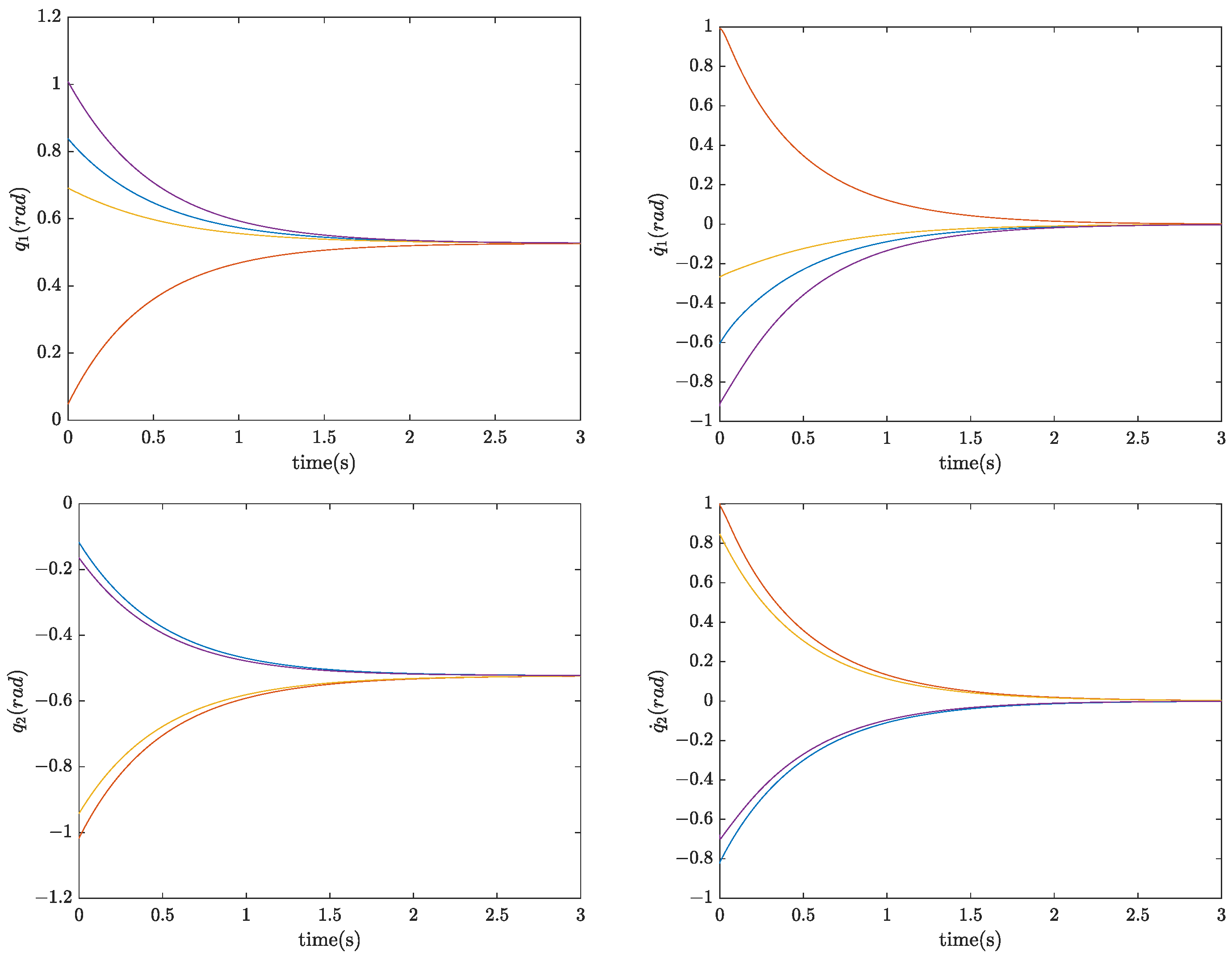

| Initial Condition , , | Initial Policy’s Cost | Final Policy’s Cost | Final Policy’s Cost (Without Prescribed Performance) |
|---|---|---|---|
| (kg) | (m) | (kg/s) | (kg) | (m) | (kg/s) | |||
|---|---|---|---|---|---|---|---|---|
| 3.2 | 0.5 | 0.96 | 1 | 2.0 | 0.4 | 0.81 | 1 | 9.81 |
| Initial Condition , , , , , | Initial Policy’s Cost | Final Policy’s Cost |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vlachos, C.; Malli, I.; Bechlioulis, C.P.; Kyriakopoulos, K.J. Inducing Optimality in Prescribed Performance Control for Uncertain Euler–Lagrange Systems. Appl. Sci. 2023, 13, 11923. https://doi.org/10.3390/app132111923
Vlachos C, Malli I, Bechlioulis CP, Kyriakopoulos KJ. Inducing Optimality in Prescribed Performance Control for Uncertain Euler–Lagrange Systems. Applied Sciences. 2023; 13(21):11923. https://doi.org/10.3390/app132111923
Chicago/Turabian StyleVlachos, Christos, Ioanna Malli, Charalampos P. Bechlioulis, and Kostas J. Kyriakopoulos. 2023. "Inducing Optimality in Prescribed Performance Control for Uncertain Euler–Lagrange Systems" Applied Sciences 13, no. 21: 11923. https://doi.org/10.3390/app132111923
APA StyleVlachos, C., Malli, I., Bechlioulis, C. P., & Kyriakopoulos, K. J. (2023). Inducing Optimality in Prescribed Performance Control for Uncertain Euler–Lagrange Systems. Applied Sciences, 13(21), 11923. https://doi.org/10.3390/app132111923








