Construction and Application of Fuzzy Comprehensive Evaluation Model for Rockburst Based on Microseismic Monitoring
Abstract
:1. Introduction
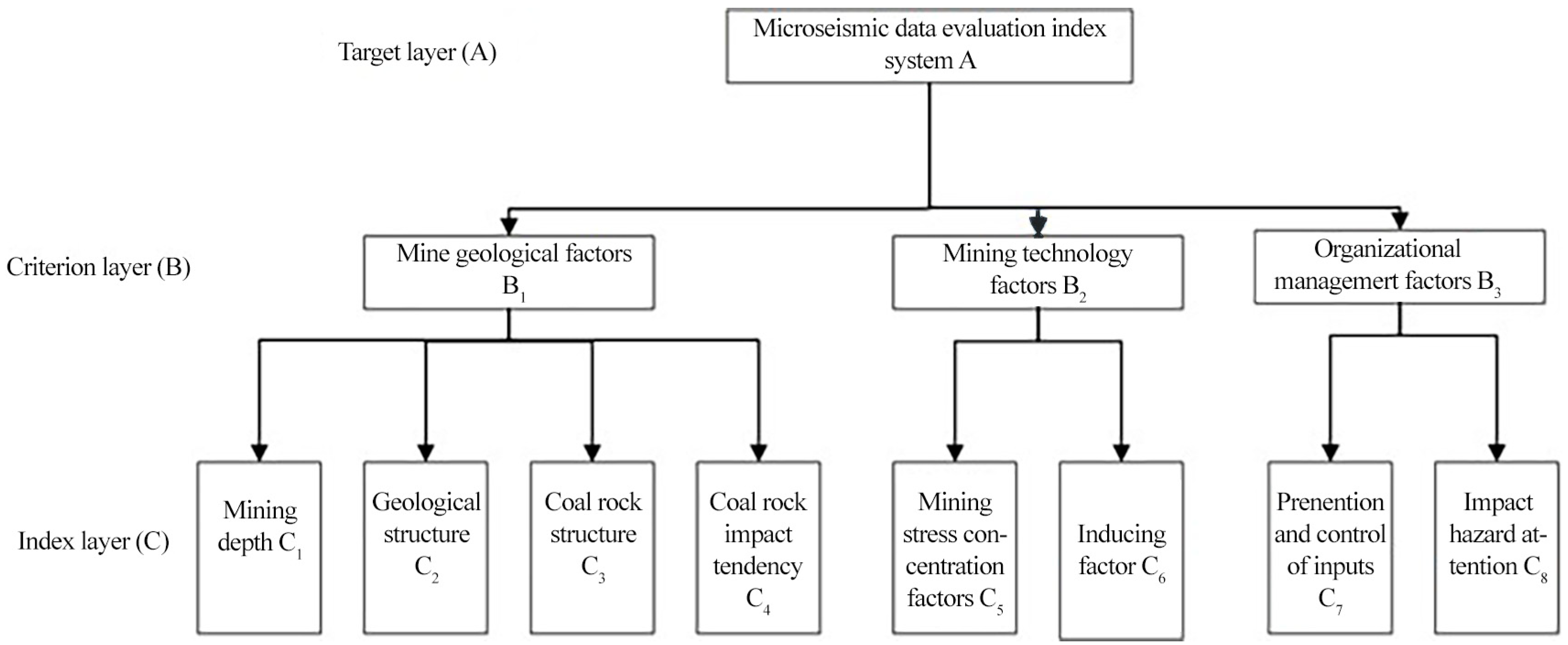
2. Evaluation Index System of Rockburst Based on Microseismic Events
2.1. Principles for the Establishment of Index System
2.2. Determination of Evaluation Indexes
2.3. Establishment of Evaluation Index System
3. Fuzzy Hierarchical Comprehensive Evaluation Model of Rockburst
3.1. Establishment of Analytic Hierarchy Process and Weight Calculation
3.2. Mathematical Model of the Fuzzy Level Comprehensive Evaluation
4. Fuzzy Hierarchical Comprehensive Evaluation of Impact Risk in Yanbei Coal Mine
4.1. Mine Overview
4.2. AHP Calculation of Index Weight in Index Layer
4.2.1. Calculation of Weight of Mine Geological Factors
4.2.2. Calculation of the Weight of Mining Technology Factors
4.2.3. Calculation of Weight of Organizational Management Factors
4.3. Single-Factor Membership Degree
4.4. Results of the Fuzzy Comprehensive Evaluation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duan, H.F.; Zhao, L.J. Prevention technology for strong mine pressure disaster in the hard-roof large-mining-height working face. Shock Vib. 2020, 2020, 8846624. [Google Scholar] [CrossRef]
- Qiu, L.M.; Liu, Z.T.; Wang, E.Y.; Li, B.L. Early-warning of rockburst in coal mine by low-frequency electromagnetic radiation. Eng. Geol. 2020, 279, 105755. [Google Scholar] [CrossRef]
- Liu, H.M.; Li, X.L.; Yu, Z.Y. Influence of hole diameter on mechanical properties and stability of granite rock surrounding tunnels. Phys. Fluids 2023, 35, 064121. [Google Scholar]
- Chen, S.J.; Du, Z.W.; Zhang, Z. Effects of chloride on the early mechanical properties and microstructure of gangue-cemented paste backfill. Constr. Build. Mater. 2020, 235, 117504. [Google Scholar] [CrossRef]
- Li, A.; Ma, Q.; Lian, Y.Q.; Ma, L.; Mu, Q.; Chen, J.B. Numerical simulation and experimental study on floor failure mechanism of typical working face in thick coal seam in Chenghe mining area of Weibei, China. Environ. Earth Sci. 2020, 79, 118. [Google Scholar] [CrossRef]
- Kumar, J.; Chitikela, S. Seismic passive earth pressure coefficients using the method of characteristics. Can. Geotech. J. 2002, 39, 463–471. [Google Scholar] [CrossRef]
- Wang, M.; Mine, X. Safe mining technology of working face under complex geological conditions with large mining depth and deep earth pressure. Coal Chem. Ind. 2019, 42, 34–40. [Google Scholar]
- Qiao, C.; Li, C.H.; Wei, X.M.; Hu, Y.Y. Numerical simulation study on the evolution law of mine pressure in deep mining. Arab. J. Geosci. 2020, 13, 471. [Google Scholar] [CrossRef]
- Fu, J.H.; Li, X.P.; Yu, G.L.; Shi, W.F.; Yuan, X. Exploration and practice of new method for rock burst hazard comprehensive evaluation. Saf. Coal Mines 2014, 45, 46–50. [Google Scholar]
- He, S.Q.; Song, D.Z.; Li, Z.L.; He, X.Q.; Chen, J.Q.; Zhong, T.P.; Lou, Q. Mechanism and prevention of rockburst in steeply inclined and extremely thick coal seams for fully mechanized top-coal caving mining and under gob filling conditions. Energies 2020, 13, 1362. [Google Scholar] [CrossRef]
- He, S.Y.; Lai, J.X.; Zhong, Y.J.; Wang, K.; Xu, W.; Wang, L.X.; Liu, T.; Zhang, C.P. Damage behaviors, prediction methods and prevention methods of rockburst in 13 deep traffic tunnels in China. Eng. Fail. Anal. 2021, 121, 105178. [Google Scholar] [CrossRef]
- Huo, B.J.; Tai, Y.; Meng, X.B.; Kuang, T.J. Deformation and failure mechanism of full seam chamber with extra-large section and its control technology. Open Geosci. 2020, 12, 390–405. [Google Scholar] [CrossRef]
- Wang, A.H.; Song, D.Z.; He, X.Q.; Dou, L.M.; Li, Z.L.; Luo, Q.; Zhao, Y.J. Investigation of coal and gas outburst risk by microseismic monitoring. PLoS ONE 2019, 14, e0216464. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.H.; Lin, D.Y.; Tang, C.A.; Yadav, K.P.; Feng, Z.Q.; Ma, K. Microseismic monitoring, positioning principle, and sensor layout strategy of rock mass engineering. Geofluids 2020, 2020, 8810391. [Google Scholar] [CrossRef]
- Xie, H.P.; Gao, F.; Ju, Y. Research and development of rock mechanics in deep ground engineering. Chin. J. Rock Mech. Eng. 2015, 34, 2161–2178. [Google Scholar]
- Shan, R.L.; Peng, Y.H.; Kong, X.S.; Xiao, Y.H.; Yuan, H.H.; Huang, B.; Zheng, Y. Research progress of coal roadway support technology at home and abroad. Chin. J. Rock Mech. Eng. 2019, 38, 2377–2403. [Google Scholar]
- Zhang, J.R.; Shi, Z.D.; Yan, Z.G.; Huang, Y.X.; Wang, Z.P.; Liu, R.Q. Double-prevention information management system for coal mine safety. Coal Eng. 2020, 52, 181–185. [Google Scholar]
- Zhang, G.Z.; Guo, J.Z.; Xu, B.; Xu, L.L.; Dai, Z.X.; Yin, S.X.; Soltanian, M.R. Quantitative analysis and evaluation of coal mine geological structures based on fractal theory. Energies 2021, 14, 1925. [Google Scholar] [CrossRef]
- Li, H.T.; Li, X.L.; Fu, J.H.; Zhu, N.Q.; Chen, D.Y.; Wang, Y.; Ding, S. Experimental study on compressive behavior and failure characteristics of imitation steel fiber concrete under uniaxial load imitation steel fiber concrete under uniaxial load. Constr. Build. Mater. 2023, 399, 132599. [Google Scholar] [CrossRef]
- Li, H.T.; Li, X.L.; Fu, J.H.; Gao, Z.L.; Chen, P.; Zhang, Z.B. Research on acoustic emission multi-parameter characteristics in the failure process of imitation steel fiber reinforced concrete. Phys. Fluids 2023, 35, 107109. [Google Scholar] [CrossRef]
- Wang, L.J. Application of safety system engineering in safe coal mine production. Energy Energy Conserv. 2018, 4, 25–26. [Google Scholar]
- Wang, B.; Cui, C.Q.; Zhao, Y.X.; Chen, M.; Yuan, X.C. Climate change mitigation in the coal mining industry: Low-carbon pathways and mine safety indicators. Nat. Hazards 2019, 95, 25–38. [Google Scholar] [CrossRef]
- Liu, Q.L.; Li, X.C.; Meng, X.F. Effectiveness research on the multi-player evolutionary game of coal-mine safety regulation in China based on system dynamics. Saf. Sci. 2019, 111, 224–233. [Google Scholar] [CrossRef]
- Chen, S.J.; Zhao, Z.H.; Feng, F.; Zhang, M.Z. Stress evolution of deep surrounding rock under characteristics of bi-modulus and strength drop. J. Cent. South Univ. 2022, 29, 680–692. [Google Scholar] [CrossRef]
- Qi, Q.X.; Li, Y.Z.; Zhao, S.K.; Zhang, N.B.; Zheng, W.Y.; Li, H.T.; Li, H.Y. The 70 years of coal mine burst development in china: The establishment and thinking of theory and technology system. Coal Sci. Technol. 2019, 47, 1–40. [Google Scholar]
- Yang, T.; Chen, P.; Li, B.; Nie, B.S.; Zhu, C.J.; Ye, Q.S. Potential safety evaluation method based on temperature variation during gas adsorption and desorption on coal surface. Saf. Sci. 2019, 113, 336–344. [Google Scholar] [CrossRef]
- Zhang, Z.B.; Wang, E.Y.; Zhang, H.T.; Bai, Z.M.; Zhang, Y.H.; Chen, X. Research on nonlinear variation of elastic wave velocity dispersion characteristic in limestone dynamic fracture process. Fractals 2023, 31, 2350008. [Google Scholar] [CrossRef]
- Si, T.; Wang, C.B.; Liu, R.Q.; Guo, Y.S.; Yue, S.; Ren, Y.J. Multi-criteria comprehensive energy efficiency assessment based on fuzzy-ahp method: A case study of post-treatment technologies for coal-fired units. Energy 2020, 200, 117533. [Google Scholar] [CrossRef]
- Zhai, M.H.; Jiang, F.X.; Qi, Q.X.; Guo, X.S.; Liu, Y.; Zhu, S.T. Research and practice of rockburst classified control system. J. China Coal Soc. 2017, 42, 3116–3124. [Google Scholar]
- Li, H.Y.; Mo, Y.L.; Sun, Z.X.; Li, L. Research status and prospect of coal bumps prevention and control technology. Coal Sci. Technol. 2019, 47, 62–68. [Google Scholar]
- Wang, J.C.; Liu, F.; Wang, Z.H. Experimental investigation on the movement mechanism of top coal in steeply inclined ultra-thick coal seams. Acta Mech. Sin. 2021, 37, 631–648. [Google Scholar] [CrossRef]
- Zhang, Z.B.; Wang, E.Y.; Li, N.; Zhang, H.T.; Bai, Z.M.; Zhang, Y.H. Research on macroscopic mechanical properties and microscopic evolution characteristic of sandstone in thermal environment. Constr. Build. Mater. 2023, 366, 130152. [Google Scholar] [CrossRef]
- Hu, H. Adhere to the development and safety of system concepts. China Emerg. Manag. Sci. 2021, 3, 4–12. [Google Scholar]
- Li, Z.L.; He, X.Q.; Dou, L.M.; Song, D.Z.; Wang, G.F.; Xu, X.L. Investigating the mechanism and prevention of coal mine dynamic disasters by using dynamic cyclic loading tests. Saf. Sci. 2019, 115, 215–228. [Google Scholar] [CrossRef]
- Zhao, Y.; Bi, J.; Zhou, X.P. Quantitative analysis of rockburst in the surrounding rock masses around deep tunnels. Eng. Geol. 2020, 273, 105669. [Google Scholar] [CrossRef]
- Du, S.W.; Feng, G.R.; Li, Z.X.; Sarkodie-Gyan, T.; Wang, J.M.; Ma, Z.J.; Li, W.H. Measurement and prediction of granite damage evolution in deep mine seams using acoustic emission. Meas. Sci. Technol. 2019, 30, 114002. [Google Scholar] [CrossRef]
- Zhang, W.P.; Li, B.; Liu, Z.J.; Zhang, B.B. Application of improved fuzzy comprehensive evaluation method in karst groundwater quality evaluation: A case study of Cengong county. Earth Sci. Inform. 2021, 14, 1101–1109. [Google Scholar] [CrossRef]
- Wang, X.T.; Li, S.C.; Xu, Z.H.; Xue, Y.G.; Hu, J.; Li, Z.Q.; Zhang, B. An interval fuzzy comprehensive assessment method for rockburst in underground caverns and its engineering application. Bull. Eng. Geol. Environ. 2019, 78, 5161–5176. [Google Scholar] [CrossRef]
- Zhang, W.H. Geological disaster monitoring and early warning system based on big data analysis. Arab. J. Geosci. 2020, 13, 946. [Google Scholar] [CrossRef]
- Wei, P.C.; He, F.C. Research on security trust measure model based on fuzzy mathematics. Chaos Solitons Fractals 2019, 128, 139–143. [Google Scholar] [CrossRef]
- Liu, X.M.; Liu, H.Y.; Wan, Z.; Wang, L.F.; Chen, Q. Study on evaluation index system of sustainable development of mine water resources based on PSO-AHP model and fuzzy comprehensive evaluation. J. Intell. Fuzzy Syst. 2021, 41, 4253–4264. [Google Scholar] [CrossRef]
- Zheng, J.H. The impact of residential area opening on road traffic—Based on multilevel fuzzy comprehensive evaluation method. Adv. Appl. Math. 2019, 8, 838–851. [Google Scholar] [CrossRef]
- Zhang, G.L. Optimization and application of mine ventilation system. Energy Energy Sav. 2018, 8, 138–139. [Google Scholar]
- Bao, Z.Y.; Li, X.M.; Lam, H.K.; Peng, Y.; Liu, F.C. Membership-function-dependent stability analysis for polynomial fuzzy-model-based control systems via chebyshev membership functions. IEEE Trans. Fuzzy Syst. 2020, 29, 3280–3292. [Google Scholar] [CrossRef]
- Chai, Z.L. An indirect variable weights method to compute fuzzy comprehensive evaluation values. Soft Comput. 2019, 23, 12511–12519. [Google Scholar] [CrossRef]
- Xue, Y.G.; Bai, C.H.; Kong, F.M.; Qiu, D.H.; Li, L.P.; Su, M.X.; Zhao, Y. A two-step comprehensive evaluation model for rockburst prediction based on multiple empirical criteria. Eng. Geol. 2020, 268, 105515. [Google Scholar] [CrossRef]
- Chen, Y.C.; Dai, J.Y.; Xie, D. Comprehensive evaluation of mine ventilation system based on combined weighting cloud model. Syst. Eng. 2020, 38, 39–46. [Google Scholar]
- Diest, F.H. A non-linear continuum approach to the problem of fracture zones and rockbursts. J. South. Afr. Inst. Min. Metall. 1965, 65, 502–522. [Google Scholar]
- Cook, N.G.W.; Hoek, E.; Pretorius, J.P.G.; Ortlepp, W.D.; Salamon, H.D.G. Rock mechanics applied to study of rockbursts. J. South Afr. Inst. Min. Metall. 1966, 10, 435–528. [Google Scholar]
- Aven, T. The cautionary principle in risk management: Foundation and practical use. Reliab. Eng. Syst. Saf. 2019, 191, 106585. [Google Scholar] [CrossRef]
- Rybak, A.; Rybak, A. Analysis of the main coal mining restructuring policy objectives in the light of polish mining companies’ ability to change. Energies 2020, 13, 3281. [Google Scholar] [CrossRef]
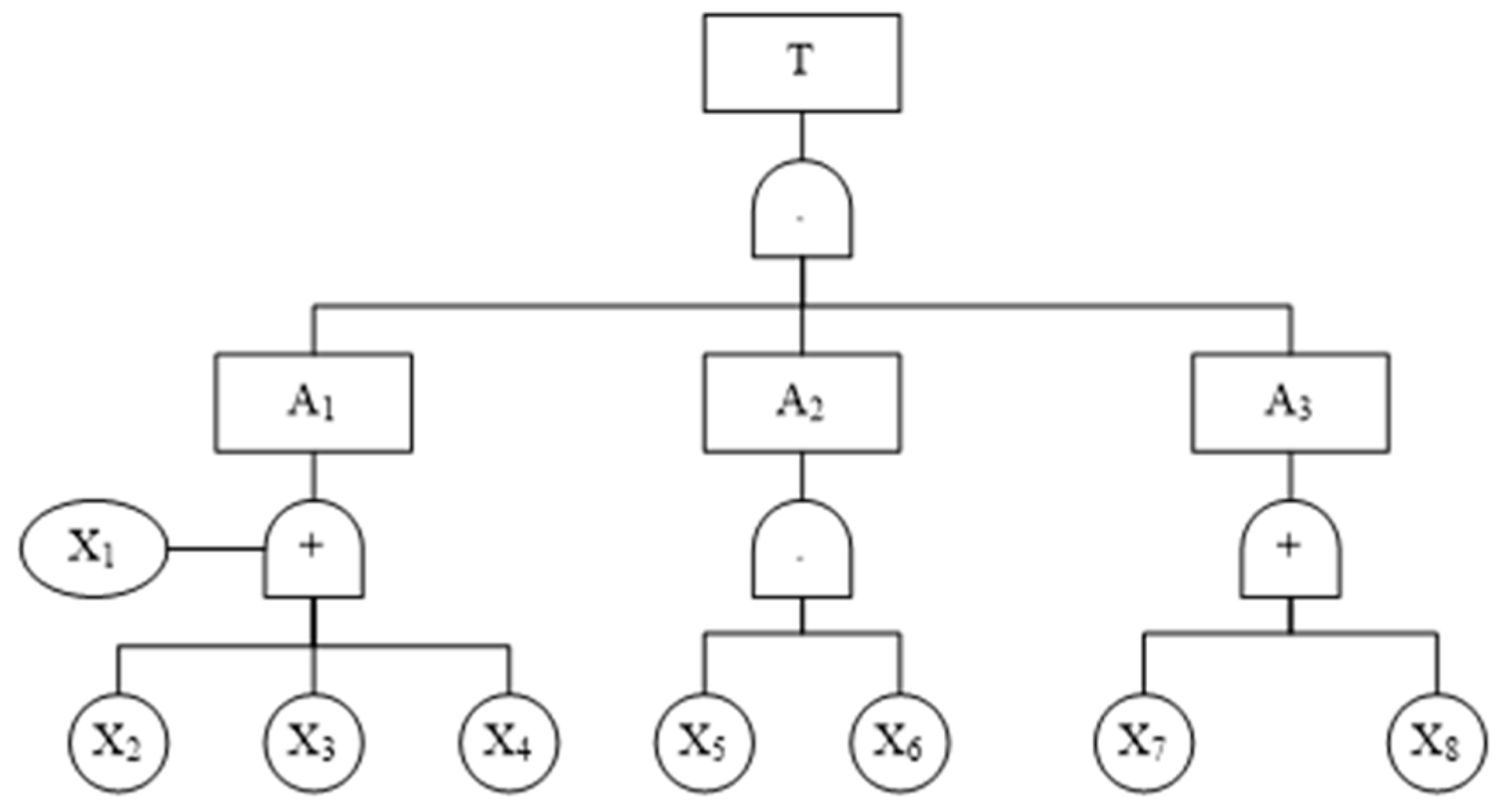
| Label | Event | Label | Event |
|---|---|---|---|
| T | “Double high” energy and frequency of microseismic events | X3 | Geological structure |
| A1 | Geological factor of mine | X4 | Coal and rock structure |
| A2 | Technical factor of production | X5 | Mining stress concentration factor |
| A3 | Organizational management factor | X6 | Inducing factors |
| X1 | The bursting liability of coal rock | X7 | Control input factor |
| X2 | Mining depth | X8 | Impact risk attention |
| Serial Number | Type | Meaning |
|---|---|---|
| 1 | Principal determinant type M (∧, ∨) | ∧ means taking a small operation, ∨ means taking large operation |
| 2 | The main factor is highlighted as Ⅰ type M (·, ∨) | · stands for ordinary multiplication operation, ∨ means taking large operation |
| 3 | The main factor is highlighted as Ⅱ type M (∧, ⊕) | ∧ means taking a small operation, ⊕ means sum with an upper limit of one, namely: x⊕y = min(1,x + y) |
| 4 | Weighted mean type M (·, +) | · is normal multiplication, and + is a normal addition |
| Judgment Matrix | B1 | B2 | B3 |
|---|---|---|---|
| B1 | 1 | 2 | 4 |
| B2 | 1/2 | 1 | 2 |
| B3 | 1/4 | 1/2 | 1 |
| Judgment Matrix B1 | C1 | C2 | C3 | C4 | W1 | λmax | |
|---|---|---|---|---|---|---|---|
| C1 | 1 | 1/5 | 1/2 | 1/5 | 0.075 | 4.004 | 0.001 < 0.1 |
| C2 | 5 | 1 | 3 | 1 | 0.393 | ||
| C3 | 2 | 1/3 | 1 | 1/3 | 0.138 | ||
| C4 | 5 | 1 | 3 | 1 | 0.393 |
| Judgment Matrix B2 | C5 | C6 | W2 | λmax | |
|---|---|---|---|---|---|
| C5 | 1 | 1/2 | 0.333 | 2.0 | 0.0 |
| C6 | 2 | 1 | 0.667 |
| Judgment Matrix B3 | C7 | C8 | W2 | λmax | |
|---|---|---|---|---|---|
| C7 | 1 | 1/3 | 0.25 | 2.0 | 0.0 |
| C8 | 3 | 1 | 0.75 |
| Factors | Detailed Inspection Items | Evaluation Grade | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| Mining depth | Actual working depth | √ | ||
| Mining above critical depth | √ | |||
| Depth of mining membership | 0.000 | 0.500 | 0.500 | |
| Geological structure | Fold (anticline, syncline) | √ | ||
| Fault | √ | |||
| The coal seam dip angle and thickness change sharply zone | √ | |||
| Tectonic change zone and tectonic stress zone | √ | |||
| Geological structure membership degree | 0.000 | 0.250 | 0.750 | |
| Coal and rock structure | Hard, thick, integrated roof | √ | ||
| Hard coal seam floor | √ | |||
| Coal with high strength, large elastic modulus, small moisture content, large metamorphic degree, and a large proportion of dark coal | √ | |||
| Subjection degree of coal structure | 0.000 | 0.000 | 1.000 | |
| The bursting liability of coal rock | Dynamic failure time of coal | √ | ||
| The impact energy index of coal | √ | |||
| The elastic energy index of coal | √ | |||
| Unidirectional compressive strength of coal | √ | |||
| Subjection degree of coal rockburst liability | 0.000 | 0.500 | 0.500 | |
| Mining stress concentration factor | Mining method (whether long arm or dry mining) | √ | ||
| Roof management method | √ | |||
| Mining procedures (whether to mine the working face, whether to advance and return to each other, whether to excavate the roadway in the supporting pressure zone) | √ | |||
| Face length | √ | |||
| Caving ratio | √ | |||
| Close to the residual mining area and stop-mining line | √ | |||
| Coal pillar | √ | |||
| Mined-out area | √ | |||
| Mining speed | √ | |||
| Mining stress concentration factor membership degree | 0.111 | 0.333 | 0.556 | |
| Inducing factors | Blasting | √ | ||
| Roof | √ | |||
| Initial pressure and periodic pressure | √ | |||
| Coal mining (support shifting) | √ | |||
| Membership degree of inducing factors | 0.000 | 0.500 | 0.500 | |
| Prevention and control of inputs | Support technology equipment is not in place | √ | ||
| No effective monitoring and forecasting equipment were selected | √ | |||
| Reasonable and effective anti-flushing measures have not been considered | √ | |||
| Control input membership | 0.000 | 0.667 | 0.333 | |
| Impact risk attention | Weak awareness of anti-impact | √ | ||
| The law of rock movement is not grasped | √ | |||
| No special administrative body has been established | √ | |||
| The knowledge of rockburst has not been studied | √ | |||
| Attachment degree of impact risk | 0.000 | 0.750 | 0.250 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Chen, D.; Fu, J.; Liu, S.; Geng, X. Construction and Application of Fuzzy Comprehensive Evaluation Model for Rockburst Based on Microseismic Monitoring. Appl. Sci. 2023, 13, 12013. https://doi.org/10.3390/app132112013
Li X, Chen D, Fu J, Liu S, Geng X. Construction and Application of Fuzzy Comprehensive Evaluation Model for Rockburst Based on Microseismic Monitoring. Applied Sciences. 2023; 13(21):12013. https://doi.org/10.3390/app132112013
Chicago/Turabian StyleLi, Xuelong, Deyou Chen, Jianhua Fu, Shumin Liu, and Xuesheng Geng. 2023. "Construction and Application of Fuzzy Comprehensive Evaluation Model for Rockburst Based on Microseismic Monitoring" Applied Sciences 13, no. 21: 12013. https://doi.org/10.3390/app132112013
APA StyleLi, X., Chen, D., Fu, J., Liu, S., & Geng, X. (2023). Construction and Application of Fuzzy Comprehensive Evaluation Model for Rockburst Based on Microseismic Monitoring. Applied Sciences, 13(21), 12013. https://doi.org/10.3390/app132112013







