Numerical Simulation on Corneal Surface Behavior Applying Luminous Beam Levels
Abstract
:1. Introduction
2. Materials and Methods
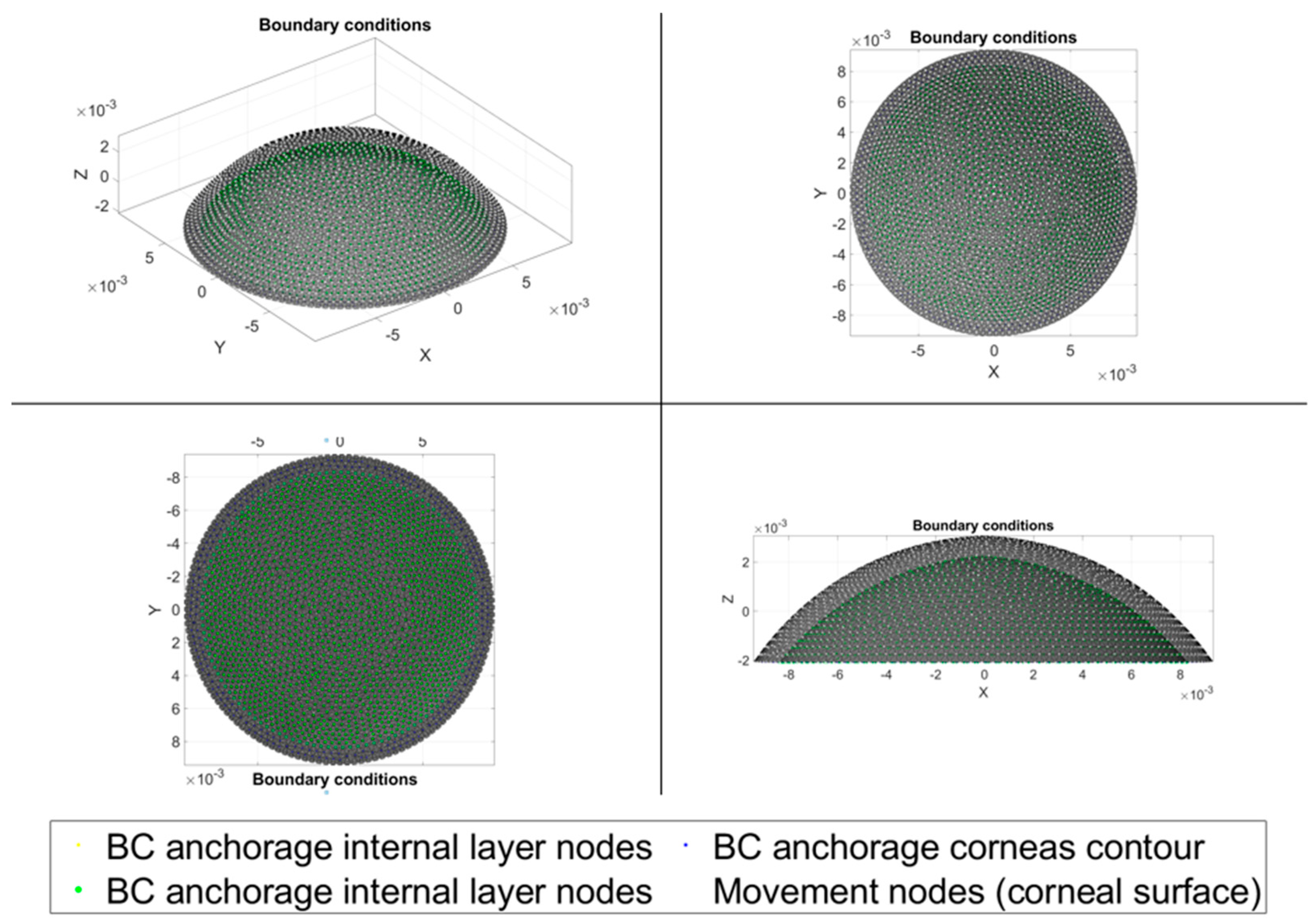
2.1. Three-Dimensional Model
2.2. Numerical Requirements
3. Results
3.1. Beam Type versus Incident Charge Ratio
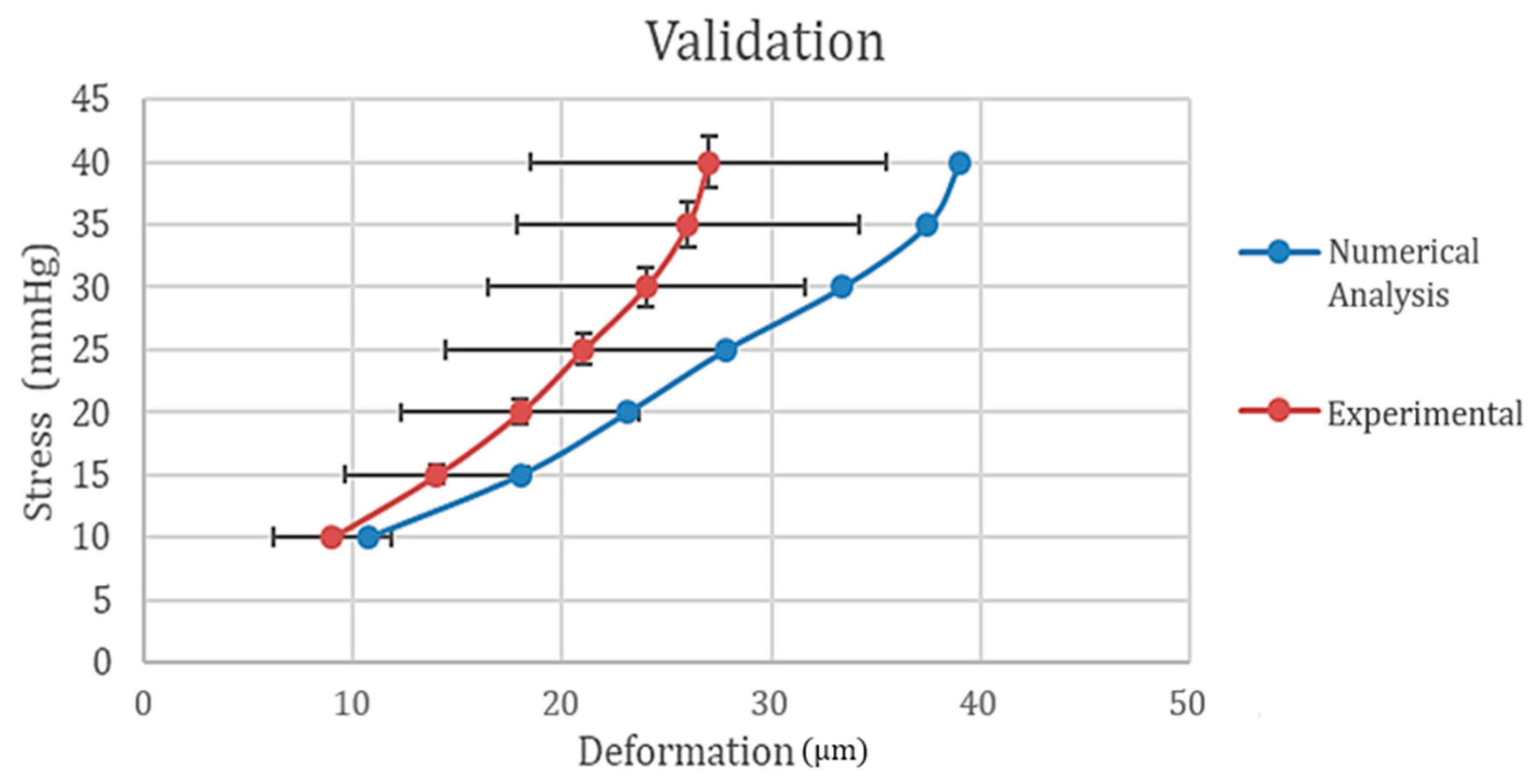
3.2. Model Validation
4. Discussion
- LASIK: 5 × 1010 Pa
- PRK: 7 × 1020 Pa
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weisentha, R.W. 2014–2015 Basic and Clinical Science Course (BCSC): Section 8: External Disease and Cornea; American Academy of Ophthalmology: San Francisco, CA, USA, 2014. [Google Scholar]
- Nan, L.; Zhang, Y.; Song, H.; Ye, Y.; Jiang, Z.; Zhao, S. Influence of Light-Emitting Diode-Derived Blue Light Overexposure on Rat Ocular Surface. J. Ophthalmol. 2023, 2023, 1097704. [Google Scholar] [CrossRef]
- Gulzar, A.; Yıldız, E.; Kaleli, H.N.; Nazeer, M.A.; Zibandeh, N.; Malik, A.N.; Taş, A.Y.; Lazoğlu, I.; Şahin, A.; Kizilel, S. Ruthenium-induced corneal collagen crosslinking under visible light. Acta Biomater. 2022, 147, 198–208. [Google Scholar] [CrossRef] [PubMed]
- Liou, H.L.; Brennan, N.A. Anatomically accurate, finite model eye for optical modeling. JOSA A 1997, 14, 1684–1695. [Google Scholar] [CrossRef] [PubMed]
- Feretis, E.; Theodorakopoulos, P.; Varotsos, C.; Efstathiou, M.; Tzanis, C.; Xirou, T. On the plausible association between environmental conditions and human eye damage. Environ. Sci. Pollut. Res. 2002, 9, 163–165. [Google Scholar] [CrossRef] [PubMed]
- Ng, E.Y.K.; Ooi, E.H. FEM simulation of the eye structure with bioheat analysis. Comput. Methods Programs Biomed. 2005, 82, 268–276. [Google Scholar] [CrossRef] [PubMed]
- Li, E.; Lui, G.T.; Tan, V.; He, Z.C. Modeling and simulation of bioheat transfer in the human eye using the 3D alpha finite element method. Int. J. Numer. Methods Biomed. Eng. 2010, 26, 955–976. [Google Scholar] [CrossRef]
- Schaumburg, F.; Guarnieri, F.A. Simulación computacional de la interacción con el campo electromagnético del tejido adyacente un implante ocular. Mecánica Comput. 2012, 16, 3883–3898. [Google Scholar]
- Álvarez, N.D.R.; Torres, C.S. Simulación y Modelamiento del ojo Humano como Herramienta Para la Prevención del Glaucoma a Través la Medición de la Presión Intraocular. Bachelor’s Thesis, Universidad Politécnica Salesiana Sede Cuenca, Cuenca, Ecuador, 2015. [Google Scholar]
- Esposito, L.; Clemente, C.; Bonora, N.; Rossi, T. Modelling human eye under blast loading. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 107–115. [Google Scholar] [CrossRef]
- Simonini, I.; Pandolfi, A. Customized finite element modelling of the human cornea. PLoS ONE 2015, 10, e0130426. [Google Scholar] [CrossRef]
- Wang, X.; Rumpel, H.; Lim, W.E.H.; Baskaran, M.; Perera, S.A.; Nongpiur, M.E.; Girard, M.J. Finite element analysis predicts large optic nerve head strains during horizontal eye movements. Investig. Ophthalmol. Vis. Sci. 2015, 57, 2452–2462. [Google Scholar] [CrossRef]
- Karimi, A.; Razaghi, R.; Navidbakhsh, M.; Sera, T.; Kudo, S. Computing the stresses and deformations of the human eye components due to a high explosive detonation using fluid–structure interaction model. Injury 2016, 47, 1042–1050. [Google Scholar] [CrossRef]
- Karimi, A.; Razaghi, R.; Navidbakhsh, M.; Sera, T.; Kudo, S. Quantifying the injury of the human eye components due to tennis ball impact using a computational fluid–structure interaction model. Sports Eng. 2016, 19, 105–115. [Google Scholar] [CrossRef]
- Whitford, C.; Joda, A.; Jones, S.; Bao, F.; Rama, P.; Elsheikh, A. Ex vivo testing of intact eye globes under inflation conditions to determine regional variation of mechanical stiffness. Eye Vis. 2016, 3, 21. [Google Scholar] [CrossRef]
- Seven, I.; Vahdati, A.; Pedersen, I.B.; Vestergaard, A.; Hjortdal, J.; Roberts, C.J.; Dupps, W.J. Contralateral eye comparison of SMILE and flap-based corneal refractive surgery: Computational analysis of biomechanical impact. J. Refract. Surg. 2017, 33, 444–453. [Google Scholar] [CrossRef] [PubMed]
- APant, D.; Kagemann, L.; Schuman, J.S.; Sigal, I.A.; Amini, R. An imaged-based inverse finite element method to determine in-vivo mechanical properties of the human trabecular meshwork. J. Model. Ophthalmol. 2017, 1, 100. [Google Scholar]
- Prieto-Vázquez, A.Y.; Cuautle-Estrada, A.; Grave-Capistrán, M.A.; Ramírez, O.; Torres-SanMiguel, C.R. Fractal Analysis and FEM Assessment of Soft Tissue Affected by Fibrosis. Fractal Fract. 2023, 7, 661. [Google Scholar] [CrossRef]
- Xu, M. Investigation of Corneal Biomechanical and Optical Behaviors by Developing Individualized Finite Element Model. Ph.D. Thesis, Mechanical Engineering, University of Rochester, Rochester, NY, USA, 2019. [Google Scholar]
- Kumar, V.; Abbas, A.K.; Fausto, N.; Astar, J.C. Patología Estructural y Funcional, 8th ed.; Elsevier: Barcelona, Spain, 2013; Volume 53. [Google Scholar]
- Bourne, R.R.A.; Flaxman, S.R.; Braithwaite, T.; Cicinelli, M.V.; Das, A.; Jonas, J.B. Magnitude, temporal trends, and projetions of the global prevalence of blindness and distance and near vision impairment: A systematic review and meta-analysis. Lancet Glob. Health 2018, 5, 3–10. [Google Scholar]
- Vaughan, N. Evolution of Biological Eye in Computer Simulation. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation(CEC), Wellington, New Zealand, 10–13 June 2019; pp. 2537–2543. [Google Scholar]
- Andre, B.; Beckanhan, R.; Chou, B.R.; Gutstein, W.; Sliney, D.; Thomas, R.; Tsubota, K. ¿Qué papel debería jugar la ciencia y/o la práctica clínica en la prevención de los problemas oculares causados por los rayos ultravioletas y la luz azul violeta? Points De Vue 2014, 71, 8–9. [Google Scholar]
- Ramirez, O.; Torres-San-Miguel, C.R.; Ceccarelli, M.; Urriolagoitia-Calderon, G. Experimental characterization of an osteosynthesis implant. In Advances in Mechanism and Machine Science; Uhl, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 53–62. [Google Scholar]
- Fada, R.; Shahgholi, M.; Azimi, R.; Babadi, N.F. Estimation of Porosity Effect on Mechanical Properties in Calcium Phosphate Cement Reinforced by Strontium Nitrate Nanoparticles: Fabrication and FEM Analysis. Arab. J. Sci. Eng. 2023, 2023, 1–11. [Google Scholar] [CrossRef]
- León, M.G.; del Valle, A.; Elizondo, B.; Ortega, P.; Siller, M.F. Comparación de la becamedición del grosor corneal central medido con el paquímetro incluido en el Wavelight® Ex500 Excimer Laser y el tomógrafo de cámara de Scheimpflug Pentacam® en sujetos sanos. Rev. Mex. De Oftalmol. 2017, 91, 25–29. [Google Scholar]
- Costanzo, L.S. Fisiología, 7th ed; Chapter 3; Neurofisiología—Fisiología; Elsevier: Amsterdam, The Netherlands; pp. 69–118. Available online: https://www-clinicalkey-com.bibliotecaipn.idm.oclc.org/student/content/book/3-s2.0-B9788413823812000039 (accessed on 13 January 2023).
- Hamilton, K.E.; Pye, D.C. Young’s modulus in normal corneas and the effect on applanation tonometry. Optom. Vis. Sci. 2008, 85, 445–450. [Google Scholar] [CrossRef] [PubMed]
- Radiation Pressure, Wikipedia, The Free Encyclopedia, Year Last Revised 2022. Available online: https://en.wikipedia.org/wiki/Radiation_pressure (accessed on 24 August 2022).
- Grytz, R.; Krishnan, K.; Whitley, R.; Libertiaux, V.; Sigal, I.A.; Girkin, C.A.; Crwford, J. A mesh-free approach to incorporate complex anisotropic and heterogeneous material properties into the eye-specific finite element models. Comput. Methods Appl. Mech. Eng. 2020, 358, 112654. [Google Scholar] [CrossRef]
- Woo, S.L.; Kobayashi, A.S.; Schlegel, W.A.; Lawrence, C. Nonlinear material properties of intact cornea and sclera. Exp. Eye Res. 1972, 14, 29–39. [Google Scholar] [CrossRef] [PubMed]
- Mark, N.; Farmer, K.C. Sun Damage and Prevention; Electronic Textbook of Dermatology; The Internet Dermatology Society, Inc.: New York, NY, USA, 2008. [Google Scholar]
- Dang, D.H.; Riaz, K.M.; Karamichos, D. Treatment of Non-Infectious Corneal Injury: Review of Diagnostic Agents, Therapeutic Medications, and Future Targets. Drugs 2022, 82, 145–167. [Google Scholar] [CrossRef] [PubMed]
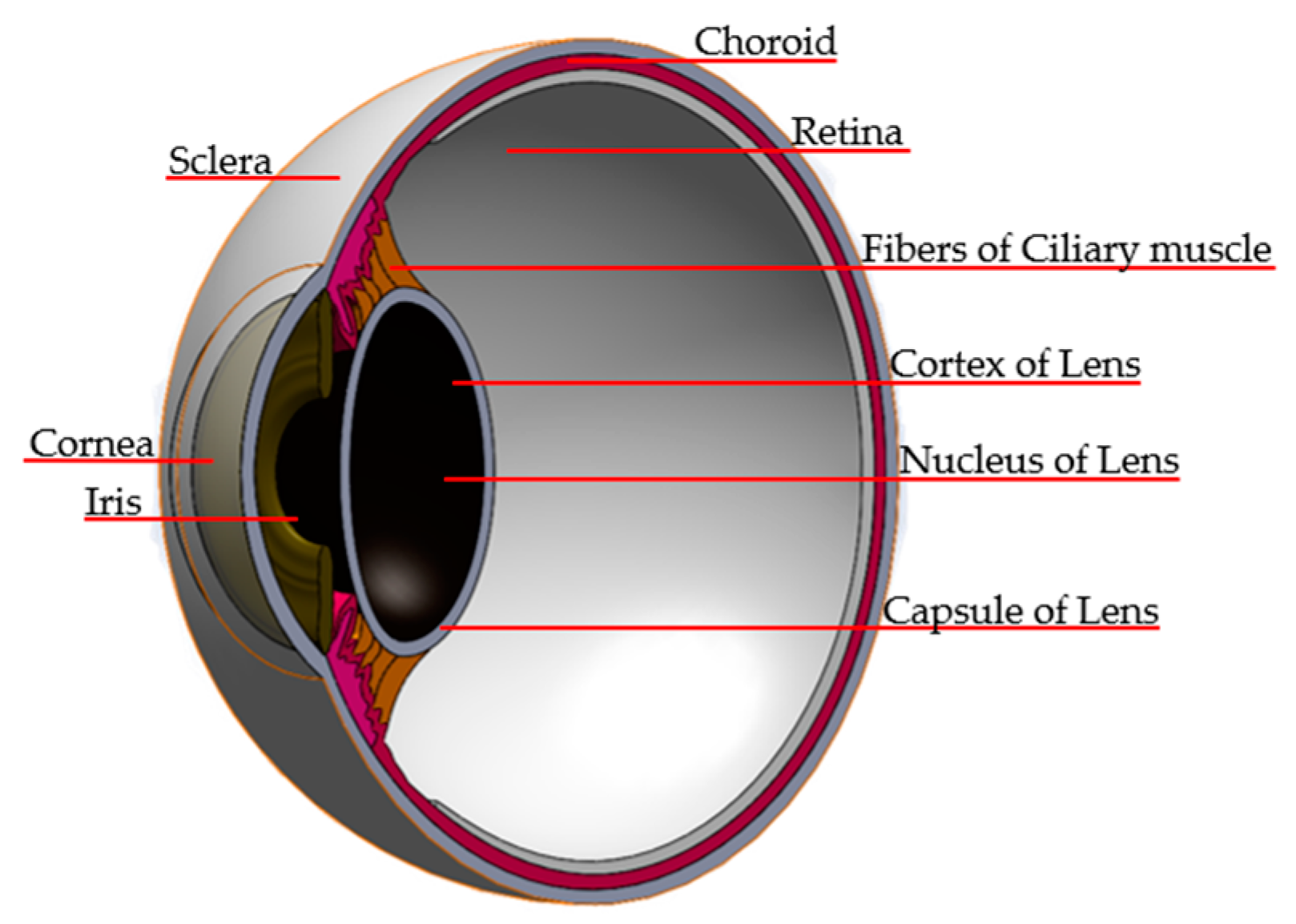
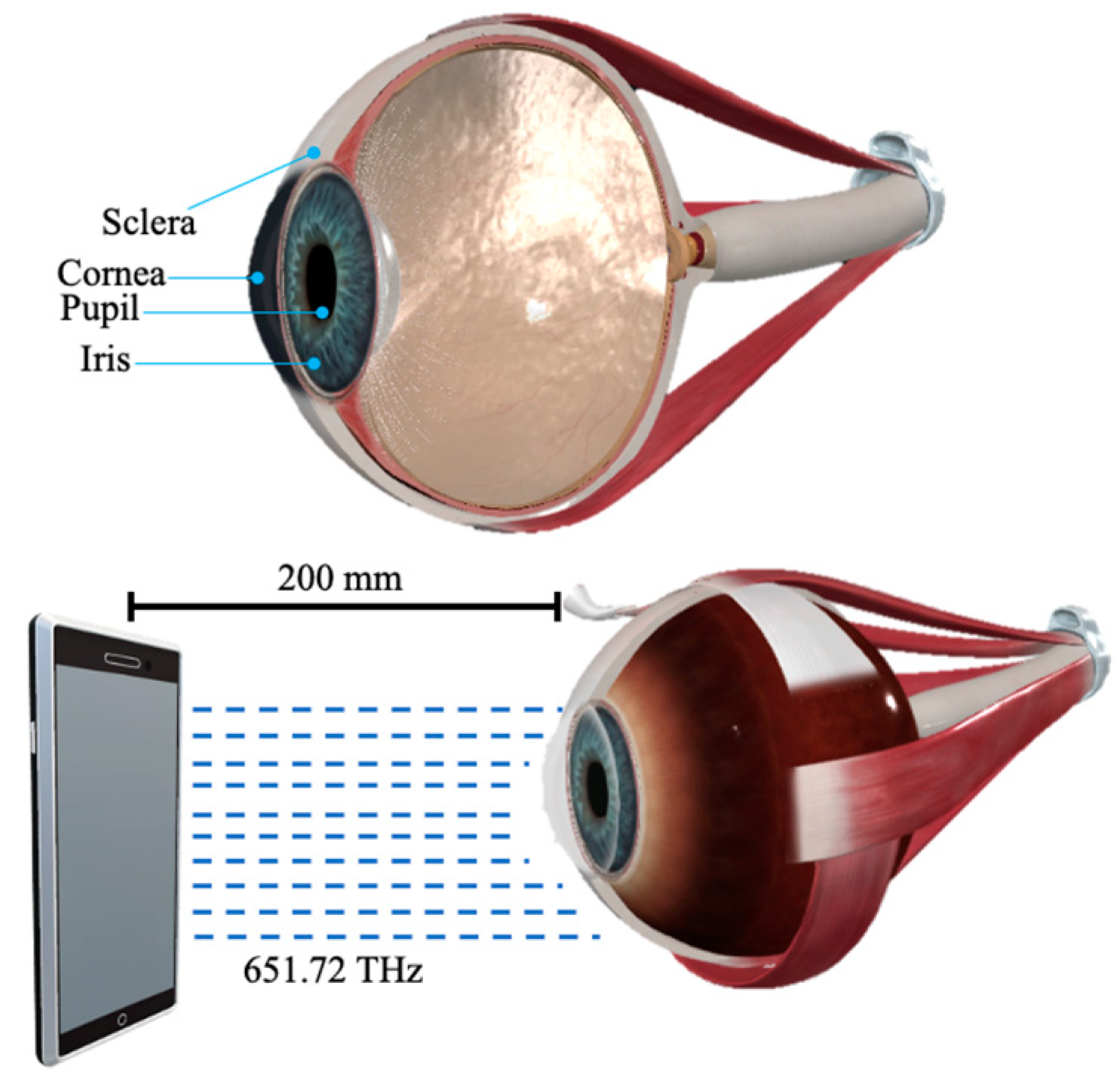

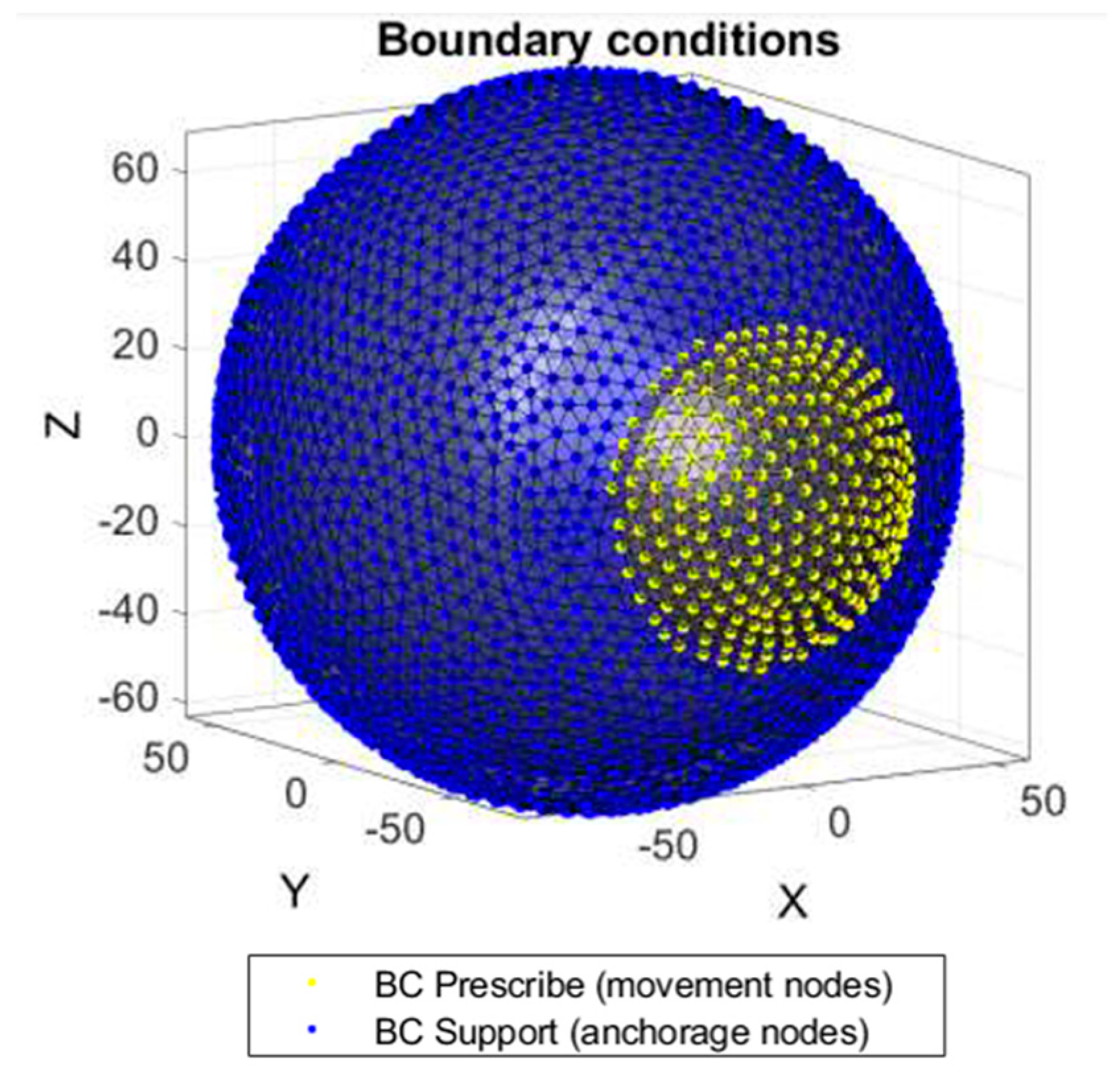
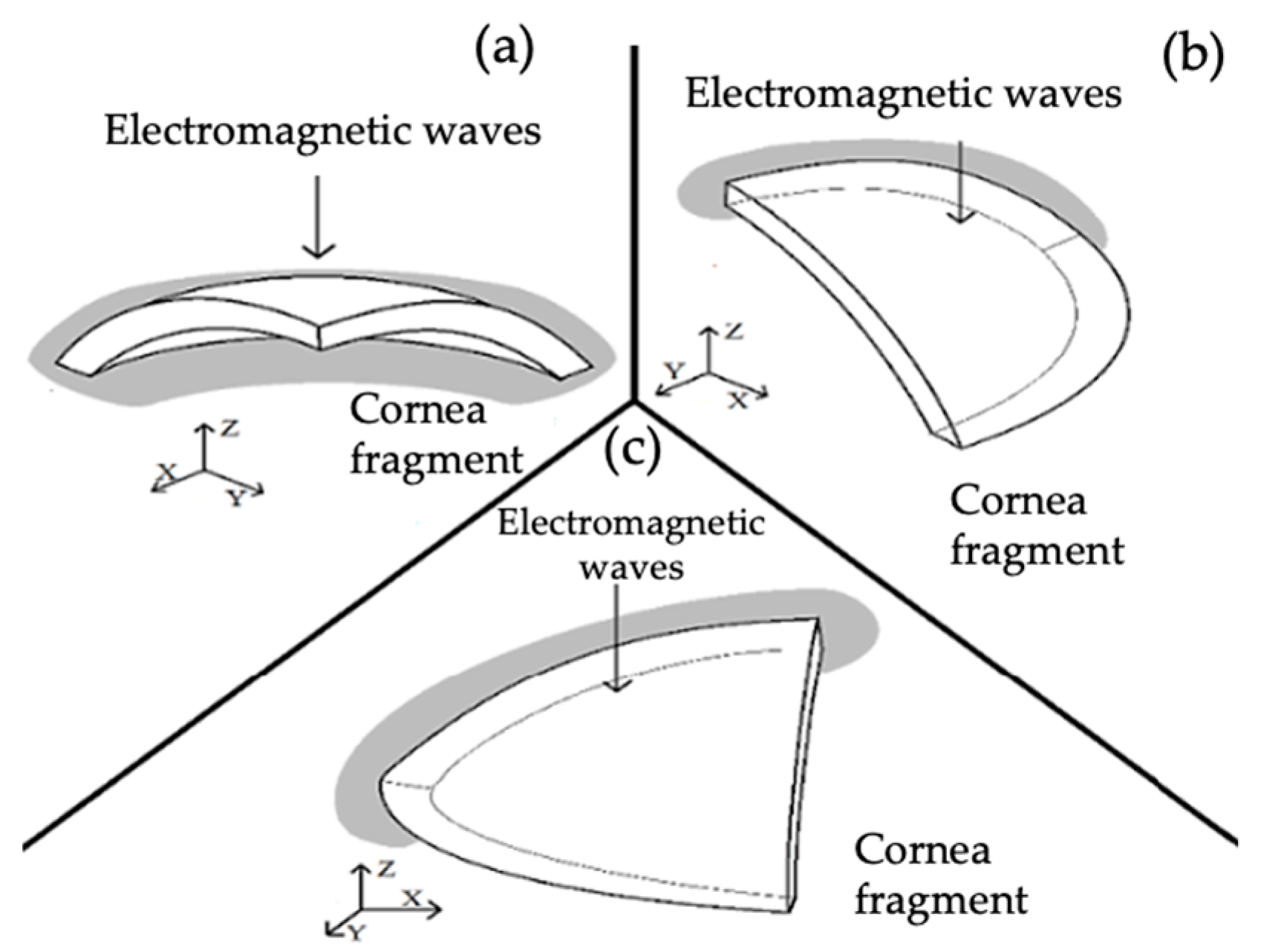


| Zone | Dimensions |
|---|---|
| Cornea | D: 10 mm. Volume: 57.5 mm3. Thickness: 0.5 mm. |
| Sclera | Different thicknesses. Leaf blade: 0.8 mm. Equator: 0.4 mm. Optic nerve insertion: 4.5 mm. |
| Iris | D: 12.33 mm. Ang. iris–cornea = 56°. Iris–crystalline distance 1.8 mm. Corrugated. |
| Pupil | D: 3 mm. “Its diameter is between 3 and 4.5 millimeters in the human eye. It can widen to between 5 to 9 mm in the dark”. |
| Crystalline | Three layers and greater curvature is the back face. Capsule thickness: 0.5 mm. Core: 2.1 mm. |
| Ciliary muscle/ciliary body | Thickness: 0.6 mm. Distance between the ciliary muscle and ciliary body: 0.35–0.3 mm. |
| Choroid | Thickness: 0.4 mm |
| Retina | Different thicknesses. Periphery: 2 mm, optic nerve insertion: 5 mm. |
| Pos/Ante Camera | Vol ante: 192 mm3. |
| Eyelids/Corneal cavity | Different thicknesses. Leaf blade: 1 mm. Equator: 1.5 mm/sclera–cavity space: 0.1 mm. Thickness: 1.5 mm. “Their distances vary between 12–14.5 mm at their maximum opening, and 3.5 mm is considered the minimum”. |
| Axial length | 24.66 mm. |
| Case No. | Wavelength | Frequency | Electromagnetic Spectrum |
|---|---|---|---|
| 1 | 300 nm | 999.31 THz | UV-B |
| 2 | 350 nm | 856.55 THz | UV-A |
| 3 | 460 nm | 651.72 THz | Visible Spectrum (Blue) |
| 4 | 1000 nm | 299.79 THz | Near Infrared |
| 5 | 1500 nm | 199.86 THz | Medium Infrared |
| Case | Load (mmHg) | Deformation (µm) | Experimental Values Range (µm) |
|---|---|---|---|
| 1 | 10 | 10.7 | 1.7–11.8 |
| 2 | 15 | 17.989 | 9.59–18.4 |
| 3 | 20 | 23.1 | 12.3–23.7 |
| 4 | 25 | 27.8315 | 14.4–27.6 |
| 5 | 30 | 33.387 | 16.4–31.6 |
| 6 | 35 | 37.4516 | 17.8–34.2 |
| 7 | 40 | 39.01 | 18.5–35.5 |
| Case | Power [W] | Source | Distance (mm) | Photon Load (Pa) | Photons | Total Load Applied (Pa) |
|---|---|---|---|---|---|---|
| 1 | 0.1 | Sun | 200 | 6.966 × 10−15 | 15.106 × 1016 | 1052.2616 |
| 2 | 0.0857 | Sun | 200 | 5.99 × 10−15 | 15.106 × 1016 | 905.8763 |
| 3 | 0.5 | Smartphone’s screen | 200 | 4.5439 × 10−15 | 157.85 × 1016 | 7172.637 |
| 4 | 0.01 | Commercial laser | 200 | 2.09022 × 10−15 | 5.0474 × 1016 | 105.22616 |
| 5 | 1 | Commercial laser | 200 | 1.3934 × 10−15 | 755.12 × 1016 | 10,522.62 |
| Case No. | Source (W) | Photon Load (Pa) | Photons Number | Total Load (Pa) | Maximum Displacement (µm) |
|---|---|---|---|---|---|
| 1 | 0.1 | 6.966 × 10−15 | 15.106 × 1016 | 1052.2616 | 1.33 |
| 2 | 0.0857 | 5.99 × 10−15 | 15.106 × 1016 | 905.8763 | 1.14 |
| 3 | 0.5 | 4.5439 × 10−15 | 157.85 × 1016 | 7172.637 | 9.07 |
| 4 | 0.01 | 2.09022 × 10−15 | 5.0474 × 1016 | 105.22616 | 0.0837 |
| 5 | 1 | 1.3934 × 10−15 | 755.12 × 1016 | 10,522.62 | 13.3 |
| Surgeries Type | Applied Energy | Exposure Time | Wave Frequency | Area | Distance | Power |
|---|---|---|---|---|---|---|
| LASIK | 2.5 µJ | 350 fs | 300 GHz | 50.6 µm | 150 mm | 0.5 MW |
| PRK | 2.5 µJ | 350 fs | 30 PHz | 7.06 pm | 150 mm | 0.5 GW |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guevara-Leon, F.; Grave-Capistrán, M.A.; Flores-Campos, J.A.; Torres-Ariza, J.L.; Alcántara-Arreola, E.A.; Torres-SanMiguel, C.R. Numerical Simulation on Corneal Surface Behavior Applying Luminous Beam Levels. Appl. Sci. 2023, 13, 12132. https://doi.org/10.3390/app132212132
Guevara-Leon F, Grave-Capistrán MA, Flores-Campos JA, Torres-Ariza JL, Alcántara-Arreola EA, Torres-SanMiguel CR. Numerical Simulation on Corneal Surface Behavior Applying Luminous Beam Levels. Applied Sciences. 2023; 13(22):12132. https://doi.org/10.3390/app132212132
Chicago/Turabian StyleGuevara-Leon, Fernando, Mario Alberto Grave-Capistrán, Juan Alejandro Flores-Campos, Jose Luis Torres-Ariza, Elliot Alonso Alcántara-Arreola, and Christopher René Torres-SanMiguel. 2023. "Numerical Simulation on Corneal Surface Behavior Applying Luminous Beam Levels" Applied Sciences 13, no. 22: 12132. https://doi.org/10.3390/app132212132
APA StyleGuevara-Leon, F., Grave-Capistrán, M. A., Flores-Campos, J. A., Torres-Ariza, J. L., Alcántara-Arreola, E. A., & Torres-SanMiguel, C. R. (2023). Numerical Simulation on Corneal Surface Behavior Applying Luminous Beam Levels. Applied Sciences, 13(22), 12132. https://doi.org/10.3390/app132212132









