Analysis of the Mechanism and Control of the Unbalanced Operation of Three-Phase Four-Wire Inverters
Abstract
:1. Introduction
2. Three-Closed-Loop Control of an Unbalanced Three-Phase Four-Wire Inverter
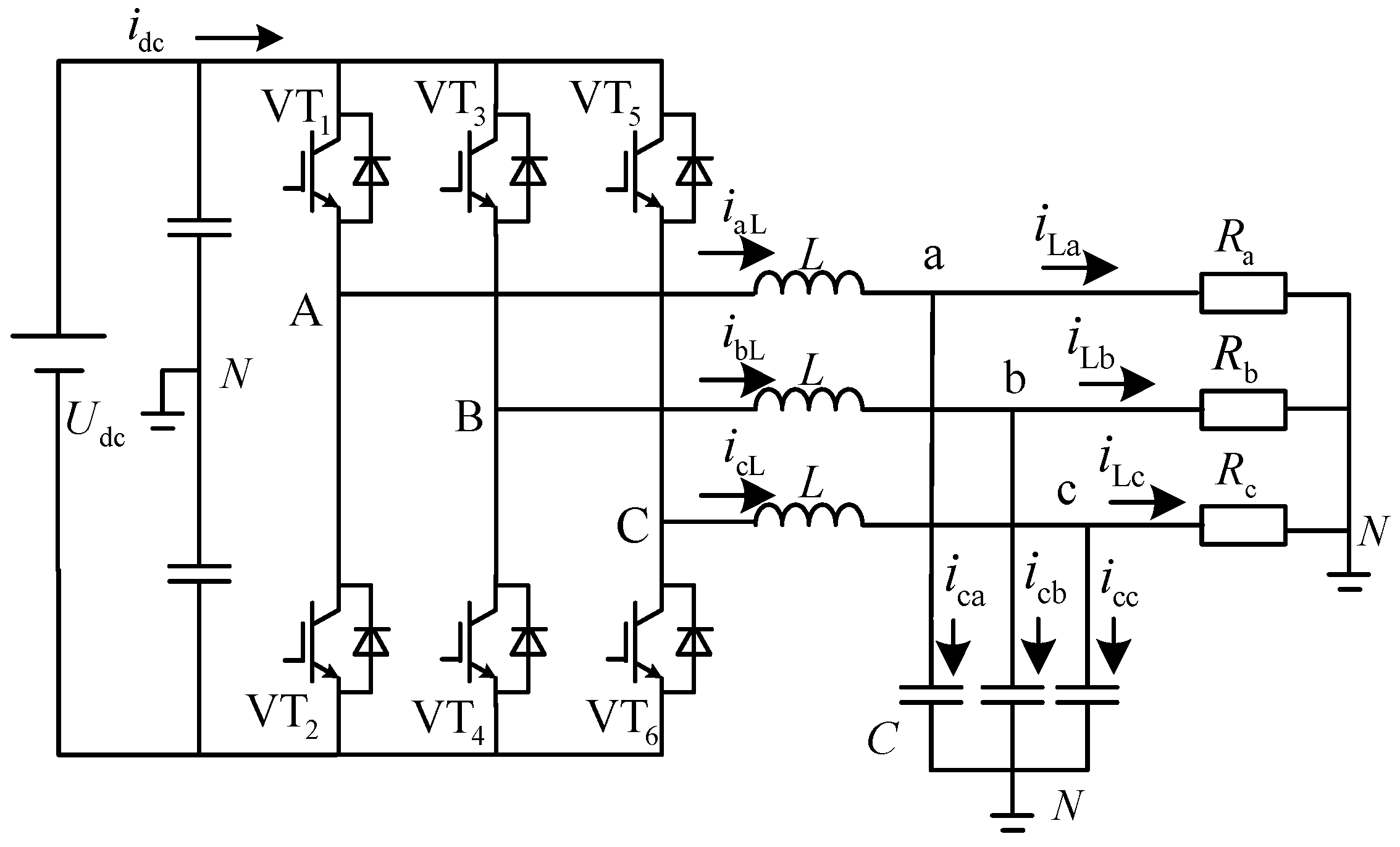
2.1. Control Principle of a Three-Phase Four-Wire Inverter
2.2. Modelling of Three-Phase Four-Wire Inverter
2.3. Control Analysis of Three-Phase Four-Wire Inverters
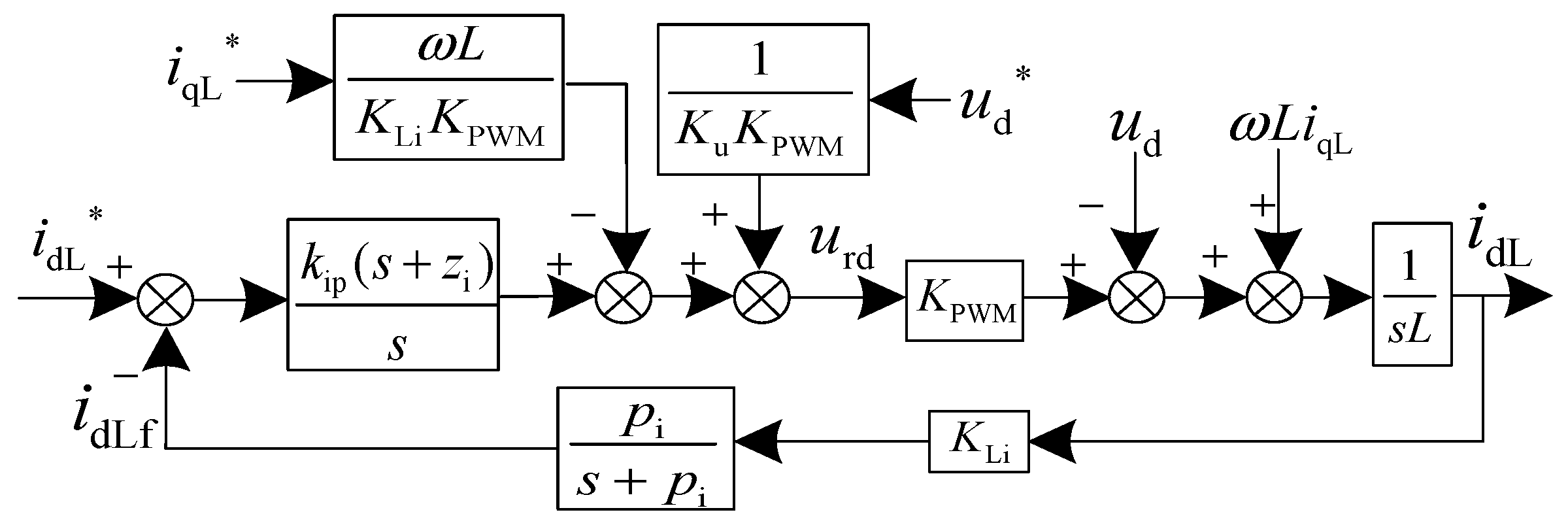
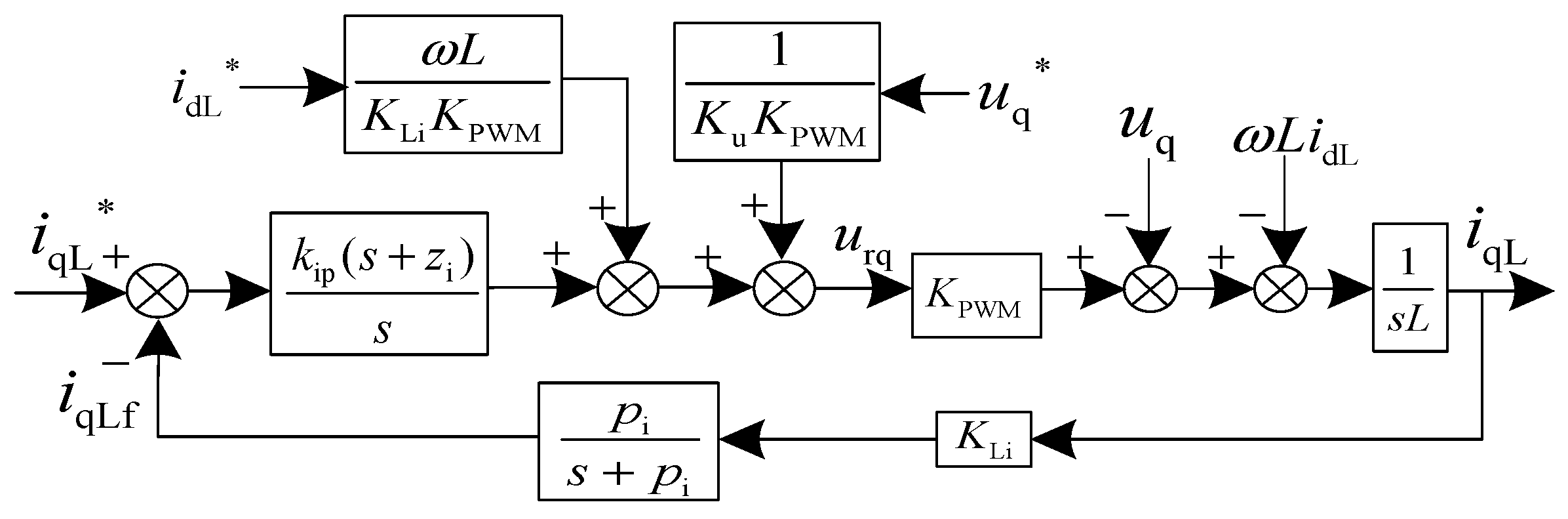
2.3.1. Current Loop Control
Open Loop Transfer Function of the Current Loop
Selection of the Zero Pole of the Compensation Link in the Current Link
Calculation of Current Loop Compensation Link Parameters
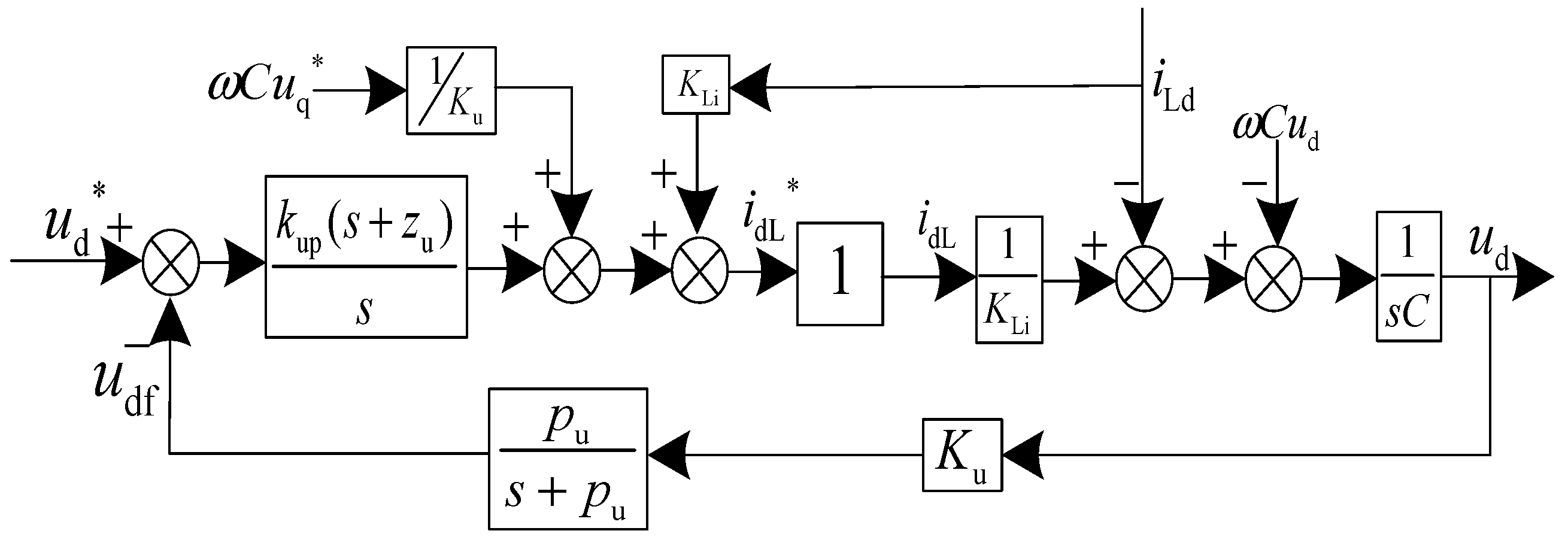
2.3.2. Voltage Loop Control
Open Loop Transfer Function of the Voltage Loop
Selection of the Zero Pole of the Compensation Link in the Voltage Link
Calculation of Voltage Loop Compensation Link Parameters
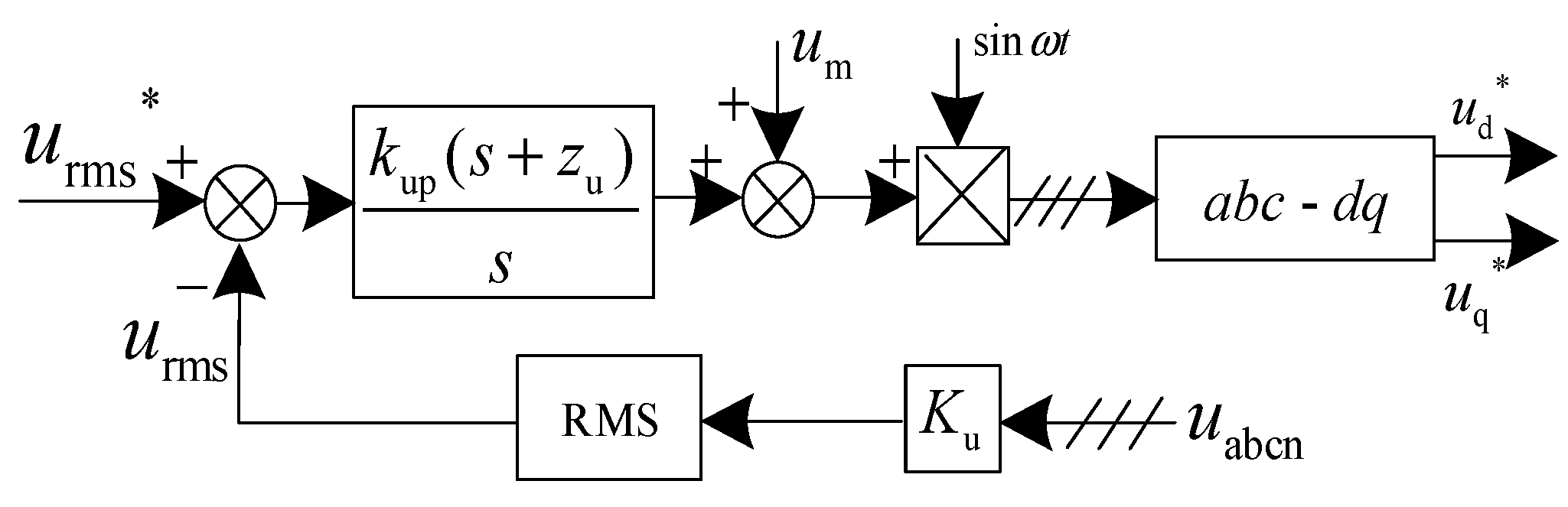
2.3.3. Voltage RMS Outer Loop Control
3. DC-Side Capacitance Analysis
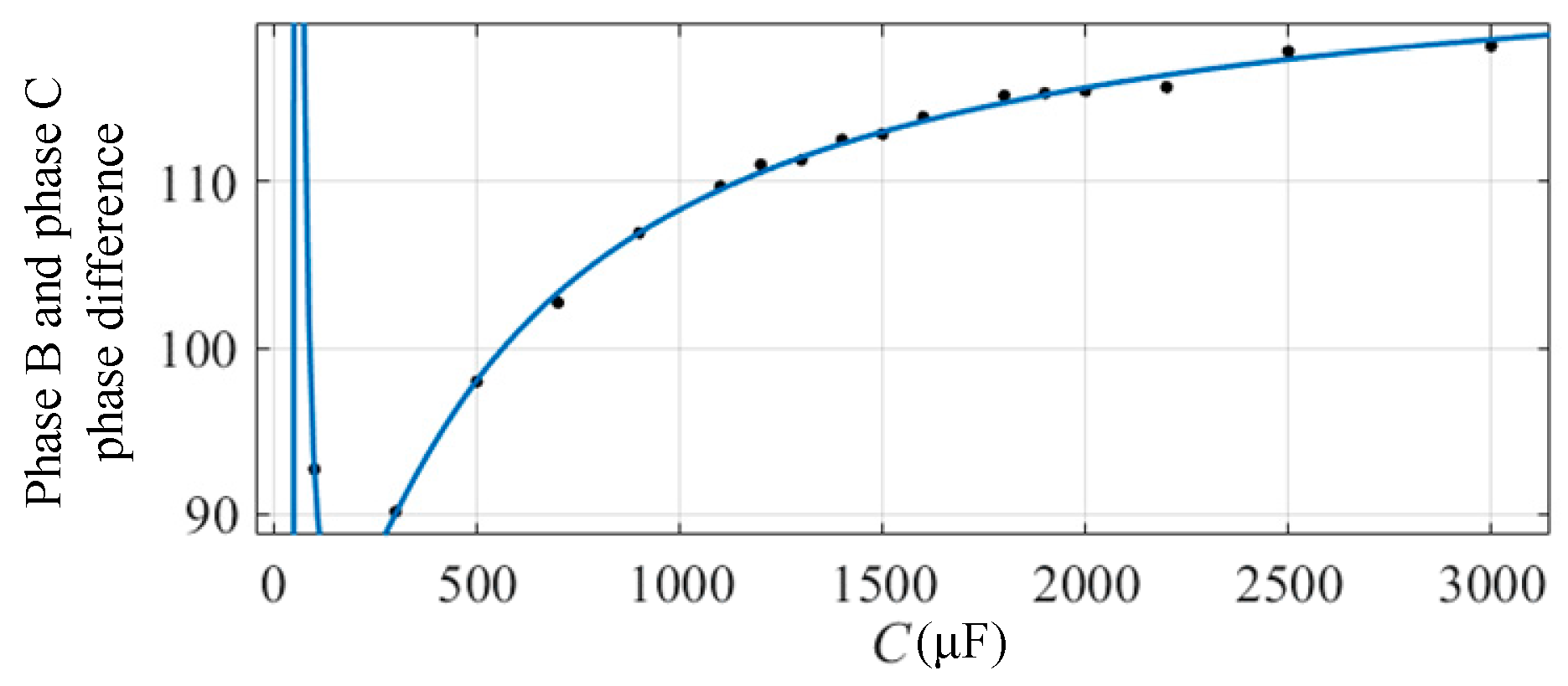
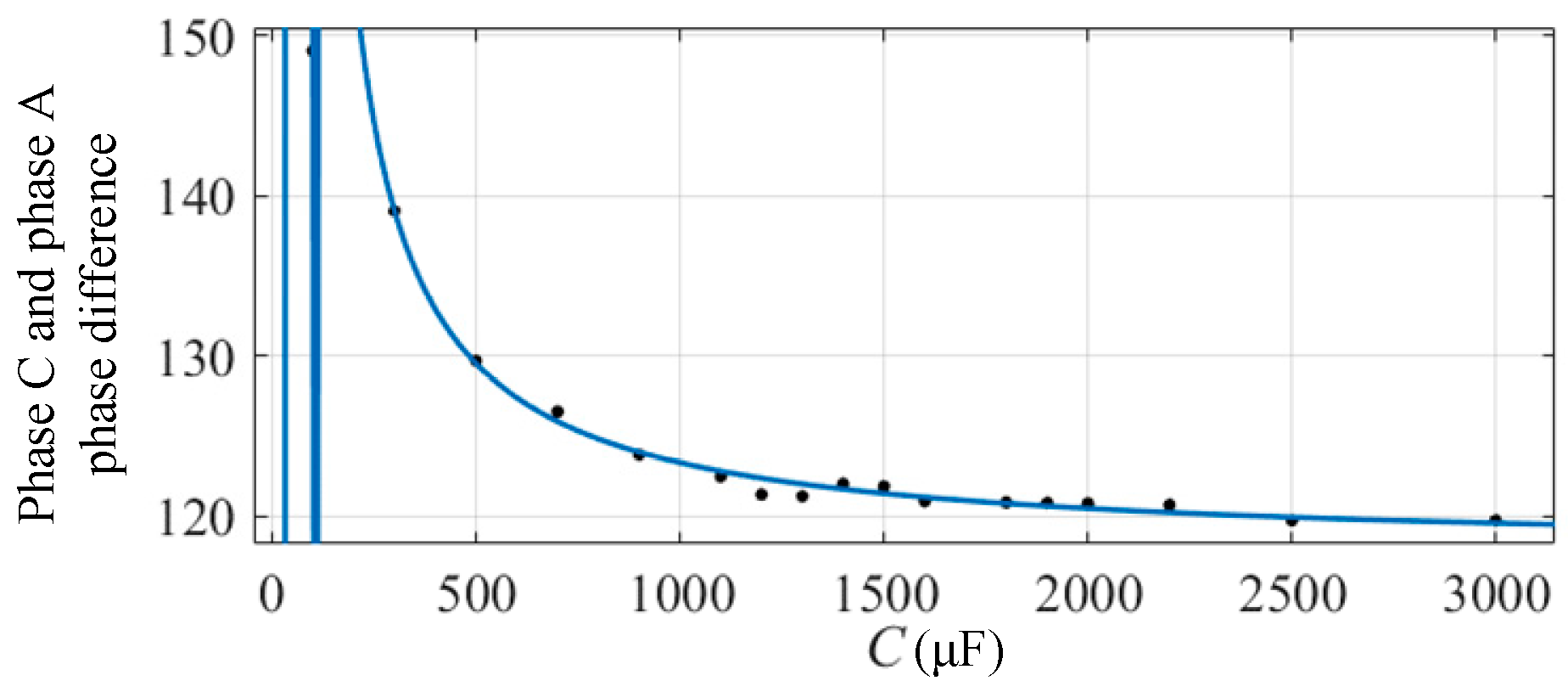
3.1. Effect of DC-Side Capacitance on Phase between Phases
3.2. Effect of DC Voltage Fluctuations on Load Voltage
3.3. Effect of Unbalanced Current on Voltage Fluctuations in the DC-Side Capacitor
3.4. Determination of DC-Side Capacitance
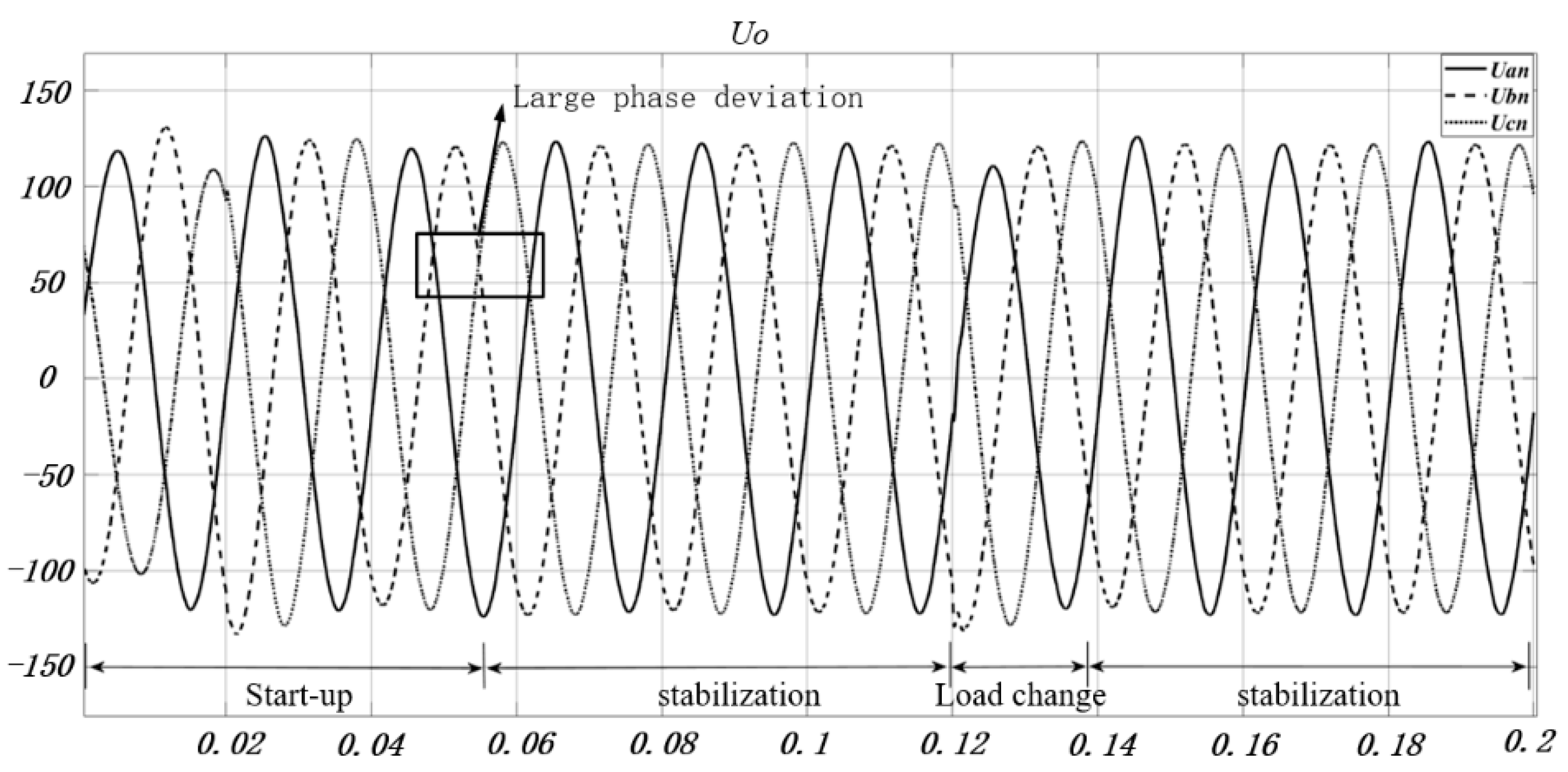
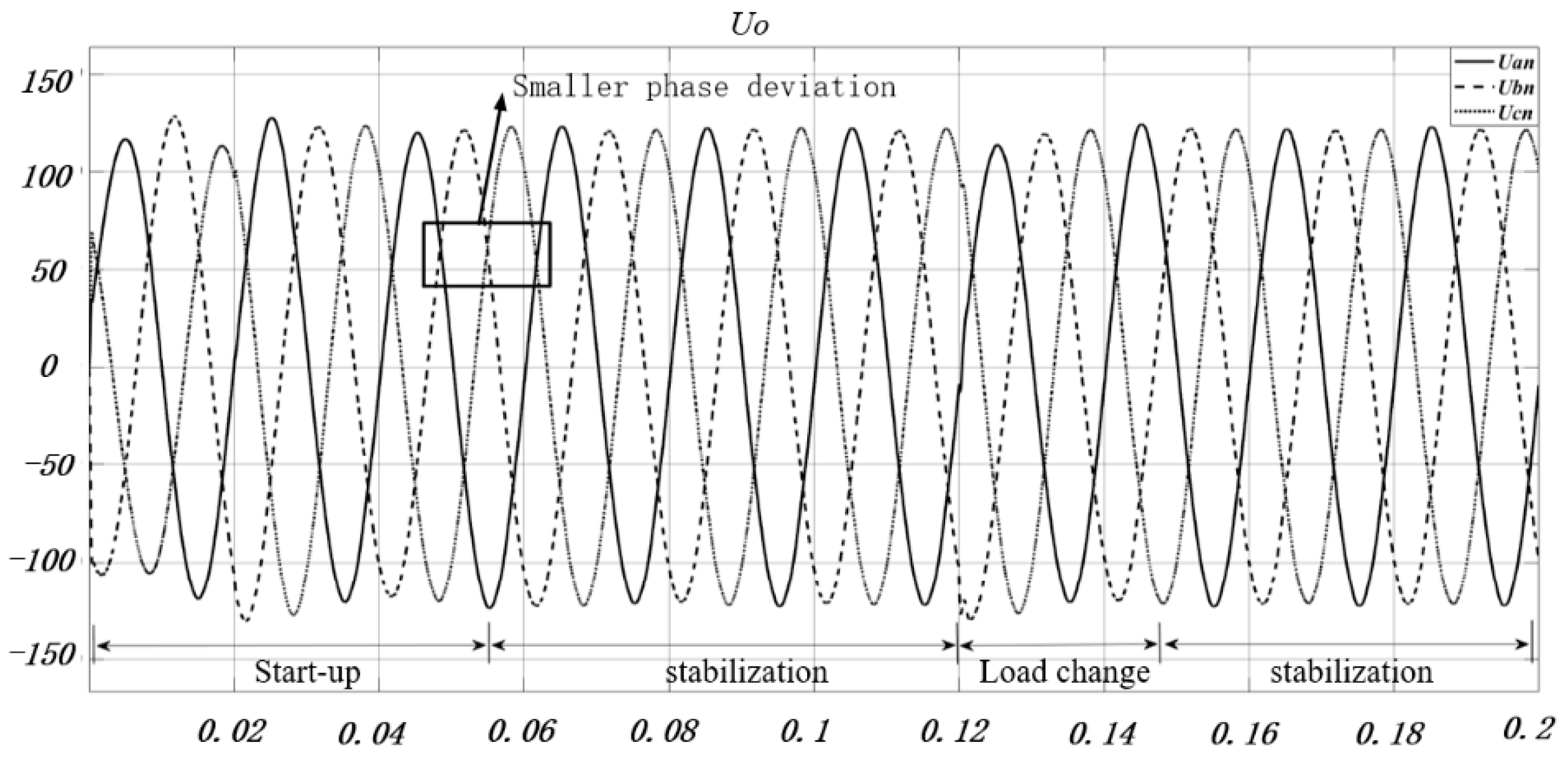
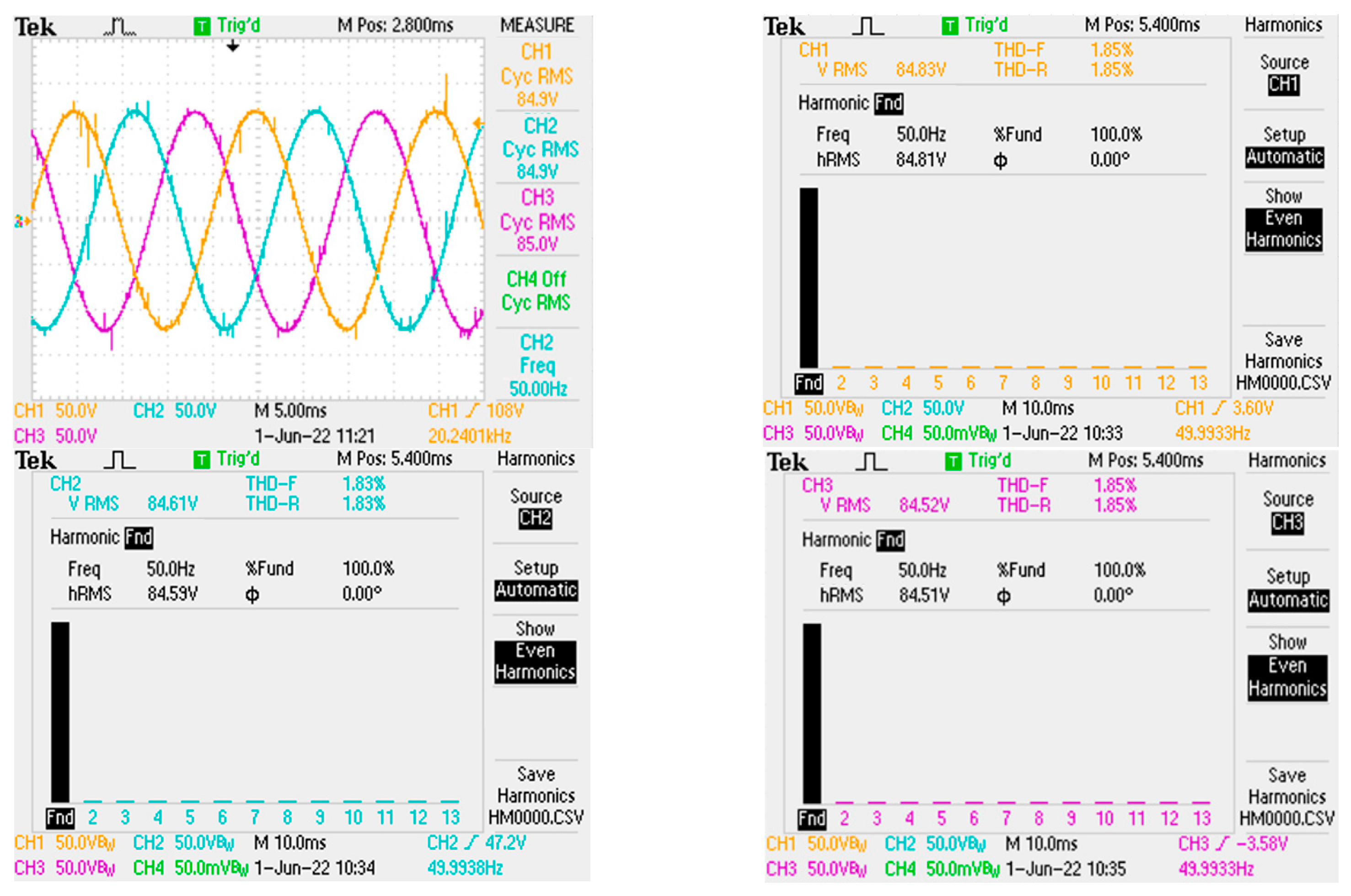
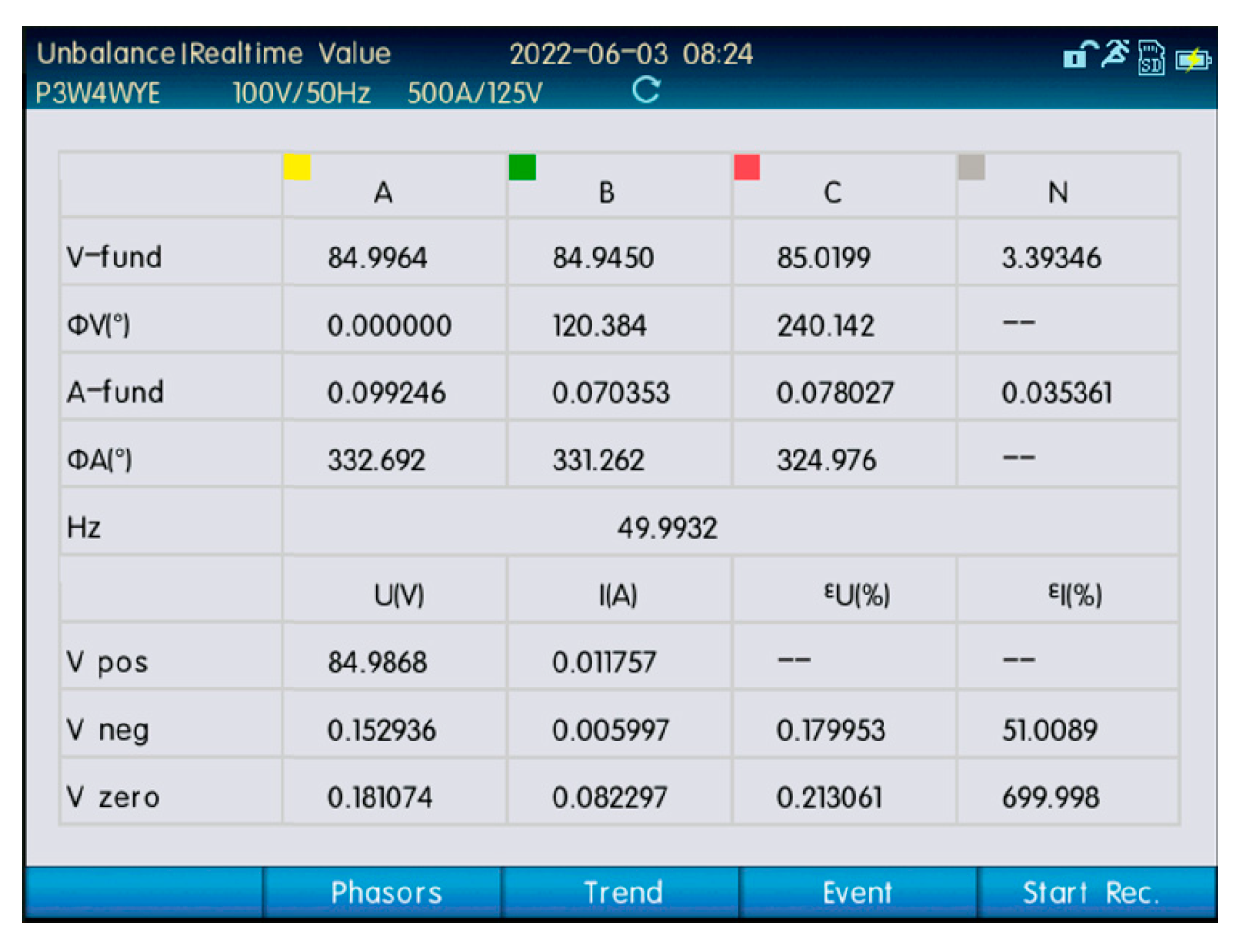
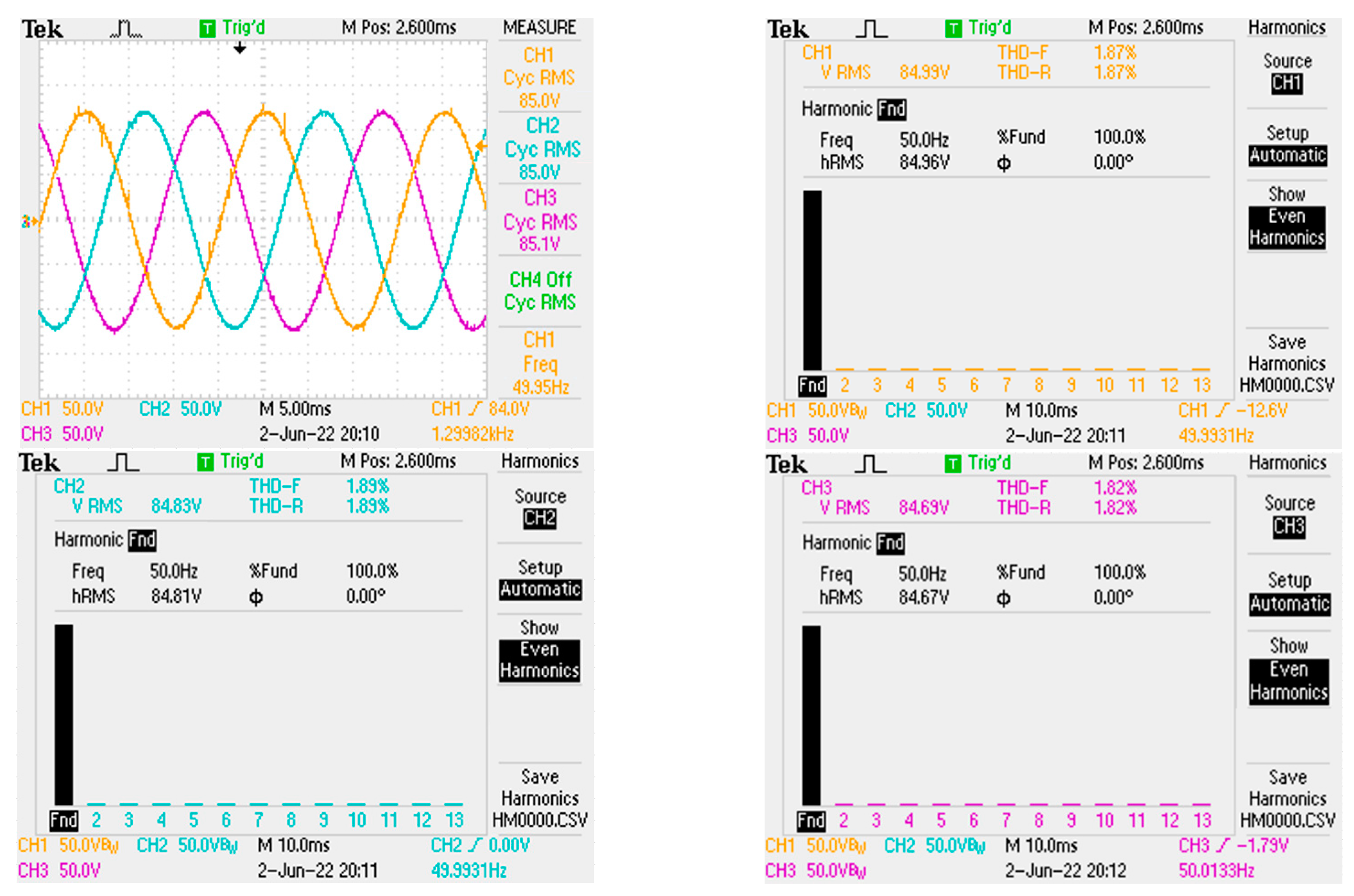
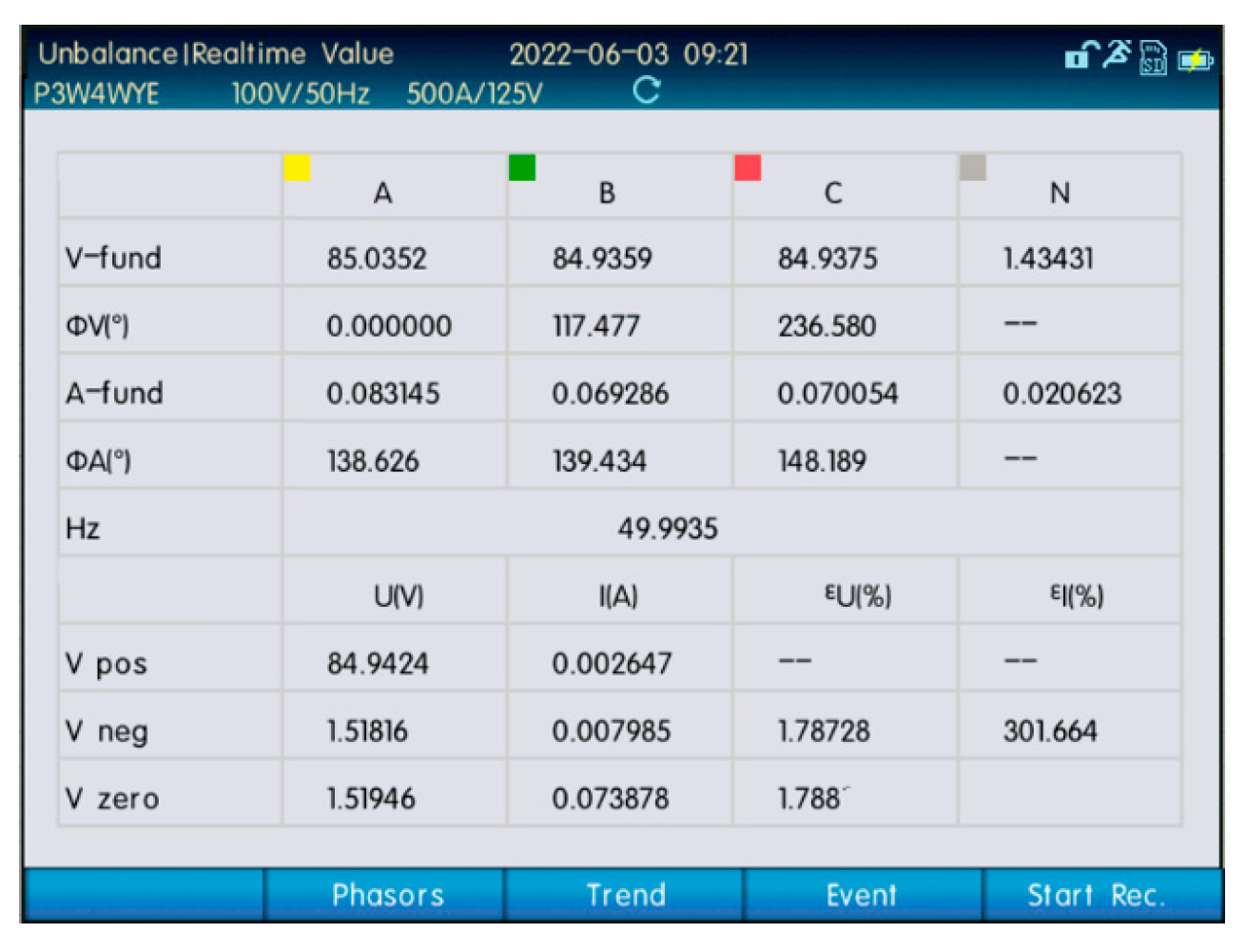
4. Simulation and Experimental Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, X.H.; Chang, C.W.; Chang-Chien, L.R. An Automatic Voltage Compensation technique for Three-Phase Stand-Alone Inverter to serve unbalanced or nonlinear load. In Proceedings of the IEEE 2nd International Future Energy Electronics Conference (IFEEC), Taipei, Taiwan, 1–4 November 2015; pp. 1–6. [Google Scholar]
- Fan, M.; Liu, H.K. Research on control method of load under the strong disturbance of wave power inverter. Electr. Meas. Instrum. 2015, 52, 78–81. [Google Scholar]
- Luo, J.; Zhang, H.; Zhang, S.; Wu, W.; Ouyang, H.; Chen, Y. Modeling and characteristic analysis of sequential impedance of three-phase off-grid inverter under unbalanced load. Power Syst. Prot. Control 2020, 48, 30–40. [Google Scholar]
- Feng, G.; Ye, Z.; Xia, Y.; Nian, H.; Huang, L.; Wang, Z. High Frequency Resonance Suppression Strategy of Three-Phase Four-Wire Split Capacitor Inverter Connected to Parallel Compensation Grid. Energies 2022, 15, 1486. [Google Scholar] [CrossRef]
- Feng, G.; Ye, Z.; Xia, Y.; Huang, L.; Wang, Z. Impedance Modeling and Stability Analysis of Three-Phase Four-Wire Inverter with Grid-Connected Operation. Energies 2022, 15, 2754. [Google Scholar] [CrossRef]
- Yang, L.; Cao, T.; Cai, Z.; Xia, X.; Jia, C.; Dong, X.; Zhang, S. Stability Analysis and Robust Control Method for LCL-Type Three-Phase Four-Wire Split Capacitor Inverter Considering Zero-Sequence Loop. Electronics 2022, 11, 3286. [Google Scholar] [CrossRef]
- Ren, B.Y.; Zhao, X.R.; Sun, X.D.; Yang, H. Improved droop control based three-phase combined inverters for unbalanced load. Power Syst. Technol. 2016, 40, 1163–1168. [Google Scholar]
- Yang, K.; Chen, L.; Chen, G.Z. Individual sequence control of DSTATCOM compensation for unbalanced load. Electr. Power Autom. Equip. 2012, 32, 36–41. [Google Scholar]
- Zhou, X.; Jin, X.M.; Tang, F. Improved Sequence Decomposition Control Strategy for Three-phase Four-leg Inverter with Unbalanced Load. High Volt. Eng. 2014, 40, 2504–2512. [Google Scholar]
- Sun, C.; Ma, W.M.; Lu, J.Y. Analysis of the Unsymmetrical Output Voltages Distortion Mechanism of Three-Phase Inverter and Its Corrections. Proc. CSEE 2006, 26, 57–64. [Google Scholar]
- Xu, S.G. Research into Control Method of Three-phase Inverter Power Supply Under Unbalanced Load. J. Chong Qing Norm. Univ. (Nat. Sci.) 2009, 26, 103–107. [Google Scholar]
- Cao, T.Q.; Qi, Q.; Wang, J. Study on unbalanced load of three-phase inverter. Electr. Mach. Control 2012, 16, 50–55. [Google Scholar]
- Zhou, C.; Zheng, Y.H.; Wang, X.; Li, L.X. Control strategy based on dual-loop controller for split-capacitor-type three-phase four-wire DSTATCOM. Electr. Power Autom. Equip. 2014, 34, 114–121. [Google Scholar]
- Shan, T.M.; Yang, R.G. Reactive power compensation for unbalanced current. Electr. Power Autom. Equip. 2004, 24, 26–29. [Google Scholar]
- Cheng, J.; Zhao, B.; Chen, X. Droop Control of Three-Phase Four-Wire Parallel Inverters under Unbalanced Load Condition. Trans. China Electrotech. Soc. 2018, 33, 4790–4801. [Google Scholar]
- Wang, Y.B. Principles, Design and Engineering Practice of Advanced Power Electronics Technology; Shandong University Press: Shandong, China, 2020. [Google Scholar]
- Xu, D.H. Power Electronic System Modeling and Control; China Machine Press: Beijing, China, 2006. [Google Scholar]
- Pei, X.J.; Chen, C.; Kang, Y. Analysis of Voltage Ripple and Design for DC-Link Capacitor in Three-Phase Voltage Source Inverters. Trans. China Electrotech. Soc. 2014, 29, 254–259+269. [Google Scholar]
- Chen, D.H.; Xie, S.J. Research on Current-Mode Control Half-Bridge Inverter(I)—Voltage Un-Balance of Input Capacitors. Trans. China Electrotech. Soc. 2004, 19, 85–88+51. [Google Scholar]




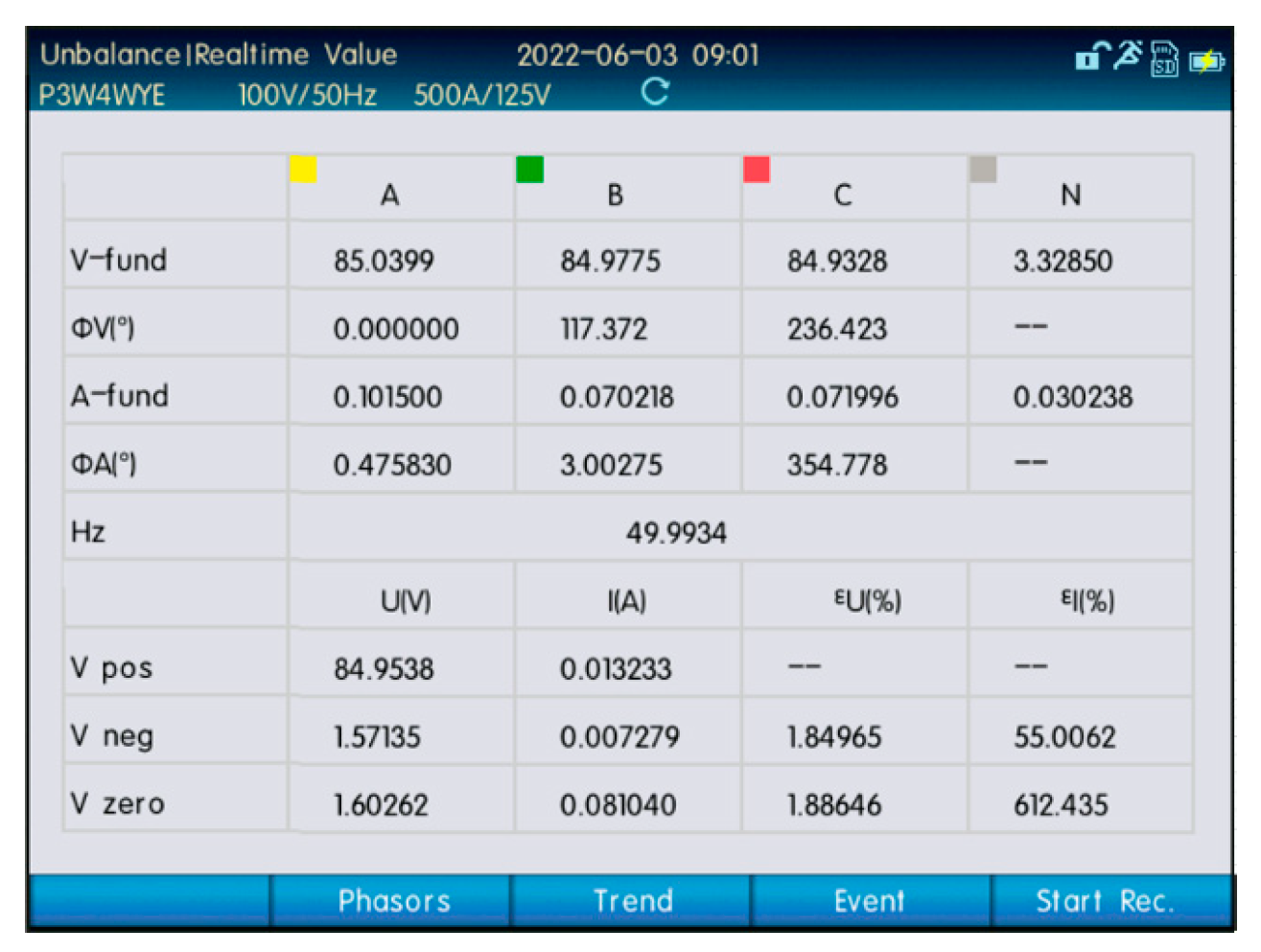
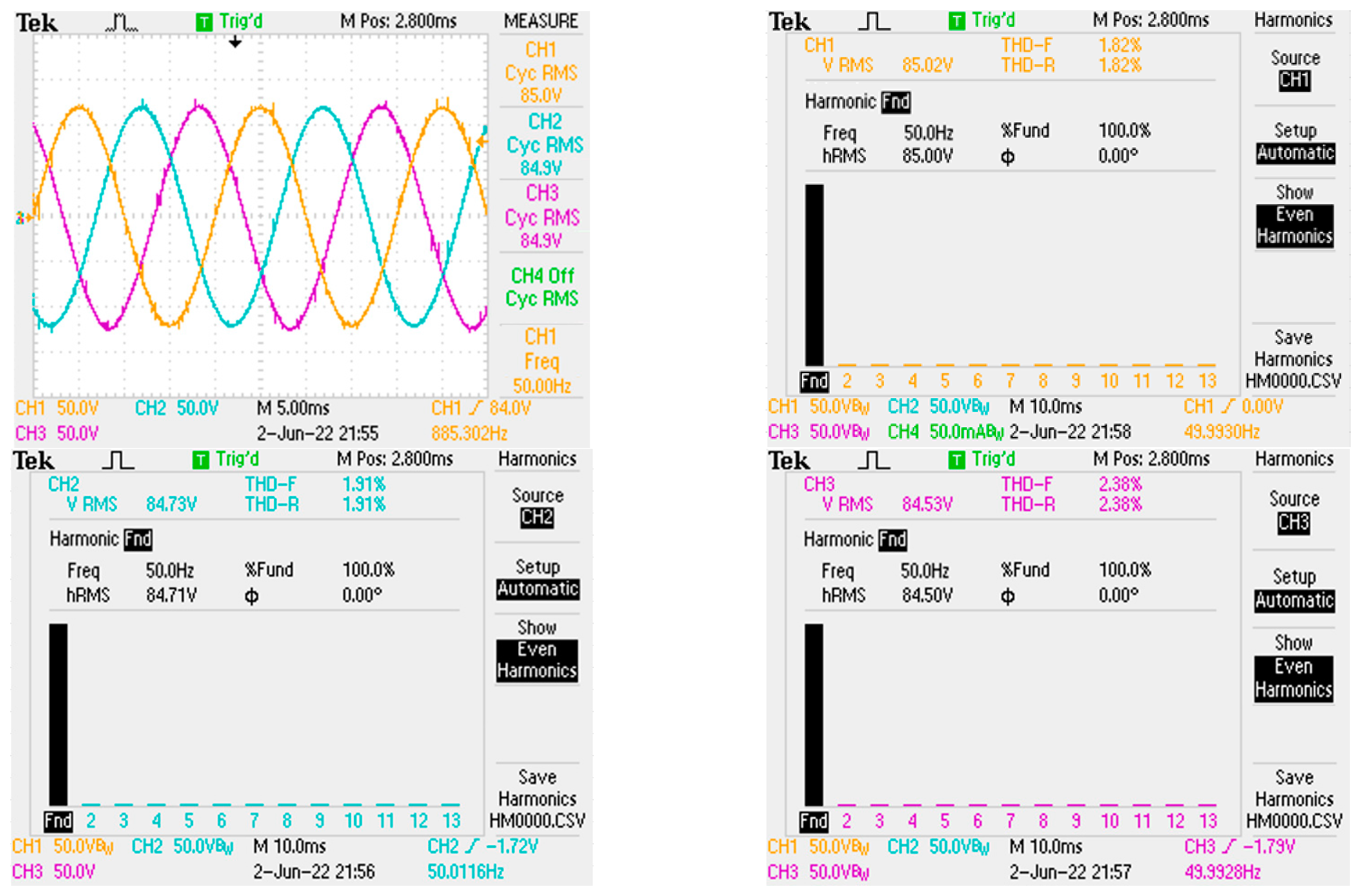

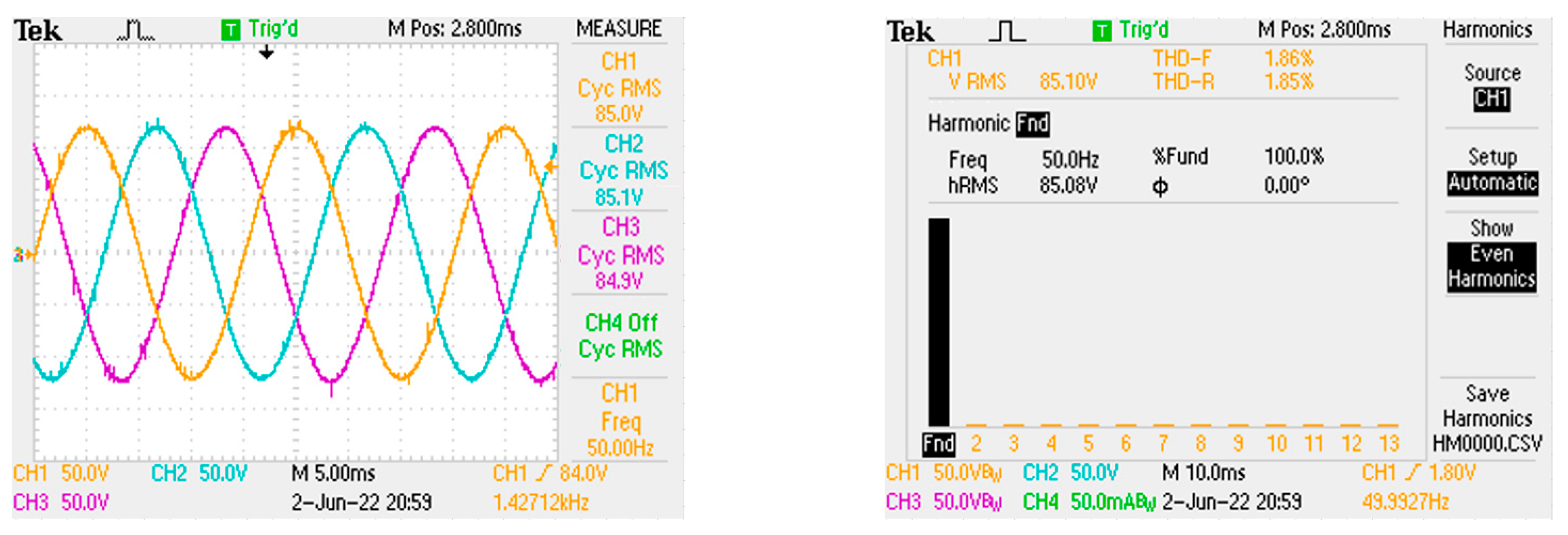
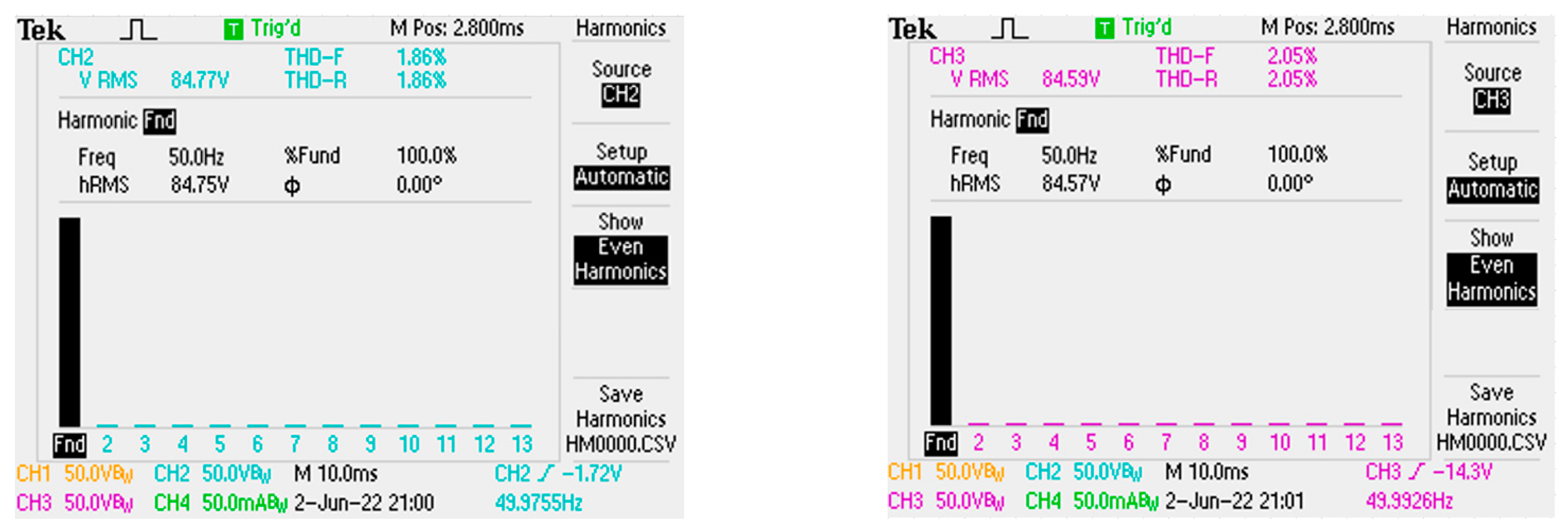

| Parameters | Value |
|---|---|
| DC-side voltage Udc | 300 V |
| Load phase voltage Uan, Ubn and Ucn | (85) 120 V |
| Filter inductance L | 2 mH |
| Filter capacitor C | 10 μF |
| Three-phase load Ra, Rb and Rc | 10 Ω, 20 Ω, 10 Ω |
| Load voltage frequency f | 50 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, F.; Miao, B.; Peng, S.; Li, M.; Wen, S. Analysis of the Mechanism and Control of the Unbalanced Operation of Three-Phase Four-Wire Inverters. Appl. Sci. 2023, 13, 12253. https://doi.org/10.3390/app132212253
Wu F, Miao B, Peng S, Li M, Wen S. Analysis of the Mechanism and Control of the Unbalanced Operation of Three-Phase Four-Wire Inverters. Applied Sciences. 2023; 13(22):12253. https://doi.org/10.3390/app132212253
Chicago/Turabian StyleWu, Fuzhuan, Binyu Miao, Sheng Peng, ManMan Li, and Shengjun Wen. 2023. "Analysis of the Mechanism and Control of the Unbalanced Operation of Three-Phase Four-Wire Inverters" Applied Sciences 13, no. 22: 12253. https://doi.org/10.3390/app132212253
APA StyleWu, F., Miao, B., Peng, S., Li, M., & Wen, S. (2023). Analysis of the Mechanism and Control of the Unbalanced Operation of Three-Phase Four-Wire Inverters. Applied Sciences, 13(22), 12253. https://doi.org/10.3390/app132212253





