Stochastic Subspace Identification-Based Automated Operational Modal Analysis Considering Modal Uncertainty
Abstract
:Featured Application
Abstract
1. Introduction
2. Stochastic Subspace Identification with Uncertainty
2.1. Stochastic Subspace Identification (SSI)
2.2. Calculation of Uncertainty
3. Automated Operational Modal Analysis Based on Modal Uncertainty
3.1. Pre-Cleaning: Removal of Spurious Modes
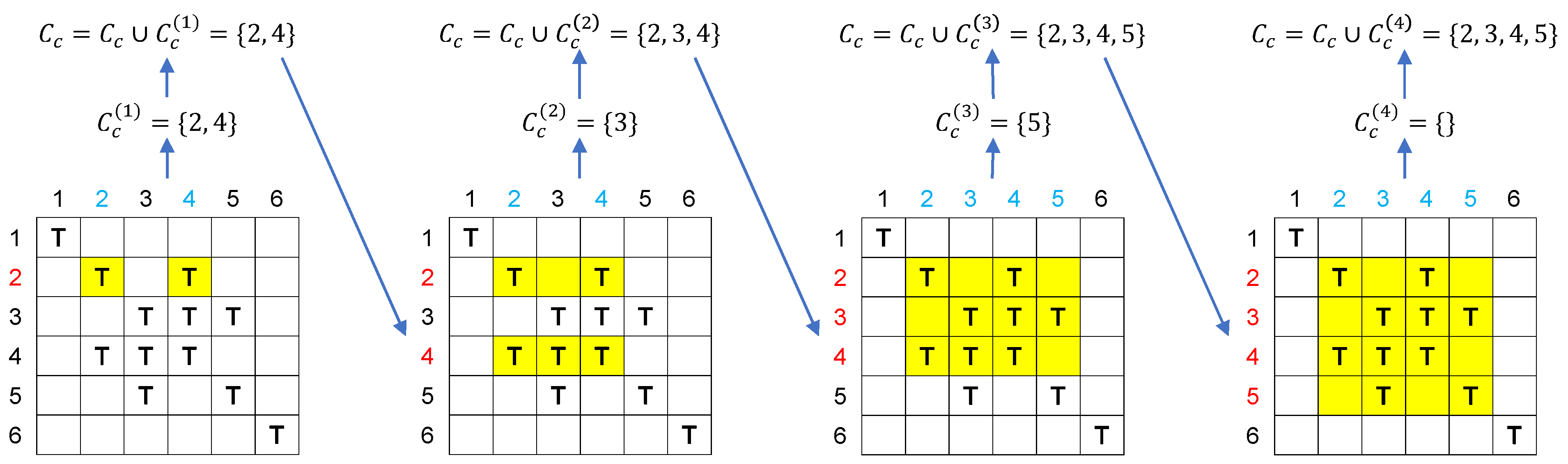
3.2. Clustering
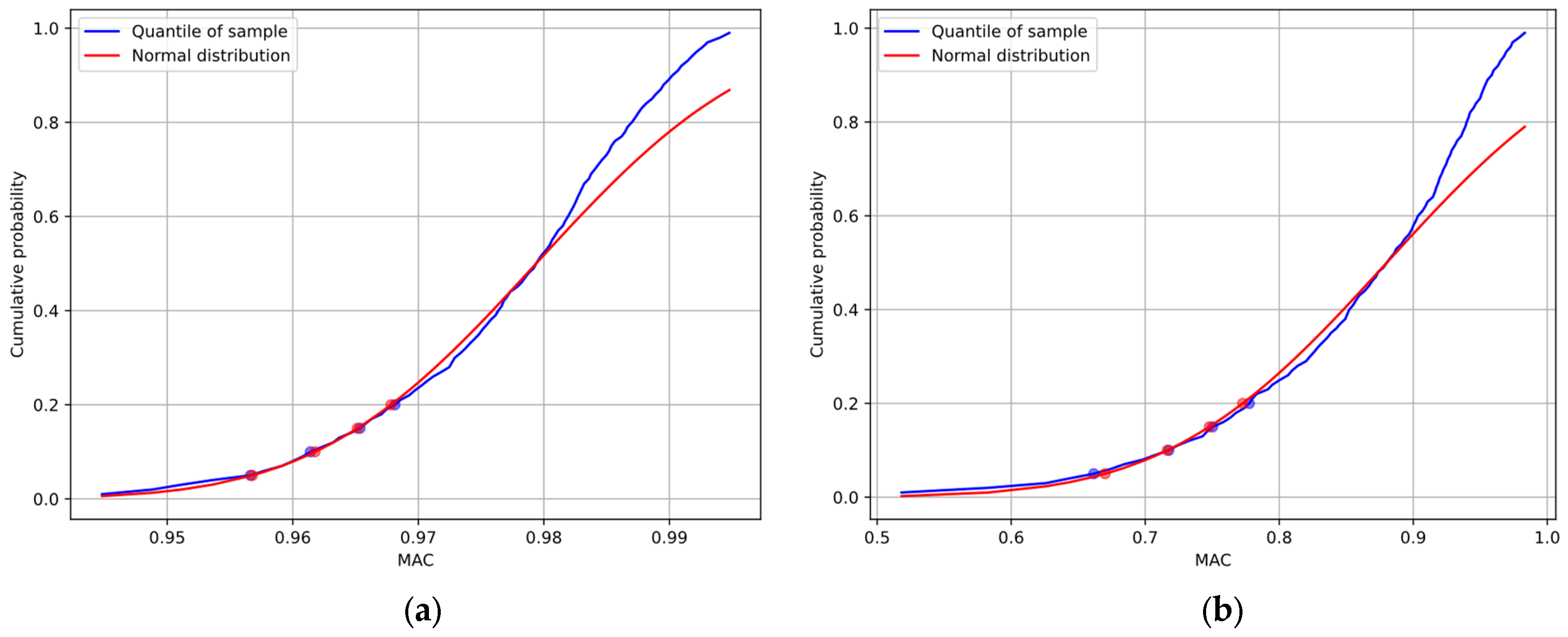
3.3. Removal of Outlier Modes
3.4. Calculation of Mode per Cluster
3.5. Discussion
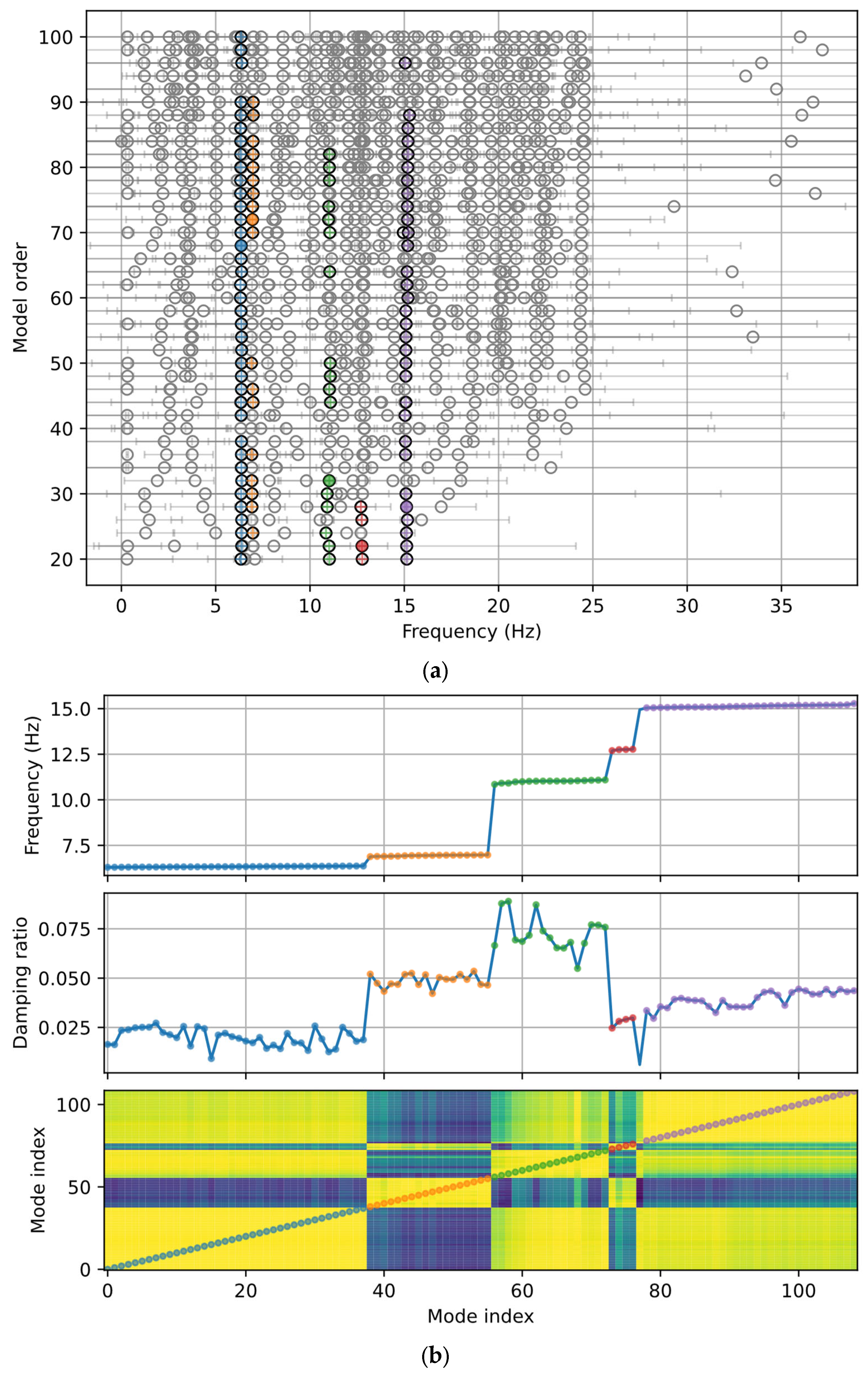
4. Case Studies
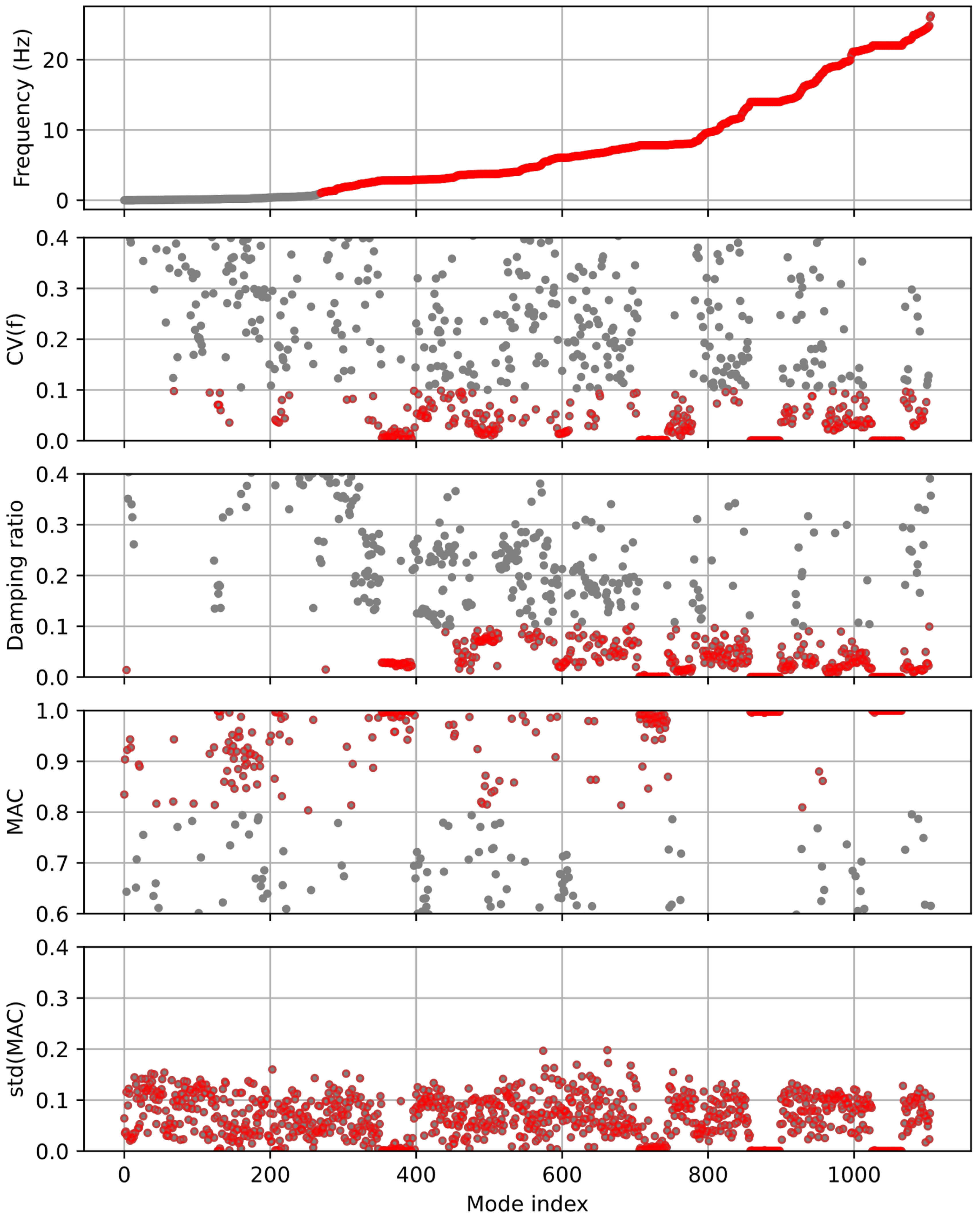
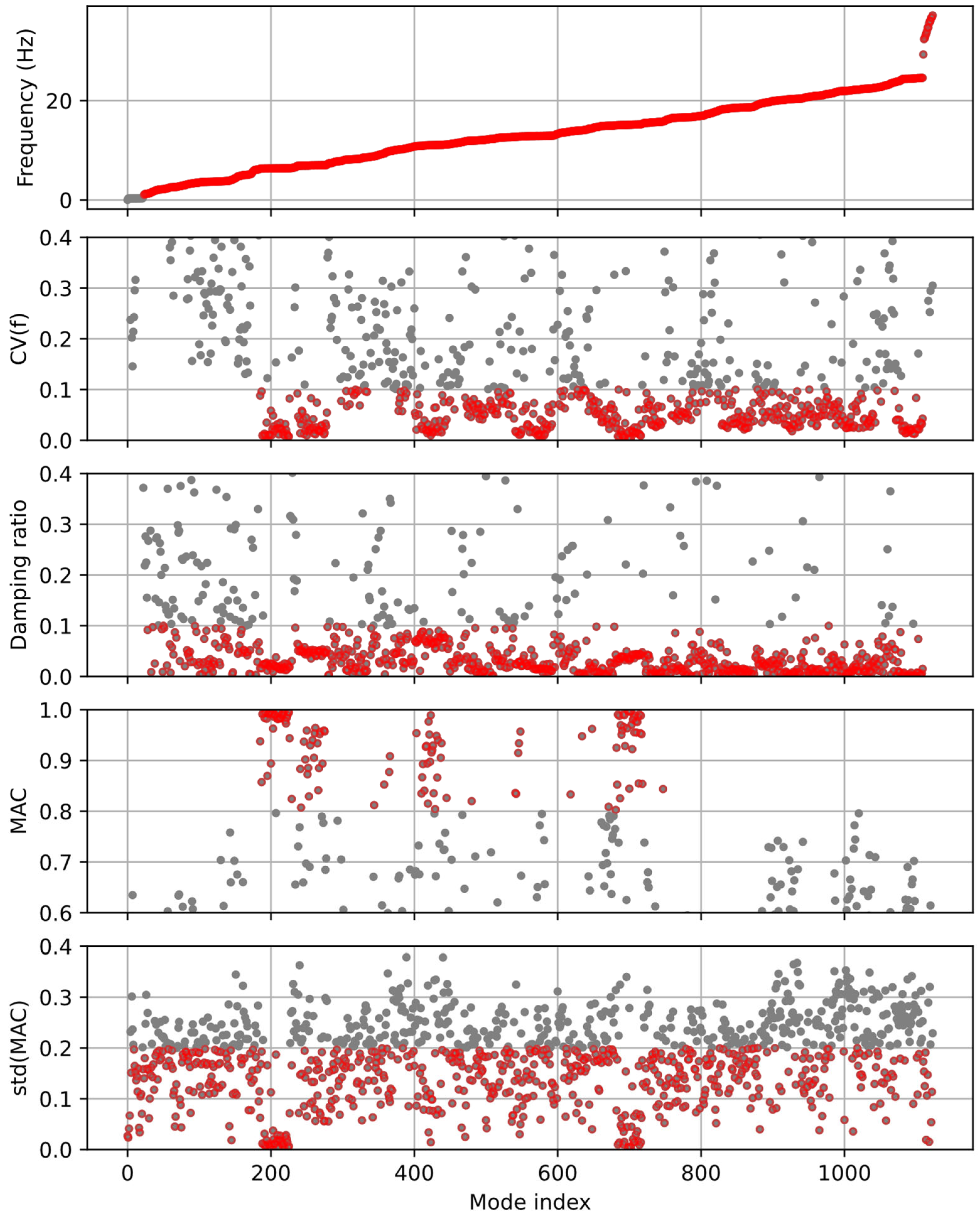
4.1. Case Study 1: Prestressed Concrete Box-Shape Girder Bridge
4.2. Case Study 2: Reinforced Concrete Rigid-Frame Bridge
4.3. Case Study 3: Prestressed Concrete I-Shape Girder Bridge
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Van Overschee, P.; De Moor, B. Subspace Identification for Linear Systems: Theory, Implementation, Applications; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Peeters, B.; De Roeck, G. Reference-based stochastic subspace identification for output-only modal analysis. Mech. Syst. Signal Process. 1999, 13, 855–878. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification from ambient responses using frequency domain decomposition. In Proceedings of the 18th International Modal Analysis Conference (IMAC), San Antonio, TX, USA, 7–10 February 2000; pp. 625–630. [Google Scholar]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441–445. [Google Scholar] [CrossRef]
- Brincker, R.; Andersen, P.; Jacobsen, N.-J. Automated frequency domain decomposition for operational modal analysis. In Proceedings of the Conference Proceedings: IMAC-XXIV: A Conference & Exposition on Structural Dynamics, St. Louis, MO, USA, 30 January–2 February 2006. [Google Scholar]
- Magalhães, F.; Cunha, Á.; Caetano, E. Dynamic monitoring of a long span arch bridge. Eng. Struct. 2008, 30, 3034–3044. [Google Scholar] [CrossRef]
- Allemang, R.J. The modal assurance criterion—Twenty years of use and abuse. Sound Vib. 2003, 37, 14–23. [Google Scholar]
- Vanlanduit, S.; Verboven, P.; Guillaume, P.; Schoukens, J. An automatic frequency domain modal parameter estimation algorithm. J. Sound Vib. 2003, 265, 647–661. [Google Scholar] [CrossRef]
- Peeters, B.; De Roeck, G. One-year monitoring of the Z24-Bridge: Environmental effects versus damage events. Earthq. Eng. Struct. Dyn. 2001, 30, 149–171. [Google Scholar] [CrossRef]
- Andersen, P.; Brincker, R.; Goursat, M.; Mevel, L. Automated modal parameter estimation for operational modal analysis of large systems. In Proceedings of the 2nd International Operational Modal Analysis Conference, Copenhagen, Denmark, 30 April–2 May 2007; pp. 299–308. [Google Scholar]
- Magalhaes, F.; Cunha, A.; Caetano, E. Online automatic identification of the modal parameters of a long span arch bridge. Mech. Syst. Signal Process. 2009, 23, 316–329. [Google Scholar] [CrossRef]
- Reynders, E.; Houbrechts, J.; De Roeck, G. Fully automated (operational) modal analysis. Mech. Syst. Signal Process. 2012, 29, 228–250. [Google Scholar] [CrossRef]
- Cabboi, A.; Magalhaes, F.; Gentile, C.; Cunha, A. Automated modal identification and tracking: Application to an iron arch bridge. Struct. Control Health Monit. 2017, 24, e1854. [Google Scholar] [CrossRef]
- Reynders, E.; Pintelon, R.; De Roeck, G. Uncertainty bounds on modal parameters obtained from stochastic subspace identification. Mech. Syst. Signal Process. 2008, 22, 948–969. [Google Scholar] [CrossRef]
- Döhler, M.; Mevel, L. Efficient multi-order uncertainty computation for stochastic subspace identification. Mech. Syst. Signal Process. 2013, 38, 346–366. [Google Scholar] [CrossRef]
- Reynders, E.; Maes, K.; Lombaert, G.; De Roeck, G. Uncertainty quantification in operational modal analysis with stochastic subspace identification: Validation and applications. Mech. Syst. Signal Process. 2016, 66–67, 13–30. [Google Scholar] [CrossRef]
- Pereira, S.; Reynders, E.; Magalhaes, F.; Cunha, A.; Gomes, J.P. The role of modal parameters uncertainty estimation in automated modal identification, modal tracking and data normalization. Eng. Struct. 2020, 224, 111208. [Google Scholar] [CrossRef]
- Greś, S.; Döhler, M.; Mevel, L. Uncertainty quantification of the modal assurance criterion in operational modal analysis. Mech. Syst. Signal Process. 2021, 152, 107457. [Google Scholar] [CrossRef]
- Greś, S.; Riva, R.; Süleyman, C.Y.; Andersen, P.; Łuczak, M.M. Uncertainty quantification of modal parameter estimates obtained from subspace identification: An experimental validation on a laboratory test of a large-scale wind turbine blade. Eng. Struct. 2022, 256, 114001. [Google Scholar] [CrossRef]
- He, Y.; Yang, J.P.; Li, Y.F. A three-stage automated modal identification framework for bridge parameters based on frequency uncertainty and density clustering. Eng. Struct. 2022, 255, 113891. [Google Scholar] [CrossRef]
- Zeng, J.C.; Hu, Z. Automated operational modal analysis using variational Gaussian mixture model. Eng. Struct. 2022, 273, 115139. [Google Scholar] [CrossRef]
- Favarelli, E.; Giorgetti, A. Machine Learning for Automatic Processing of Modal Analysis in Damage Detection of Bridges. IEEE Trans. Instrum. Meas. 2021, 70, 2504013. [Google Scholar] [CrossRef]
- Mugnaini, V.; Fragonara, L.Z.; Civera, M. A machine learning approach for automatic operational modal analysis. Mech. Syst. Signal Process. 2022, 170, 108813. [Google Scholar] [CrossRef]
- Civera, M.; Mugnaini, V.; Fragonara, L.Z. Machine learning-based automatic operational modal analysis: A structural health monitoring application to masonry arch bridges. Struct. Control Health Monit. 2022, 29, e3028. [Google Scholar] [CrossRef]
- Cheema, P.; Alamdari, M.M.; Vio, G.A.; Zhang, F.L.; Kim, C.W. Infinite mixture models for operational modal analysis: An automated and principled approach. J. Sound Vib. 2021, 491, 115757. [Google Scholar] [CrossRef]
- Reynders, E.; Roeck, G.D. Reference-based combined deterministic–stochastic subspace identification for experimental and operational modal analysis. Mech. Syst. Signal Process. 2008, 22, 617–637. [Google Scholar] [CrossRef]
- Rainieri, C.; Fabbrocino, G.; Cosenza, E. Near real-time tracking of dynamic properties for standalone structural health monitoring systems. Mech. Syst. Signal Process. 2011, 25, 3010–3026. [Google Scholar] [CrossRef]
- Ubertini, F.; Gentile, C.; Materazzi, A.L. Automated modal identification in operational conditions and its application to bridges. Eng. Struct. 2013, 46, 264–278. [Google Scholar] [CrossRef]






| Pre-Cleaning Criteria | Criteria for Clustering and Removal of Outliers |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, K.; Cho, J.-R. Stochastic Subspace Identification-Based Automated Operational Modal Analysis Considering Modal Uncertainty. Appl. Sci. 2023, 13, 12274. https://doi.org/10.3390/app132212274
Cho K, Cho J-R. Stochastic Subspace Identification-Based Automated Operational Modal Analysis Considering Modal Uncertainty. Applied Sciences. 2023; 13(22):12274. https://doi.org/10.3390/app132212274
Chicago/Turabian StyleCho, Keunhee, and Jeong-Rae Cho. 2023. "Stochastic Subspace Identification-Based Automated Operational Modal Analysis Considering Modal Uncertainty" Applied Sciences 13, no. 22: 12274. https://doi.org/10.3390/app132212274
APA StyleCho, K., & Cho, J.-R. (2023). Stochastic Subspace Identification-Based Automated Operational Modal Analysis Considering Modal Uncertainty. Applied Sciences, 13(22), 12274. https://doi.org/10.3390/app132212274







