Study of Load Calculation Models for Anti-Sliding Short Piles Using Finite Difference Method
Abstract
:1. Introduction
2. Structural Calculation Model for Anti-Sliding Short Piles
2.1. Basic Assumptions
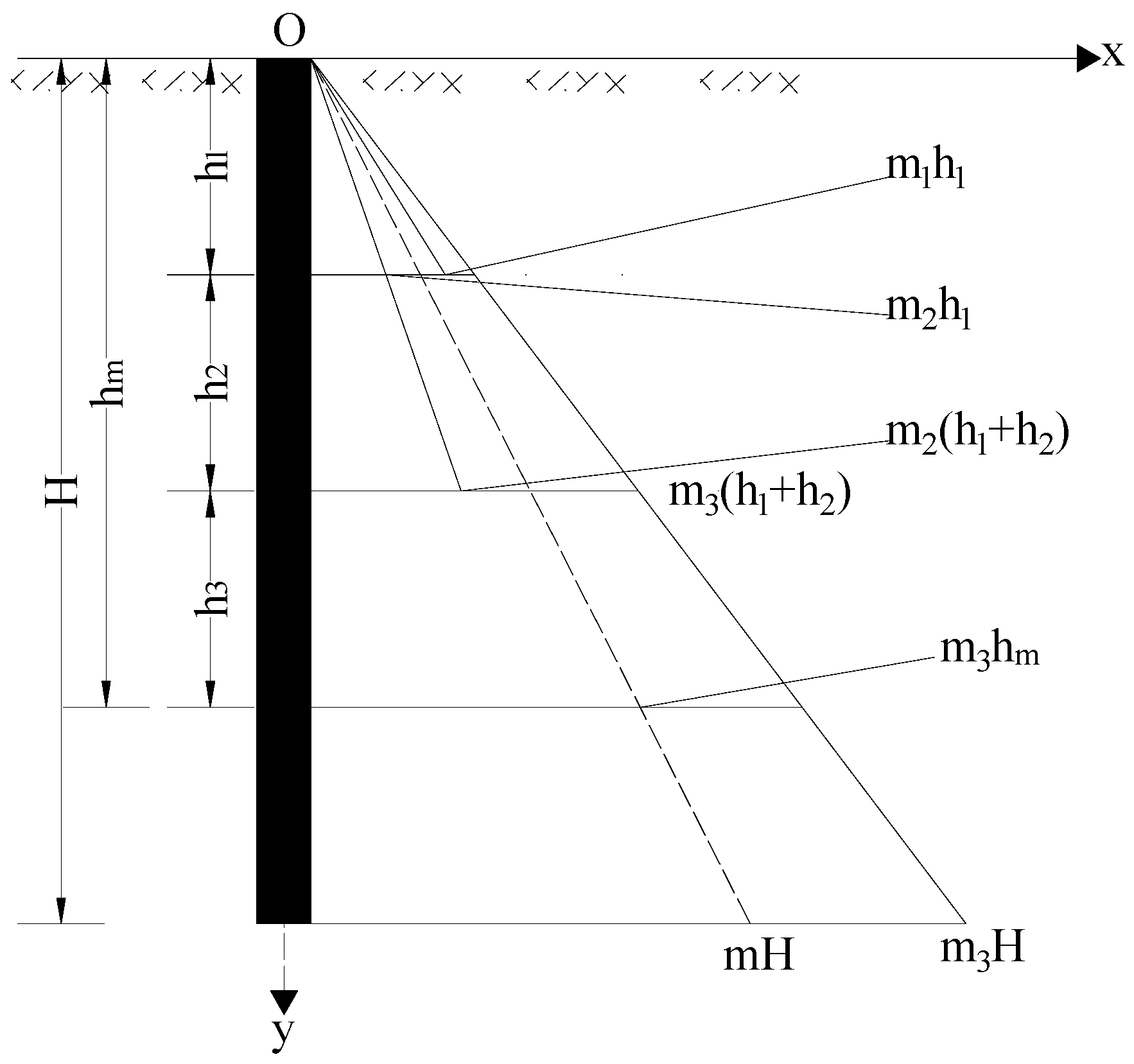
2.2. Analysis of the Forces on Anti-Sliding Short Piles
2.3. Finite Difference Solution for the Anti-Sliding Short Pile Model
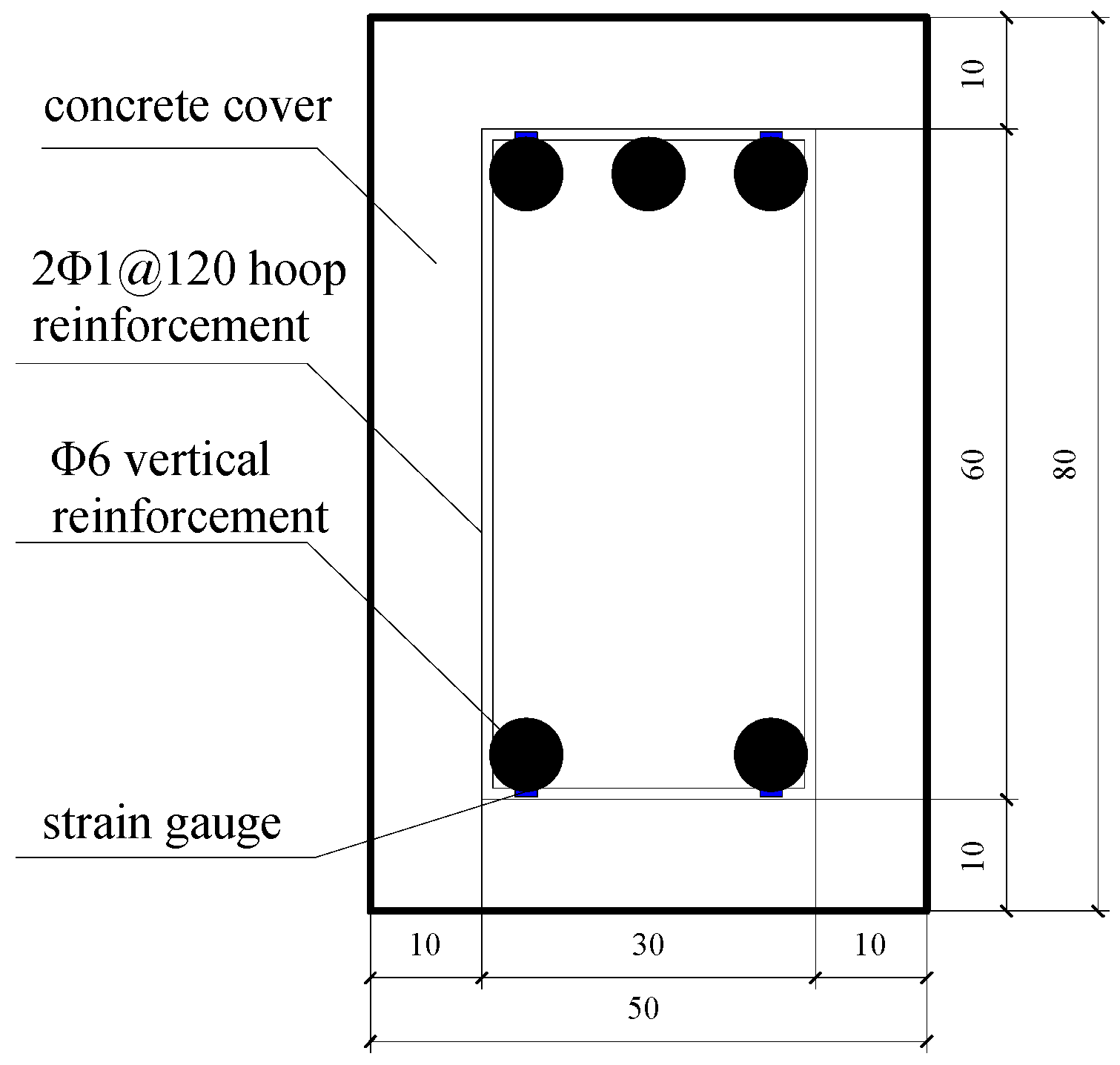
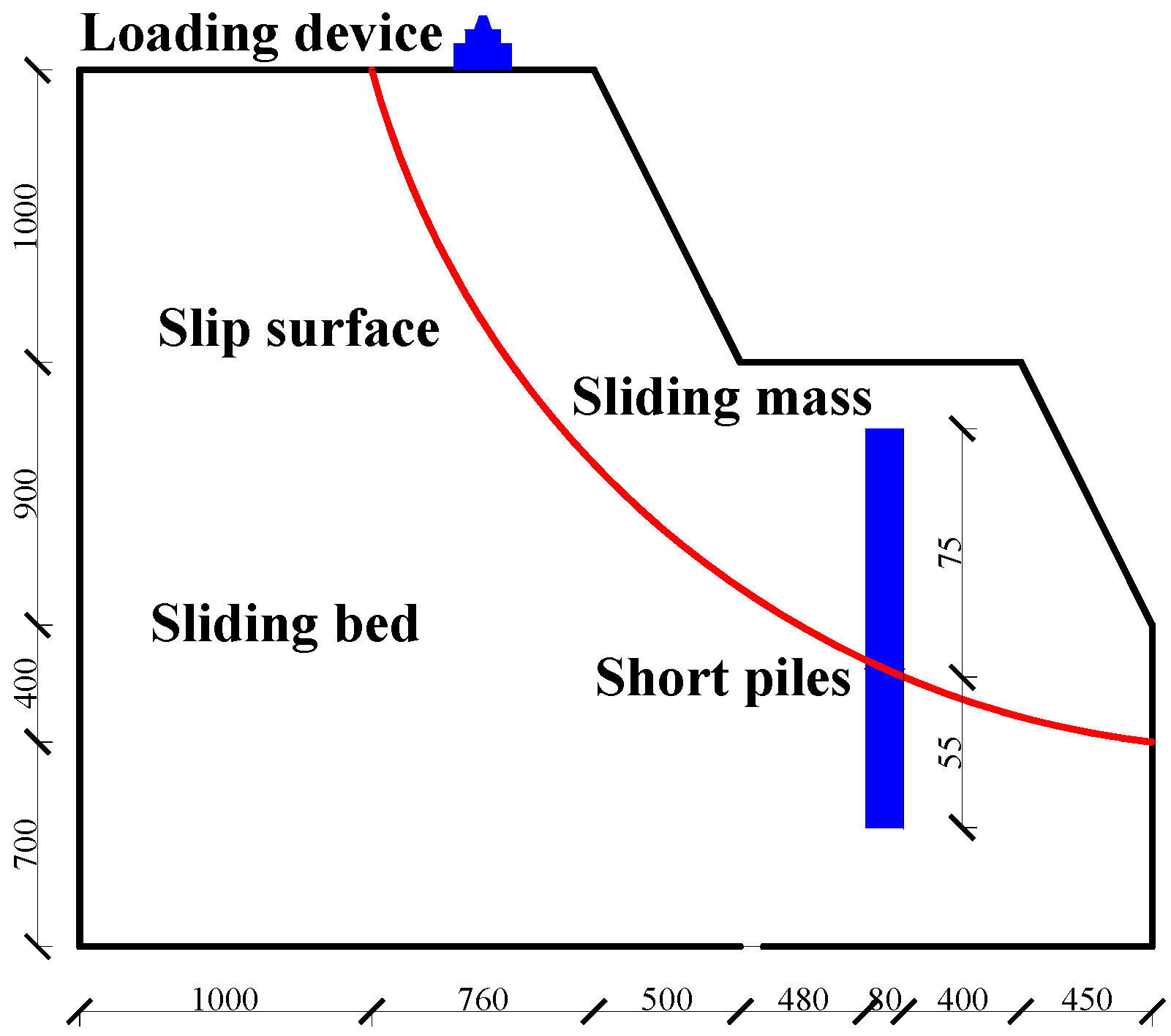
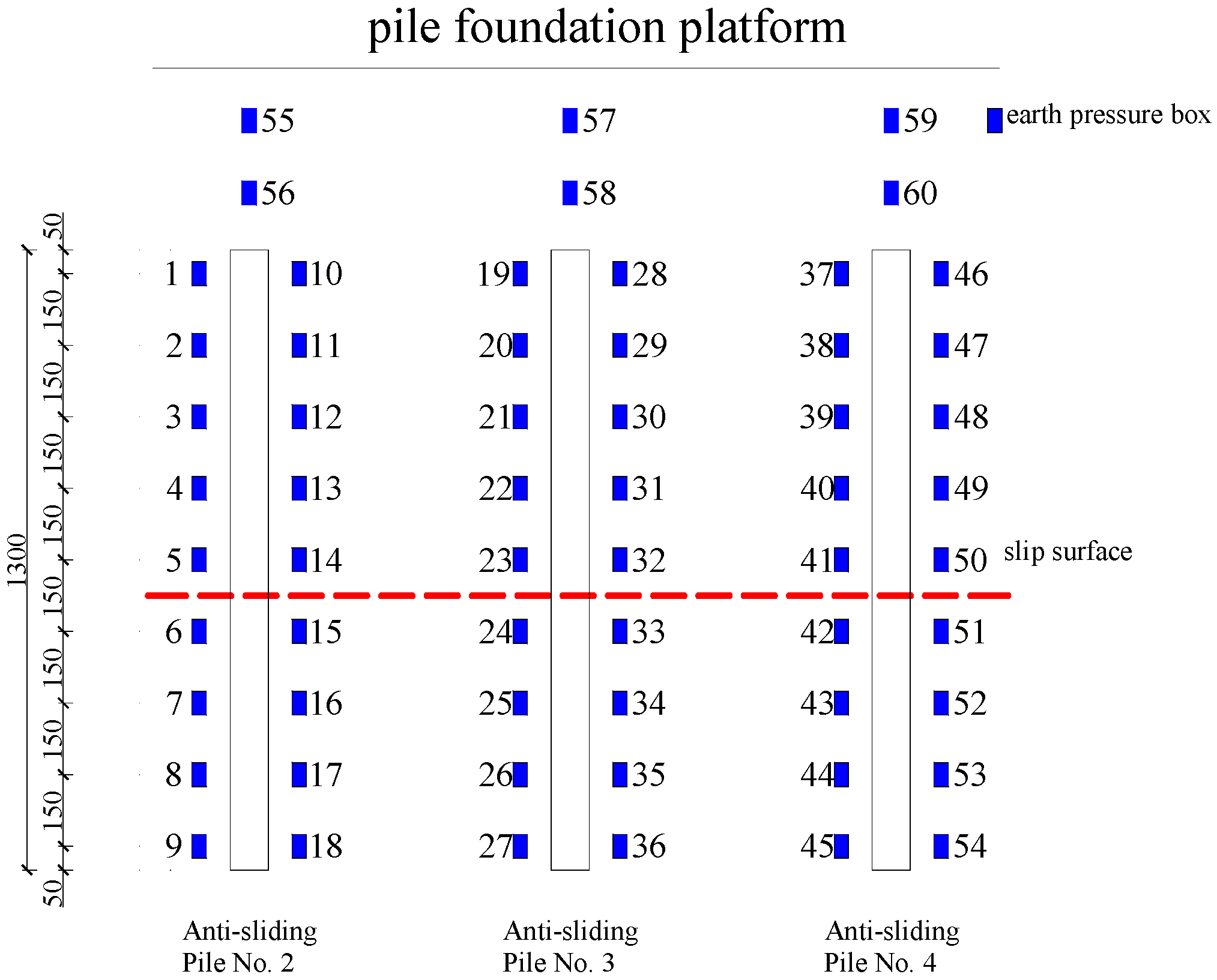
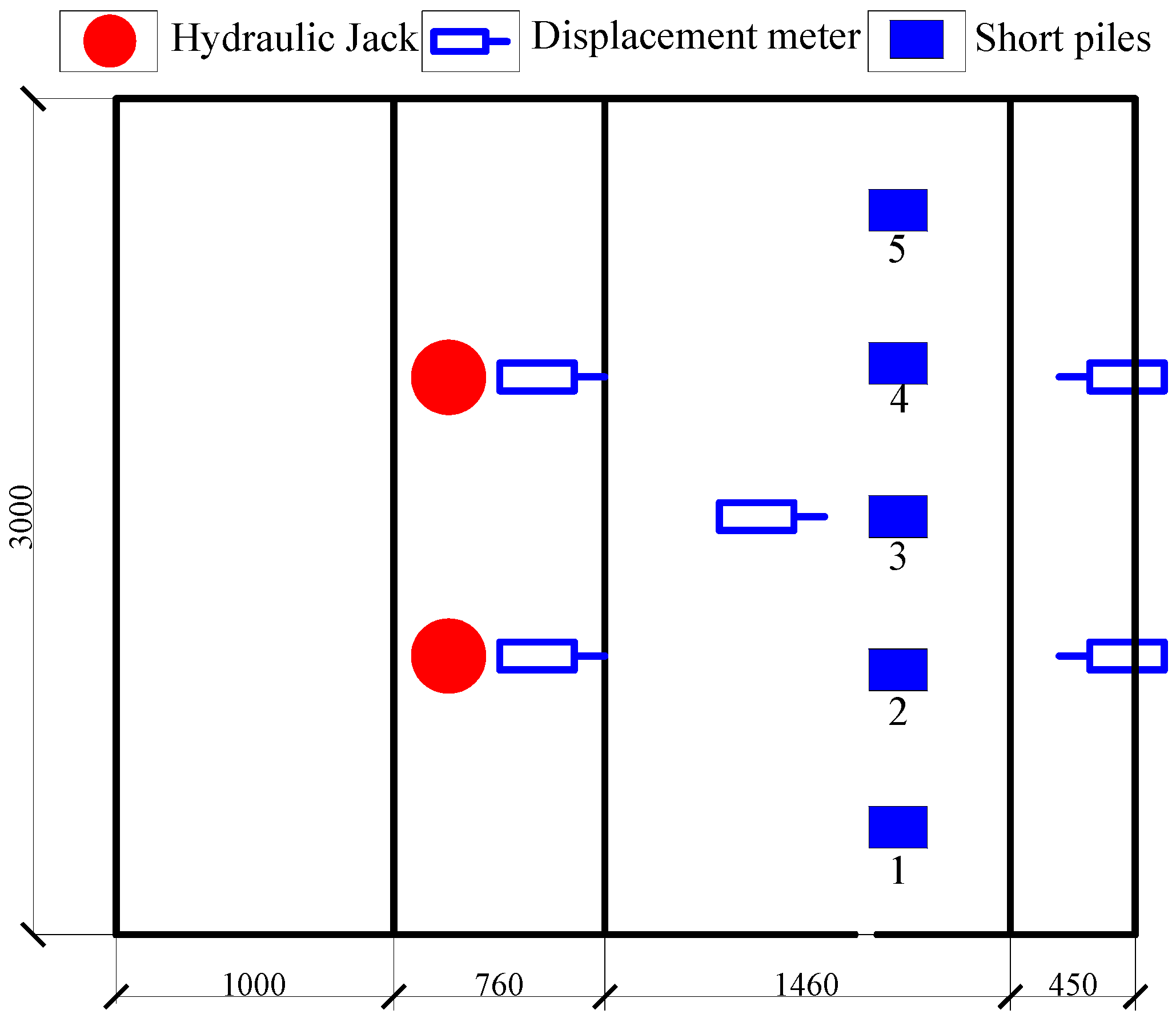
3. Model Experiment
3.1. Experimental Design
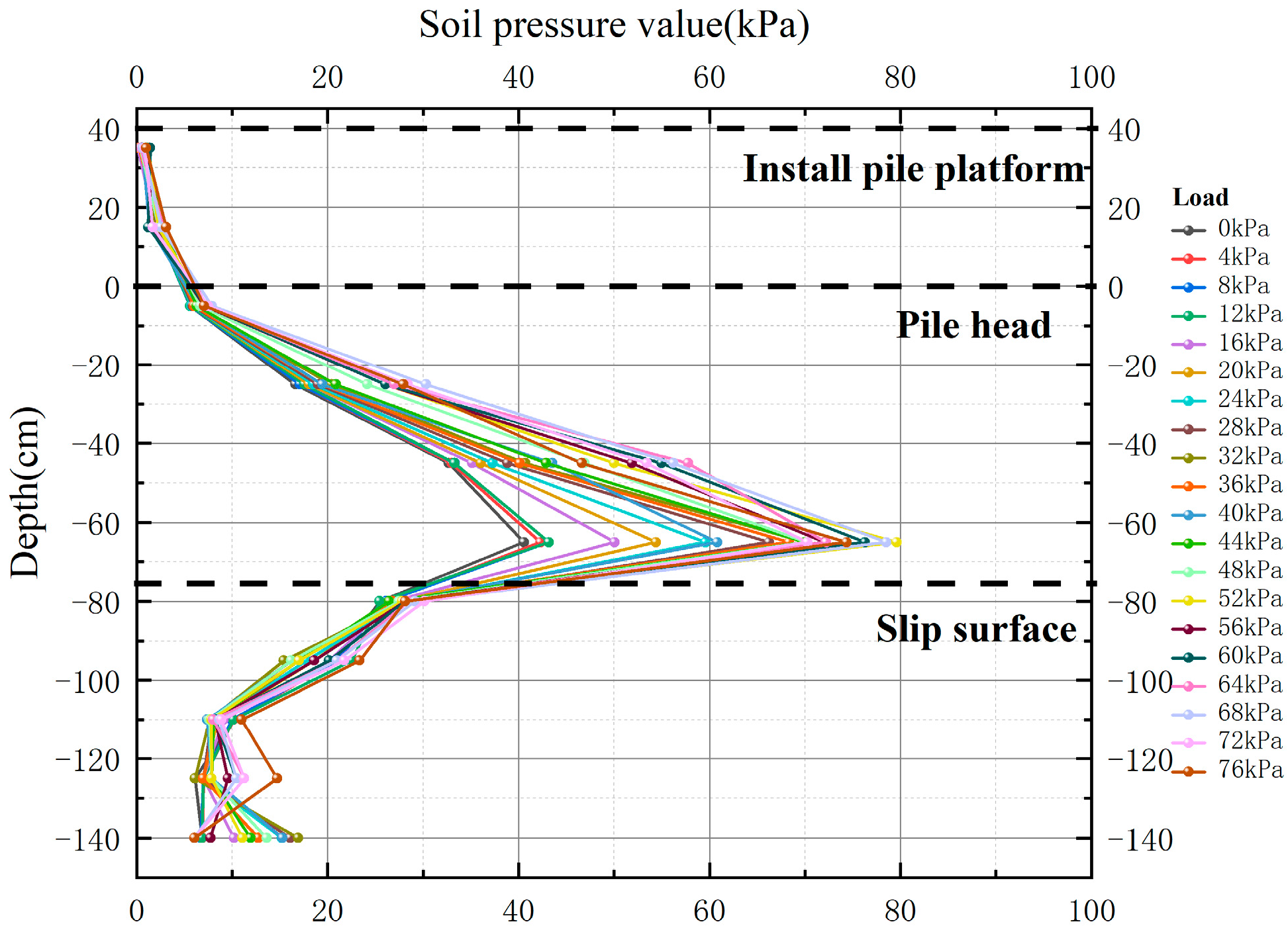
3.2. Analysis of Experiment Results
4. Data Comparison
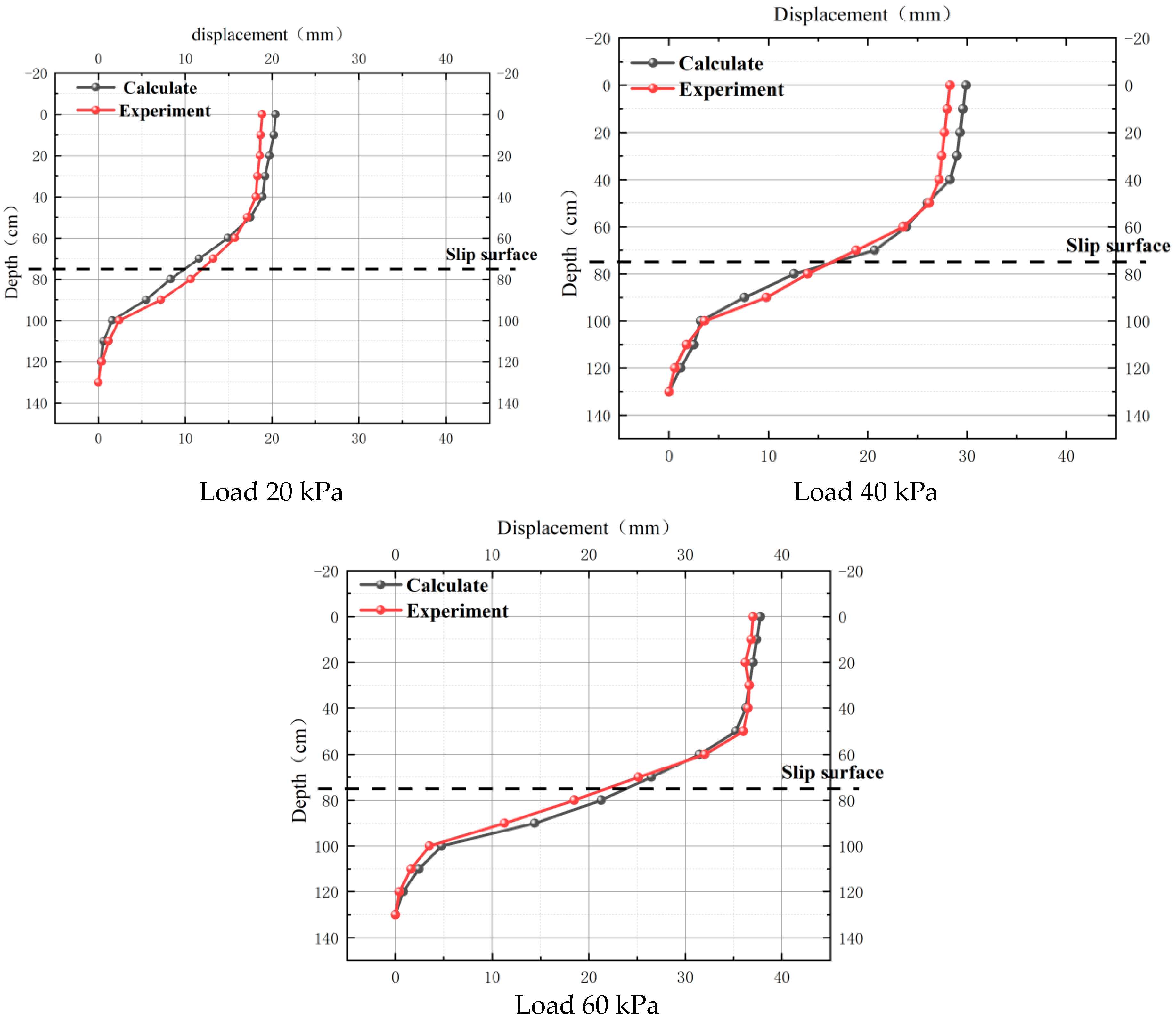
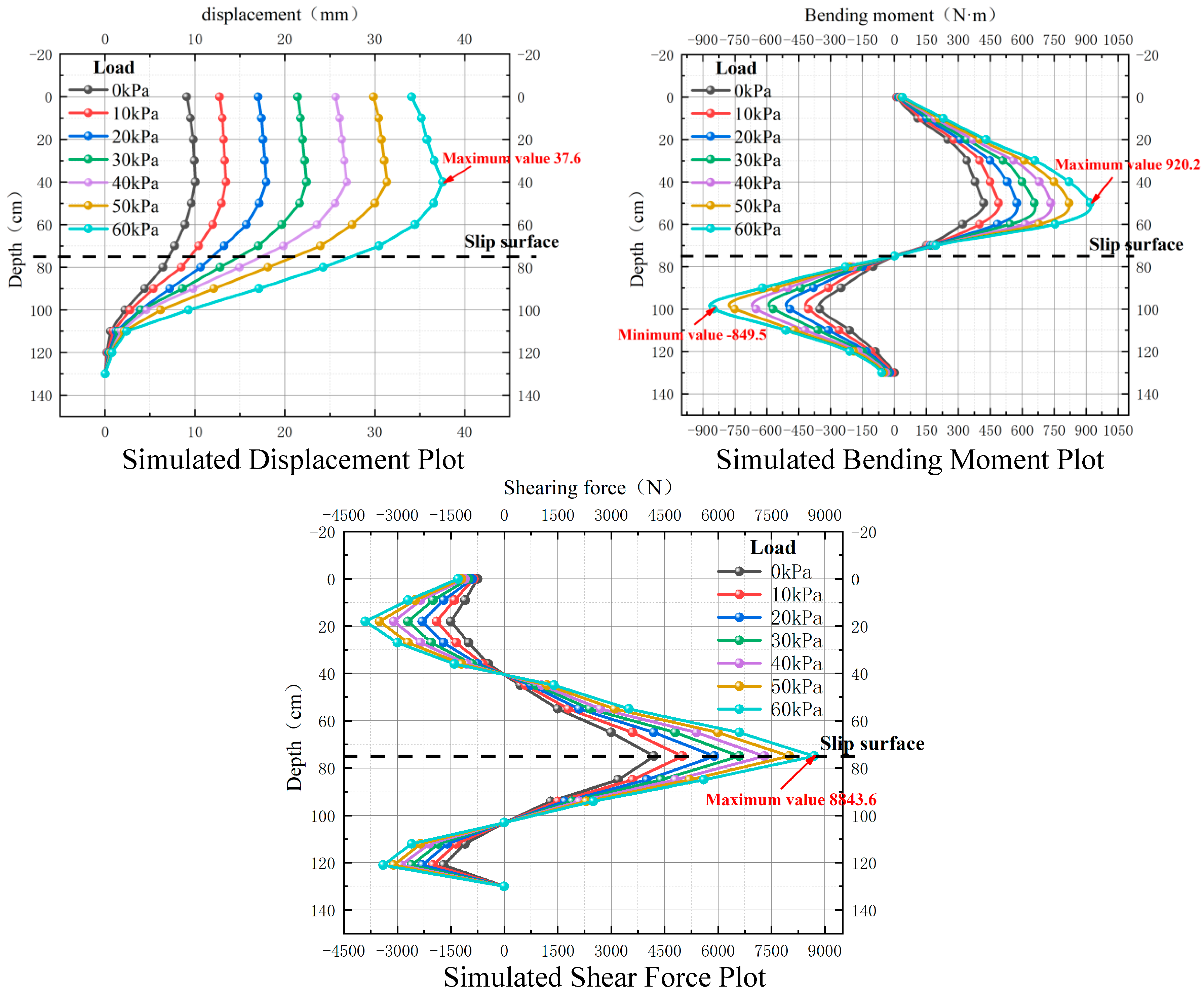
4.1. Comparison of Pile Head Displacement
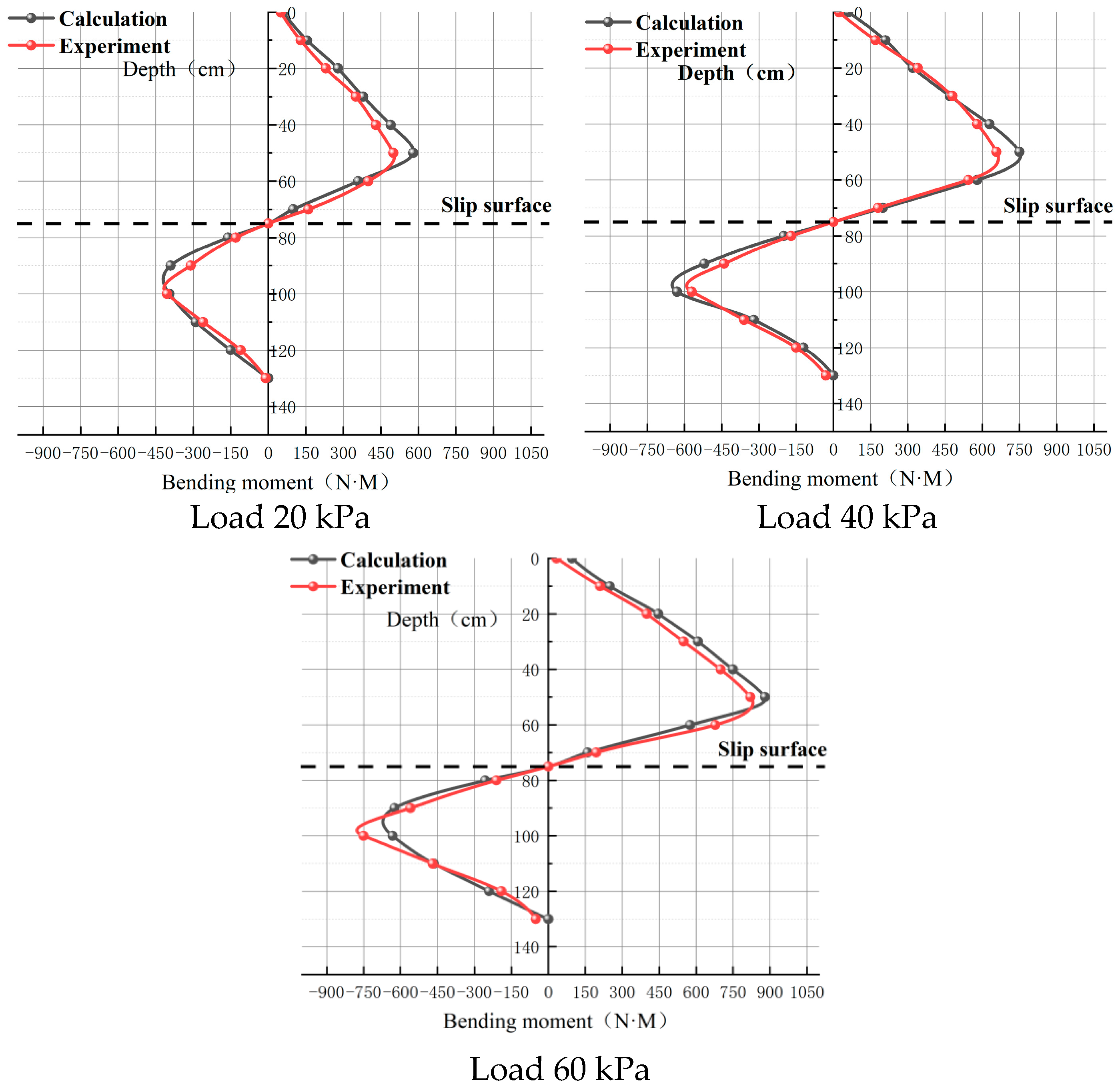
4.2. Comparison of Bending Moments
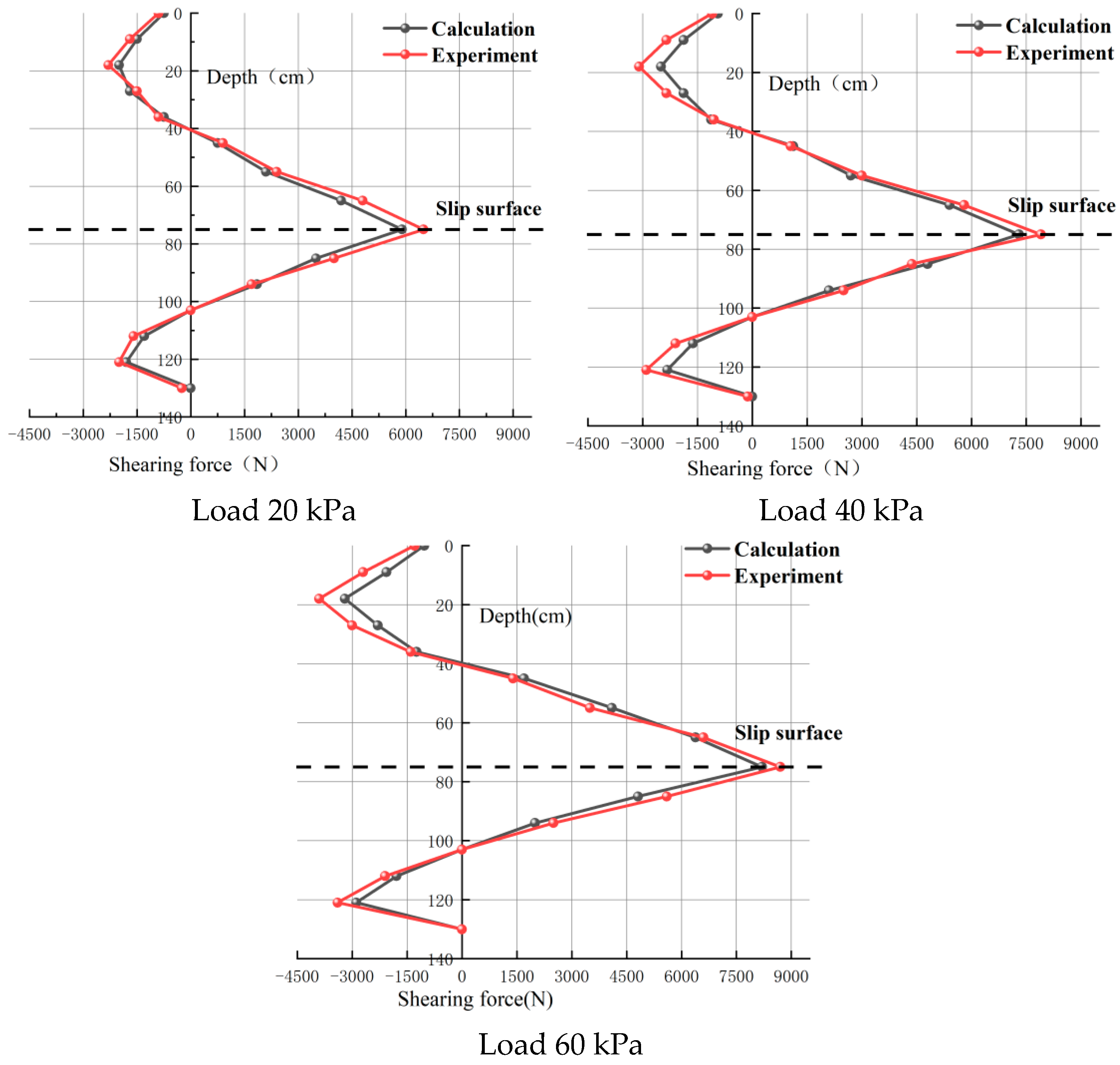
4.3. Shear Force Comparison
5. Discussion
5.1. The Calculation Method for ‘m’ in Multilayered Foundations
5.2. Numerical Simulation of Anti-Slip Short Piles
6. Conclusions
- (1)
- Leveraging the Euler–Bernoulli beam theory, this study formulates a finite difference calculation model tailored for short anti-slide piles. Equation (10) enables the unified calculation of internal forces across the entire pile. This method obviates the requirement for intricate iterative computations between the load-bearing and embedded sections while relying on continuous conditions, thereby markedly enhancing computational efficiency.
- (2)
- Both experimental and calculated data demonstrate that short anti-slide piles undergo three discernible stages of displacement variation when subjected to identical loading conditions. The distribution of bending moments along the pile follows an “S” shape, with the maximum bending moments occurring in proximity to the sliding surface. Simultaneously, shear values peak at the sliding surface, while they attain zero values at positions corresponding to maximum positive and negative bending moments. These observations suggest that short anti-slide piles effectively strengthen the soil in the vicinity of the sliding surface.
- (3)
- The finite difference calculation model is utilized to independently compute displacements, bending moments, and shear values, subsequently subjecting them to comparison with experimental data. The observed discrepancies fall within an acceptable range, affirming the reliability and precision of the calculation model introduced in this paper. This novel approach offers a rapid method for determining the internal forces across short anti-slide piles. The study underscores the significance of the stress analysis model for short anti-slide piles in advancing sustainable engineering practices. It furnishes insights into the stress state and distribution patterns of short anti-slide piles, thereby providing valuable references for geological disaster prevention and control, as well as the promotion of sustainable engineering practices.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K.-T. Landslide inventory maps: New tools for an old problem. Earth-Sci. Rev. 2012, 112, 42–66. [Google Scholar] [CrossRef]
- Lei, Y.; Zheng, Y.; Chen, K. Discussion on the Concept of ‘Anti-Slide Short Piles’ and Its Influence on Force. J. Undergr. Space Eng. 2009, 5, 608–615. [Google Scholar]
- Li, X.; Gong, Z.; Zhou, C.; Chen, Q.; He, Y. Numerical Simulation of Slope Reinforcement by Anti-Slide Short Piles with Vertical Reinforcement Bands. J. Water Resour. Archit. Eng. 2022, 20, 124–129. [Google Scholar]
- Fu, X.; Xie, Q.; Zhang, Y.; Qiu, P.; Wan, R. Indoor Model Test Study on Overturned Failure of Fully Buried Anti-Slide Piles. Rock Soil Mech. 2014, 35, 2205–2211+2218. [Google Scholar] [CrossRef]
- Zeng, H.; Han, L.; Zhou, C.; Liu, W.; Tan, C. Model Test and Numerical Analysis of Anti-Slide Pile Reinforced Soil Slopes. Chin. J. Geotech. Eng. 2020, 42 (Suppl. S1), 132–136. [Google Scholar]
- Li, Z.; Zhu, Z.; Zhang, J.; Cao, S.; Li, Y. In-Situ Model Tests of Cantilever and Fully Buried Single-Row Two-Pile Anti-Slide Piles on Loess Slopes. China J. Highw. Transp. 2020, 33, 14–23. [Google Scholar]
- Yang, X.L.; Yin, J.H. Slope stability analysis with nonlinear failure criterion. J. Eng. Mech. 2004, 130, 267–273. [Google Scholar] [CrossRef]
- Itasca Consulting Group Inc. FLAC3D (Fast Lagrangian Analysis of Continua in Three-Dimensions), version 2.1. User’s Manual. Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2002.
- Hu, J. Research on Analytical Calculation Method and Mechanical Properties of Ultra-Long Anti-Slide Piles. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2015. [Google Scholar]
- Won, J.; You, K.; Jeong, S.; Kim, S. Coupled Effects in Stability Analysis of Pile-Slope Systems. Comput. Geotech. 2005, 32, 304–315. [Google Scholar] [CrossRef]
- Lane, P.A.; Griffiths, D.V. Assessment of Stability of Slopes under Drawdown Condition. J. Geotech. Geoenviron. Eng. 2000, 126, 443–450. [Google Scholar] [CrossRef]
- Ashour, M.; Ardalan, H. Analysis of Pile Stabilized Slopes Based on Soil-Pile Interaction. Comput. Geotech. 2012, 39, 85–97. [Google Scholar] [CrossRef]
- Lei, Y.; Jiang, W.; Deng, X. Numerical Analysis of Horizontal Resistance of Anti-Slide Piles in Rock Slopes. In Proceedings of the Annual Conference of the Chinese Society of Civil Engineering, Chongqing, China, 2 November 2007; pp. 756–760. [Google Scholar]
- Liang, R.; Zeng, S. Numerical study of soil arching mechanism in drilled shafts for slope stabilization. Soils Found. 2002, 42, 83–92. [Google Scholar] [CrossRef]
- Vermeer, P.A.; Punlor, A.; Ruse, N. Arching Effects Behind a Soldier Piles. Geotech. Investig. Surv. 2009, 8–13, 33. [Google Scholar] [CrossRef]
- Wei, Y.; Fu, W.; Ye, F. Estimation of the equivalent Mohr–Coulomb parameters using the Hoek–Brown criterion and its application in slope analysis. Eur. J. Environ. Civ. Eng. 2021, 25, 599–617. [Google Scholar] [CrossRef]
- Chen, C.Y.; Martin, G.R. Soil structure interaction for landslide stabilizing piles. Comput. Geotech. 2002, 29, 363–386. [Google Scholar] [CrossRef]
- Hu, S.; Cai, Q.; Li, Q.; Zhang, Y.; Shi, S. Three-Dimensional Numerical Simulation Analysis of Model Test on Reinforcement of Landslide by Anti-Slide Piles. J. Eng. Geol. 2018, 26, 969–977. [Google Scholar] [CrossRef]
- Dai, Z.; Peng, Z. Finite Difference Method for Internal Force Calculation of Anti-Slide Piles ‘m-k’ Method. Rock Soil Mech. 2002, 23, 5. [Google Scholar]
- Liu, D.; Liao, X.; Wang, H.; Cheng, J. Finite Difference Method for Full-Pile Calculation of Anti-Slide Piles. J. Geol. Hazards Prev. 2007, 42–46. [Google Scholar] [CrossRef]
- Dai, Z.; Wang, Y.; Lu, C. Numerical Solution of Comprehensive Stiffness and Two-Parameter System of Horizontal Load Pile Calculation. Chin. J. Rock Mech. Eng. 2016, 35, 2115–2123. [Google Scholar]
- Wang, Y.; Zhao, B.; Wang, Q.; Hua, X.; Zhai, Y. H-Type Anti-Slide Pile Structural Calculation Model Based on Finite Difference Method. J. Disaster Prev. Mitig. Eng. 2015, 35, 464–470. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, L.; Song, X.; Guo, S.; Yan, M. Finite Difference Method for Calculating the Anti-Slide Pile of Drilled Rigid Frame in Stratified Soil Foundation. Railw. Stand. Des. 2023, 1–9. [Google Scholar] [CrossRef]
- Dai, Z.; Shen, P.; Peng, Z. New Mode of Elastic Anti-Slide Pile Internal Force Calculation and Its Finite Difference Solution. China Civ. Eng. J. 2003, 36, 6. [Google Scholar]
- Fan, Q.Y.; Wang, M.Q.; Xu, S.C. Calculation on the Internal Force of Deeply Buried Anti-Slide Pile by Using Finite Difference Method Based on the m-k Type Method. AMM 2011, 130, 128–134. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, X. Computer-Aided Design of Anti-Slide Piles Based on Finite Difference Method. J. Geol. Hazards Prev. 2006, 17, 4. [Google Scholar]
- TB10093–2017; Code for the Design of Foundation and Foundation of Railway Bridge and Culvert. China Railway Publishing House: Beijing, China, 2017.
- JTG 3363-2019; Introduction to the Revision of the ‘Code for Design of Foundations and Foundations of Highway Bridges and Culverts’. Ministry of Transport of the People’s Republic of China: Beijing, China, 2021; Volume 66, pp. 162–164.
- Dai, Z.; Chen, L. Two Numerical Solutions for the Horizontal Load Pile Calculation ‘m Method’ in Multilayer Ground. J. Rock Mech. Eng. 2007, 29, 690–696. [Google Scholar]
- Dai, Z. Study on the Distribution of Landslide Thrust and Pile Front Resistance of Anti-Slide Pile. Chin. J. Rock Mech. Eng. 2002, 21, 517–521. [Google Scholar]
- Zhang, X.; He, S.; Yin, P. Optimization Design of Embedded Anti-Slide Pile. China Civ. Eng. J. 2012, 45, 143–149. [Google Scholar]
- Zhang, H.; Song, X.; Guo, S. Improved Finite Difference Method for Anti-Slide Pile Calculation under Layered Soil Conditions. Railw. Stand. Des. 2023, 1–7. [Google Scholar] [CrossRef]
- Lei, Y.; Xu, J.; Zheng, Y. Study on the Applicability of Anti-Slide Piles. J. Undergr. Space Eng. 2010, 6 (Suppl. S2), 1647–1651+1664. [Google Scholar]
- Yang, S.; Ren, X.; Zhang, J. Study on Embedded Length of Piles for Slope Reinforced with One Row of Piles. J. Rock Mech. Geotech. Eng. 2011, 3, 167–178. [Google Scholar] [CrossRef]
- Yan, Y.P.; Xiao, S.G. Physical Model Testing of Rear Thrust Distribution of Double-Row Anti-Slide Piles. J. Geol. Hazards Prev. 2022, 33, 79–87. [Google Scholar] [CrossRef]
- Luo, X.; Song, C.; Yao, W.; Kou, H.; He, X. Load-Deformation Characteristics and Application Research of Composite Multilayered Soil Slope Combination Circular Section Anti-Slide Pile. Saf. Environ. Eng. 2023, 30, 120–130+140. [Google Scholar] [CrossRef]
- Lee, H.P. Dynamic of a Timoshenko Beam on a Winkler Foundation Subjected to a Moving Mass. Appl. Acoust. 1998, 55, 203–204. [Google Scholar] [CrossRef]
- Yang, T.; Zhou, D.; Zhang, J.; Feng, J. Determination of the Calculation Form of Thrust Distribution for Anti-Slide Piles in Landslide. Chin. J. Geotech. Eng. 2006, 03, 322–326. [Google Scholar]
- Huang, S. Similarity Study of Small-Scale Models for Reinforced Concrete Structures. Ph.D. Thesis, Institute of Engineering Mechanics, China Earthquake Administration, Beijing, China, 2008. [Google Scholar]
- Xu, W.; Wu, S.; Yang, C.; Guo, Z.; Qu, X. Experimental Study on Proportioning of Similar Materials with Different Water-to-Cement Ratios. Powder Coal Ash Compr. Util. 2022, 38, 86–91. [Google Scholar]










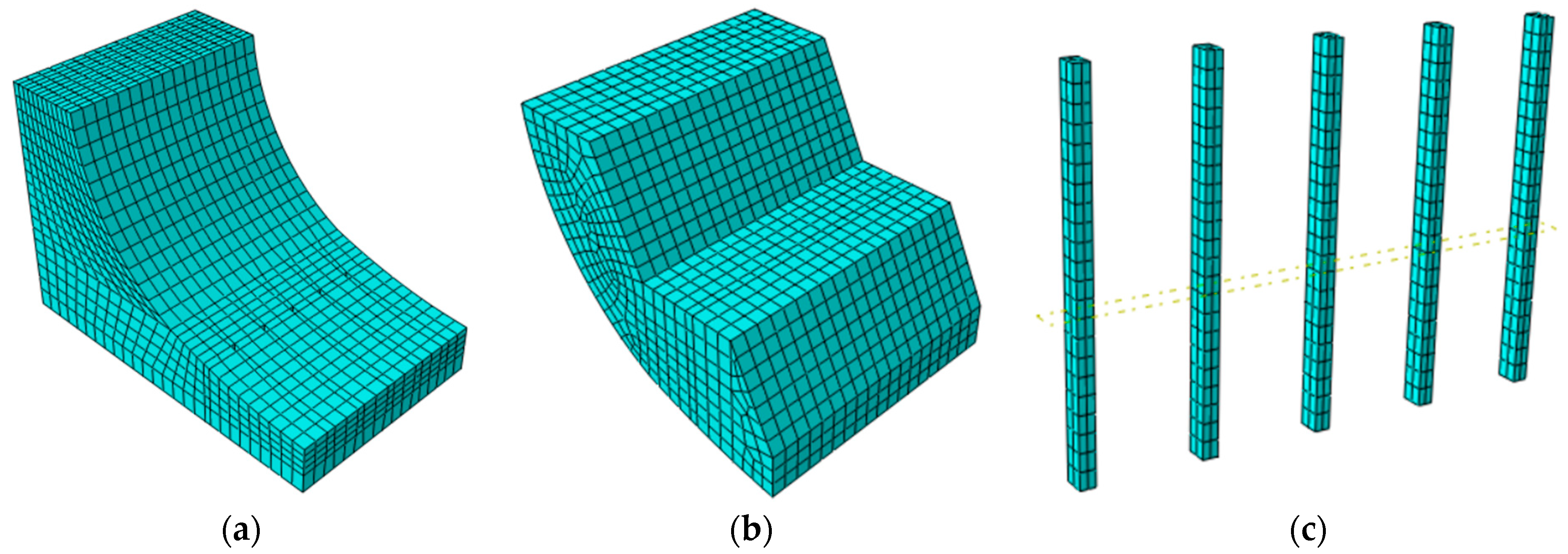
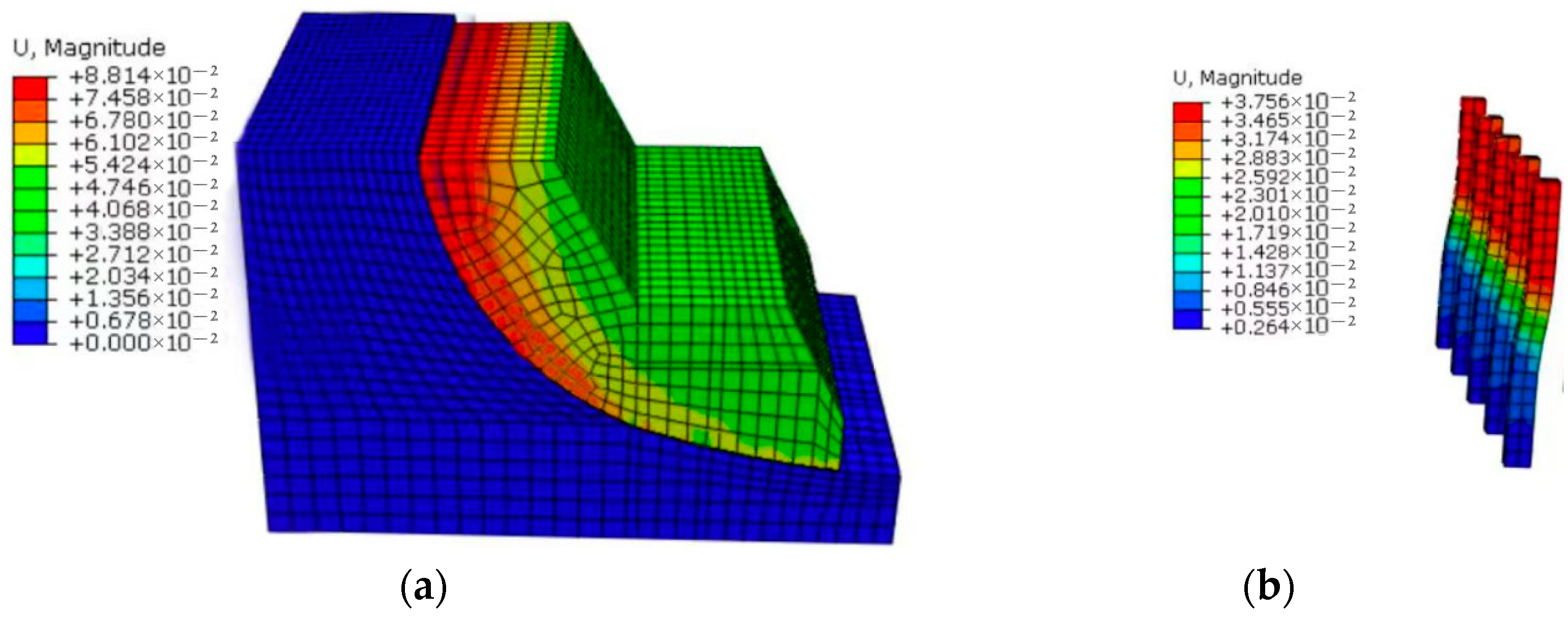
| Type | Simulation Quantity | Dimension | General Model | Practical Model | Experiment Model |
|---|---|---|---|---|---|
| Material property | Stress σ | FL−2 | Kσ | 1 | 20 |
| Strain ε | - | 1 | 1 | 1 | |
| Elastic modulus E | FL−2 | Kσ | 1 | 20 | |
| Shear modulus Gm | FL−2 | Kσ | 1 | 20 | |
| Compressive strength R | FL−2 | Kσ | 1 | 20 | |
| Cohesive strength C | FL−2 | Kσ | 1 | 20 | |
| Friction angle φ | - | 1 | 1 | 1 | |
| Bulk density γ | FL−3 | Kγ | 1 | 1 | |
| Geometric property | Length L | L | KL | KL | 20 |
| Linear displacement δ | L | KL | KL | 20 | |
| Angular displacement β | - | 1 | 1 | 1 | |
| Area A | L2 | KL2 | KL2 | 202 | |
| Load | Point load P | F | KσKL2 | KL2 | 203 |
| Distributed load W | FL−1 | KσKL | KL | 202 | |
| Surface load q | FL−2 | Kσ | 1 | 20 | |
| Torque M | FL | KσKL3 | KL3 | 204 |
| Bulk Density γ (kN/m3) | Moisture Content ρ | Cohesive Strength C (kPa) | Internal Friction Angle φ (°) | |
|---|---|---|---|---|
| Sliding mass | 18.6 | 15.2 | 10.2 | 20.4 |
| Sliding bed | 18.8 | 14.7 | 10.2 | 20.6 |
| Sliding strip | -- | -- | 7 | 13 |
| Load (kpa) | Numerical Value (N·m) | Distance from Sliding Surface (cm) | Error | ||
|---|---|---|---|---|---|
| 20 | Calculated Value | Positive Bending Moment | 572 | 20 | 5.0% |
| Negative Bending Moment | −395 | 20 | |||
| Experimental Value | Positive Bending Moment | 513 | 19.6 | ||
| Negative Bending Moment | −408 | 21.5 | |||
| 40 | Calculated Value | Positive Bending Moment | 748 | 20 | 12.4% |
| Negative Bending Moment | −634 | 20 | |||
| Experimental Value | Positive Bending Moment | 659 | 21.4 | ||
| Negative Bending Moment | −570 | 22.3 | |||
| 60 | Calculated Value | Positive Bending Moment | 882 | 20 | 3.3% |
| Negative Bending Moment | −642 | 20 | |||
| Experimental Value | Positive Bending Moment | 819 | 18.7 | ||
| Negative Bending Moment | −747 | 21.6 | |||
| Load (kpa) | Numerical Value (kN) | Error | ||
|---|---|---|---|---|
| 20 | Calculated Value | Positive Shear | 5.973 | 8.5% |
| Negative Shear | −2.085 | |||
| Experimental Value | Positive Shear | 6.545 | ||
| Negative Shear | −2.258 | |||
| 40 | Calculated Value | Positive Shear | 7.366 | 9.8% |
| Negative Shear | −2.535 | |||
| Experimental Value | Positive Shear | 8.024 | ||
| Negative Shear | −2.947 | |||
| 60 | Calculated Value | Positive Shear | 8.188 | 8.0% |
| Negative Shear | −2.986 | |||
| Experimental Value | Positive Shear | 8.792 | ||
| Negative Shear | −3.358 | |||
| Bulk Density γ (N·m−3) | Elastic Modulus E (MPa) | Internal Friction Angle Φ(°) | Poisson’s Ratio μ | Cohesion c (kPa) | |
|---|---|---|---|---|---|
| Sliding body | 18,600 | 80 | 20.4 | 0.3 | 10.2 |
| Sliding bed | 18,800 | 80 | 20.6 | 0.3 | 10.2 |
| Anti-sliding piles | 21,000 | 18,000 | -- | 0.2 | -- |
| Sliding strip | -- | -- | 13 | -- | 7 |
| Loading Times | Earth Stress | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 1 | found | transmit | transmit | transmit | transmit | transmit | transmit |
| 2 | 10 kPa | 10 kPa | 10 kPa | 10 kPa | 10 kPa | 10 kPa | |
| 3 | 10 kPa | 10 kPa | 10 kPa | 10 kPa | 10 kPa | ||
| 4 | 10 kPa | 10 kPa | 10 kPa | 10 kPa | |||
| 5 | 10 kPa | 10 kPa | 10 kPa | ||||
| 6 | 10 kPa | 10 kPa | |||||
| 7 | 10 kPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Ran, Y.; Wang, K.; Shi, Z. Study of Load Calculation Models for Anti-Sliding Short Piles Using Finite Difference Method. Appl. Sci. 2023, 13, 12399. https://doi.org/10.3390/app132212399
Li X, Ran Y, Wang K, Shi Z. Study of Load Calculation Models for Anti-Sliding Short Piles Using Finite Difference Method. Applied Sciences. 2023; 13(22):12399. https://doi.org/10.3390/app132212399
Chicago/Turabian StyleLi, Xunchang, Yutong Ran, Kang Wang, and Zhengzheng Shi. 2023. "Study of Load Calculation Models for Anti-Sliding Short Piles Using Finite Difference Method" Applied Sciences 13, no. 22: 12399. https://doi.org/10.3390/app132212399
APA StyleLi, X., Ran, Y., Wang, K., & Shi, Z. (2023). Study of Load Calculation Models for Anti-Sliding Short Piles Using Finite Difference Method. Applied Sciences, 13(22), 12399. https://doi.org/10.3390/app132212399






