Sensorless HSPMSM Control of an Improved SMC and EKF Based on Immune PSO
Abstract
:1. Introduction
- (1)
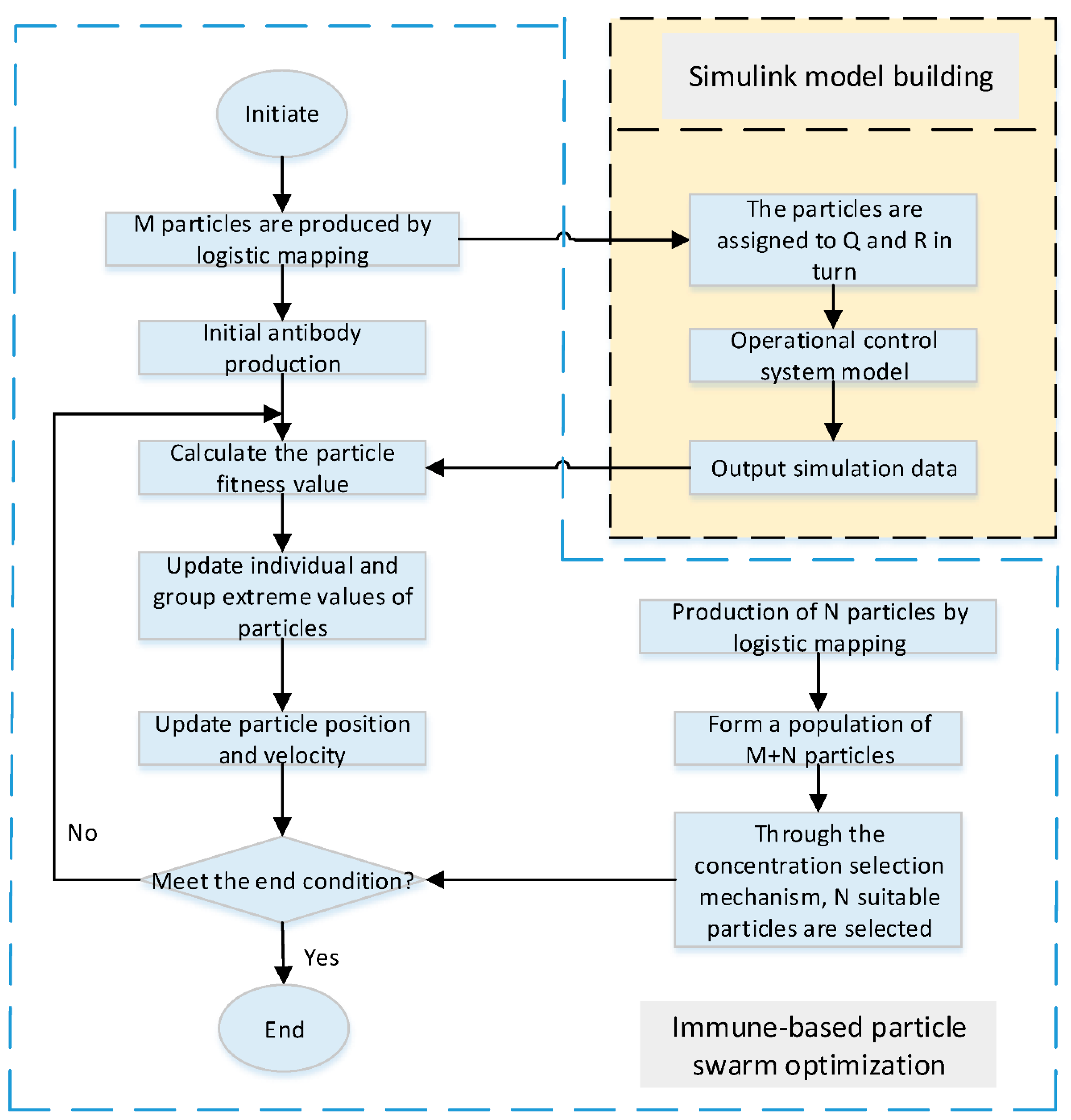
- A traditional 6-dimensional array composed of a noise matrix and measurement matrix requires considerable trial-and-error and computation time for optimization; this paper provides a new particle swarm optimization algorithm for overcoming this limit through optimization. This algorithm is based on the basic particle swarm algorithm and adds the concept of adaptive weighting and immunity. The method can shorten the optimization time and accelerate the convergence speed. Testing in MATLAB assesses the viability of matrix calculation and calculation speed acceleration.
- (2)
- To optimize the dynamic control performance of an HSPMSM, a novel convergence law is proposed to design a sliding-mode speed controller in terms of the controller, and the continuous function sat(s) is utilized instead of the symbolic function sgn(s), which further attenuates system jitter. This new integral sliding mode controller can reach the sliding mode surface quickly to optimize static and dynamic performance.
2. Methodology
2.1. Mathematical Model of a Flywheel Motor
2.2. Estimation and Optimization of the EKF Rotor Angular Velocity and Rotor Position
2.2.1. EKF Design
2.2.2. Optimizing the EKF Noise Covariance Matrix Using Immune-Based PSO
- (a)
- Elementary PSO:
- (b)
- PSO based on adaptive weights of immunity:
- (c)
- PSO based on adaptive weights of immunity optimization of the EKF covariance matrix by a novel particle swarm:
2.2.3. Optimizing the EKF Noise Covariance Matrix using Immune-Based PSO Convergence Analysis of the Novel PSO Algorithm
3. Design of the Speed Controller Based on Improved SMC
3.1. Design of Traditional-Speed SMC
3.2. Improvement of Speed SMC
3.3. Controller Stability Proof
3.4. Controller Stability Proof Analysis of New Approach Law Characteristics
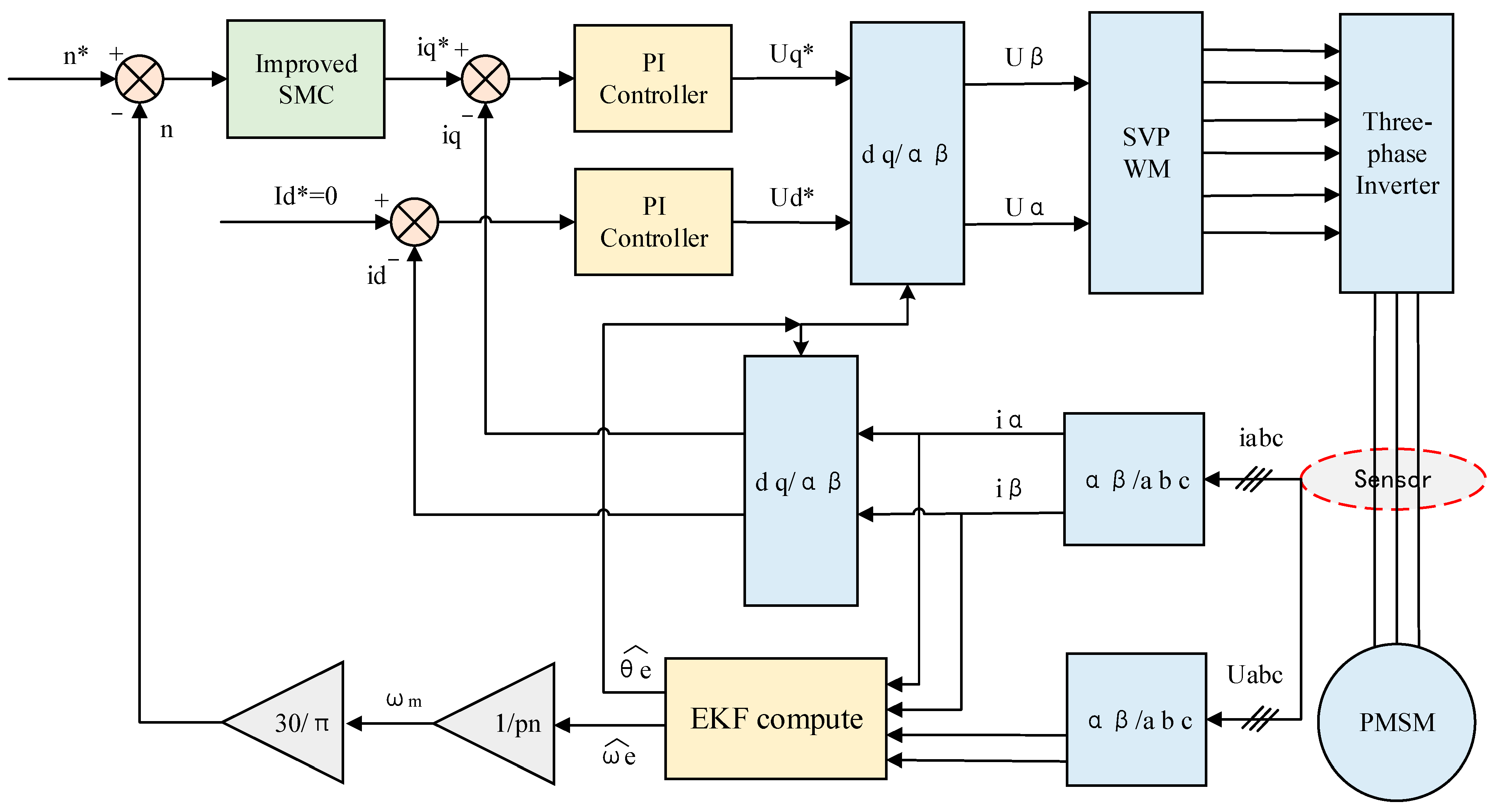
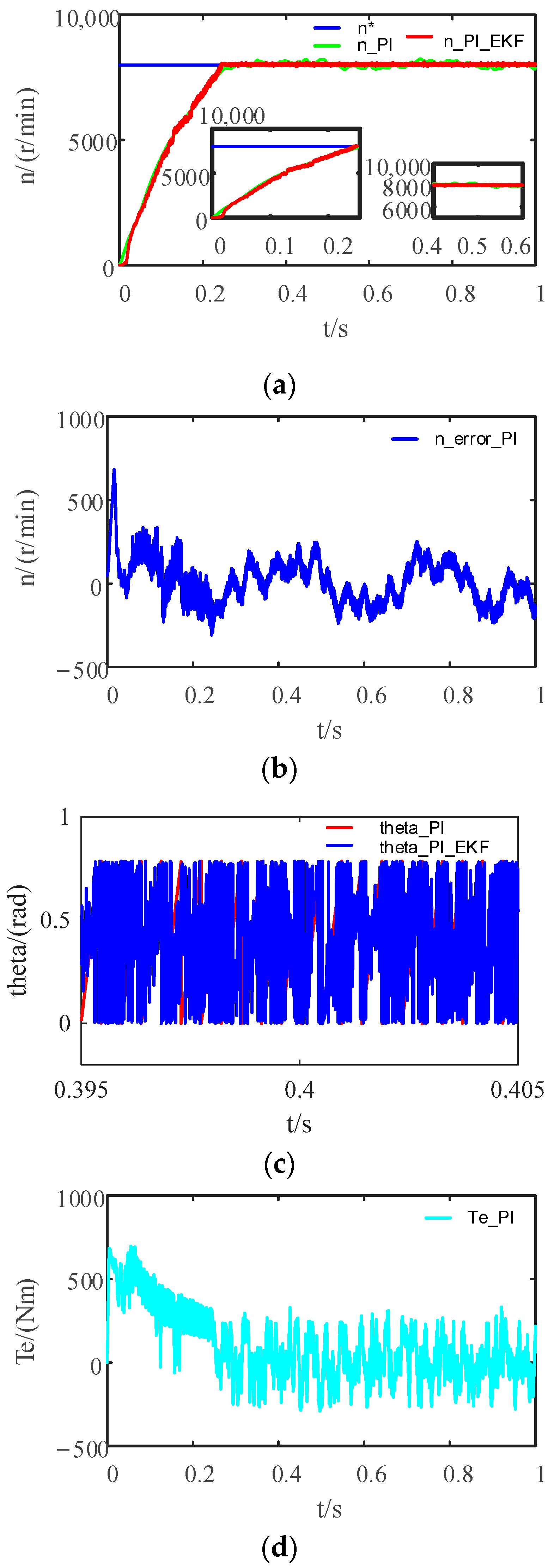
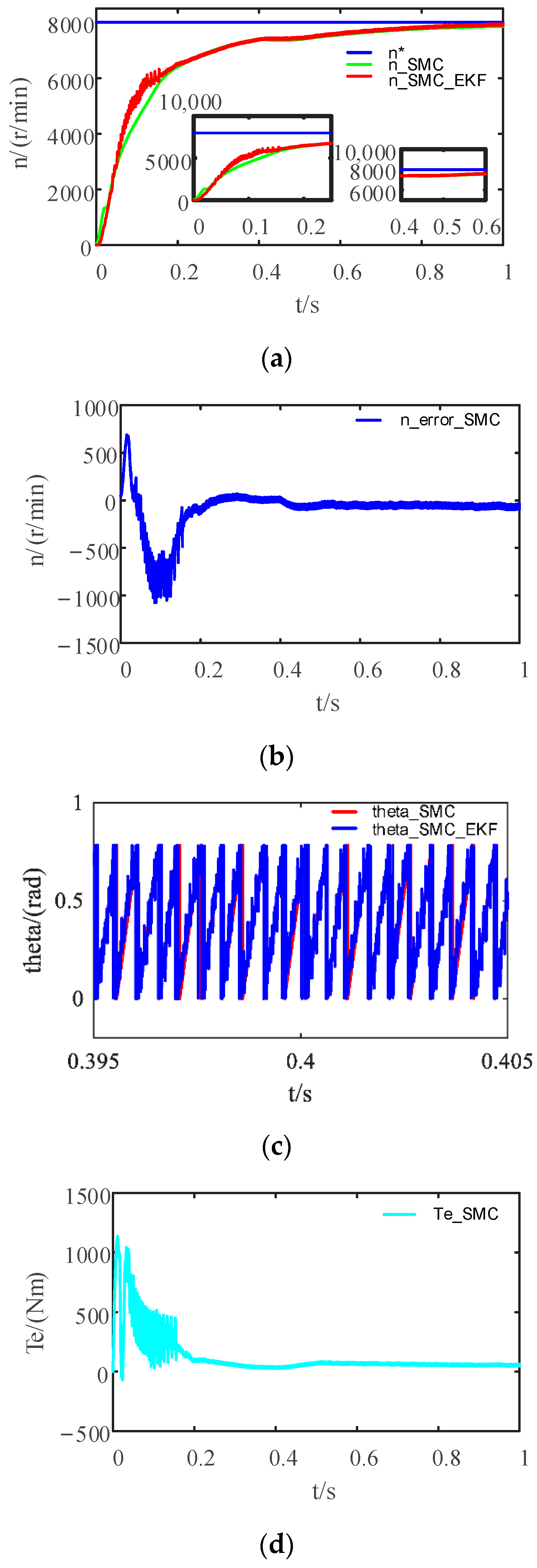
4. Case Study
4.1. Simulation Experimental Design
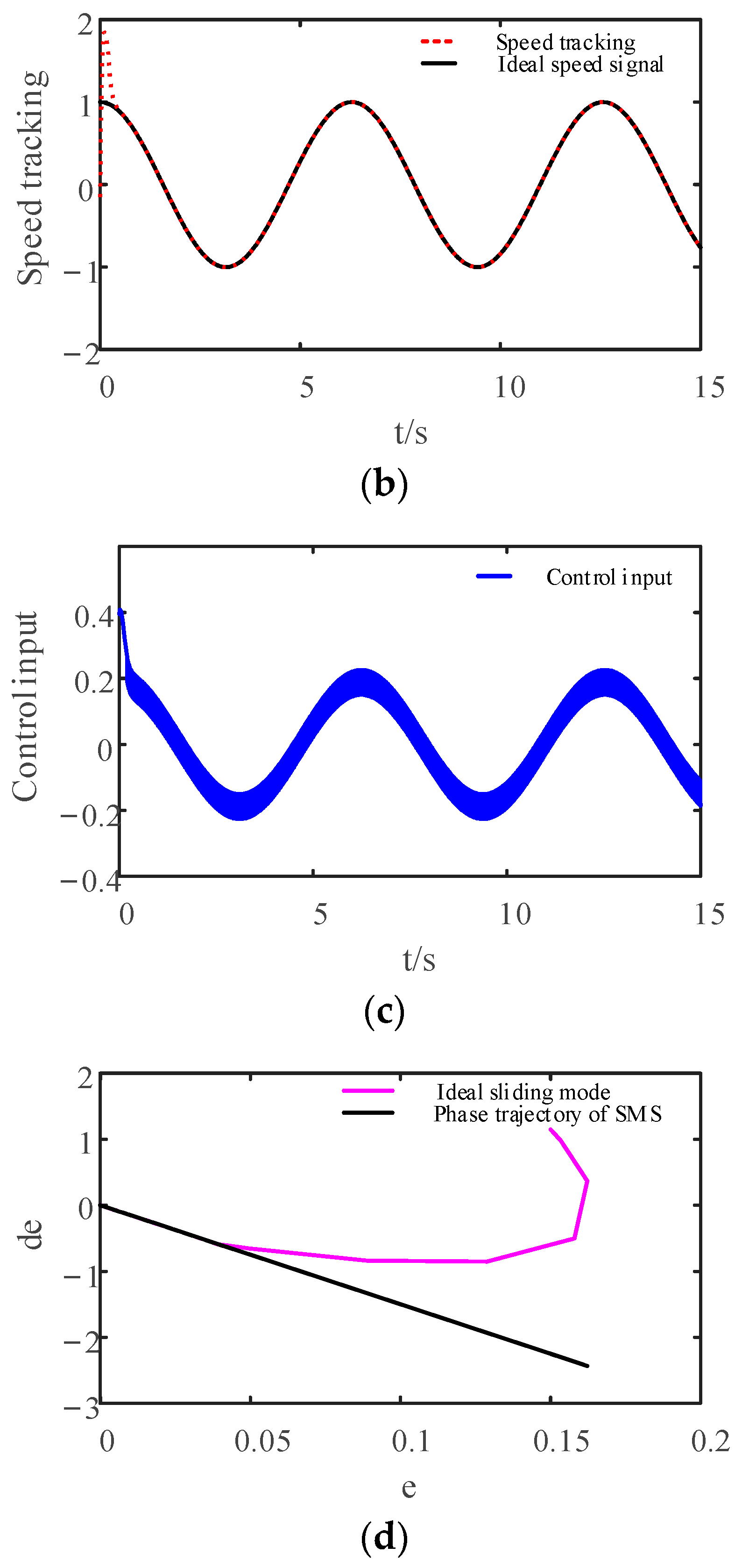
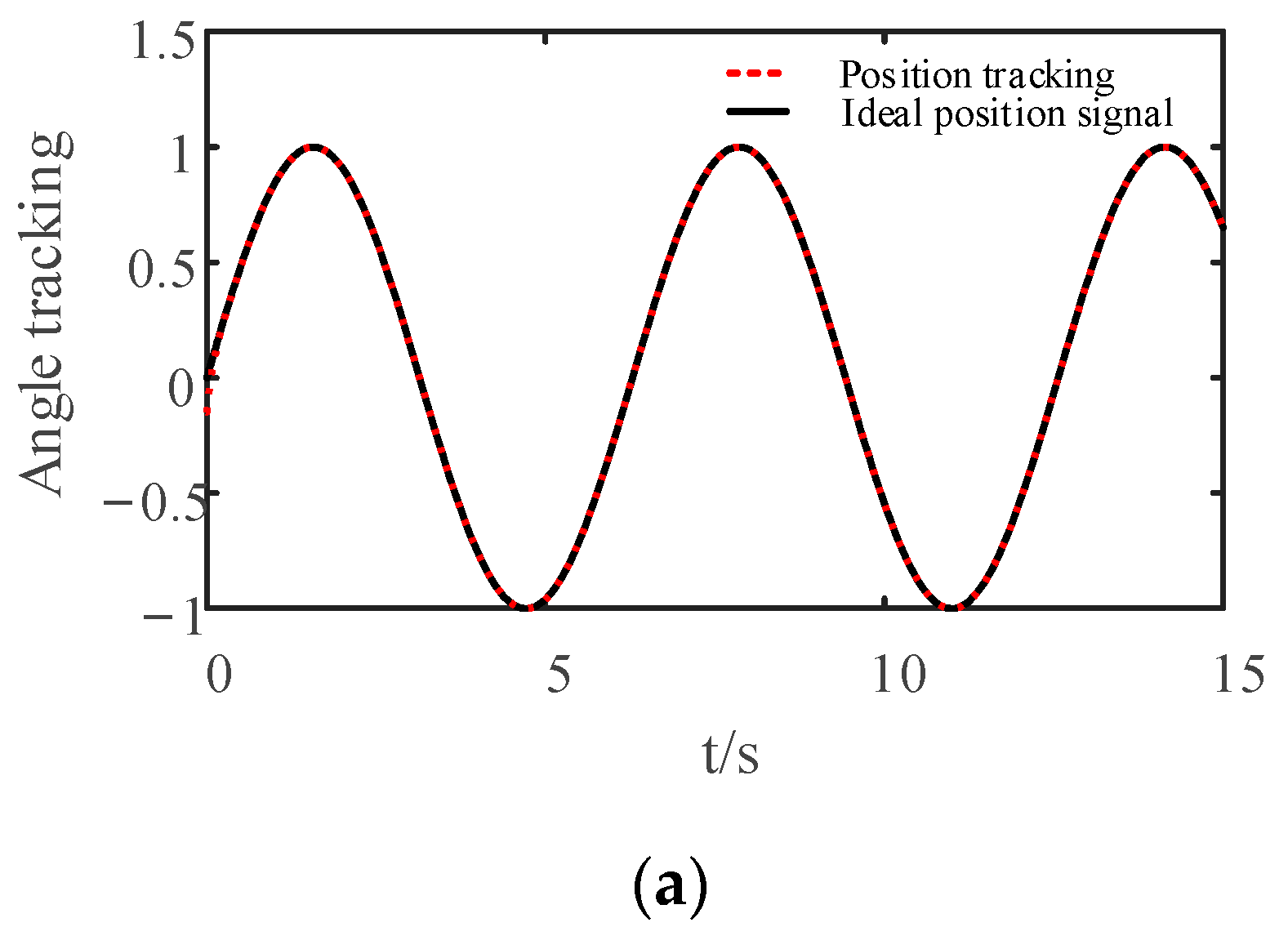
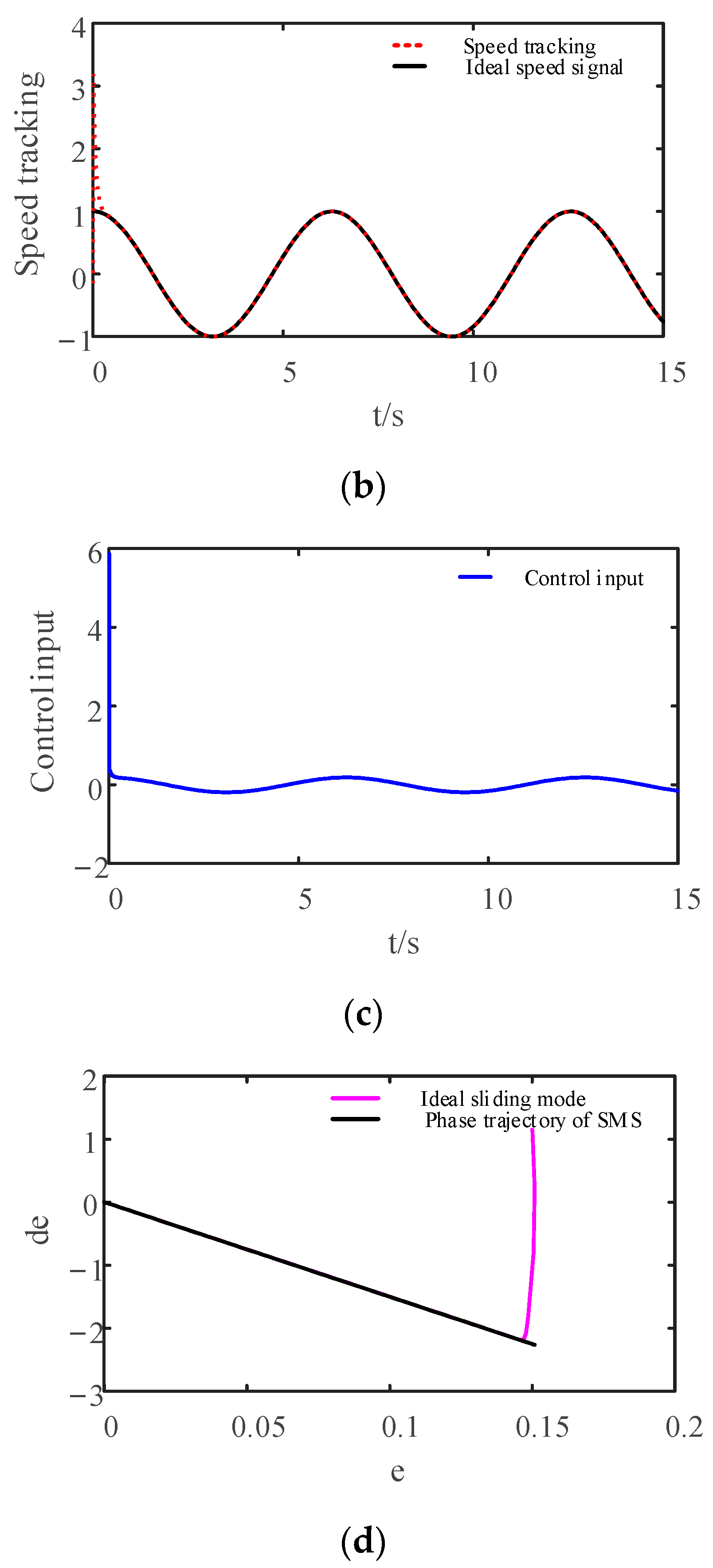
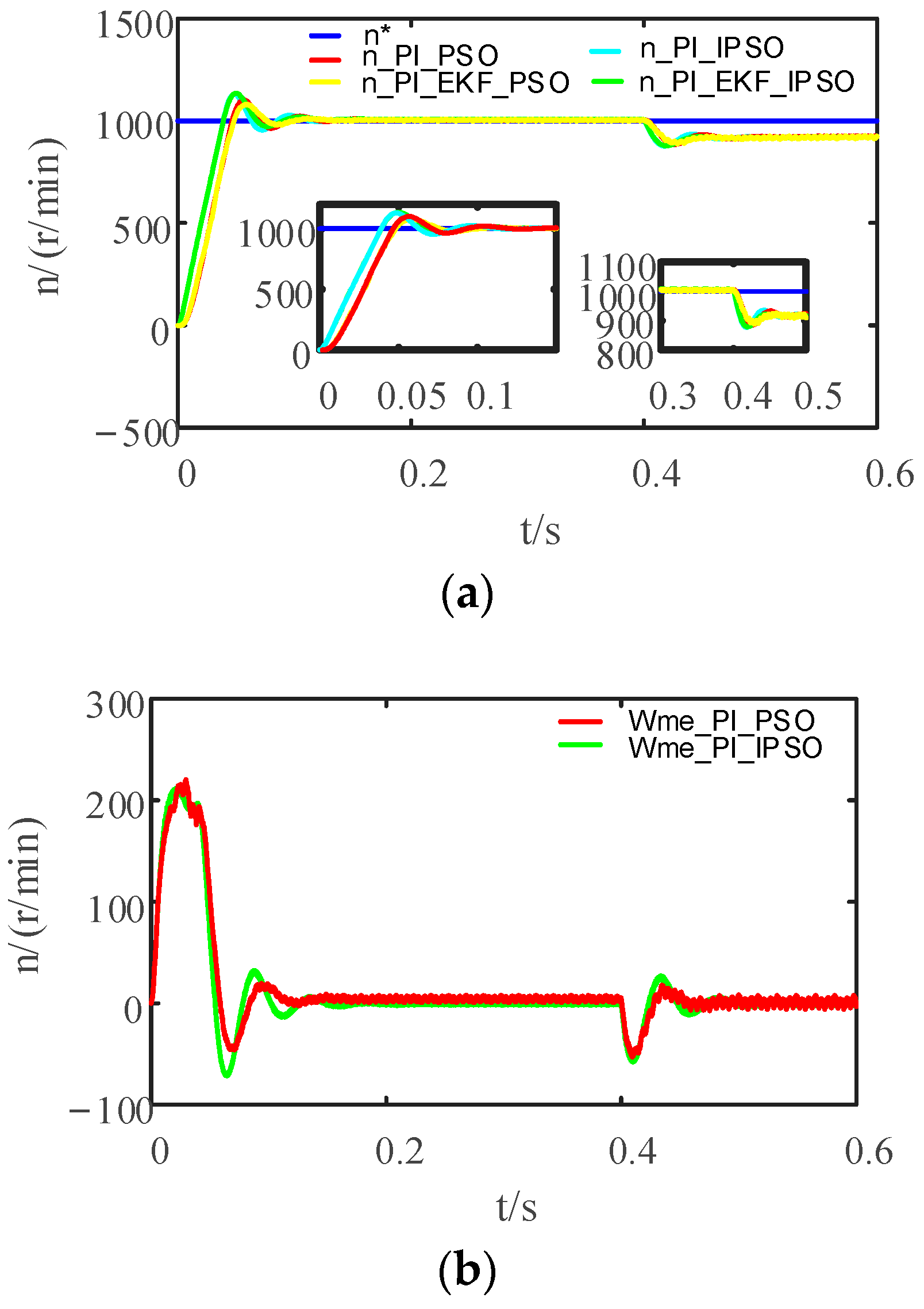
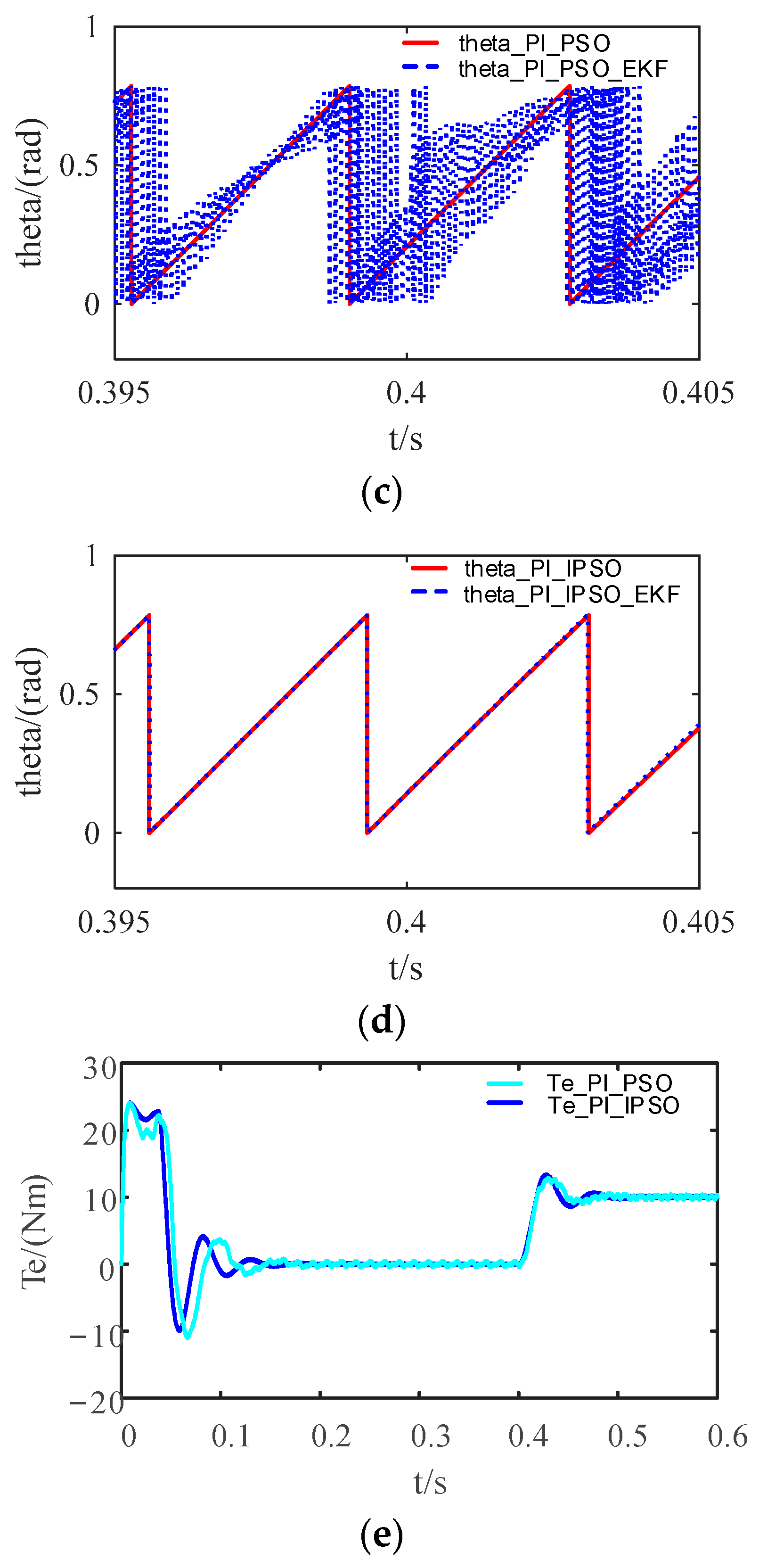
4.2. Simulation Experiment I
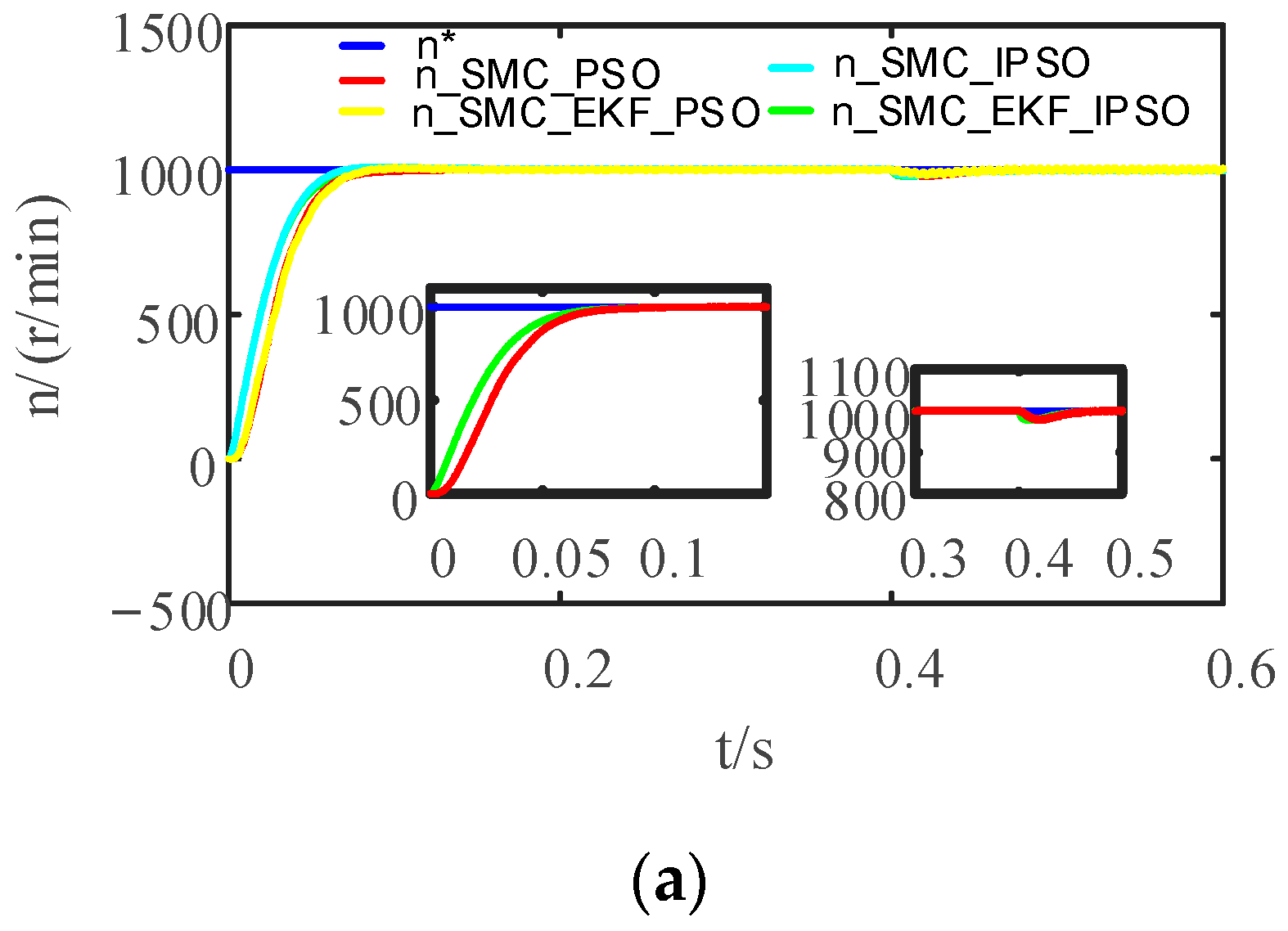
4.3. Simulation Experiment II
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alessandro, S.; Federico, D.; Gianluca, G.; Ignazio, M. Performance Analysis of PMSM for High-Speed Flywheel Energy Storage Systems in Electric and Hybrid Electric Vehicles. In Proceedings of the 2014 IEEE International Electric Vehicle Conference, Florence, Italy, 17–19 December 2014. [Google Scholar]
- Zhang, X.; Yang, J. An Improved Discharge Control Strategy with Load Current and Rotor Speed Compensation for High-Speed Flywheel Energy Storage System. In Proceedings of the IEEE Transactions on Industrial Electronics, Hangzhou, China, 22–25 October 2014. [Google Scholar]
- Liu, J.; Xiao, F.; Shen, Y.; Mai, Z.; Li, C. Position-Sensorless Control Technology of Permanent-Magnet Permanent-Magnet Synchronous Motor—A Review. Trans. China Electrotech. Soc. 2017, 32, 76–88. [Google Scholar]
- Hofer, M.; Nikowitz, M.; Schroedl, M. Sensorless Control of a Reluctance Synchronous Machine in the Whole Speed Range without Voltage Pulse Injections. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017-ECCE ASIA), Kaohsiung, Taiwan, 3–7 June 2017. [Google Scholar]
- Bolognani, S.; Zigliotto, M.; Zordan, M. Extended-Range PMSM Sensorless Speed Drive Based on Stochastic Filtering. IEEE Trans. Power Electron. 2001, 16, 110–117. [Google Scholar] [CrossRef]
- Favata, A.; Toso, F.; Torchio, R.; Bolognani, S. Integral Model Predictive Current Control for Synchronous Motor Drives. IEEE Tranactions Power Electron. 2021, 36, 13293–13303. [Google Scholar] [CrossRef]
- Wang, G.; Valla, M.; Solsona, J. Position Sensorless Permanent Magnet Synchronous Machine Drives—A Review. IEEE Trans. Ind. Electron. 2019, 67, 5830–5842. [Google Scholar] [CrossRef]
- Lee, Y.; Sul, S.K. Model-based Sensorless Control of an IPMSM with Enhanced Robustness against Load Disturbances based on Position and Speed Estimator using a Speed Error. IEEE Trans. Ind. Electron. 2017, 24, 1448–1459. [Google Scholar] [CrossRef]
- Andersson, A.; Thiringer, T. Motion Sensorless IPMSM Control Using Linear Moving Horizon Estimation with Luenberger Observer State Feedback. IEEE Trans. Transp. Electrif. 2018, 4, 464–473. [Google Scholar] [CrossRef]
- Bao, D.; Pan, X.; Wang, X. Adaptive Synchronous-Frequency Tracking-Mode Observer for the Sensorless Control of a Surface PMSM. IEEE Trans. Ind. Appl. 2017, 54, 6460–6471. [Google Scholar] [CrossRef]
- Xue, S.; Wei, L.; Ling, Y. Sensorless Vector Control of Permanent Magnet Synchronous Motor Based on Extended Kalman Filter. Electr. Control Appl. 2011, 38, 15–18. [Google Scholar]
- Li, Y.; Xie, L.; Qi, R.; Lin, H. Design of PMSM sensorless speed regulating system. Electr. Mach. Control 2003, 7, 307–309. [Google Scholar]
- Zheng, S.; Meng, K.; Hai, R.; Wang, T. Sensorless DPMSM sliding Mode on Particle Swarm Optimization EKF. Modul. Mach. Tool Autom. Manuf. Technol. 2022, 7, 66–70. [Google Scholar]
- Wang, A.; Wang, Q.; Hu, C.; Qian, Z.; Ju, L.; Liu, J. An EKF for PMSM Sensorless Control Based on Noise Model Identification Using Ant Colony Algorithm. In Proceedings of the 2009 International Conference on Electrical Machines and Systems, Tokyo, Japan, 15–18 November 2009. [Google Scholar]
- Ding, H.; Qin, X.; Wei, L. Extended Kalman filters combined with feed-forward compensation for permanent magnet synchronous motor position estimation. Control Theory Appl. 2016, 33, 1312–1318. [Google Scholar]
- Ding, H.; Qin, X.; Wei, L. Sensorless Control of Surface-Mounted Permanent Magnet Synchronous Motor Using Adaptive Robust UKF. J. Electr. Eng. Technol. 2022, 17, 2995–3013. [Google Scholar] [CrossRef]
- Janiszewski, D. Load Torque estimation in sensorless PMSM drive using Unscented Kalmana Filter. In Proceedings of the 2014 IEEE Interantional Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011. [Google Scholar]
- Aydogmus, O.; Sunter, S. Implementation of EKF based sensorless drive system using vector controlled PMSM fed by a matrix converter. Electr. Power Energy Syst. 2012, 43, 736–743. [Google Scholar] [CrossRef]
- Bolognani, S.; Oboe, R.; Zigliotto, M. Sensorless Full-Digital PMSM Drive with EKF Estimation of Speed and Rotor Position. IEEE Tranactions Power Electron. 2021, 46, 184–191. [Google Scholar] [CrossRef]
- Park, J.B.; Wang, X. Sensorless Direct Torque Control of Surface-Mounted Permanent Magnet Synchronous Motors with Nonlinear Kalman Filtering. Energies 2018, 11, 969. [Google Scholar] [CrossRef]
- Wang, X.; Cao, B.; Mahfuz Alam, S.M. Sensorless Direct Torque Control of Surface Permanent Magnet Synchronous Motors with Resilient Extended Kalman Filtering. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo(ITEC), Chicago, IL, USA, 22–24 June 2017; pp. 714–719. [Google Scholar]
- Yi, B.; Kang, L.; Tao, S.; Zhao, X.; Jing, Z. Adaptive Two-stage Extended Kalman Filter Theory in Application of Sensorless Control for Permanent Magnet Synchronous Motor. Math. Probl. Eng. 2013, 2013, 974974. [Google Scholar] [CrossRef]
- Quang, N.K.; Ha, Q.P.; Hieu, N.T. FPGA Sensorless PMSM Drive with Adaptive Fading Extended Kalman Filtering. In Proceedings of the 2014 13th International Conference on Control Automation Robotics and Vision (ICARCV), Singapore, 10–12 December 2017. [Google Scholar]
- Khan, N.; Jabbar, A.; Bilal, H.; Gul, U. Compensated Closed-loop Kalman Filtering for nonlinear systems. Measurement 2020, 151, 1–11. [Google Scholar] [CrossRef]
- Park, J.B.; Wang, X. Nonlinear Filtering Based Sensorless Direct Torque Control of Surface-Mounted Permanent Synchronous Motors. Energies 2018, 11, 448–453. [Google Scholar]
- Xue, S.; Wei, L.; Ling, Y. Sensorless Vector Control of Permanent Magnet Synchronous Motors Based on EKF and SMC. Inf. Control 2012, 41, 267–272. [Google Scholar]
- Zhang, P.; Shi, Z.; Lin, J.; Yu, B.; Sun, Y.; Ding, H. Improved Sensorless Vector Control System for Permanent Magnet Synchronous Motors Based on Hyperbolic Tangent Functions. J. Harbin Eng. Univ. 2021, 42, 710–718. [Google Scholar]
- Hasan, D.E.; Hasan, K.; Afsin, K.A. A novel unified maximum power extraction framework for PMSG based WECS using chaotic particle swarm optimization derivatives. Eng. Sci. Technol.-Int. J.-Jestech 2021, 24, 158–170. [Google Scholar]
- Hasan, K. GM-CPSO A new viewpoint to chaotic particle swarm optimization via Gauss map. Neural Process. Lett. 2020, 52, 241–266. [Google Scholar]
- Hasan, D.E.; Afsin, K.A. Second-order sliding mode voltage-regulator for improving MPPT efficiency of PMSG-based WECS. Int. J. Electr. Power Energy Syst. 2020, 121, 106149. [Google Scholar]
- Xiuxing, Y.; Zhansi, J.; Li, P. Recurrent neural network based adaptive integral sliding mode power maximization control for wind power systems. Renew. Energy 2020, 145, 1149–1157. [Google Scholar]
- Xiong, L.; Li, P.; Wang, J. High-order sliding mode control of DFIG under unbalanced grid voltage conditions. Int. J. Electr. Power Energy Syst. 2020, 117, 105608. [Google Scholar] [CrossRef]
- Yu, Q.; Yan, S.; Zhao, H. Simulation Experiment of Sliding Mode Control Based on Simulink. Sci. Technol. Innov. Her. 2018, 35, 97–98. [Google Scholar]
- Yuan, L.; Hu, B.X.; Wei, K.Y.; Chen, S. Modern Permanent Magnet Synchronous Motor Control Principle and MATLAB Simulation; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2016; pp. 151–165. [Google Scholar]
- Wen, Z.; Sun, H. MATLAB Intelligent Algorithm; Tsinghua University Press: Beijing, China, 2017; pp. 108–144. [Google Scholar]
- Xing, Y.; Wang, X.; Yang, D.; Zhang, Z. Novel Stator flux linkage estimator and choice of its parameters. Electr. Mach. Control 2016, 20, 29–35. [Google Scholar]
- Liu, J. Sliding Mode Control Design and MATLAB Simulation the Basic Theory and Design Method, 4th ed.; Tsinghua University Press: Beijing, China, 2012; pp. 38–55. [Google Scholar]
- Yu, L. Modern Control Theory, 3rd ed.; Tsinghua University Press: Beijing, China, 2007; pp. 100–104. [Google Scholar]




| Parameters | Value |
|---|---|
| Learning factor c1 | 2 |
| Learning factor c2 | 2 |
| Minimum weight wmin | 0.4 |
| Maximum weight wmax | 0.9 |
| Inertia weight w | 0.6 |
| Initialized population number | 30 |
| Maximum number of iterations | 50 |
| Search space dimension D | 6 |
| Arithmetic | Iterations | Value | Iterations | Optimal Fitness Value |
|---|---|---|---|---|
| PI-PSO | 12 | 71.2878320918268 | 48 | 26.7295406097632 |
| SMC-PSO | 12 | 29.1013543176795 | 47 | 26.8191574261835 |
| SMC-w-PSO | 12 | 31.2474590327885 | 45 | 25.9442102638115 |
| SMC-w-IPSO | 12 | 25.3497159998008 | 46 | 17.3148124002699 |
| Arithmetic | Iterations | Value | Iterations | Optimal Fitness Value |
|---|---|---|---|---|
| PI-PSO | 17 | 67.0864712052134 | 29 | 52.057357828006 |
| SMC-PSO | 6 | 29.1013543176795 | 47 | 26.8191574261835 |
| SMC-w-PSO | 4 | 26.6556819783912 | 4 | 26.6556819783912 |
| SMC-w-IPSO | 17 | 24.272268595533 | 49 | 17.0101770076945 |
| Parameters | Value |
|---|---|
| Stator Inductance/μH | 91.3 |
| Stator Resistance/mΩ | 8.17 |
| Rated Voltage/V | 690 |
| Number of Motor Poles | 2 |
| Rated Power/kW | 75 |
| Friction Coefficient/Nms/rad | 0 |
| Flywheel Moment of Inertia/kgm2 | 0.115 |
| Busbar Capacitance/mF | 3 |
| Bus Voltage Rating/mF | 1100 |
| Minimum Speed/rpm | 10,000 |
| Maximum Speed/rpm | 20,000 |
| Parameters | PI_PSO | PI_EKF_PSO | PI_IPSO | PI_EKF_IPSO | SMC_PSO | SMC_EKF_PSO | SMC_IPSO | SMC_EKF_IPSO |
|---|---|---|---|---|---|---|---|---|
| rising time(tr)/s | 0.0465 | 0.0481 | 0.0389 | 0.0390 | 0.0845 | 0.1292 | 0.0699 | 0.1378 |
| peak time(tp)/s | 0.0566 | 0.0585 | 0.0485 | 0.0502 | 0.1001 | 0.1542 | 0.0847 | 0.1684 |
| Adjusting time(ts)/s | 0.0799 | 0.0849 | 0.0753 | 0.0763 | 0.1293 | 0.1047 | 0.0698 | 0.1396 |
| overtone(σ)/% | 7.356 | 9.533 | 12.637 | 12.587 | 0.4 | 0.8 | 1.1 | 0.2 |
| steady-state error/rpm | 7 | 6 | 5 | 9 | 4 | 7 | −3.5 | 1 |
| 0.4 s after load recovery time/s | 0.0463 | 0.0463 | 0.0467 | 0.0463 | 0.059 | 0.056 | 0.0769 | 0.0729 |
| 0.4 s after load recovery value/rpm | 928.4 | 919.9 | 932.5 | 923.1 | 1001 | 1000 | 996 | 1001 |
| 0.4 s after load recovery value fluctuation range/rpm | 928.4 | 912~925 | 932.5 | 923.1 | 990~1005 | 991~1007 | 996~997 | 1001 |
| Parameters | PI_IPSO | PI_EKF_IPSO | SMC_IPSO | SMC_EKF_IPSO |
|---|---|---|---|---|
| rising time(tr)/s | 0.2862 | 0.2453 | 0.7691 | 0.7666 |
| peak time(tp)/s | 0.4476 | 0.2467 | 0.9936 | 0.9979 |
| Adjusting time(ts)/s | 0.4886 | 0.25 | 0.9949 | 0.9989 |
| overtone(σ)/% | 2.84 | 0.975 | 1.5 | 1.575 |
| steady-state error/rpm | 242 | 107 | 120 | 126 |
| 0.4 s after load recovery value/rpm | 8242 | 8107 | 8120 | 8126 |
| 0.4 s after load recovery value fluctuation range/rpm | 7817~8242 | 7932~8107 | 8120 | 8109~8126 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, K.; Liu, Q.; Zhang, Z.; Wu, H.; Feng, H.; Kang, T. Sensorless HSPMSM Control of an Improved SMC and EKF Based on Immune PSO. Appl. Sci. 2023, 13, 12407. https://doi.org/10.3390/app132212407
Meng K, Liu Q, Zhang Z, Wu H, Feng H, Kang T. Sensorless HSPMSM Control of an Improved SMC and EKF Based on Immune PSO. Applied Sciences. 2023; 13(22):12407. https://doi.org/10.3390/app132212407
Chicago/Turabian StyleMeng, Keqilao, Qing Liu, Zhanqiang Zhang, Huijuan Wu, Haining Feng, and Taifeng Kang. 2023. "Sensorless HSPMSM Control of an Improved SMC and EKF Based on Immune PSO" Applied Sciences 13, no. 22: 12407. https://doi.org/10.3390/app132212407
APA StyleMeng, K., Liu, Q., Zhang, Z., Wu, H., Feng, H., & Kang, T. (2023). Sensorless HSPMSM Control of an Improved SMC and EKF Based on Immune PSO. Applied Sciences, 13(22), 12407. https://doi.org/10.3390/app132212407






