Prediction of Failure Modes of Steel Tube-Reinforced Concrete Shear Walls Using Blending Fusion Model Based on Generative Adversarial Networks Data Augmentation
Abstract
:1. Introduction
- (1)
- The use of GAN for database augmentation of STRC shear walls enables various ML models to fully learn the patterns in the data, addressing the issue of limited training samples of STRC shear walls.
- (2)
- The establishment of a Blending-CRKL fusion model that combines the advantages of Catboost, RF, KNN, and LASSO models significantly improves the prediction accuracy of failure modes of STRC shear walls compared to single ML models tested. The stability and robustness of this model are also validated.
- (3)
- The application of model interpretability methods provides explanations for the Blending-CRKL fusion model, addressing the “black box” issue of ML models. The important features of failure modes of STRC shear walls and the ranges of feature values under different failure modes are analyzed.
2. STRC Shear Wall Failure Modes and Small Sample Database Establishment
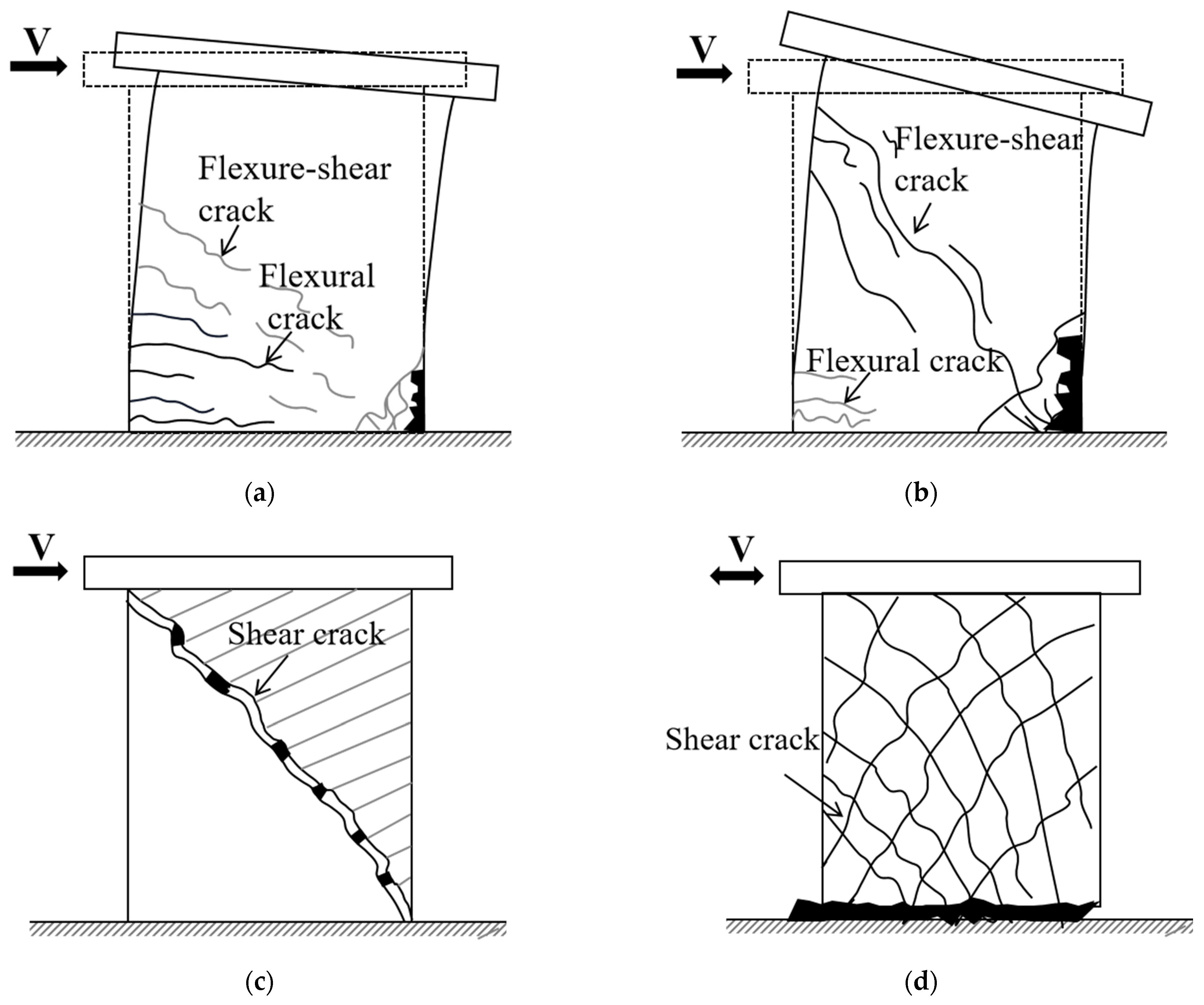
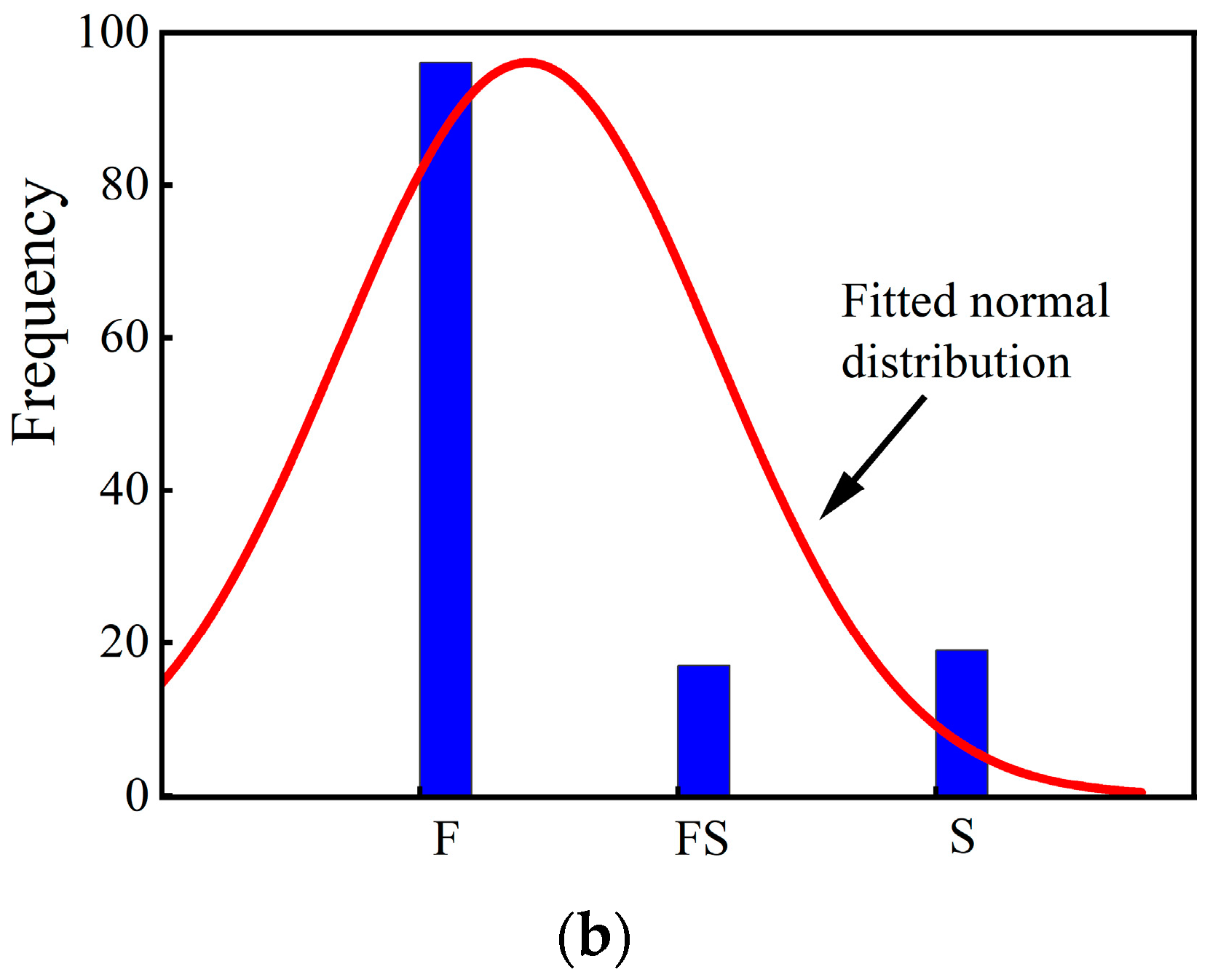
2.1. Failure Modes of STRC Shear Walls
2.2. Data Collection
- (1)
- The steel tubes are arranged in the boundary unit or the middle of the wall.
- (2)
- The STRC shear walls are single-layered with a symmetrical rectangular cross-section and no openings.
- (3)
- The vertical reinforcement and steel tubes of all STRC shear walls are continuous, without lap splices.
- (4)
- The loading method for testing is cyclic loading.
- (5)
- Walls without special structures, such as hidden steel frames, hidden steel trusses, or shear keys, are excluded from the study.
2.3. Feature Settings
3. Methodology
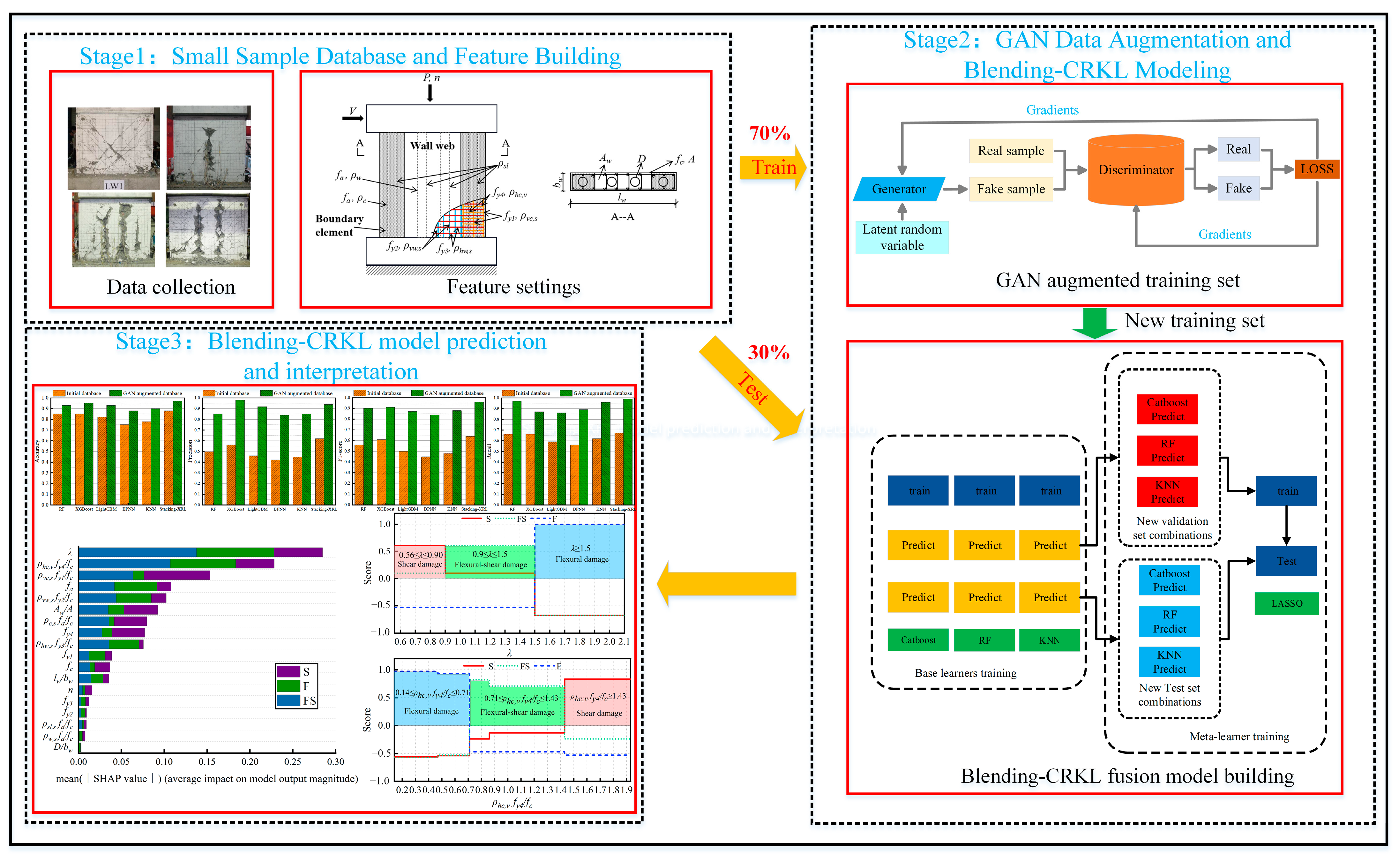
3.1. Proposed Framework
- (1)
- (2)
- In the second stage, the deep learning GAN is applied to augment the training set data, and a two-layer Blending algorithm framework is used to establish a fusion model (Blending-CRKL) for RF, Catboost, K-Nearest Neighbors (KNN), and Least Absolute Shrinkage and Selection Operator (LASSO).
- (3)
- In the third stage, the effectiveness of the proposed GAN augmented training set method is verified, and the Blending-CRKL fusion model is used to predict and explain the failure modes of STRC shear walls, analyzing their important features and the characteristic value ranges of different failure modes.
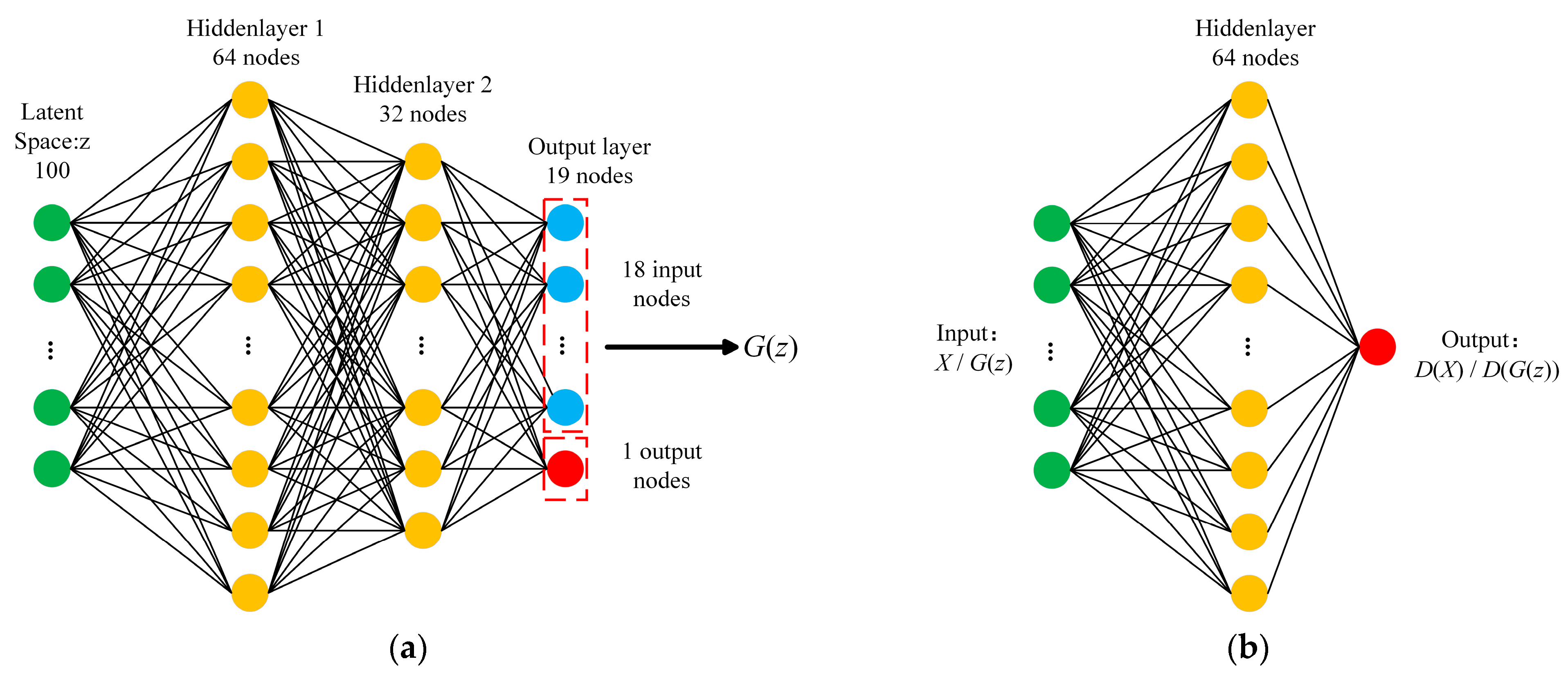
3.2. Generative Adversarial Networks
3.3. Blending Fusion Prediction Model Building
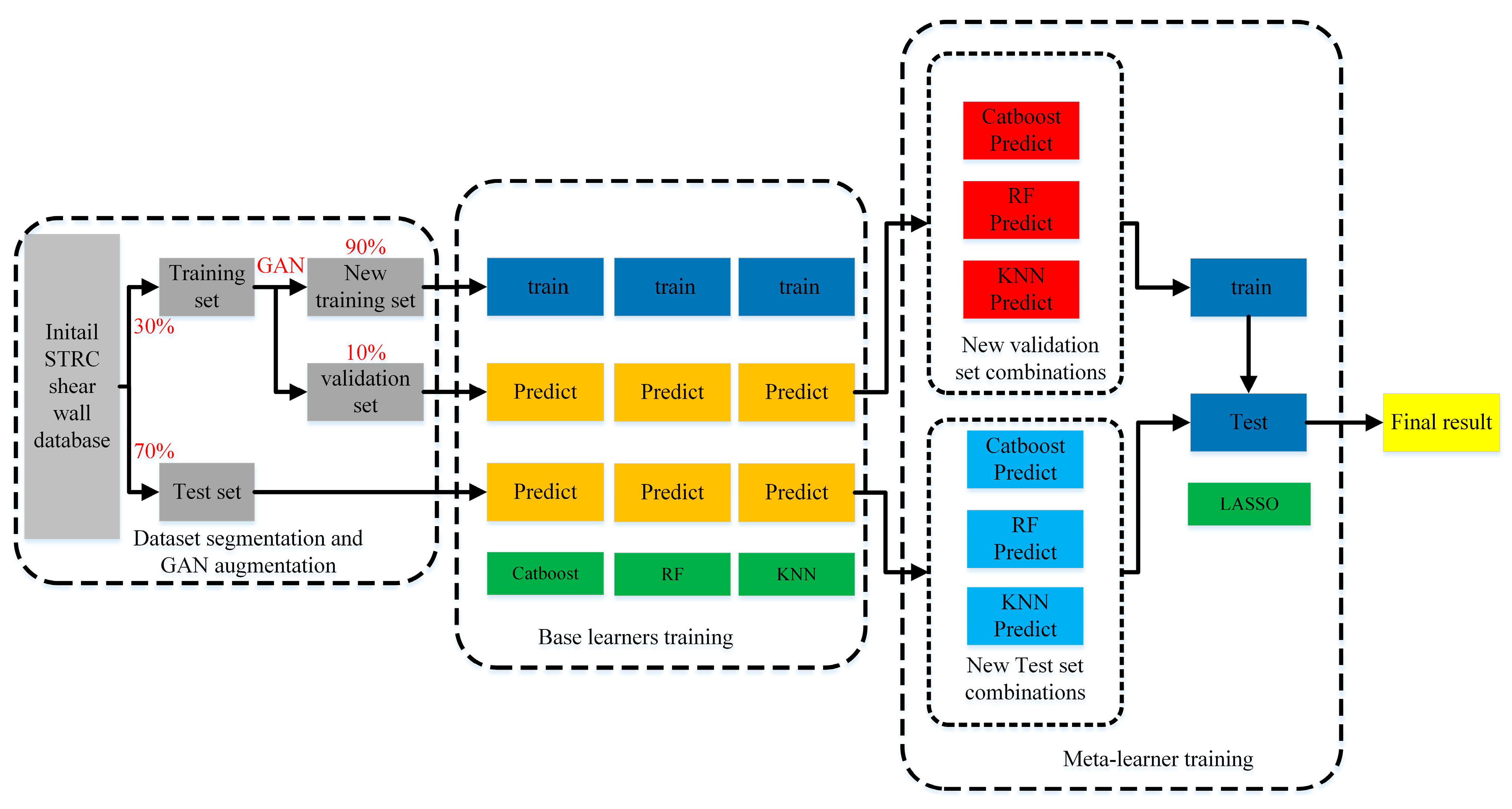
- (1)
- Dataset segmentation and GAN augmentation. In this study, the initial collected STRC shear wall database was randomly divided into a 70% training set and a 30% testing set. The training set was used for model training, while the testing set was used for model validation. To fully train the model, the 242 new samples generated by GAN were merged with the training set samples, resulting in a new training set containing 347 samples. And 10% of the samples of the new training set are randomly selected as the validation set.
- (2)
- Training process of base learners. The Blending fusion model utilizes Catboost, RF, and KNN models as base learners, training them separately on the new training set and making predictions on the validation and test sets. The predicted values of the validation set by the Catboost, RF, and KNN models are used as the training set for the next layer, while the predictions on the test set are used as the test set for the next layer.
- (3)
- Training process of the meta-learner. In the training process of the LASSO meta-learner, a new training set is formed using the predicted values of the base learners on the validation set, and the LASSO model is trained on this new training set. The final prediction results are obtained by testing the model on a new test set, which consists of the predicted values of the base learners on the test set.
3.4. Model Evaluation Criteria
4. Analysis of Results and Discussion
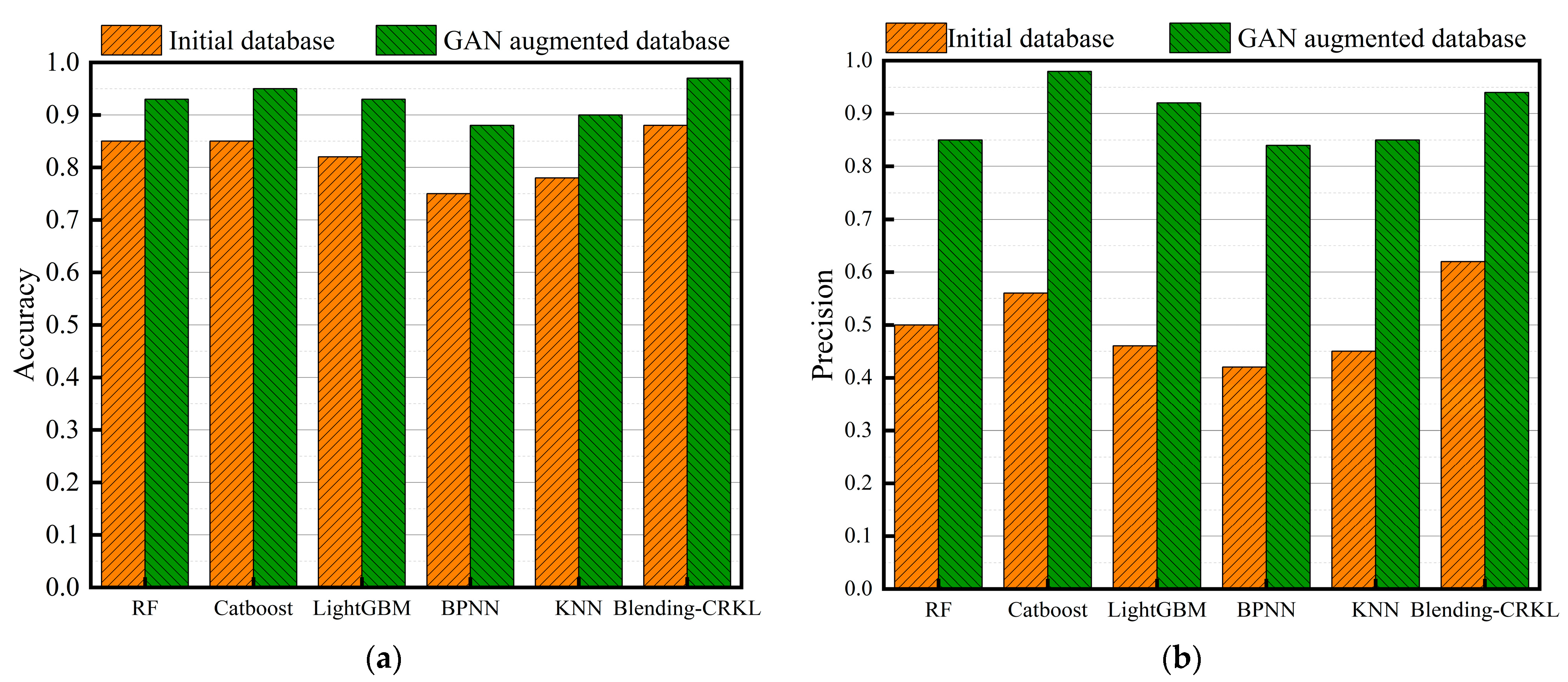
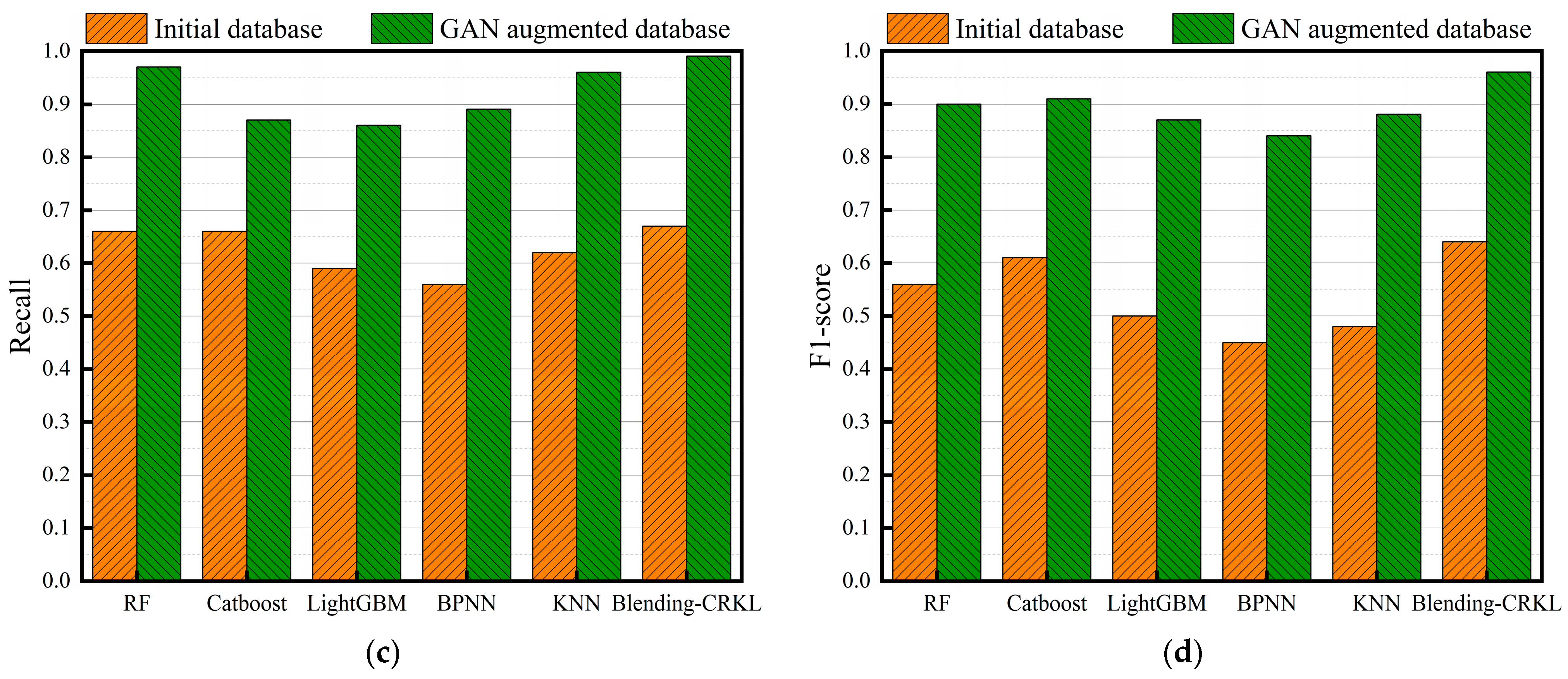
4.1. Comparison of Model Prediction Performance before and after GAN Augmented Training Set
4.2. Comparison of Various ML Models
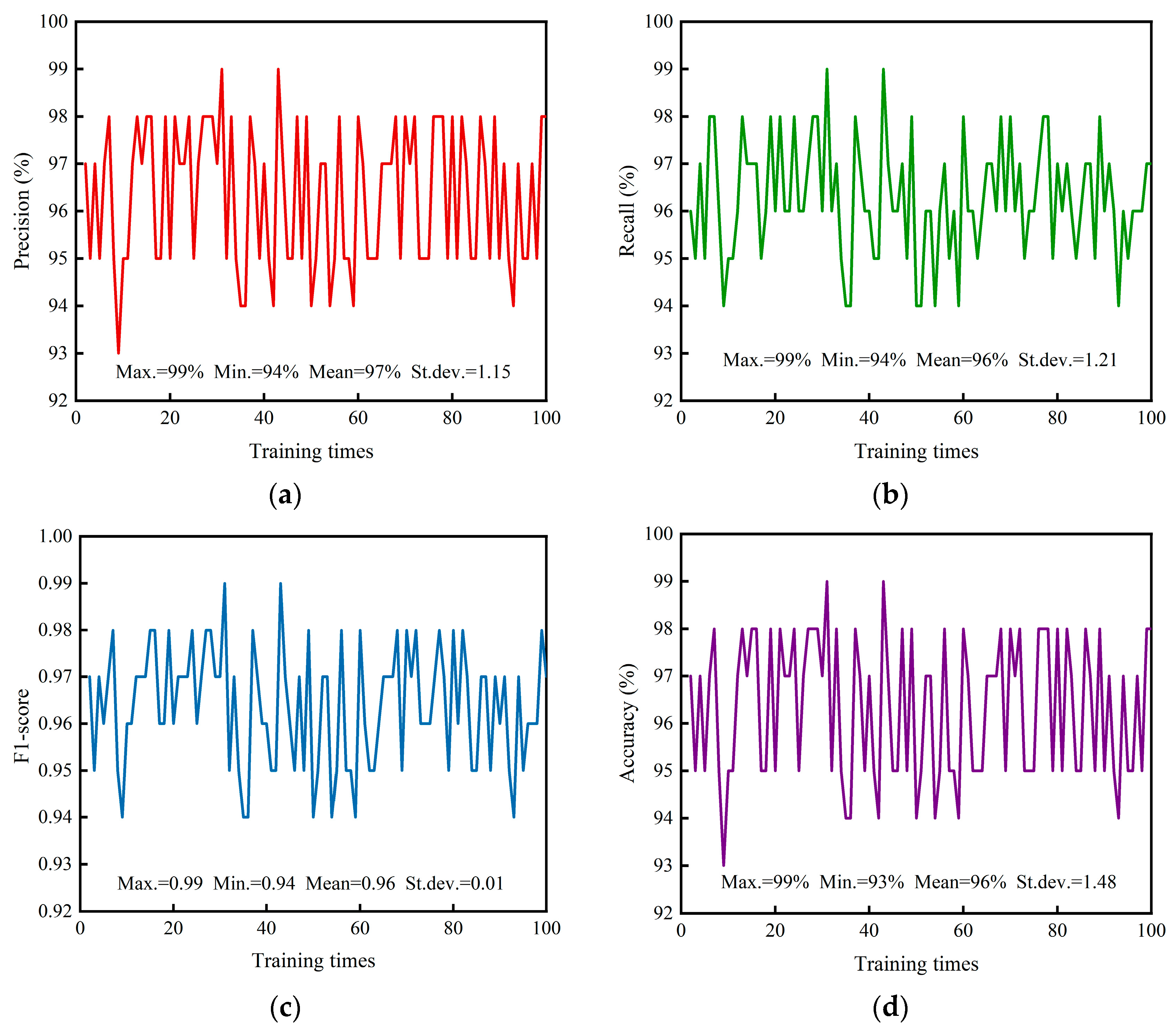
4.3. Checking of Robustness and Reliability for Stacking-CRK Model
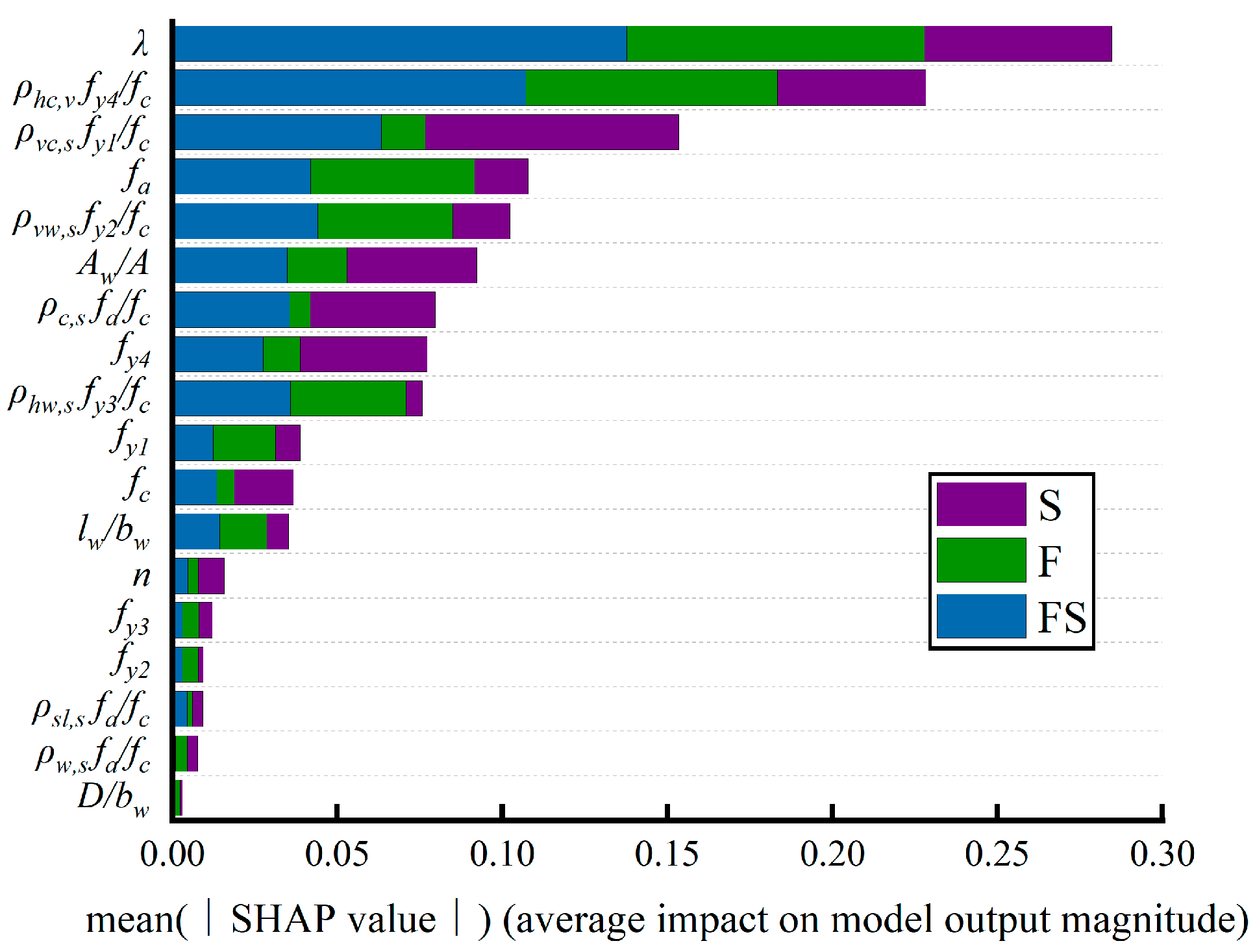
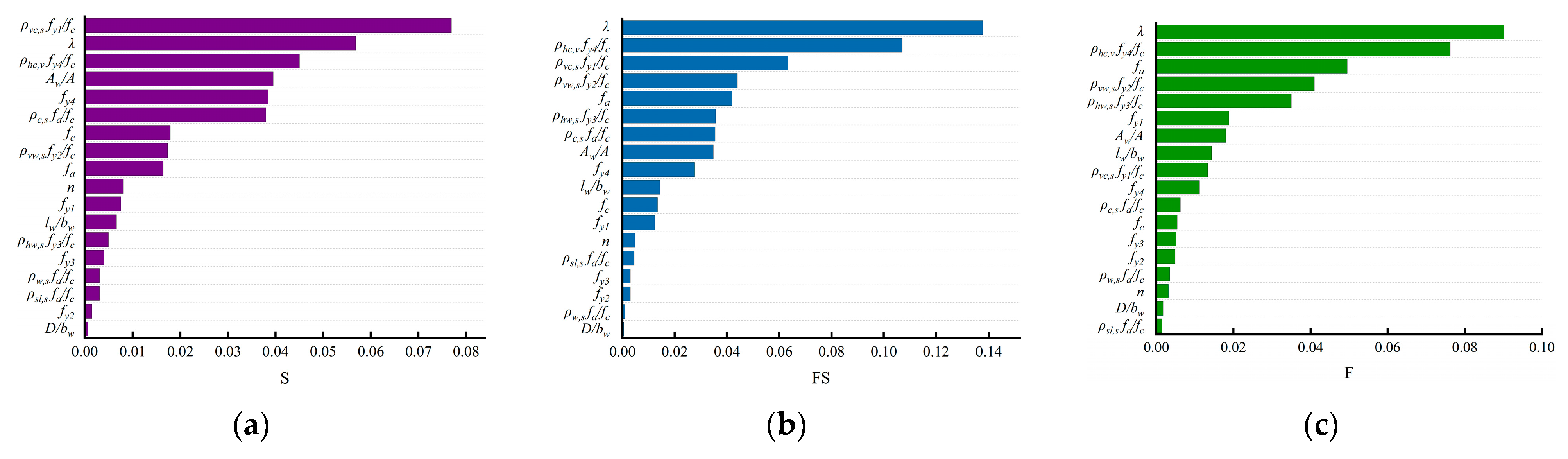
4.4. Interpretation of STRC Shear Walls Failure Modes Prediction Model
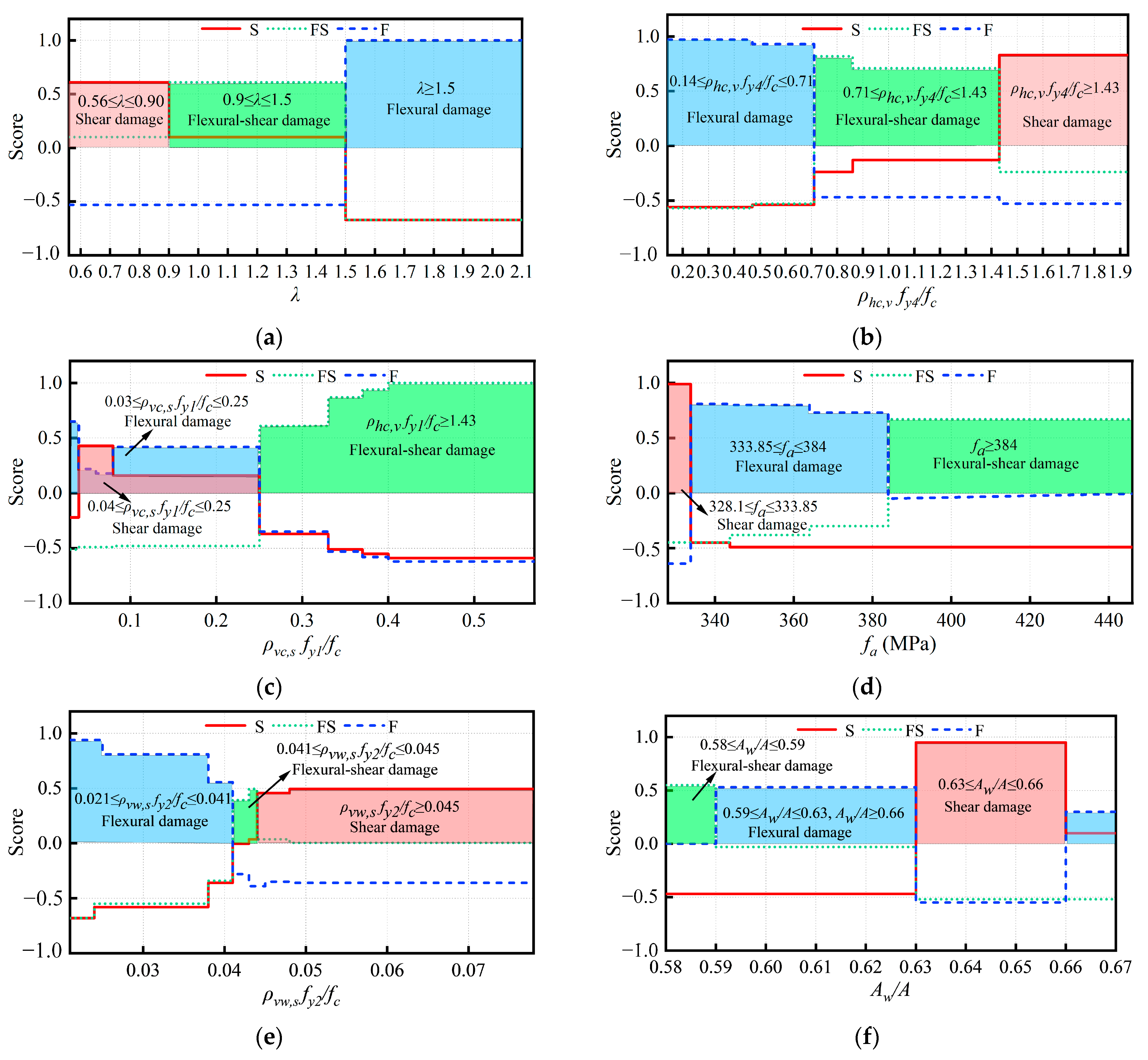
4.5. STRC Shear Walls Failure Modes Boundary Analysis
5. Conclusions
- (1)
- By augmenting the training dataset with GAN, we improved the predictive performance of STRC shear wall failure mode models. Compared to the initial dataset, the six models exhibited significant enhancements with average increases of 13% in accuracy, 81% in precision, 48% in recall, and 67% in F1-score. This approach effectively addresses the poor predictive performance issue in small sample databases, enhancing the accuracy of models.
- (2)
- The Blending-CRKL fusion model proposed in this study outperformed the other models in predicting the failure modes of STRC shear walls. It achieved an outstanding accuracy of 97% when trained with the GAN-augmented dataset, surpassing the performance of KNN, BPNN, RF, LightGBM, and Catboost models. Additionally, the Blending-CRKL model demonstrated good robustness and stability, making it highly suitable for accurately predicting the failure modes of STRC shear walls.
- (3)
- The Blending-CRKL fusion model was explained using SHAP. The results showed that the shear–span ratio (λ) is the most important feature for identifying the failure modes of STRC shear walls, followed by the horizontal bar index in the boundary element (ρhc,v fy4/fc) and the vertical bar index in the boundary element (ρvc,s fy1/fc). Additionally, the reinforcement configuration of the boundary elements plays a crucial role in the shear and flexural failure of STRC shear walls.
- (4)
- Analysis of the features value range of different failure modes of STRC shear walls reveals that as the shear–span ratio (λ) increases, the probability of flexural failure also increases. A larger value of the boundary element horizontal bar index (ρhc,v fy4/fc), the vertical bar index of the web (ρvw,s fy2/fc), and the web area ratio (Aw/A) indicates a higher likelihood of shear failure in the shear wall. On the other hand, a larger value of the boundary element vertical bar index (ρvc,s fy1/fc) and the compressive strength of concrete (fa) indicates a higher likelihood of flexural shear failure in the shear wall.
- (5)
- In future research, the Blending-CRKL model proposed in this study can be further improved by expanding the experimental data and validating the predictive results of the model in engineering practice. These efforts will contribute to continuously enhancing the prediction accuracy of the model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wan, L.C.; Hong, Y.D.; Jian, W.Z. Experimental Study and Theoretical Analysis on Seismic Performance of RC Shear Wall with STRC Columns and Embedded Steel Plate. Adv. Mater. Res. 2012, 446–449, 1006–1013. [Google Scholar]
- Zhou, J.; Fang, X.; Yao, Z. Mechanical behavior of a steel tube-confined high-strength concrete shear wall under combined tensile and shear loading. Eng. Struct. 2018, 171, 673–685. [Google Scholar] [CrossRef]
- Li, X.; Zhao, Z.; Qian, J.; Liu, S.; Le, H.E.; Han, X. Experimental studies on seismic performance of precast shear walls with hybrid vertical rebar connections. J. Harbin Inst. Technol. 2020, 52, 1–9. [Google Scholar]
- Greifenhagen, C.; Lestuzzi, P. Static cyclic tests on lightly reinforced concrete shear walls. Eng. Struct. 2005, 27, 1703–1712. [Google Scholar] [CrossRef]
- Teng, S.; Chandra, J. Cyclic Shear Behavior of High-Strength Concrete Structural Walls. ACI Struct. J. 2016, 113, 1335–1345. [Google Scholar] [CrossRef]
- Vadyala, S.R.; Betgeri, S.N.; Matthews, J.C.; Matthews, E. A Review of Physics-based Machine Learning in Civil Engineering. Results Eng. 2022, 13, 100316. [Google Scholar] [CrossRef]
- Mangalathu, S.; Jang, H.; Hwang, S.-H.; Jeon, J.-S. Data-driven machine-learning-based seismic failure mode identification of reinforced concrete shear walls. Eng. Struct. 2020, 208, 110331. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, X.; Li, Y.; Du, X. Prediction of failure modes, strength, and deformation capacity of RC shear walls through machine learning. J. Build. Eng. 2022, 50, 104145. [Google Scholar] [CrossRef]
- Liang, D.; Xue, F. Integrating automated machine learning and interpretability analysis in architecture, engineering and construction industry: A case of identifying failure modes of reinforced concrete shear walls. Comput. Ind. 2023, 147, 103883. [Google Scholar] [CrossRef]
- Siam, A.; Ezzeldin, M.; El-Dakhakhni, W. Machine learning algorithms for structural performance classifications and predictions: Application to reinforced masonry shear walls. Structures 2019, 22, 252–265. [Google Scholar] [CrossRef]
- Ma, G.; Wang, Y. Failure mode prediction and explanation of concrete-filled steel tubular shear walls based on machine learning. Earthq. Eng. Eng. Dyn. 2022, 42, 143–152. (In Chinese) [Google Scholar]
- Kim, E.-J. Analysis of Travel Mode Choice in Seoul Using an Interpretable Machine Learning Approach. J. Adv. Transp. 2021, 2021, 6685004. [Google Scholar] [CrossRef]
- Barbados, A.; Corcho, S. Vehicle Fuel Optimization Under Real-World Driving Conditions: An Explainable Artificial Intelligence Approach. arXiv 2021, arXiv:2107.06031. [Google Scholar]
- Štrumbelj, E.; Kononenko, I. Explaining prediction models and individual predictions with feature contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Mangalathu, S.; Hwang, S.-H.; Jeon, J.-S. Failure mode and effects analysis of RC members based on machine-learning-based SHapley Additive exPlanations (SHAP) approach. Eng. Struct. 2020, 219, 110927. [Google Scholar] [CrossRef]
- Lai, D.; Demartino, C.; Xiao, Y. Interpretable machine-learning models for maximum displacements of RC beams under impact loading predictions. Eng. Struct. 2023, 281, 115723. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Islam, K.; Bekdaş, G.; Kim, S.; Geem, Z.W. Interpretable Machine Learning Algorithms to Predict the Axial Capacity of FRP-Reinforced Concrete Columns. Materials 2022, 15, 2742. [Google Scholar] [CrossRef]
- Ding, H.; Lu, Y.; Sze, N.; Chen, T.; Guo, Y.; Lin, Q. A deep generative approach for crash frequency model with heterogeneous imbalanced data. Anal. Methods Accid. Res. 2022, 34, 100212. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y. Credibility evaluation method of small sample data based on cluster cloud model. J. Syst. Simul. 2019, 31, 1263. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Wang, T.; Trugman, D.; Lin, Y. SeismoGen: Seismic Waveform Synthesis Using GAN with Application to Seismic Data Augmentation. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020077. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, J.; Feng, Y.; Wang, R.; Zhao, Z.; Chen, H. Hydrogen yield prediction for supercritical water gasification based on generative adversarial network data augmentation. Appl. Energy 2023, 336, 120814. [Google Scholar] [CrossRef]
- Chen, N.; Zhao, S.; Gao, Z.; Wang, D.; Liu, P.; Oeser, M.; Wang, L. Virtual mix design: Prediction of compressive strength of concrete with industrial wastes using deep data augmentation. Constr. Build. Mater. 2022, 323, 126580. [Google Scholar] [CrossRef]
- Qian, J.; Jiang, Z.; Ji, X. Behavior of steel tube-reinforced concrete composite walls subjected to high axial force and cyclic loading. Eng. Struct. 2012, 36, 173–184. [Google Scholar] [CrossRef]
- Deger, Z.T.; Kaya, G.T. Glass-box model representation of seismic failure mode prediction for conventional reinforced concrete shear walls. Neural Comput. Appl. 2022, 34, 13029–13041. [Google Scholar] [CrossRef]
- Moehle, J.P. Seismic Design of Reinforced Concrete Buildings; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Paulay, T.; Priestley, M. Seismic design of reinforced concrete and masonry buildings. In Seismic Design of Reinforced Concrete and Masonry Buildings; Wiley: New York, NY, USA, 1992. [Google Scholar]
- American Society of Civil Engineers. Seismic Evaluation and Retrofit of Existing Buildings; American Society of Civil Engineers: Reston, VA, USA, 2017. [Google Scholar]
- Yang, G. Study on Seismic Behavior of CFT Composite Shear Walls under High Axial Compression Ratio; Tsinghua University: Beijing, China, 2013. (In Chinese) [Google Scholar]
- Luo, W. The Studies on Force Mechanism of Steel Pipe Concrete Structural Wall of Small Shear Span Ratio; Chang’an University: Xi’an, China, 2014. (In Chinese) [Google Scholar]
- Bai, L.; Zhou, T.H.; Luo, X.W.; Zhang, Y.; Luo, W. Experimental study on the seismic behavior of steel tube confined high-strength concrete shear walls. China Civ. Eng. J. 2014, 47, 9–17. (In Chinese) [Google Scholar]
- Li, Q. Experimental Study on Axial-Flexural Behavior of Shear Walls with Steel Tube-Confined High Performance Concrete; South China University of Technology: Guangzhou, China, 2012. (In Chinese) [Google Scholar]
- Sun, X.M. Experimental Study on Shear Behavior of Shear Wall with Steel Tube-Confined High-Strength Concrete; South China University of Technology: Guangzhou, China, 2013. (In Chinese) [Google Scholar]
- Qiang, J.R.; Jiang, Z.; Ji, X.D. Experimental study on seismic behavior of steel tube-reinforced concrete composite shear walls with high axial compressive load ratio. J. Build. Struct. 2010, 31, 40–48. (In Chinese) [Google Scholar]
- Maleki, A.; Haghighi, A.; Mahariq, I. Machine learning-based approaches for modeling thermophysical properties of hybrid nanofluids: A comprehensive review. J. Mol. Liq. 2021, 322, 114843. [Google Scholar] [CrossRef]
- JGJ 3-2010; Technical Specification for Concrete Structures of Tall Building. China Ministry of Construction: Beijing, China, 2010. (In Chinese)
- CECS 188; Technical Specification for Steel Tube-Reinforced Concrete Column Structure. China Planning Press: Beijing, China, 2005. (In Chinese)
- JGJ 138–2001; Standard Chinese. Technical Specification for Steel Reinforced Concrete Composite Structures. China Architecture and Building Press: Beijing, China, 2002. (In Chinese)
- ACI 318-19; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2019.
- EN 1998-1; Eurocode 8: Design of Structures for Earthquake Resistance, Part-1. European Union; CEN: Brussels, Belgium, 2005.
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- García, C.A.; Gil-de-la-Fuente, A.; Barbas, C.; Otero, A. Probabilistic metabolite annotation using retention time prediction and meta-learned projections. J. Cheminform. 2022, 14, 33. [Google Scholar] [CrossRef]
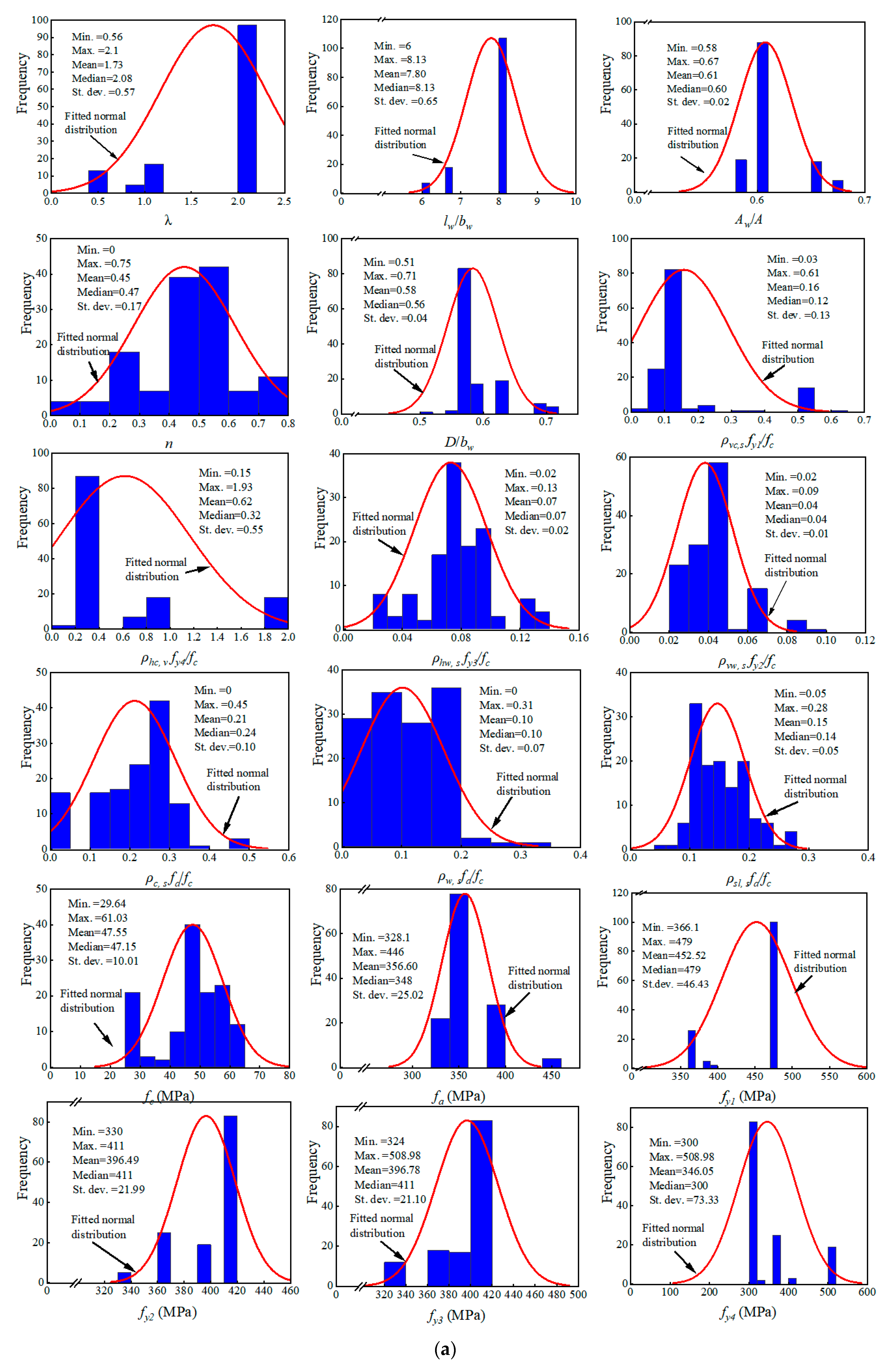
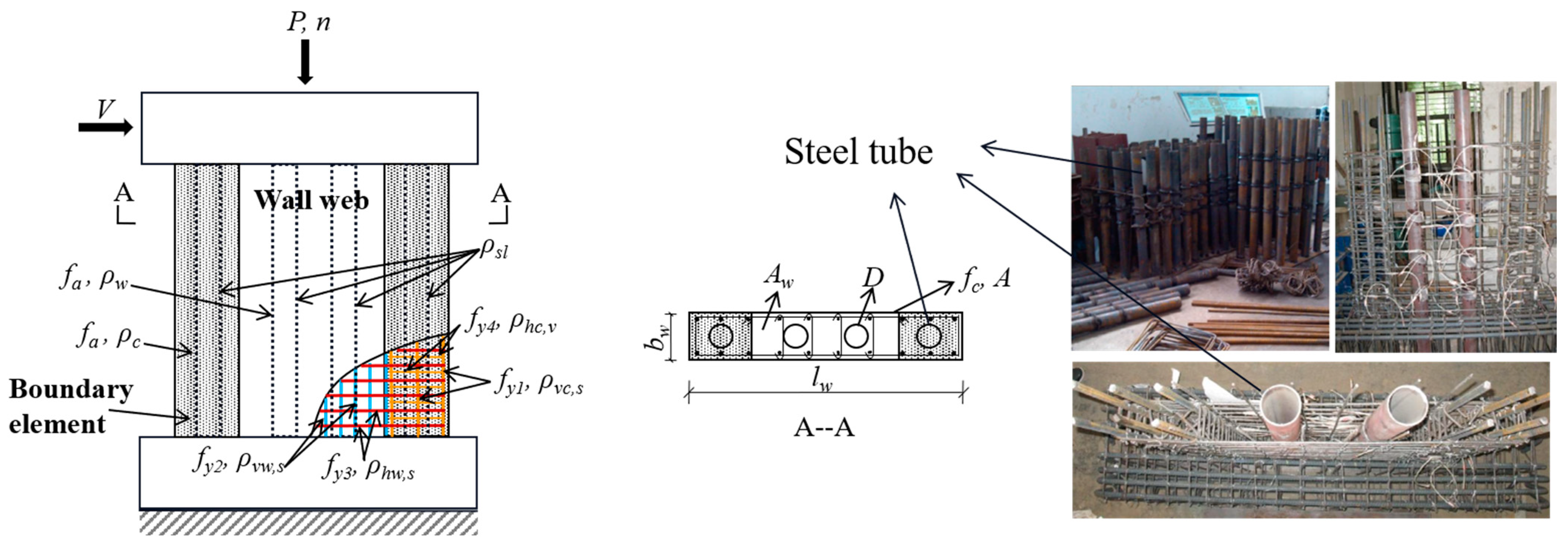


| Group | Symbol | Unit | Feature Description |
|---|---|---|---|
| Geometric characteristics | λ | (-) | Shear–span ratios. |
| lw/bw | (-) | Wall length and thickness ratios. | |
| Aw/A | (-) | Area share of webs. | |
| D/bw | (-) | Steel tubular diameter to wall thickness ratio. | |
| Material properties | fc | MPa | Yield stress of steel tubular. |
| fa | MPa | Concrete compressive strength. | |
| fy1 | MPa | Yield stress of vertical bars in boundary element. | |
| fy2 | MPa | Yield stress of vertical bars in the web. | |
| fy3 | MPa | Yield stress of horizontal bars in the web. | |
| fy4 | MPa | Yield stress of horizontal bars in boundary element. | |
| Mechanical properties | n | (-) | Axial force ratio. |
| ρvc,sfy1/fc | (-) | Vertical bars index in boundary element. | |
| ρvw,sfy2/fc | (-) | Vertical bars index in the web. | |
| ρhw,sfy3/fc | (-) | Horizontal bars index in the web. | |
| ρhc,vfy4/fc | (-) | Horizontal bars index in boundary element. | |
| ρc,sfa/fc | (-) | Configuration steel tubular index in boundary element. | |
| ρw,sfa/fc | (-) | Configuration steel tubular index in the web. | |
| ρsl,sfa/fc | (-) | Whole section configuration steel tubular index. |
| Accuracy | Improved Rate | Precision | Improved Rate | Recall | Improved Rate | F1-Score | Improved Rate | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial | GAN | Initial | GAN | Initial | GAN | Initial | GAN | |||||
| RF | 0.85 | 0.93 | 9% | 0.50 | 0.85 | 70% | 0.66 | 0.97 | 47% | 0.56 | 0.90 | 61% |
| Catboost | 0.85 | 0.95 | 12% | 0.56 | 0.98 | 75% | 0.66 | 0.87 | 32% | 0.61 | 0.91 | 49% |
| LightGBM | 0.82 | 0.93 | 13% | 0.46 | 0.92 | 100% | 0.59 | 0.86 | 46% | 0.50 | 0.87 | 74% |
| BPNN | 0.75 | 0.88 | 17% | 0.42 | 0.84 | 100% | 0.56 | 0.89 | 59% | 0.45 | 0.84 | 87% |
| KNN | 0.78 | 0.9 | 15% | 0.45 | 0.85 | 89% | 0.62 | 0.96 | 55% | 0.48 | 0.88 | 83% |
| Blending-CRKL | 0.88 | 0.97 | 10% | 0.62 | 0.94 | 94% | 0.67 | 0.99 | 48% | 0.64 | 0.96 | 50% |
| Average | 13% | 81% | 48% | 67% | ||||||||
| Features | Failure Modes | ||
|---|---|---|---|
| S | FS | F | |
| λ | 0.56 ≤ λ ≤ 0.90 | 0.90 ≤ λ ≤ 1.50 | λ ≥ 1.50 |
| ρhc,vfy4/fc | ρhc,vfy4/fc≥ 1.43 | 0.71 ≤ ρhc,v fy4/fc ≤ 1.43 | 0.14 ≤ ρhc,v fy4/fc ≤ 0.71 |
| ρvc,s fy1/fc | 0.04 ≤ ρvc,s fy1/fc ≤ 0.25 | ρvc,s fy1/fc≥ 1.43 | 0.03 ≤ ρvc,s fy1/fc ≤ 0.25 |
| fa(MPa) | 328.1 ≤ fa≤ 333.85 | fa≥ 384 | 333.85 ≤ fa≤ 384 |
| ρvw,s fy2/fc | ρvw,s fy2/fc≥ 0.045 | 0.041 ≤ ρvw,s fy2/fc≤ 0.045 | 0.021 ≤ ρvw,s fy2/fc≤ 0.041 |
| Aw/A | 0.63 ≤ Aw/A ≤ 0.66 | 0.58 ≤ Aw/A ≤ 0.59 | 0.59 ≤ Aw/A ≤ 0.63, Aw/A ≥ 0.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Zhang, J.; Ma, Z.; Xu, W. Prediction of Failure Modes of Steel Tube-Reinforced Concrete Shear Walls Using Blending Fusion Model Based on Generative Adversarial Networks Data Augmentation. Appl. Sci. 2023, 13, 12433. https://doi.org/10.3390/app132212433
Yang G, Zhang J, Ma Z, Xu W. Prediction of Failure Modes of Steel Tube-Reinforced Concrete Shear Walls Using Blending Fusion Model Based on Generative Adversarial Networks Data Augmentation. Applied Sciences. 2023; 13(22):12433. https://doi.org/10.3390/app132212433
Chicago/Turabian StyleYang, Guangchao, Jigang Zhang, Zhehao Ma, and Weixiao Xu. 2023. "Prediction of Failure Modes of Steel Tube-Reinforced Concrete Shear Walls Using Blending Fusion Model Based on Generative Adversarial Networks Data Augmentation" Applied Sciences 13, no. 22: 12433. https://doi.org/10.3390/app132212433
APA StyleYang, G., Zhang, J., Ma, Z., & Xu, W. (2023). Prediction of Failure Modes of Steel Tube-Reinforced Concrete Shear Walls Using Blending Fusion Model Based on Generative Adversarial Networks Data Augmentation. Applied Sciences, 13(22), 12433. https://doi.org/10.3390/app132212433






