Optimizing Two-Dimensional Irregular Packing: A Hybrid Approach of Genetic Algorithm and Linear Programming

Abstract

The problem of two-dimensional irregular packing involves the arrangement of objects with diverse shapes and sizes within a given area. This challenge arises across various industrial sectors, where effective packing optimization can yield cost savings, enhanced productivity, and reduced material waste. Existing methods for addressing the two-dimensional irregular packing problem encounter several challenges, such as limited computing resources, a prolonged solving time, and the propensity to converge to local optima. To address this issue, this study proposes a hybrid algorithm called the GA-LP algorithm to optimize the two-dimensional irregular packing problem in the manufacturing industry. The algorithm combines the global search capability of a genetic algorithm with the precise solving characteristics of linear programming. Matheuristics merges the advantages of metaheuristics, such as genetic algorithms, and mathematical programming, such as linear programming. The algorithm employs the no-fit-polygon technique along with the bottom-left and lowest-gravity center mixing placement strategies to acquire an initial solution via the utilization of a genetic algorithm. The algorithm then optimizes the solution obtained by the genetic algorithm using linear programming to obtain the final packing result. Experimental results, drawn from a real case involving the European Special Interest Group on Cutting and Packing (ESICUP) demonstrate that the GA-LP algorithm outperforms two hybrid algorithms from the relevant literature. Compared with recent methods, this algorithm can increase the best and average utilization rates by up to 5.89% and 4.02%, respectively, with important implications for improving work quality in areas such as packing and cutting.

1. Introduction

The problem of two-dimensional irregular packing entails the placement of irregular shapes within a limited area with the objective of optimizing material utilization. The utilization of sheets is prevalent in various industry sectors, including mechanical manufacturing, metal processing, aerospace engineering, automobile manufacturing, and furniture manufacturing [1]. At the societal level, the enhancement of material utilization can have a substantial impact on environmental conservation. In addition, even a slight increase in packing density can result in significant economic gain.

The primary focus of manufacturing industries is undeniably the optimization of material utilization, a task of utmost importance in their efforts to mitigate the rising expenses associated with raw materials. To exemplify the significant cost reduction possibilities, it is worth examining the leather industry in China, which, in the year 2021, achieved an astonishing production output of 597 million square meters of leather [2]. Even a slight increase of 0.01% in material utilization has the potential to save up to 60,000 square meters of leather. Additionally, during the period of January to December 2021, China recorded an import of 612,500 tons of cattle and horse leather, with a total value amounting to US $2.096 billion [3]. The potential to increase leather utilization rates not only offers significant economic advantages, but also aligns with the urgent requirement for environmental sustainability, emphasizing the critical necessity for inventive approaches. The primary objective of this research is to enhance material utilization rates, acknowledging this as the fundamental focus of the study’s purpose. While prioritizing material utilization, the ultimate objective is to achieve the best possible balance with respect to calculation time. Striking an optimal balance between these two critical elements is essential for the success of the study.

Currently, there has been significant research conducted on the problem of two-dimensional irregular packing, resulting in the proposal of various solutions. These solutions are commonly classified into three distinct categories: mathematical programming methods, heuristic algorithms, and machine learning methods [4]. Mathematical programming methods can be used to handle complex constraints and obtain optimal solutions. For instance, Imamichi et al. proposed a separation overlap polygon algorithm based on nonlinear programming, which finds a new position with the least overlap on a material board by exchanging the placement positions of the two polygons on the original material board [5]. Toledo et al. introduced a mixed integer model that establishes a correlation between discrete points, commonly represented as grids, on the material board and each specific type of workpiece using binary decision variables. The representation of the workpiece type in the model requires the use of binary variables to indicate whether a particular workpiece type is selected. Additionally, discrete points are employed to determine the placement position of the workpiece [6]. Leao et al. proposed an innovative semi-continuous mixed integer programming model for the two-dimensional cutting and packing problem of irregularly shaped workpieces, and partially simplified the developed mathematical model [7]. Cherri et al., introduced a mixed integer quadratically constrained programming model to address the irregular strip packing problem, taking into account the continuous rotation of workpieces. The authors also conducted an analysis of the model’s strengths and weaknesses [8]. Oliveira et al. proposed a mathematical programming model that addresses the integration of irregular strip packing and cutting path determination problems [9]. Heuristic algorithms, including greedy algorithms, simulated annealing algorithms, and genetic algorithms, have the capability to yield satisfactory solutions within a limited timeframe. For instance, Terashima-Marín introduced a comprehensive hyper-heuristic algorithm utilizing genetic algorithms, specifically designed to address the challenges posed by two-dimensional regular (rectangular) and irregular (convex polygon) bin packing problems [10]. Hu proposed a greedy adaptive search algorithm that involves the construction of an evaluation function and the introduction of a restricted local search strategy [11]. Fang proposed a novel algorithm called Sequence Transfer-Based Particle Swarm Optimization (ST-PSO) to address the challenges of multi-constraint layout problems. This algorithm was inspired by transfer learning and takes into account the characteristics of two-dimensional irregular layouts [12]. Rao proposed a hybrid search algorithm (BSTS) to solve the irregular packing problem. The algorithm combines beam search (BS) and tabu search (TS) to search for an optimal sequence of irregular pieces on a plate [13]. Guerriero introduced a dynamic hierarchical hyper-heuristic approach that involves the utilization of low-level heuristics. These heuristics are combined in various manners using the main hyper-heuristic in order to determine the most effective heuristic operators for solving the two-dimensional irregular bin packing problem [14]. Pinheiro presented a random-key genetic algorithm (RKGA) for solving the nesting problem. This algorithm combines the power of a metaheuristic approach, the random-key genetic algorithm, with well-known placement strategies, such as the bottom-left strategy [15]. In recent years, researchers have begun to explore machine learning methods to solve two-dimensional irregular packing problems. These techniques forecast the potential packing solutions based on historical data. For instance, Huang proposed a deep hierarchical reinforcement learning approach to effectively plan the packing order and placement of irregular objects [16]. In a similar vein, Tu investigated a deep reinforcement learning hyper-heuristic with feature fusion to address online packing problems [17].

Despite the advantages associated with these techniques, they also possess several drawbacks and limitations. Insufficient computational resources and lengthy solution durations for larger problems are two challenges that may arise when employing mathematical programming approaches. These challenges can significantly diminish the effectiveness of problem-solving efforts. Heuristic algorithms necessitate a gradual improvement in algorithm performance through the incorporation of additional variable elements and the adjustment of algorithm parameters. This is essential as heuristic algorithms are susceptible to becoming trapped in local optimal solutions. The effectiveness of machine learning techniques in processing heavily depends on the training set. This particular dataset necessitates a substantial quantity of meticulously curated samples for the purposes of training and algorithm refinement. Consequently, a longer duration is required to acquire a more refined set of samples. For packing problems on a large scale, the utilization of machine learning-based searches can result in significant time consumption.

To tackle the aforementioned challenges, this study presents a pioneering and inventive solution: the GA-LP optimization algorithm. By integrating genetic algorithms (GAs) with linear programming (LP), our algorithm presents a distinctive and robust solution that surpasses the constraints of current methodologies. In contrast to prior research, the GA-LP algorithm capitalizes on the synergistic capabilities of genetic algorithms (GAs) and linear programming (LP). This approach enables a more streamlined and successful optimization of packing configurations, effectively balancing efficiency and utilization in the resolution of irregular two-dimensional packing problems. By conducting rigorous experimental evaluations on problem instances of varying sizes provided by the European Special Interest Group on Cutting and Packing (ESICUP), the GA-LP algorithm has exhibited superior performance in comparison to both the BSTS algorithm and the RKGA-NP algorithm. This superiority is evident across multiple metrics, such as optimal utilization rate, average utilization rate of the board, and packing time. It has proven the effectiveness and versatility of this algorithm in practical work scenarios.

The subsequent sections of this paper are organized in the following manner. In Section 2, the mathematical model of the two-dimensional irregular packing problem is presented. Section 3 presents the hybrid placement strategy based on NFP. Section 4 offers a comprehensive description of the GA-LP algorithm and its optimization procedures. The computational results and comparisons are presented in Section 5. Finally, the paper is concluded in Section 6.

2. Problem Statement

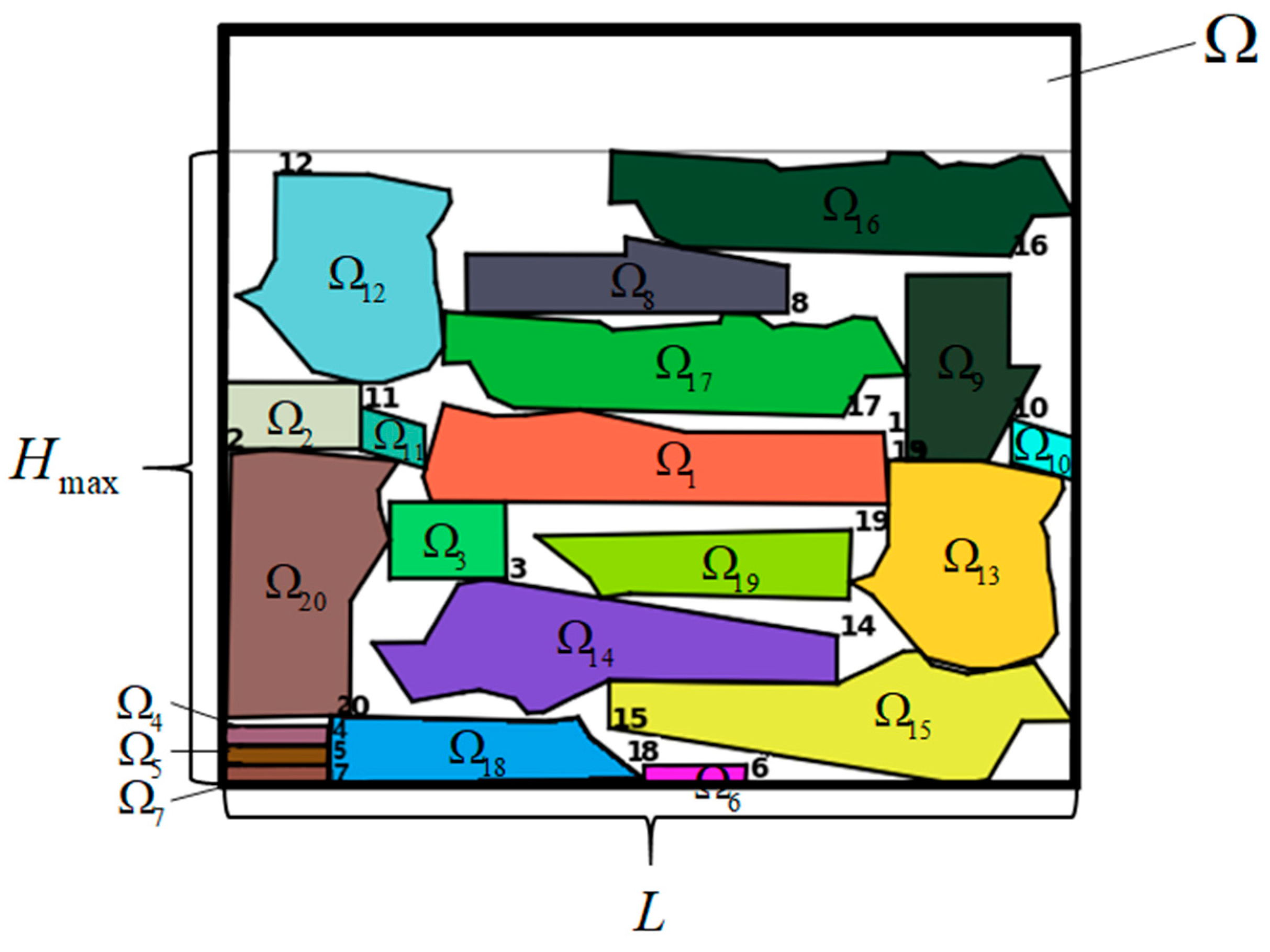
In the realm of manufacturing, specifically in the field of sheet cutting, it is a prevalent necessity to arrange and cut various shapes and quantities of workpieces on a predetermined size of raw material sheet. The objective is to optimize the utilization of each sheet by either maximizing its usage or minimizing the number of sheets required. This study exclusively addresses the issue of irregular packing in rectangular raw material areas. Mathematically, this problem can be described as follows:

Given a rectangular raw material board $\Omega$ with a length of $L$ and $p$ pieces of workpieces to be arranged, the $i-th$ and $j-th$ workpieces to be arranged are ${\Omega }_i$ and ${\Omega }_j$, respectively, with areas of $S_i$ and $S_j$. The initial position of each workpiece to be arranged is represented by a coordinate list composed of all its vertices coordinates. The initial position of the $i-th$ workpiece to be arranged is $\left[\left[x_{i1},y_{i1}\right],\left[x_{i2},y_{i2}\right],\cdots ,\left[x_{in},y_{in}\right]\right]$ ($n$ is the number of its vertices), that is, the coordinate list of all workpieces to be arranged is $\left[\left[\left[x_{11},y_{11}\right],\left[x_{12},y_{12}\right],\cdots ,\left[x_{1n},y_{1n}\right]\right],\left[\left[x_{21},y_{21}\right],\left[x_{22},y_{22}\right],\cdots ,\left[x_{2n},y_{2n}\right]\right],\cdots ,\left[\left[x_{p1},y_{p1}\right],\left[x_{p2},y_{p2}\right],\cdots ,\left[x_{pn},y_{pn}\right]\right]\right]$. The angle that the workpiece to be arranged can be rotated relative to the initial posture is $\theta$ (i.e., the workpiece to be arranged can be placed in different directions by a certain angle, typically 90° or its multiples, to increase the position variation of the workpiece, improve the search efficiency of the algorithm, and help the algorithm find more possible solutions and increase the probability of obtaining higher-quality optimal solutions). The maximum contour height of the packing result is $H_{\max }$, and the utilization rate of the board material is $U$. A schematic diagram with some symbol meanings is shown in Figure 1.

The objective is to minimize the maximum contour height of the packing result, denoted as $H_{\max }$, while ensuring that each workpiece is fully contained within the rectangular sheet (${\Omega }_i\in \Omega$), that workpieces do not overlap (${\Omega }_i\cap {\Omega }_j=\varnothing$), and that the allowable rotation angle ${\theta }_i$ meets the specific process requirements. Moreover, the utilization rate of the board material $U$ is constrained to fall within the range [0, 1]. Therefore, we define the two-dimensional irregular packing problem as follows:

$$\mathrm{minimize} H_{\max }$$

(1)

$$\mathrm{subject} \mathrm{to} {\Omega }_i\in {\Omega }^{}{,}^{} {{}^{}}^{}1\le i\le p$$

(2)

$${\Omega }_i\cap {\Omega }_j={\varnothing }^{}{,}^{} {{}^{}}^{}1\le i<j\le p$$

(3)

$${\theta }_i\in {\theta }^{}{,}^{} {{}^{}}^{}1\le i\le p{,}^{} {{}^{}}^{}0\le \theta \le 2\pi$$

(4)

$$U\in \left[0,1\right]$$

(5)

$$H_{\max }\in ℝ$$

(6)

Formula (2) indicates that all the workpieces to be arranged must be completely contained within the rectangular sheet, Formula (3) indicates that the workpieces to be arranged cannot overlap, and Formula (4) indicates that the allowable rotation angle of the workpieces to be arranged must meet the process requirements, for example, some leather workpieces need to be cut in the same direction to maintain the consistency of their surface texture.

This mathematical model provides a foundation for the subsequent algorithmic approach that will effectively solve the irregular packing problem, with the primary objective being to minimize $H_{\max }$ and optimize material utilization.

3. NFP-Based Hybrid Placement Strategy

3.1. No-Fit Polygon

This study adopted the method of constructing a no-fit polygon (NFP) to satisfy the constraint that the workpieces to be arranged do not overlap. Moreover, the inner polygon is introduced to determine whether all the workpieces to be arranged are completely contained within the boundary of the raw material sheet.

There are three main construction methods for the no-fit polygon: (1) the Minkowski sum [18,19,20,21], (2) the decomposition algorithm [22], and (3) the orbital sliding algorithm [23,24,25]. The Minkowski sum method has a high computational complexity and requires a large amount of computational resources. The execution time of the algorithm significantly increases as the polygon’s number of vertices increases. The decomposition algorithm may be ineffective and unable to manage polygons with concave or convex structures due to the decomposition algorithm’s potential to produce a large number of vertices and tangents.

In comparison, the track sliding algorithm can accommodate a variety of irregular shapes and is relatively simple to implement. In addition, it has good applicability and versatility. Furthermore, by altering the parameters, this method can increase the accuracy by reducing the distance between the created NFP and actual components. The track sliding approach has a low computing complexity when compared to other methods, which allows for the quick completion of a significant amount of calculation work. Additionally, the independent calculation steps of this method make it simple to parallelize and boost the computational efficiency. The calculation of the NFP in this study utilizes the orbital sliding algorithm. The operational procedure is outlined as follows:

Given two polygons ${\Omega }_i$ and ${\Omega }_j$, polygon ${\Omega }_i$ remains fixed while a reference point (e.g., the top-right corner) is selected on polygon ${\Omega }_j$. Polygon ${\Omega }_j$ is then slid along the edges of polygon ${\Omega }_i$ for one full rotation, keeping the edges of both polygons in contact and non-overlapping. Neither of the polygons undergo rotation throughout the entire movement. The trajectory of the reference point forms a new polygon, called $NF{P}_{ij}$, as shown in Figure 2.

If the reference point is inside $NF{P}_{ij}$, the two polygons will overlap, denoted as ${\Omega }_i\cap {\Omega }_j\ne \varnothing$, which means that the packing solution is not feasible, as shown in Figure 3a. If the reference point is on the edge of $NF{P}_{ij}$, the two polygons will touch only at the edges, and if the reference point is outside of $NF{P}_{ij}$, the two polygons will not overlap, denoted as ${\Omega }_i\cap {\Omega }_j=\varnothing$. Both cases satisfy the condition and the packing solution is feasible, as shown in Figure 3b,c.

3.2. Construction of Inner Fit Polygon

The inner fit polygon (IFP) refers to the most suitable position for placing one polygon inside another polygon, which is the overlapping area between the minimum area bounding rectangle of the polygon and the other polygon. Since the raw material sheet studied in this study is rectangular, the IFP of the irregular parts relative to the rectangular raw material is also in the shape of a rectangle. Therefore, the inner fit polygon can also be called an inner fit rectangle (IFR). Its definition is as follows: given a raw material rectangle $\Omega$ and an arbitrary irregular polygon ${\Omega }_i$, polygon ${\Omega }_i$ can be completely placed inside rectangle $\Omega$. Select a point on polygon ${\Omega }_i$ as a reference point. While keeping rectangle $\Omega$ fixed, polygon ${\Omega }_i$ rigidly slides along the inner wall of rectangle $\Omega$. Throughout the entire sliding process, the boundary of the polygon remains in contact with the rectangle without overlapping. After a complete sliding cycle, the reference point trajectory on polygon ${\Omega }_i$ is its IFP relative to rectangle $\Omega$, which is represented as $IF{P}_{\Omega }{}_{{\Omega }_i}$. The specific calculation method is as follows:

Step 1: Define the inner fit rectangle IFR. Select a reference point on polygon ${\Omega }_i$ arbitrarily (e.g., choose a vertex of the polygon).

Step 2: Calculate the maximum width $w$ and maximum height $h$ of the minimum bounding rectangle of polygon ${\Omega }_i$.

Step 3: Move polygon ${\Omega }_i$ to the lower-left corner of the raw material rectangle $\Omega$. At this position, the reference point on polygon ${\Omega }_i$ is a vertex of the inner fit rectangle IFR.

Step 4: Move polygon ${\Omega }_i$ to the four corners of raw material rectangle $\Omega$, and the reference point of polygon ${\Omega }_i$ is now located at the four vertices of the inner fit rectangle. The width of IFR is $Widt{h}_{IFP}=Widt{h}_{\Omega }-w$ and the height is $Heigh{t}_{IFP}=Heigh{t}_{\Omega }-h$. Figure 4 shows the process of generating an IFR for polygon ${\Omega }_i$ relative to the rectangular raw material $\Omega$, and polygon ABCD, that is, $IF{P}_{\Omega }{}_{{\Omega }_i}$ is calculated.

3.3. Positioning Principles Based on Bottom-Left Strategy and Lowest-Gravity-Center Strategy

3.3.1. “Bottom-Left” Placement Strategy

The “bottom-left” placement strategy works by sorting the parts in a specific order (such as by size or other rules). Then, starting from the bottom-left corner, each part is placed one by one until the top-right corner, with the aim of placing them as far left and down as possible [26]. This strategy aims to minimize waste and maximize material utilization as much as possible. Compared to the simple “downward” strategy, the bottom-left strategy can more effectively fill gaps and has been observed to be an empirically better use of raw materials, as shown in Figure 5.

3.3.2. Lowest-Gravity-Center Strategy

The lowest-gravity-center strategy considers that the shape to be placed has a planar shape with a uniform mass distribution. Calculating its center of mass helps select the free area with the smallest distance to the centers of mass of the other already placed shapes for the best packing [27].

Its working principle is to first calculate the center of gravity of each part, and then sort the parts in order of vertical position, placing the part with the lowest center of gravity first. After the first part is placed in a certain position on the material table, the subsequent parts will be placed in the most stable position based on their center of gravity relative to the position of the previous part. This process is repeated until all parts are placed on the material table.

3.4. NFP-Based Hybrid Placement Strategy

Based on the NFP, the hybrid placement strategy places polygons within a given rectangle to minimize the height of the placed polygons. The input of the algorithm is a list of polygons, each of which can be considered as a closed area composed of multiple continuous line segments [12].

Firstly, set the width and height of the rectangle and the list of polygons to be placed, and place the first polygon in the bottom-left corner of the rectangle. Each polygon to be placed must be placed within the rectangle, and the current lowest height is updated every time a polygon is placed. When placing a polygon, first, obtain the inner fit rectangle (IFR) of the polygon, and then place the polygon inside the rectangle. In order to ensure that the polygons do not overlap, this algorithm uses the NFP algorithm to obtain the non-intersecting area between the polygons, intersects the IFR and all calculated NFPs, obtains the area in which the polygon can be placed, and translates the polygon to the bottom-left corner of the placeable area. Then, calculate the lowest point of the centroid of the area and move the polygon to that point. Finally, check the highest point of each placed polygon to calculate the lowest height within the current rectangle, which is the maximum contour height $H_{\max }$ of the final packing result. This algorithm combines the bottom-left strategy and the lowest-gravity-center strategy to ensure a compact arrangement of polygons while reducing gaps and waste.

The pseudocode for the hybrid placement strategy algorithm based on the NFP is shown in Algorithm 1. Among them, n represents the total number of workpieces to be arranged.

Algorithm 1 Hybrid Placement Strategy Based on NFP

1   Initialize the placement process   2   Place the first polygon in the bottom-left corner   3   for i = 1 to n, do   4       Calculate the IFR of the polygon   5       Calculate the NFP between the polygon and the already placed polygon   6       Calculate the intersection of two regions   7       Calculate the lowest point of the center of gravity in the region   8       Move the polygon to the calculated position   9        Calculate the height of all current polygons 10   end 11   Display all polygons and write the results in the text 12   return the maximum height $H_{\max }$

4. Hybrid Packing Strategy Based on Genetic Algorithm—Linear Programming

The two-dimensional irregular packing problem was solved using a genetic algorithm, and then the generated feasible solution was improved using the linear programming method to fully utilize the advantages of both and improve the accuracy and feasibility of solving the packing problem. By combining the global search ability of genetic algorithms with the exact solution of linear programming, material utilization can be improved while ensuring the best feasible solution is found, thereby further improving the efficiency of the algorithm.

4.1. Genetic Algorithm

4.1.1. Population Initialization

The first step in solving the two-dimensional irregular packing problem using a genetic algorithm is to create an initial population. To account for the chosen orientation of each workpiece, we encode the orientation information as integer values. For instance, if a workpiece can be placed in four different orientations (0°, 90°, 180°, and 270°), we represent each of these orientations with the integer values 0, 1, 2, and 3, respectively. The population consists of multiple solutions to the packing problem, and each solution includes a coordinate list of all workpieces to be scheduled and their corresponding rotation angle relative to the initial posture. To ensure diversity within the initial population, the order of all workpieces to be scheduled is randomly shuffled.

4.1.2. Determine the Fitness Function

The reciprocal of the maximum contour height $H_{\max }$ of the final packing result calculated using an NFP-based hybrid placement strategy is used as the fitness value, while an impact factor $a$ is added to avoid the fitness value being too small, in order to improve the performance and robustness of the algorithm. Specifically, the value of the impact factor $a$ depends on the restricted height of the packing space $\Omega$. The quality of each solution is evaluated using the fitness function to measure the degree to which it meets the problem requirements. For a feasible packing solution $x_i$, the fitness function can be expressed as:

$$f\left(x_i\right)=\frac{a}{H_{\max }}$$

(7)

The objective of two-dimensional irregular packing is to optimize the utilization of materials. Hence, when the length is held constant, it is desirable to have a smaller maximum contour height for the final packing outcome, indicating a higher fitness level.

4.1.3. Perform Selection Operation

This study employs the fitness selection ratio, commonly referred to as “roulette wheel selection”, as a method for selecting parents. In this approach, the probability of an individual being chosen is directly proportional to its fitness value. The following are the specific steps:

Step 1: Calculate the fitness function $f\left(x_i\right)$ for all packing solutions in this generation, as well as the probability of their selection for inheritance in the next generation $P_i$:

$$P_i={\frac{f\left(x_i\right)}{{\displaystyle \sum _{i=1}^{n}f\left(x_i\right)}}}^{}\left(i=1,2,\cdots ,n\right)$$

(8)

Step 2: The cumulative probability is the sum of all individual probabilities in front of the individual in the individual list. The cumulative probability of each individual $q_i$ is calculated as follows:

$$q_i={\displaystyle \sum _{j=1}^{i}P\left(x_j\right)}$$

(9)

Step 3: Generate a uniformly distributed pseudo-random number $r$ within the $\left[0,1\right]$ interval.

Step 4: If $q_1>r$, select individual 1 as the parent. Otherwise, select individual $k$ so that $q_{k-1}<r\le q_k$ is established.

Step 5: Repeat steps 3 and 4 until the population update is completed.

Meanwhile, this article employs an elitism strategy in the algorithm to ensure the preservation of the highest-performing individuals from one generation to the next. The objective of elitism is to guarantee the ongoing presence of outstanding solutions, hinder premature convergence to local optima, and augment the algorithm’s global search capability. The process of implementing elitism entails the following steps:

Step 1: Identify the individual with the maximum fitness function value in the current population.

Step 2: Preserve this selected individual for the next generation, ensuring its exclusion from the pool of parents.

4.1.4. Implementing a Cross-Operation

In genetic algorithms, crossover operation is one of the important operations for generating new individuals. Crossover operation refers to exchanging the chromosomes of two individuals in a certain way to produce new individuals. Its essence is to simulate the genetic recombination phenomenon in nature, that is, to combine the excellent genes of two individuals in the hope of obtaining more excellent offspring. Simultaneously, crossover operations can increase the genetic diversity of the population and improve the global search ability of genetic algorithms.

In this study, we used an ordered crossover (OX) to generate offspring. Ordered crossover is a commonly used crossover operation in genetic algorithms. It is a crossover method based on sequential coding that is suitable for solving optimization problems, particularly permutation optimization problems.

Specifically, the operation steps of ordered crossover are as follows:

Step 1: Randomly select two individuals as parents and randomly select two intersection points. Take Figure 6 as an example, where each number indicates the initial number of the workpiece to be arranged.

Step 2: In parent 1, copy the gene segment between the two intersections to offspring 1, and then insert the unselected genes into offspring 1 in sequence according to the gene sequence in parent 2 to create the chromosome of offspring 1. The generation method for offspring 2 is the same as that for offspring 1. Figure 7 shows this process.

Compared with other crossover methods, ordered crossover can keep the order and position of genes unchanged, effectively maintaining the constraints of the problem. In addition, because only gene segments are exchanged, ordered crossover can improve the convergence speed and search efficiency of the genetic algorithm.

4.1.5. Implement Mutation Operation

Mutation serves as a mechanism to prevent evolutionary stagnation and promote population diversity. When conducting reversal mutations on chromosomes utilizing binary or integer representations, it is necessary to choose a random gene sequence and reverse the order of genes within that sequence. In genetic algorithms, mutation plays an important role in exploring other parts of the solution space by introducing new paths, thereby avoiding becoming swamped by local optima.

When mutating, it is necessary to consider the rule that all pending packing shapes must be arranged and no shape can be discarded for irregular 2D packing. Therefore, the present study employs the reverse mutation technique. This mutation method randomly selects two mutation points and reverses the gene order between the mutation points. That is to say, in the context of a specific low probability, two shapes have the potential to swap positions within the packing solution. Figure 8 shows this process.

4.1.6. Determining the Stopping Criteria

The utilization of a stopping criterion is essential in determining the appropriate termination point for a genetic algorithm. This objective can typically be accomplished by establishing the termination criteria, such as the maximum number of generations or the maximum computation time. When the specified stopping criterion is met, the algorithm will return the best found feasible solution that has been discovered up to that point. In the present study, the fitness function converges within 20 generations during the computation of the instance. Therefore, the maximum number of generations in this study has been established as 30. Algorithm 2 provides the specific steps of the genetic algorithm iteration.

Algorithm 2 Genetic Algorithm

1   Initialize population size to 40, chromosome length to N, mutation rate to 0.1, and max generations to 30   2   Create an empty list population   3   Initialize best solution variable as None   4   for i in range(population size), do   5       Create a new chromosome the length of the number of workpieces to be arranged   6       Append the chromosome to the population list   7   end   8   for generation in range(max generations), do   9       Calculate the fitness value for each chromosome in the population 10       Select the parents from the population using a selection process and their corresponding fitness values 11       Create offspring by applying the crossover operator to the selected parents with a certain crossover rate 12       Apply mutation to the offsprings with a certain mutation rate 13       Use the replacement function to create a new population by replacing the worst chromosomes in the population with the mutants 14       if a better solution is found in the new population 15          Update the best solution variable 16       Output the best solution and its fitness value using the output function 17   end

4.2. Linear Programming

This study employs coin-or branch and cut (CBC) solvers for the purpose of solving linear programming models and obtaining the optimal solution. A CBC solver uses an improved simplex algorithm to solve the linear programming problem. The simplex algorithm is an iterative method that starts with feasible vertices (i.e., feasible solutions) and moves along the edges of the feasible region until it reaches the optimal vertex. In each iteration, the algorithm selects a variable that can be increased or decreased to improve the objective function, while remaining within the feasible region. The algorithm terminates when the optimal solution conditions are satisfied or when the specified maximum number of iterations is reached. The improved simplex algorithm reduces the number of operations required for each iteration and lowers the computational complexity of each iteration, thereby making it more efficient in practice and able to converge to an optimal solution faster. In addition, the CBC solver uses techniques such as degenerate handling and numerical stability checks to improve the performance and accuracy of the simplex algorithm.

After obtaining the packing solution, it is checked to ensure that it meets the requirements of the constraint conditions and objective functions in the mathematical formulation section. Simultaneously, necessary adjustments and modifications are made to the packing solution to meet the requirements of the constraint conditions and objectives, and the final packing solution is obtained.

The procedure for improving the solution using linear programming can be outlined as follows:

Step 1: Initialization of the algorithm. The coordinate sequence of the optimal solution obtained by the genetic algorithm is obtained as the initial workpiece coordinate list. Additionally, the width of raw materials and the maximum time allowed for the algorithm operation are set.

Step 2: Generate possible workpiece discharge directions. Traverse each potential direction (e.g., 0°, 90°, 180°, and 270°, represented by integer values 0, 1, 2, and 3) in order to compile a comprehensive list of the potential workpiece orientations.

Step 3: Develop a linear programming model. The model is expressed as a collection of constraints and an objective function. Constraints dictate that every workpiece must be contained within the raw material board and must not overlap with any other workpiece. The objective function aims to maximize the utilization of packing materials. The linear programming model is as follows:

$$\mathrm{maximize} Ma{x}^{}U=\frac{{\displaystyle \sum _{i=1}^n{S}_i}}{L\times H_{\max }}\times 100\%$$

(10)

$$\mathrm{subject} \mathrm{to} {\Omega }_i\in {\Omega }^{}{,}^{} {{}^{}}^{}1\le i\le p$$

(11)

$$0\le S_i\le {\displaystyle \sum _{i=1}^n{S}_i}{,}^{} {{}^{}}^{}1\le i\le p$$

(12)

$${\displaystyle \sum _{i=1}^n{S}_i}\le L\times H_{\max }{,}^{} {{}^{}}^{}1\le i\le p$$

(13)

$${\Omega }_i\cap {\Omega }_j={\varnothing }^{}{,}^{} {{}^{}}^{}1\le i<j\le p$$

(14)

$${\theta }_i\in {\theta }^{}{,}^{} {{}^{}}^{}1\le i\le p{,}^{} {{}^{}}^{}0\le \theta \le 2\pi$$

(15)

$$L,H_{\max }\in ℝ$$

(16)

Formula (11) indicates that all workpieces to be arranged must be completely contained within the rectangular sheet. Formula (12) indicates that the area of each workpiece cannot exceed the sum of the areas of all the workpieces, while Formula (13) indicates that the sum of the areas of all the workpieces cannot exceed the product of the plate length and the maximum contour height of the packing result. Formula (14) indicates that the workpieces to be arranged cannot overlap, while Formula (15) indicates that the allowable rotation angle of the workpieces to be arranged must meet the process requirements.

Step 4: Utilize the CBC solver to solve the linear programming model. If a feasible solution is identified, meaning a solution that adheres to all constraints, the program will output the optimal packing solution. If a feasible solution is not found, expand the boundaries to explore more search space. The search process should be repeated until either a better packing solution is found or the maximum time limit is reached.

4.3. Genetic Algorithm—Linear Programming Hybrid Algorithm

A practical and effective hybrid algorithm, named GA-LP, was devised by integrating a genetic algorithm with linear programming. Similar to the operational process of the genetic algorithm, the hybrid algorithm achieves superior packing solutions by improving the feasible solution of the genetic algorithm via the utilization of linear programming. In the hybrid algorithm, the initialization of the linear programming phase is accomplished by randomly permuting the optimal solution sequence generated by the genetic algorithm (GA), rather than initializing it based on the original packing instance. Combining genetic algorithms (GAs) and linear programming (LP) can effectively address the limitations inherent in each method and leverage the global search capabilities of GAs alongside the precise solution characteristics offered by LP. The procedure of the hybrid algorithm is illustrated in Figure 9.

5. Computational Experiment

5.1. Problem Instance

The algorithm employed in this research was implemented using Python 3.9 and its performance was evaluated on a computer equipped with an AMD Ryzen 7 5800H with a Radeon Graphics CPU, operating at a clock speed of 3.20 GHz. The computer had eight cores and 8 GB of memory. The test data are sourced from the European Special Interest Group on Cutting and Packing (ESICUP), which operates under the European Operational Research Society (EURO). The data can be accessed at the following website: https://www.euro-online.org/websites/esicup/ (accessed on 11 January 2023). The packing instance data utilized in this study are displayed in

Table 1. Packing instance data.

Instance	Total Number of Pieces	Number of Pieces Types	Sheet Width	Feasible Orientations (Degrees)
Albano	24	8	4900	0 and 180
Blaz1	28	7	15	0 and 180
Fu	12	12	38	0, 90 and 180
Dagli	30	10	60	0 and 180
Jakobs1	25	25	40	0, 90, 180 and 270
Mao	20	9	2550	0, 90 and 180
Marques	24	8	104	0, 90, 180 and 270
Shapes0	43	4	40	0
Shapes1	43	4	40	0 and 180
Shirts	99	8	40	0 and 180
Swim	48	10	5752	0 and 180
Trousers	64	17	79	0 and 180

, encompassing a range of combinations involving concave polygons and convex polygons. The provided test instances encompass a range of complexities and configurations, thereby mirroring the irregular packing challenges encountered in diverse industries. This extensive assortment of cases facilitates a comprehensive assessment of the performance of our proposed algorithm across various packing scenarios.

Concerning the genetic algorithm, the parameters were set to the values presented in

Table 2. The GA parameters.

Parameter	Value
Population size	40
Elite individual ratio	0.125
Mutation rate	0.1
Fitness calculation	$\frac{a}{H_{\max }}$
Stopping criteria	Stop after 30 generations

after conducting the preliminary experiments.

Population size: A deliberate decision was made to select an initial population size of 40 individuals in order to strike a balance between ensuring an adequate level of diversity for the optimization process and avoiding the computational burden associated with excessively complex calculations. While an increased population size has the potential to offer a wider range of solutions, it also results in an elevated computational overhead. By conducting a thorough analysis of the trade-off between diversity and computational efficiency, we have empirically determined that a population size of 40 is appropriate. This choice allows for an adequate level of diversity while still keeping the computational complexity at a manageable level.

Elite individual ratio: In order to ensure the preservation and promotion of the highest-performing individuals for the next generation, we implemented an elite individual ratio of 0.125. This phenomenon facilitated the survival of the most capable individuals across generations, thereby promoting the attainment of optimal solutions.

Mutation rate: In relation to genetic mutation, a mutation rate of 0.1 was employed for the specified gene. We conducted a comprehensive series of experiments and found that increasing the mutation rate leads to greater exploration within the solution space, thereby enabling escape from local optima. Conversely, a reduced rate facilitates the exploitation of refined solutions, but it also carries the potential risk of premature convergence. After conducting a thorough evaluation, a mutation rate of 0.1 was selected in order to strike an optimal balance between exploration and exploitation. This choice allows for a moderate level of exploration while still ensuring convergence of promising solutions.

Fitness calculation: In the context of fitness calculation, we utilized a fitness function that is defined as the product of the reciprocal of the maximum contour height (H) and the impact factor (a). This fitness calculation approach is designed to prioritize solutions that have lower contour heights, as these heights are considered to be indicative of more optimal packing arrangements in the context of sequence transmission.

The stopping criterion for the algorithm was established to ensure an adequate number of generations for population evolution while avoiding excessive computational burden. Specifically, the algorithm was programmed to terminate after 30 generations. This facilitated a thorough examination of the search space and the attainment of optimal or nearly optimal solutions, given the available computational resources.

The determination of various parameter values in our approach is a result of thorough and comprehensive consideration. We meticulously considered various factors, including diversity, computational efficiency, exploration, exploitation, and convergence. The chosen parameter values were meticulously adjusted using experimentation in order to attain an optimal balance between the exploration and convergence of promising solutions. The parameter settings played a crucial role in ensuring the effectiveness and efficiency of the optimization process in solving the two-dimensional irregular packing problem.

5.2. Calculation Result

This study involved conducting 20 experiments for each packing instance and comparing the experimental results using the BSTS [13] algorithm, RKGA-NP [15] algorithm, and the widely recognized algorithm “A New Bottom-Left-Fill Heuristic Algorithm” (BLF) [26] obtained from the literature. The comparison was based on the optimal utilization rate, average utilization rate of the board, and packing time. There exist variations in the programming languages and computer specifications employed by these algorithms, as illustrated in

Table 3. Computational environment.

Algorithm	#lan	Computer Type	CPU	RAM
GA-LP	Python	Laptop	AMD Ryzen 7 5800H CPU at 3.20 GHz	8 G
BSTS	C++	-	Core 2 D CPU at 2.0 GHz	1 G
RKGA-NP	Java	Desktop	Intel i5 CPU at 3.60 GHz	4 G
BLF	-	PC	2 GHz Intel Pentium 4 processor	256 MB

.

We selected a subset of instances from our study that is also included in the comparison papers, allowing for a direct evaluation of the GA-LP algorithm’s performance against the reference algorithms. Compared with the best results obtained using BSTS, the GA-LP algorithm proposed in this study produced six better best results (Albano, Dagli, Jakobs1, Mao, Marques, and Shapes0), five better average results (Albano, Fu, Dagli, Jakobs1, and Shapes0), and three faster results (Albano, Swim, and Trousers) among 10 comparable standard instances. Compared with the best results obtained using RKGA-NP, the GA-LP algorithm proposed in this study produced three better best results (Albano, Jakobs1, and Marques), five better average results (Albano, Jakobs1, Marques, and Shapes0), and seven faster results (Albano, Swim, and Trousers) among 7 comparable standard instances. Compared with the best results obtained by BLF, the GA-LP algorithm proposed in this study produced nine better best results (Albano, Fu, Dagli, Jakobs1, Mao, Marques, Shapes0, Swim, and Trousers), and two faster results (Swim and Trousers) among 11 comparable standard instances.

Table 4. GA-LP algorithm results compared with the results of BSTS, RKGA-NP, and BLF.

Instance	GA-LP			BSTS			RKGA-NP			BLF
	Best (%)	Avg (%)	Time (s)	Best (%)	Avg (%)	Time (s)	Best (%)	Avg (%)	Time (s)	Best (%)	Time (s)
Albano	86.53	85.66	874	84.46	83.37	926	84.74	84.69	10,230	84.6	93.39
Fu	88.64	86.87	811	88.79	86.38	282	-	-	-	86.9	20.78
Dagli	86.23	84.02	3326	83.01	80.93	413	-	-	-	83.7	188.8
Jakobs1	84.91	82.81	709	83.55	81.87	639	81.67	78.79	10,268	82.6	43.49
Mao	82.06	80.03	914	81	80.12	759	-	-	-	79.5	29.74
Marques	87.70	85.15	776	87.31	86.40	591	84.47	84.31	6871	86.5	4.87
Shapes0	66.39	63.79	1071	62.19	60.38	363	67.25	63.50	1826	60.5	21.33
Shapes1	66.13	64.49	1215	67.55	65.26	557	66.37	65.98	3025	66.5	2.19
Shirts	82.24	80.99	762	-	-	-	-	-	-	84.6	58.36
Swim	68.92	66.56	620	71.74	69.46	855	73.59	70.78	14,352	68.4	607.37
Trousers	88.56	83.81	570	88.84	86.41	641	90.91	88.67	16,025	88.5	756.15

Among the results of GA-LP, results better than BSTS are shown in bold, results better than RKGA-NP are shown underlined, and results better than BLF are shown in italics.

presents a comparison of the experimental results, and Figure 10 shows the best packing results for the 12 instances.

In terms of the programming languages, Python is a high-level and dynamically typed language, which may result in a relatively slower execution compared to lower-level languages like C++ and Java, especially for CPU-intensive tasks like solving the two-dimensional irregular packing problem. Regarding the CPUs used in the experiments, the Intel i5 CPU at 3.60 GHz has a slightly higher clock speed than the AMD Ryzen 7 5800H CPU at 3.20 GHz. A higher clock speed allows the CPU to perform more operations per second, leading to a better overall processing performance. However, despite these limitations, the GA-LP algorithm proposed in this study still achieved impressive experimental results, outperforming the BSTS and RKGA-NP algorithms in multiple instances (as indicated in Table 4).

Figure 11 shows the evolutionary convergence curves of some packing instance optimal solutions. It can be observed from the figure that for each instance, the population tends to converge within 20 generations, indicating that the GA-LP algorithm has a fast global convergence speed.

6. Conclusions

This article presents a novel hybrid algorithm, named GA-LP, that integrates the global search capability of genetic algorithms with the precise solving characteristics of linear programming. The proposed algorithm aims to address the two-dimensional irregular packing problem. The experimental results demonstrate that the GA-LP algorithm demonstrates superior and effective performance in addressing this problem. The performance of the GA-LP algorithm is evaluated by comparing it with and analyzing it against the BSTS algorithm, the RKGA-NP algorithm, and the BLF algorithm. This evaluation focuses on the best utilization, average utilization, and required time. The experimental results demonstrate that, in the majority of test instances, the GA-LP algorithm outperforms the BSTS algorithm, the RKGA-NP algorithm, and the BLF algorithm in terms of both the best utilization and the average utilization. In certain cases, the GA-LP algorithm and the BLF algorithm demonstrate a quicker computation time compared to BSTS. Furthermore, when compared to the RKGA-NP algorithm, the GA-LP algorithm consistently achieves a faster processing speed across all test instances.

To further augment the performance and applicability of the algorithm, we will investigate the feasibility of integrating the LP phase as a procedure called within the GA. This adaptation has the potential to improve the performance of the GA-LP algorithm, especially in situations where the efficiency of the LP phase can be more dynamically leveraged. Future research can also investigate the potential of integrating additional advanced optimization techniques, including metaheuristics, reinforcement learning, and deep learning. These approaches have the potential to provide novel perspectives and opportunities for enhancing the algorithm’s efficiency and efficacy in addressing intricate optimization problems. Furthermore, additional research can be conducted to explore the utilization of the GA-LP algorithm in addressing other optimization challenges that are closely related, thereby broadening its applicability and potential influence across diverse industrial and logistical sectors.