Process Modularity Impact on Manufacturing Lead Time and Throughput Rate in Terms of Mass Customization
Abstract
:1. Introduction
2. Related Work
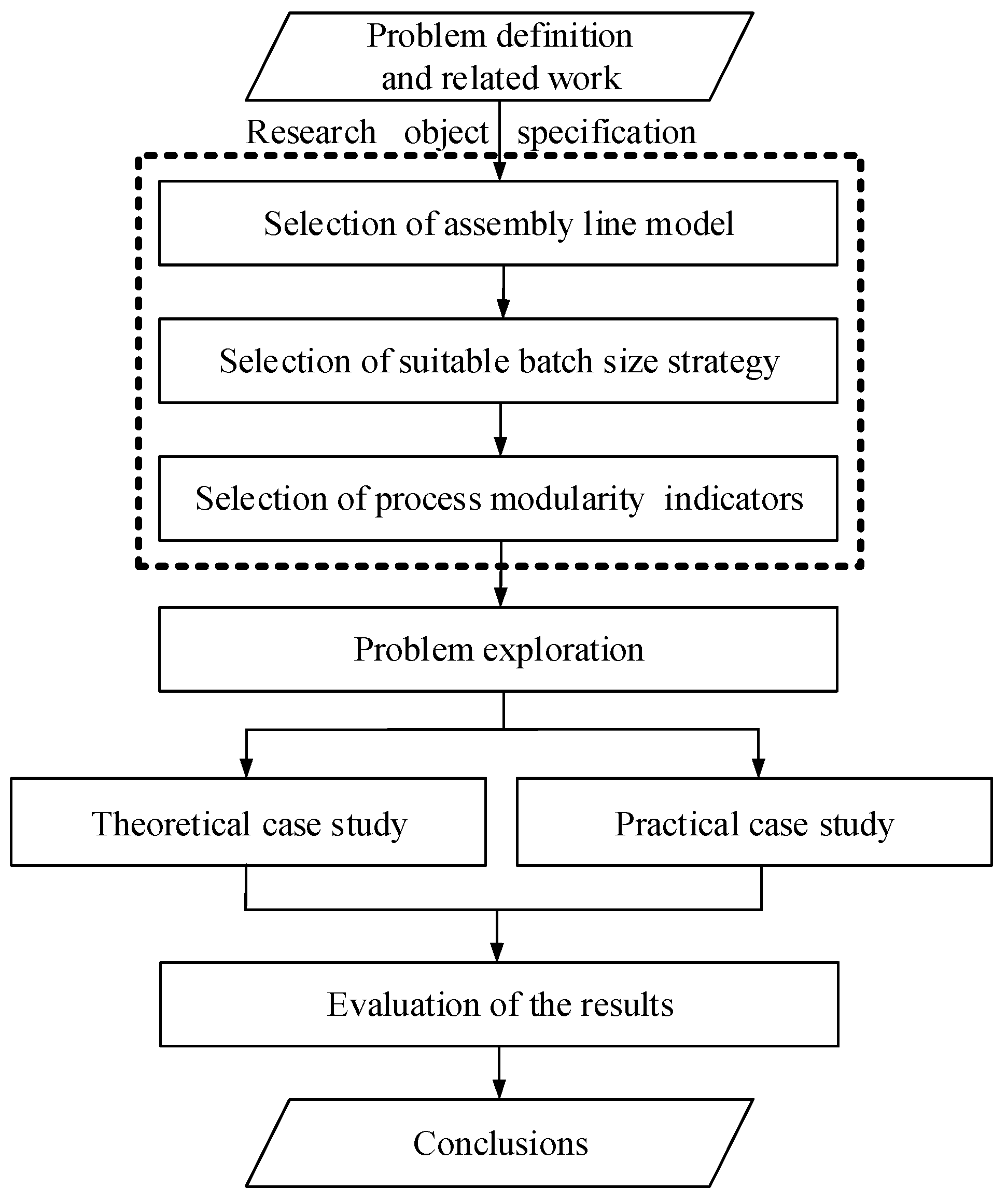
3. Methodology and Research Object Specification
3.1. Selection of the Assembly Line Model
3.2. Selection of Batch Size Strategy
3.3. Selection of Process Modularity Indicators
3.3.1. Optimal Modularity Indicator Qd
3.3.2. Optimal Modularity Indicator M(G)
3.3.3. Cross-Module Independence CMI
4. Problem Exploration
4.1. Theoretical Case Study
4.2. Practical Case Study
- -
- Moderate negative correlation (ρ = −0.45) between M(G) and MLT;
- -
- Moderate positive correlation (ρ = 0.45) between M(G) and THR;
- -
- Moderate negative correlation (ρ = −0.41) between Qd and MLT;
- -
- Moderate positive correlation (ρ = 0.41) between Qd and THR.
5. Results Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Müller, J.M.; Kiel, D.; Voigt, K.-I. What Drives the Implementation of Industry 4.0? The Role of Opportunities and Challenges in the Context of Sustainability. Sustainability 2018, 10, 247. [Google Scholar] [CrossRef]
- Da Cunha, C.; Agard, B.; Kusiak, A. Design for cost: Module-based mass customization. IEEE Trans. Autom. Sci. Eng. 2007, 4, 350–359. [Google Scholar] [CrossRef]
- ElMaraghy, H.; Monostori, L.; Schuh, G.; ElMaraghy, W. Evolution and future of manufacturing systems. CIRP Ann. 2021, 70, 635–658. [Google Scholar] [CrossRef]
- Modrak, V.; Bednar, S. Using axiomatic design and entropy to measure complexity in mass customization. Procedia CIRP 2015, 34, 87–92. [Google Scholar] [CrossRef]
- Suh, N.P. Axiomatic Design: Advances and Applications; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Modrak, V.; Soltysova, Z. Process modularity of mass customized manufacturing systems: Principles, measures and assessment. Procedia CIRP 2018, 67, 36–40. [Google Scholar] [CrossRef]
- Ethiraj, S.K.; Levinthal, D. Modularity and innovation in complex systems. Manag. Sci. 2004, 50, 159–173. [Google Scholar] [CrossRef]
- Baldwin, C.Y.; Clark, K.B. Chapter 3: What Is Modularity? In Design Rules: The Power of Modularity; MIT Press: Cambridge, MA, USA, 2000; pp. 63–92. [Google Scholar]
- Modrak, V.; Soltysova, Z. Novel complexity indicator of manufacturing process chains and its relations to indirect complexity indicators. Complexity 2017, 2017, 9102824. [Google Scholar] [CrossRef]
- Kirschner, M.; Gerhart, J. Evolvability. Proc. Natl. Acad. Sci. USA 1998, 95, 8420–8427. [Google Scholar] [CrossRef]
- B Kashtan, N.; Alon, U. Spontaneous evolution of modularity and network motifs. Proc. Natl. Acad. Sci. USA 2005, 102, 13773–13778. [Google Scholar] [CrossRef]
- Wagner, C. Robustness and Evolvability in Living Systems; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Salhieh, S.E.M.; Kamrani, A.K. Collaborative Engineering: Theory and Practice. In Modular Design; Salhieh, S.E.M., Kamrani, A.K., Eds.; Springer: New York, NY, USA, 2008; pp. 207–226. [Google Scholar]
- Reijers, H.; Mendling, J. Modularity in process models: Review and effects. In International Conference on Business Process Management; Springer: Berlin/Heidelberg, Germany, 2008; pp. 20–35. [Google Scholar]
- Vickery, S.K.; Koufteros, X.; Dröge, C.; Calantone, R. Product modularity, process modularity, and new product introduction performance: Does complexity matter? Prod. Oper. Manag. 2016, 25, 751–770. [Google Scholar] [CrossRef]
- Jacobs, M.; Droge, C.; Vickery, S.K.; Calantone, R. Product & process modularity’s effects on manufacturing agility & firm growth performance. J. Prod. Innov. Manag. 2011, 28, 123–137. [Google Scholar]
- Kusiak, A. Integrated product and process design: A modularity perspective. J. Eng. Des. 2002, 13, 223–231. [Google Scholar] [CrossRef]
- Piran, F.A.S.; Lacerda, D.P.; Camargo, L.F.R.; Viero, C.F.; Teixeira, R.; Dresch, A. Product modularity and its effects on the production process: An analysis in a bus manufacturer. Int. J. Adv. Manuf. Technol. 2017, 88, 2331–2343. [Google Scholar] [CrossRef]
- Gualandris, J.; Kalchschmidt, M. Product and process modularity: Improving flexibility and reducing supplier failure risk. Int. J. Prod. Res. 2013, 51, 5757–5770. [Google Scholar] [CrossRef]
- Soltysova, Z.; Modrak, V.; Nazarejova, J. Scheduling Optimization for Mass Customized Production Using Simulation Tool. In Managing and Implementing the Digital Transformation; Matt, D.T., Vidoni, R., Rauch, E., Dallasega, P., Eds.; ISIEA 2022; Lecture Notes in Networks and Systems; Springer International Publishing: Cham, Switzerland, 2022; pp. 214–226. [Google Scholar]
- Hoogeweegen, M.R.; Teunissen, W.J.; Vervest, P.H.; Wagenaar, R.W. Modular network design: Using information and communication technology to allocate production tasks in a virtual organization. Decis. Sci. 1999, 30, 1073–1103. [Google Scholar] [CrossRef]
- Fine, C.H.; Golany, B.; Naseraldin, H. Modeling tradeoffs in three-dimensional concurrent engineering: A goal programming approach. J. Oper. Manag. 2005, 23, 389–403. [Google Scholar] [CrossRef]
- Watanabe, C.; Ane, B.K. Constructing a virtuous cycle of manufacturing agility: Concurrent roles of modularity in improving agility and reducing lead time. Technovation 2004, 24, 573–583. [Google Scholar] [CrossRef]
- Piran, F.S.; Lacerda, D.P.; Sellitto, M.A.; Morandi, M.I.W.M. Influence of modularity on delivery dependability: Analysis in a bus manufacturer. Prod. Plan. Control 2021, 32, 688–698. [Google Scholar] [CrossRef]
- Zidi, S.; Harmani, N.; Kermad, L. Modularity metric in reconfigurable supply chain. In Proceedings of the Advances in Production Management Systems, Artificial Intelligence for Sustainable and Resilient Production Systems: IFIP WG 5.7 International Conference, APMS 2021, Nantes, France, 5–9 September 2021; Proceedings, Part V. Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 455–464. [Google Scholar]
- Chiu, M.C.; Okudan, G.L.E. An Investigation of Product Modularity and Supply Chain Performance at the Product Design Stage. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 August 2011; Volume 54860, pp. 681–689. [Google Scholar]
- Verma, N.K.; Chatterjee, A.K. Process flexibility in the presence of product modularity: Does modularity help? Int. J. Prod. Econ. 2023, 256, 108723. [Google Scholar] [CrossRef]
- Rodríguez-Escudero, A.I.; Camarero-Izquierdo, C.; Redondo-Carretero, M. Towards profitable customized solutions in small firms: A matter of relationships, modularity and expertise. J. Bus. Ind. Mark. 2023, 38, 137–154. [Google Scholar] [CrossRef]
- Alptekinoglu, A.; Stadler Blank, A.; Meloy, M.G.; Guide, V.D.R., Jr. Can mass customization slow fast fashion down? The impact on time-to-disposal and willingness-to-pay. J. Oper. Manag. 2023. [Google Scholar] [CrossRef]
- Osman, O.M.A.; Jian, Z. Does service modularity enhance new service development performance in supply chains: An empirical study. J. Bus. Ind. Mark. 2023. [Google Scholar] [CrossRef]
- Cowan, R.; Jonard, N. Modular organization and informal structure: Modularity, performance, and the alignment of organizational networks. Ind. Corp. Change 2023, 32, 181–207. [Google Scholar] [CrossRef]
- Christiansen, T.; Bruun, P.; Ward, P. Lean manufacturing, mass customization and their relationships–empirical findings. In Proceedings of the EurOMA Conference, Fontainebleau, France, 27–29 June 2004; p. 727. [Google Scholar]
- Vanderfeesten, I.T.P.; Reijers, H.A.; van der Aalst, W.M. Evaluating workflow process designs using cohesion and coupling metrics. Comput. Ind. 2007, 7, 420–437. [Google Scholar] [CrossRef]
- Epasto, A.; Lattanzi, S.; Paes Leme, R. Ego-splitting framework: From non-overlapping to overlapping clusters. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 145–154. [Google Scholar]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2003, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Haddou Benderbal, H.; Dahane, M.; Benyoucef, L. Modularity assessment in reconfigurable manufacturing system (RMS) design: An Archived Multi-Objective Simulated Annealing-based approach. Int. J. Adv. Manuf. Technol. 2018, 94, 729–749. [Google Scholar] [CrossRef]
- Singh, A.; Gupta, S.; Asjad, M.; Gupta, P. Reconfigurable manufacturing systems: Journey and the road ahead. Int. J. Syst. Assur. Eng. Manag. 2017, 8, 1849–1857. [Google Scholar] [CrossRef]
- Fotsoh, E.C.; Castagna, P.; Mebarki, N.; Berruet, P. Modularity of RMS: What about the Aggregation? In Proceedings of the 13th Nternational Conference on Modeling, Optimization and Simulation, Agadir, Morocco, 12–14 November 2020.
- Tu, Q.; Vonderembse, M.A.; Ragu-Nathan, T.S.; Ragu-Nathan, B. Measuring modularity-based manufacturing practices and their impact on mass customization capability: A customer-driven perspective. Decis. Sci. 2004, 35, 147–168. [Google Scholar] [CrossRef]
- Modrak, V.; Soltysova, Z. Exploration of the optimal modularity in assembly line design. Sci. Rep. 2022, 12, 20414. [Google Scholar] [CrossRef]
- Abdelkafy, N. Variety Induced Complexity in Mass Customization: Concepts and Management; Erich Schmidt Verlag GmbH & Co KG: Berlin, Germany, 2008. [Google Scholar]
- Modrak, V.; Soltysova, Z. Management of product configuration conflicts to increase the sustainability of mass customization. Sustainability 2020, 12, 3610. [Google Scholar] [CrossRef]
- Groover, M.P. Automation, Production Systems, and Computer-Integrated Manufacturing, 4th ed.; Pearson: London, UK, 2016; pp. 1–816. [Google Scholar]
- On-Line Encyclopedia of Integer Sequences (OEIS). Available online: https://oeis.org/A000669 (accessed on 15 June 2023).
- Little, J.D. A proof for the queuing formula: L = λ W. Oper. Res. 1961, 9, 383–387. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation coefficients: Appropriate use and interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Modrak, V.; Soltysova, Z. Modularity measurement as a crucial design element. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Sanya, China, 12–14 November 2021; IOP Publishing: Bristol, UK, 2021; Volume 1174, p. 10. [Google Scholar]









| Scenario 1 | P1 | P2 | P3 | Scenario 2 | P1 | P2 | P3 |
|---|---|---|---|---|---|---|---|
| PB | 10 | 5 | 3 | PB | 10 | 5 | 3 |
| L | 1 | 1 | 1 | L | 10 | 5 | 3 |
| TBS | 10 | 5 | 3 | TBS | 1 | 1 | 1 |
| m × n | P1 | P2 | P3 | P4 |
|---|---|---|---|---|
| WS1 | 20 | 30 | 20 | 30 |
| WS2 | 50 | 50 | 60 | 60 |
| Parts Assembly | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 |
|---|---|---|---|---|---|---|---|---|---|---|
| A + B | 20 | 20 | 20 | - | 20 | 20 | 20 | 20 | - | - |
| A + B + V1 | 30 | 30 | 30 | - | 30 | 30 | 30 | 30 | - | - |
| AB + C + D + E + F | 50 | - | - | - | - | - | - | - | - | - |
| AB + C + D + E + F + V2 | 60 | - | - | - | - | - | - | - | - | - |
| ABV1 + C + D + E + F | 50 | - | - | - | - | - | - | - | - | - |
| ABV1 + C + D + E + F + V2 | 60 | - | - | - | - | - | - | - | - | - |
| AB + C + D | - | 30 | - | - | - | - | - | - | - | - |
| ABV1 + C + D | - | 30 | - | - | - | - | - | - | - | - |
| ABCD + E + F | - | 30 | - | - | - | - | 30 | - | 30 | - |
| ABCDV1 + E + F | - | 30 | - | - | - | - | 30 | - | 30 | - |
| ABCD + E + F + V2 | - | 40 | - | - | - | - | 40 | - | 40 | - |
| ABCDV1 + E + F + V2 | - | 40 | - | - | - | - | 40 | - | 40 | - |
| AB + C | - | - | 20 | - | - | - | - | - | - | - |
| ABV1 + C | - | - | 20 | - | - | - | - | - | - | - |
| ABC + D + E | - | - | 30 | - | - | - | - | - | - | - |
| ABCV1 + D + E | - | - | 30 | - | - | - | - | - | - | - |
| ABCDE + F | - | - | 20 | - | - | 20 | 20 | - | - | 20 |
| ABCDEV1 + F | - | - | 30 | - | - | - | - | - | - | - |
| ABCDE + F + V2 | - | - | 30 | - | - | 30 | 30 | - | - | 30 |
| ABCDE + V1 + F + V2 | - | - | 40 | - | - | - | - | - | - | - |
| A + B + C | - | - | - | 30 | - | - | - | - | - | - |
| A + B + C + V1 | - | - | - | 40 | - | - | - | - | - | - |
| D + E + F | - | - | - | 30 | - | - | - | - | - | - |
| D + E + F + V2 | - | - | - | 40 | - | - | - | - | - | - |
| ABC + DEF | - | - | - | 20 | - | - | - | - | - | - |
| ABCV1 + DEF | - | - | - | 20 | - | - | - | - | - | - |
| ABC + DEFV2 | - | - | - | 20 | - | - | - | - | - | - |
| ABCV1 + DEFV2 | - | - | - | 20 | - | - | - | - | - | - |
| C + D + E | - | - | - | - | 30 | - | - | - | - | - |
| AB + CDE | - | - | - | - | 20 | - | - | - | - | - |
| ABV1 + CDE | - | - | - | - | 20 | - | - | - | - | 20 |
| ABCDV1 + F | - | - | - | - | 20 | 20 | - | - | - | 20 |
| ABCDEV1 + F + V2 | - | - | - | - | 30 | 30 | - | - | - | - |
| C + D | - | - | - | - | - | 20 | 20 | 20 | - | - |
| AB + CD | - | - | - | - | - | 20 | 20 | - | - | - |
| ABV1 + CD | - | - | - | - | - | 20 | 20 | - | - | - |
| ABCD + E | - | - | - | - | - | 20 | - | - | - | 20 |
| ABCDV1 + E | - | - | - | - | - | - | - | - | - | 20 |
| AB + CD + E + F | - | - | - | - | - | - | - | 40 | - | - |
| ABV1 + CD + E + F | - | - | - | - | - | - | - | 40 | - | - |
| AB + CD + E + F + V2 | - | - | - | - | - | - | - | 50 | - | - |
| ABV1 + CD + E + F + V2 | - | - | - | - | - | - | - | 50 | - | - |
| A + B + C + D | - | - | - | - | - | - | - | - | 40 | 40 |
| A + B + C + D + V1 | - | - | - | - | - | - | - | - | 50 | 50 |
| APSs | Qd | CMI | M(G) | MLT (Minutes) | THR (Parts/ h) |
|---|---|---|---|---|---|
| No.1 | 0.36 | 0.1 | 0.043 | 92.3 | 65.01 |
| No.9 | 0.4 | 0.1 | 0.039 | 75.88 | 79.07 |
| No.8 | 0.471 | 0.182 | 0.055 | 75.63 | 79.33 |
| No.10 | 0.438 | 0.182 | 0.042 | 76.18 | 78.76 |
| No.4 | 0.463 | 0.182 | 0.0496 | 67.3 | 89.49 |
| No.2 | 0.47934 | 0.182 | 0.047 | 60.1 | 99.83 |
| No.7 | 0.472 | 0.25 | 0.054 | 59.68 | 100.53 |
| No.3 | 0.493 | 0.25 | 0.048 | 51.82 | 115.79 |
| No.5 | 0.486 | 0.25 | 0.0504 | 51.02 | 117.61 |
| No.6 | 0.47929 | 0.308 | 0.0494 | 43.24 | 138.25 |
| No. of Assembled Parts | Assembly Time |
|---|---|
| 2 (e.g., A + E) | 20 |
| 3 (e.g., A + E + B) | 30 |
| 4 (e.g., A + D + B + F) | 40 |
| 5 (e.g., AD + B + F + C + H) | 50 |
| 6 (e.g., A + D + B + F + C + H) | 60 |
| 7 (e.g., A + D + B + F + C + H + G) | 70 |
| APSs No. | Qd | CMI | M(G) | MLT (min) | THR (Parts/h) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0.033 | 29.12 | 61.81 |
| 79 | 0.4 | 0.2 | 0.0465 | 24.68 | 72.9 |
| 2 | 0.296 | 0.111 | 0.0529 | 24.57 | 73.27 |
| 58 | 0.296 | 0.111 | 0.0424 | 24.55 | 73.4 |
| 34 | 0.37 | 0.111 | 0.0449 | 22.73 | 79.18 |
| 46 | 0.41 | 0.2 | 0.0574 | 22.62 | 79.57 |
| 5 | 0.37 | 0.111 | 0.05 | 22.04 | 80.36 |
| 6 | 0.4 | 0.2 | 0.06 | 21.3 | 84.51 |
| 3 | 0.44 | 0.2 | 0.066 | 21.067 | 85.44 |
| 86 | 0.446 | 0.273 | 0.0486 | 19.97 | 90.14 |
| 17 | 0.44 | 0.2 | 0.0554 | 19.52 | 92.23 |
| 14 | 0.395 | 0.111 | 0.048 | 19.4 | 92.78 |
| 19 | 0.46 | 0.2 | 0.0603 | 19.23 | 93.59 |
| 24 | 0.45 | 0.2 | 0.0581 | 19.07 | 94.4 |
| 29 | 0.4546 | 0.273 | 0.0646 | 19.07 | 94.4 |
| 47 | 0.471 | 0.273 | 0.0636 | 18.47 | 97.46 |
| 35 | 0.46 | 0.2 | 0.0546 | 18.18 | 98.99 |
| 18 | 0.446 | 0.273 | 0.0596 | 18.13 | 99.27 |
| 15 | 0.45 | 0.2 | 0.057 | 18.017 | 99.91 |
| 16 | 0.446 | 0.273 | 0.0636 | 18.017 | 99.91 |
| 67 | 0.465 | 0.333 | 0.058 | 18 | 99.9 |
| 84 | 0.458 | 0.333 | 0.053 | 17.8 | 101.1 |
| 74 | 0.446 | 0.273 | 0.0548 | 17.8 | 101.1 |
| 66 | 0.463 | 0.273 | 0.0551 | 17.8 | 101.1 |
| 64 | 0.4793 | 0.273 | 0.0566 | 17.8 | 101.1 |
| 8 | 0.471 | 0.273 | 0.069 | 17.8 | 101.12 |
| 7 | 0.47 | 0.2 | 0.063 | 17.73 | 101.5 |
| 4 | 0.4959 | 0.273 | 0.075 | 17.57 | 102.47 |
| 89 | 0.458 | 0.333 | 0.0495 | 16.92 | 106.4 |
| 82 | 0.471 | 0.273 | 0.0499 | 16.63 | 108.2 |
| 44 | 0.463 | 0.273 | 0.0538 | 16.63 | 108.2 |
| 63 | 0.463 | 0.273 | 0.0548 | 16.63 | 108.2 |
| 78 | 0.449 | 0.385 | 0.057 | 16.57 | 108.6 |
| 77 | 0.458 | 0.333 | 0.0564 | 16.5 | 109.1 |
| 81 | 0.472 | 0.333 | 0.0541 | 16.45 | 109.4 |
| 65 | 0.472 | 0.333 | 0.0593 | 16.42 | 109.6 |
| 70 | 0.465 | 0.333 | 0.0559 | 16.4 | 109.7 |
| 75 | 0.465 | 0.333 | 0.0576 | 16.37 | 110 |
| 37 | 0.47 | 0.2 | 0.0528 | 16.35 | 110.09 |
| 73 | 0.465 | 0.333 | 0.0534 | 16.22 | 110.9 |
| 60 | 0.4796 | 0.273 | 0.0581 | 16.2 | 111.1 |
| 49 | 0.4793 | 0.273 | 0.0617 | 16.18 | 111.21 |
| 22 | 0.4794 | 0.273 | 0.0644 | 16.18 | 111.23 |
| 72 | 0.471 | 0.273 | 0.0517 | 16.03 | 112.3 |
| 71 | 0.4793 | 0.273 | 0.0529 | 16.03 | 112.3 |
| 27 | 0.471 | 0.273 | 0.0625 | 16.02 | 112.38 |
| 32 | 0.465 | 0.333 | 0.0671 | 16.02 | 112.38 |
| 80 | 0.463 | 0.273 | 0.0512 | 16 | 112.5 |
| 38 | 0.471 | 0.273 | 0.0572 | 15.97 | 120.27 |
| 48 | 0.4792 | 0.333 | 0.0676 | 15.97 | 112.7 |
| 69 | 0.45 | 0.2 | 0.0484 | 15.85 | 113.5 |
| 62 | 0.46 | 0.2 | 0.0502 | 15.85 | 113.5 |
| 41 | 0.44 | 0.2 | 0.0508 | 15.85 | 113.54 |
| 59 | 0.43 | 0.2 | 0.0519 | 15.85 | 113.54 |
| 53 | 0.455 | 0.273 | 0.0596 | 15.85 | 113.89 |
| 11 | 0.48 | 0.2 | 0.061 | 15.73 | 114.41 |
| 9 | 0.4959 | 0.273 | 0.072 | 15.73 | 114.41 |
| 83 | 0.465 | 0.333 | 0.0518 | 15.25 | 118.01 |
| 45 | 0.458 | 0.333 | 0.0552 | 15.25 | 118.01 |
| 42 | 0.471 | 0.273 | 0.0552 | 15.12 | 119.1 |
| 87 | 0.465 | 0.333 | 0.0505 | 15.03 | 119.7 |
| 57 | 0.456 | 0.385 | 0.0607 | 14.92 | 120.67 |
| 43 | 0.458 | 0.333 | 0.0579 | 14.8 | 121.6 |
| 23 | 0.472 | 0.333 | 0.0664 | 14.8 | 121.62 |
| 54 | 0.472 | 0.333 | 0.062 | 14.75 | 122.41 |
| 90 | 0.449 | 0.385 | 0.0498 | 14.72 | 122.34 |
| 56 | 0.465 | 0.333 | 0.0606 | 14.72 | 122.34 |
| 50 | 0.472 | 0.333 | 0.0639 | 14.72 | 122.34 |
| 33 | 0.456 | 0.385 | 0.0684 | 14.72 | 122.34 |
| 40 | 0.458 | 0.333 | 0.0616 | 14.7 | 122.52 |
| 36 | 0.4793 | 0.273 | 0.0608 | 14.68 | 122.59 |
| 25 | 0.4793 | 0.273 | 0.0644 | 14.68 | 122.59 |
| 20 | 0.4876 | 0.273 | 0.0664 | 14.68 | 122.59 |
| 30 | 0.472 | 0.333 | 0.0689 | 14.68 | 122.59 |
| 12 | 0.479 | 0.273 | 0.067 | 14.52 | 123.86 |
| 21 | 0.472 | 0.333 | 0.0703 | 14.52 | 123.99 |
| 39 | 0.463 | 0.273 | 0.0591 | 14.35 | 125.44 |
| 76 | 0.4497 | 0.385 | 0.0594 | 14.35 | 125.44 |
| 68 | 0.449 | 0.385 | 0.0599 | 14.35 | 125.44 |
| 85 | 0.449 | 0.385 | 0.0539 | 14.3 | 125.9 |
| 61 | 0.4792 | 0.333 | 0.0624 | 14.3 | 125.9 |
| 88 | 0.4497 | 0.385 | 0.0516 | 14.28 | 126 |
| 55 | 0.456 | 0.385 | 0.0634 | 14.28 | 126 |
| 28 | 0.465 | 0.333 | 0.0648 | 14.28 | 126 |
| 51 | 0.465 | 0.333 | 0.0656 | 14.28 | 126 |
| 52 | 0.456 | 0.385 | 0.067 | 14.28 | 126 |
| 26 | 0.465 | 0.333 | 0.0685 | 14.28 | 126 |
| 13 | 0.472 | 0.333 | 0.071 | 14.28 | 126 |
| 31 | 0.456 | 0.385 | 0.0718 | 14.28 | 126 |
| 10 | 0.486 | 0.333 | 0.0759 | 14.27 | 126.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Modrak, V.; Soltysova, Z.; Nazarejova, J. Process Modularity Impact on Manufacturing Lead Time and Throughput Rate in Terms of Mass Customization. Appl. Sci. 2023, 13, 12487. https://doi.org/10.3390/app132212487
Modrak V, Soltysova Z, Nazarejova J. Process Modularity Impact on Manufacturing Lead Time and Throughput Rate in Terms of Mass Customization. Applied Sciences. 2023; 13(22):12487. https://doi.org/10.3390/app132212487
Chicago/Turabian StyleModrak, Vladimir, Zuzana Soltysova, and Julia Nazarejova. 2023. "Process Modularity Impact on Manufacturing Lead Time and Throughput Rate in Terms of Mass Customization" Applied Sciences 13, no. 22: 12487. https://doi.org/10.3390/app132212487
APA StyleModrak, V., Soltysova, Z., & Nazarejova, J. (2023). Process Modularity Impact on Manufacturing Lead Time and Throughput Rate in Terms of Mass Customization. Applied Sciences, 13(22), 12487. https://doi.org/10.3390/app132212487








