Abstract
Replacing traditional manual sweeping with unmanned sweepers in closed parks can not only greatly reduce labor costs, but also improve sweeping efficiency. Efficient path planning is the key technology for unmanned sweepers to complete the sweeping task. Existing unmanned sweepers are often based on fixed path sweeping or completely traversing the sweeping mode, this mode does not have the environmental adaptability, in the actual sweeping is often high energy cost, and sweeping is not complete. In this paper, an environment-adaptive sweeping path planning method is proposed to improve the sweeping intelligence and environmental adaptability of unmanned sweepers, reduce the energy consumption of sweeping and improve the efficiency of sweeping. Specifically, in this paper, we first use YOLOv5 to complete the accurate identification of individual garbage and obstacles in the road, and then work with LIDAR and Gaussian Mixture Model(GMM) to remove redundant targets. We also propose a Permutation Entropy(PE) value-based discrimination method to complete the target distribution posture analysis of each complex garbage pile. Finally, the traditional path planning problem is transformed into a combinatorial optimization problem of garbage areas, and a sweeping path accurate method based on Simulated Annealing(SA) algorithm is proposed. Through comprehensive theoretical analysis and simulation study, the optimality and effectiveness of the proposed method are proved by comparing A star and Coverage Path Planning(CPP) algorithms in a variety of experimental scenarios.
1. Introduction
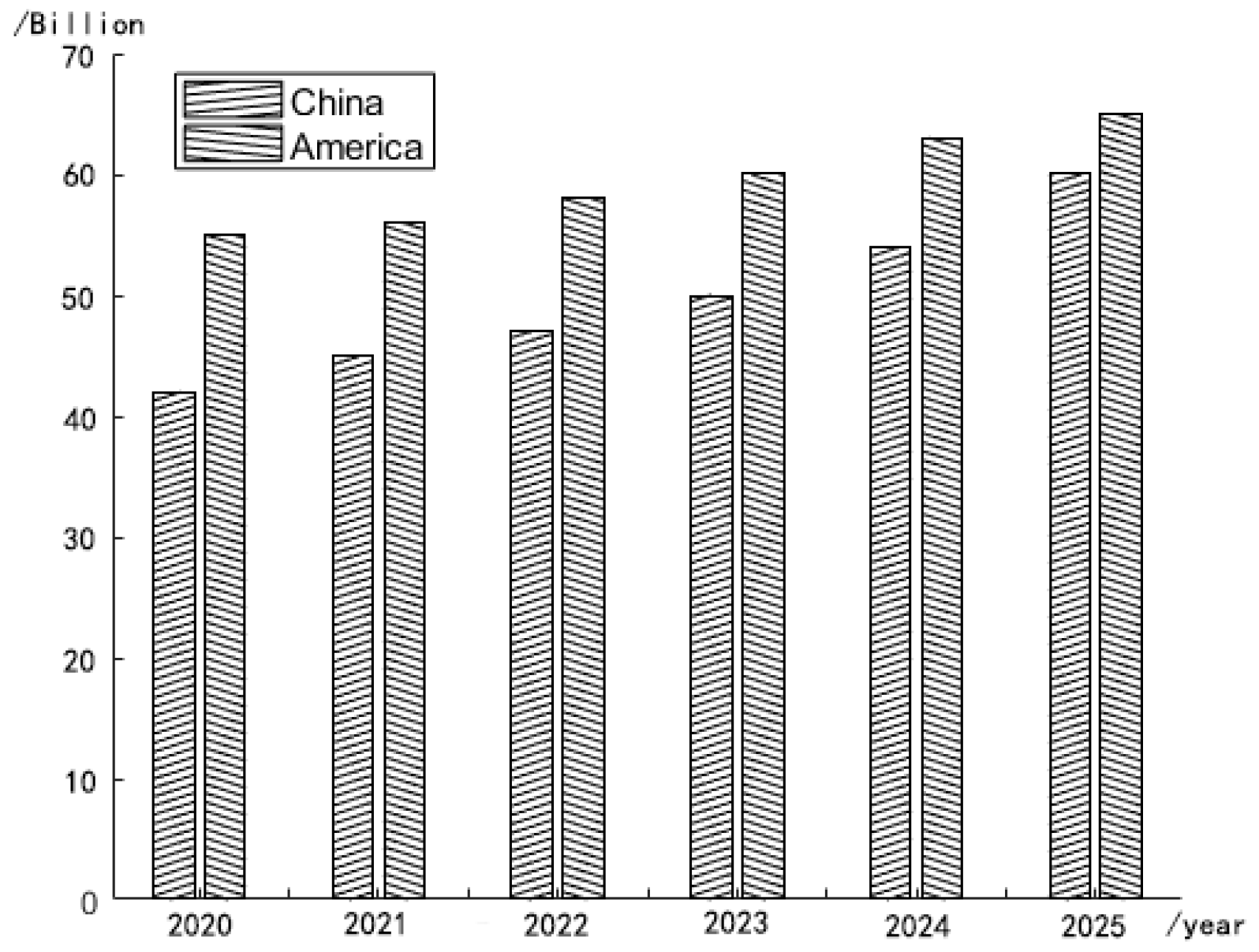
With the development of autonomous driving technology and the structural adjustment, transformation and upgrading of the sanitation industry, the market demand for intelligent equipment is expanding, primarily including the demand for automatic driving sweeping equipment. The realization of unmanned sweepers’ unique use and driving characteristics has important practical significance and broad market prospects [1]. The market volume of unmanned sweepers in China and the U.S. in recent years is shown in Figure 1, where 2020–2022 is the data from research and 2023–2025 is the forecast data.
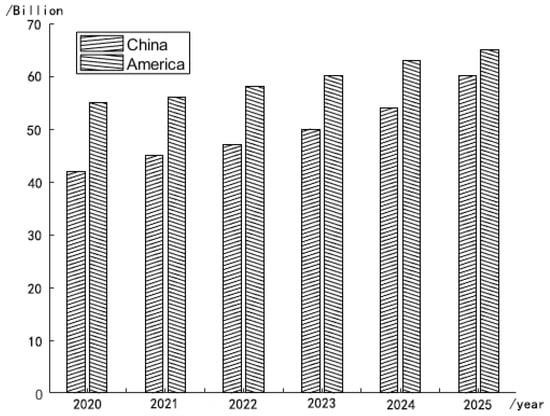
Figure 1.
The market volume of unmanned sweepers in China and the U.S. in recent years and in the future (source: Statistical Bulletin on the Development of the Transport Sector).
As shown in Figure 2, for urban roads, garbage is usually distributed at the edge of the road, so it is more appropriate to use a fixed path for cleaning strategy, but for closed parks such as schools, parks, airports, etc., the garbage is more dispersed and the efficiency of the traditional directional cleaning is difficult to guarantee. The full-coverage path can be used in parks, but too long a path will consume a lot of energy, and the efficiency is low; it will also interfere with the normal passage of pedestrians and vehicles in the park.

Figure 2.
Different garbage distribution patterns for urban roads and enclosed parks.
Existing robots lack a global view, so sweeping can be blind. An effective approach is to enhance the target perception within the current visible sweeping, and then design a corresponding sweeping strategy to improve the environmental adaptability of the sweeper. However, this process faces two challenges: on the one hand, the existing perception strategy can hardly meet the demand of forming a qualitative and dense perception of the road garbage distribution when the sweeper plans its route. The existing machine vision perception of existing sweepers or sweeping robots is based on target classification, and although some road targets can be identified through machine vision, and even obstacles and garbage can be distinguished [2], the spatial continuity of information obtained by target identification is poor [3], and it is difficult to form accurate continuous perception for densely distributed garbage. Although semantic segmentation can be enhanced in terms of spatio-temporal continuity, it can only recognize regions with a single feature and has poor performance in recognizing regions composed of complex features.
On the other hand, existing intelligent body planning algorithms for self-driving vehicles and robots use a heuristic search as the computational core. Such methods often have the shortest path as the optimization goal to form optimal path planning. However, for unmanned sweepers, their planning core is optimally sweeping-oriented, forming the shortest path possible under the guarantee of sweeping efficiency. The change in optimization goals driven by the sweeping task makes the original path planning based on the heuristic search form an inefficient sweeping route. In addition, the randomness and dispersion of the garbage distribution in the cleaning make the target in the cleaning path planning process no longer a collection that can be spatially characterized in traditional planning methods, but a class of spatially discrete sets of each anisotropy. More complex planning objectives make the traditional planning algorithm no longer applicable, and there is an urgent need to study an environment-adaptive dynamic planning algorithm for unmanned sweepers.
Therefore, in this paper, we study a novel unmanned sweeper vehicle sweeping method based on target distribution posture analysis, which firstly uses the inverse perspective transformation (IPM) together with You Only Look Once version 5 (YOLOv5) to identify obstacles and monolithic garbage in the roadway, followed by the use of LIDAR local elevation and Gaussian mixture model (GMM) to tolerate similar obstacles as well as garbage targets, and for the complex garbage piles by identifying the PE (permutation entropy) entropy for their complementary detection. Finally, all the garbage regions are subjected to convex packet ensemble generation by Graham’s scanning method, and the optimal sweeping path problem for unmanned sweepers is solved using a simulated annealing (SA) algorithm.
In summary, our contributions are as follows:
- (1)
- The accurate identification of monolithic trash and obstacles was accomplished using YOLOv5 and combined with GMM to reduce redundant parts.
- (2)
- For complex garbage piles, a novel roadway garbage area discrimination method based on PE value analysis is proposed to obtain accurate garbage area information in the roadway plane.
- (3)
- The traditional unmanned sweeper vehicle sweeping path planning problem is transformed into a Traveling Salesman Problem-Coverage Path Planning(TSP-CPP) problem based on Contributions 1 and 2, and a simulated-annealing-algorithm-based unmanned sweeper vehicle path planning method is proposed.
This paper is organized as follows. Section 2 provides a literature review on target detection, situation analysis, and a literature review on path planning for unmanned sweepers. In Section 3, a detailed framework of a sweeping method based on target distribution posture analysis is described. Experiments and results are presented in Section 4. Finally, we conclude the discussion of this study in Section 5.
2. Related Works
In this section, we provide a brief overview of the latest research on garbage detection, classification methods and path planning for unmanned sweepers.
2.1. Research on Garbage Detection and Classification
Accurate garbage identification will greatly improve the automation and intelligence of cleaning vehicles. Earlier researchers have used RFID readers, load cells, gas sensors, etc., to implement garbage classification [4]. Ranjana et al. [5] designed a dry and wet garbage sorting bin based on RFID readers with an Android application, where the public needs to display RFID tags to throw the garbage into the bin. However, this approach is not applicable to the sweeper scenario. Nowadays, with the rapid development of deep learning techniques, increasing amounts of researchers are trying to accomplish image processing problems using CNN, VGG, ResNet, UNet++, etc. Bansal et al. [6] proposed a robotic system using CNN for detecting garbage on the ground. After detecting the garbage, the location of the garbage is calculated and communication sharing is completed with the microcontroller controlling the robot arm. MA et al. [7] proposed a lightweight feature fusion single short multi-box detector (L-SSD) algorithm to achieve intelligent garbage classification and recognition, which solves the problem of the small size of garbage and low image resolution of garbage in garbage classification. ResNet-101 is used instead of VGG16 to achieve more accurate detection in the training set. Liao et al. [8] proposed deep supervision UNet++ to solve the problem of road garbage classification and semantic segmentation; this method can directly identify the type of garbage and occupied ground area with an MIoU (mean intersection over union) of 76.73 ± 0.11, which greatly improves the accuracy of garbage segmentation compared with advanced methods.
In addition, the YOLO family of algorithms is gradually becoming the leading computer-vision-based target detection and classification method [9]. Deep learning methods such as R-CNN (region-based CNN) typically use a two-stage target detection model that generates and selects regions of interest in the first and second stages, sends region suggestions down and uses convolutional neural networks for target classification and bounding box regression. Such models have high accuracy but are less real-time and less efficient [10]. The YOLO family of algorithms treats target recognition as a simple regression problem by creating a feature map of the input image and learning the category probabilities and the bounding box coordinates of the entire image, allowing the algorithm to run only once. Such a model is much faster than a two-stage target detector, although with reduced accuracy, and is commonly used for real-time target detection tasks [11]. A number of scholars have applied the improved YOLO algorithm to garbage detection and classification. Kong et al. [12] trained the YOLOv3 network widely used in the field of high-speed accurate object detection on a floating garbage dataset to achieve accurate real-time garbage detection. To improve the anti-interference capability, a visual steering control method based on a sliding mode controller was proposed. Zhu et al. [13] proposed a YOLOX for detecting seventeen types of garbage, and after the camera detects the garbage, it automatically identifies and analyzes the type and specific location of the garbage and is automatically picked up by a mechanical jaw; the test results show that the can exceed 97%.
2.2. Research on Path Planning of Unmanned Sweepers
Path planning technology is one of the core elements of the research on sweeping robots, and the so-called robot path planning technology works by the robot planning a safe route by itself based on its own sensors’ perception of the environment, while efficiently completing the operational tasks [14]. The path planning of mobile robots can be divided into two types according to their purpose—one is full-coverage path planning (CPP) and the other is traditional point-to-point path planning. Full-coverage path planning has been extensively studied by several authors. Galceran et al. [15] considered that full-coverage path planning is related to the covering salesman problem and studied in detail the advantages and disadvantages of several CPP algorithms. Tan [16] reviews the principles of CPP, creatively discusses the use of deep reinforcement learning methods to solve the CPP problem and discusses its development trends, and the authors argue that coverage algorithms can be divided into classical and heuristic-based algorithms, depending on the a priori knowledge of the environment surrounding the on-board sensors. Point-to-point path planning is more like the well-known traveling salesman problem (TSP), SOUISSI et al. [17] detailed the state-of-the-art path planning in automation, robotics and video games, respectively, A star and its variants [18], RRT algorithm [19], artificial potential field method [20], etc.
The traditional sweeping robot’s operation task is to clean the room, so its path planning belongs to fully traversing path planning, and it needs to satisfy the traversability and non-repetitiveness. Zhang et al. [21] designed an inward spiral traversal method and proposed a shortest path out of a dead zone scheme based on the A star algorithm to avoid the problem of inward spiral traversal of the sweeping robot into the dead zone. Luo et al. [22] considered the global planning of cell paths for inter-cell transfer by exhaustive search and the ant colony algorithm, so that the sweeping robot can work better in complex environments. As for what needs to be accomplished in this task, the path planning in which the unmanned sweeper will pass all the garbage from the starting point to the end point belongs to the traditional point-to-point path planning. Path optimality is related to the shortest cover path or TSP, which is usually the planning of a path with minimum travel cost to visit all points that pass through multiple images containing garbage. The new path planning problem explored here can be called the TSP-CPP problem, considered as an integration of the TSP and CPP problems [23]. The multiple-TSP problem was explored by Khamis et al. [24], and Xie et al. [25] provided a mixed-integer planning formulation for this new problem, and then developed a dynamic-based approach based on a CPP method covering a single convex polygon region planning exact method that finds the optimal path, in addition to proposing a heuristic method that can generate high-quality plans very efficiently.
3. Proposed Methodology
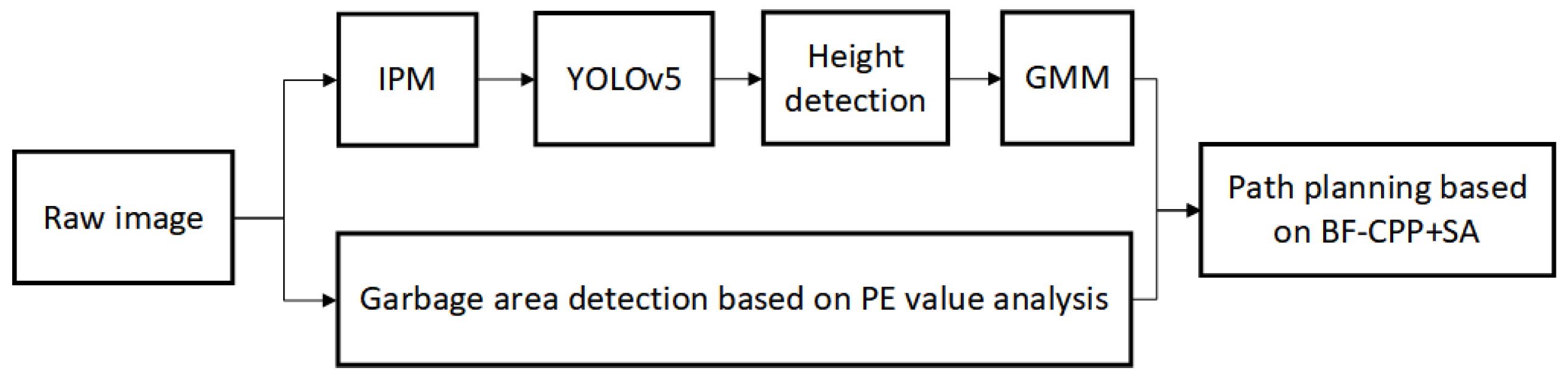
In this section, we will give the detailed design process of the proposed sweeping method based on target distribution posture analysis. In the sweeping area, we categorize the sensed objects into obstacles that affect the passage of the unmanned sweeper and the targets or areas that the sweeper needs to sweep, and both obstacles and sweeping targets are mapped to the area distribution on the 2D plane after sensing. For single targets, we first use IPM to map the initial image to a bird’s-eye view, then use YOLOv5 for target extraction, together with LIDAR to detect the height in order to remove targets that cannot be swept, and then use GMM to further reduce redundant targets. For complex garbage areas, we designed a garbage area discrimination based on PE value analysis. The above two kinds of garbage targets are integrated to form the region to be swept. Finally, this paper designs a sweeping path planning method based on BF (back-and-forth)-CPP and SA. The planning method aims to improve the efficiency of unmanned sweeper vehicles when they sweep roadway garbage. The mind map of the unmanned sweeper vehicle’s sweeping method designed in this paper is shown in Figure 3.
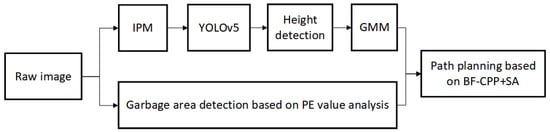
Figure 3.
The mind map of the designed unmanned sweeper vehicle sweeping method in this paper.
3.1. Garbage Distribution Sensing
3.1.1. Discrete Object Recognition
The YOLO family can extract category information. Among them, YOLOv5 has a good performance in traffic target detection, and the algorithm only needs GPU training to generate a low-cost, robust, real-time, high-quality, and convincing target detection model. YOLOv5 consists of 4 parts: input, backbone, neck, and head. In this paper, we use YOLOv5 to recognize the type and exact location of specific obstacles and individual garbage.
Many objects in the roadway, such as leaves or bottles, tend to be distributed within close proximity, thus forming a group or cluster. Treating them as discrete objects would only increase the number of nodes to be passed in the TSP, leading to a steep increase in computation cost. Therefore, as shown in Figure 3, we introduce the group in which neighboring targets of the same type are treated as a cluster so as to lower computational cost.
Further, in practical scenarios, the irregular distribution of complex garbage piles often causes stacking of garbage, which leads to garbage higher than the brush height of the sweeper, making it impossible for the sweeper to complete the sweeping work. For this kind of situation, we will process the LIDAR point cloud information. LIDAR can emit laser beams to detect the position, velocity and other characteristic quantities of a target. As shown in Figure 4, which shows the process of converting our radar point cloud into a local elevation map, the gray rectangle is the vehicle model of this vehicle, and the orange cube is the recognized elevation terrain. Once the height of the garbage pile is detected to be higher than the threshold value, this pile of garbage is determined as an obstacle and the avoidance strategy is executed.

Figure 4.
Mapping local terrain to elevation terrain, where gray rectangle is the vehicle model of this vehicle, and the orange cube is the recognized elevation terrain.
The inverse perspective transformation is the inverse process of perspective imaging, which acquires a bird’s eye view of the road plane by back-projecting the image coordinates to the spatial coordinates. Ref. [26] proposed the inverse perspective transformation based on the pitch angle and yaw angle of the vanishing point, which finally realizes the solution of the position of the image plane corresponding to the road plane captured during the working process of the sweeper.
In this paper, the inverse perspective transformation is used to eliminate the perspective effect and obtain the top view of the real road surface, and the YOLOv5 algorithm completes the recognition of single garbage and obstacles. As shown in Figure 5, it is the result of recognizing obstacles and single items of garbage with the YOLOv5 algorithm after inverse perspective transformation of multiple initial images.

Figure 5.
Detecting results of objects on the road based on (Inverse Perspective Transformation) IPM and YOLOv5. (The number represents the angle of rotation of the recognized object in the image).
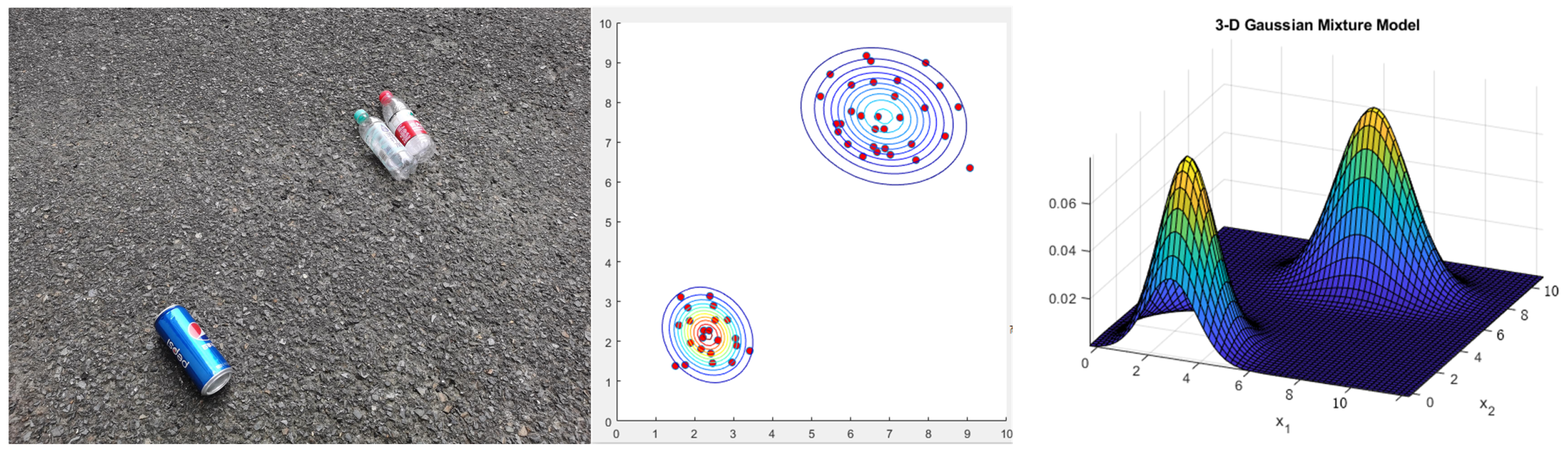
YOLOv5 is used to recognize a single garbage target. In order to make the recognition information more qualitatively dense and reduce the planning redundant points, we further fused the feature points for recognition by a GMM-based skeleton feature downscaling method, which maps the skeleton features of the garbage into a two-dimensional plane and makes the feature points more characteristic. GMM is a K-means-like model that quantizes things precisely with Gaussian probability density function [27].
Firstly, we discretize the recognized sweeping targets, i.e., we sparsify the features of a single target by selecting some random points in the target box. The random points in the perceptual domain form a set, and the region formed by similar targets can often be characterized by independent normal distributions, so we adopt the GMM model to characterize each discrete region. As shown in Figure 6, the initial image is a Gaussian mixed distribution, and the accurate detection and target localization of garbage is accomplished.
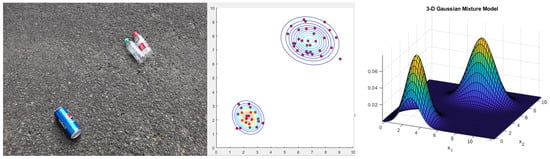
Figure 6.
Gaussian Mixture Model (GMM)-based garbage clustering.
3.1.2. Continuous Sensing of Complex Garbage Area Based on PE Analysis
Through the fusion of object detection and GMM, we can obtain the distribution of discrete targets; however, in real environments, there also exist some garbage regions with sparser features. As shown in Figure 7a, the road garbage is continuously distributed on the road and is not composed of significant independent targets, while the pixel characteristic of the garbage area is not regular. At this point, the methods relying simply on deep features struggle to accomplish the area judgment task.

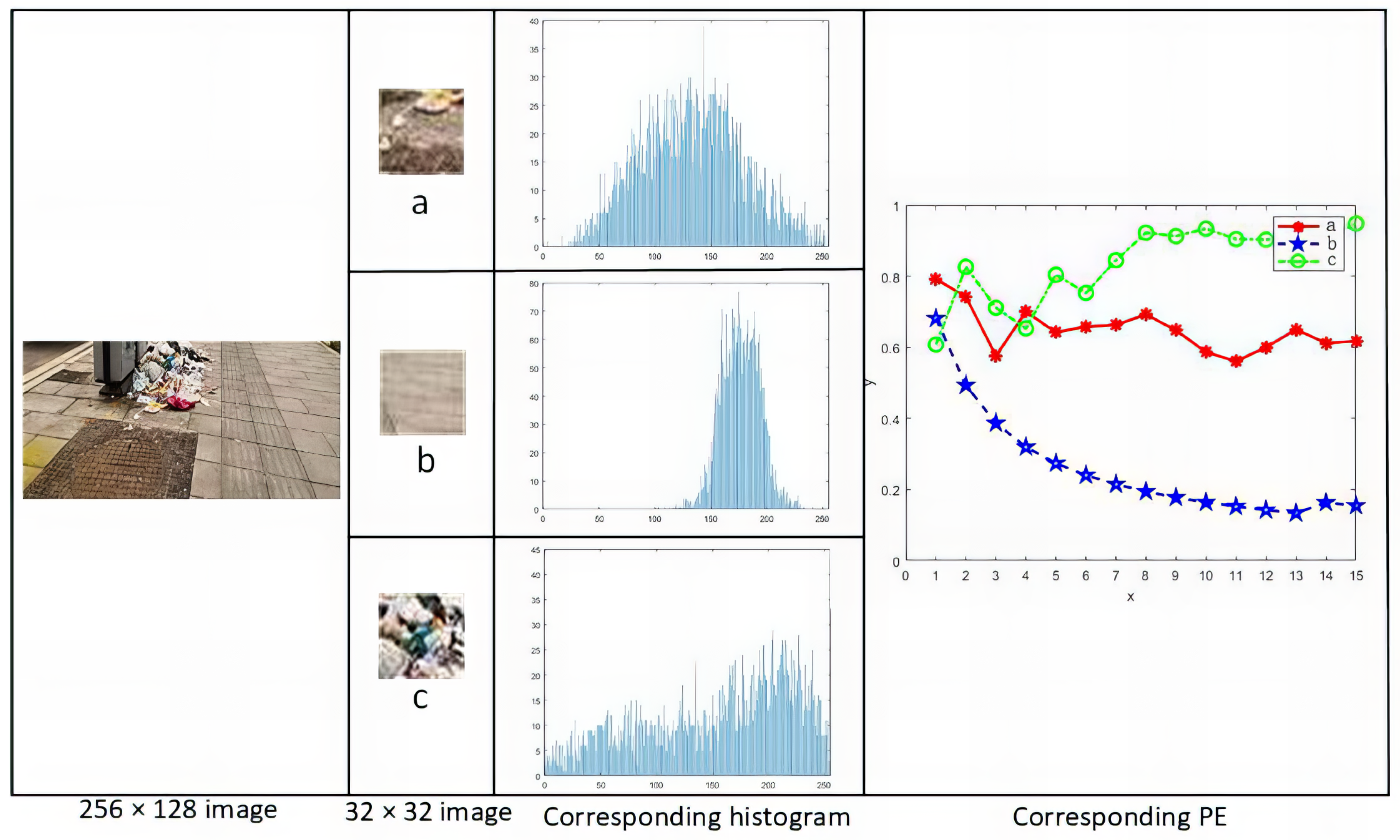
Figure 7.
The (a) is an image of a road containing a complex garbage pile. (b) is the solution to the road complex garbage pile. The circle is the process of iterative computation of PE, and the red dot is the complexity threshold, above which the complexity pavement is indicated.
In order to form a qualitatively dense identification for road garbage regions, inspired by [28,29], we design a road image information entropy identification method to predict the distribution of garbage regions by recognizing the heterogeneity of garbage regions. As shown in Figure 7b, we first perform gradient histogram detection on the camera front view image and select the centroid of the anomalous partition, then gradually expand and calculate the complexity of each partition. We will use the PE-a method of approximating the entropy by ordinal analysis to evaluate the complexity of the given partition, and ultimately determine whether it belongs to the complex garbage heap.
The specific calculation steps are as follows: We first perform gradient histogram detection on the camera’s front view image to extract possible garbage distribution areas and select the center of the garbage area. The lower half part of the front view image with a size of 256 × 128 is transformed into a BEV image and then the whole image is divided into 32 regions with a size of 32 × 32. The histogram information is extracted from each region, and the potential garbage distribution is obtained based on the feature of the histogram information. The histogram of each 32 × 32 image block is calculated to predict the potential garbage distribution region. As shown in Figure 8, the road area tends to have a very narrow histogram for the pixel feature, which is relatively pure. In contrast, the histogram of the potential garbage area tends to have a very wide distribution. Based on this histogram, the potential garbage area could be selected preliminarily.
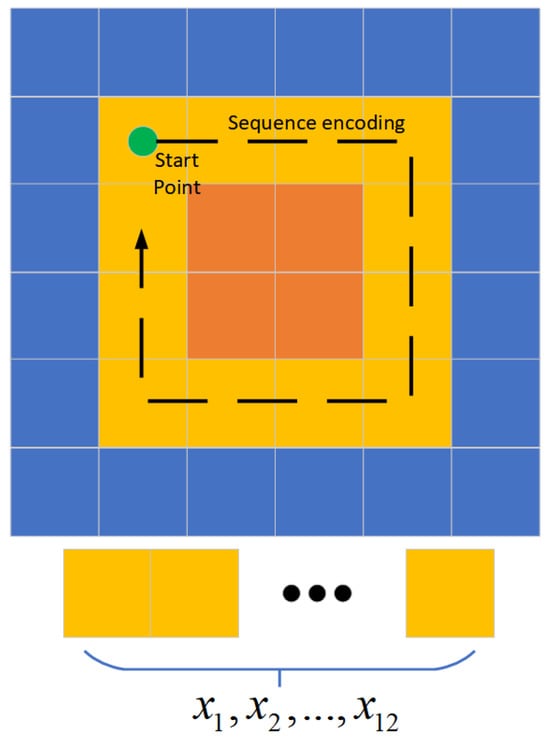
Figure 8.
Selection process for a 4 × 4 circle (12 pixels).
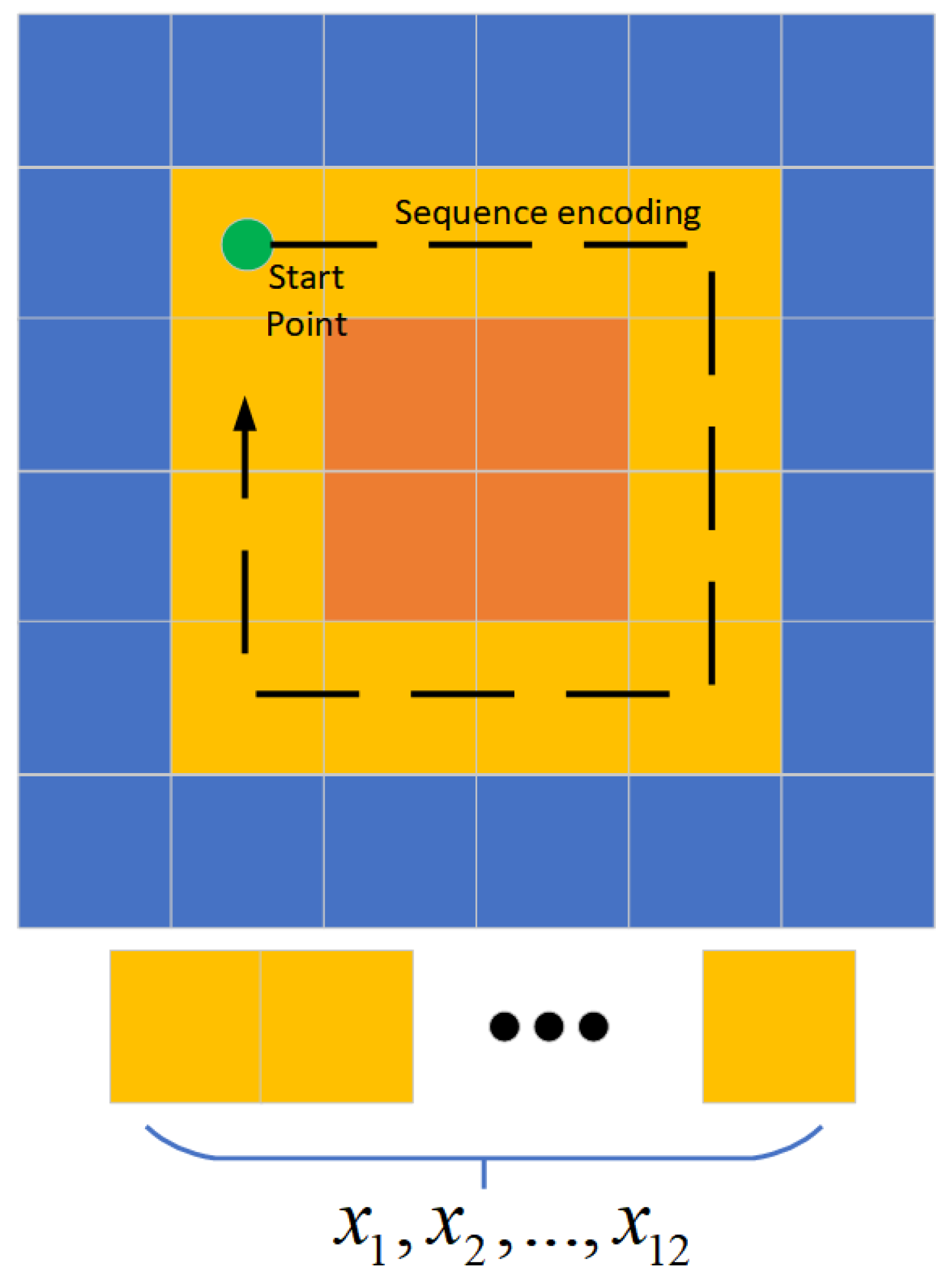
Since each image block is not necessarily fully covered by garbage, we need to further determine the specific intra-block garbage regions by fine scanning. Thus, we proposed an inference method based on the region PE evaluation [28]. For each potential garbage distribution region, as shown in Figure 7b, we encode the area image into sequence by outwardly expanded encoding from the center of the garbage area. Then, encoding process scans the area from the inside out in an expanding search, and the image features are encoded as a sequence set . Each scanned sequence is stacked to calculate the PE value, which could describe the changing of the image feature [29].
The original sequence is a set of RGB points, and RGB only represents the details of the color composition with very weak order features. Therefore, before we input to the PE calculation, we convert the pixel features of the image to HSV format and retain only the H that characterizes the color interval, while S and V characterize the saturation and luminance of the color, for which the two values are homogenized as the average of all pixel points within the color block. By converting the image feature format, we preserve the image features and give them sequential attributes with H values as the ordering criterion.
By converting the image feature format, we preserve the image features and assign them sequence properties using the H-value as the sorting criterion. For each 32 × 32 × 1 pixel block, the PE calculation process starts from the internal 4 × 4 circle (12 pixels) and ends with the external 32 × 32 circle (124 pixels). The specific calculation method is shown in Figure 8. The HSV-based sequence is considered as a time series with a time delay of 1. Assuming that a one-dimensional time sequence represents the HSV features of a circle of images, the elements within it are sorted in ascending order according to the reconstructed sequence , and the computational steps are shown in Algorithm 1.
It is worth noting that after calculating one region of 32 × 32 according to the steps of the algorithm, we still further decompose the potential region into four regions of the same size, i.e., 8 × 8 regions, for which further PE entropy calculations are carried out to determine a more detailed region of garbage distribution.
| Algorithm 1: PE . |
 |
As shown in Figure 7b, the substitution entropy detection box on the right does not detect pixel anomalies, so it will not continue to expand the detection outward. After the detection box on the left detects the pixel abnormality, it will continue to select the center point in the direction of the maximum replacement entropy and continue to expand the detection in all directions until there is no pixel abnormality. Further, this method can also be used to circumvent anomalous regions caused by continuous waterlogging and road reflections.
As shown in Figure 9, taking three 32 × 32 pixel regions as an example, Figure 9a is the junction of garbage and road, Figure 9b is the part of the clean road, and Figure 9c is the complex garbage pile. Then, for each region, the histogram information is extracted based on the histogram information to obtain the potential garbage distribution region. Then, PE entropy calculation is performed for the collection of sequences to obtain the complexity of the sequences. As shown in the line graph of Figure 9, the PE value of the sequence of Figure 9c is growing, which indicates that the pixels of the current loop are more complex and have not been iterated to the background region with a more uniform color. The PE value of the sequence of Figure 9a decreases to a certain extent, which indicates that the current expansion circle has been located in the solid color background region on the periphery of the garbage region.
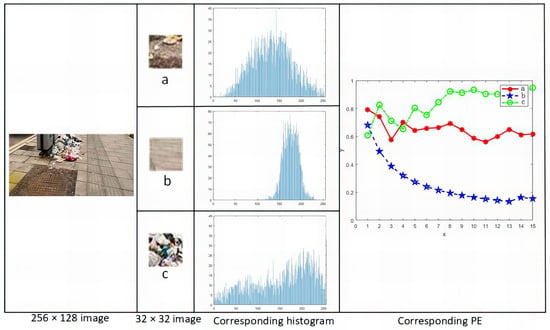
Figure 9.
Calculated process of road image complexity. Where (a) is the junction of garbage and road, (b) is the part of the clean road, (c) is the complex garbage pile.
3.2. Optimal Sweeping Path Planning Based on Simulated Annealing Algorithm
Different from the traditional robot path planning algorithm to obtain the shortest obstacle avoidance path as the optimization goal, the unmanned sweeper not only needs to avoid obstacles but also needs to obtain the optimal sweeping path. In order to obtain the optimal sweeping path, inspired by [25], in this paper, we propose a fusion path planning algorithm based on BF-CPP + SA, which firstly takes the discrete garbage distribution region as the traversal target, considers the global scavenging path planning as TSP-CPP (traveling salesman problem–coverage path planning), and solves the optimal traversal strategy by simulated annealing algorithm. On the basis of global planning, we cover the independent discrete regions for traversal by BF-CPP method.
3.2.1. Generation of Convex Hull in the Region to Be Cleaned
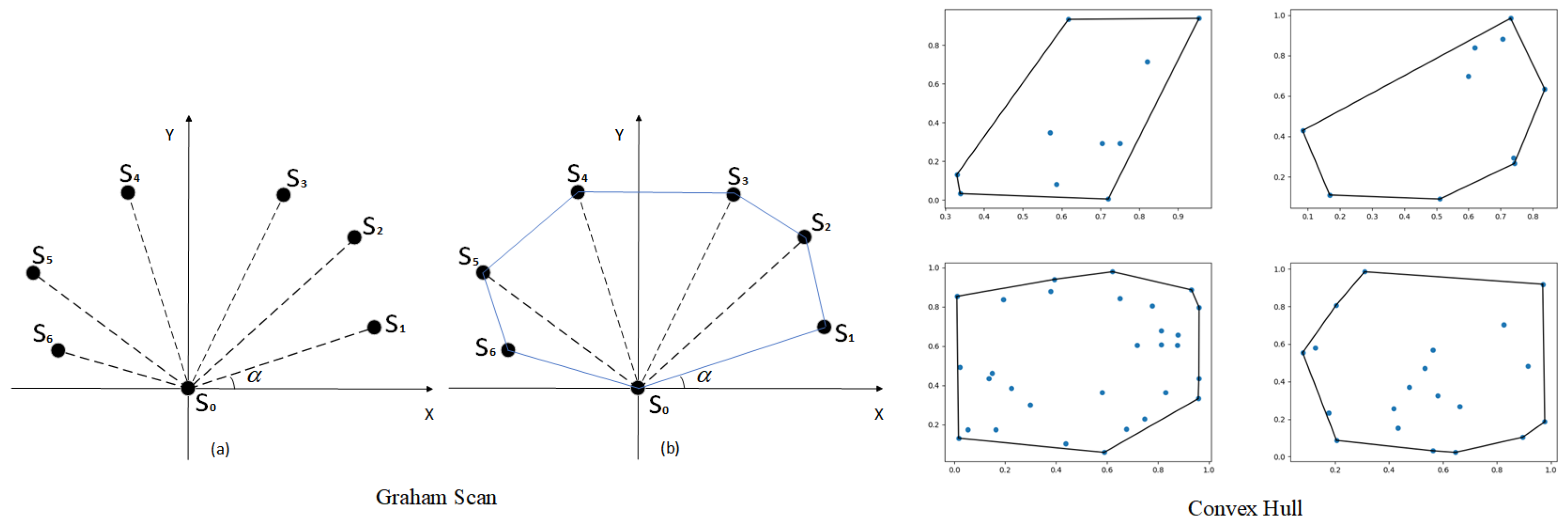
Convex Hull refers to the convex polygonal region where all the garbage exists in the two-dimensional plane space, forming the Convex Hull set for the garbage region. In this paper, we will use the Graham scanning method; the idea is to find a point on the Convex Hull first, and then start from that point to look for the points on the Convex Hull one by one in a counter-clockwise direction. The main steps are as follows:
- (1)
- Put all the points in a two-dimensional coordinate system as shown in Figure 10; then, the point with the smallest vertical coordinate must be the point on the Convex Hull with as the starting point.
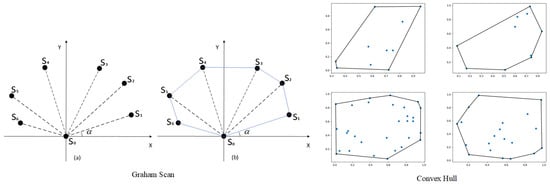 Figure 10. Transformation of garbage regions into Convex Hull sets. Where (a) represents the set of points to be included. (b) represents the Convex Hull by using the Graham scanning method.
Figure 10. Transformation of garbage regions into Convex Hull sets. Where (a) represents the set of points to be included. (b) represents the Convex Hull by using the Graham scanning method. - (2)
- Calculate the magnitude angle of each point with respect to and sort each point in order from smallest to largest. When is the same, the point closer to is ranked first. For example, the following figure shows that the results are , , , , , and .
- (3)
- Put , and into the stack, and then repeat step 2 above with as the current point to obtain the stack that characterizes the vertex of the convex packet.
- (4)
- Sequentially connect the neighboring points in the stack, and finally connect and the point at the top of the stack, as in Figure 10, to map the final convex envelope region.
Specifically, first, we randomly take some farther points inside the GMM distribution and then form a Convex Hull set, as shown in Figure 9 for the set of Convex Hulls formed using the above Graham scanning method.
3.2.2. Path Planning for a Single Convex Hull Set
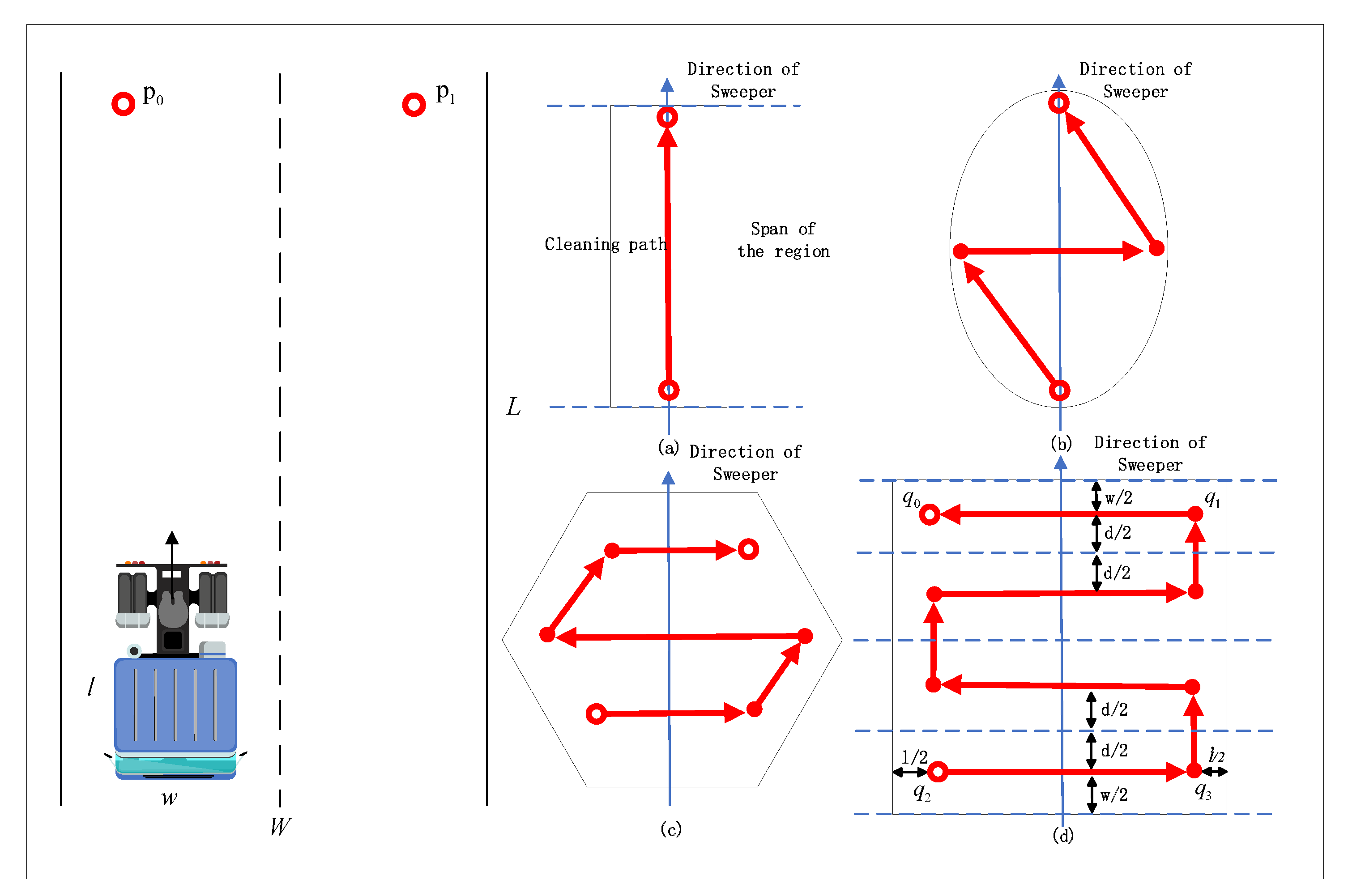
Then, full-coverage path planning for a single Convex Hull set of garbage regions is performed. Depending on the size of the convex Hull, there will be different sweeping strategies as shown in Figure 11. For long striped areas, the paths are straight lines. For oval areas, the paths are zigzags, and for large polygonal areas, the paths are bow ties.
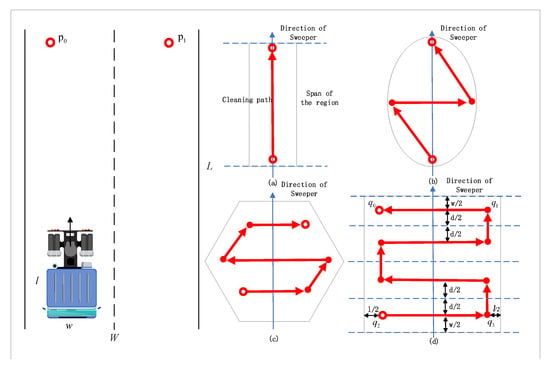
Figure 11.
Left: Two-dimensional spatial description of the cleaning task. Right: Coverage path planning schematic for a single garbage area. Where (a) is straight lines. (b) is zigzag, (c,d) are bow ties. And the arrows show the direction of the sweeper’s progress, the dots show the start and end points.
The sweeping task can be described in two dimensions, and the size of the camera footprint, i.e., the area of the ground captured in one frame, is , as shown in Figure 11, where l and w are the length and width of the sweeper. Assuming that there is no forbidden area to visit in the target area, we assume that the unmanned sweeper will travel to the location or after completing the sweeping work in this camera frame. Therefore, the goal of the TSP-CPP problem considered here is to find the best path that traverses all garbage points so that the unmanned sweeper will sweep the garbage along the path and minimize the total travel cost.
The back-and-forth pattern can generate a back-and-forth pattern path (BFPs) for covering a single convex polygon region. Back-and-forth-CPP (BF-CPP) greatly simplifies path design and is easy to implement, so it is adopted by many CPP methods. As shown in Figure 11a, the BFP of a convex polygonal region can be found by a set of parallel lines of support (LOS). The distance between the two lines of support becomes the span of the convex polygon region. The direction of path generation, i.e., the direction of the sweep line, is the forward direction of the sweeper.
As shown in Figure 11d, a rectangular area to be swept has been identified according to the previous steps, and given the direction of sweeping, where W is the width of the area to be swept and w is the width of the sweeper, the minimum number of flight lines to completely cover the area is . Then, cell decomposition is executed to decompose the region into a set of sub-regions along the flight line. Then, rectangular cells that only cover the sub-regions are constructed. To ensure full coverage, we set the width of the first and last cell to w and the width of the middle cell to , with d being the distance between the two flight lines, where
Since the frequent acceleration and deceleration of the sweeper tend to increase the travel time and travel cost, the algorithm of this module needs to reduce the number of turns of the BFPs as much as possible. As shown in Figure 11a, the width of the convex polygon is smaller than the width w of the sweeper when the minimum number of turns is 1. As shown in Figure 11b–d, the number of turns of the BFP is when the width of the garbage area . The exact computation progress is described in Algorithm 2.
| Algorithm 2: BF-CPP . |
 |
The optimal travel path is constrained by the order of visiting individual garbage areas as well as the entry and exit locations, and although a BFP can be found within a single area with a minimum number of turns, its combination with other areas may not lead to the optimal travel path. Therefore, we tend to pre-select 2–4 feasible BFPs with lower travel costs when CPP is performed for a single area. are all possible starting points for travel paths as shown in Figure 11d, and the exact choice of which one to use as the starting point is derived by the exact method of the TSP-CPP clearance paths based on simulated annealing in the next section.
3.2.3. Solutions for Multiple Convex Hull Set
Finally, a simulated annealing-based TSP-CPP scavenging path accuracy method is executed.
The TSP problem is an NP-hard problem in combinatorial optimization, where the difficulty lies in the fact that as the number of objectives increases, so does the amount of data to be processed. For this task, the problem consists of solving the shortest path to visit each area to be cleaned once, given a series of areas to be cleaned and the distance between the areas. Specifically, this problem is a symmetric TSP problem, i.e., the distances between two regions to be cleaned are equal. We propose to use the simulated annealing algorithm to solve the TSP-CPP problem.
SA is a stochastic optimization algorithm based on the Monte-Carlo iterative solution strategy. The algorithmic optimization is carried out by continuously rearranging the current solution internally and gradually arranging it into the solution that achieves the minimum value of the objective function. The process of continuously optimizing the solution needs to remove the limitations of the greedy algorithm and can have a certain probability of jumping out of the local optimum to reach the global optimum. The exact computation progress is described in Algorithm 3.
| Algorithm 3: SA . |
 |
Therefore, attention should be paid to the connection of local and global coverage paths to address the integrated TSP-CPP, including the full coverage paths in each ROI (region of interest), the access order within the area to be cleaned, and the entrance/exit locations.
The city location data are the entrance and exit locations in the area to be cleaned, and for the large area to be cleaned as described in the previous section, the entrance and exit locations are at most 4 groups. The algorithm will calculate the travel cost for each of these 4 city distributions.
Set the initial temperature and randomly select a traversal path as the initial path and calculate its length ; then, randomly generate a new traversal path and calculate its length . If , then receive as the new path; otherwise, receive with the probability of simulated annealing, and then cool down the temperature. The above steps are repeated until the temperature reaches the minimum value .
There are 3 main methods for generating new traversal paths:
- (1)
- Randomly select 2 nodes and swap the order of these 2 nodes in the path.
- (2)
- Randomly select 2 nodes and reverse the order of the nodes between these 2 nodes in the path.
- (3)
- Randomly select 3 nodes , and then shift the nodes between nodes m and n to behind node k.
The higher the number of iterations, the more accurate the result will be; however, too many iterations will require too long a calculation time, so the number of iterations needs to be chosen appropriately.
In path planning, the algorithm will compute the coverage of the Convex Hull set in real time and enter the next region when the target sweep is detected without turning back, avoiding the problem of the SA having to go back to the starting point.
3.2.4. Static and Dynamic Obstacle Avoidance Strategies
Static and dynamic obstacles will affect the unmanned sweeper to perform the task, the function of detecting obstacles and predicting their future trends through sensors, and performing path planning according to certain algorithms so as to avoid obstacles is essential. The unmanned sweeper can obtain the point cloud information in the environment by LiDAR and match and analyze the obstacles in the environment in real time, and the objects that do not exist in the high-precision map will be judged as obstacles. Obstacles without positional changes are static obstacles, while the positional changes in obstacles in different frames of data characterize the historical motion trajectories of dynamic obstacles. In order to make the robot safer during obstacle avoidance, we will make a reasonable expansion of obstacles.
For static obstacles, if the expanded static obstacles appear on the paths of the two cities planned by SA, we will replan the paths of this section of the road based on the A star algorithm [18].
For dynamic obstacles, we use particle filters to make trajectory predictions for them. The historical trajectories of dynamic obstacles are pre-stored into a passive mode behavioral planner, then all feasible trajectories are extracted from the map based on the embedded traffic rules, then the particles are sampled from the behavioral model, the weights are computed for each sampled particle, and finally the weights are normalized and the likelihood of each predicted trajectory is computed. The trajectory with the highest likelihood is passed into the local planning and used for path replanning.
4. Experimental Results
4.1. Experiment Platform
In this section, we perform a simulation study to evaluate the performance of the proposed methods, including YOLOv5, IPM, GMM, BF-CPP and SA-based cleared path accurate methods. Among them, YOLOv5 is carried out on Pytorch (version: 1.7) and the rest of the methods are implemented using MATLAB (version: 2021b). The experiments are performed on a PC with Intel Core i5, RTX 3060ti, 16 GB RAM and 1 TB storage.
Among the garbage detection part, we use the actual scene to complete, as shown in Figure 12, where the left is the unmanned sweeper used for this experiment, the car is 1.2 m long, 0.8 m wide and 1.4 m high, and the camera is installed at 1 m from the ground. We think the car can be swept clean after being on the road. Figure 12 (right) is the scene oriented for this experiment, which is a 50 m long and 4.5 m wide sidewalk in the park.

Figure 12.
Experimental sweeping vehicle platform and actual scene.
4.2. Garbage Detection Experiments Based on YOLOv5 and PE
This experiment uses the common garbage detection and obstacle dataset on the roadway. This dataset contains 14,964 pictures, of which there are 20 categories of GT frame labels, which are as follows: bag, book paper, can, paper box, traffic sign, roadblock, stone pier, etc. Since the experiment mainly detects the common garbage targets on the sidewalks of enclosed parks, only six of these categories are detected for garbage: leaf, tissue, paper, can, carton, and bottle. Only three of these categories are detected for obstacles: roadblocks, stone piers, and bicycles. Some of the images in the dataset are shown in Figure 13. After filtering the dataset and removing the images that do not contain the above objectives, 10,000 images are retained, of which 9000 and 1000 are in the training and validation sets, respectively.

Figure 13.
Selected images from the Obstacles and Spam dataset.
For comparison, we choose Faster RCNN [30], YOLOv3 [31], YOLOv4 [32] and our algorithm. We use time, precision, recall, and mAP (mean average precision) as the evaluation metrics of the model to measure the performance of the model. Time represents the time spent for testing 100 validation sets. Precision is the rate of correct predictions among all results where the prediction is a positive sample, and here we focus on checking the accuracy of the most common garbage on the road, i.e., bottles. Recall is the rate of correct predictions among all positive samples. mAP is the mean pixel accuracy of the total category N, which measures how good the model is over all the categories. The comparison results of different network models are shown in Table 1.

Table 1.
Performance comparison of YOLOv5 with different network models.
For the complex garbage pile, this experiment additionally uses a dataset open-sourced by G Mittal [33], which contains 2561 images and 956 images containing garbage; the rest are non-trash images that are very similar to the trash in terms of various visual attributes. Therefore, this dataset cannot fully meet the needs of the road garbage scenario and needs to be collected by ourselves. As shown in Figure 13, for the various types of garbage images used in this experiment, the first row is the image of a single garbage, the second row is part of the images in the SpotGarbage dataset, and the third row is the self-acquired images of road garbage.
For comparison, we choose UNet++ [34], DUNet++ [8], YOLOv3+Self-Cluster and our algorithm YOLOv5+PE. We still use time, AP (average precision), and MIoU (mean intersection over union) as model evaluation metrics to measure the performance of the model. Time represents the time spent for testing 100 validation sets. AP is the pixel accuracy, where the ratio of correct pixels is calculated on a per-category basis. MIoU is the ratio between the intersection and the union of the ground truth and algorithm-predicted segmentation of the garbage region. Performance comparisons of the YOLOv5+PE algorithm with different network models are shown in Table 2. It can be seen that the YOLOv5+PE algorithm has a significant increase in detection accuracy, although the detection time is longer.

Table 2.
Performance comparison of YOLOv5+PE algorithm with different network models.
4.3. A Sweeping Path Accuracy Method Based on Situation Analysis and BF-CPP + SA
4.3.1. Multi-Region Situational Analysis and Route Planning
We set up three sets of experimental scenes. For Scene 1, we designed multiple small garbage to verify the effectiveness of the SA algorithm. For Scene 2, we set up a non-rectangular unit to verify the effectiveness of the BF-CPP algorithm. For Scene 3, we set up small garbage with multiple non-rectangular units to verify the synergistic effect of BF-CPP and SA. Finally, we combine the three experimental scenarios together to test the coherence and smoothness of the algorithm between different camera frames.
As shown in Figure 14, the first line is the initial camera image, the second line is the effect image after IPM, the third line is the effect image after YOLOv5+GMM, the fourth line is the path calculated under the three scenarios, respectively, and the last one is the resulting image after the three experimental scenarios are combined. From the figure, it can be seen that both IPM and GMM can complete the analysis of the distribution situation of the garbage target better, and the final planned path can also complete the cleaning task better.

Figure 14.
Accurate method of sweeping path based on BF-CPP + SA. Where the red line is the planned path and the arrow is the direction of travel.
4.3.2. Path Planning in Static and Dynamic Obstacle Scenarios
Considering the presence of complex garbage piles and static and dynamic obstacles in real scenarios, we set up a set of experiments to verify the performance of the BF-CPP and SA algorithms. Among them:
- (1)
- Discrete waste and complex waste piles with lower heights.
- (2)
- Discrete waste and complex piles with higher heights.
- (3)
- Discrete waste and complex piles with static obstacles.
- (4)
- Discrete waste and complex piles with dynamic obstacles.
- (5)
- Discrete garbage, complex piles of garbage with low height and static obstacles.
- (6)
- Discrete garbage, complex piles of garbage with low height and dynamic obstacles.
The experimental results are shown in Figure 15, where the white irregular box indicates the area to be cleared, the yellow irregular box indicates the complex garbage pile conforming to the clearing rules, the blue irregular box indicates the complex garbage pile whose height exceeds the threshold, the black rectangular box indicates the static obstacles, and the gray rectangular box indicates the prediction of the motion trend of the dynamic obstacles.

Figure 15.
Performance of BF-CPP and SA algorithms combined with obstacle avoidance algorithms. where the white irregular box indicates the area to be cleared, the yellow irregular box indicates the complex garbage pile conforming to the clearing rules, the blue irregular box indicates the complex garbage pile whose height exceeds the threshold, the black rectangular box indicates the static obstacles, and the gray rectangular box indicates the prediction of the motion trend of the dynamic obstacles.
As can be seen from Scenes 1 and 2, according to the local elevation map, complex dumps below the height threshold will be considered areas to be cleared, while complex dumps above the threshold will be considered obstacles. As can be seen from Scene 3, for the case of obstacles between two sites (areas to be cleared), this algorithm will replan this journey with the A star algorithm and then replace the original path. As can be seen from Scene 4, the particle filter can reasonably predict the motion trend of dynamic obstacles, making the path planned by the A star algorithm more robust. Scenes 5 and 6 are a collection of the above scenarios, and it can be seen that the BF-CPP and SA algorithms can also accomplish the task of path planning very efficiently in relatively complex situations.
4.3.3. A Comparative Study of Scenarios with Different Sparsities
Considering the existence of real scenarios with different garbage heap sparsity, we set up a set of experiments to verify the performance of the BF-CPP and SA algorithms. Among them:
- (1)
- Ten situations where pavement garbage is clustered but overall sparse.
- (2)
- Ten scenarios with a balanced distribution of pavement garbage.
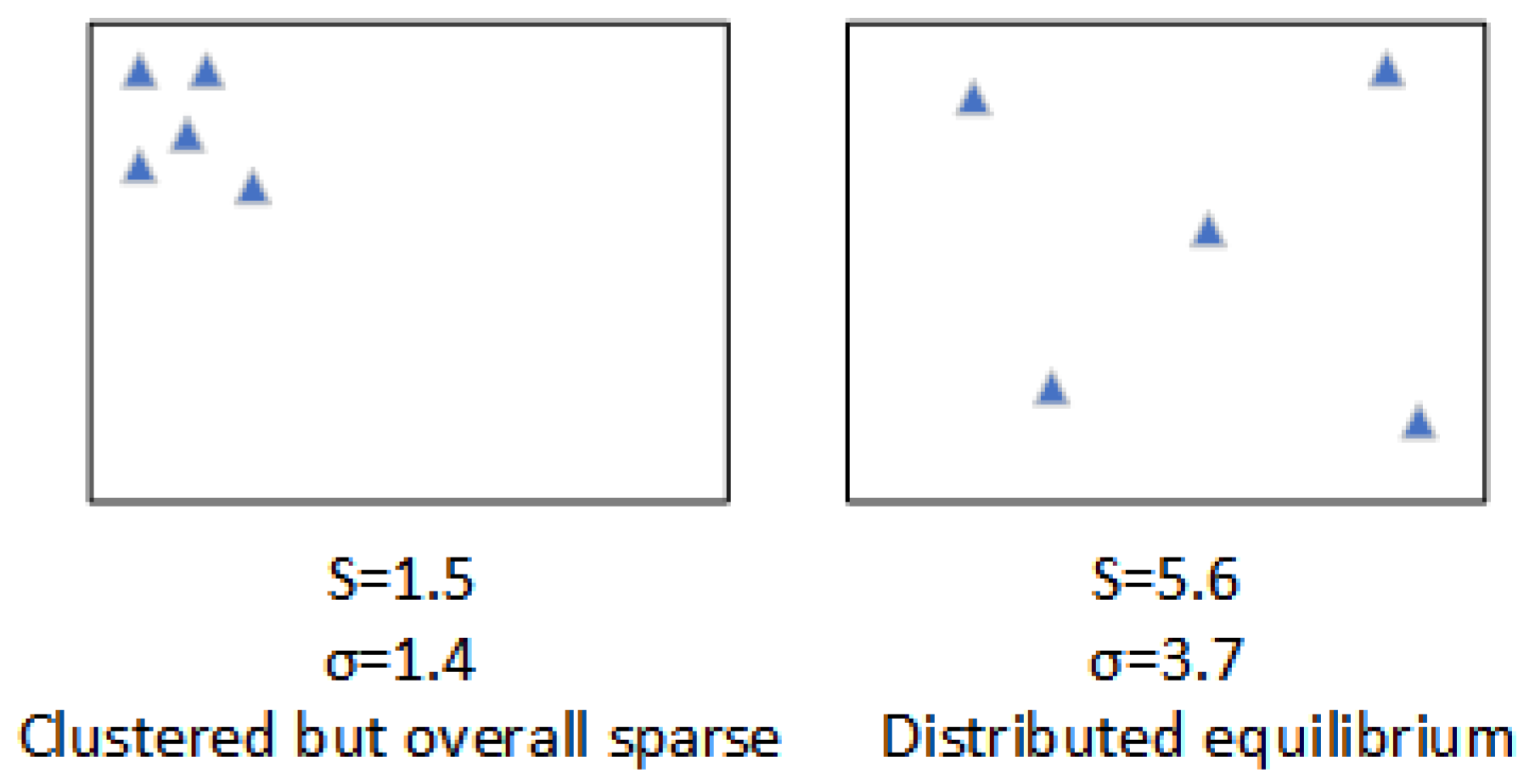
The scene schematic is shown in Figure 16, where the mean s and variance of the distance between obstacles are used to denote the scene sparsity. We set up simulation experiments to verify the performance of the A star algorithm, CPP algorithm and BF-CPP + SA algorithm under two scenarios, respectively. The experimental results are shown in Table 3 and Table 4. According to the experimental results, we found that the A star algorithm can also work well in the case of roadway trash aggregation but overall sparseness, but it is not satisfactory in the case of balanced distribution of roadway trash. The CPP algorithm has better coverage, but the energy loss is serious. After a comprehensive analysis, BF-CPP + SA is found to be more suitable for all kinds of complex situations.
Figure 16.
Scenarios with varying sparsity. Where blue triangles are obstacles.

Table 3.
Comparison of algorithms’ performance in scenarios with aggregated but overall sparse road debris.

Table 4.
Comparison of the performance of algorithms under the scenario of equalization of road garbage distribution.
4.4. Discussion
We also use the simulation environment to implement three path-planning algorithms to compare with the algorithms proposed in this paper:
- (1)
- A star: Using the intelligent backtracking mechanism of greedy A star (GA) search to pass through a given garbage area.
- (2)
- CPP: Use precise cell decomposition methods to decompose free space into simple, non-overlapping regions. Enable robots to easily sweep through these unobstructed areas.
- (3)
- KNN: Path planning is accomplished using the locally optimal KNN algorithm.
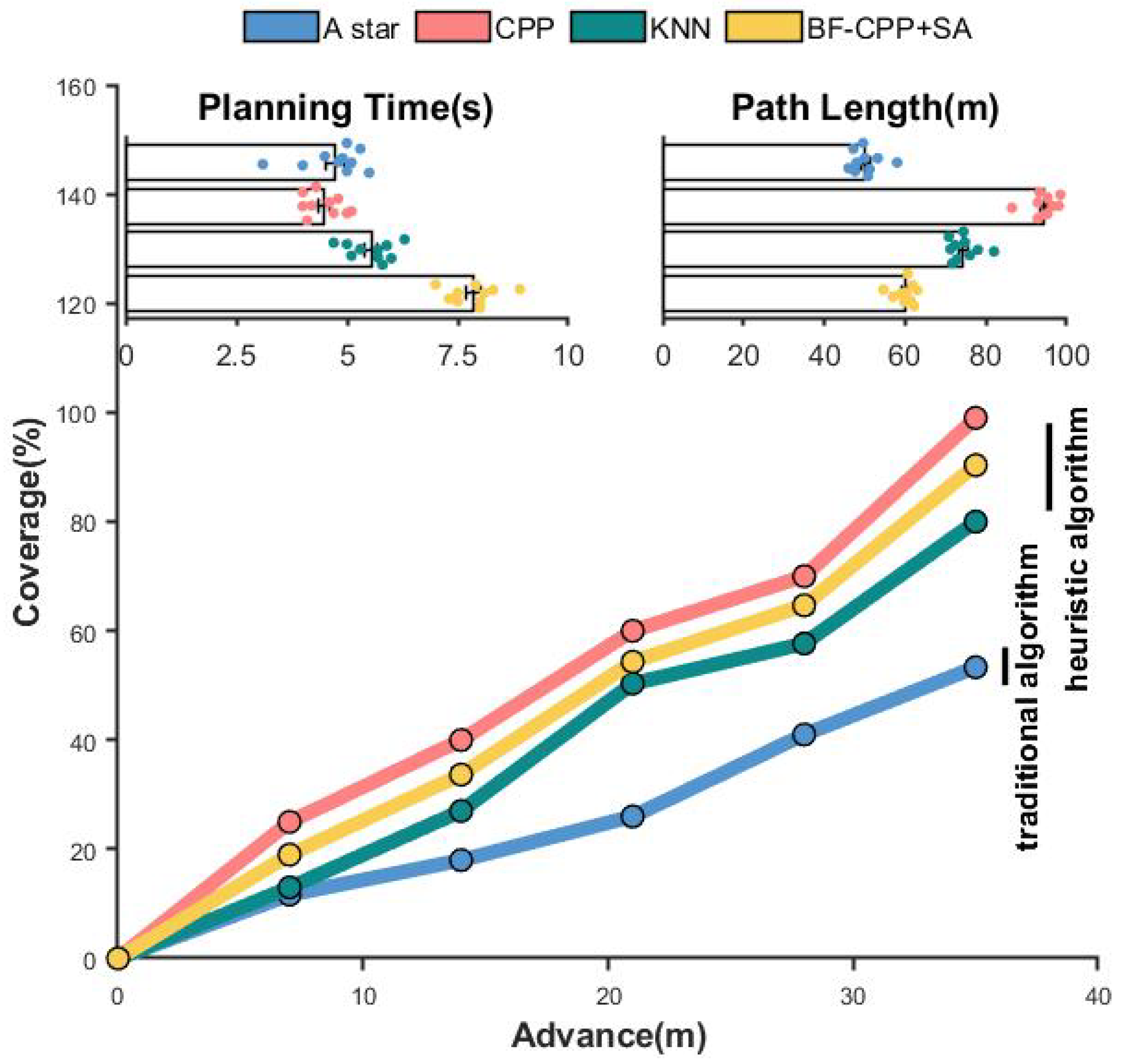
As shown in Table 5, the A star algorithm does not have the ability to recognize the target region; we turn the garbage region into the corresponding path point, and the result is that the performance of the A star algorithm is still unsatisfactory. In the CPP algorithm, due to its mechanical nature and blind obedience rows, the planning path is too long although the planning time and coverage are very excellent. In contrast to the KNN algorithm, the BF-CPP + SA-based sweeping path accuracy method performs well in terms of path length and garbage area coverage, although the planning time is slightly inferior.

Table 5.
Performance of BF-CPP + SA algorithm compared with traditional path planning.
The specific performance of each algorithm is shown in Figure 17. The line graph reflects the cleaning efficiency of each algorithm, and the two subplots are the planning time and the path length obtained from the planning, respectively. The floating points on the subplots indicate the average value taken after multiple experiments.
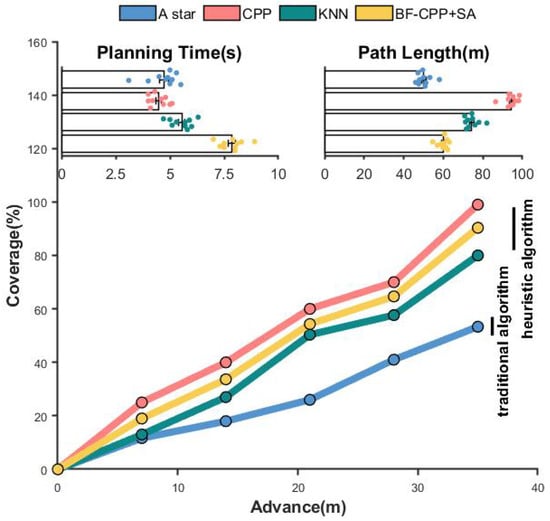
Figure 17.
Performance of BF-CPP + SA algorithm compared with traditional path planning.
In summary, the exact cleaning path method based on BF-CPP + SA proposed in this article can comprehensively solve the mechanical and aimless nature of CPP while maintaining the completion of cleaning. Compared with traditional path planning algorithms, it can also better solve the problem of traditional algorithms being unable to correctly identify garbage and obstacles. Compared to the A star algorithm and the CPP algorithm, there is also a significant performance improvement.
Through theoretical analysis and experimental study, we demonstrate the performance and capability of the proposed BF-CPP + SA method from various aspects. In the experiments, traditional algorithms such as the A star algorithm and KNN algorithm have less than optimal sweeping efficiency because they do not have the ability to identify the target area. The CPP algorithm is able to traverse the garbage area, but its path length and inefficiency are discouraging. In particular, the exact method based on BF-CPP + SA can guarantee an optimal solution for TSP-CPP, but due to the more complex processing flow, it is able to produce high-quality tours but still needs to be optimized in terms of planning speed.
5. Conclusions
In this paper, we introduce a novel unmanned sweeper vehicle sweeping method based on target distribution posture analysis. Firstly, we use IPM and YOLOv5 to identify the classes of obstacles and garbage present on the road surface, and then we tolerate similar obstacles as well as garbage targets by GMM, and for complex garbage piles, we use PE to differentiate the regional complexity. The target-based distribution posture analysis is completed by combining the single target with the complex garbage pile. After the above operations, we convert the trash sweeping task into a TSP-CPP problem, and finally, we use the exact method of BF-CPP + SA for trash sweeping to find an efficient and robust sweeping path with the lowest travel cost. This method enhances the target perception ability within the currently visible sweeping, eliminates blindness, and improves the environmental adaptability of the unmanned sweepers. In order to ensure the efficiency of sweeping, the shortest path is formed as far as possible so that the original path planning based on heuristic search forms an efficient sweeping path. It improves the cleaning efficiency and reduces energy consumption. After experimental validation, the path planning method based on target distribution posture analysis performs beneficially in both planning path length and coverage, but the planning time is unsatisfactory due to the complicated computational process of identifying the area to be swept. In the future, we will simplify the computational model of the area to be swept to reduce the planning time and try to extend the proposed method to cope with various traffic situations.
Author Contributions
Methodology, Y.L., P.P. and H.C.; Software, Y.L.; Validation, Y.L. and Q.Y.; Formal analysis, P.P. and H.C.; Data curation, Q.Y.; Supervision, Q.S. and J.L.; Project administration, J.L.; Funding acquisition, P.P., Q.S. and J.L. All authors have read and agreed to the published version of the manuscript.
Funding
Fund project: National Natural Science Foundation of China (52202496); the Natural Science Foundation for Colleges and Universities in Jiangsu Province (22KJB520007); The 333 Talent Technology Research Project of Jiangsu (2022021); Nantong social livelihood science andtechnology project [MS12022015]; Postgraduate Research & Practice Innovation Program of Jiangsu Province (SJCX22_1619) and National Natural Science Foundation of China (42001239).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the privacy of the follow-up study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rayguru, M.M.; Mohan, R.E.; Parween, R.; Yi, L.; Roy, S. An Output Feedback Based Robust Saturated Controller Design for Pavement Sweeping Self-Reconfigurable Robot. IEEE/ASME Trans. Mechatron. 2021, 26, 1236–1247. [Google Scholar]
- Nguyen, V.D.; Van Nguyen, H.; Tran, D.T.; Lee, S.J.; Jeon, J.W. Learning framework for robust obstacle detection, recognition, and tracking. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1633–1646. [Google Scholar]
- Botha, F.J.; van Daalen, C.E.; Treurnicht, J. Data fusion of radar and stereo vision for detection and tracking of moving objects. In Proceedings of the 2016 Pattern Recognition Association of South Africa and Robotics and Mechatronics International Conference (PRASA-RobMech), Stellenbosch, South Africa, 30 November–2 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–7. [Google Scholar]
- Zhang, T.; Li, M.; Li, L.; Luo, W. Design of garbage classification system based on RFID. J. Phys. Conf. Ser. 2021, 1744, 022111. [Google Scholar]
- Ranjana, P.; Varsha, S.; Eliyas, S. IoT Based Smart Garbage Collection Using RFID Andsensors. J. Phys. Conf. Ser. 2021, 1818, 012225. [Google Scholar] [CrossRef]
- Bansal, S.; Patel, S.; Shah, I.; Patel, P.; Makwana, P.; Thakker, D. AGDC: Automatic garbage detection and collection. arXiv 2019, arXiv:1908.05849. [Google Scholar]
- Ma, W.; Wang, X.; Yu, J. A lightweight feature fusion single shot multibox detector for garbage detection. IEEE Access 2020, 8, 188577–188586. [Google Scholar] [CrossRef]
- Liao, J.; Luo, X.; Cao, L.; Li, W.; Feng, X.; Li, J.; Yuan, F. Road garbage segmentation and cleanliness assessment based on semantic segmentation network for cleaning vehicles. IEEE Trans. Veh. Technol. 2021, 70, 8578–8589. [Google Scholar]
- Dai, Y.; Liu, W.; Wang, H.; Xie, W.; Long, K. YOLO-Former: Marrying YOLO and Transformer for Foreign Object Detection. IEEE Trans. Instrum. Meas. 2022, 71, 5026114. [Google Scholar]
- Yuan, H.; Shao, Y.; Liu, Z.; Wang, H. An Improved Faster R-CNN for Pulmonary Embolism Detection From CTPA Images. IEEE Access 2021, 9, 105382–105392. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the Computer Vision & Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Kong, S.; Tian, M.; Qiu, C.; Wu, Z.; Yu, J. IWSCR: An Intelligent Water Surface Cleaner Robot for Collecting Floating Garbage. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6358–6368. [Google Scholar] [CrossRef]
- Zhu, C.; Qian, J.; Wang, B. YOLOX on Embedded Device With CCTV & TensorRT for Intelligent Multicategories Garbage Identification and Classification. IEEE Sens. J. 2022, 22, 16522–16532. [Google Scholar]
- Cabreira, T.M.; Brisolara, L.B.; Ferreira, P.R. Survey on coverage path planning with unmanned aerial vehicles. Drones 2019, 3, 4. [Google Scholar] [CrossRef]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Tan, C.S.; Mohd-Mokhtar, R.; Arshad, M.R. A comprehensive review of coverage path planning in robotics using classical and heuristic algorithms. IEEE Access 2021, 9, 119310–119342. [Google Scholar] [CrossRef]
- Souissi, O.; Benatitallah, R.; Duvivier, D.; Artiba, A.; Feyzeau, P. Path planning: A 2013 survey. In Proceedings of the 2013 International Conference on Industrial Engineering and Systems Management (IESM), Rabat, Morocco, 28–30 October 2013. [Google Scholar]
- Viet, H.H.; Dang, V.H.; Choi, S.; Chung, T.C. BoB: An online coverage approach for multi-robot systems. Appl. Intell. 2015, 42, 157–173. [Google Scholar]
- Yehoshua, R.; Agmon, N.; Kaminka, G.A. Robotic adversarial coverage of known environments. Int. J. Robot. Res. 2016, 35, 1419–1444. [Google Scholar] [CrossRef]
- Stentz, A. Optimal and efficient path planning for partially known environments. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994. [Google Scholar]
- Zhang, H.; Hong, W.; Chen, M. A Path Planning Strategy for Intelligent Sweeping Robots. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019. [Google Scholar]
- Luo, B.; Huang, Y.; Deng, F.; Li, W.; Yan, Y. Complete Coverage Path Planning for Intelligent Sweeping Robot. In Proceedings of the 2021 IEEE Asia-Pacific Conference on Image Processing, Electronics and Computers (IPEC), Dalian, China, 14–16 April 2021. [Google Scholar]
- Xie, J.; Carrillo, L.R.G.; Jin, L. An integrated traveling salesman and coverage path planning problem for unmanned aircraft systems. IEEE Control Syst. Lett. 2018, 3, 67–72. [Google Scholar] [CrossRef]
- Khamis, A.; Hussein, A.; Ehnogy, A. Multi-robot Task Allocation: A Review of the State-of-the-Art. Coop. Robot. Sens. Netw. 2015, 2015, 31–51. [Google Scholar]
- Xie, J.; Carrillo, L.; Jin, L. Path Planning for UAV to Cover Multiple Separated Convex Polygonal Regions. IEEE Access 2020, 8, 51770–51785. [Google Scholar] [CrossRef]
- Zhang, D.; Fang, B.; Yang, W.; Luo, X.; Tang, Y. Robust inverse perspective mapping based on vanishing point. In Proceedings of the 2014 IEEE International Conference on Security, Pattern Analysis, and Cybernetics (SPAC), Wuhan, China, 18–19 October 2014. [Google Scholar]
- Ping, P.; Huang, C.; Ding, W.; Liu, Y.; Chiyomi, M.; Kazuya, T. Distracted driving detection based on the fusion of deep learning and causal reasoning. Inf. Fusion 2023, 89, 121–142. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Garland, J.; James, R.; Bradley, E. Model-free quantification of time-series predictability. Phys. Rev. E 2014, 90, 052910. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar] [CrossRef]
- Choi, J.; Chun, D.; Kim, H.; Lee, H.J. Gaussian yolov3: An accurate and fast object detector using localization uncertainty for autonomous driving. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 502–511. [Google Scholar]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Mittal, G.; Yagnik, K.B.; Garg, M.; Krishnan, N.C. Spotgarbage: Smartphone app to detect garbage using deep learning. In Proceedings of the 2016 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Heidelberg, Germany, 12–16 September 2016; pp. 940–945. [Google Scholar]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. Unet++: A nested u-net architecture for medical image segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, Proceedings of the 4th International Workshop, DLMIA 2018, and 8th International Workshop, ML-CDS 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, 20 September 2018; Proceedings 4; Springer: Berlin/Heidelberg, Germany, 2018; pp. 3–11. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).