Ore Rock Fragmentation Calculation Based on Multi-Modal Fusion of Point Clouds and Images
Abstract
:1. Introduction
2. Related Works
2.1. Computation Methods Based on the Image Modality
2.2. Computation Methods Based on the Point Cloud Modality
2.3. Analysis
3. Ore Rock Fragmentation Calculation Method
3.1. Image Preprocessing
3.2. SDM Calculation
3.2.1. Gradient Map Calculation
3.2.2. SDM Calculation
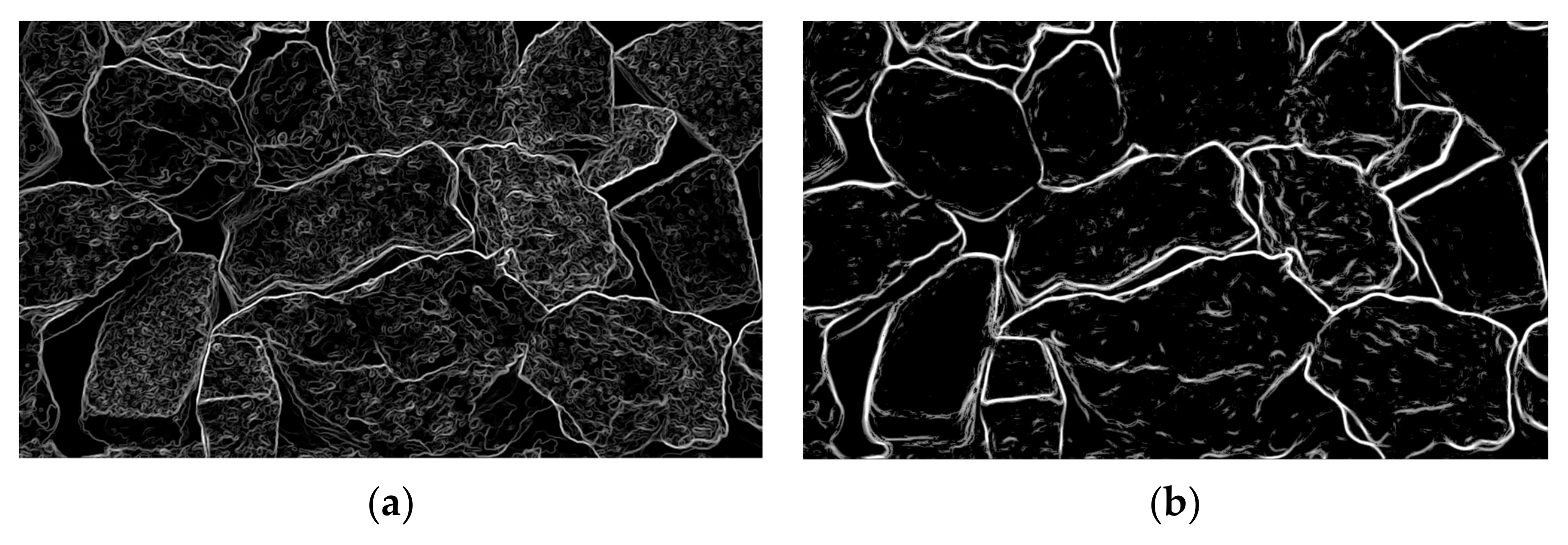
3.3. Multiscale Adaptive Edge Detection Based on SDM
3.4. Edge-Ehanced SDM Calculation
3.5. Watershed Segmentation
3.6. Ore Rock Fragmentation Calculation Based on Multi-Modal Calibration Mapping
3.6.1. Calibration Mapping
- (1)
- Point cloud and image data acquisition. Multiple sets of 3D LiDAR point clouds and 2D images, featuring a black and white chessboard calibration board, are captured in various poses using the 3D LiDAR and camera from a multimodal 3D environmental perception system. Figure 8 showcases the simultaneous collection results of each set of point clouds and images;
- (2)
- Camera intrinsic calibration. We utilize multiple sets of images, featuring a calibration board with chessboard patterns captured in different poses, to compute the camera’s intrinsic matrix using Zhang’s calibration method [24]. Simultaneously, through intrinsic calibration, we determine the positional relationship between the calibration board coordinate system and the camera coordinate system for various poses;
- (3)
- The extrinsic calibration of the 3D LiDAR and camera involves determining the geometric mapping relationship between the 3D point cloud and image pixels. Our research group has developed a method for calibrating the extrinsic parameters [25]. This method incorporates both line–plane and plane–plane geometric constraints to create a set of linear equations. The initial extrinsic matrix is obtained using the least squares method. Subsequently, a global error is formed by combining the pixel projection error from the camera’s intrinsic calibration and the vertical distance error of laser points resulting from the initial extrinsic calibration. To refine the calibration, this global error undergoes nonlinear global optimization based on the Levenberg–Marquardt method. Through this optimization process, the final extrinsic calibration is achieved, establishing the desired geometric mapping relationship between the 3D point cloud and image pixels.

3.6.2. Point Cloud Segmentation and High-Density Ore Rock Fragments Screening
3.6.3. Pixel Size Calibration and Ore Rock Fragment Calculation
4. Experiments
4.1. Evaluation Metrics
- (1)
- Equivalent diameter : It is the diameter of a circle with an area that is identical to the rock block region . The computational approach is as follows:where signifies the number of pixels contained in the rock block and denotes the pixel size calibration coefficient.
- (2)
- Elliptical long diameter : The edge contour of the rock block is subjected to elliptical fitting, and the major axis of the fitted ellipse is represented by . is the product of the pixel number encompassed within the major axis and the pixel calibration coefficient . The calculation method can be summarized as follows:
- (3)
- Elliptical short diameter : The edge contour of the rock block is subjected to elliptical fitting, and the short axis of the fitted ellipse is represented by . is the product of the pixel number encompassed within the short axis and the pixel calibration coefficient . The calculation method can be summarized as follows:
4.2. Experiments and Analysis
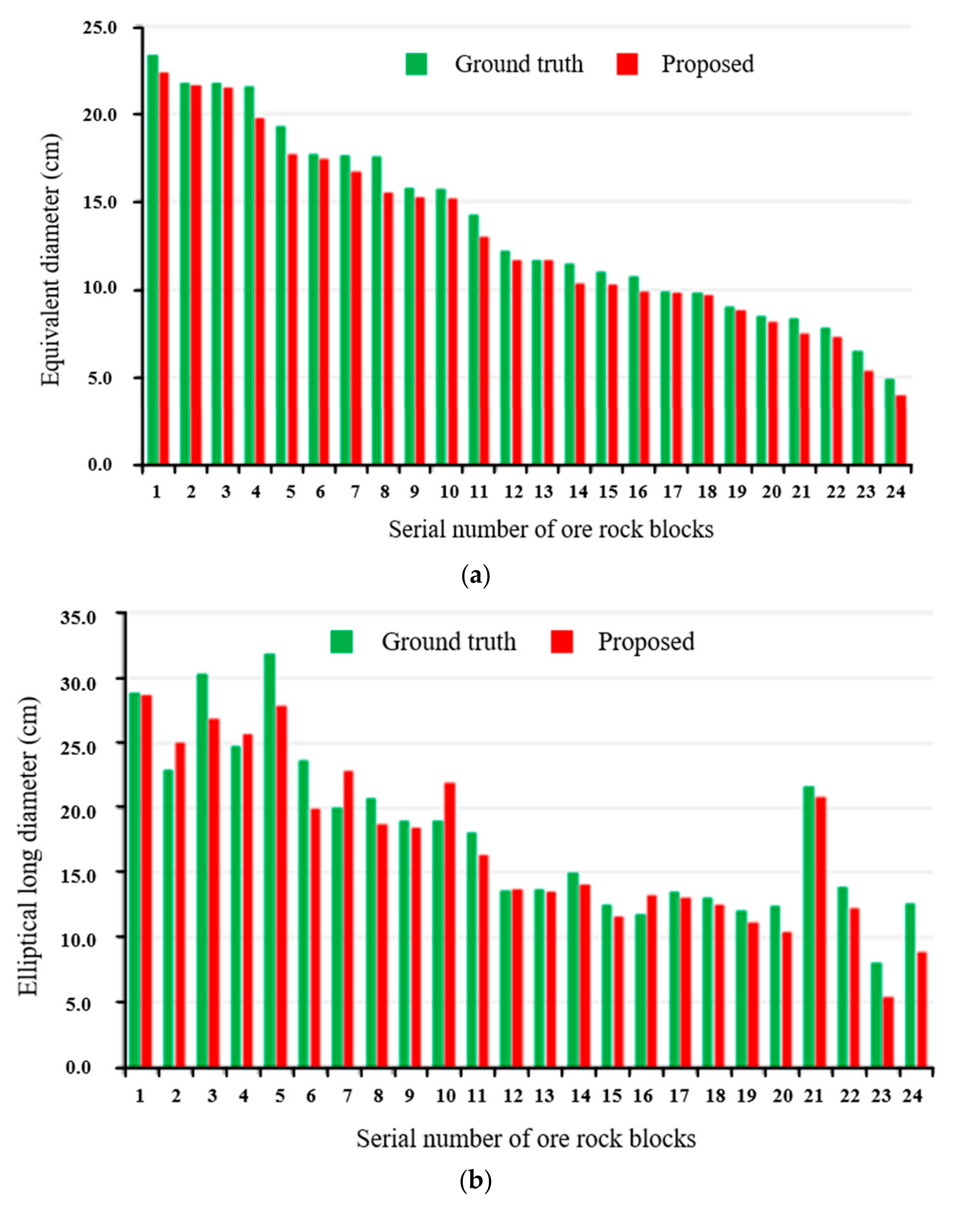
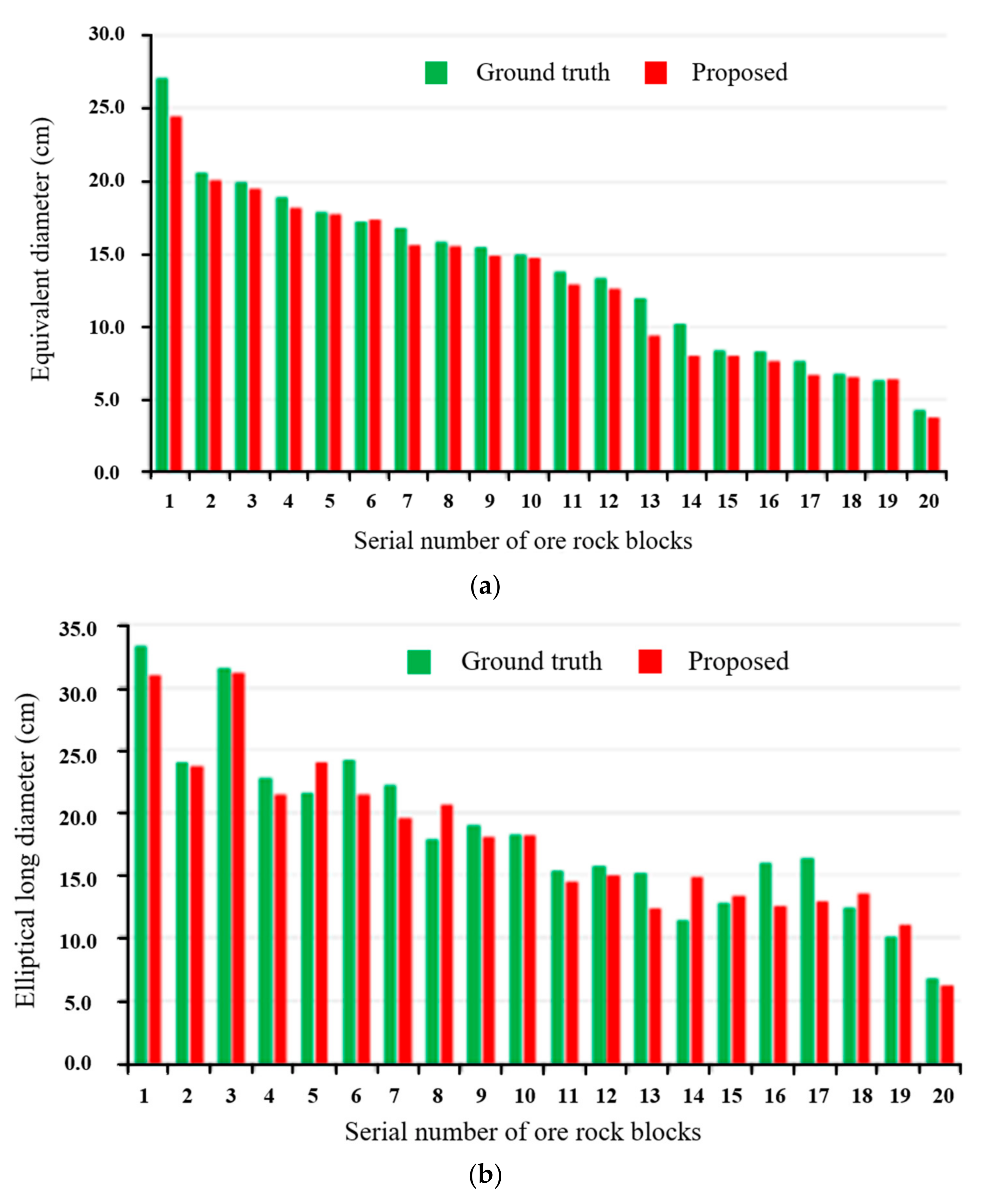
4.2.1. Visualization Segmentation Results for Ore Rock Images and Point Clouds
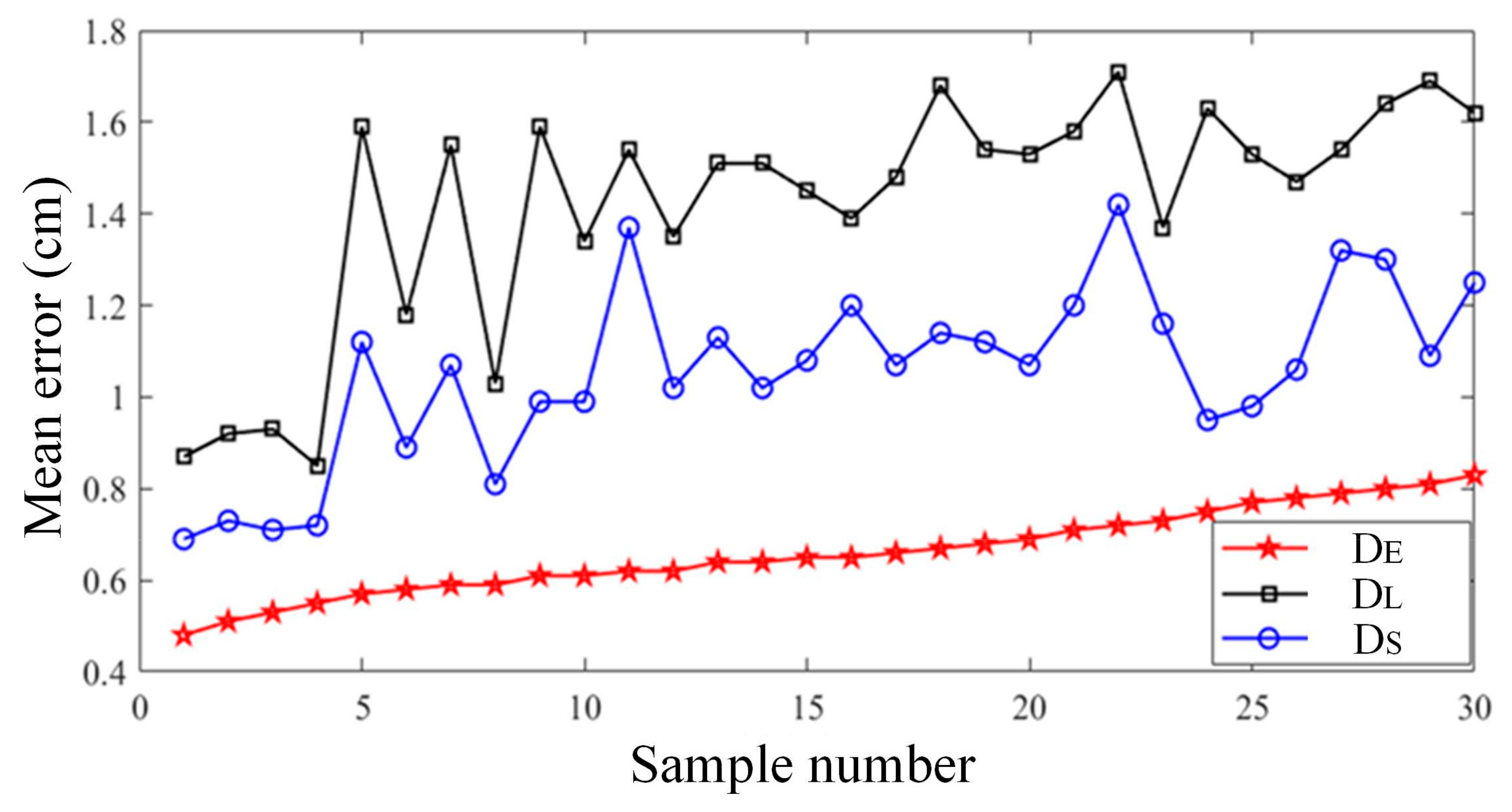
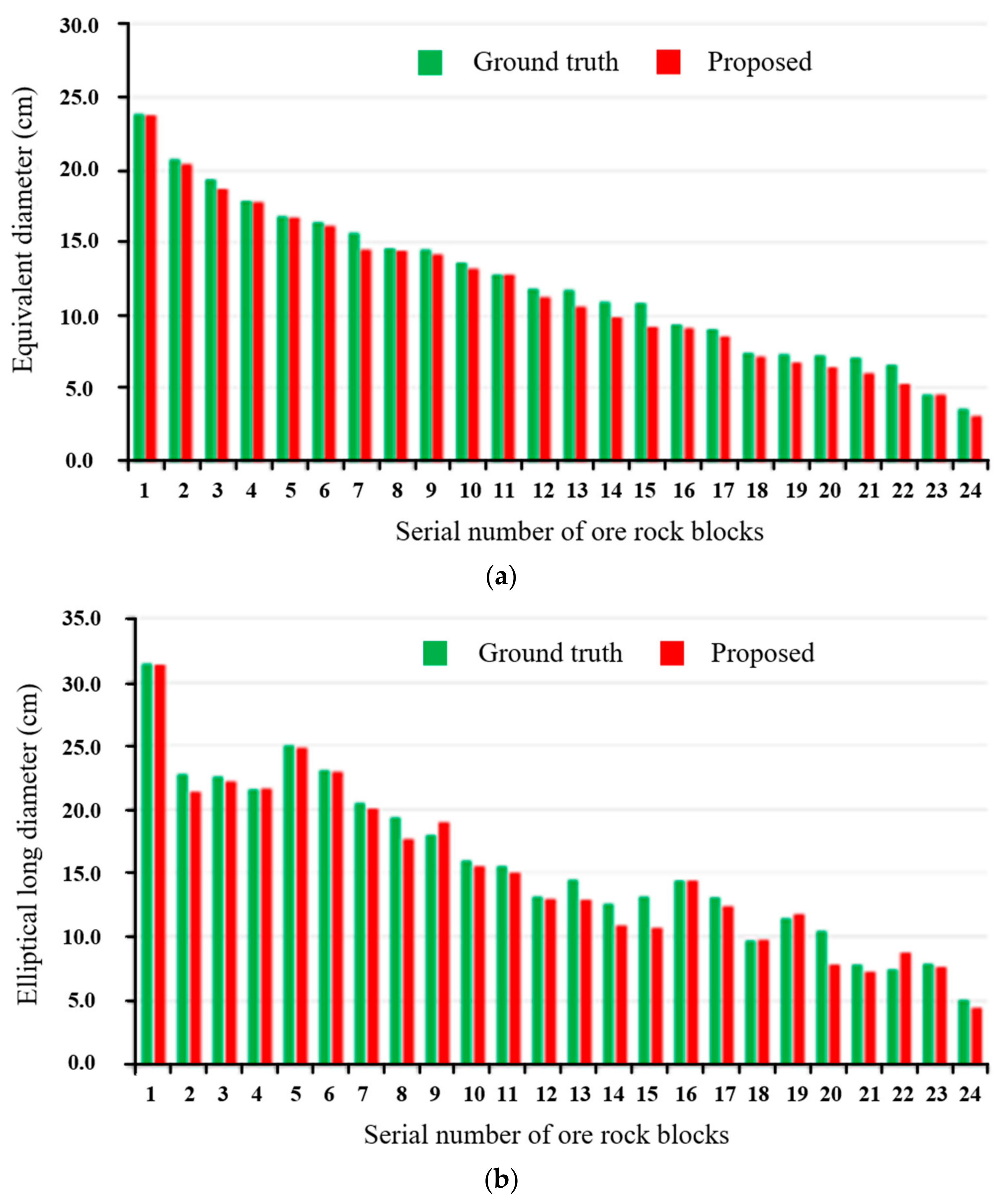
4.2.2. Quantitative Experiments
4.2.3. Comparative Experiments
4.2.4. Ablation Experiments
4.2.5. Discussion
5. Conclusions
- (1)
- Aiming at the problem that a single mode cannot accurately calculate the ore rock fragmentation, a multi-mode fusion algorithm was proposed, which used the spatial position information of the point cloud to calibrate the size of image pixels, and accurately achieved ore rock fragmentation calculation without relying on external markers to calibrate the pixel size;
- (2)
- To solve the problem of image under-segmentation caused by weak edges, the construction of the standard deviation map and multi-scale adaptive edge detection had effectively enhanced weak edges. This achieved an improvement in the marked watershed image segmentation algorithm and improved the accuracy of image segmentation;
- (3)
- Experiments demonstrated that the proposed method could accurately calculate the fragmentation of ore rock blocks with different morphologies in the local excavation area of the bucket. The average error of the equivalent diameter of ore rock blocks was 0.66 cm, the average error of elliptical long diameter was 1.42 cm, and the average error of elliptical short diameter was 1.06 cm, which could effectively meet practical engineering needs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Siddiqui, F.; Ali, S.; Behan, M. Measurement of size distribution of blasted rock using digital image processing. Eng. Sci. 2009, 20, 81–93. [Google Scholar] [CrossRef]
- Si, L.; Wang, Z.B.; Liu, P.; Tan, C.; Chen, H.; Wei, D. A Novel Coal-Rock Recognition Method for Coal Mining Working Face Based on Laser Point Cloud Data. IEEE Trans. Instrum. Meas. 2021, 70, 2514118. [Google Scholar] [CrossRef]
- Amankwah, A.; Aldrich, C. Automatic ore image segmentation using mean shift and watershed transform. In Proceedings of the 21st International Conference Radioelektronika 2011, Brno, Czech Republic, 19–20 April 2011; pp. 1–8. [Google Scholar]
- Zhang, G.; Li, M.; Zhan, Y. Ore image thresholding segmentation using double windows with fisher discrimination. In Proceedings of the 2017 13th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Guilin, China, 29–31 July 2017; pp. 18–25. [Google Scholar]
- Wang, R.; Zhang, W.; Shao, L. Research of Ore Particle Size Detection Based on Image Processing; Springer: Singapore, 2018; pp. 505–514. [Google Scholar]
- Guo, Q.P.; Wang, Y.C.; Yang, S.J.; Xiang, Z.B. A method of blasted rock image segmentation based on improved watershed algorithm. Sci. Rep. 2022, 12, 7143. [Google Scholar] [CrossRef]
- Ding, X.; Zhou, W.; Lu, X. Distribution characteristics of fragments size and optimization of blasting parameters under blasting impact load in open-pit mine. IEEE Access 2019, 7, 137501–137516. [Google Scholar] [CrossRef]
- Wang, W.; Bergholm, F. Fragment size estimation without image segmentation. Imaging Sci. J. 2007, 56, 91–96. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, J.H.; Yu, H.Y.; Wang, Y.Y.; Zhou, X.K. An Improved Grey Wolf Optimizer Based on Differential Evolution and OTSU Algorithm. Appl. Sci. 2020, 10, 6343. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, G.; Zhu, H. Ore image thresholding using bi-neighbourhood Otsu’s approach. Electron. Lett. 2010, 46, 1–3. [Google Scholar] [CrossRef]
- Hadi, Y.; Hamid, M.; Mohammad, A. Determining the fragmented rock size distribution using textural feature extraction of images. Powder Technol. 2019, 342, 630–641. [Google Scholar]
- Xie, C.; Nguyen, H.; Bui, X.N. Predicting rock size distribution in mine blasting using various novel soft computing models based on meta-heuristics and machine learning algorithms. Geosci. Front. 2021, 12, 35–42. [Google Scholar] [CrossRef]
- Yuan, L.; Duan, Y. A Method of Ore Image Segmentation Based on Deep Learning; Springer: Cham, Switzerland, 2018; pp. 508–519. [Google Scholar]
- Ko, Y.; Shang, H. A neural network-based soft sensor for particle size distribution using image analysis. Powder Technol. 2011, 212, 359–366. [Google Scholar] [CrossRef]
- Shubham, S.; Debasis, D.; Sudipta, B. Prediction of particle size distribution curves of dump materials using convolutional neural networks. Rock Mech. Rock Eng. 2021, 21, 15–24. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Xiao, D.; Liu, X.; Le, B. An ore image segmentation method based on RDU-Net model. Sensors 2020, 17, 4979. [Google Scholar] [CrossRef]
- Jin, Q.; Meng, Z.; Pham, T. DUNet: A deformable network for retinal vessel segmentation. Knowl.-Based Syst. 2019, 178, 149–162. [Google Scholar] [CrossRef]
- Matthew, J. Automated image segmentation and analysis of rock piles in an open-pit mine. In Proceedings of the 2013 International Conference on Digital Image Computing: Techniques and Applications (DICTA), Hobart, TAS, Australia, 26–28 November 2013. [Google Scholar]
- Onederra, I.; Thurley, M.; Catalan, A. Measuring blast fragmentation at Esperanza mine using 3D laser scanning. Min. Technol. 2015, 124, 34–46. [Google Scholar] [CrossRef]
- Campbell, A.; Thurley, M. Application of laser scanning to measure fragmentation in underground mines. Min. Technol. 2017, 126, 240–247. [Google Scholar] [CrossRef]
- Engin, I.; Maerz, N.; Boyko, K. Practical measurement of size distribution of blasted rocks using LiDAR scan data. Rock Mech. Rock Eng. 2020, 53, 4653–4671. [Google Scholar] [CrossRef]
- Cui, Y.H.; An, Y.; Sun, W.; Hu, H.S.; Song, X.G. Multiscale adaptive edge detector for images based on a novel standard deviation map. IEEE Trans. Instrum. Meas. 2021, 70, 5010913. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- An, Y.; Li, B.; Wang, L. Calibration of a 3D laser rangefinder and a camera based on optimization solution. J. Ind. Manag. Optim. 2021, 17, 427–445. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef]
- Topal, C.; Akinlar, C. Edge drawing: A combined real-time edge and segment detector. J. Vis. Commun. Image Represent. 2012, 23, 862–872. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, C.; Zhang, L. A novel centroid update approach for clustering-based superpixel methods and superpixel-based edge detection. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020. [Google Scholar]









| Method | Mean Error of DE (cm) | Mean Error of DL (cm) | Mean Error of DS (cm) |
|---|---|---|---|
| Our method | 0.66 | 1.42 | 1.06 |
| [3] | 0.85 | 1.94 | 1.87 |
| [6] | 0.68 | 1.52 | 1.08 |
| [21] | 0.93 | 1.68 | 1.92 |
| Method | Mean Error of DE (cm) | Mean Error of DL (cm) | Mean Error of DS (cm) |
|---|---|---|---|
| Our method | 0.66 | 1.42 | 1.06 |
| Gradient map | 1.09 | 2.87 | 2.31 |
| Canny | 0.97 | 2.53 | 1.94 |
| Edge drawing | 0.84 | 2.24 | 1.76 |
| SBED | 0.76 | 1.96 | 1.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, J.; Cui, Y.; Zhong, Z.; An, Y. Ore Rock Fragmentation Calculation Based on Multi-Modal Fusion of Point Clouds and Images. Appl. Sci. 2023, 13, 12558. https://doi.org/10.3390/app132312558
Peng J, Cui Y, Zhong Z, An Y. Ore Rock Fragmentation Calculation Based on Multi-Modal Fusion of Point Clouds and Images. Applied Sciences. 2023; 13(23):12558. https://doi.org/10.3390/app132312558
Chicago/Turabian StylePeng, Jianjun, Yunhao Cui, Zhidan Zhong, and Yi An. 2023. "Ore Rock Fragmentation Calculation Based on Multi-Modal Fusion of Point Clouds and Images" Applied Sciences 13, no. 23: 12558. https://doi.org/10.3390/app132312558
APA StylePeng, J., Cui, Y., Zhong, Z., & An, Y. (2023). Ore Rock Fragmentation Calculation Based on Multi-Modal Fusion of Point Clouds and Images. Applied Sciences, 13(23), 12558. https://doi.org/10.3390/app132312558






