Electron Impact Cross Sections and Transport Studies of C3F6O
Abstract
:1. Introduction
2. Calculation Methods
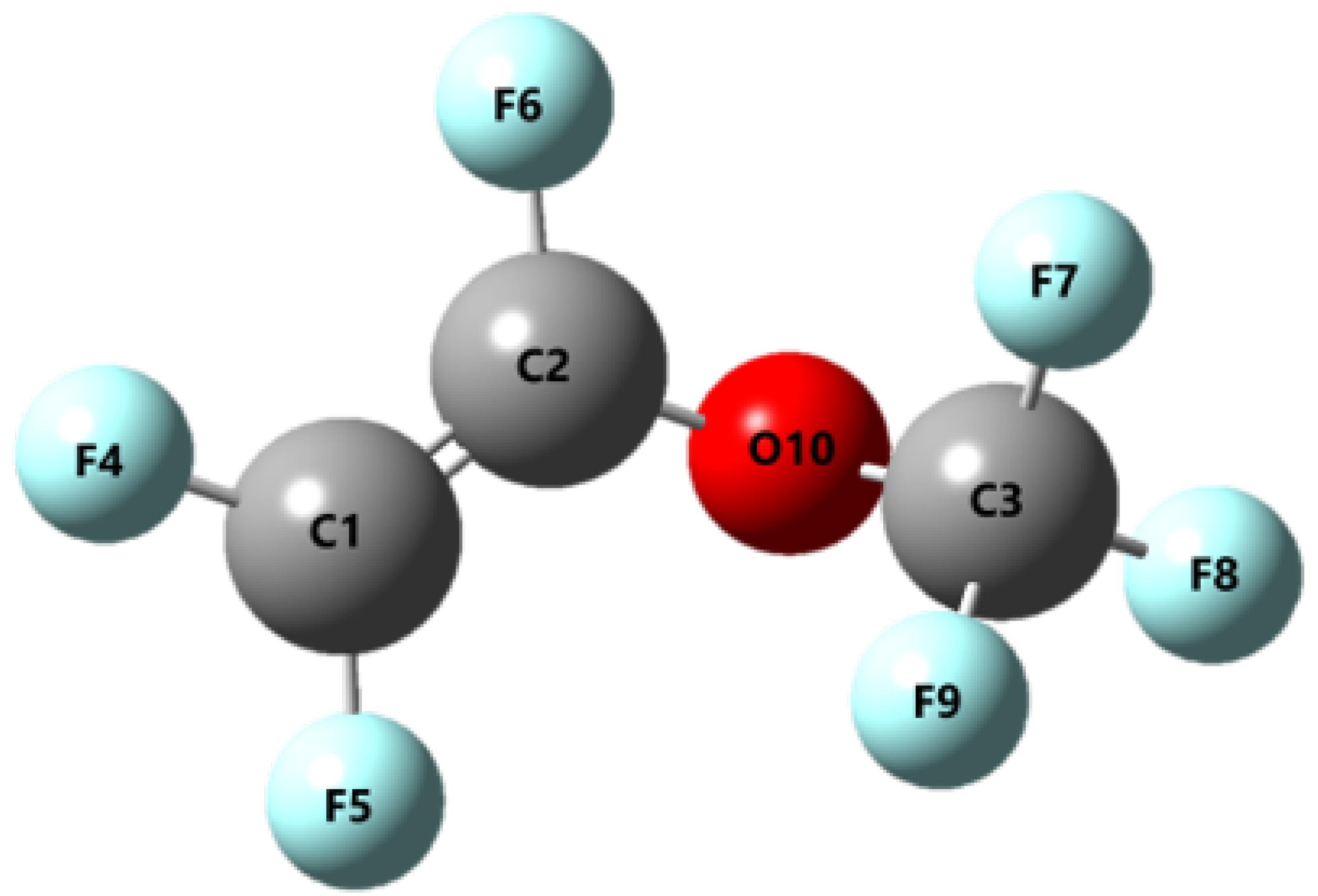
2.1. Electron Impact Cross Section Calculation
2.2. Transport Studies
2.3. Buffer Gas Mixtures
3. Results and Discussion
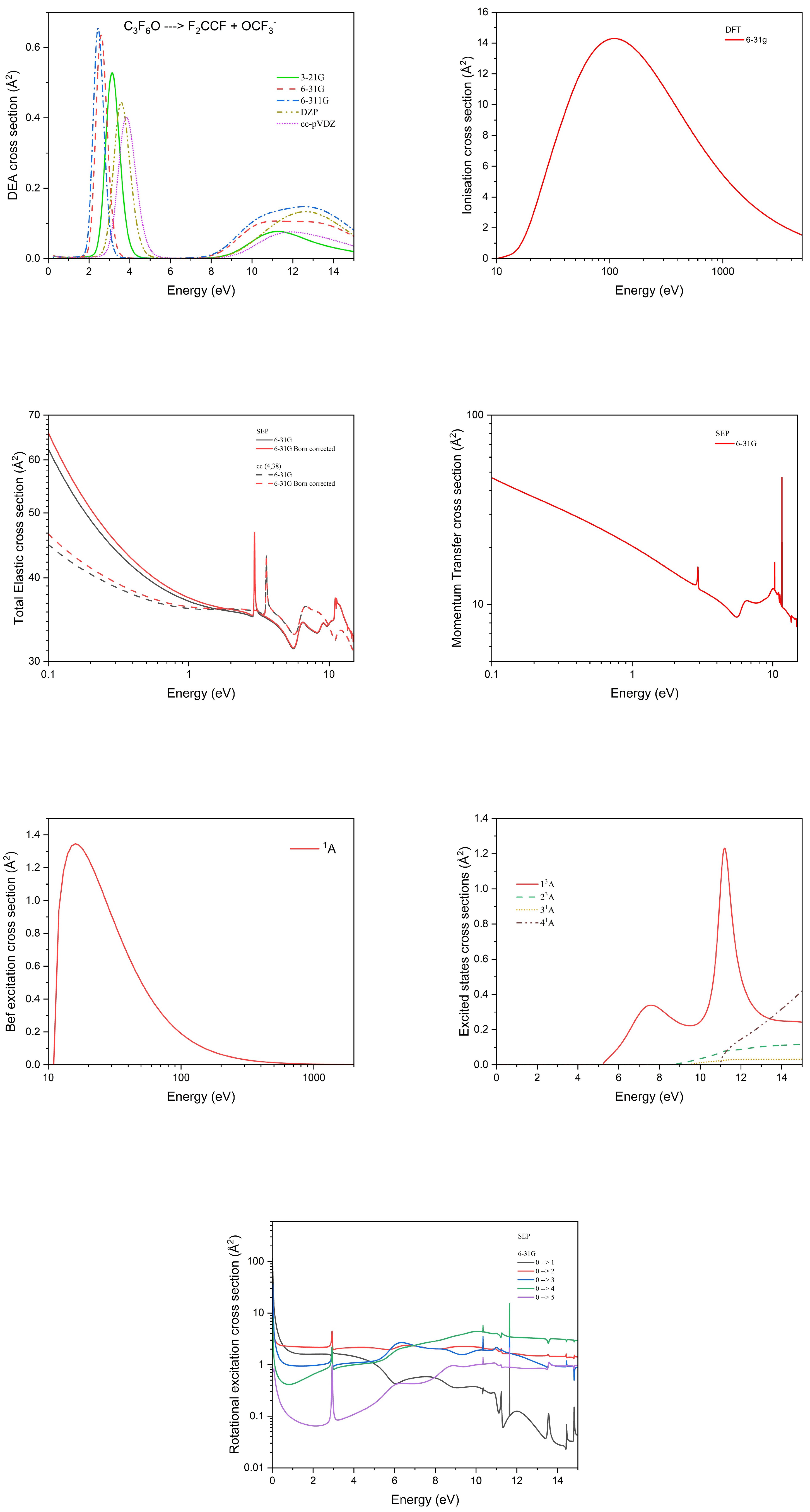
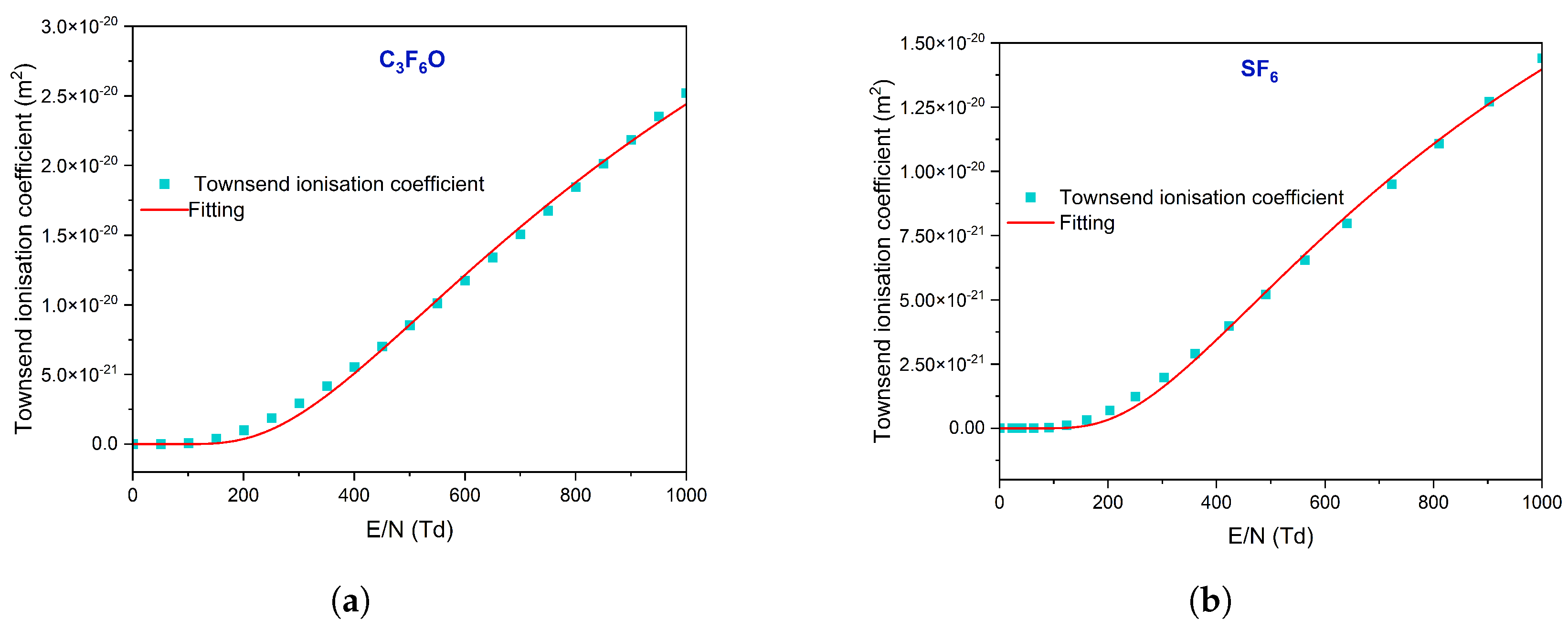
3.1. Electron Impact Cross Section
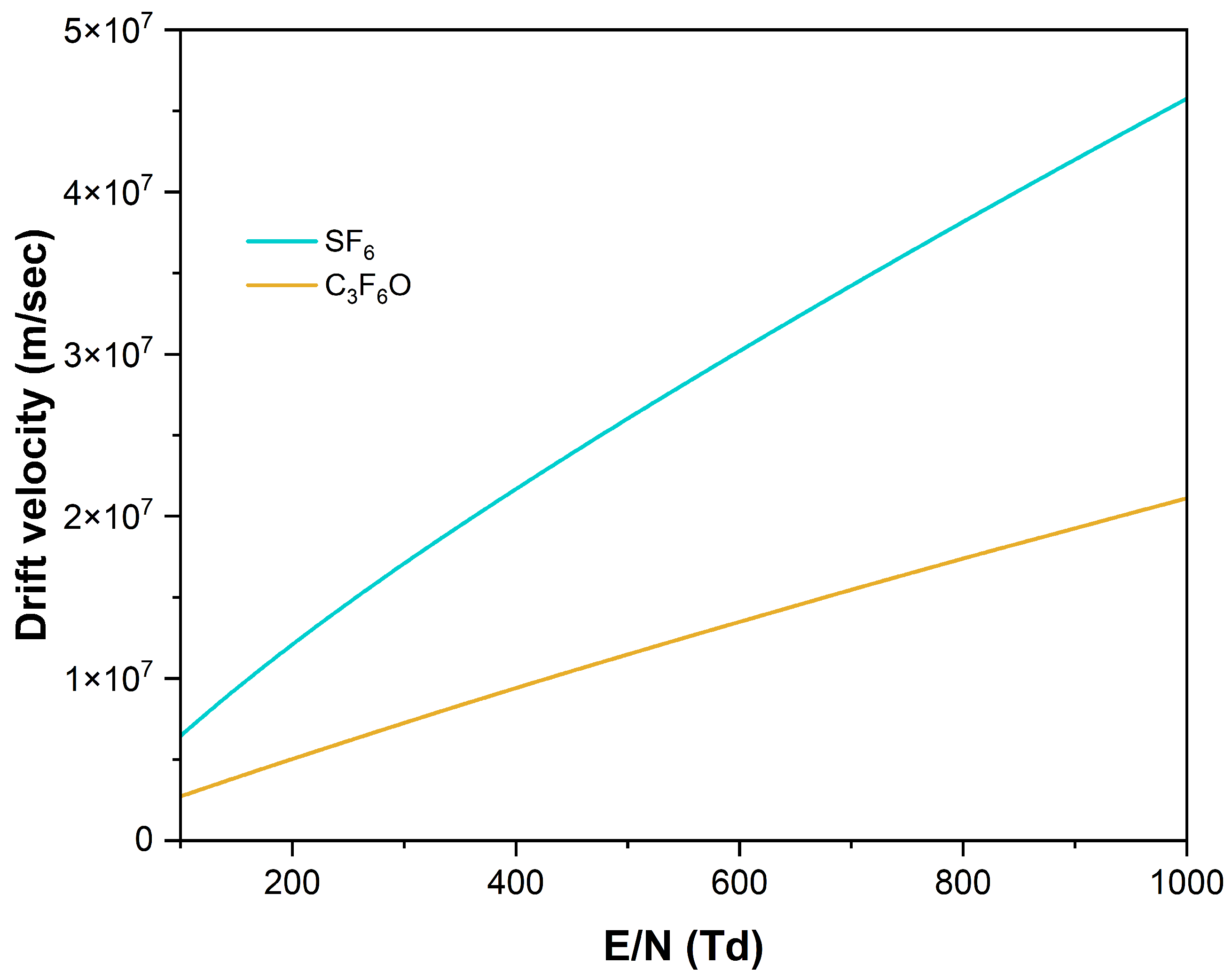
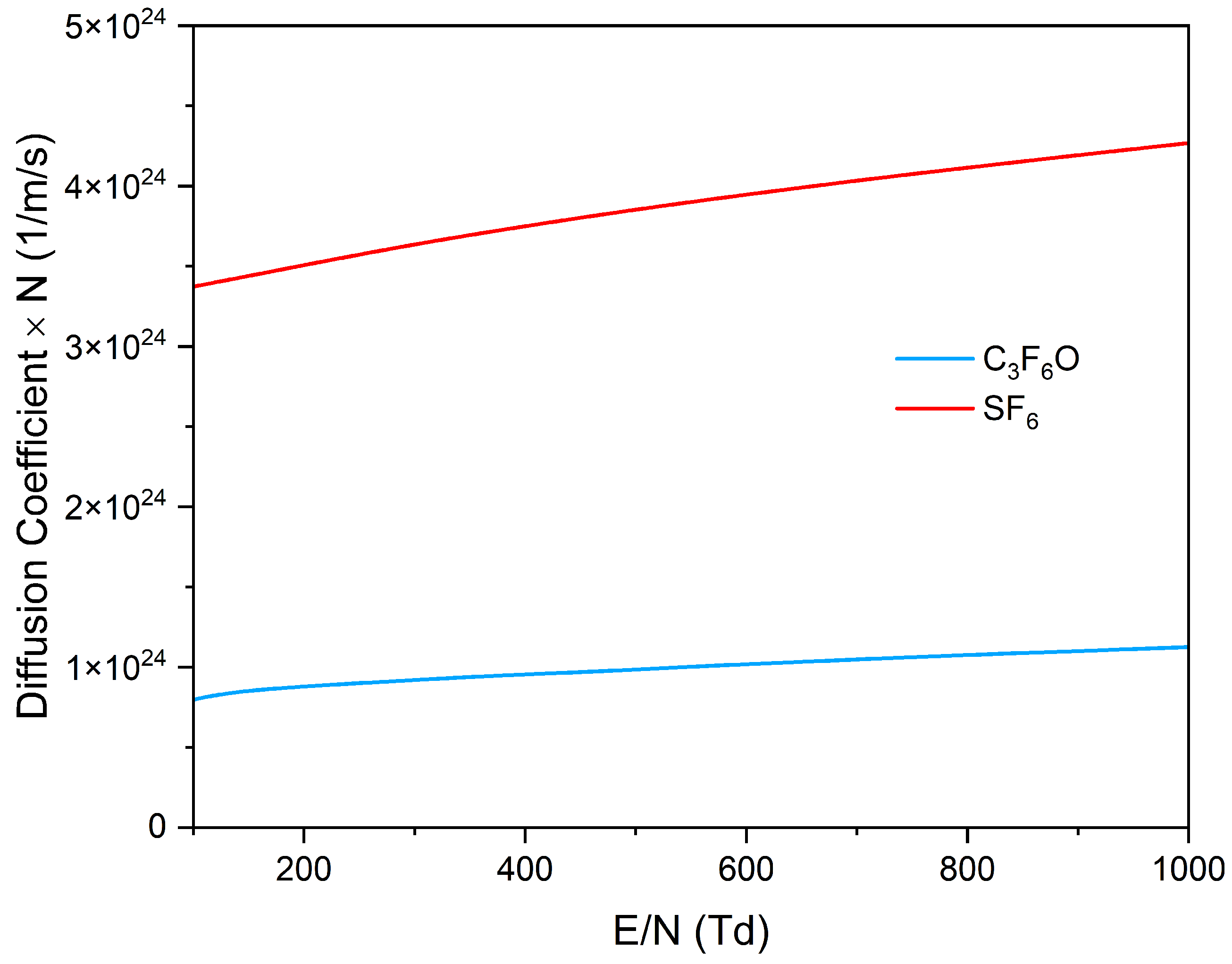
3.2. Transport Parameters
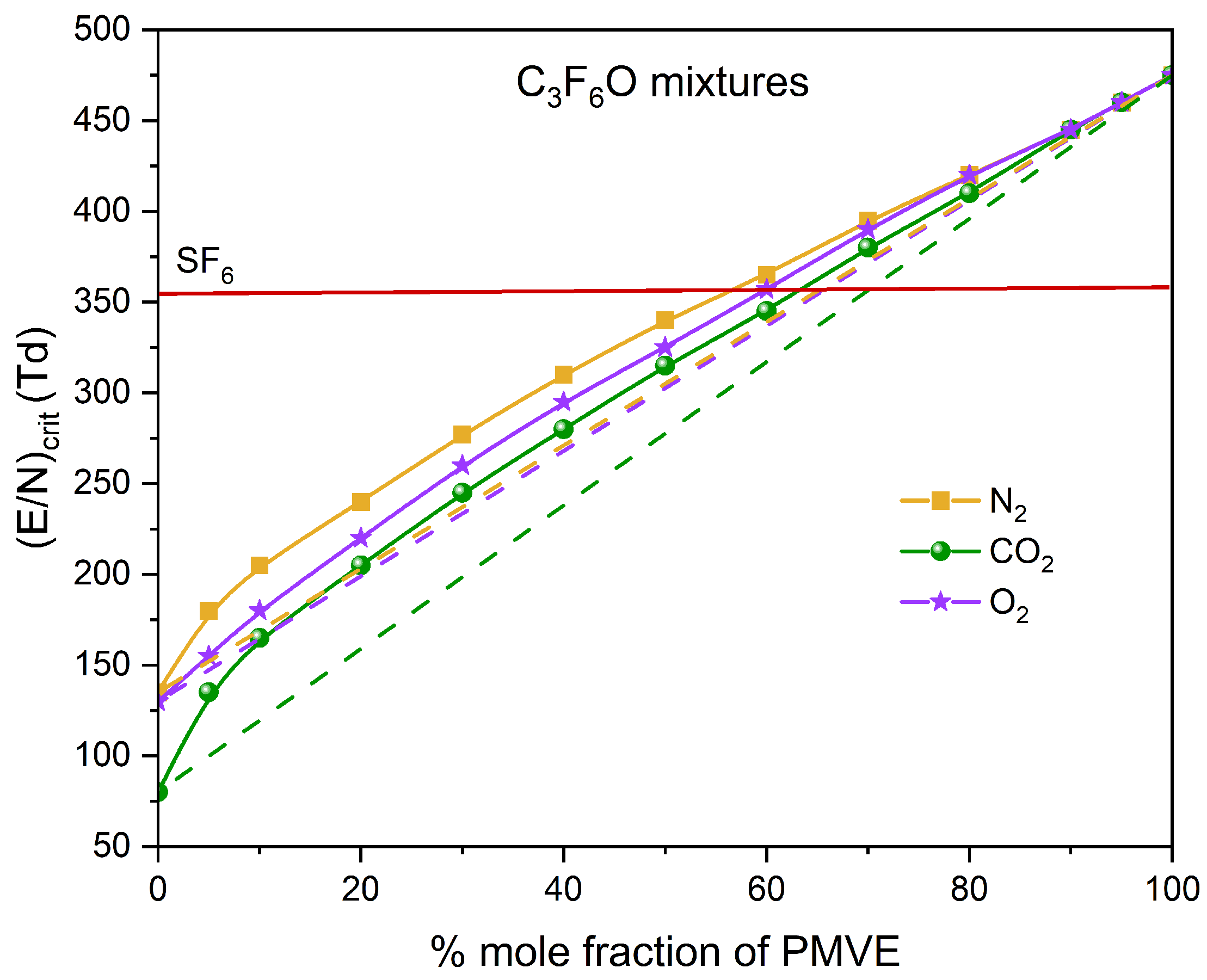
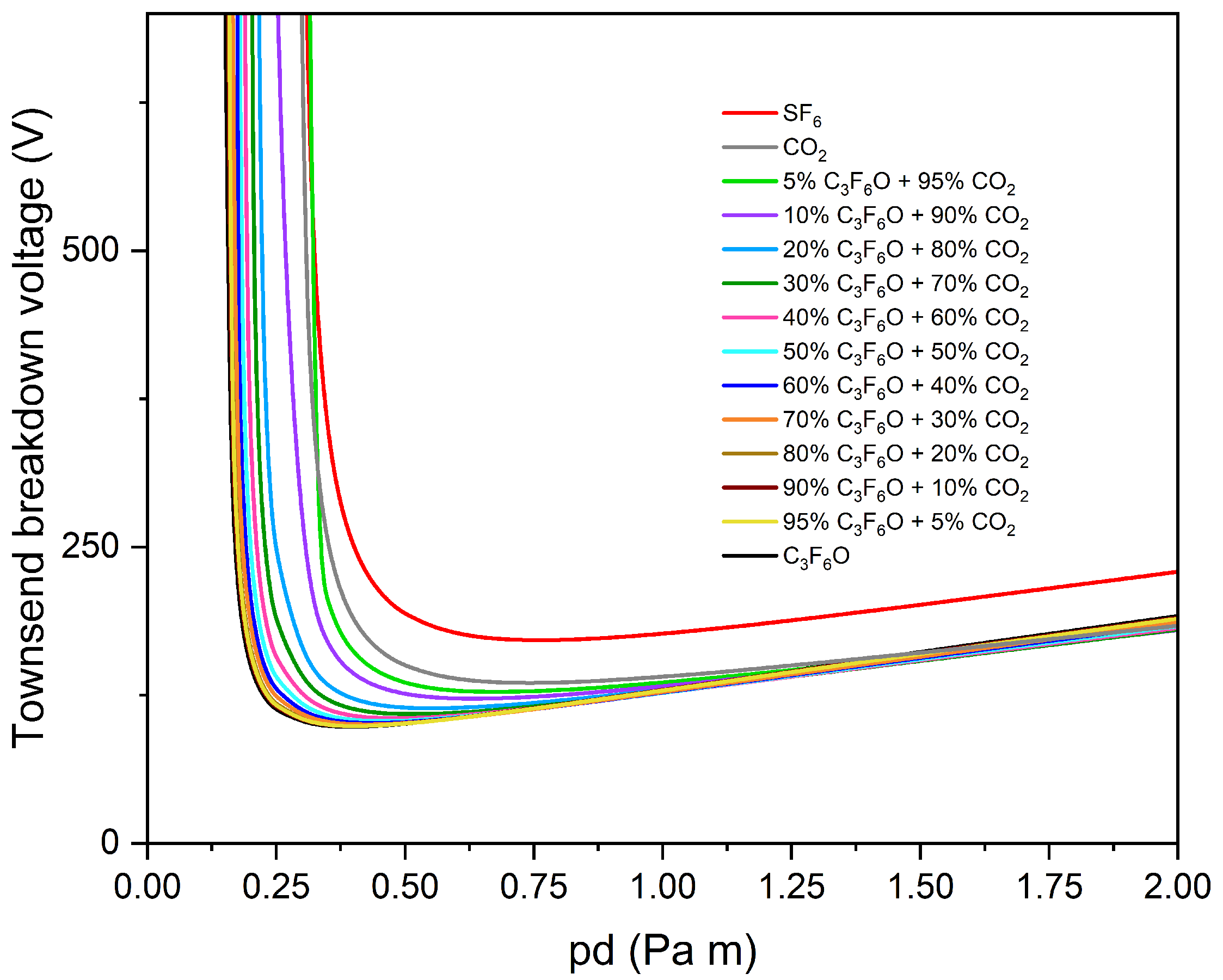
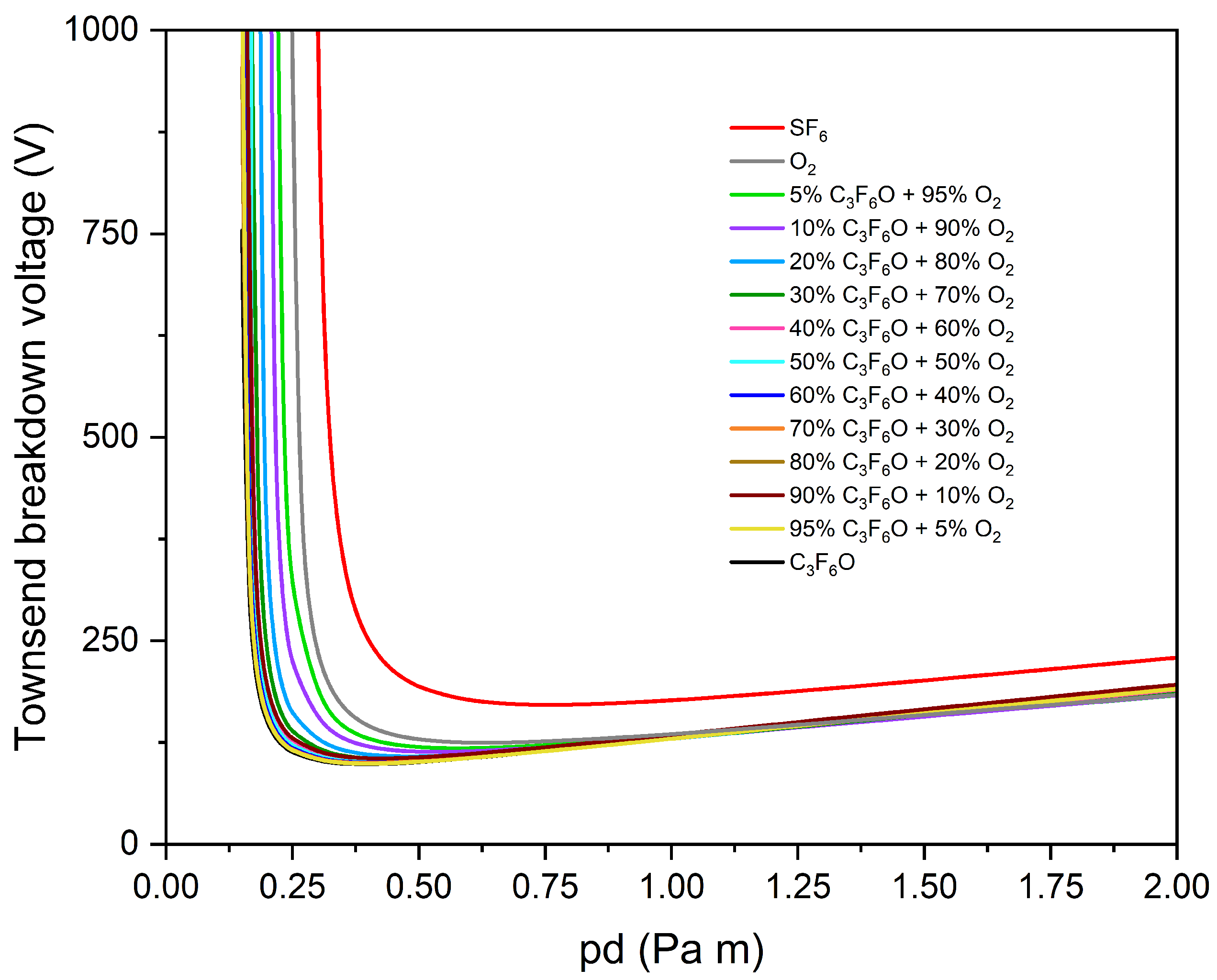
3.3. Buffer Gas Mixtures
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Zhao, H.; Murphy, A.B. SF6-alternative gases for application in gas-insulated switchgear. J. Phys. D Appl. Phys. 2018, 51, 153001. [Google Scholar] [CrossRef]
- Pan, B.; Wang, G.; Shi, H.; Shen, J.; Ji, H.K.; Kil, G.S. Green gas for grid as an eco-friendly alternative insulation gas to SF6: A Review. Appl. Sci. 2020, 10, 2526. [Google Scholar] [CrossRef]
- Tian, S.; Zhang, X.; Cressault, Y.; Hu, J.; Wang, B.; Xiao, S.; Li, Y.; Kabbaj, N. Research status of replacement gases for SF6 in power industry. AIP Adv. 2020, 10, 050702. [Google Scholar] [CrossRef]
- Sinha, N.; Choi, H.; Song, M.Y.; Jang, H.J.; Oh, Y.H.; Song, K.D. Perfluoro-methyl-vinyl-ether as SF6 alternative in insulation applications: A DFT study on the physiochemical properties and decomposition pathways. Comput. Theor. Chem. 2023, 1225, 114159. [Google Scholar] [CrossRef]
- Li, Z.; Tao, Z.; Naik, V.; Good, D.A.; Hansen, J.C.; Jeong, G.R.; Francisco, J.S.; Jain, A.K.; Wuebbles, D.J. Global warming potential assessment for CF3OCF=CF2. J. Geophys. Res. Atmos. 2000, 105, 4019–4029. [Google Scholar] [CrossRef]
- ChemSpider. Available online: https://www.chemspider.com/ (accessed on 14 May 2022).
- Zhong, R.; Su, Z.; Dengming, X.; Hui, W.; Jiang, X.; Zhongmin, Y.; Yunkun, D. Investigation of the performance of CF3I/c-C4F8/N2 and CF3I/c-C4F8/CO2 gas mixtures from electron transport parameters. Plasma Sci. Technol. 2020, 22, 055402. [Google Scholar] [CrossRef]
- Hagelaar, G.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Technol. 2005, 14, 722. [Google Scholar] [CrossRef]
- Radmilović-Radjenović, M.; Sabo, M.; Radjenović, B. Transport Characteristics of the Electrification and Lightning of the Gas Mixture Representing the Atmospheres of the Solar System Planets. Atmosphere 2021, 12, 438. [Google Scholar] [CrossRef]
- Yang, W.; Meng, X.; Zhou, Q.; Dong, Z. Boltzmann equation studies on electron swarm parameters in Townsend breakdown of copper vapor plasma using independently assessed electron-collision cross sections. AIP Adv. 2019, 9, 035041. [Google Scholar] [CrossRef]
- Park, Y.; Choi, Y.R.; Kim, D.C.; Kim, Y.; Song, M.Y.; Kim, Y.W.; Cho, H.; Jang, H.J.; Oh, Y.H.; Song, K.D. Total electron scattering cross section of C3F6O at the intermediate-energy region for developing an alternative insulation gas to SF6. Curr. Appl. Phys. 2022, 41, 111–115. [Google Scholar] [CrossRef]
- Cooper, B.; Tudorovskaya, M.; Mohr, S.; O’Hare, A.; Hanicinec, M.; Dzarasova, A.; Gorfinkiel, J.D.; Benda, J.; Mašín, Z.; Al-Refaie, A.F.; et al. Quantemol electron collisions (QEC): An enhanced expert system for performing electron molecule collision calculations using the R-matrix method. Atoms 2019, 7, 97. [Google Scholar] [CrossRef]
- Tennyson, J. Electron–molecule collision calculations using the R-matrix method. Phys. Rep. 2010, 491, 29–76. [Google Scholar] [CrossRef]
- Kim, Y.K.; Rudd, M.E. Binary-encounter-dipole model for electron-impact ionization. Phys. Rev. A 1994, 50, 3954. [Google Scholar] [CrossRef] [PubMed]
- Sanna, N.; Gianturco, F.A. Differential cross sections for electron/positron scattering from polyatomic molecules. Comput. Phys. Commun. 1998, 114, 142–167. [Google Scholar] [CrossRef]
- Munro, J.J.; Stephen, H.; Milton, M.F.; Jonathan, T. A dissociative electron attachment cross-section estimator. J. Phys. Conf. Ser. 2012, 388, 012013. [Google Scholar] [CrossRef]
- Kim, Y.K. Scaling of plane-wave Born cross sections for electron-impact excitation of neutral atoms. Phys. Rev. A 2001, 64, 032713. [Google Scholar] [CrossRef]
- Frisch, M.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.; et al. Gaussian 09 (Revision D. 01); Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Kondo, Y.; Ishikawa, K.; Hayashi, T.; Sekine, M.; Hori, M. Electron impact ionization of perfluoro-methyl-vinyl-ether C3F6O. Plasma Sources Sci. Technol. 2018, 27, 015009. [Google Scholar] [CrossRef]
- LXcat. Available online: http://www.lxcat.laplace.univ-tlse.fr (accessed on 6 December 2021).



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sinha, N.; Song, M.-Y.; Chang, H.; Choi, H.; Jang, H.-J.; Oh, Y.-H.; Song, K.-D. Electron Impact Cross Sections and Transport Studies of C3F6O. Appl. Sci. 2023, 13, 12612. https://doi.org/10.3390/app132312612
Sinha N, Song M-Y, Chang H, Choi H, Jang H-J, Oh Y-H, Song K-D. Electron Impact Cross Sections and Transport Studies of C3F6O. Applied Sciences. 2023; 13(23):12612. https://doi.org/10.3390/app132312612
Chicago/Turabian StyleSinha, Nidhi, Mi-Young Song, Hyonu Chang, Heechol Choi, Hyun-Jae Jang, Yeon-Ho Oh, and Ki-Dong Song. 2023. "Electron Impact Cross Sections and Transport Studies of C3F6O" Applied Sciences 13, no. 23: 12612. https://doi.org/10.3390/app132312612




